Effect of Radiation Defects on Thermo–Mechanical Properties of UO2 Investigated by Molecular Dynamics Method
Abstract
:1. Introduction
2. Computational Method
3. Results and Discussion
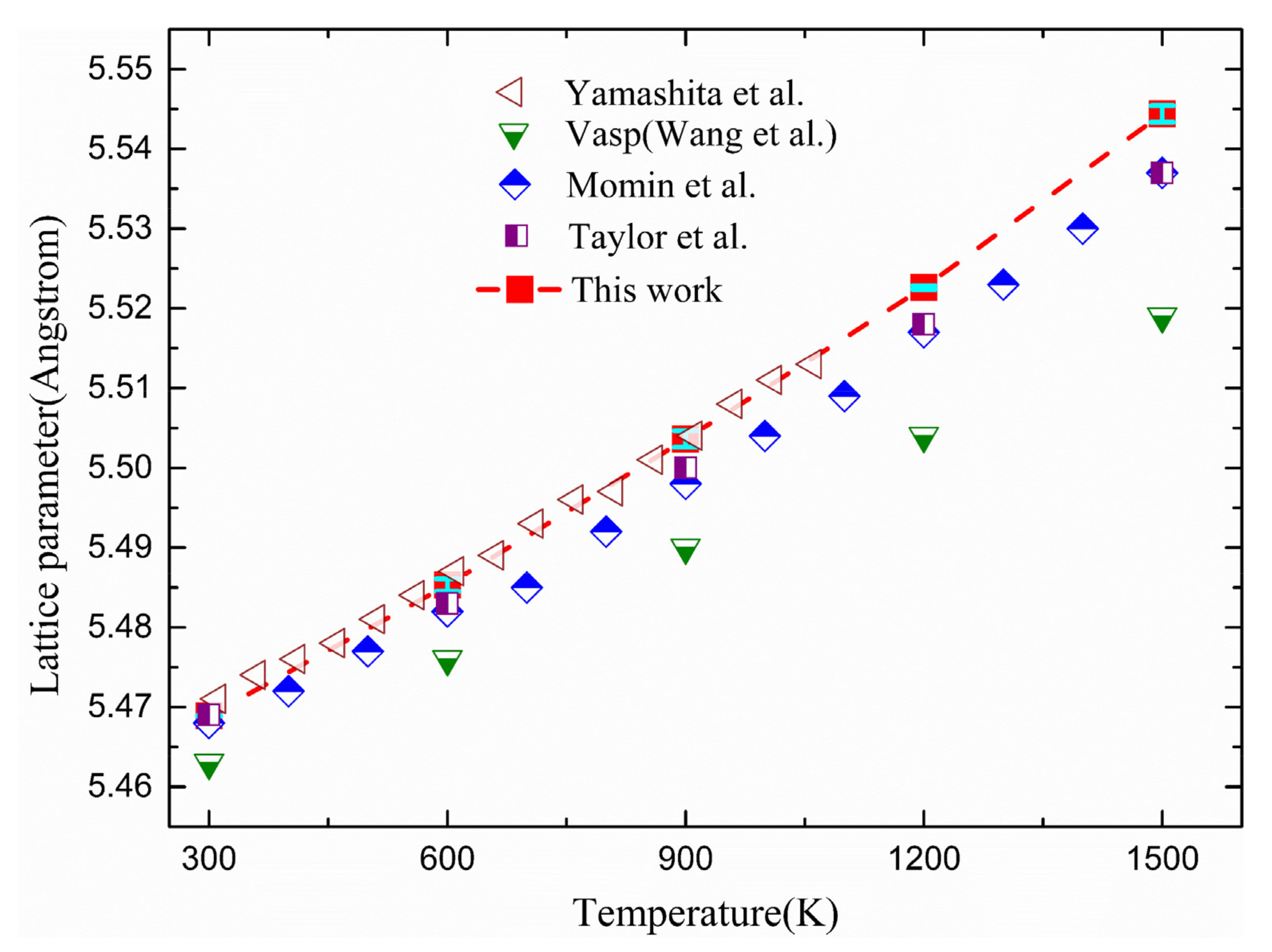
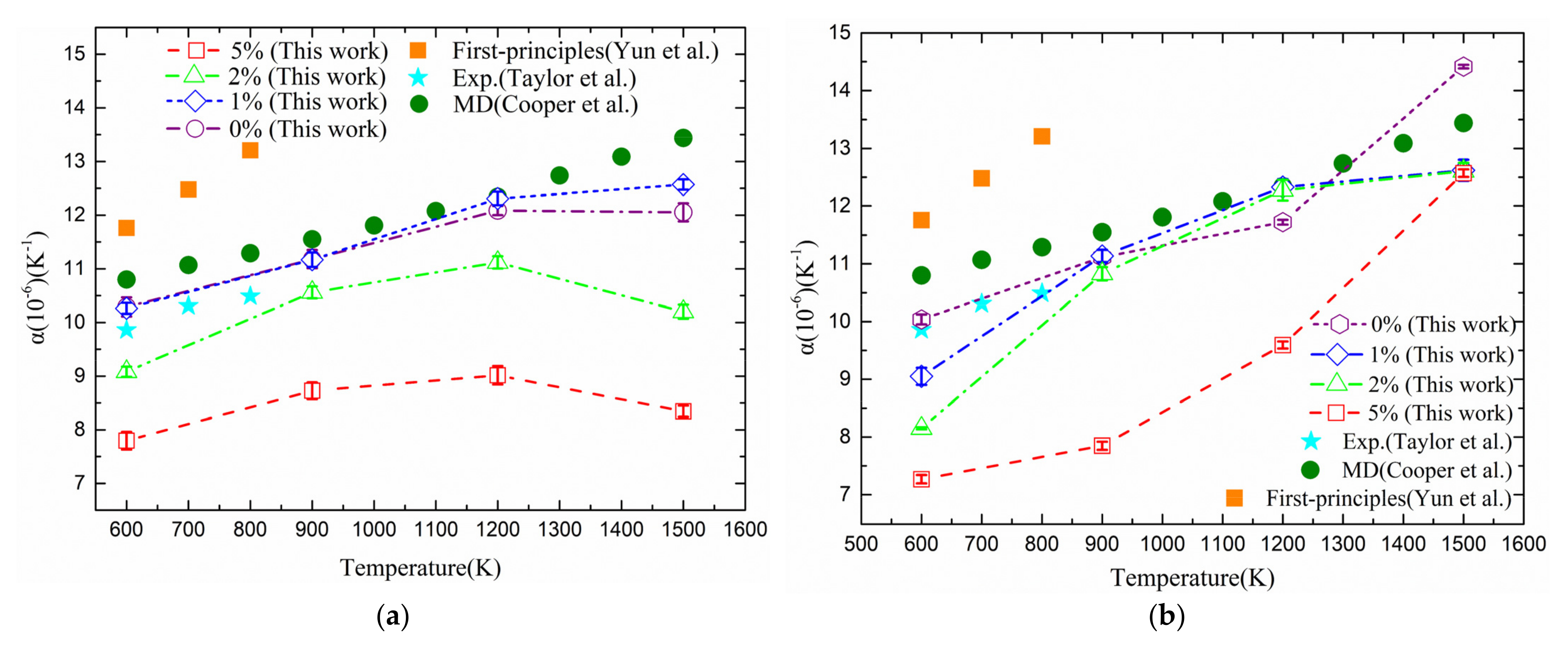
3.1. Effect of Defects on Lattice Parameter and Thermal Expansion Coefficient
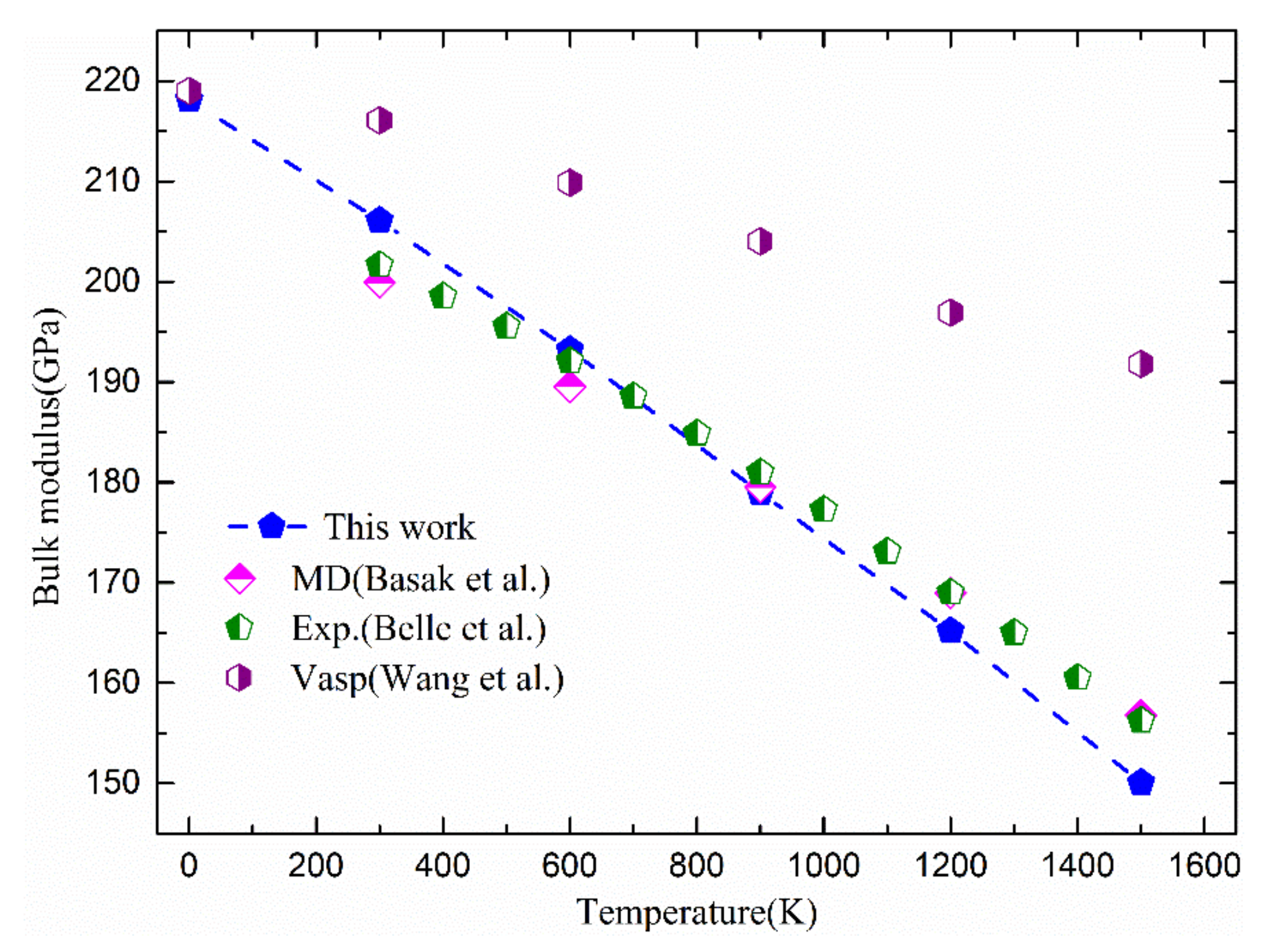
3.2. Elastic Modulus of UO2
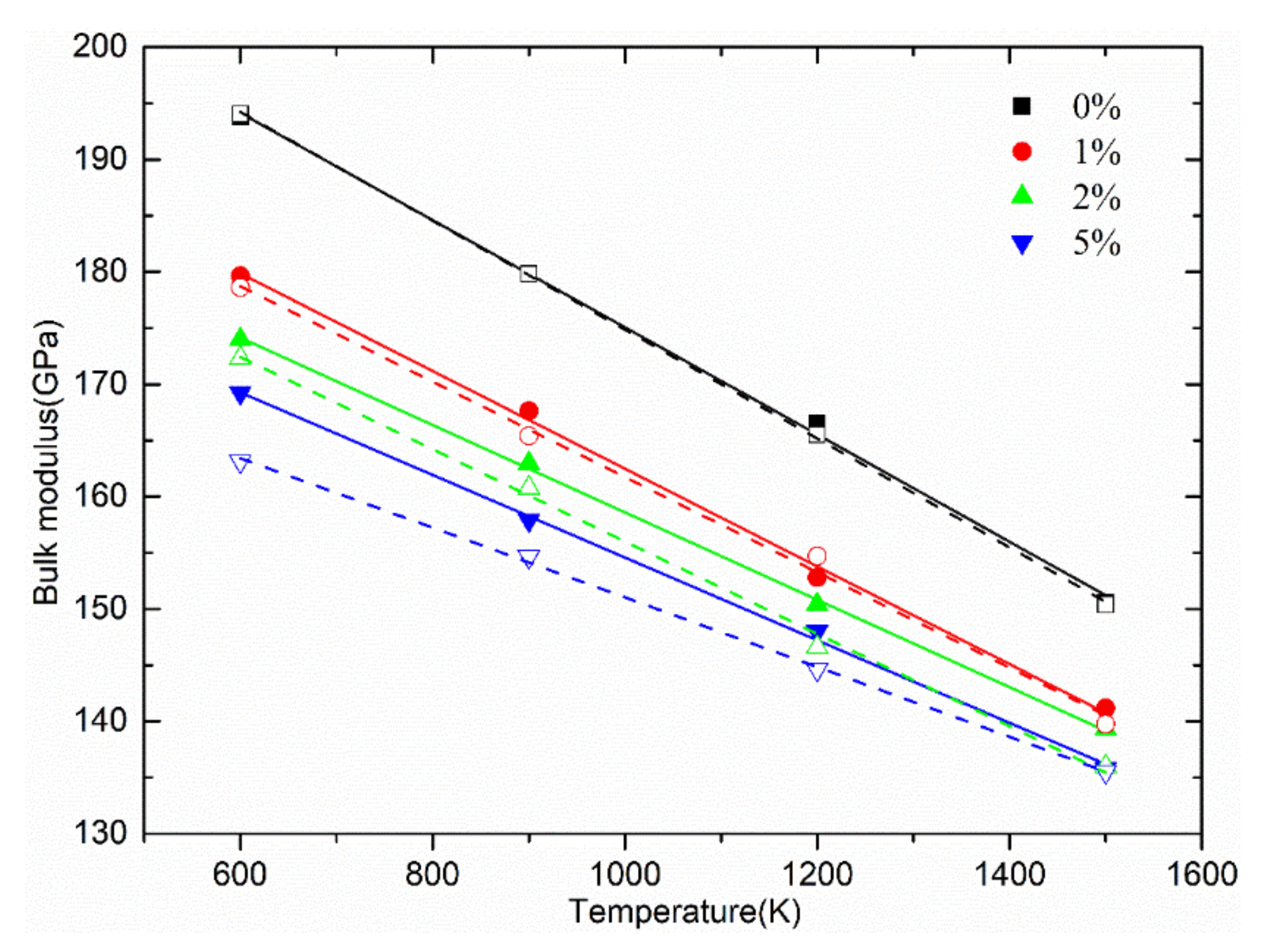
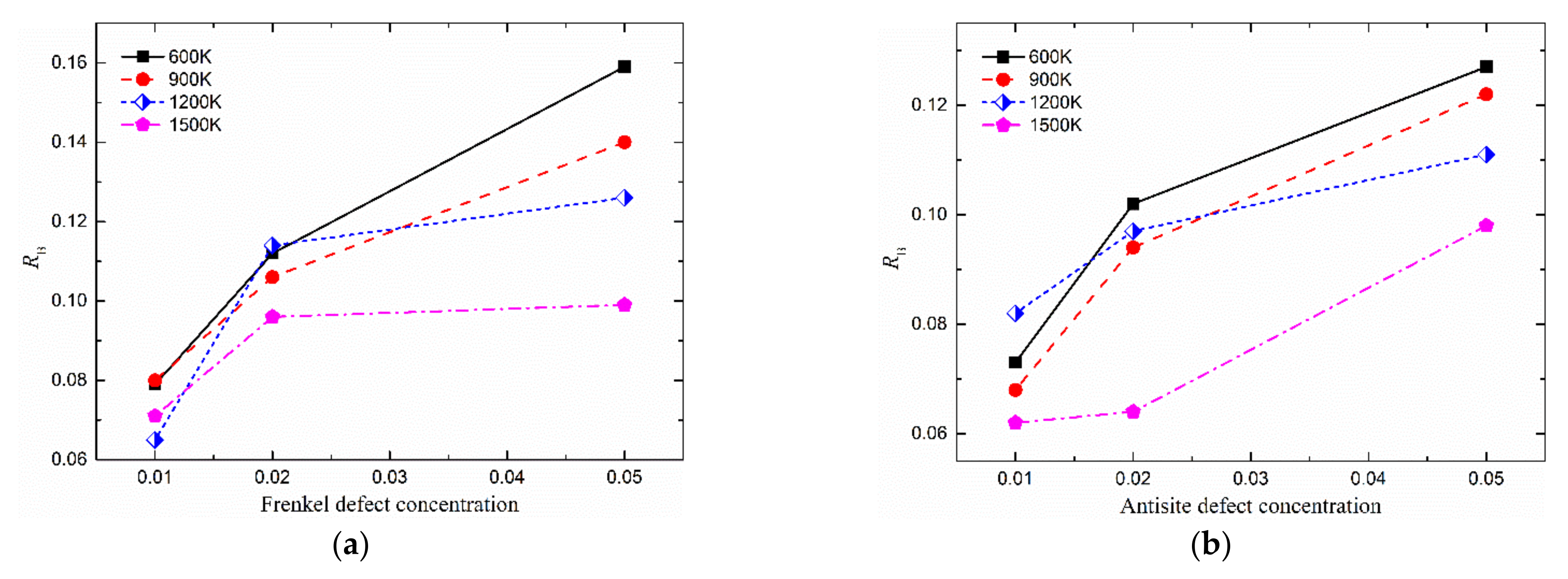
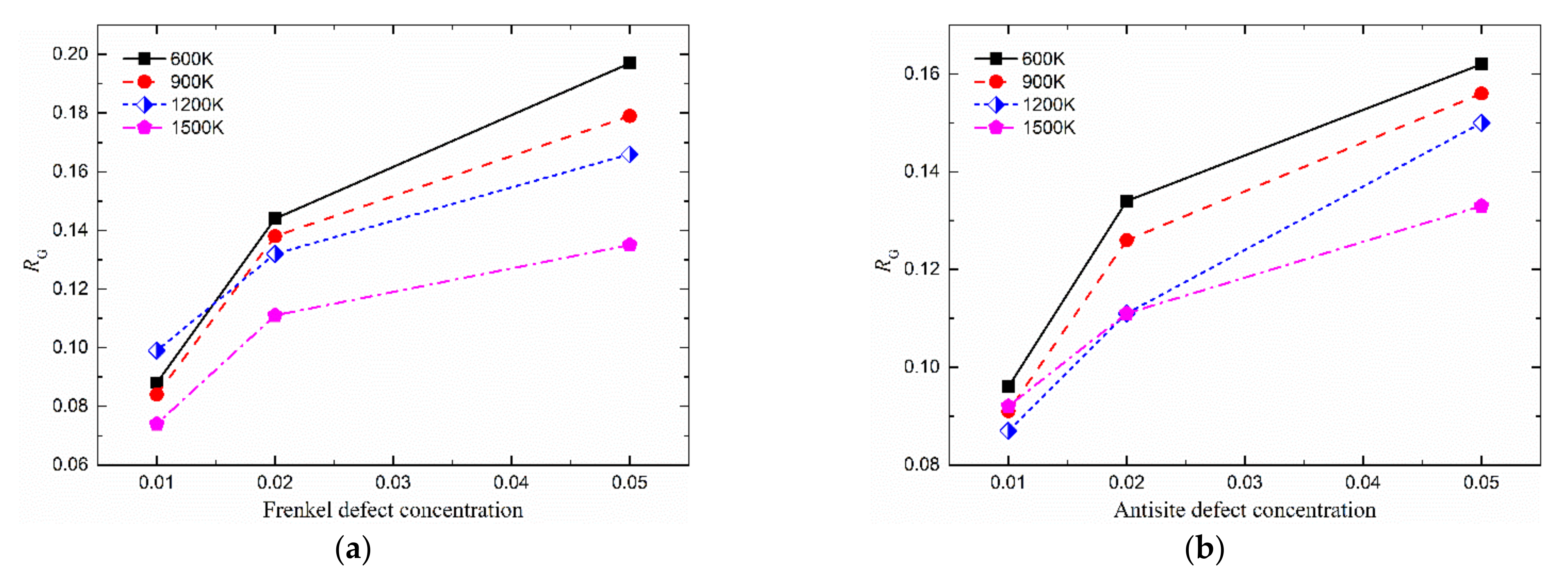
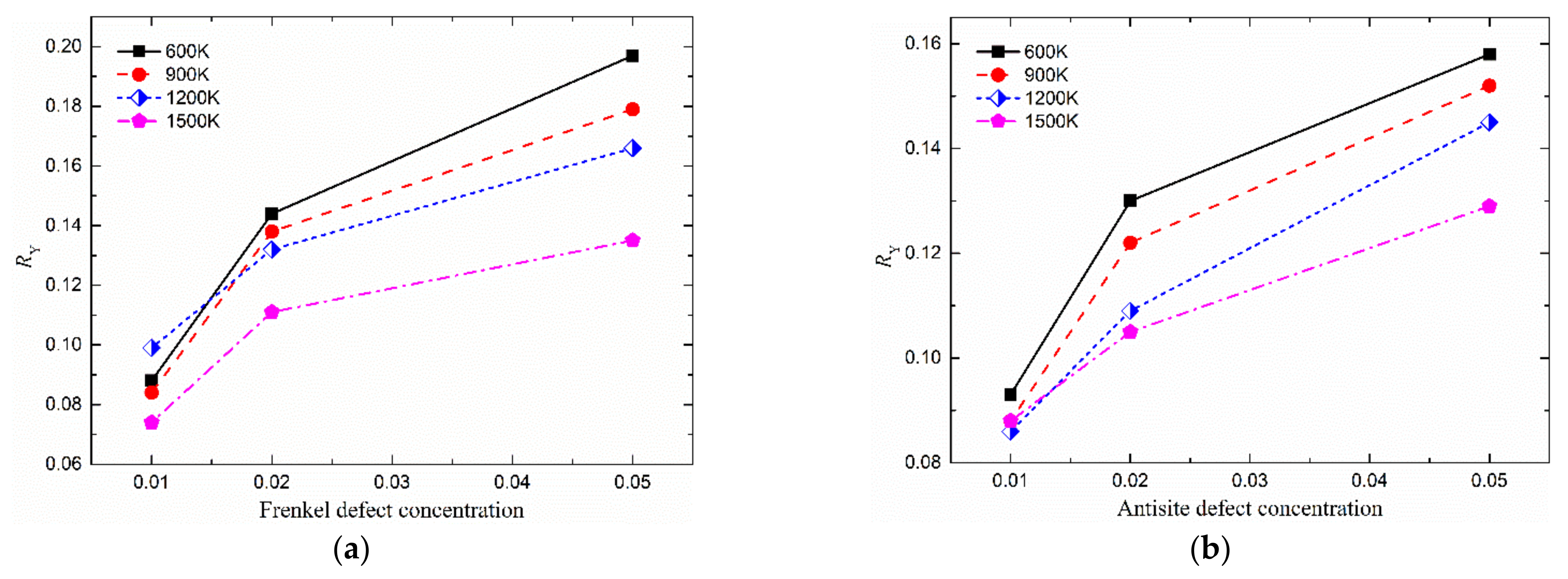
3.3. Reduction of Elastic Modulus of UO2 by Frenkel Defects and Antisites
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cooper, M.W.D.; Murphy, S.T.; Rushton, M.J.D.; Grimes, R.W. Thermophysical properties and oxygen transport in the (Ux,Pu1−x)O2 lattice. J. Nucl. Mater. 2015, 461, 206–214. [Google Scholar] [CrossRef] [Green Version]
- Devanathan, R.; Van Brutzel, L.; Chartier, A.; Guéneau, C.; Mattsson, A.E.; Tikare, V.; Bartel, T.; Besmann, T.; Stan, M.; Van Uffelen, P. Modeling and simulation of nuclear fuel materials. Energy Environ. Sci. 2010, 3, 1406–1426. [Google Scholar] [CrossRef]
- Martin, G.; Maillard, S.; Brutzel, L.V.; Garcia, P.; Dorado, B.; Valot, C. A molecular dynamics study of radiation induced diffusion in uranium dioxide. J. Nucl. Mater. 2009, 385, 351–357. [Google Scholar] [CrossRef]
- Cooper, M.W.D.; Rushton, M.J.D.; Grimes, R.W. A many-body potential approach to modelling the thermomechanical properties of actinide oxides. J. Phys. Condens. Matter 2014, 26, 105401. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.; Szpunar, B.; Szpunar, J. Dependence of thermal conductivity on fission-product defects and vacancy concentration in thorium dioxide. J. Nucl. Mater. 2020, 532, 152050. [Google Scholar] [CrossRef]
- Hobson, I.C.; Taylor, R.; Ainscough, J.B. Effect of porosity and stoichiometry on the thermal conductivity of uranium dioxide. J. Phys. D Appl. Phys. 1974, 7, 1003–1015. [Google Scholar] [CrossRef]
- Ishimoto, S.; Hirai, M.; Ito, K.; Korei, Y. Effects of Soluble Fission Products on Thermal Conductivities of Nuclear Fuel Pellets. J. Nucl. Sci. Technol. 1994, 31, 796–802. [Google Scholar] [CrossRef]
- Liu, X.Y.; Cooper, M.W.D.; McClellan, K.J.; Lashley, J.C.; Byler, D.D.; Bell, B.D.C.; Grimes, R.W.; Stanek, C.R.; Andersson, D.A. Molecular Dynamics Simulation of Thermal Transport in UO2 Containing Uranium, Oxygen, and Fission-product Defects. Phys. Rev. Appl. 2016, 6, 044015. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Cooper, M.W.D.; Xiao, Z.; Andersson, D.A.; Bai, X.-M. Effect of Xe bubble size and pressure on the thermal conductivity of UO2—A molecular dynamics study. J. Mater. Res. 2019, 34, 2295–2305. [Google Scholar] [CrossRef] [Green Version]
- Uchida, T.; Sunaoshi, T.; Kato, M.; Konashi, K. Thermal properties of UO2 by molecular dynamics simulation. In Progress in Nuclear Science and Technology; Atomic Energy Society of Japan: Tokyo, Japan, 2011; Volume 2, pp. 598–602. [Google Scholar]
- Park, J.; Farfán, E.B.; Mitchell, K.; Resnick, A.; Enriquez, C.; Yee, T. Sensitivity of thermal transport in thorium dioxide to defects. J. Nucl. Mater. 2018, 504, 198–205. [Google Scholar] [CrossRef]
- Rahman, M.J.; Szpunar, B.; Szpunar, J.A. Comparison of thermomechanical properties of (Ux,Th1−x)O2, (Ux,Pu1−x)O2 and (Pux,Th1−x)O2 systems. J. Nucl. Mater. 2019, 513, 8–15. [Google Scholar] [CrossRef]
- Jelea, A.; Colbert, M.; Ribeiro, F.; Tréglia, G.; Pellenq, R.J.M. An atomistic modelling of the porosity impact on UO2 matrix macroscopic properties. J. Nucl. Mater. 2011, 415, 210–216. [Google Scholar] [CrossRef]
- Rahman, M.J.; Szpunar, B.; Szpunar, J.A. Effect of fission generated defects and porosity on thermo-mechanical properties of thorium dioxide. J. Nucl. Mater. 2018, 510, 19–26. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Galvin, C.O.T.; Cooper, M.W.D.; Rushton, M.J.D.; Grimes, R.W. Thermophysical properties and oxygen transport in (Thx,Pu1−x)O2. Sci. Rep. 2016, 6, 36024. [Google Scholar] [CrossRef] [Green Version]
- Cooper, M.; Middleburgh, S.; Grimes, R. Modelling the thermal conductivity of (UxTh1−x)O2 and (UxPu1−x)O2. J. Nucl. Mater. 2015, 466, 29–35. [Google Scholar] [CrossRef]
- Qin, M.; Cooper, M.; Kuo, E.; Rushton, M.; Grimes, R.; Lumpkin, G.; Middleburgh, S. Thermal conductivity and energetic recoils in UO2 using a many-body potential model. J. Phys. Condens. Matter 2014, 26, 495401. [Google Scholar] [CrossRef]
- Martin, G.; Garcia, P.; Sabathier, C.; Van Brutzel, L.; Dorado, B.; Garrido, F.; Maillard, S. Irradiation-induced heterogeneous nucleation in uranium dioxide. Phys. Lett. A 2010, 374, 3038–3041. [Google Scholar] [CrossRef]
- Devanathan, R.; Yu, J.; Weber, W.J. Energetic recoils in UO2 simulated using five different potentials. J. Chem. Phys. 2009, 130, 174502. [Google Scholar] [CrossRef]
- Van Brutzel, L.; Rarivomanantsoa, M. Molecular dynamics simulation study of primary damage in UO2 produced by cascade overlaps. J. Nucl. Mater. 2006, 358, 209–216. [Google Scholar] [CrossRef]
- Van Brutzel, L.; Chartier, A.; Crocombette, J.P. Basic mechanisms of Frenkel pair recombinations in UO2 fluorite structure calculated by molecular dynamics simulations. Phys. Rev. B 2008, 78, 024111. [Google Scholar] [CrossRef]
- Basak, C.B.; Sengupta, A.K.; Kamath, H.S. Classical molecular dynamics simulation of UO2 to predict thermophysical properties. J. Alloys Compd. 2003, 360, 210–216. [Google Scholar] [CrossRef]
- Dai, H.; Yu, M.; Dong, Y.; Setyawan, W.; Gao, N.; Wang, X. Effect of Cr and Al on Elastic Constants of FeCrAl Alloys Investigated by Molecular Dynamics Method. Metals 2022, 12, 558. [Google Scholar] [CrossRef]
- Zuo, L.; Humbert, M.; Esling, C. Elastic properties of polycrystals in the Voigt-Reuss-Hill approximation. J. Appl. Crystallogr. 1992, 25, 751–755. [Google Scholar] [CrossRef]
- Wang, B.-T.; Zhang, P.; Lizárraga, R.; Di Marco, I.; Eriksson, O. Phonon spectrum, thermodynamic properties, and pressure-temperature phase diagram of uranium dioxide. Phys. Rev. B 2013, 88, 104107. [Google Scholar] [CrossRef] [Green Version]
- Taylor, D. Thermal expansion data. II: Binary oxides with the fluorite and rutile structures, MO2, and the antifluorite structure, M2O. Trans. J. Br. Ceram. Soc. 1984, 83, 32–37. [Google Scholar]
- Yamashita, T.; Nitani, N.; Tsuji, T.; Inagaki, H. Thermal expansions of NpO2 and some other actinide dioxides. J. Nucl. Mater. 1997, 245, 72–78. [Google Scholar] [CrossRef]
- Momin, A.C.; Mirza, E.B.; Mathews, M.D. High temperature X-ray diffractometric studies on the lattice thermal expansion behaviour of UO2, ThO2 and (U0.2Th0.8)O2 doped with fission product oxides. J. Nucl. Mater. 1991, 185, 308–310. [Google Scholar] [CrossRef]
- Cooper, M.W.D.; Murphy, S.T.; Fossati, P.C.M.; Rushton, M.J.D.; Grimes, R.W. Thermophysical and anion diffusion properties of (Ux, Th1−x) O2. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470, 20140427. [Google Scholar]
- Yun, Y.; Legut, D.; Oppeneer, P.M. Phonon spectrum, thermal expansion and heat capacity of UO2 from first-principles. J. Nucl. Mater. 2012, 426, 109–114. [Google Scholar] [CrossRef] [Green Version]
- Sun, C.Q. An approach to local band average for the temperature dependence of lattice thermal expansion. arXiv 2008, arXiv:0801.0771. [Google Scholar]
- Belle, J.; Berman, R. Thorium Dioxide: Properties and Nuclear Applications; USDOE Assistant Secretary for Nuclear Energy: Washington, DC, USA, 1984. [Google Scholar]
- Dorado, B.; Freyss, M.; Martin, G. GGA+U study of the incorporation of iodine in uranium dioxide. Eur. Phys. J. B 2009, 69, 203–209. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Yu, M.; Yang, C.; Long, X.; Gao, N.; Yao, Z.; Dong, L.; Wang, X. Effect of Radiation Defects on Thermo–Mechanical Properties of UO2 Investigated by Molecular Dynamics Method. Metals 2022, 12, 761. https://doi.org/10.3390/met12050761
Wang Z, Yu M, Yang C, Long X, Gao N, Yao Z, Dong L, Wang X. Effect of Radiation Defects on Thermo–Mechanical Properties of UO2 Investigated by Molecular Dynamics Method. Metals. 2022; 12(5):761. https://doi.org/10.3390/met12050761
Chicago/Turabian StyleWang, Ziqiang, Miaosen Yu, Chen Yang, Xuehao Long, Ning Gao, Zhongwen Yao, Limin Dong, and Xuelin Wang. 2022. "Effect of Radiation Defects on Thermo–Mechanical Properties of UO2 Investigated by Molecular Dynamics Method" Metals 12, no. 5: 761. https://doi.org/10.3390/met12050761
APA StyleWang, Z., Yu, M., Yang, C., Long, X., Gao, N., Yao, Z., Dong, L., & Wang, X. (2022). Effect of Radiation Defects on Thermo–Mechanical Properties of UO2 Investigated by Molecular Dynamics Method. Metals, 12(5), 761. https://doi.org/10.3390/met12050761






