An Experimental Study of the Tension-Compression Asymmetry of Extruded Ti-6.5Al-2Zr-1Mo-1V under Quasi-Static Conditions at High Temperature
Abstract
:1. Introduction
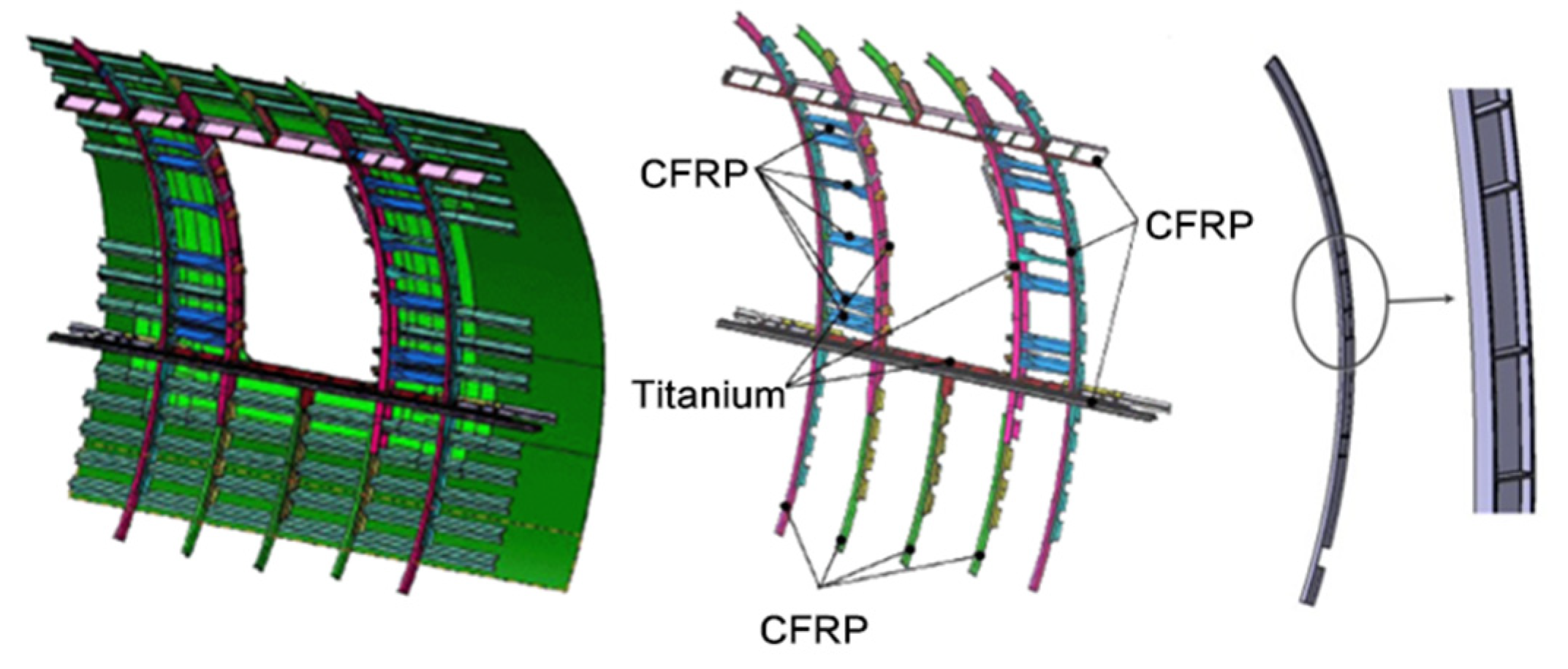
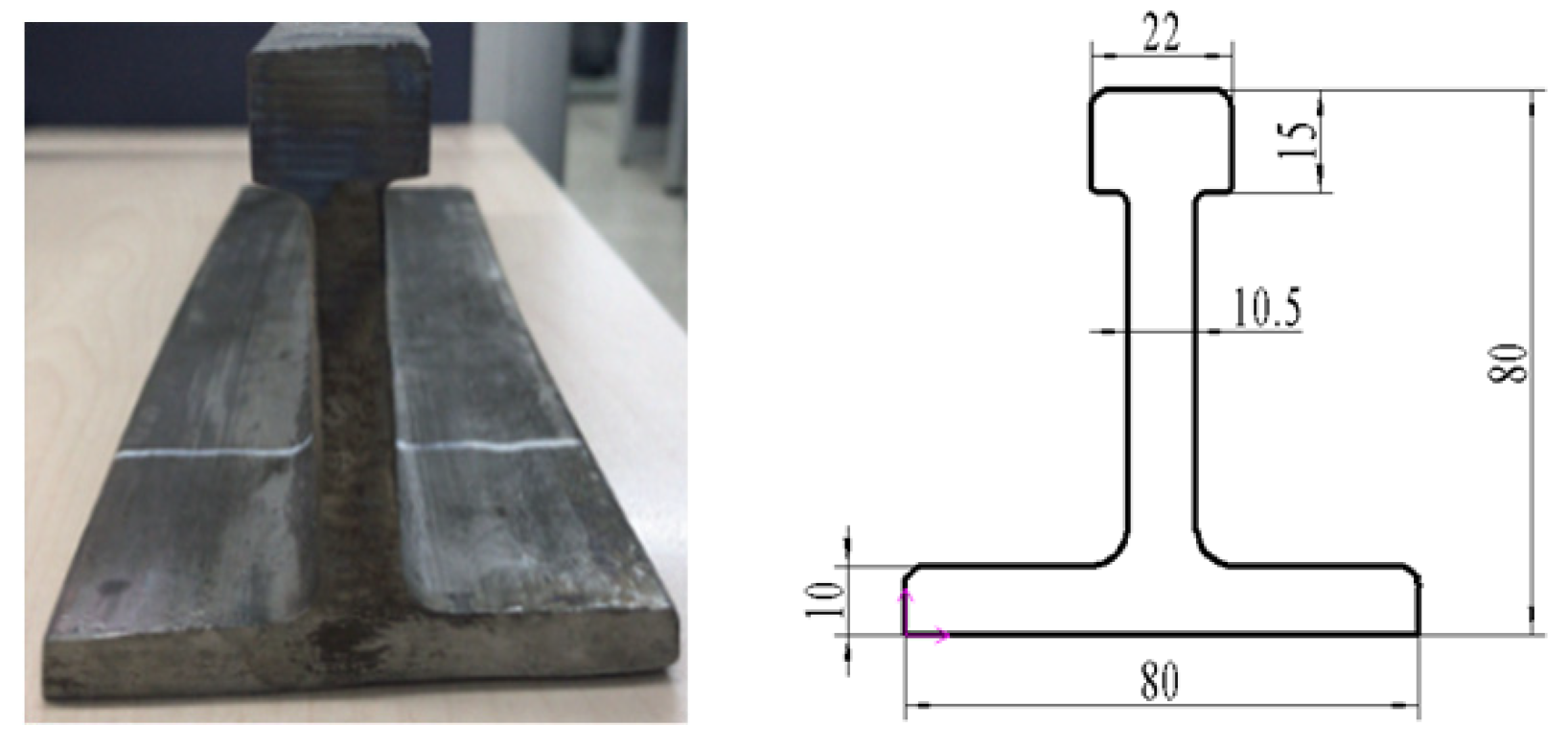
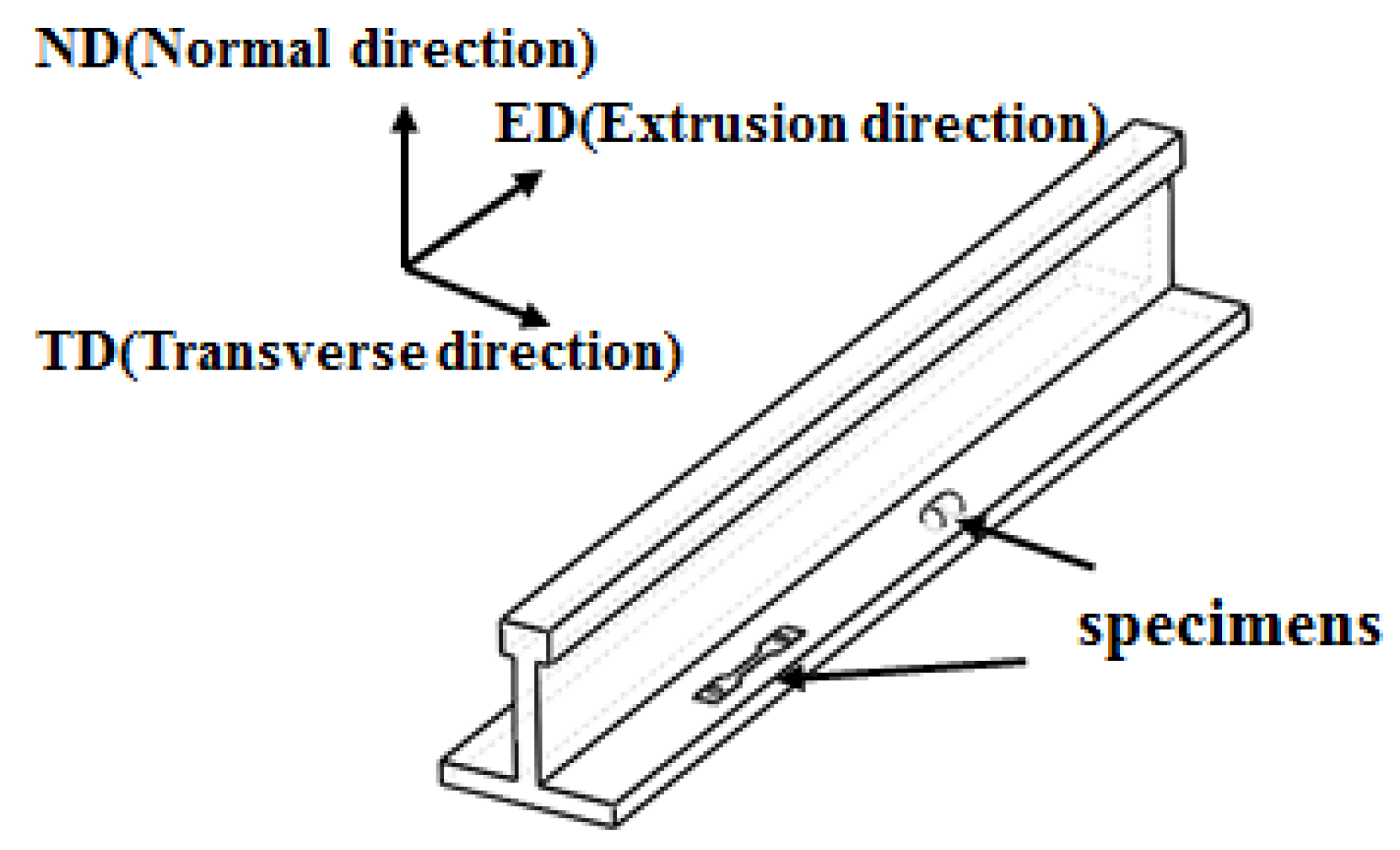
2. Materials and Methods
2.1. Material
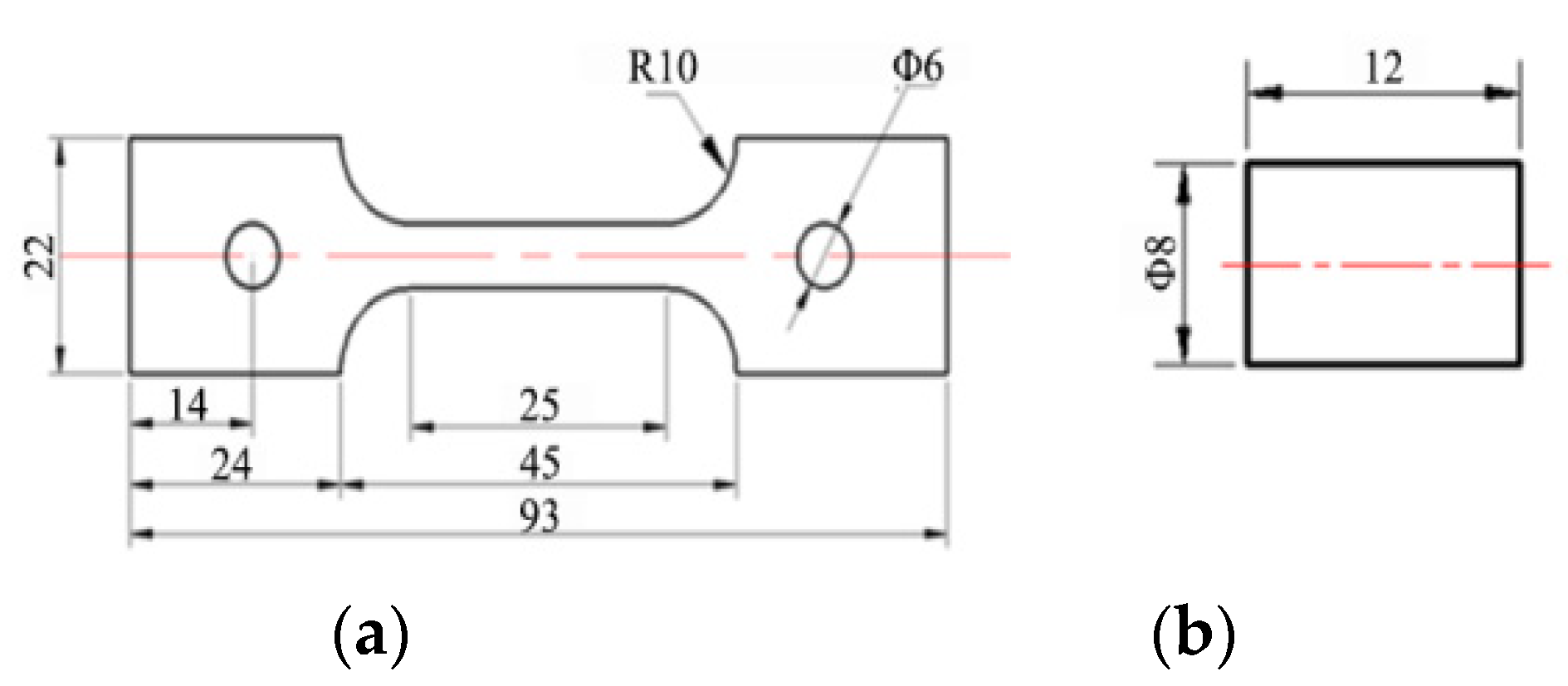
2.2. Mechanical Tests
2.3. OM Observations
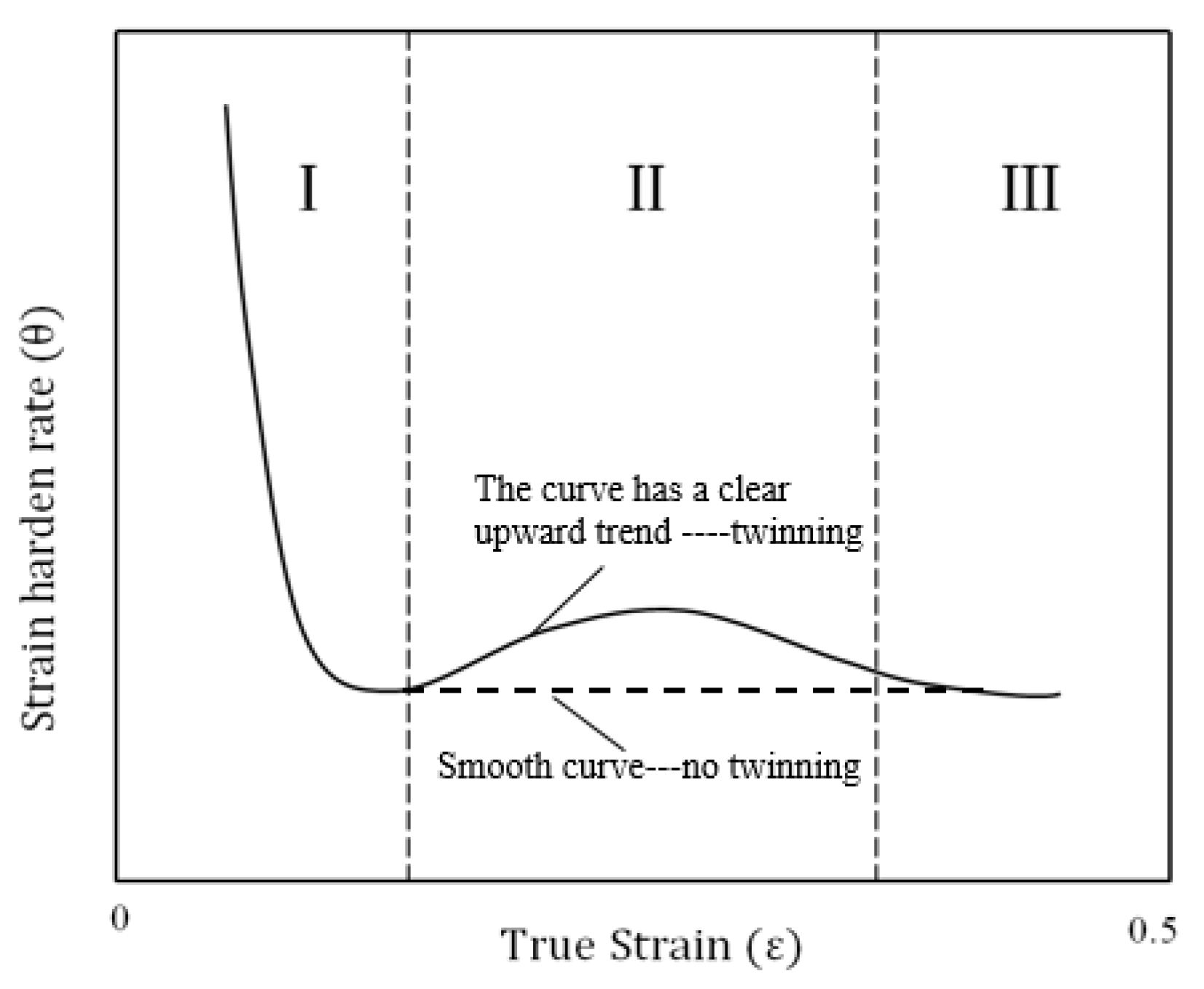
3. Results
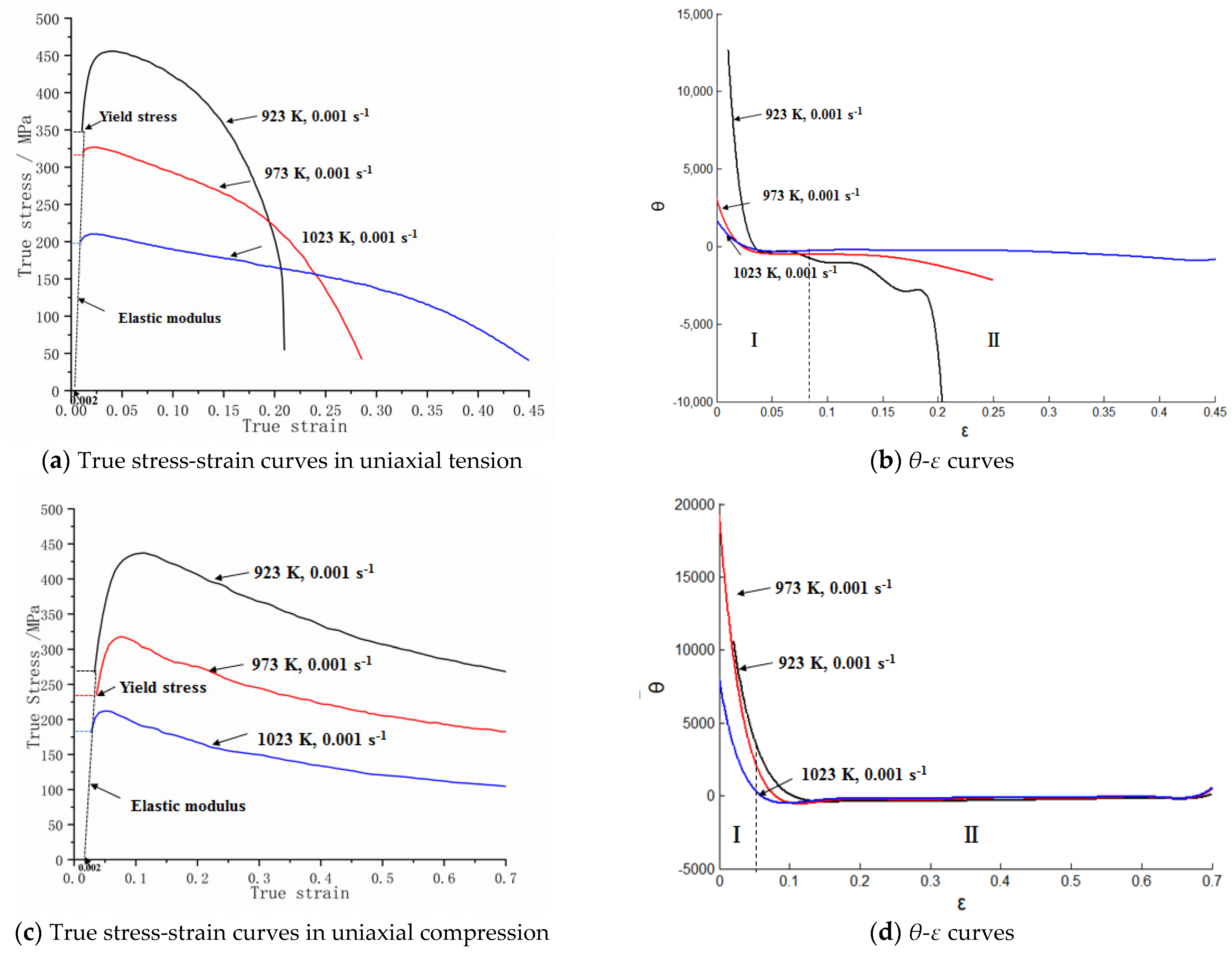
3.1. Stress–Strain Behavior at Different Temperatures
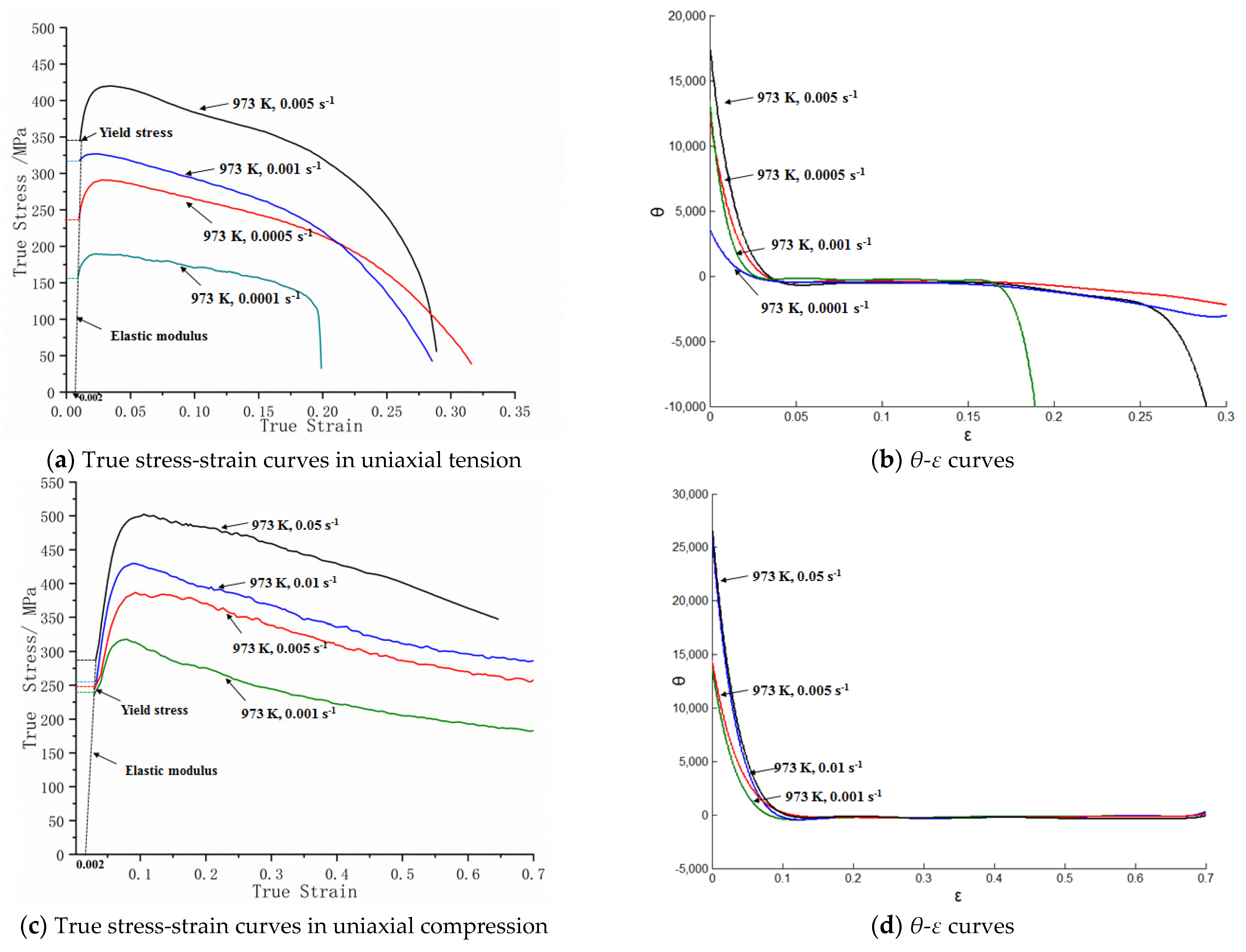
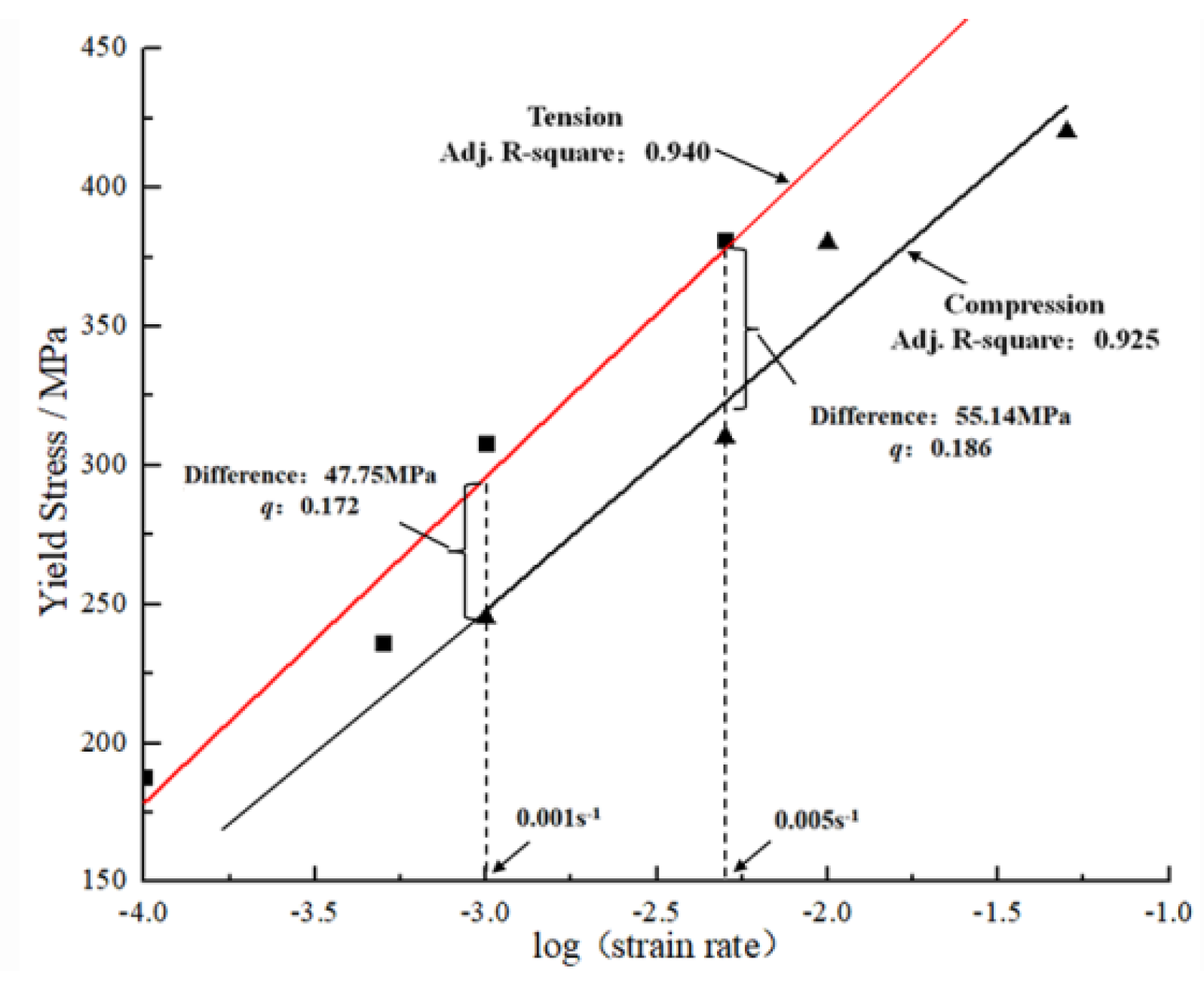
3.2. Stress-Strain Behavior at Different Strain Rates
3.3. OM Microstructure
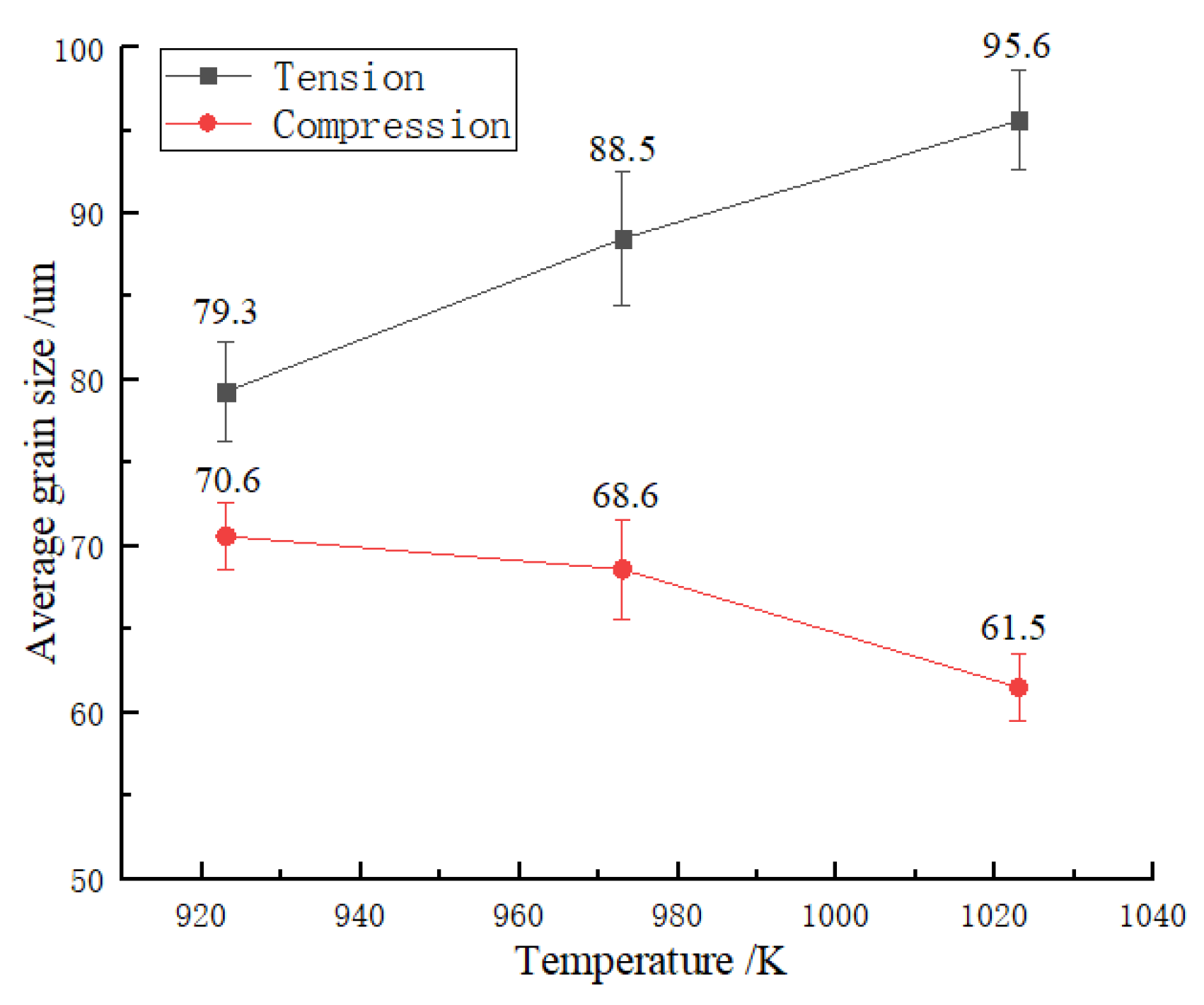
3.3.1. The Average Grain Size
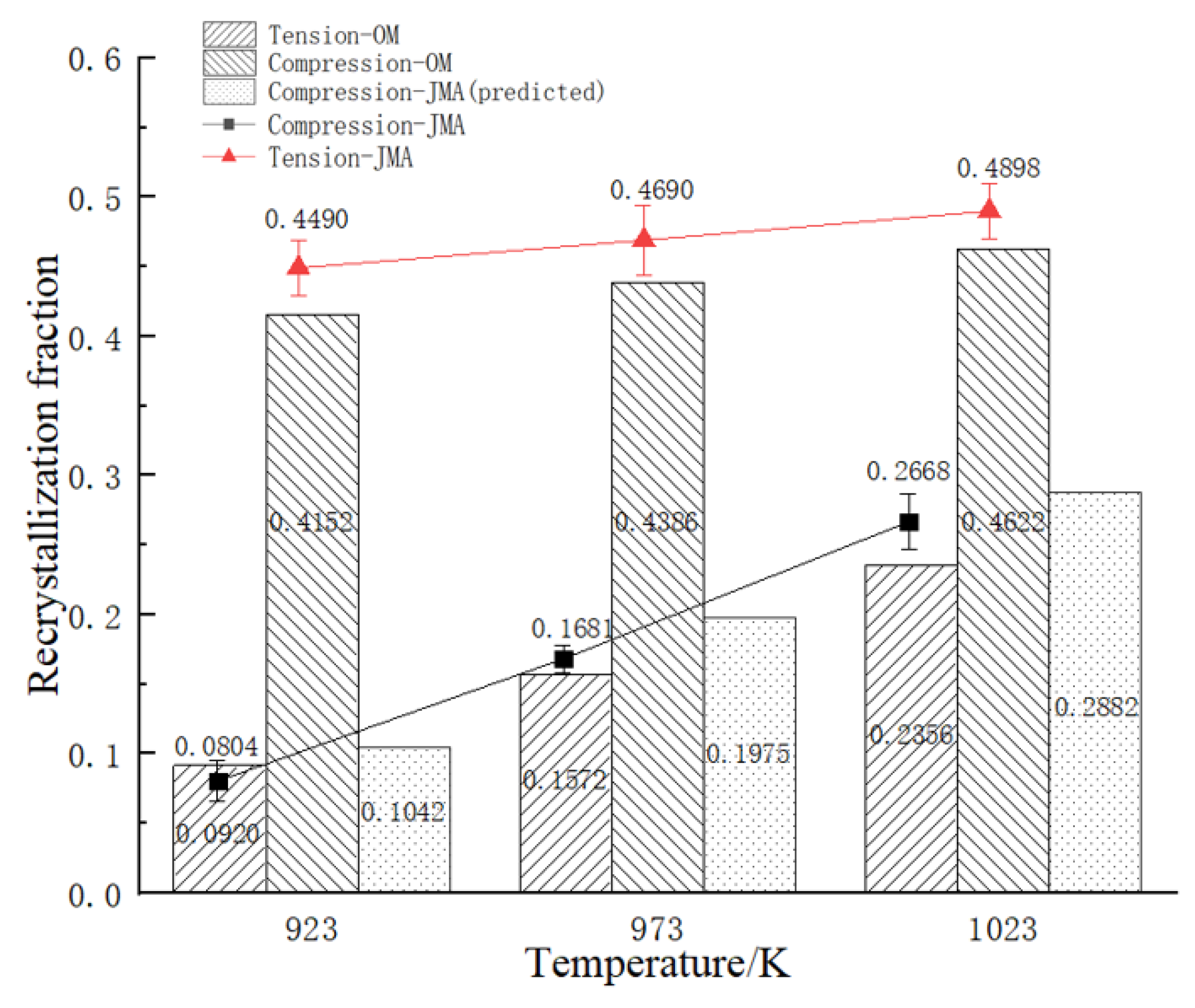
3.3.2. The Recrystallization Fraction
4. Discussion
4.1. Effect of Deformation Temperature on TCA
4.2. Effect of Strain Rates on TCA
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boyer, R. An overview on the use of titanium in the aerospace industry. Mater. Sci. Eng. A 1996, 213, 103–114. [Google Scholar] [CrossRef]
- Li, C.-L.; Mi, X.-J.; Ye, W.-J.; Hui, S.-X.; Yu, Y.; Wang, W.-Q. A study on the microstructures and tensile properties of new beta high strength titanium alloy. J. Alloy. Compd. 2012, 550, 23–30. [Google Scholar] [CrossRef]
- Li, Y.; Loretto, M.; Rugg, D.; Voice, W. Effect of heat treatment and exposure on microstructure and mechanical properties of Ti–25V–15Cr–2Al–0.2C (wt%). Acta Mater. 2001, 49, 3011–3017. [Google Scholar] [CrossRef]
- Odenberger, E.-L.; Pederson, R.; Oldenburg, M. Finite element modeling and validation of springback and stress relaxation in the thermo-mechanical forming of thin Ti-6Al-4V sheets. Int. J. Adv. Manuf. Technol. 2019, 104, 3439–3455. [Google Scholar] [CrossRef] [Green Version]
- Xiao, J.; Li, D.; Li, X.; Deng, T. Constitutive modeling and microstructure change of Ti–6Al–4V during the hot tensile deformation. J. Alloy. Compd. 2012, 541, 346–352. [Google Scholar] [CrossRef]
- Astarita, A.; Armentani, E.; Ceretti, E.; Giorleo, L.; Mastrilli, P.; Paradiso, V.; Scherillo, F.; Squillace, A.; Velotti, C. Hot Stretch Forming of a Titanium Alloy Component for Aeronautic: Mechanical and Modeling. Key Eng. Mater. 2013, 554–557, 647–656. [Google Scholar] [CrossRef]
- Guo, G.; Li, D.; Li, X.; Deng, T.; Wang, S. Finite element simulation and process optimization for hot stretch bending of Ti-6Al-4V thin-walled extrusion. Int. J. Adv. Manuf. Technol. 2017, 92, 1707–1719. [Google Scholar] [CrossRef]
- Astarita, A.; Giorleo, L.; Scherillo, F.; Squillace, A.; Ceretti, E.; Carrino, L. Titanium Hot Stretch Forming: Experimental and Modeling Residual Stress Analysis. Key Eng. Mater. 2014, 611–612, 149–161. [Google Scholar] [CrossRef]
- Lin, P.; Hao, Y.; Zhang, B.; Zhang, S.; Chi, C.; Shen, J. Tension-compression asymmetry in yielding and strain hardening behavior of CP-Ti at room temperature. Mater. Sci. Eng. A 2017, 707, 172–180. [Google Scholar] [CrossRef]
- Tuninetti, V.; Gilles, G.; Milis, O.; Pardoen, T.; Habraken, A. Anisotropy and tension–compression asymmetry modeling of the room temperature plastic response of Ti–6Al–4V. Int. J. Plast. 2015, 67, 53–68. [Google Scholar] [CrossRef]
- Hao, Y.G.; Lin, P.; Zhang, B.Y.; Cui, X.L.; Zhang, C.J.; Chi, C.Z. Effect of Planar Anisotropy and Tension-Compression Asymmetry of CP-Ti on its Deep Drawing Behavior at Room Temperature. Mater. Sci. Forum 2018, 913, 190–195. [Google Scholar] [CrossRef]
- Neeraj, T.; Savage, M.; Tatalovich, J.; Kovarik, L.; Hayes, R.; Mills, M. Observation of tension–compression asymmetry in α and titanium alloys. Philos. Mag. 2005, 85, 279–295. [Google Scholar] [CrossRef]
- Sarsfield, H.; Wang, L.; Petrinic, N. An experimental investigation of rate-dependent deformation and failure of three titanium alloys. J. Mater. Sci. 2007, 42, 5085–5093. [Google Scholar] [CrossRef]
- Khan, A.S.; Kazmi, R.; Farrokh, B.; Zupan, M. Effect of oxygen content and microstructure on the thermo-mechanical response of three Ti–6Al–4V alloys: Experiments and modeling over a wide range of strain-rates and temperatures. Int. J. Plast. 2007, 23, 1105–1125. [Google Scholar] [CrossRef]
- Adharapurapu, R.R.; Jiang, F.; Vecchio, K.S.; Gray, G.T. Response of NiTi shape memory alloy at high strain rate: A systematic investigation of temperature effects on tension–compression asymmetry. Acta Mater. 2006, 54, 4609–4620. [Google Scholar] [CrossRef]
- Qin, H.; Jonas, J.J.; Yu, H.; Brodusch, N.; Gauvin, R.; Zhang, X. Initiation and accommodation of primary twins in high-purity titanium. Acta Mater. 2014, 71, 293–305. [Google Scholar] [CrossRef]
- Haertel, S.; Graf, M.; Lehmann, T.; Ullman, M. Influence of Tension-Compression Anomaly during Bending of Magnesium Alloy AZ31. Mater. Sci. Eng. A 2017, 705, 62–71. [Google Scholar] [CrossRef]
- Lei, Z.; Gao, P.; Li, H.; Cai, Y.; Li, Y.; Zhan, M. Comparative analyses of the tensile and damage tolerance properties of tri-modal microstructure to widmanstätten and bimodal microstructures of TA15 titanium alloy. J. Alloy. Compd. 2019, 788, 831–841. [Google Scholar] [CrossRef]
- Zhang, C.; Li, D.; Li, X.; Xia, Q. Numerical simulation and process optimization for hot stretch bending of Ti-6.5Al-2Zr-1Mo-1V large-section extrusion. Procedia Manuf. 2020, 50, 483–487. [Google Scholar] [CrossRef]
- AMST9046B. Titanium and Titanium Alloy, Sheet, Strip, and Plate; Society of Automotive Engineers (SAE): Washington, DC, USA, 2006. [Google Scholar]
- ISO 6892-2. Metallic Materials-Tensile Testing-Part2: Method of Test at Elevated Temperature; Case Postale; International Organization for Standardization: Geneva, Switzerland, 2011. [Google Scholar]
- Shen, F.J.; Chen, M.H.; Feng, J.C. Stress Relaxation and Flow Stress of TA15 Alloy at Elevated Temperature. Aerosp. Mater. Technol. 2013, 3, 114–118. [Google Scholar]
- ISO 4499-1. Hardmetals-Metallographic Determination of Microstructure-Part 1: Photomicrographs and Description; International Organization for Standardization: Geneva, Switzerland, 2020. [Google Scholar]
- Park, S.H.; Lee, J.H.; Moon, B.G.; You, B.-S. Tension–compression yield asymmetry in as-cast magnesium alloy. J. Alloy. Compd. 2014, 617, 277–280. [Google Scholar] [CrossRef]
- Xu, W.C.; Shan, B.D.; Lv, Y.; Li, C.F. Effects of hot deformation parameters on flow stress and establishment of constitutive relationship system of BT20 titanium alloy. Trans. Nonferrous Met. Soc. China 2005, 15, 167–172. [Google Scholar] [CrossRef]
- Shi, Y.; Zhong, F.; Li, X.; Gong, S.; Chen, L. Effect of laser beam welding on fracture toughness of a Ti-6.5Al-2Zr-1Mo-1V alloy sheet. J. Mater. Sci. 2007, 42, 6651–6657. [Google Scholar] [CrossRef]
- Wang, T.; Li, B.; Wang, Z.; Nie, Z. Hot deformation behavior and microstructure evolution of a high-temperature titanium alloy modified by erbium. J. Mater. Res. 2017, 32, 1517–1527. [Google Scholar] [CrossRef]
- Meng, Q.G.; Zhao, G.D.; Wang, L.N.; Wang, Y.F.; Guo, J.; Han, D. A Method for Determining the Volume Fraction of Dynamic Recrystallization of Metals Av-rami’s Method of Mathematical Model Coefficient. CN 201910387211.8, 17 September 2019. [Google Scholar]
- Ouyang, D.L.; Lu, S.; Cui, X.; Wang, K.L.; Wu, C. Dynamic Recrystallization of Titanium Alloy TA15 during β Hot Process at Different Strain Rates. Rare. Metal. Mat. Eng. 2011, 40, 325–330. [Google Scholar]
- Avrami, M. Kinetics of Phase Change. I General Theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar]
- Avrami, M. Kinetics of Phase Change. II Transformation-Time Relations for Random Distribution of Nuclei. J. Chem. Phys. 1939, 8, 212–224. [Google Scholar] [CrossRef]
- Yue, L.Y.; Huang, Z.F.; He, Z.L.; Jiang, M.G.; Chen, W. Microstructure Evolution and Numerical Simulation of DP Steel TWBs During Warm Tensile Deformation. Adv. Mater. Res. 2012, 418–420, 1222–1227. [Google Scholar] [CrossRef]
- Nagarajan, V.; Palmiere, E.J.; Sellars, C.M. New approach for modelling strain induced precipitation of Nb(C,N) in HSLA steels during multipass hot deformation in austenite. Mater. Sci. Technol. 2009, 25, 1168–1174. [Google Scholar] [CrossRef] [Green Version]
- Medina, S.F.; Hernandez, C.A. General expression of the Zener-Hollomon parameter as a function of the chemical composition of low alloy and microalloyed steels. Acta Mater. 1996, 44, 137–148. [Google Scholar] [CrossRef]
- Jia, Y.; Xu, L.; Ma, P.; Gokuldoss Prashanth, K.; Yao, C.; Wang, G. Microstructure evolution and hot deformation behavior of spray-deposited Ti-Al alloy. J. Mater. Res. 2018, 33, 1–9. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, J.; Wang, Y. Effect of strain rate on the tension–compression asymmetric responses of Ti–6.6Al–3.3Mo–1.8Zr–0.29Si. Mater. Des. 2014, 61, 281–285. [Google Scholar] [CrossRef]
- Yin, D.L.; Wang, J.T.; Liu, J.Q.; Zhao, X. On tension–compression yield asymmetry in an extruded Mg–3Al–1Zn alloy. J. Alloy. Compd. 2009, 478, 789–795. [Google Scholar] [CrossRef]
- Salem, A.; Semiatin, S. Anisotropy of the hot plastic deformation of Ti–6Al–4V single-colony samples. Mater. Sci. Eng. A 2009, 508, 114–120. [Google Scholar] [CrossRef]
- Mann, G.; Griffiths, J.R.; Cáceres, C.H. Hall-Petch parameters in tension and compression in cast Mg-2Zn alloys. J. Alloys Compd. 2004, 378, 188–191. [Google Scholar] [CrossRef]
- Duc-Toan, N.; Seung-Han, Y.; Dong-Won, J.; Tien-Long, B.; Young-Suk, K. A study on material modeling to predict spring-back in V-bending of AZ31 magnesium alloy sheet at various temperatures. Int. J. Adv. Manuf. Technol. 2011, 62, 551–562. [Google Scholar] [CrossRef]
- Dieter, G.E. Mechanical Metallurgy, 3rd ed.; McGraw-Hill Book Company: London, UK, 1988. [Google Scholar]




| Al | Zr | Mn | V | Ti |
|---|---|---|---|---|
| 5.5~7.0 | 1.5~2.5 | 0.5~2.0 | 0.8~2.5 | allowance |
| Groups | Temperature/K | Strain Rate/s−1 | Microstructure Test |
|---|---|---|---|
| 1 | 923 | 0.001 | Optical microscope |
| 973 | |||
| 102 | |||
| 2 | 973 | 0.0001 | - |
| 0.0005 | |||
| 0.001 | - | ||
| 0.005 |
| Temperature (K) | Strain Rate (s−1) | Z | ||||
|---|---|---|---|---|---|---|
| Tension | Compression | Tension | Compression | |||
| 923 | 0.001 | 8.0075 × 109 | 0.109 | 0.068 | 0.0704 | 0.4390 |
| 973 | 0.001 | 1.7402 × 109 | 0.096 | 0.062 | 0.1681 | 0.4690 |
| 1023 | 0.001 | 4.3866 × 108 | 0.085 | 0.057 | 0.2668 | 0.4898 |
| Temperature/K | Tension/MPa | Compression/MPa | Asymmetry Coefficient q | Strain Rates/s−1 |
|---|---|---|---|---|
| 923 | 355.25 | 272 | 0.23 | 0.001 |
| 973 | 308.03 | 248 | 0.20 | |
| 1023 | 212.93 | 185 | 0.13 | |
| 973 | 348.25 | 251 | 0.28 | 0.005 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Li, D.; Li, X.; Li, Y. An Experimental Study of the Tension-Compression Asymmetry of Extruded Ti-6.5Al-2Zr-1Mo-1V under Quasi-Static Conditions at High Temperature. Metals 2021, 11, 1299. https://doi.org/10.3390/met11081299
Zhang C, Li D, Li X, Li Y. An Experimental Study of the Tension-Compression Asymmetry of Extruded Ti-6.5Al-2Zr-1Mo-1V under Quasi-Static Conditions at High Temperature. Metals. 2021; 11(8):1299. https://doi.org/10.3390/met11081299
Chicago/Turabian StyleZhang, Chen, Dongsheng Li, Xiaoqiang Li, and Yong Li. 2021. "An Experimental Study of the Tension-Compression Asymmetry of Extruded Ti-6.5Al-2Zr-1Mo-1V under Quasi-Static Conditions at High Temperature" Metals 11, no. 8: 1299. https://doi.org/10.3390/met11081299
APA StyleZhang, C., Li, D., Li, X., & Li, Y. (2021). An Experimental Study of the Tension-Compression Asymmetry of Extruded Ti-6.5Al-2Zr-1Mo-1V under Quasi-Static Conditions at High Temperature. Metals, 11(8), 1299. https://doi.org/10.3390/met11081299






