Quantification of Solid Solution Strengthening and Internal Stresses through Creep Testing of Ni-Containing Single Crystals at 980 °C
Abstract
:1. Introduction
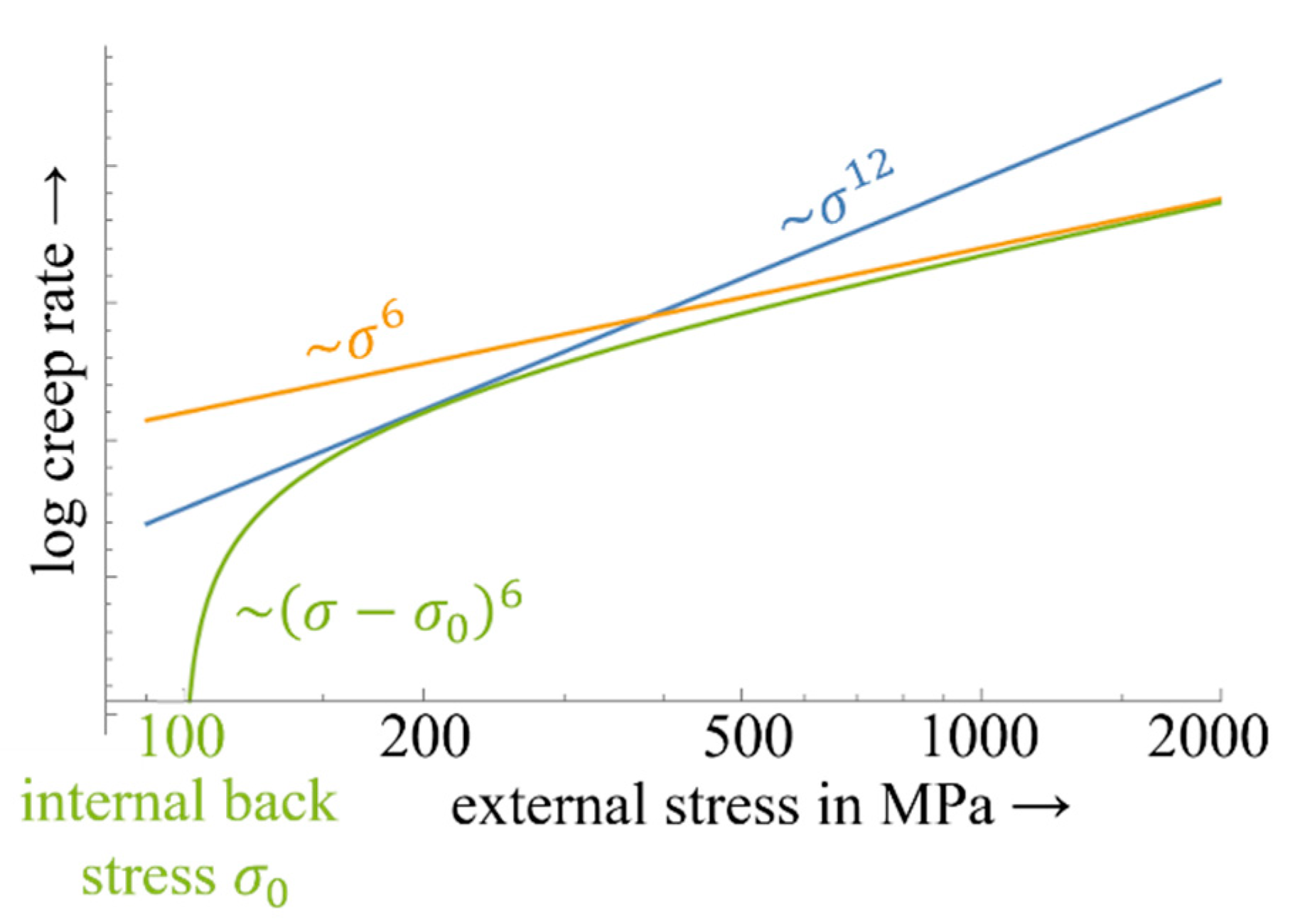
1.1. Internal Back Stress
1.2. Solid Solution Strengthening
1.3. Dislocation Density Induced Internal Back Stress
1.4. Misfit Stress
1.5. Orowan Stress
1.6. Cutting of γ′-Phase
1.7. Summary Stress Contributions
- Dislocation density varies depending on the orientation of individual matrix channels with respect to external load direction.
- The misfit can vary locally from 0 to −4 × 10−3 in interdendritic areas as compared to the dendrite center, respectively [19].
- The distance L between -precipitates is distributed between 10 and 150 nm, resulting in a change of the Orowan stress within a factor of 15. Additionally, coarsening occurs during long-time creep, resulting in an increase of L.
- The stresses can convert into each other, e.g., misfit-induced stress can turn into dislocation-induced stress.
2. Materials and Methods
2.1. Material
- (A)
- Pure Ni (single-phase fcc) with 99.9 at.% technical purity and configurational entropy equal to zero. No heat treatment was carried out. Solid solution strengthening can be excluded. For the sake of readability, this sample composition will also be referred to as an “alloy”, knowing that this might not be a precise denomination.
- (B)
- Equiatomic alloys with single-phase fcc microstructure: CrCoNi with 33.3 at.% for each element and the so-called Cantor alloy (CrMnFeCoNi with 20 at.% each) [26]. These two compositions exemplify a configurational entropy of 1.10·R (generally called medium entropy alloy) and 1.61·R (high entropy alloy). No heat treatment was carried out on CrCoNi and Cantor alloy. Due to the evaporation of Mn during the SX casting procedure, the Mn content was adjusted before casting to obtain 20 ± 1 at.% in the cast single-crystal sample.
- (C)
- Single-phase solid solution strengthened Ni-based alloys with fcc structure. The two alloys of this group have the composition of the matrix of the two alloys of Group (D). The compositions of the matrix phases were calculated with Thermo-Calc Software and database TTNi7 at 800 °C [27] and compared with experimentally determined matrix composition. A temperature of 800 °C was used to ensure the single-phase state at 980 °C. No precipitates were observed in these alloys; hence, they remain single-phase, see, for example, Figure 2a. Homogenization treatment was performed at 1290 °C for 48 h, see Table 3. The two alloys within this group have similar compositions, except for the element Re. Thereby, the contribution of solid solution strengthening of Re can be quantitatively determined. It should be noted that 3.1 atomic% of Re converts into 9.0 weight%.
- (D)
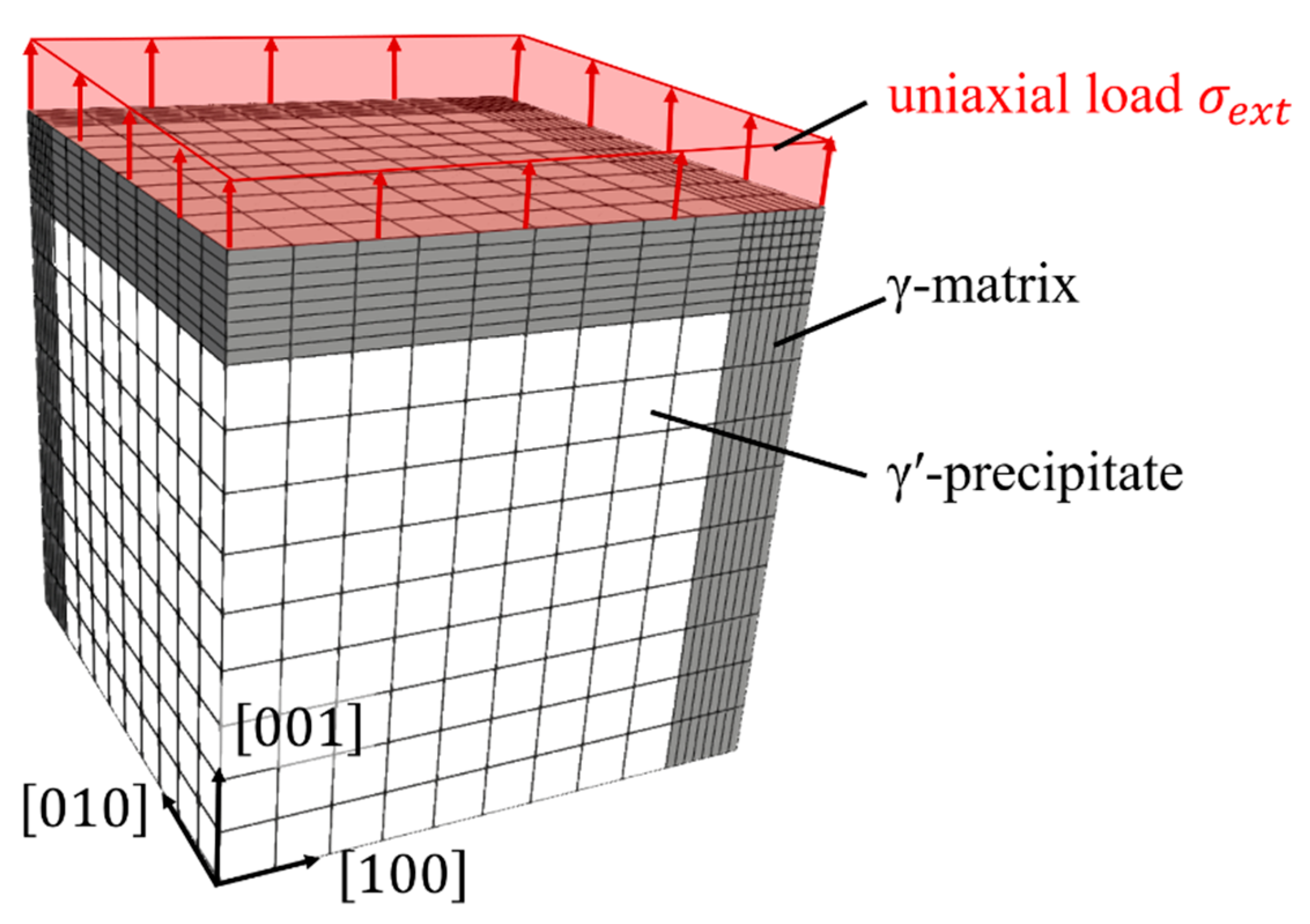
- The commercially available two-phase Ni-based superalloys CMSX-3 (no Re, 1st generation) and CMSX-4 (1.0 at.% (3 wt.%) Re, 2nd generation) [28]. The exceptionally good mechanical properties of Ni-based superalloys at high temperatures are mainly due to the two-phase matrix/-microstructure (Figure 2b). A specific heat treatment, see Table 3, was used after single-crystal casting in order to obtain such a microstructure, resulting in an average edge length of the cuboidal -particles of 410 ± 30 nm (CMSX-3) and 470 ± 50 nm (CMSX-4). The -volume fraction for the alloys is about 60% for CMSX-3 and about 70% for CMSX-4 at 980 °C.
2.2. Sample Processing
2.3. Creep Testing
2.4. Simulation of Two-Phase Steady-State Creep by Finite Element Calculations
3. Results and Discussion
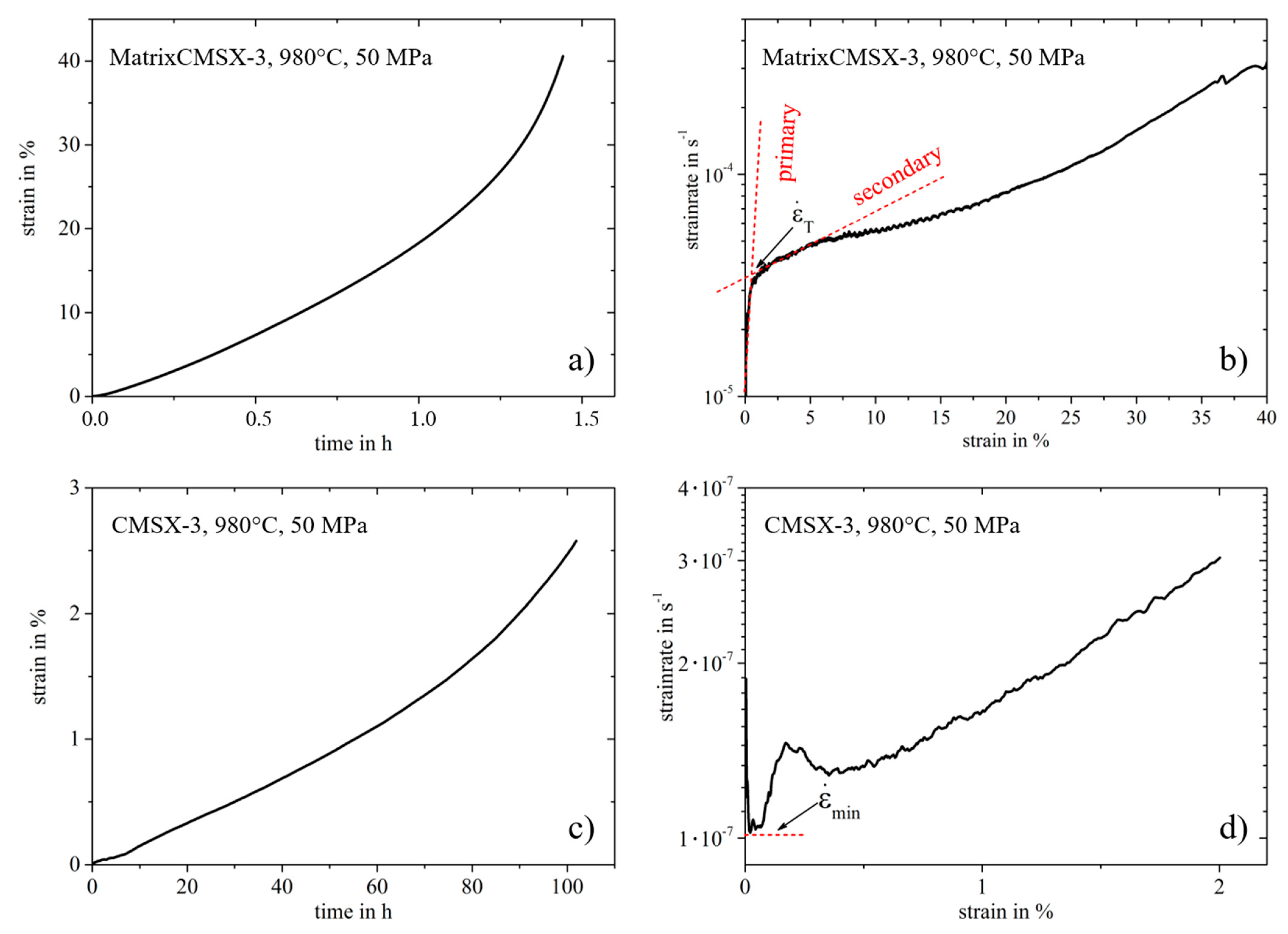
3.1. Experimental Evaluation of the Steady-State Creep Rate
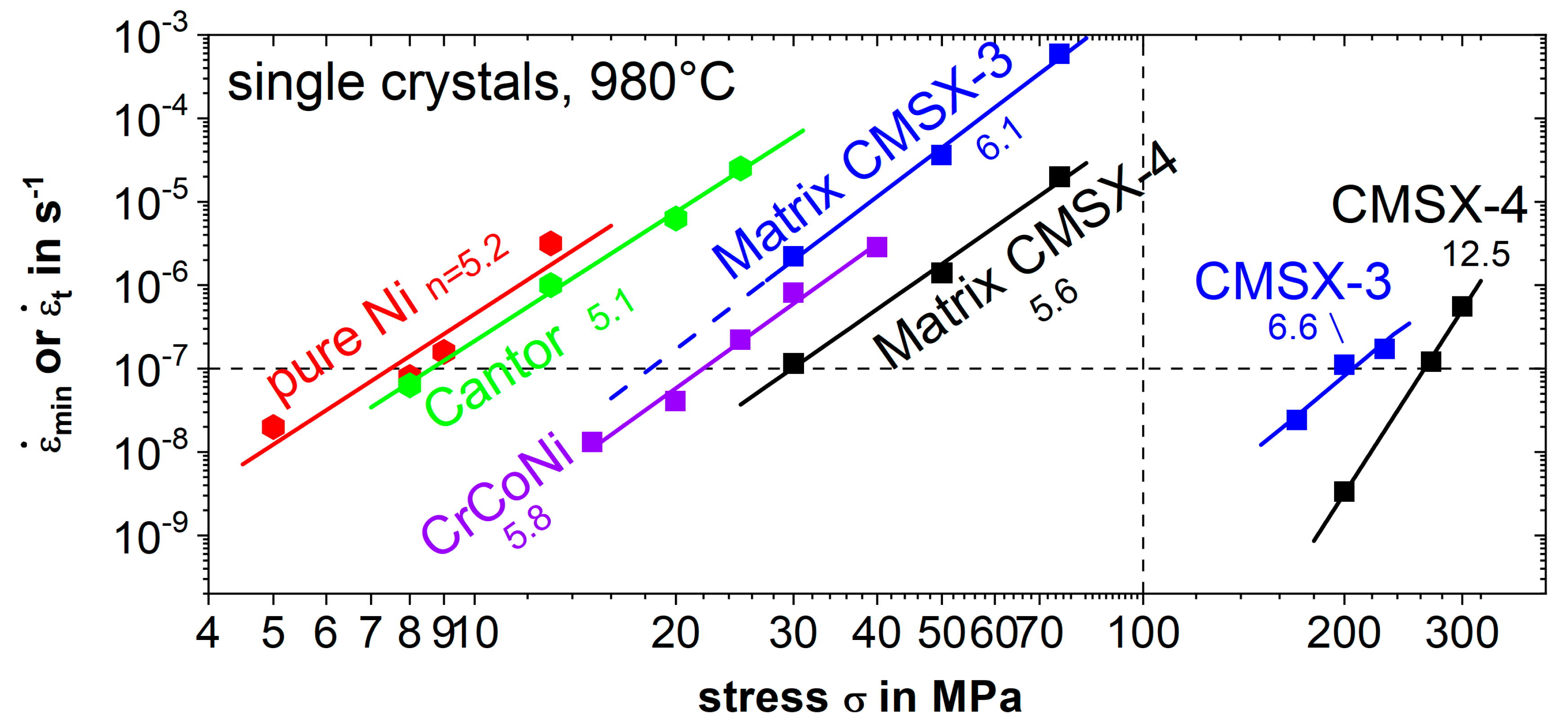
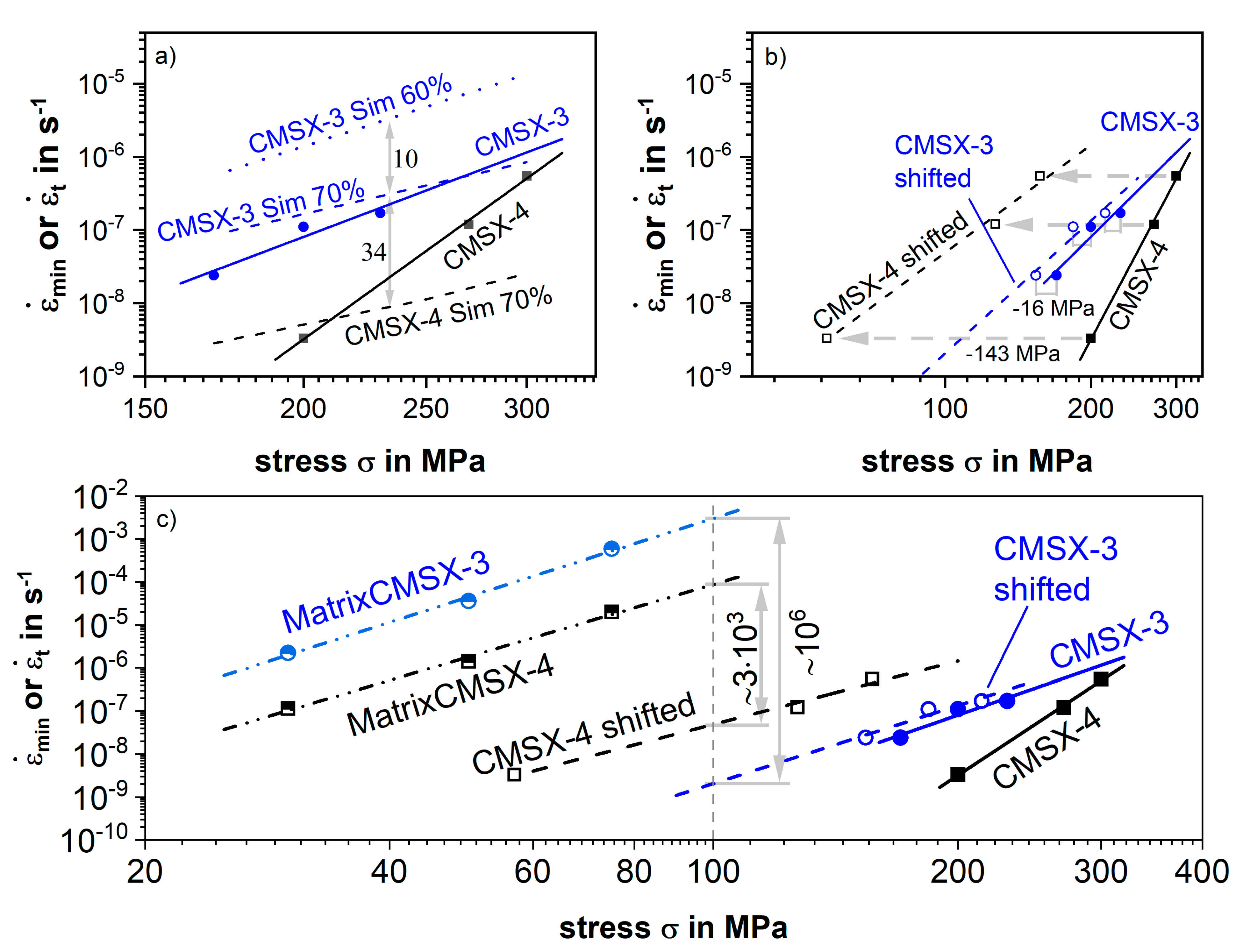
3.2. Creep Results at 980 °C over a Wide Range of Applied Stress
3.3. Quantification of Solid Solution Strengthening and Internal Back Stresses by Precipitation Hardening
3.4. Combined Effect of Various Strengthening Mechanism
4. Conclusions
- An influence of solely configurational entropy on creep strength is not observed. However, solid solution strengthening is of course of very high importance. Bearable stresses are four times higher for the matrix of CMSX-4 compared to pure Ni.
- We quantify the combined internal back stresses due to the various acting strengthening mechanisms in two-phase superalloys to be:
- –
- for the Ni-based superalloy CMSX-4.
- –
- for CMSX-3.
- Additions of Re: 1.0 at.% (3 wt.%, respectively) Re in the superalloys, corresponding to 3.1 at.% (9 wt.%, respectively) in the single-phase matrix, result in a strength increase of the matrix by a factor of 1.7 (1.2, respectively) in the two-phase material.
- The element Re influences the lattice misfit, the γ′ precipitate size, and morphology and thereby increases the internal back stress.
- Quantification of these effects is only possible by using single-crystal samples.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Reed, R.C. The Superalloys: Fundamentals and Applications; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2006; ISBN 9780511541285. [Google Scholar]
- Sims, C.T.; Stoloff, N.S.; Hagel, W.C. (Eds.) Superalloys II: High-Temperature Materials for Aerospace and Industrial Power; Wiley: New York, NY, USA, 1987; ISBN 978-0-471-01147-7. [Google Scholar]
- Fleischmann, E.; Miller, M.K.; Affeldt, E.; Glatzel, U. Quantitative experimental determination of the solid solution hardening potential of rhenium, tungsten and molybdenum in single-crystal nickel-based superalloys. Acta Mater. 2015, 87, 350–356. [Google Scholar] [CrossRef] [Green Version]
- Harada, H.; Murakami, H. Design of Ni-Base Superalloys. In Computational Materials Design; Zunger, A., Osgood, R.M., Hull, R., Sakaki, H., Saito, T., Eds.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 1999; pp. 39–70. ISBN 978-3-642-08404-1. [Google Scholar]
- Bird, J.E.; Mukherjee, A.K.; Dorn, J.E. Correlations between High-Temperature Creep Behaviour and Structure. In Quantitative Relation Between Properties and Microstructure: Proceedings of an International Conference; Israel University Press: Haifa, Israel, 1969; pp. 255–342. [Google Scholar]
- Biberger, M.; Blum, W. On the natural law of steady state creep. Scr. Metall. 1989, 23, 1419–1424. [Google Scholar] [CrossRef]
- Zakine, C.; Prioul, C.; François, D. Creep behaviour of ODS steels. Mater. Sci. Eng. A 1996, 219, 102–108. [Google Scholar] [CrossRef]
- Blum, W.; Finkel, A. New technique for evaluating long range internal back stresses. Acta Metall. 1982, 30, 1705–1715. [Google Scholar] [CrossRef]
- Kassner, M.E. Fundamentals of Creep in Materials, 3rd ed.; Butterworth-Heinemann: Amsterdam, The Netherlands, 2014; ISBN 9780080994277. [Google Scholar]
- Fleischer, R. Solution hardening. Acta Metall. 1961, 9, 996–1000. [Google Scholar] [CrossRef]
- Fleischer, R. Substitutional solution hardening. Acta Metall. 1963, 11, 203–209. [Google Scholar] [CrossRef]
- Labusch, R. A Statistical Theory of Solid Solution Hardening. Phys. Stat. Sol. B 1970, 41, 659–669. [Google Scholar] [CrossRef]
- Labusch, R. Statistische theorien der mischkristallhärtung. Acta Metall. 1972, 20, 917–927. [Google Scholar] [CrossRef]
- Wu, X.; Makineni, S.K.; Liebscher, C.H.; Dehm, G.; Rezaei Mianroodi, J.; Shanthraj, P.; Svendsen, B.; Bürger, D.; Eggeler, G.; Raabe, D.; et al. Unveiling the Re effect in Ni-based single crystal superalloys. Nat. Commun. 2020, 11, 389. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heckl, A.; Neumeier, S.; Göken, M.; Singer, R.F. The effect of Re and Ru on γ/γ′ microstructure, γ-solid solution strengthening and creep strength in nickel-base superalloys. Mater. Sci. Eng. A 2011, 528, 3435–3444. [Google Scholar] [CrossRef]
- Pettinari-Sturmel, F.; Douin, J.; Krieg, F.; Fleischmann, E.; Glatzel, U. Evidence of Short-Range Order (SRO) by Dislocation Analysis in Single-Crystal Ni-Based Matrix Alloys with Varying Re Content After Creep. In Superalloys 2020; Tin, S., Hardy, M.C., Clews, J., Cormier, J., Feng, Q., Marcin, J., O’Brien, C., Suzuki, A., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 253–259. ISBN 978-3-030-51833-2. [Google Scholar]
- Pollock, T.M.; Argon, A.S. Creep resistance of CMSX-3 nickel base superalloy single crystals. Acta Metall. Et Mater. 1992, 40, 1–30. [Google Scholar] [CrossRef]
- Glatzel, U.; Feller-Kniepmeier, M. Calculations of internal stresses in the γ/γ′ microstructure of a nickel-base superalloy with high volume fraction of γ′-phase. Scr. Metall. 1989, 23, 1839–1844. [Google Scholar] [CrossRef]
- Völkl, R.; Glatzel, U.; Feller-Kniepmeier, M. Measurement of the lattice misfit in the single crystal nickel based superalloys CMSX-4, SRR99 and SC16 by convergent beam electron diffraction. Acta Mater. 1998, 46, 4395–4404. [Google Scholar] [CrossRef]
- Glatzel, U.; Forbes, K.R.; Nix, W.D. Dislocation energies for an anisotropic cubic crystal calculations and observations for NiAl. Philos. Mag. A 1993, 67, 307–323. [Google Scholar] [CrossRef]
- Scattergood, R.O.; Bacon, D.J. The Orowan mechanism in anisotropic crystals. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1975, 31, 179–198. [Google Scholar] [CrossRef]
- Bensch, M.; Konrad, C.H.; Fleischmann, E.; Rae, C.; Glatzel, U. Influence of oxidation on near-surface γ′ fraction and resulting creep behaviour of single crystal Ni-base superalloy M247LC SX. Mater. Sci. Eng. A 2013, 577, 179–188. [Google Scholar] [CrossRef]
- Pollock, T.M.; Argon, A.S. Intermediate Temperature Creep Deformation in CMSX-3 Single Crystals. In Proceedings of the Superalloys 1988 (Sixth International Symposium), Superalloys, Champion, PA, USA, 18–22 September 1988; pp. 285–294, ISBN 0-87339-076-8. [Google Scholar]
- Hirth, J.P.; Lothe, J. Theory of Dislocations, 2nd ed.; Wiley: New York, NY, USA, 1982; ISBN 0471091251. [Google Scholar]
- Konrad, C.H.; Brunner, M.; Kyrgyzbaev, K.; Völkl, R.; Glatzel, U. Determination of heat transfer coefficient and ceramic mold material parameters for alloy IN738LC investment castings. J. Mater. Process. Technol. 2011, 211, 181–186. [Google Scholar] [CrossRef]
- Cantor, B.; Chang, I.; Knight, P.; Vincent, A. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375–377, 213–218. [Google Scholar] [CrossRef]
- Andersson, J.-O.; Helander, T.; Höglund, L.; Shi, P.; Sundman, B. Thermo-Calc & DICTRA, computational tools for materials science. Calphad 2002, 26, 273–312. [Google Scholar] [CrossRef]
- Harris, K.; Wahl, J.B. Improved Single Crystal Superalloys, CMSX-4 (SLS)[La+Y] and CMSX-486. In Proceedings of the Superalloys 2004 (Tenth International Symposium), Seven Springs, PA, USA, 19–23 September 2004; pp. 45–52. [Google Scholar]
- Knobloch, C.; Saβ, V.; Siebörger, D.; Glatzel, U. Anisotropie creep behavior of a nickel-based superalloy compared with single phase nickel solid solution and γ′ phase single crystals. Mater. Sci. Eng. A 1997, 234–236, 237–241. [Google Scholar] [CrossRef]
- Völkl, R.; Fischer, B.; Beschliesser, M.; Glatzel, U. Evaluating strength at ultra-high temperatures—Methods and results. Mater. Sci. Eng. A 2008, 483–484, 587–589. [Google Scholar] [CrossRef]
- Brunner, M.; Bensch, M.; Völkl, R.; Affeldt, E.; Glatzel, U. Thickness influence on creep properties for Ni-based superalloy M247LC SX. Mater. Sci. Eng. A 2012, 550, 254–262. [Google Scholar] [CrossRef]
- Preußner, J.; Rudnik, Y.; Völkl, R.; Glatzel, U. Finite-element modelling of anisotropic single-crystal superalloy creep deformation based on dislocation densities of individual slip systems. Z. für Met. 2005, 96, 595–601. [Google Scholar] [CrossRef]
- Probst-Hein, M.; Dlouhy, A.; Eggeler, G. Interface dislocations in superalloy single crystals. Acta Mater. 1999, 47, 2497–2510. [Google Scholar] [CrossRef]
- Schleifer, F.; Holzinger, M.; Lin, Y.-Y.; Glatzel, U.; Fleck, M. Phase-field modeling of γ/γ″ microstructure formation in Ni-based superalloys with high γ″ volume fraction. Intermetallics 2020, 120, 106745. [Google Scholar] [CrossRef] [Green Version]
- Fleck, M.; Schleifer, F.; Holzinger, M.; Glatzel, U. Phase-Field Modeling of Precipitation Growth and Ripening During Industrial Heat Treatments in Ni-Base Superalloys. Met. Mater. Trans. A 2018, 49, 4146–4157. [Google Scholar] [CrossRef]
- Glatzel, U.; Müller, A. Neutron scattering experiments with a nickel base superalloy part I: Material and experiment. Scr. Metall. Et Mater. 1994, 31, 285–290. [Google Scholar] [CrossRef]
- Glatzel, U. Neutron scattering experiments with a nickel base superalloy part II: Analysis of intensity profiles. Scr. Metall. Et Mater. 1994, 31, 291–296. [Google Scholar] [CrossRef]
- Fleischmann, E.; Konrad, C.; Preußner, J.; Völkl, R.; Affeldt, E.; Glatzel, U. Influence of Solid Solution Hardening on Creep Properties of Single-Crystal Nickel-Based Superalloys. Met. Mater. Trans. A 2015, 46, 1125–1130. [Google Scholar] [CrossRef]
- Hemker, K.J.; Nix, W.D. High-temperature creep of the intermetallic alloy Ni3Al. Metall. Trans. 1993, 24, 335–341. [Google Scholar] [CrossRef]
- Preußner, J.; Rudnik, Y.; Brehm, H.; Völkl, R.; Glatzel, U. A dislocation density based material model to simulate the anisotropic creep behavior of single-phase and two-phase single crystals. Int. J. Plast. 2009, 25, 973–994. [Google Scholar] [CrossRef]
- Hoffman, R.E.; Pikus, F.W.; Ward, R.A. Self-Diffusion in Solid Nickel. J. Met. 1956, 8. [Google Scholar]
- Ardell, A.J.; Huang, J.C. Antiphase boundary energies and the transition from shearing to looping in alloys strengthened by ordered precipitates. Philos. Mag. Lett. 1988, 58, 189–197. [Google Scholar] [CrossRef]
- Mitra, S.K.; McLean, D. Cold Work and Recovery in Creep at Ostensibly Constant Structure. Met. Sci. J. 1967, 1, 192–198. [Google Scholar] [CrossRef]
- Drew, G.L.; Reed, R.C.; Kakehi, K.; Rae, C.M.F. Single Crystal Superalloys: The Transition from Primary to Secondary Creep. In Proceedings of the Superalloys 2004 (Tenth International Symposium), Seven Springs, PA, USA, 19–23 September 2004; pp. 127–136, ISBN 0-87339-576-X. [Google Scholar]


| in at.% | Group | Al | Ti | Cr | Mn | Fe | Co | Ni | Mo | Hf | Ta | W | Re |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ni | (A) | - | - | - | - | - | - | 100 | - | - | - | - | - |
| CrCoNi | (B) | - | - | 33 | - | - | 33 | 33 | - | - | - | - | - |
| Cantor | - | - | 20 | 20 | 20 | 20 | 20 | - | - | - | - | - | |
| matrixCMSX-3 | (C) | 3.1 | 0.1 | 21.4 | - | - | 20.3 | 51.1 | 0.9 | - | 0.1 | 3.0 | - |
| matrixCMSX-4 | 3.3 | 0.1 | 20.0 | - | - | 19.6 | 50.0 | 0.9 | - | 0.1 | 2.9 | 3.1 | |
| CMSX-3 | (D) | 12.4 | 1.3 | 9.1 | - | - | 4.7 | 67.6 | 0.3 | 0.05 | 2.0 | 2.6 | - |
| CMSX-4 | 12.6 | 1.3 | 7.7 | - | - | 9.9 | 62.8 | 0.4 | 0.05 | 2.2 | 2.1 | 1.0 |
| Alloy | Group | Phases | |
|---|---|---|---|
| Ni | (A) | single-phase fcc | 0.00 |
| CrCoNi | (B) | 1.10 | |
| Cantor | 1.61 | ||
| matrixCMSX-3 | (C) | 1.27 | |
| matrixCMSX-4 | 1.37 | ||
| CMSX-3 | (D) | two-phase fcc + L12 | 0.51 * |
| CMSX-4 | 0.41 * |
| Alloy | Group | Heat Treatment | Literature |
|---|---|---|---|
| Ni | (A) | - | |
| CrCoNi | (B) | ||
| Cantor | - | ||
| MatrixCMSX-3 MatrixCMSX-4 | (C) | 1290 °C/48 h | this work |
| CMSX-3 | (D) | 1293 °C/2 h + 1298 °C/3 h, cooling with > 100 °C/min, 1080 °C/4 h, 870 °C/20 h | [17] |
| CMSX-4 | 1320 °C/2 h, cooling with > 100 °C/min, 1140 °C/6 h, cooling with > 100 °C/min, 870 °C/20 h | [29] |
| Parameter | Value | |
|---|---|---|
| Elastic constants | γ-matrix | C11 = 210 GPa C12 = 160 GPa C44 = 90 GPa |
| γ′-phase | C11 = 200 GPa C12 = 140 GPa C44 = 100 GPa | |
| Lattice misfit | −2.2 × 10−3 | |
| Creep parameters at = 100 MPa | matrix CMSX-3 | = 2 × 10−3 s−1 n = 5.5 |
| matrix CMSX-4 | = 8 × 10−5 s−1 n = 5.5 | |
| Mass density | 8900 kg m−3 | |
| γ′ volume fraction | CMSX-3 | 60% |
| CMSX-4 | 70% | |
| Alloy | Norton Exponent | Stress in MPa to Reach a Steady-State Strain Rate of 10−7 s−1 | Extrapolated Life Time | |
|---|---|---|---|---|
| Ni | 5.2 | 7.5 | −1.2 | 2 s |
| CrCoNi | 5.8 | 22 | −3.2 | 3 min |
| Cantor | 5.1 | 8.4 | −1.5 | 3 s |
| MatrixCMSX-3 | 6.1 | 18 | −2.5 | 32 s |
| MatrixCMSX-4 | 5.6 | 30 | −4.1 | 21 min |
| CMSX-3 | 6.6 | 210 | −9.1 | 4 years |
| CMSX-4 | 12.5 | 260 | −12.3 | >6000 years |
| Stress Type | Estimated Internal Back Stress Contribution | Lateral Extension | Location | Remarks |
|---|---|---|---|---|
| solid solution strengthening | w, f0 unknown and r−3 dependence | very short range~r−3 | matrix | always active during plastic deformation as long as a continuous matrix exists |
| dislocation density | 250 MPa | const. | matrix | varies strongly locally, in exchange with misfit stress |
| misfit | 220 MPa | const. | matrix | varies strongly locally on two different length scales, in exchange with dislocation density, can be negative |
| Orowan | 500 MPa | const. | matrix | reduced during creep if coarsening occurs, increases with increasing dislocation density (apparent smaller separation of γ′ phase) |
| cutting | 600 MPa | const. | γ′ phase | constant within γ′ phase |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glatzel, U.; Schleifer, F.; Gadelmeier, C.; Krieg, F.; Müller, M.; Mosbacher, M.; Völkl, R. Quantification of Solid Solution Strengthening and Internal Stresses through Creep Testing of Ni-Containing Single Crystals at 980 °C. Metals 2021, 11, 1130. https://doi.org/10.3390/met11071130
Glatzel U, Schleifer F, Gadelmeier C, Krieg F, Müller M, Mosbacher M, Völkl R. Quantification of Solid Solution Strengthening and Internal Stresses through Creep Testing of Ni-Containing Single Crystals at 980 °C. Metals. 2021; 11(7):1130. https://doi.org/10.3390/met11071130
Chicago/Turabian StyleGlatzel, Uwe, Felix Schleifer, Christian Gadelmeier, Fabian Krieg, Moritz Müller, Mike Mosbacher, and Rainer Völkl. 2021. "Quantification of Solid Solution Strengthening and Internal Stresses through Creep Testing of Ni-Containing Single Crystals at 980 °C" Metals 11, no. 7: 1130. https://doi.org/10.3390/met11071130
APA StyleGlatzel, U., Schleifer, F., Gadelmeier, C., Krieg, F., Müller, M., Mosbacher, M., & Völkl, R. (2021). Quantification of Solid Solution Strengthening and Internal Stresses through Creep Testing of Ni-Containing Single Crystals at 980 °C. Metals, 11(7), 1130. https://doi.org/10.3390/met11071130






