Abstract
Molecular dynamic simulations of polyacrylic acid polyelectrolyte (PAA) analyzed its interaction with the main minerals that make up characteristic tailings of the mining industry, in this case, quartz, kaolinite, and montmorillonite. The simulations were carried out with the package Gromacs 2020.3. The interaction potentials used were General AMBER Force Field (GAFF) for PAA and CLAYFF-MOH for mineral surfaces. The SPC/E model described water molecules and Lennard-Jones 12-6 parameters adjusted for SPC/E model were used for Na+ and Cl− ions. The studied systems were carried out at pH 7, obtaining stable adsorption between the PAA and the studied surfaces. Interestingly, the strongest adsorptions were for montmorillonite at both low and high salt concentrations. The effect of salinity differs according to the system, finding that it impairs the absorption of the polymer on montmorillonite surfaces. However, a saline medium favors the interaction with quartz and kaolinite. This is explained because montmorillonite has a lower surface charge density and a greater capacity to adsorb ions. This facilitated the adsorption of PAA. It was possible to identify that the main interaction by which the polymer is adsorbed is through the hydroxyl of the mineral surface and the COO−Na+ complexes. Molecular dynamics allows us to advance in the understanding of interactions that define the behavior of this promising reagent as an alternative for sustainable treatment of complex tailings in highly saline environments.
1. Introduction
The large amount of waste generated annually is one of the main problems presented by the mining industry. Some researchers classify mineral waste as the second-largest impact of mining activity [1]. This amount will increase due to the massive exploitation of minerals that presents lower grades of valuable minerals, generating a negative impact on the environmental footprint and increasing the volume of mining waste (tailings) transported long distances before reaching the tailings deposits. Proper management of tailings is essential to ensure sustainability at an environmental, social, and economic level in mining, mainly in arid and semi-arid areas in Chile, Australia, and South Africa, where the expensive water resources are scarce [2,3].
Tailings management comprises two stages. The first seeks to recover and recirculate the processed water resource for upstream operations and concentrates the solid phase for disposal or elimination through gravity thickeners. These types of equipment use flocculating chemical reagents that induce a solid–liquid separation and subsequent settlement of the flocs, causing an increase in the sedimentation speed of the pulp and an improvement in the clarification of wastewater [4]. In the second stage, the thickened tailings are extracted from the thickener from a lower equipment cone. They are pumped through a pipe to the tailings storage facility, where the thickened solid is expected to continue to consolidate over time and possibly increase water recovery [5]. The high water content trapped in particle aggregates from conventional thickeners, the low solids compaction, and economic and environmental considerations, have generated interest in the use of paste thickeners. These thickeners can reach levels of percentage of solids greater than 70 wt%, increases water recovery, favors evaporation, minimizes storage volume, significantly reduces the risks in tailings deposits due to earthquakes, avoids the generation of acidic waters and leaching of metals, and notably reduces water loss due to infiltration [5,6]. However, the non-Newtonian behavior and the high yield stress of highly thickened slurries lead to a challenging discharge from the thickener underflow and make it challenging to transport tailings through the pipes through pumping [6,7,8].
Various studies have shown that rheology is significantly affected by salts, the presence of clays, and the content of fine minerals in the tailings [9,10,11,12,13]. Clays are fine solids ubiquitous in mineral processing, often only a few microns in diameter. They are challenging to separate from tailings and negatively impact most mineral-processing stages such as thickening and transport of tailings [9]. Depending on the response that clay surfaces present in the presence of water, they can be classified as swelling (for example, sodium montmorillonite) or non-swelling (for example, kaolinite). The kaolinite (Al2Si2O5(OH)4) comprises an octahedral sheet of aluminum hydroxide and a tetrahedral sheet of silica. This clay has two crystallographically different surfaces: the basal faces that have a negative charge throughout the pH range, and the edges, which vary in charge (negative or positive) with the variation of the pH as a response to the protonation or deprotonation of the groups aluminol (Al-OH) and silanol (Si-OH) in the exposed planes with hydroxyl termination. In response to their anisotropic structure and loading properties, clay sheets can associate in three different ways: face-face (FF), edge-edge (EE), and edge-face (EF) [14,15]. Montmorillonite with the composition MxAl3Si8O24H4Na⋅nH2O (Mx: Mg or Fe) comprises an octahedral sheet of alumina and two tetrahedral sheets of silica. The central layer contains octahedrally coordinated Al and Mg in oxides and hydroxides and is surrounded by two outer layers formed by tetrahedrally coordinated silicon oxides. Sodium montmorillonite shows a high degree of swelling in the presence of freshwater; however, in the presence of saline water, swelling decreases due to the excess of cations that reduce the electrostatic repulsion between the layers of the phyllosilicate, causing a decrease in the separation distance and preventing the entry of water molecules into the clay [16,17].
One of the main operational challenges of thickening paste is to reduce the rheological properties of the pulps at the exit of the thickeners. Common strategies used in the plant to deal with highly rheological tailings consider generally inefficient methods, such as dilution with water or pH modifications. The latter presents certain uncertainties when complex gangs do not present monotonous behaviors for pH. Another alternative is to use chemical reagents that alter the surface characteristics of the particles, promoting the action of repulsive forces, which cause dispersion. For example, Labanda and Llorens [18] showed that sodium polyacrylate could adhere to the Laponite surface and produce a steric barrier that prevents its agglomeration. Simultaneously, this anionic polyelectrolyte increased the net anionic charge of particles generating a greater electrostatic dispersion. The rheological consequence was a reduction of viscosity until an optimum polymer dose. Then, Robles et al. [19] analyzed the effect of low molecular weight sodium polyacrylate on kaolin pulps’ rheological behavior in the presence of seawater. They showed that the anionic polyacrylate considerably decreased the rheological parameters due to reducing the strength of the bonds between the particles through steric stabilization. At the same time, the effect of the polymer on electrostatic forces was not very significant. This resulted from the high presence of Na+ and Mg2+ counterions in seawater, which reduce the ionic atmosphere surrounding the colloidal particles’ surface. Subsequently, Jeldres et al. [20] studied the effect of anionic polyacrylate in synthetic quartz-kaolin and quartz-montmorillonite tailings in seawater by measuring yield stress and viscosity at pH 8. The authors showed that the yield stress of both tailings was reduced when dosing with the polymer of low molecular weight.
The complexity of the system creates difficulties when studying and quantifying effects rigorously. The current efforts have yielded valuable results to understand how to modify the rheology with polyacrylate species from polyacrylic acid (PAA) dispersant additives. In this case, computational tools have prompted the research to concisely describe the phenomena on a macroscopic scale. Several researchers have studied the interactions between additives and surfaces through molecular simulation [21,22]. Zhong et al. [23] have studied by simulation how to modify the quartz surface by aliphatic agents. Xu et al. [24] analyzed the adsorption of ammonium collectors on muscovite, describing the degree of hydrophobicity that can confer to the surface. Hao et al. [25] studied the interaction between starch and oleate on siderite, hematite, and quartz surfaces, obtaining responses from the activation and depression of the minerals. In the study in the thickening stage, it was possible to describe the effects of salt on the adsorption of hydrolyzed polyacrylamide flocculants (HPAM) on quartz [26]. The affinity of HPAM with minerals present in the copper tailings and with the presence of magnesium precipitate has recently been quantified [27], which demonstrated the detriment of this precipitate in thickening processes using conventional flocculants. Such studies have demonstrated the usefulness of molecular dynamics in describing phenomena related to mineral processing, helping to improve knowledge about the phenomena that intervene at the microscale and define the efficiency of operations.
This work focuses on understanding, through molecular dynamics, the mechanisms that determine the adsorption of sodium polyacrylate on the surface of minerals that generally constitute the tailings generated by the mining industry, in this case, quartz, kaolinite, and sodium montmorillonite. Considering the potential uses offered by this reagent in highly saline media, the influence of sodium chloride on the adsorption mechanisms and on the relevant functional groups to generate stable adsorption is analyzed.
2. Theoretical Background
Computational advances have allowed the implementation of theoretical physics in complex systems, for example, particle systems on a molecular scale [28]. One of the most widely used techniques is molecular dynamics (MD) [29], which uses Newton’s equations considering spherical particles (Figure 1). Newton’s second law indicates that an applied force generates an acceleration to the particles, translated into velocity and motion.
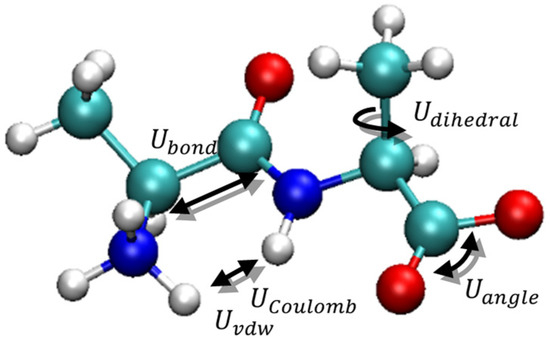
Figure 1.
Schematic representation of equations used in MD for a particular molecule.
The applied force is derived from an energy potential constructed from intramolecular and intermolecular interactions (Figure 1) for each atom in established functional groups.
The literature offers various models to describe force fields chosen depending on the system’s characteristics [29]. Some of these force fields are AMBER [30], OPLS [31], GROMOS [32], INTERFACEFF [33], CLAYFF [34], CFF [35], and COMPASS [36]. This made it possible to complement experimental methodologies with simulations at a molecular scale and explain the underlying phenomenology. Then, the more reliable the force fields become, the better the description of physical phenomena from MD, complementing or even replacing experimental methods when these are expensive and difficult to implement.
The MD simulations are performed numerically, so the proper control of the propagation of numerical errors is imperative to avoid statistically ambiguous simulations. For this, the Newton’s equations require the implementation of integration methods that conserve the system’s energy and are known as symplectic [37,38]. For this, it is also necessary to consider the integration steps of the integrated equations; a correct time step preserves the trajectory of the particles and conserves the associated energy. It is essential to include variations in the energy of the atoms when one has an interest in studying systems at constant temperature or pressure, which can modify the position of the particles and disturb the conserved energy. Therefore, one of the precautions is to implement thermostats that minimize these disturbances. The best-known thermostats include Berendsen [39] or Nose-Hoover [40]. MD simulations do not generally consider chemical reactions, but advances in this area, such as ReaxFF, allow the creation or breaking of bonds. Such details show that carrying out MD simulations requires a robust methodology to represent natural systems as correctly as possible.
3. Materials and Methods
Molecular dynamics simulations were used to determine the adsorption of PAA on electrically charged mineral surfaces in NaCl solutions. Representations of the polymer and the quartz and kaolinite are based on recent work available in the literature [26,41,42,43], and therefore the main details are reproduced here. In this work, we include a montmorillonite slab taken from a pyrophyllite structure where substitutions are placed in the silica and alumina atoms creating a montmorillonite structure with a chemical formula of Na0.75[Si7.75Al0.25][Al3.5Mg0.5]O20(OH)4 [44,45]. We choose for d-spacing of 1.2 nm for montmorillonite as shown in the X-ray diffraction data [46]. The unit cell for kaolinite is (a, b, c, α, β, γ) = (5.148, 7.153, 8.920, 90, 90, 72.2) and the supercell was 16 × 12 × 2 with a surface area of 67.45 nm2. For montmorillonite the unit cell is (a, b, c, α, β, γ) = (5.180, 15.00, 8.98, 90, 90, 90) and the supercell is 16 × 6 × 2 with a surface area of 74.59 nm2. For quartz the unit cell is (a, b, c, α, β, γ) = (4.916, 13.757, 5.4057, 141.8, 90, 90) and the supercell is 16 × 6 × 4 with a surface area of 64.92 nm2. The z dimension was extended up to 10 nm to add the salt solution with PAA. A 72-monomer PAA polymer chain was placed between the mineral surfaces. The monomers are hydrolyzed in the form of acrylate (-CH2-CHCOO−). Then, SPC/E water molecules and Na+ and Cl− ions were placed between the two mineral surfaces avoiding overlap between them and the PAA polymer. The NaCl concentration was 0.06 and 0.6 M, which range from a brackish water to seawater conditions (for details see Table S11 in the Supplementary Materials). The temperature was 300 K always, and the pH was 7.
At this pH quartz, montmorillonite and kaolinite are deprotonated. Quartz is negatively charged at pH > 2 [47], for kaolinite, the edge surface is negatively charged at pH > 4.6 [48], and the edge of the montmorillonite surface is negatively charged at pH > 3.2 [49]. In this work, quartz (010), montmorillonite (010), and kaolinite (010) surfaces were used, the first being the most recurrent cleavages [48,50] and the clays ones for being the most reactive of kaolinite [43]. Corresponding charge densities at −0.051 C/m2 for montmorillonite [49], −0.03 C/m2 for quartz [50], and −0.115 C/m2 for kaolinite [48]. We proceeded as Kroutil et al. [50] based on the DFT calculations [42,43,51]. The polymer has a pKa of 3.5–4, and thus, the degree of ionization is 100% at pH ≥ 6. This means that COOH groups are charged like COO− at pH 7.
Computer simulations were carried out with the package Gromacs 2020.3. The interaction potentials used were GAFF with antechamber package for PAA, [52,53,54] CLAYFF-MOH for mineral surfaces [34,55], the SPC/E water model [56] constrained with Settle [57] to describe water, and for the Na+ and Cl− ions, Lennard-Jones 12-6 parameters derived from Li et al. [58] were used adjusted to the SPC/E water model. The similarity of these potentials facilitates their use together. Partial charge of PAA was used as previous work with HPAM [41]. All parameters used in this work are presented in Tables S1–S10 (see the Supplementary Materials). The particle mesh Ewald method (PME) was used to compute the long-range interactions [59]. An initial energy minimization step was performed by the steepest descent method. This step was followed by (i) a constant particle, volume, and temperature (NVT) simulation of 1 ns to generate corresponding hydration layers, and ions remained at fixed positions, and (ii) a constant particle, pressure, and temperature (NPT) step of 2 ns, initially using annealing with a temperature increase from 300 K to 430 K during 250 ps and then a temperature drop to 300 K, thus eliminating metastable PAA configurations. Finally, an NVT simulation of 80 ns was used to generate the results. The integration step is 2 fs, and the constants of the thermostat and barostat of modified Berendsen were 0.1 and 2.0 ps, respectively [60].
4. Results
4.1. Surface Adsorption of PAA and Ions
The computational simulation was used to analyze PAA interaction on quartz, kaolinite, and montmorillonite surfaces. This is achieved by counting the effective atomic interactions between the surface and the polymer, mainly the hydrogen bonds and the interactions mediated by the ions present in the water as cationic bridges. Then, the adsorption was quantified by summing all interactions, averaged over the simulation with six repetitions. Then, the average surface adsorption was calculated.
The experiments were carried out at pH 7 considering two concentrations of sodium chloride (0.06 M and 0.6 M). The surface charge densities at this pH are −0.051 C/m2 for montmorillonite, −0.03 C/m2 for quartz, and −0.115 C/m2 for kaolinite. Figure 2 shows negligible adsorption of the polymer in both kaolinite and quartz at low salinity, with values lower than 0.001 nm−2 in both cases. On the other hand, the adsorption of the polymer on montmorillonite is very different, presenting surface adsorption of ~0.12 nm−2. When the salinity increases to 0.6 M, the adsorption of kaolinite and quartz increases, more significant in kaolinite with ~0.02 nm−2 and then quartz with ~0.004 nm−2. At the same time, montmorillonite decreases to ~0.03 nm−2, even so, higher than kaolinite and quartz. Jeldres et al. [20] applied sodium polyacrylate to modify the rheological properties of synthetic tailings composed of mixtures of quartz and clays prepared in seawater. The authors found that a tailing containing montmorillonite requires lower dosages to reduce the yield stress value by 63.2%, compared to tailings containing kaolinite. It is then possible that the results are linked to better adsorption of the polymer on the montmorillonite surface. Interestingly, the effect of salts enhances the adsorption of PAA on quartz and kaolinite, while the opposite occurs in montmorillonite.
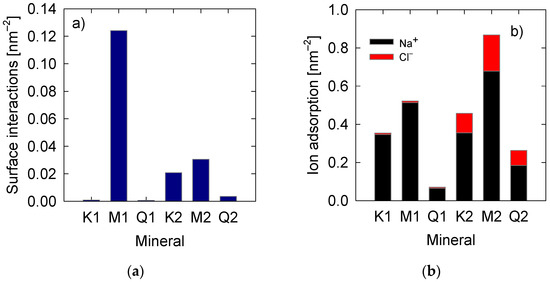
Figure 2.
Surface adsorption of (a) PAA and (b) Na+ and Cl− on kaolinite (K), montmorillonite (M) and quartz (Q). K1, M1, and Q1 are at 0.06 M salt concentration. K2, M2, and Q2 are at 0.6 M salt concentration.
The adsorption of Na+ and Cl− ions were quantified (see Figure 2b) as counting the ions by a cutoff radius defined as the first layer in the radial distribution functions (RDF) between surface oxygen and sodium ions (Figure S1 in the Supplementary Materials). A trend similar to PAA obtained appears since the adsorption decreases in montmorillonite > kaolinite > quartz. Increasing salinity generates changes that depend on the mineral. For kaolinite, there is a slight increase in Na+ adsorption, suggesting saturation of these cations. On the other hand, Cl− adsorption increases with increasing salt concentration. The adsorption on the surface of montmorillonite increases both in cations and anions, demonstrating the strong adsorption capacity of this mineral [61]. Quartz also shows a significant increase in adsorbed ions. The quartz surface has adsorption capacity, but it is hampered by its low charge density that does not attract the ions effectively. Only at high concentrations is it possible to generate effective adsorption.
4.2. PAA-Mineral Interactions
The results shown in Figure 2a allow us to classify the surface interactions into hydrogen bond or cationic bridges, considering the atoms present in the effective interactions [27]. PAA has only deprotonated oxygens (PO) that allow hydrogen and ionic bridge-type interactions. For mineral surfaces, there are mainly hydroxyl groups (OH) and deprotonated oxygens (OM), and oxygens (OS) appear only on quartz surface.
The interactions were calculated with a specific cutoff radius. In the case of hydrogen bond, the equilibrium distances from the literature were followed [62] where they were used as criteria to identify the hydrogen bond, these are between 0.24 and 0.3 nm for donor–acceptor distance. We use this interval to identify the hydrogen bond in our simulation.
In the case of cationic bridges, to determine this bridge, cutting radii related to the first layer in the RDFs are used between sodium–oxygens of the PAA molecules and sodium–oxygens of the surfaces (see Figure S1 in the Supplementary Materials), as has been done in previous works [41].
The classification of the interactions is shown in Figure 3. Hydrogen bonds between OM and OP are possible for kaolinite and montmorillonite because deprotonated oxygens have hydrogen-bonded as AlOH− [43,63]. When observing the hydrogen bond between the mineral surface and the PAA (Figure 3a), it is observed that, in general, their interaction is very slight. This implies that these types of interactions do not represent the primary mechanisms by which PAA is adsorbed. Montmorillonite surfaces produce most hydrogen bonds in low salinity water and kaolinite in saline water. The cationic bridge interactions are the primary PAA adsorption mechanism because the polymer has only charged groups, which generate a high affinity for forming COO−Na+ complexes, as has already been observed in previous works [26,64].
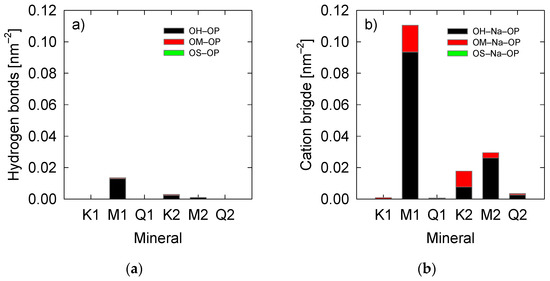
Figure 3.
PAA-mineral interactions (a) hydrogen bond and (b) cation bridging. K1, M1, and Q1 are at 0.06 M salt concentration. K2, M2, and Q2 are at 0.6 M salt concentration. OP: deprotonated PAA oxygen, OH: hydroxide oxygen, OM: deprotonated kaolinite oxygen, OS: surface neutral oxygen.
According to Figure 3b, the primary type of cationic bridge is OH-Na-OP, then OM-Na-OP, and almost zero interactions of the OS-Na-OP type are observed. The more significant interaction by OH-type oxygens is the product of two reasons: (i) There is a higher density of these sites; and (ii) partial charges of the OH-type are less negative than the OM-type. Therefore, they have a higher affinity for COO−Na+ complexes than sodium ions alone. In the case of OS-type oxygens, they only exist in quartz and do not interact with the COO−Na+ complexes.
4.3. PAA Adsorbed Conformation
This section analyzes the conformation that PAA acquires when it is adsorbed on the surfaces of the different minerals. First, the train, tails, and loops conformation was quantified [65] to determine later their fraction concerning the total carbon atoms of the main chain. These results are summarized in Figure 4. At low salt concentration (0.06 M), kaolinite has a higher proportion of the main chain as tails, showing a quiet presence of loops and trains. This is expected considering the low adsorption that the polymer has on the mineral surface, but as salinity increases (0.6 M), the number of loops increases, keeping the trains practically constant. This means that the molecule has a higher affinity and is more attracted to the surface. PAA considerably increases its proportion of loops and trains configurations on montmorillonite surfaces to 0.06 M, clearly responding to the higher affinity that the polymer has on this mineral compared to that obtained on kaolinite and quartz. Such effects are diminished with increasing salinity, as is the trend is shown in the results of Figure 2a. Finally, the behavior of the polymer on the surface of quartz is similar to that obtained on kaolinite. There is a larger formation of loops, both at low and high salts in the solution. Although quartz adsorbs less PAA than the other cases, its topology helps the polymer form more widely spaced interactions, increasing their loops.
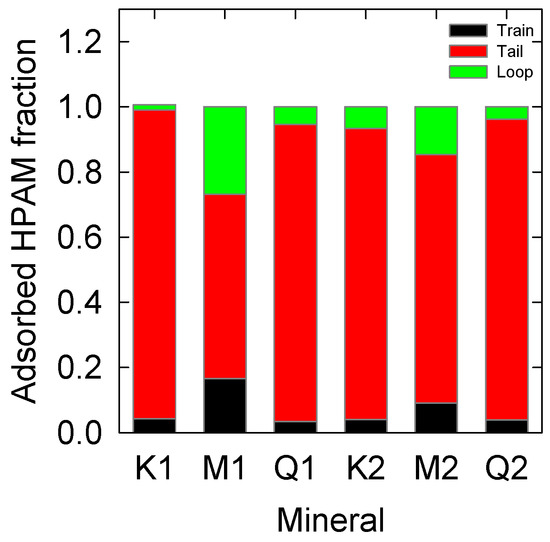
Figure 4.
PAA conformation on kaolinite (K), montmorillonite (M) and quartz (Q). K1, M1, and Q1 are at 0.06 M salt concentration. K2, M2, and Q2 are at 0.6 M salt concentration.
The discussed results are supported by simulated top and side view images of the conformation of adsorbed PAA on the different surfaces (Figure 5). For kaolinite and quartz, a snapshot simulation was used at 0.6 M and for montmorillonite at 0.06 M because these conditions generate greater polymer adsorption on each mineral. Simulation snapshots were selected that were representative of the simulation, that is, they had values of train, tail, and loop close to those obtained on average. For kaolinite, it is observed that a large part of the chain is exposed to the medium, and a low portion is actually adsorbed on the surface. This effect can be generated by the high density of PAA and kaolinite active sites, making effective adsorption difficult. The d-spacing separates the active sites of montmorillonite, improving its interaction with PAA, increasing loops and tails configurations. Even with the 1.2-nm d-spacing used, the polymer cannot internally adsorb in the montmorillonite, as sodium cations do. Finally, the quartz shows that the adsorption is low, and a portion of the chain is in the vicinity of the surface. This may imply that the polymer has an affinity with the surface but not enough to be adsorbed because it does not have surface sites strong enough to generate effective contact.
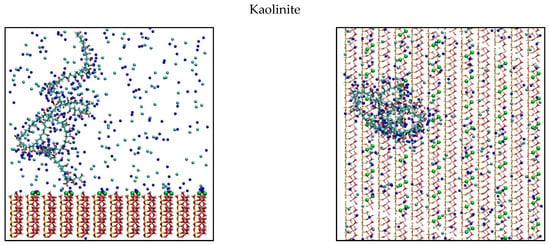
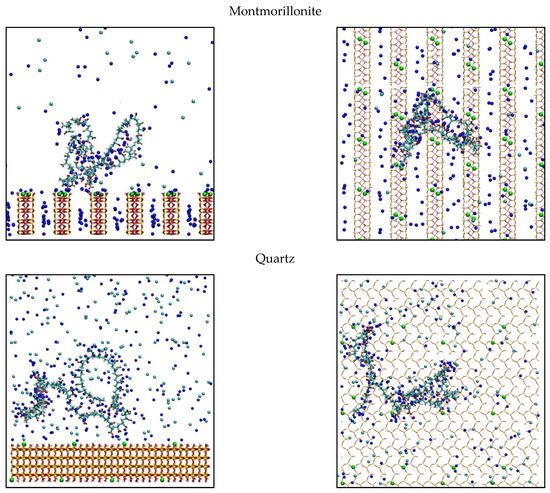
Figure 5.
Snapshot of PAA adsorbed configuration onto kaolinite, montmorillonite, and quartz. Green spheres represent charged sites in the mineral surfaces, blue and cyan spheres are the Na+ and Cl− ions. Left: side view, Right: top view. Water is not shown for visibility.
5. Conclusions
Molecular dynamics simulations are performed to study PAA interaction on mineral surfaces of quartz, kaolinite, and montmorillonite, commonly found in tailings generated in the mining industry. This study shows that PAA can be adsorbed on clay surfaces better than on quartz, especially on montmorillonite surfaces, due to the greater d-spacing between the sheets that compose it. By increasing the spacing, the strong active sites of the montmorillonite are further separated allowing a better anchoring of the PAA on the surface. The results showed that the primary adsorption mechanism in all cases was through the hydroxyl groups on the surface and the carboxylic groups of PAA mediated by a sodium cation. The hydroxyl groups have a lower charge density, which is suitable for the COO−Na+ complex to be adsorbed. Effective adsorption of PAA on kaolinite surfaces was also found, but it is lower than in montmorillonite, given the higher density of sites it has. Finally, the adsorption of PAA on quartz is low because its active sites are weak and of low surface density, which prevents effective contact with PAA.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/met11060987/s1. Figure S1: Average radial distribution function of cation reference to an oxygen from PAA and oxygen type from the three surfaces, Table S1: Nonbonded Lennar Jones parameters, Table S2: Bond parameters, harmonic function for PAA, morse function for Surfaces, Table S3: Angle parameters, harmonic function, Table S4: Torsion parameters, RB function, Table S5: Planar torsion parameters, cosine function, Table S6: PAA partial charges, Table S7: Kaolinite partial charges for individual cells (supercell 16x12x2 (384)), Table S8: Montmorillonite partial charges for individual cells (supercell 16x6x2 (192)), Table S9: Quartz partial charges for individual cells (supercell 16x6x4 (384)), Table S10: DFT-NBO corrections of deprotonated atoms, Table S11: Number of cations, anions and water molecules for all systems. The reported volume excludes the slab mineral volume. (c.i. means counterion).
Author Contributions
Conceptualization, R.I.J. and S.N.; methodology, G.R.Q.; software, G.R.Q.; validation, R.I.J., E.P. and S.N.; formal analysis, E.G., P.R. and C.M.; investigation, S.N.; resources, P.R.; data curation, E.G.; writing—original draft preparation, G.R.Q.; writing—review and editing, R.I.J. and S.N.; visualization, R.I.J.; supervision, R.I.J.; funding acquisition, P.R. and C.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by ANID/FONDAP/15130015.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
G.R.Q. and R.I.J. thank Centro CRHIAM Project ANID/FONDAP/15130015. G.R.Q. thanks ANID FONDECYT 3200978 and The Southern GPU-cluster (SGPUC) UDEC funded by FONDEQUIP EQM150134 for computational support. S.N. acknowledges the infrastructure and support of the Programa de Doctorado en Ingeniería de Procesos de Minerales of the Universidad de Antofagasta. P.R. thanks the Pontificia Universidad Católica de Valparaíso for the support provided.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kulczycka, J. LCA for Minimisation of Environmental Impact of Wastes from Zinc and Lead Industry; Polish Academy of Sciences, Mineral and Energy Economy Research Institute: Krakow, Poland, 2008. [Google Scholar]
- Northey, S.A.; Mudd, G.M.; Werner, T.T.; Jowitt, S.M.; Haque, N.; Yellishetty, M.; Weng, Z. The exposure of global base metal resources to water criticality, scarcity and climate change. Glob. Environ. Chang. 2017, 44, 109–124. [Google Scholar] [CrossRef]
- Cisternas, L.A.; Gálvez, E.D. The use of seawater in mining. Miner. Process. Extr. Metall. Rev. 2018, 39, 18–33. [Google Scholar] [CrossRef]
- Kane, J.C.; la Mer, V.K.; Linford, H.B. The effect of solid content on the adsorption and flocculation behavior of silica suspensions. J. Phys. Chem. 1964, 68, 3539–3544. [Google Scholar] [CrossRef]
- De Kretser, R.; Scales, P.J.; Boger, D.V. Improving clay-based tailings disposal: Case study on coal tailings. AIChE J. 1997, 43, 1894–1903. [Google Scholar] [CrossRef]
- Wang, C.; Harbottle, D.; Liu, Q.; Xu, Z. Current state of fine mineral tailings treatment: A critical review on theory and practice. Miner. Eng. 2014, 58, 113–131. [Google Scholar] [CrossRef]
- Boger, D.V. Rheology of slurries and environmental impacts in the mining industry. Annu. Rev. Chem. Biomol. Eng. 2013, 4, 239–257. [Google Scholar] [CrossRef]
- Jones, R.L.; Horsley, R.R. Viscosity modifiers in the mining industry. Miner. Process. Extr. Metall. Rev. 2000, 20, 215–223. [Google Scholar] [CrossRef]
- Franks, G.V. Zeta potentials and yield stresses of silica suspensions in concentrated monovalent electrolytes: Isoelectric point shift and additional attraction. J. Colloid Interface Sci. 2002, 249, 44–51. [Google Scholar] [CrossRef] [PubMed]
- Jeldres, R.I.; Piceros, E.C.; Wong, L.S.; Leiva, W.H.; Herrera, N.; Toledo, P.G. Dynamic moduli of flocculated kaolinite sediments: Effect of salinity, flocculant dose, and settling time. Colloid Polym. Sci. 2018, 296, 1935–1943. [Google Scholar] [CrossRef]
- Jeldres, R.I.; Piceros, E.C.; Leiva, W.H.; Toledo, P.G.; Herrera, N. Viscoelasticity and yielding properties of flocculated kaolinite sediments in saline water. Colloids Surf. A Physicochem. Eng. Asp. 2017, 529, 1009–1015. [Google Scholar] [CrossRef]
- Romero, C.P.; Jeldres, R.I.; Quezada, G.R.; Concha, F.; Toledo, P.G. Zeta potential and viscosity of colloidal silica suspensions: Effect of seawater salts, pH, flocculant, and shear rate. Colloids Surf. A Physicochem. Eng. Asp. 2018, 538, 210–218. [Google Scholar] [CrossRef]
- Quezada, G.R.; Jeldres, R.I.; Goñi, C.; Toledo, P.G.; Stickland, A.D.; Scales, P.J. Viscoelastic behaviour of flocculated silica sediments in concentrated monovalent chloride salt solutions. Miner. Eng. 2017, 110. [Google Scholar] [CrossRef]
- Hong, E.; Herbert, C.M.; Yeneneh, A.M.; Sen, T.K. Rheological characteristics of mixed kaolin–sand slurry, impacts of pH, temperature, solid concentration and kaolin–sand mixing ratio. Int. J. Environ. Sci. Technol. 2016, 13, 2629–2638. [Google Scholar] [CrossRef]
- Ndlovu, B.; Becker, M.; Forbes, E.; Deglon, D.; Franzidis, J.P. The influence of phyllosilicate mineralogy on the rheology of mineral slurries. Miner. Eng. 2011, 24, 1314–1322. [Google Scholar] [CrossRef]
- Elmashad, M.E.; Ata, A.A. Effect of seawater on consistency, infiltration rate and swelling characteristics of montmorillonite clay. HBRC J. 2015, 12, 175–180. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.F.; Zhang, Q.H.; Maa, J.P.Y. Coagulation processes of kaolinite and montmorillonite in calm, saline water. Estuar. Coast. Shelf Sci. 2018, 202, 18–29. [Google Scholar] [CrossRef]
- Labanda, J.; Llorens, J. Influence of sodium polyacrylate on the rheology of aqueous Laponite dispersions. J. Colloid Interface Sci. 2005, 289, 86–93. [Google Scholar] [CrossRef]
- Robles, P.; Piceros, E.; Leiva, W.H.; Valenzuela, J.; Toro, N.; Jeldres, R.I. Analysis of sodium polyacrylate as a rheological modifier for kaolin suspensions in seawater. Appl. Clay Sci. 2019. [Google Scholar] [CrossRef]
- Jeldres, M.; Robles, P.; Toledo, P.G.; Saldaña, M.; Quezada, L.; Jeldres, R.I. Improved dispersion of clay-rich tailings in seawater using sodium polyacrylate. Colloids Surf. A Physicochem. Eng. Asp. 2021, 612. [Google Scholar] [CrossRef]
- Costa, D.; Savio, L.; Pradier, C.M. Adsorption of amino acids and peptides on metal and oxide surfaces in water environment: A synthetic and prospective review. J. Phys. Chem. B 2016, 120, 7039–7052. [Google Scholar] [CrossRef]
- Ozboyaci, M.; Kokh, D.B.; Corni, S.; Wade, R.C. Modeling and simulation of protein-surface interactions: Achievements and challenges. Q. Rev. Biophys. 2016, 49. [Google Scholar] [CrossRef] [Green Version]
- Zhong, J.; Wang, P.; Zhang, Y.; Yan, Y.; Hu, S.; Zhang, J. Adsorption mechanism of oil components on water-wet mineral surface: A molecular dynamics simulation study. Energy 2013, 59, 295–300. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, Y.L.; Liu, G.S. Molecular dynamics simulation of primary ammonium ions with different alkyl chains on the muscovite (001) surface. Int. J. Miner. Process. 2015. [Google Scholar] [CrossRef]
- Hao, H.; Li, L.; Yuan, Z.; Liu, J. Molecular arrangement of starch, Ca2+ and oleate ions in the siderite-hematite-quartz flotation system. J. Mol. Liq. 2018, 254, 349–356. [Google Scholar] [CrossRef]
- Quezada, G.R.; Jeldres, R.I.; Fawell, P.D.; Toledo, P.G. Use of molecular dynamics to study the conformation of an anionic polyelectrolyte in saline medium and its adsorption on a quartz surface. Miner. Eng. 2018, 129. [Google Scholar] [CrossRef]
- Quezada, G.R.; Jeldres, M.; Toro, N.; Robles, P.; Toledo, P.G.; Jeldres, R.I. Understanding the flocculation mechanism of quartz and kaolinite with polyacrylamide in seawater: A molecular dynamics approach. Colloids Surf. A Physicochem. Eng. Asp. 2021, 608, 125576. [Google Scholar] [CrossRef]
- Alder, B.J.; Wainwright, T.E. Studies in molecular dynamics. I. General method. J. Chem. Phys. 1959, 31, 459–466. [Google Scholar] [CrossRef] [Green Version]
- Hollingsworth, S.A.; Dror, R.O. Molecular dynamics simulation for all. Neuron 2018, 99, 1129–1143. [Google Scholar] [CrossRef] [Green Version]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef] [Green Version]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Scott, W.R.P.; Hünenberger, P.H.; Tironi, I.G.; Mark, A.E.; Billeter, S.R.; Fennen, J.; Torda, A.E.; Huber, T.; Krüger, P.; van Gunsteren, W.F. The GROMOS biomolecular simulation program package. J. Phys. Chem. A 1999, 103, 3596–3607. [Google Scholar] [CrossRef]
- Heinz, H.; Lin, T.J.; Kishore Mishra, R.; Emami, F.S. Thermodynamically consistent force fields for the assembly of inorganic, organic, and biological nanostructures: The INTERFACE force field. Langmuir 2013, 29, 1754–1765. [Google Scholar] [CrossRef]
- Cygan, R.T.; Liang, J.J.; Kalinichev, A.G. Molecular models of hydroxide, oxyhydroxide, and clay phases and the development of a general force field. J. Phys. Chem. B 2004, 108, 1255–1266. [Google Scholar] [CrossRef]
- Rasmussen, K.J.; Engelsen, S.B.; Fabricius, J.; Rasmussen, B. The consistent force field: Development of potential energy functions for conformational analysis. In Recent Experimental and Computational Advances in Molecular Spectroscopy; Springer: Dordrecht, The Netherlands, 1993; pp. 381–419. [Google Scholar]
- Sun, H. Compass: An ab initio force-field optimized for condensed-phase applications—Overview with details on alkane and benzene compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Gray, S.K.; Noid, D.W.; Sumpter, B.G. Symplectic integrators for large scale molecular dynamics simulations: A comparison of several explicit methods. J. Chem. Phys. 1998, 101, 4062. [Google Scholar] [CrossRef] [Green Version]
- Verlet, L. Computer “experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phys. Rev. 1967. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; Dinola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Evans, D.J.; Holian, B.L. The Nose-Hoover thermostat. J. Chem. Phys. 1985, 83, 4069–4074. [Google Scholar] [CrossRef]
- Quezada, G.R.; Saavedra, J.H.; Rozas, R.E.; Toledo, P.G. Molecular dynamics simulations of the conformation and diffusion of partially hydrolyzed polyacrylamide in highly saline solutions. Chem. Eng. Sci. 2019. [Google Scholar] [CrossRef]
- Quezada, G.R.; Rozas, R.E.; Toledo, P.G. Molecular dynamics simulations of quartz (101)-water and corundum (001)-water interfaces: Effect of surface charge and ions on cation adsorption, water orientation, and surface charge reversal. J. Phys. Chem. C 2017, 121. [Google Scholar] [CrossRef]
- Quezada, G.R.; Rozas, R.E.; Toledo, P.G. Ab initio calculations of partial charges at kaolinite edge sites and molecular dynamics simulations of cation adsorption in saline solutions at and above the pH of zero charge. J. Phys. Chem. C 2019, 123. [Google Scholar] [CrossRef]
- Li, Q.; Lu, X.; Zhang, L.; Cheng, Y.; Liu, X. Molecular simulation of interlayer cation exchange of montmorillonite. J. Nanjing Univ. 2019, 55, 879–887. [Google Scholar] [CrossRef]
- Rahromostaqim, M.; Sahimi, M. Molecular dynamics simulation of hydration and swelling of mixed-layer clays. J. Phys. Chem. C 2018, 122, 14631–14639. [Google Scholar] [CrossRef]
- Viani, A.; Gualtieri, A.F.; Artioli, G. The nature of disorder in montmorillonite by simulation of X-ray powder patterns. Am. Mineral. 2002, 87, 966–975. [Google Scholar] [CrossRef]
- Goloub, T.P.; Koopal, L.K.; Bijsterbosch, B.H.; Sidorova, M.P. Adsorption of cationic surfactants on silica. Surface charge effects. Langmuir 1996, 12, 3188–3194. [Google Scholar] [CrossRef]
- Gupta, V.; Hampton, M.A.; Stokes, J.R.; Nguyen, A.V.; Miller, J.D. Particle interactions in kaolinite suspensions and corresponding aggregate structures. J. Colloid Interface Sci. 2011, 359, 95–103. [Google Scholar] [CrossRef] [PubMed]
- Sperry, J.M.; Peirce, J.J. Ion exchange and surface charge on Montmorillonite clay. Water Environ. Res. 1999. [Google Scholar] [CrossRef]
- Kroutil, O.; Chval, Z.; Skelton, A.A.; Předota, M. Computer simulations of quartz (101)-water interface over a range of pH values. J. Phys. Chem. C 2015, 119, 9274–9286. [Google Scholar] [CrossRef]
- Quezada, G.R.; Toledo, P.G. Structure of the interface between lithium-rich spodumene and saltwater by density functional theory calculations and molecular dynamics simulations. J. Phys. Chem. C 2019, 124, 1446–1457. [Google Scholar] [CrossRef]
- Mintis, D.G.; Mavrantzas, V.G. Effect of pH and molecular length on the structure and dynamics of short poly(acrylic acid) in dilute solution: Detailed molecular dynamics study. J. Phys. Chem. B 2019, 123, 4204–4219. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef]
- Pouvreau, M.; Greathouse, J.A.; Cygan, R.T.; Kalinichev, A.G. Structure of hydrated gibbsite and brucite edge surfaces: DFT results and further development of the ClayFF classical force field with Metal-O-H angle bending terms. J. Phys. Chem. C 2017, 121, 14757–14771. [Google Scholar] [CrossRef] [Green Version]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Miyamoto, S.; Kollman, P.A. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
- Li, P.; Song, L.F.; Merz, K.M. Systematic parameterization of monovalent ions employing the nonbonded model. J. Chem. Theory Comput. 2015, 11, 1645–1657. [Google Scholar] [CrossRef] [PubMed]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baker, M.L.; Baas, J.H.; Malarkey, J.; Jacinto, R.S.; Craig, M.J.; Kane, I.A.; Barker, S. The effect of clay type on the properties of cohesive sediment gravity flows and their deposits. J. Sediment. Res. 2017, 87, 1176–1195. [Google Scholar] [CrossRef] [Green Version]
- Minch, M.J. An Introduction to Hydrogen Bonding (Jeffrey, George A.); Oxford University Press Inc.: New York, NY, USA, 1999; Volume 76, ISBN 0195095499. [Google Scholar]
- Zeitler, T.R.; Greathouse, J.A.; Cygan, R.T.; Fredrich, J.T.; Jerauld, G.R. Molecular dynamics simulation of resin adsorption at kaolinite edge sites: Effect of surface deprotonation on interfacial structure. J. Phys. Chem. C 2017. [Google Scholar] [CrossRef]
- Quezada, G.R.; Rozas, R.E.; Toledo, P.G. Polyacrylamide adsorption on (1 0 1) quartz surfaces in saltwater for a range of pH values by molecular dynamics simulations. Miner. Eng. 2021, 162, 106741. [Google Scholar] [CrossRef]
- Scheutjens, J.M.H.M.; Fleer, G.J. Statistical theory of the adsorption of interacting chain molecules. 2. Train, loop, and tail size distribution. J. Phys. Chem. 1980, 84, 178–190. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).