A Ternary Map of Ni–Mn–Ga Heusler Alloys from Ab Initio Calculations
Abstract
1. Introduction
2. Computational Methodology
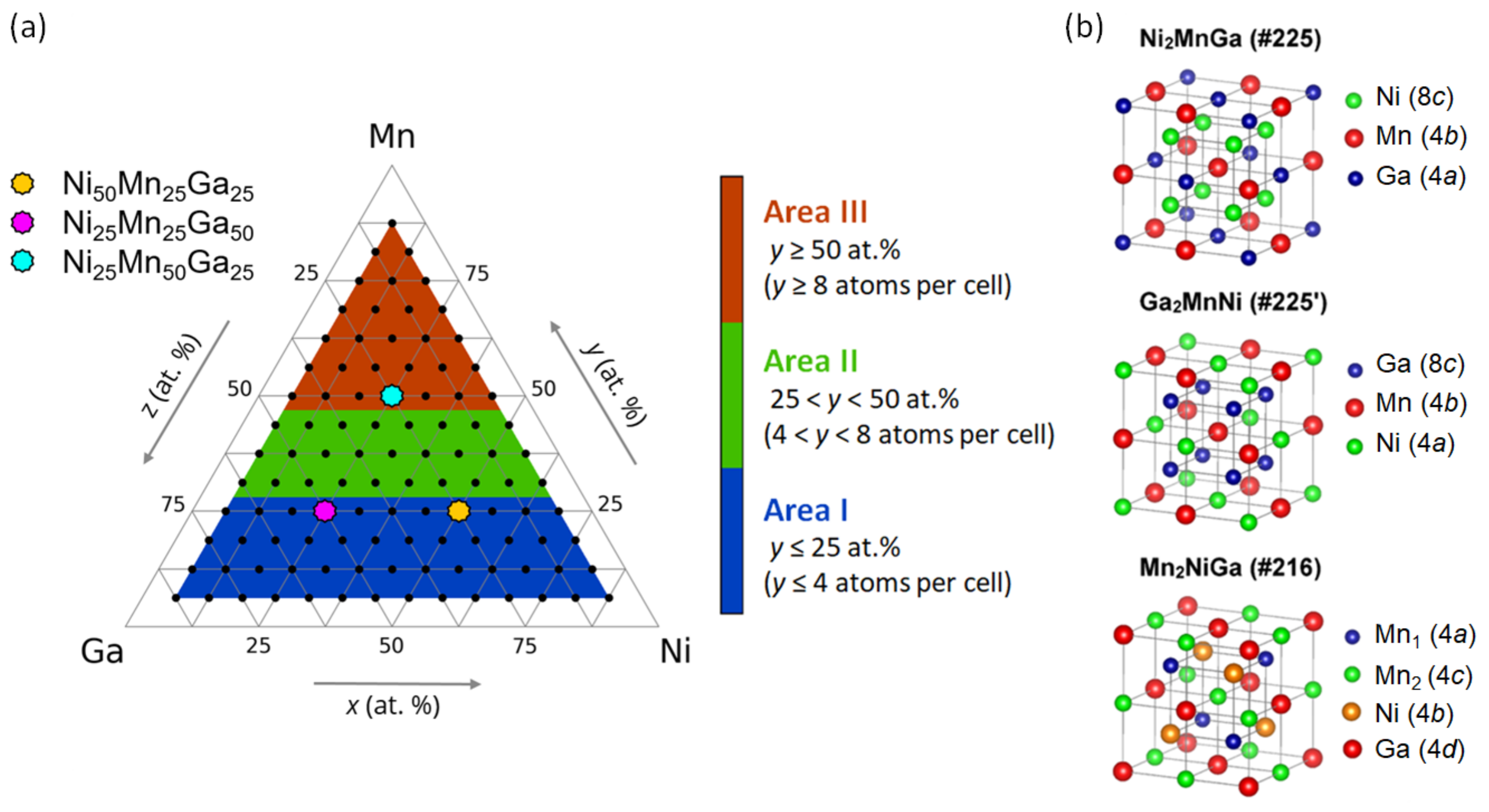
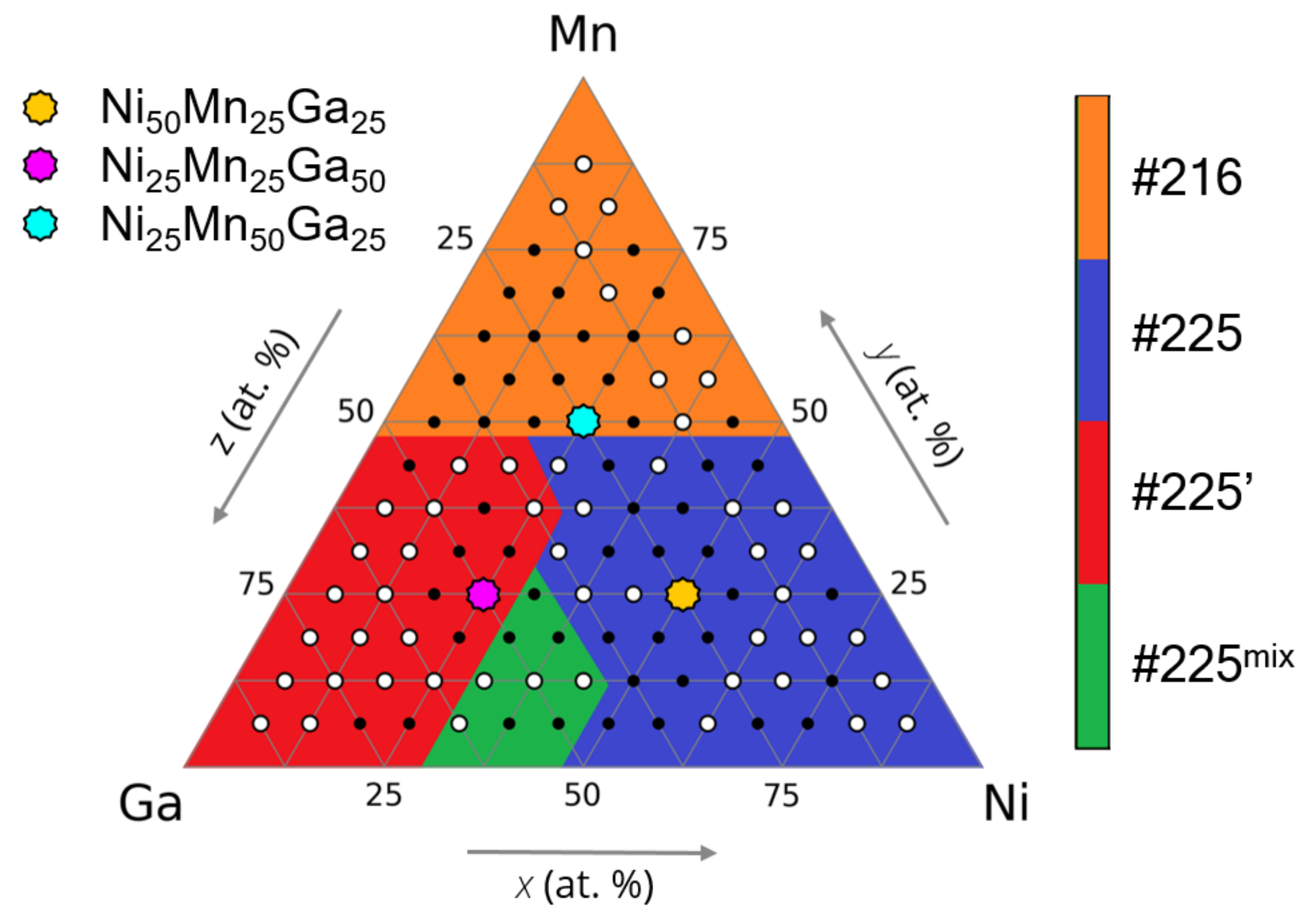
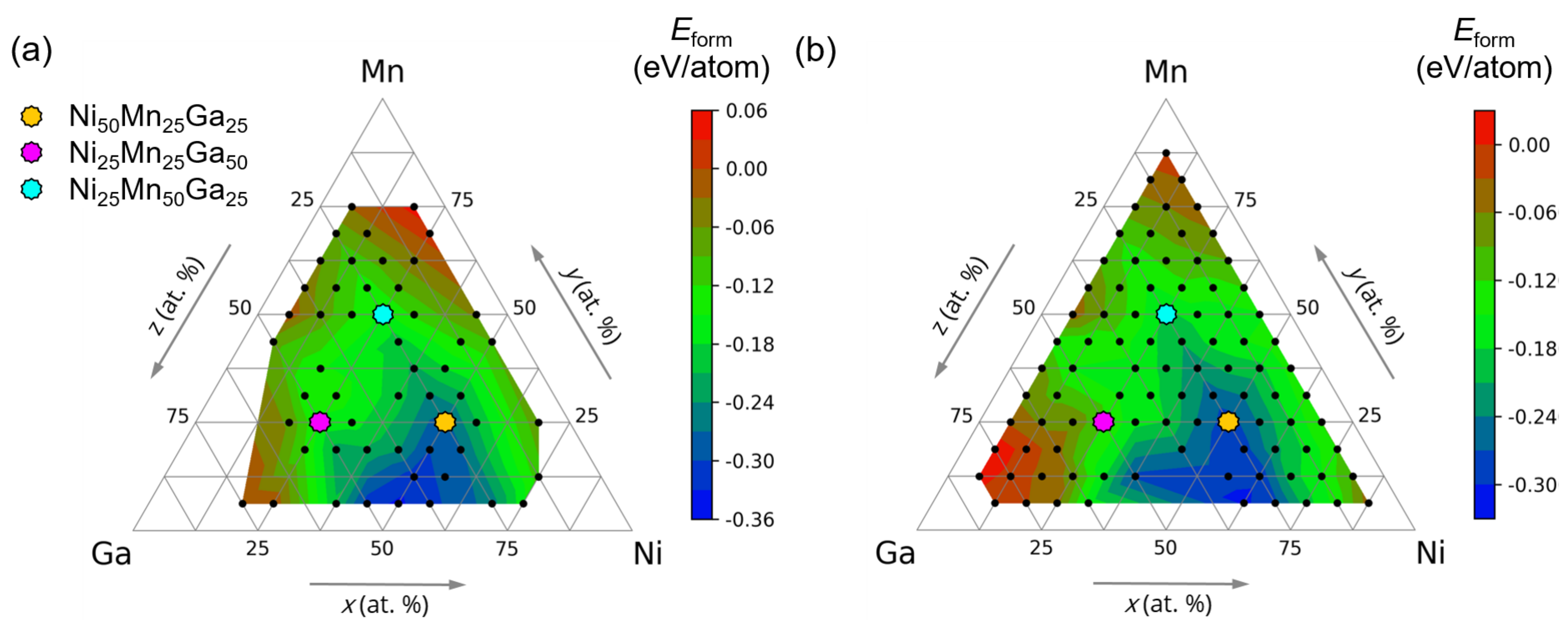
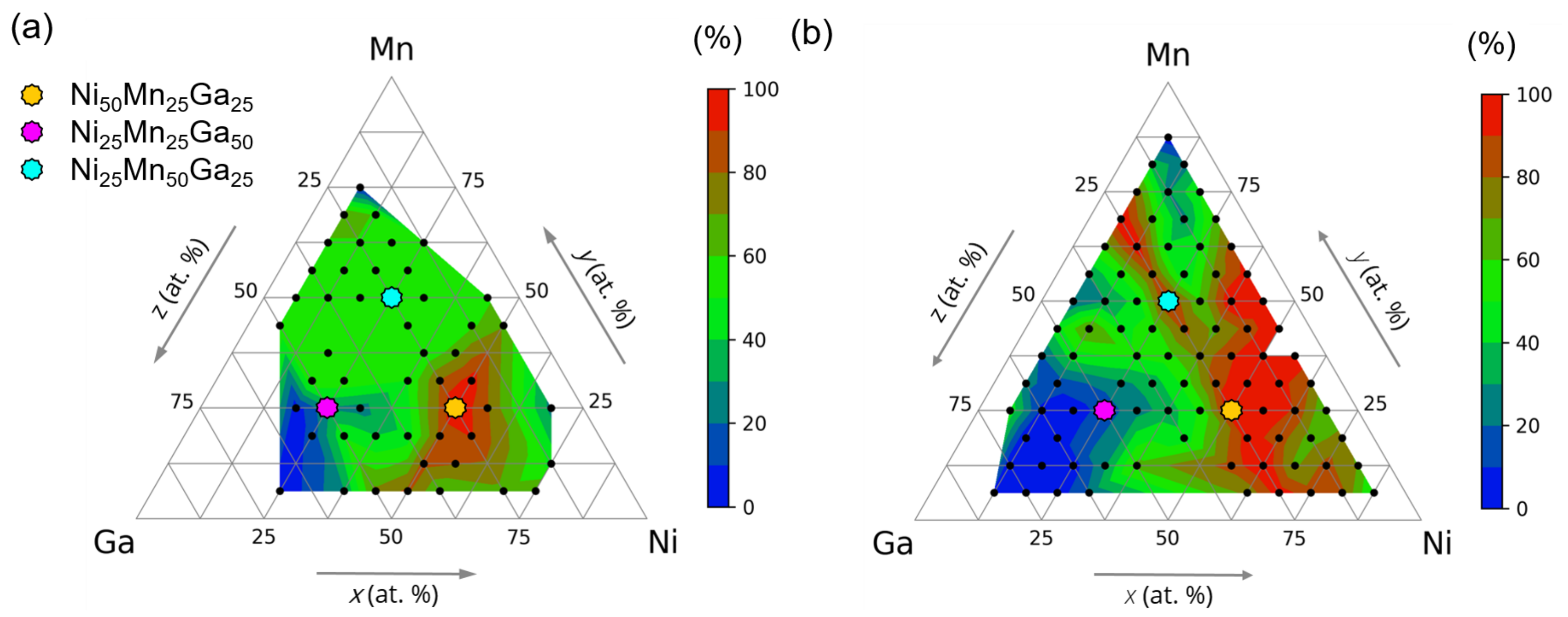
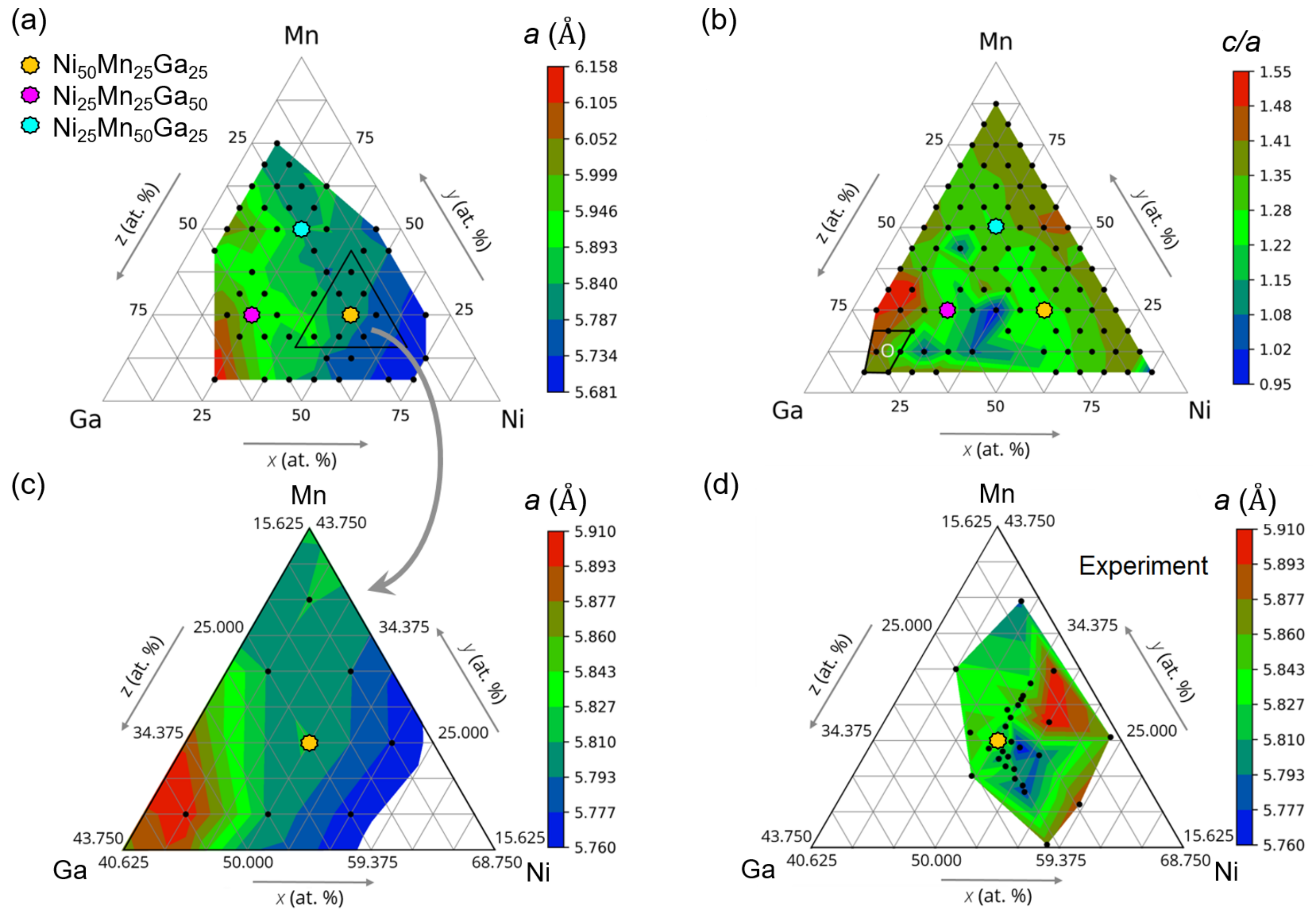
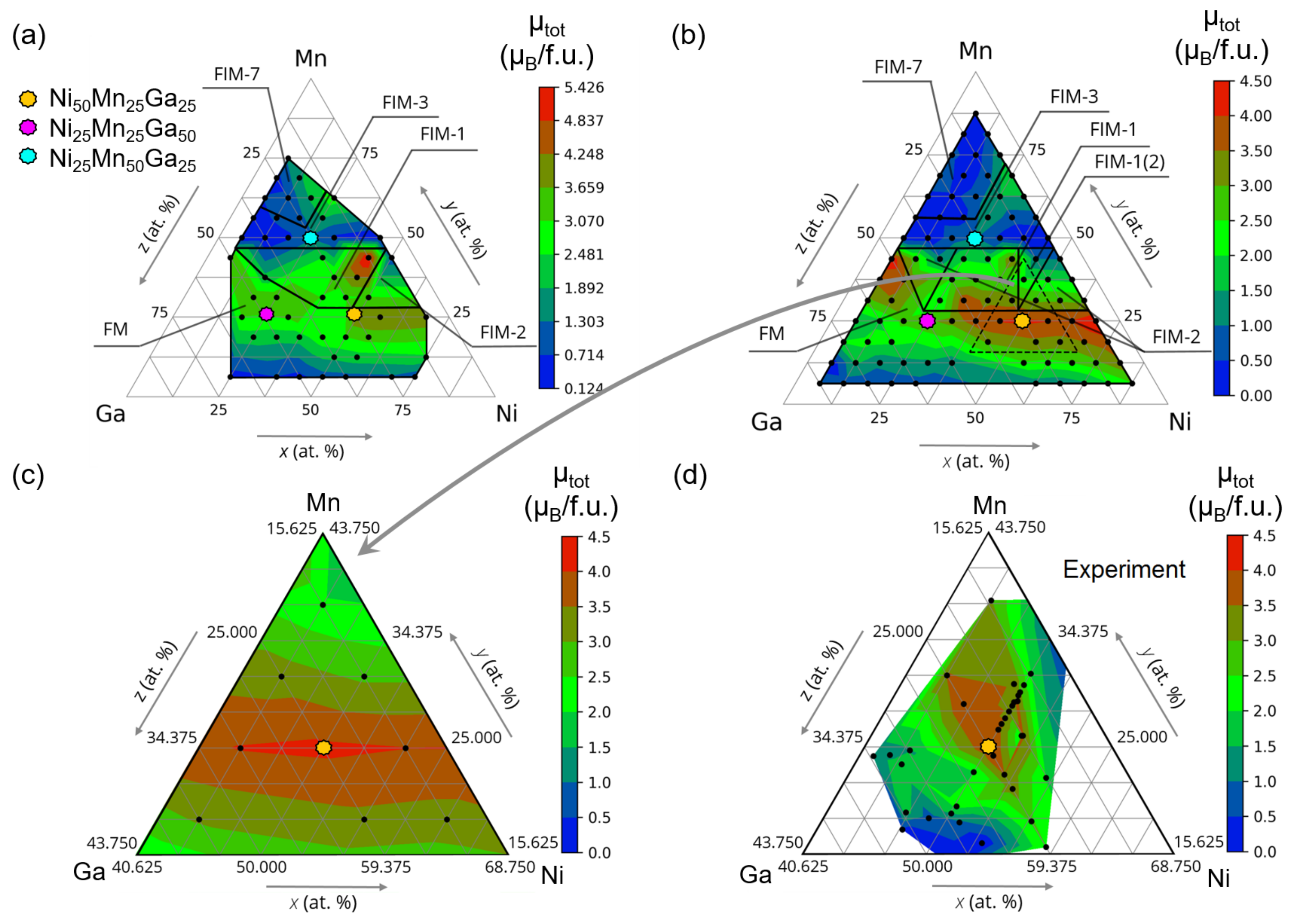
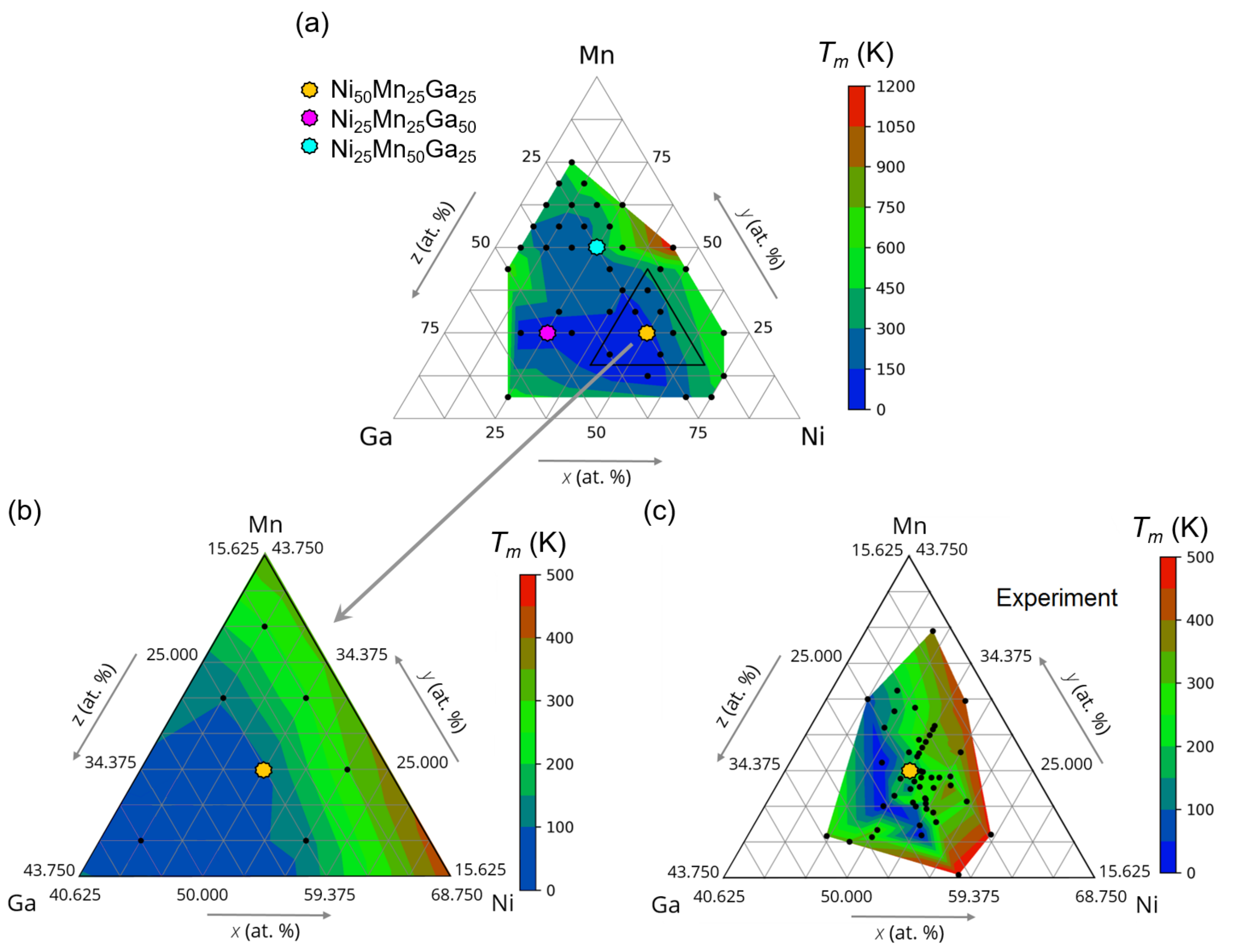
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Webster, P.J.; Ziebeck, K.R.A.; Town, S.L.; Peak, M.S. Magnetic order and phase transformation in Ni2MnGa. Philos. Mag. B 1984, 49, 295–310. [Google Scholar] [CrossRef]
- Ullakko, K.; Huang, J.K.; Kantner, C.; O’Handley, R.C. Large magnetic-field-induced strains in Ni2MnGa single crystals. Appl. Phys. Lett. 1996, 69, 1966–1968. [Google Scholar] [CrossRef]
- Chernenko, V.A.; Seguí, C.; Cesari, E.; Pons, J.; Kokorin, V.V. Sequence of martensitic transformations in Ni-Mn-Ga alloys. Phys. Rev. B 1998, 57, 2659–2662. [Google Scholar] [CrossRef]
- Wedel, B.; Suzuki, M.; Murakami, Y.; Wedel, C.; Suzuki, T.; Shindo, D.; Itagaki, K. Low temperature crystal structure of Ni-Mn-Ga alloys. J. Alloys Compd. 1999, 290, 137–142. [Google Scholar] [CrossRef]
- Glavatska, N.; Mogilniy, G.; Glavatsky, I.; Danilkin, S.; Hohlwein, D.; Beskrovnij, A.; Lindroos, V.K. Temperature dependence of martensite structure and its effect on magnetic-field-induced strain in Ni2MnGa magnetic shape memory alloys. J. Phys. IV France 2003, 112, 963–967. [Google Scholar] [CrossRef]
- Gavriljuk, V.G.; Söderberg, O.; Bliznuk, V.V.; Glavatska, N.I.; Lindroos, V.K. Martensitic transformations and mobility of twin boundaries in Ni2MnGa alloys studied by using internal friction. Scripta Mater. 2003, 49, 803–809. [Google Scholar] [CrossRef]
- Vasil’ev, A.N.; Buchel’nikov, V.D.; Takagi, T.; Khovailo, V.V.; Estrin, E.I. Shape memory ferromagnets. Phys. Usp. 2003, 46, 559–588. [Google Scholar] [CrossRef]
- Dubenko, I.; Samanta, T.; Pathak, A.K.; Kazakov, A.; Prudnikov, V.; Stadler, S.; Granovsky, A.; Zhukov, A.; Ali, N. Magnetocaloric effect and multifunctional properties of Ni-Mn-based Heusler alloys. J. Magn. Magn. Mater. 2012, 324, 3530–3534. [Google Scholar] [CrossRef]
- Dubenko, I.; Quetz, A.; Pandey, S.; Aryal, A.; Eubank, M.; Rodionov, I.; Prudnikov, V.; Granovsky, A.; Lähderanta, E.; Samanta, T.; et al. Multifunctional properties related to magnetostructural transitions in ternary and quaternary Heusler alloys. J. Magn. Magn. Mater. 2015, 383, 186–189. [Google Scholar] [CrossRef]
- Sozinov, A.; Likhachev, A.A.; Lanska, N.; Ullakko, K. Giant magnetic-field-induced strain in NiMnGa seven-layered martensitic phase. Appl. Phys. Lett. 2002, 80, 1746–1748. [Google Scholar] [CrossRef]
- Buchelnikov, V.D.; Vasiliev, A.N.; Koledov, V.; Taskaev, S.V.; Khovaylo, V.V.; Shavrov, V.G. Magnetic shape-memory alloys: Phase transitions and functional properties. Phys. Usp. 2006, 49, 871–877. [Google Scholar] [CrossRef]
- Planes, A.; Manosa, L.; Acet, M. Magnetocaloric effect and its relation to shape-memory properties in ferromagnetic Heusler alloys. J. Phys. Condens. Matter. 2009, 21, 233201. [Google Scholar] [CrossRef]
- Kamantsev, A.P.; Koledov, V.V.; Mashirov, A.V.; Dilmieva, E.T.; Shavrov, V.G.; Cwik, J.; Los, A.S.; Nizhankovskii, V.I.; Rogacki, K.; Tereshina, I.S.; et al. Magnetocaloric and thermomagnetic properties of Ni2.18Mn0.82Ga Heusler alloy in high magnetic fields up to 140 kOe. J. Appl. Phys. 2015, 117, 163903. [Google Scholar] [CrossRef]
- Pons, J.; Chernenko, V.A.; Santamarta, R.; Cesari, E. Crystal structure of martensitic phases in Ni-Mn-Ga shape memory alloys. Acta Mater. 2000, 48, 3027–3038. [Google Scholar] [CrossRef]
- Bozhko, A.D.; Vasil’ev, A.N.; Khovailo, V.V.; Buchel’nikov, V.D.; Dikshtein, I.E.; Seletskii, S.M.; Shavrov, V.G. Phase transitions in the ferromagnetic alloys Ni2+xMn1-xGa. JETP Lett. 1998, 67, 227–232. [Google Scholar] [CrossRef]
- Vasil’ev, A.N.; Bozhko, A.D.; Khovailo, V.V.; Dikshtein, I.E.; Shavrov, V.G.; Buchelnikov, V.D.; Matsumoto, M.; Suzuki, S.; Takagi, T.; Tani, J. Structural and magnetic phase transitions in shape-memory alloys Ni2+xMn1-xGa. Phys. Rev. B 1999, 59, 1113–1120. [Google Scholar] [CrossRef]
- Jin, X.; Marioni, M.; Bono, D.; Allen, S.M.; O’Handley, R.C.; Hsu, T.Y. Empirical mapping of Ni-Mn-Ga properties with composition and valence electron concentration. J. Appl. Phys. 2002, 91, 8222–8224. [Google Scholar] [CrossRef]
- Khovaylo, V.V.; Buchelnikov, V.D.; Kainuma, R.; Koledov, V.V.; Otsuka, M.; Shavrov, V.G.; Takagi, T.; Taskaev, S.V.; Vasiliev, A.N. Phase transitions in Ni2+xMn1-xGa with a high Ni excess. Phys. Rev. B 2005, 72, 224408. [Google Scholar] [CrossRef]
- Entel, P.; Buchelnikov, V.D.; Khovailo, V.V.; Zayak, A.T.; Adeagbo, W.A.; Gruner, M.E.; Herper, H.C.; Wassermann, E.F. Modelling the phase diagram of magnetic shape memory Heusler alloys. J. Phys. D Appl. Phys. 2006, 39, 865–889. [Google Scholar] [CrossRef]
- Wang, Y.F.; Wang, J.M.; Jiang, C.B.; Xu, H.B. Composition triangle diagrams of Ni-Mn-Ga magnetic shape memory alloys. Acta Metall. Sin. (Engl. Lett.) 2006, 19, 171–175. [Google Scholar] [CrossRef]
- Buchelnikov, V.D.; Taskaev, S.V.; Zagrebin, M.A.; Ermakov, D.I.; Koledov, V.V.; Shavrov, V.G.; Takagi, T. The phase diagrams of Ni-Mn-Ga alloys in the magnetic field. J. Magn. Magn. Mater. 2007, 313, 312–316. [Google Scholar] [CrossRef]
- Çakır, A.; Righi, L.; Albertini, F.; Acet, M.; Farle, M.; Aktúrk, S. Extended investigation of intermartensitic transitions in Ni-Mn-Ga magnetic shape memory alloys: A detailed phase diagram determination. J. Appl. Phys. 2013, 114, 183912. [Google Scholar] [CrossRef]
- Liu, G.D.; Chen, J.L.; Liu, Z.H.; Dai, X.F.; Wu, G.H.; Zhang, B.; Zhang, X.X. Martensitic transformation and shape memory effect in a ferromagnetic shape memory alloy: Mn2NiGa. Appl. Phys. Lett. 2005, 87, 262504. [Google Scholar] [CrossRef]
- Liu, G.D.; Dai, X.F.; Yu, S.Y.; Zhu, Z.Y.; Chen, J.L.; Wu, G.H.; Zhu, H.; Xiao, J.Q. Physical and electronic structure and magnetism of Mn2NiGa: Experiment and density-functional theory calculations. Phys. Rev. B 2006, 74, 054435. [Google Scholar] [CrossRef]
- Singh, S.; Maniraj, M.; D’Souza, S.W.; Ranjan, R.; Barman, S.R. Structural transformations in Mn2NiGa due to residual stress. Appl. Phys. Lett. 2010, 96, 081904. [Google Scholar] [CrossRef]
- Barman, S.R.; Banik, S.; Shukla, A.K.; Kamal, C.; Chakrabarti, A. Martensitic transition, ferrimagnetism and Fermi surface nesting in Mn2NiGa. Europhys. Lett. 2007, 80, 57002. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Siewert, M.; Roy, T.; Mondal, K.; Banerjee, A.; Gruner, M.E.; Entel, P. Ab initio studies of effect of copper substitution on the electronic and magnetic properties of Ni2MnGa and Mn2NiGa. Phys. Rev. B 2013, 88, 174116. [Google Scholar] [CrossRef]
- Kundu, A.; Gruner, M.E.; Siewert, M.; Hucht, A.; Entel, P.; Ghosh, S. Interplay of phase sequence and electronic structure in the modulated martensites of Mn2NiGa from first-principles calculations. Phys. Rev. B 2017, 96, 064107-13. [Google Scholar] [CrossRef]
- Barman, S.R.; Chakrabarti, A.; Singh, S.; Banik, S.; Bhardwaj, S.; Paulose, P.L.; Chalke, B.A.; Panda, A.K.; Mitra, A.; Awasthi, A.M. Theoretical prediction and experimental study of a ferromagnetic shape memory alloy: Ga2MnNi. Phys. Rev. B 2008, 78, 134406. [Google Scholar] [CrossRef]
- Uijttewaal, M.A.; Hickel, T.; Neugebauer, J.; Gruner, M.E.; Entel, P. Understanding the Phase Transitions of the Ni2MnGa Magnetic Shape Memory System from First Principles. Phys. Rev. Lett. 2009, 102, 035702. [Google Scholar] [CrossRef]
- Buchelnikov, V.D.; Sokolovskiy, V.V.; Herper, H.C.; Ebert, H.; Gruner, M.E.; Taskaev, S.V.; Khovaylo, V.V.; Hucht, A.; Dannenberg, A.; Ogura, M.; et al. First-principles and Monte Carlo study of magnetostructural transition and magnetocaloric properties of Ni2+xMn1-xGa. Phys. Rev. B 2010, 81, 094411. [Google Scholar] [CrossRef]
- Li, C.-M.; Luo, H.-B.; Hu, Q.-M.; Yang, R.; Johansson, B.; Vitos, L. Temperature dependence of elastic properties of Ni2+xMn1-xGa and Ni2Mn(Ga1-xAlx) from first principles. Phys. Rev. B 2011, 84, 174117. [Google Scholar] [CrossRef]
- Hickel, T.; Uijttewaal, M.; Al-Zubi, A.; Dutta, B.; Grabowski, B.; Neugebauer, J. Ab Initio-Based Prediction of Phase Diagrams: Application to Magnetic Shape Memory Alloys. Adv. Eng. Mater. 2012, 14, 547–561. [Google Scholar] [CrossRef]
- Xu, N.; Raulot, J.M.; Li, Z.B.; Bai, J.; Yang, B.; Zhang, Y.D.; Meng, X.Y.; Zhao, X.; Zuo, L.; Esling, C. Composition-dependent structural and magnetic properties of Ni-Mn-Ga alloys studied by ab initio calculations. J. Mater. Sci. 2015, 50, 3825–3834. [Google Scholar] [CrossRef]
- Dutta, B.; Çakır, A.; Giacobbe, C.; Al-Zubi, A.; Hickel, T.; Acet, M.; Neugebauer, J. Ab initio Prediction of Martensitic and Intermartensitic Phase Boundaries in Ni-Mn-Ga. Phys. Rev. Lett. 2016, 116, 025503. [Google Scholar] [CrossRef] [PubMed]
- Sokolovskiy, V.V.; Gruner, M.E.; Entel, P.; Acet, M.; Çakir, A.; Baigutlin, D.R.; Buchelnikov, V.D. Segregation tendency of Heusler alloys. Phys. Rev. Mater. 2019, 3, 084413. [Google Scholar] [CrossRef]
- Sokolovskaya, Y.A.; Sokolovskiy, V.V.; Zagrebin, M.A.; Buchelnikov, V.D.; Zayak, A.T. Ab Initio Study of the Composite Phase Diagram of Ni-Mn-Ga Shape Memory Alloys. J. Exp. Theor. Phys. 2017, 125, 104–110. [Google Scholar] [CrossRef]
- Sokolovskiy, V.V.; Sokolovskaya, Y.A.; Zagrebin, M.A.; Buchelnikov, V.D.; Zayak, A.T. Ternary diagrams of magnetic properties of Ni-Mn-Ga Heusler alloys from ab initio and Monte Carlo studies. J. Magn. Magn. Mater. 2019, 470, 64–68. [Google Scholar] [CrossRef]
- Sokolovskaya, Y.; Zagrebin, M.; Buchelnikov, V.; Zayak, A. Ternary phase diagram of Ni-Mn-Ga: Insights from ab initio calculations. EPJ Web Conf. 2018, 185, 05012. [Google Scholar] [CrossRef]
- Ebert, H.; Koedderitzsch, D.; Minar, J. Calculating condensed matter properties using the KKR-Green’s function method—Recent developments and applications. Rep. Prog. Phys. 2011, 74, 096501. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Anelli, A.; Engel, E.; Pickard C., J.; Ceriotti, M. Generalized convex hull construction for materials discovery. Phys. Rev. Mater. 2018, 2, 103804-8. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Chernenko, V.A.; Cesari, E.; Kokorin, V.V.; Vitenko, I.N. The development of new ferromagnetic shape memory alloys in Ni-Mn-Ga system. Scr. Metall. Mater. 1995, 33, 1239–1244. [Google Scholar] [CrossRef]
- Adachi, K.; Wayman, C.M. Transformation behavior of nearly stoichiometric Ni-Mn alloys. Metall. Trans. A 1985, 16, 1567–1579. [Google Scholar] [CrossRef]
- Entel, P.; Dannenberg, A.; Siewert, M.; Herper, H.C.; Gruner, M.E.; Buchelnikov, V.D.; Chernenko, V.A. Composition-Dependent Basics of Smart Heusler Materials from First- Principles Calculations. Mater. Sci. Forum 2011, 684, 1–29. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sokolovskaya, Y.; Miroshkina, O.; Baigutlin, D.; Sokolovskiy, V.; Zagrebin, M.; Buchelnikov, V.; Zayak, A.T. A Ternary Map of Ni–Mn–Ga Heusler Alloys from Ab Initio Calculations. Metals 2021, 11, 973. https://doi.org/10.3390/met11060973
Sokolovskaya Y, Miroshkina O, Baigutlin D, Sokolovskiy V, Zagrebin M, Buchelnikov V, Zayak AT. A Ternary Map of Ni–Mn–Ga Heusler Alloys from Ab Initio Calculations. Metals. 2021; 11(6):973. https://doi.org/10.3390/met11060973
Chicago/Turabian StyleSokolovskaya, Yulia, Olga Miroshkina, Danil Baigutlin, Vladimir Sokolovskiy, Mikhail Zagrebin, Vasilly Buchelnikov, and Alexey T. Zayak. 2021. "A Ternary Map of Ni–Mn–Ga Heusler Alloys from Ab Initio Calculations" Metals 11, no. 6: 973. https://doi.org/10.3390/met11060973
APA StyleSokolovskaya, Y., Miroshkina, O., Baigutlin, D., Sokolovskiy, V., Zagrebin, M., Buchelnikov, V., & Zayak, A. T. (2021). A Ternary Map of Ni–Mn–Ga Heusler Alloys from Ab Initio Calculations. Metals, 11(6), 973. https://doi.org/10.3390/met11060973







