Theoretical Study on Thermoelectric Properties and Doping Regulation of Mg3X2 (X = As, Sb, Bi)
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
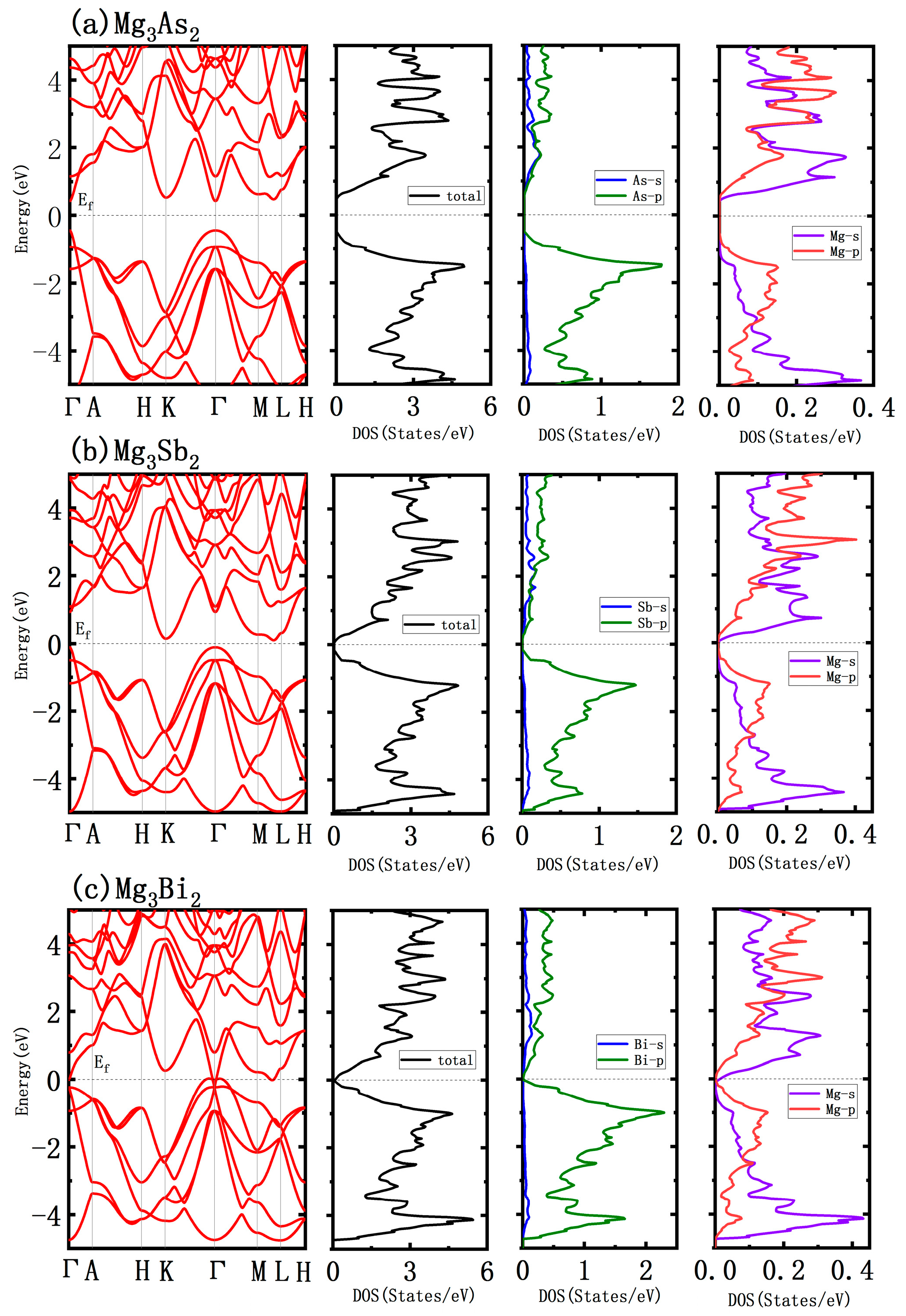
3.1. Atomic and Electronic Structure
3.2. Dynamics Stability
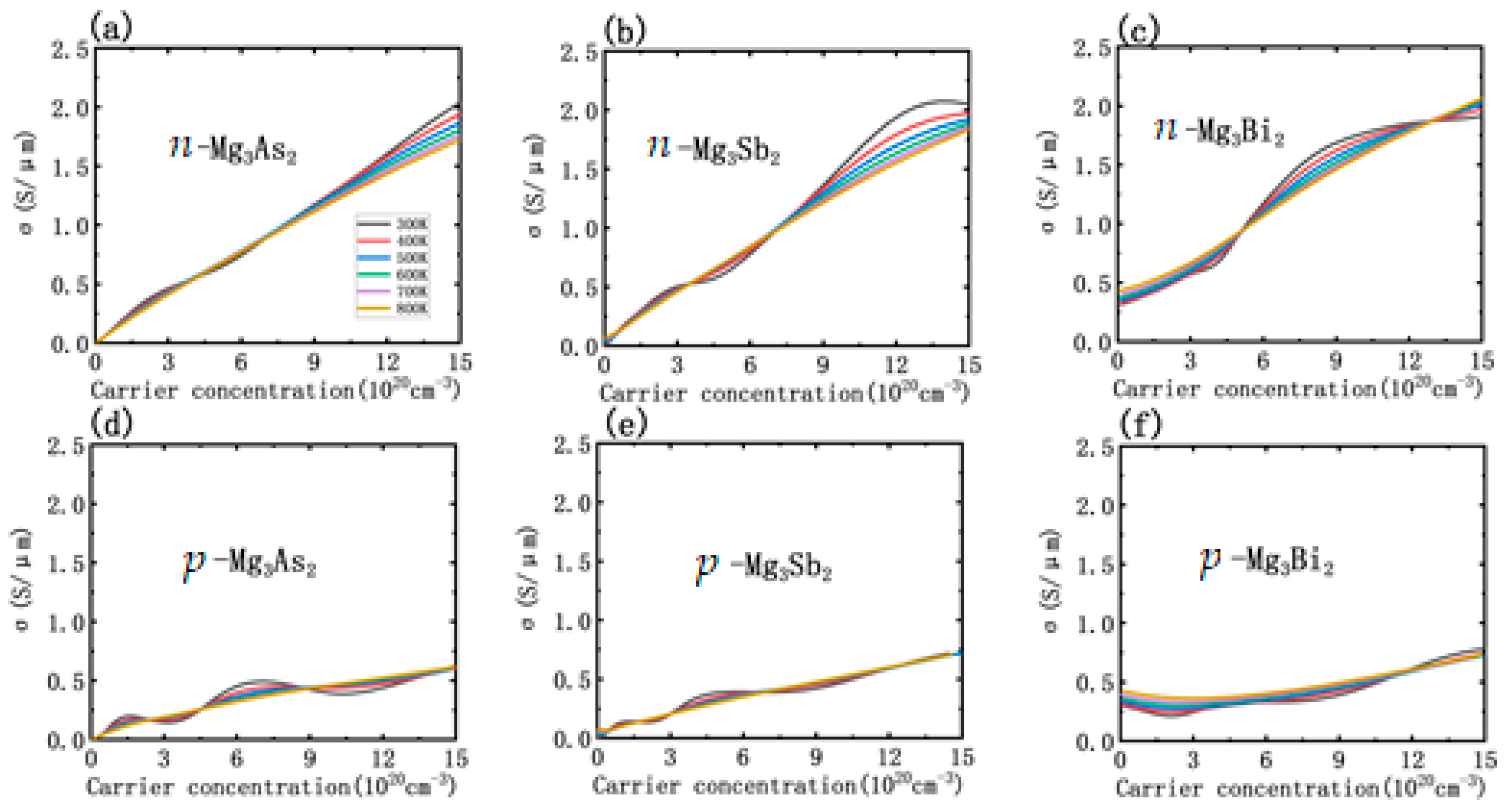
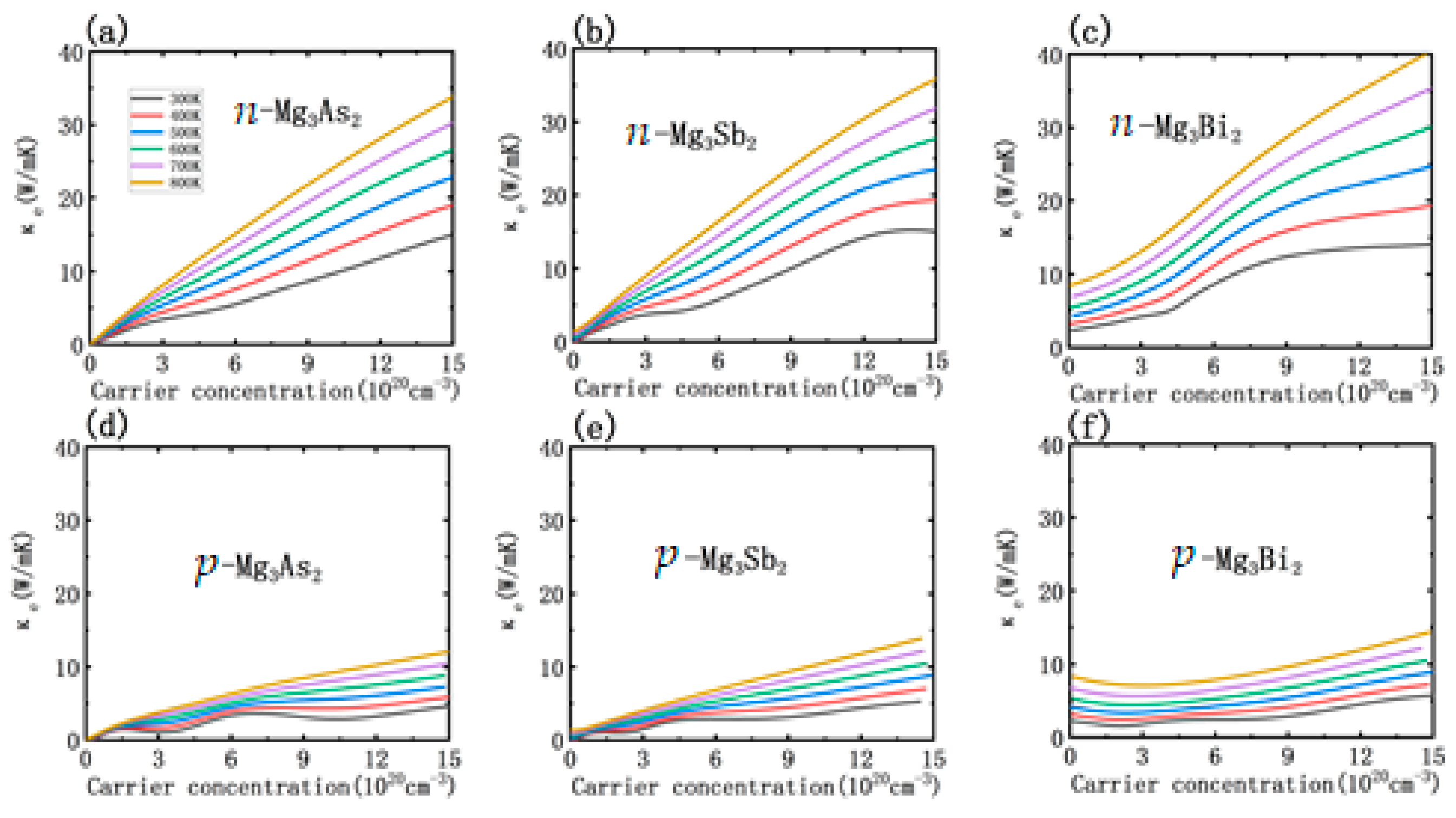
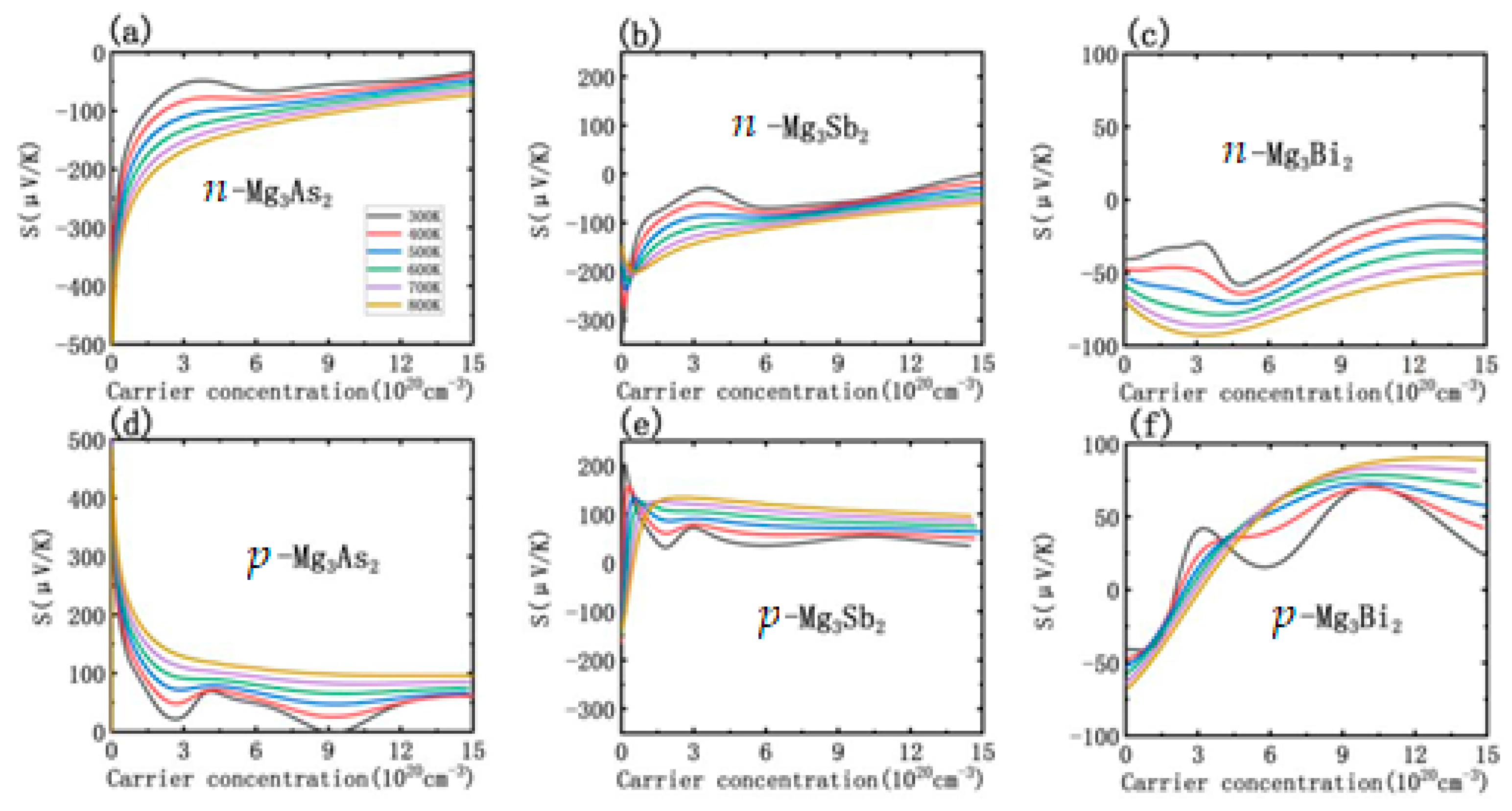
3.3. Thermoelectric Transport Properties
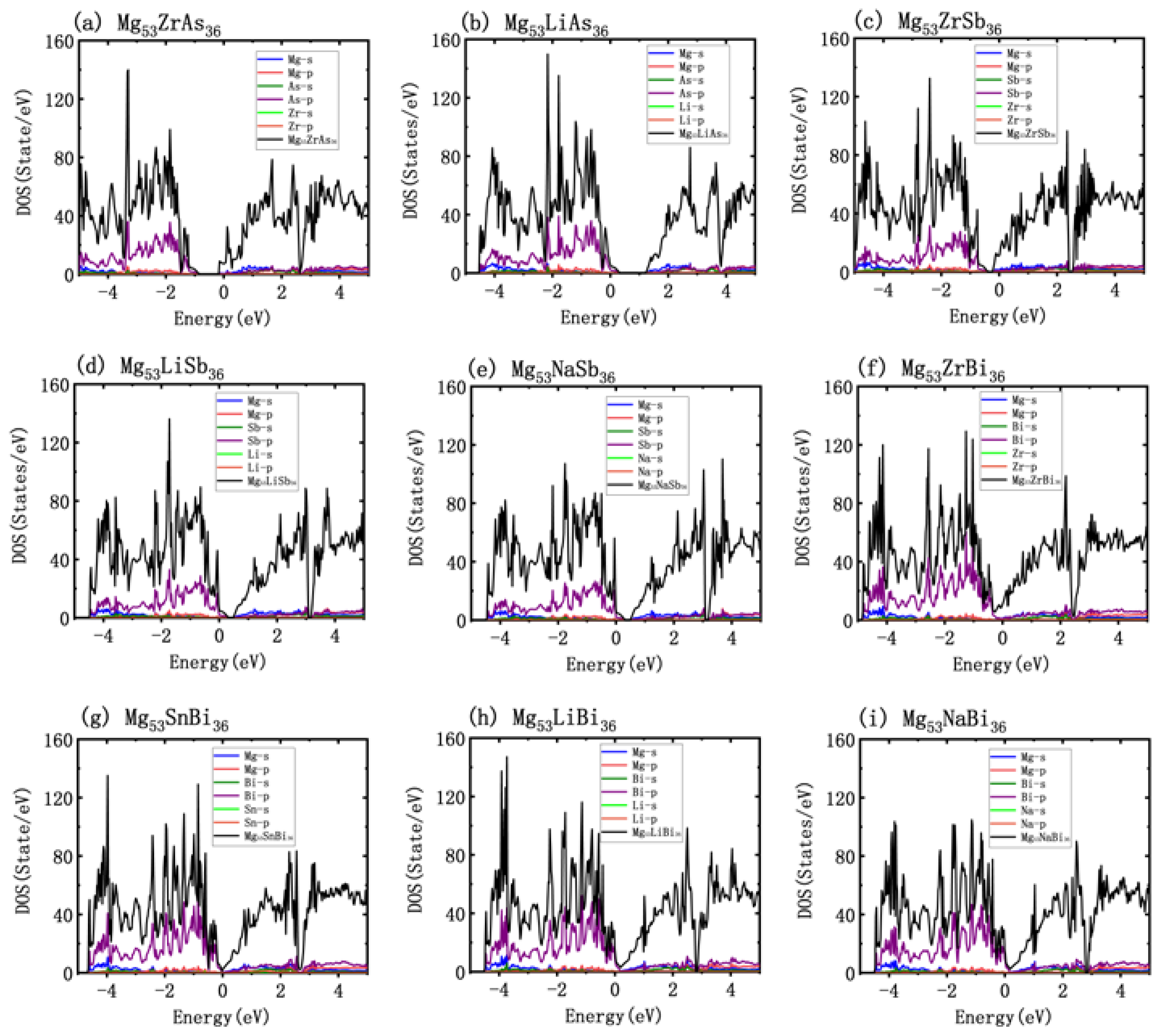
3.4. Doping Effect
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gelbstein, Y.; Davidow, J.; Leshem, E.; Pinshow, O.; Moisa, S. Significant lattice thermal conductivity reduction following phase separation of the highly efficient GexPb1–xTe thermoelectric alloys. Phys. Status Solidi B 2014, 251, 1431–1437. [Google Scholar] [CrossRef]
- Ben-Ayoun, D.; Sadia, Y.; Gelbstein, Y. High temperature thermoelectric properties evolution of Pb1-xSnxTe based alloys. J. Alloys Compd. 2017, 722, 33–38. [Google Scholar] [CrossRef]
- Xing, Y.; Liu, R.; Liao, J.; Zhang, Q.; Xia, X.; Wang, C.; Huang, H.; Chu, J.; Gu, M.; Zhu, T.; et al. High-efficiency half-Heusler thermoelectric modules enabled by self-propagating synthesis and topologic structure optimization. Energy Environ. Sci. 2019, 12, 3390. [Google Scholar] [CrossRef]
- Rull-Bravo, M.; Moure, A.; Fernández, J.F.; Martín-González, M. Skutterudites as thermoelectric materials: Revisited. RSC Adv. 2015, 5, 41653–41667. [Google Scholar] [CrossRef]
- Kauzlarich, S.M.; Brown, S.R.; Snyder, G.J. Zintl phases for thermoelectric devices. Dalton Trans. 2007, 21, 2099–2107. [Google Scholar] [CrossRef]
- Condron, C.L.; Kauzlarich, S.M.; Gascoin, F.; Snyder, G.J. Thermoelectric Properties and Microstructure of Mg3Sb2. J. Solid State Chem. 2016, 179, 2252–2257. [Google Scholar] [CrossRef]
- Chen, C.; Li, X.; Li, S.; Wang, X.; Zhang, Z.; Sui, J.; Cao, F.; Liu, X.; Zhang, Q. Enhanced thermoelectric performance of p-type Mg3Sb2 by lithium doping and its tunability in an anionic framework. J. Mater. Sci. 2018, 53, 16001–16009. [Google Scholar] [CrossRef]
- Wang, H.; Chen, J.; Lu, T.; Zhu, K.; Li, S.; Liu, J.; Zhao, H. Enhanced thermoelectric performance in p-type Mg3Sb2 via lithium doping. Chin. Phys. B. 2018, 4, 110–116. [Google Scholar]
- Xu, B.; Rao, L.; Yu, G.; Ma, S.; Wang, Y.; Wang, Y.; Yi, L. The Relation between the Electronic Structure and Thermoelectric Properties for Zintl Compounds Mg3Sb2. J. Phys. Soc. Jpn. 2017, 86, 024601. [Google Scholar] [CrossRef]
- Meng, F.; Sun, S.; Ma, J.; Chronister, C.; He, J.; Li, W. Anisotropic thermoelectric figure-of-merit in Mg3Sb2. Mater. Today Phys. 2020, 13, 100217. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Gonze, X.; Lee, C. Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory. Phys. Rev. B Condens. Matter. 1997, 55, 10355–10368. [Google Scholar] [CrossRef]
- Madsen, G.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef]
- Jun-ichi, T.; Takahashi, M.; Kido, H. Lattice dynamics and elastic properties of Mg3As2 and Mg3Sb2 compounds from first-principles calculations. Phys. B Condens. Matter 2010, 405, 4219–4225. [Google Scholar] [CrossRef]
- Lee, J.; Monserrat, B.; Seymour, I.D.; Liu, Z.; Dutton, S.E.; Grey, C.P. An ab initio investigation on the electronic structure, defect energetics, and magnesium kinetics in Mg3Bi2. J. Mater. Chem. A. 2018, 6, 16983–16991. [Google Scholar] [CrossRef]
- Juza, R.; Kroebel, R. Über eine Hochtemperaturmodifikation des Magnesiumarsenids und eine ternre Phase Mg2MnAs2 gleicher Struktur. Z. Für Anorg. Allg. Chem. 1964, 331, 187–199. [Google Scholar] [CrossRef]
- Sevast’yanova, L.G.; Kravchenko, O.V.; Gulish, O.K.; Stupnikov, V.A.; Leonova, M.E.; Zhizhin, M.G. Binary and ternary compounds in the Mg-Sb-B and Mg-Bi-B systems as catalysts for the synthesis of cubic BN. Inorg. Mater. 2006, 42, 863–866. [Google Scholar] [CrossRef]
- Imai, Y.; Watanabe, A. Electronic structures of Mg3Pn2 (Pn=N, P, As, Sb and Bi) and Ca3N2 calculated by a first-principle pseudopotential method. J. Mater. Sci. 2006, 41, 2435–2441. [Google Scholar] [CrossRef]
- Xu, R.; Groot, R.; van der Lugt, W. Resistivities and band structures of alkaline-earth-pnictide systems. J. Phys. Condens. Matter 1993, 5, 7551–7562. [Google Scholar] [CrossRef]
- Ferrier, R.P.; Herrell, D.J. Conduction in amorphous magnesium-bismuth alloys. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1969, 19, 853–868. [Google Scholar] [CrossRef]
- Ferrier, R.P.; Herrell, D.J. The structure and electrical properties of amorphous MgBi and MgSb alloys. J. Non-Cryst. Solids 1970, 4, 338–344. [Google Scholar] [CrossRef]
- Yu, W.Y.; Tang, B.Y.; Peng, L.M.; Ding, W.J. Electronic structure and mechanical properties of α-Mg3Sb2. Acta Phys. Sin. 2009, 58, 216–223. [Google Scholar]
- Wu, Z.J.; Zhao, E.J.; Xiang, H.P.; Hao, X.F.; Liu, X.J.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B. 2007, 76, 054115. [Google Scholar] [CrossRef]
- Song, L.; Zhang, J.; Iversen, B.B. Simultaneous improvement of power factor and thermal conductivity via Ag doping in p-type Mg3Sb2 thermoelectric materials. J. Mater. Chem. A. 2017, 5, 4932–4939. [Google Scholar] [CrossRef]
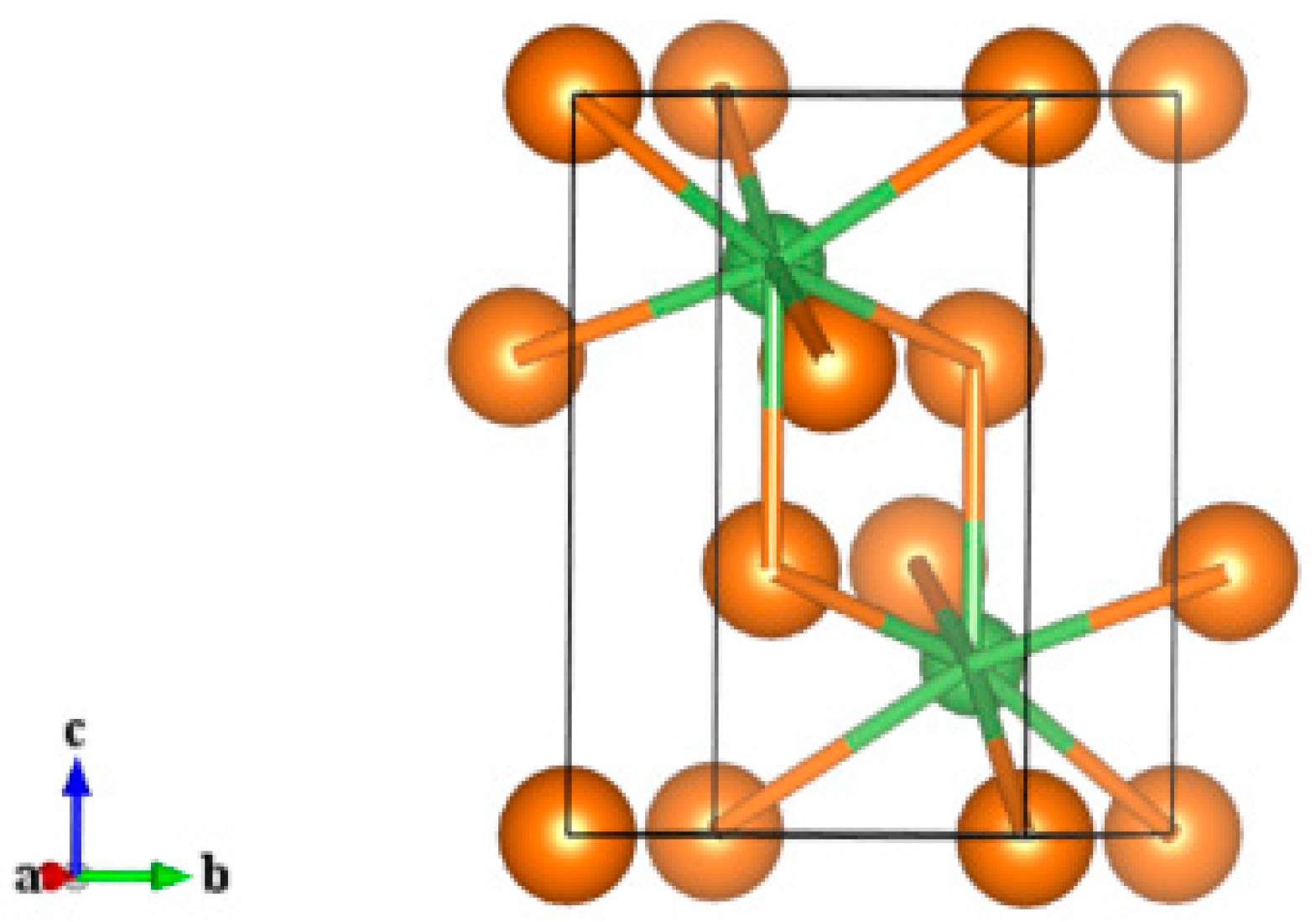



| a(Å) | c(Å) | Bond angle | |
|---|---|---|---|
| Mg3As2 | 4.293 (4.264 [16]) | 6.763 (6.738 [16]) | α = β = 90°, β = 120° |
| Mg3Sb2 | 4.596 (4.53 [17]) | 7.280 (7.24 [17]) | α = β = 90°, β = 120° |
| Mg3Bi2 | 4.723 (4.67 [18]) | 7.44 (7.40 [18]) | α = β = 90°, β = 120° |
| Mg3As2 | Mg3Sb2 | Mg3Bi2 | |
|---|---|---|---|
| c11 (GPa) | 96.63 | 71.73 | 58.77 |
| c33 (GPa) | 90.89 | 75.91 | 65.52 |
| c44 (GPa) | 23.71 | 13.79 | 12.48 |
| c12 (GPa) | 45.84 | 36.78 | 32.06 |
| c13 (GPa) | 26.63 | 21.06 | 20.13 |
| ρ (g/cm3) | 3.43 | 3.95 | 5.67 |
| V (Å3) | 21.59 | 26.64 | 28.75 |
| B (GPa) | 53.28 | 41.83 | 36.39 |
| G (GPa) | 26.54 | 17.70 | 14.62 |
| ΘD (K) | 332 | 237 | 175 |
| vt (m/s) | 2782.50 | 2117.95 | 1605.26 |
| vl (m/s) | 5085.97 | 4071.74 | 3138.67 |
| vm (m/s) | 3102.70 | 2370.11 | 1798.33 |
| κmin (W/K) | 0.76 | 0.52 | 0.38 |
| Ef (Mg53YAs36) | Ef (Mg53YSb36) | Ef (Mg53YBi36) | |
|---|---|---|---|
| Y = Hf (n) | 0.97 | 2.41 | 0.98 |
| Y = Sn (n) | 1.22 | 2.62 | 0.50 |
| Y = Zr (n) | 0.55 | 2.09 | 0.50 |
| Y = Ag (p) | 1.89 | 1.32 | 1.05 |
| Y = Li (p) | 0.26 | −0.14 | −0.35 |
| Y = Na (p) | 0.36 | −0.14 | −0.39 |
| vl (m/s) | vt (m/s) | ΘD (K) | κmin (W/mK) | |
|---|---|---|---|---|
| Mg3As2 | 5085.97 | 2782.52 | 332 | 0.76 |
| Mg53ZrAs36 (n) | 5036.81 | 2735.55 | 326 | 0.75 |
| Mg53LiAs36 (p) | 4841.40 | 2462.41 | 295 | 0.70 |
| Mg3Sb2 | 4071.74 | 2117.95 | 237 | 0.52 |
| Mg53ZrSb36 (n) | 3998.69 | 2051.21 | 229 | 0.50 |
| Mg53LiSb36 (p) | 4014.01 | 2051.68 | 229 | 0.51 |
| Mg53NaSb36 (p) | 4009.55 | 2045.79 | 228 | 0.50 |
| Mg3Bi2 | 3138.67 | 1605.26 | 175 | 0.38 |
| Mg53ZrBi36 (n) | 3134.87 | 1613.38 | 176 | 0.38 |
| Mg53SnBi36 (n) | 3149.64 | 1608.67 | 175 | 0.38 |
| Mg53LiBi36 (p) | 3053.87 | 1503.96 | 164 | 0.36 |
| Mg53NaBi36 (p) | 3050.20 | 1493.58 | 163 | 0.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Lu, Y.; Hu, Z.; Shao, X. Theoretical Study on Thermoelectric Properties and Doping Regulation of Mg3X2 (X = As, Sb, Bi). Metals 2021, 11, 971. https://doi.org/10.3390/met11060971
Wang X, Lu Y, Hu Z, Shao X. Theoretical Study on Thermoelectric Properties and Doping Regulation of Mg3X2 (X = As, Sb, Bi). Metals. 2021; 11(6):971. https://doi.org/10.3390/met11060971
Chicago/Turabian StyleWang, Xiaofang, Yong Lu, Ziyu Hu, and Xiaohong Shao. 2021. "Theoretical Study on Thermoelectric Properties and Doping Regulation of Mg3X2 (X = As, Sb, Bi)" Metals 11, no. 6: 971. https://doi.org/10.3390/met11060971
APA StyleWang, X., Lu, Y., Hu, Z., & Shao, X. (2021). Theoretical Study on Thermoelectric Properties and Doping Regulation of Mg3X2 (X = As, Sb, Bi). Metals, 11(6), 971. https://doi.org/10.3390/met11060971





