Description of the Expansion of a Two-Layer Tube: An Analytic Plane-Strain Solution for Arbitrary Pressure-Independent Yield Criterion and Hardening Law
Abstract
1. Introduction
2. Statement of the Problem
3. General Solution
4. Expansion of a Two-Layer Tube
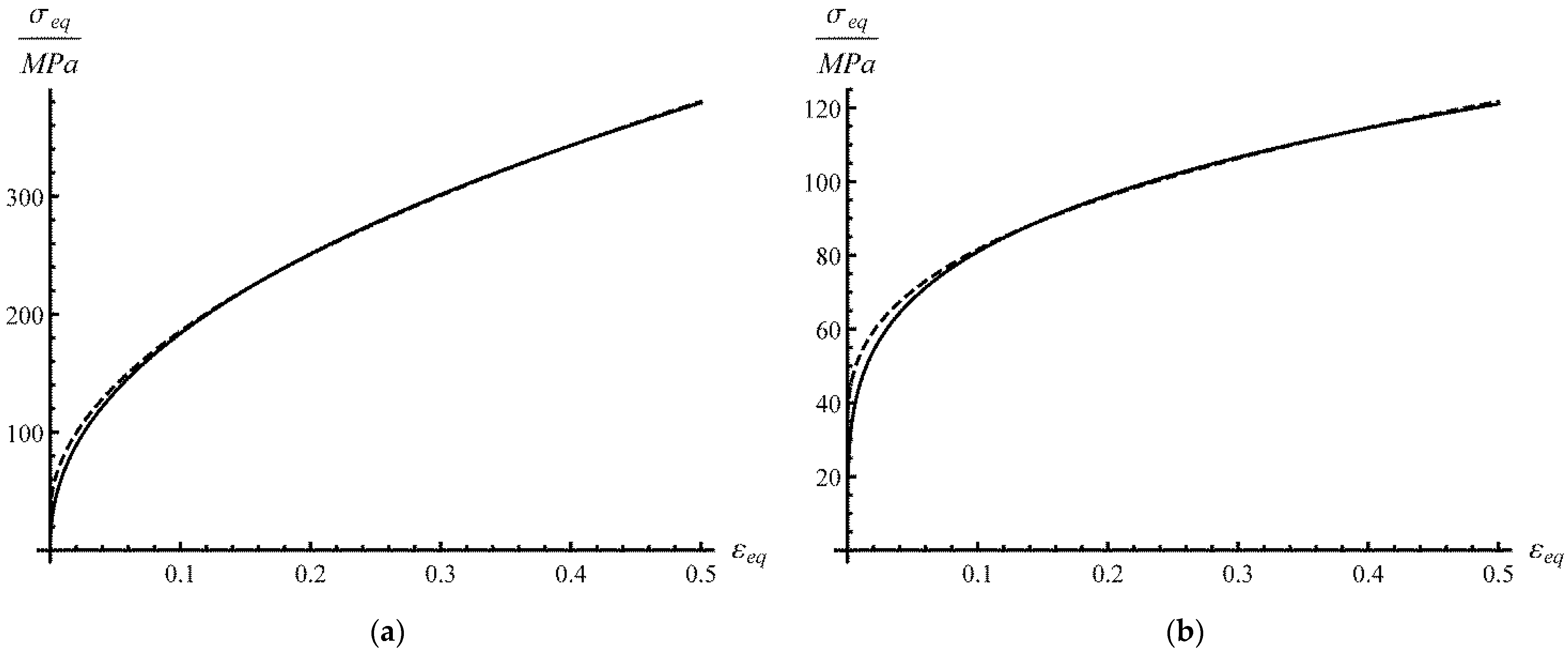
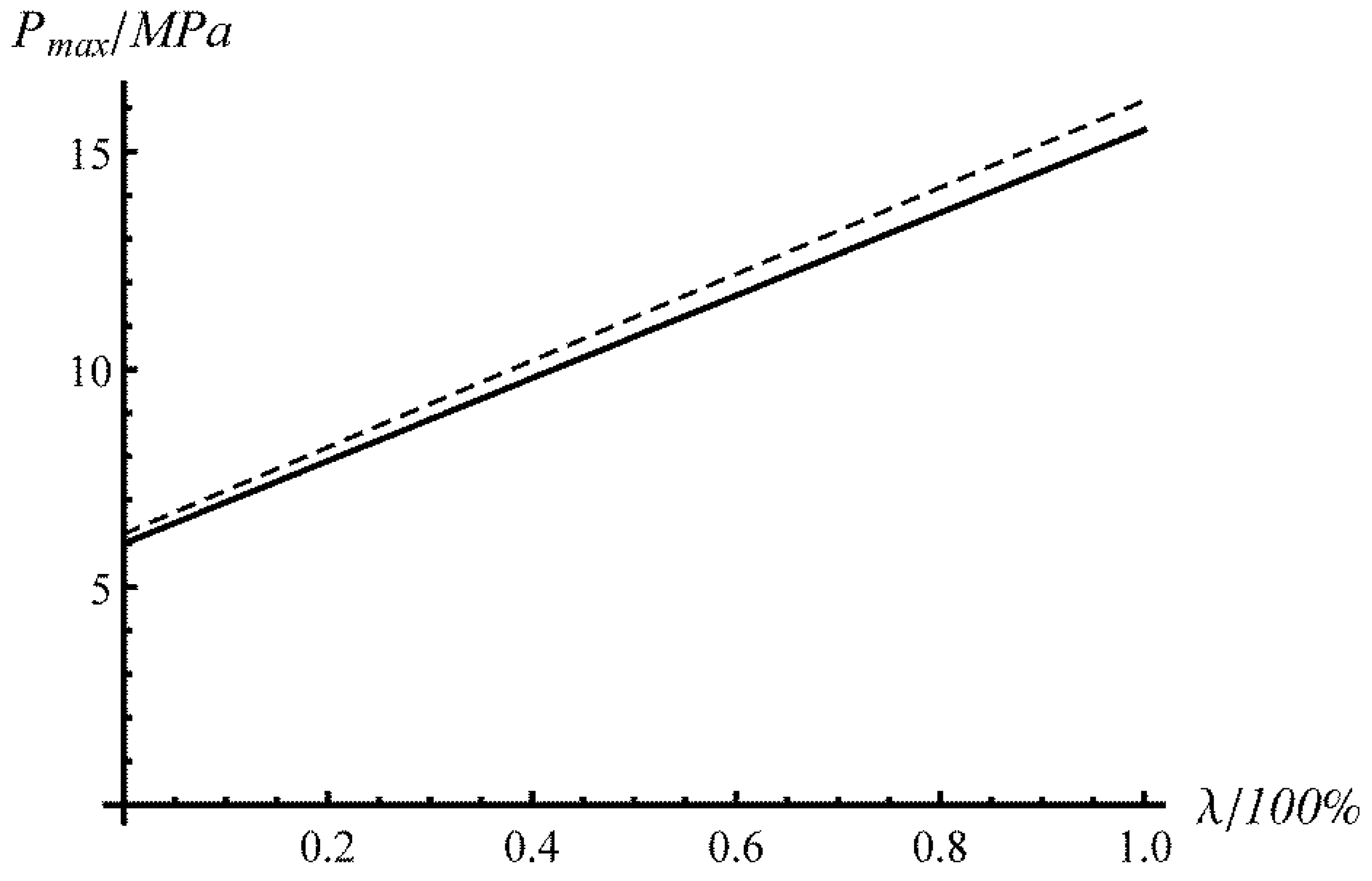
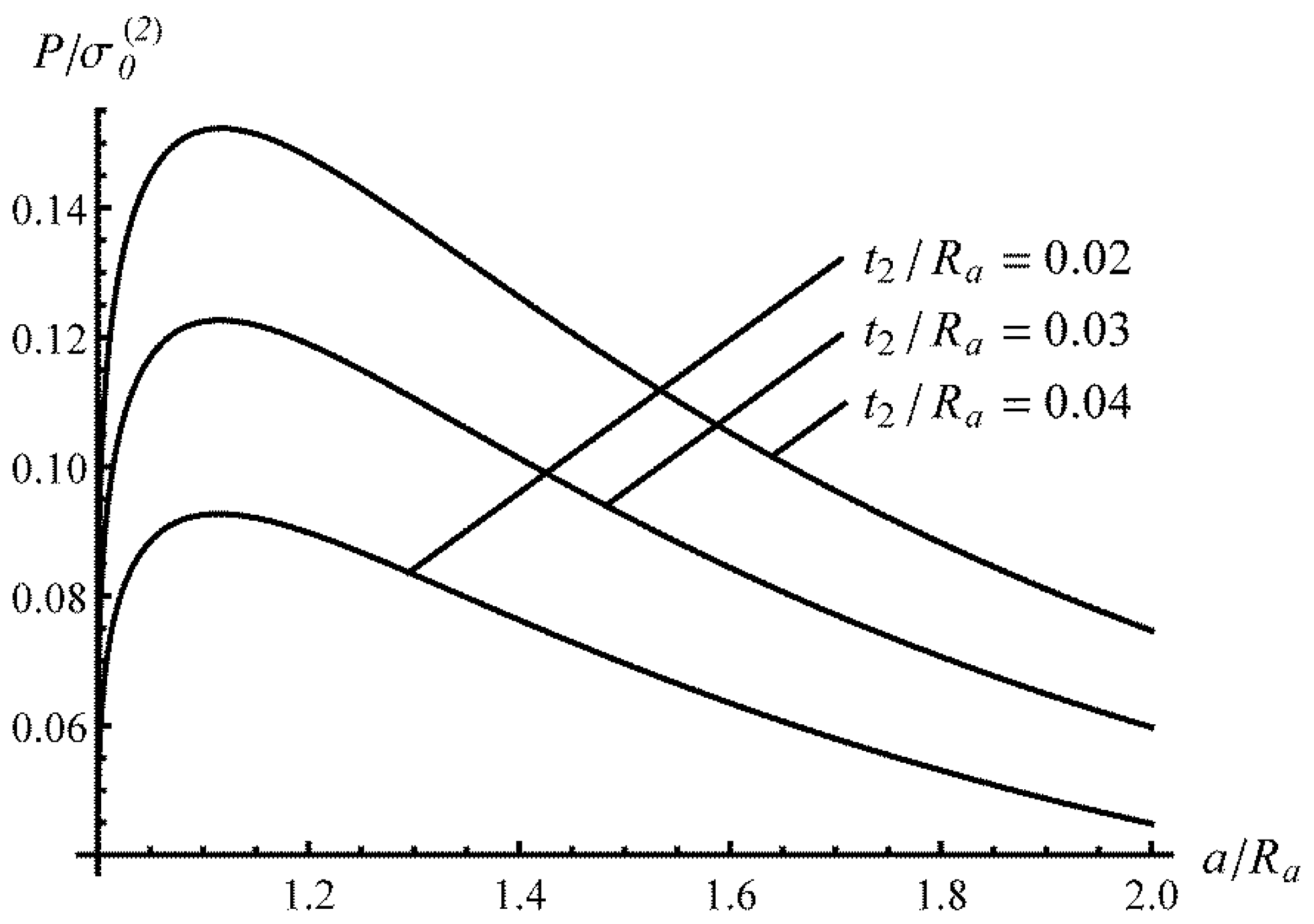
5. Experimental Verification and Illustrative Examples
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | inner radius of the tube after any amount of deformation |
| b | outer radius of the tube after any amount of deformation |
| c | radius of the interface between the layers after any amount of deformation |
| k | parameter introduced after Equation (30) |
| P | pressure over the inner radius of the tube |
| Pmax | maximum inner pressure in the course of the hydroforming process |
| R | Lagrangian coordinate |
| Ra | Lagrangian coordinate of the inner radius of the tube |
| Rb | Lagrangian coordinate of the outer radius of the tube |
| Rc | Lagrangian coordinate of the interface between the layers |
| cylindrical coordinate system | |
| t | Time |
| t1 | initial thickness of the inner layer |
| t2 | initial thickness of the outer layer |
| U | radial velocity at the inner radius of the tube |
| u | radial velocity |
| equivalent strain | |
| equivalent strain rate | |
| and | radial and circumferential strain rates, respectively |
| equivalent stress | |
| and | radial, circumferential, and axial stresses, respectively |
| initial yield stress in tension | |
| ϕ | arbitrary function of the equivalent strain introduced in Equation (6) |
| parameter introduced in Equation (1) |
References
- Fiorentino, A.; Ginestra, P.S.; Attanasio, A.; Ceretti, E. Numerical optimization of the blank dimensions in tube hydroforming using line-search and bisection methods. Materials 2020, 13, 945. [Google Scholar] [CrossRef] [PubMed]
- Kocańda, A.; Sadłowska, H. Automotive component development by means of hydroforming. Archiv. Civ. Mech. Eng. 2008, 8, 55–72. [Google Scholar] [CrossRef]
- Han, S.W.; Woo, Y.Y.; Hwang, T.W.; Oh, I.Y.; Moon, Y.H. Tailor layered tube hydroforming for fabricating tubular parts with dissimilar thickness. Int. J. Mach. Tools Manuf. 2018, 138, 51–65. [Google Scholar] [CrossRef]
- Saboori, M.; Gholipour, J.; Champliaud, H.; Wanjara, P.; Gakwaya, A.; Savoie, J. Prediction of burst pressure in multistage tube hydroforming of aerospace alloys. ASME J. Eng. Gas Turbines Power 2016, 138, 082101. [Google Scholar] [CrossRef] [PubMed]
- Sadłowska, H.; Kochański, A.; Czapla, M. Application of the numerical model to design the geometry of a unit tool in the innovative rth hydroforming technology. Materials 2020, 13, 5427. [Google Scholar] [CrossRef] [PubMed]
- Micro-Manufacturing Technologies and Their Applications: A Theoretical and Practical Guide, 1st ed.; Fassi, I., Shipley, D., Eds.; Springer International Publishing: Cham, Switzerland, 2017; p. 301. [Google Scholar] [CrossRef]
- Ngaile, G.; Lowrie, J. New micro tube hydroforming system based on floating die assembly concept. ASME J. Micro Nano-Manuf. 2014, 2, 41004. [Google Scholar] [CrossRef]
- Hartl, H.; Schiefer, H.; Chlynin, A. Evaluation of experimental and numerical investigations into micro-hydroforming of platinum tubes for an industrial application. Manuf. Rev. 2014, 1, 17. [Google Scholar] [CrossRef]
- Koç, M.; Altan, T. Overall review of the tube hydroforming (THF) technology. J. Mater. Process. Technol. 2001, 108, 384–393. [Google Scholar] [CrossRef]
- Bell, C.; Corney, J.; Zuelli, N.; Savings, D. A state of the art review of hydroforming technology: Its applications, research areas, history, and future in manufacturing. Int. J. Mater. Form. 2019, 13, 789–828. [Google Scholar] [CrossRef]
- Hartl, C. Review on advances in metal micro-tube forming. Metals 2019, 9, 542. [Google Scholar] [CrossRef]
- Reddy, P.V.; Reddy, B.V.; Ramulu, P.J. Evolution of hydroforming technologies and its applications—A review. J. Adv. Manuf. Syst. 2020, 19, 737–780. [Google Scholar] [CrossRef]
- Hwang, Y.-M.; Pham, H.-N.; Tsui, H.-S.R. Investigation of punch shape and loading path design in hydro-flanging processes of aluminum alloy tubes. Metals 2021, 11, 636. [Google Scholar] [CrossRef]
- Chung, K.; Richmond, O. Ideal forming—II. Sheet forming with optimum deformation. Int. J. Mech. Sci. 1992, 34, 617–633. [Google Scholar] [CrossRef]
- Barlat, F.; Chung, K.; Richmond, O. Anisotropic plastic potentials for polycrystals and application to the design of optimum blank shapes in sheet forming. Metall. Mater. Trans. A 1994, 25, 1209–1216. [Google Scholar] [CrossRef]
- Chung, K.; Alexandrov, S. Ideal flow in plasticity. ASME. Appl. Mech. Rev. 2007, 60, 316–335. [Google Scholar] [CrossRef]
- Zhang, S.H.; Wang, Z.R. Research into the dieless hydroforming of double layer spherical vessels. Int. J. Pres. Ves. Pip. 1994, 60, 145–149. [Google Scholar] [CrossRef]
- Kim, S.Y.; Joo, B.D.; Shin, S.; Van Tyne, C.J.; Moon, Y.H. Discrete layer hydroforming of three-layered tubes. Int. J. Mach. Tools Manuf. 2013, 68, 56–62. [Google Scholar] [CrossRef]
- Liu, S.; Lang, L.; Guan, S.; Zeng, Y. Investigation into composites property effect on the forming limits of multi-layer hybrid sheets using hydroforming technology. Appl. Compos. Mater. 2019, 26, 205–217. [Google Scholar] [CrossRef]
- Zhou, B.J.; Xu, Y.C.; Zhang, Z.C. Research on the selection principle of upper sheet in double-layer sheets hydroforming. Int. J. Adv. Manuf. Technol. 2020, 109, 1663–1669. [Google Scholar] [CrossRef]
- Blala, H.; Lang, L.; Khan, S.; Li, L.; Alexandrov, S. An analysis of process parameters in the hydroforming of a hemispherical dome made of fiber metal laminate. Appl. Compos. Mater. 2021. [Google Scholar] [CrossRef]
- Durban, D.; Baruch, M. Analysis of an elasto-plastic thick walled sphere loaded by internal and external pressure. Int. J. Non-Linear Mech. 1997, 12, 9–21. [Google Scholar] [CrossRef]
- Alexandrov, S.; Hwang, Y.-M. Plane strain bending with isotropic strain hardening at large strains. Trans. ASME J. Appl. Mech. 2010, 77. [Google Scholar] [CrossRef]
- Alexandrov, S.; Pirumov, A.; Jeng, Y.-R. Expansion/contraction of a spherical elastic/plastic shell revisited. Cont. Mech. Therm. 2015, 27, 483–494. [Google Scholar] [CrossRef]
- Manabe, K.; Nishimura, H. Influence of material properties in forming of tubes. Bander Bleche Rohre 1983, 9, 266–269. [Google Scholar]
- Mori, S.; Manabe, K.-I.; Nishimura, H. Hydraulic bulge forming of clad thin-walled tubes. Adv. Tech. Plast. 1990, 3, 1549–1554. [Google Scholar]
- Roberts, S.M.; Hall, F.; Van Bael, A.; Hartley, P.; Pillinger, I.; Sturgess, E.N.; Van Houtte, P.; Aernoudt, E. Benchmark tests for 3-D, elasto-plastic, finite-element codes for the modelling of metal forming processes. J. Mater. Process. Technol. 1992, 34, 61–68. [Google Scholar] [CrossRef]
- Abali, B.E.; Reich, F.A. Verification of deforming polarized structure computation by using a closed-form solution. Contin. Mech. Thermodyn. 2020, 32, 693–708. [Google Scholar] [CrossRef]
- Alzahrani, B.; Ngaile, G. Preliminary investigation of the process capabilities of hydroforging. Materials 2016, 9, 40. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alexandrov, S.; Lyamina, E.; Lang, L. Description of the Expansion of a Two-Layer Tube: An Analytic Plane-Strain Solution for Arbitrary Pressure-Independent Yield Criterion and Hardening Law. Metals 2021, 11, 793. https://doi.org/10.3390/met11050793
Alexandrov S, Lyamina E, Lang L. Description of the Expansion of a Two-Layer Tube: An Analytic Plane-Strain Solution for Arbitrary Pressure-Independent Yield Criterion and Hardening Law. Metals. 2021; 11(5):793. https://doi.org/10.3390/met11050793
Chicago/Turabian StyleAlexandrov, Sergei, Elena Lyamina, and Lihui Lang. 2021. "Description of the Expansion of a Two-Layer Tube: An Analytic Plane-Strain Solution for Arbitrary Pressure-Independent Yield Criterion and Hardening Law" Metals 11, no. 5: 793. https://doi.org/10.3390/met11050793
APA StyleAlexandrov, S., Lyamina, E., & Lang, L. (2021). Description of the Expansion of a Two-Layer Tube: An Analytic Plane-Strain Solution for Arbitrary Pressure-Independent Yield Criterion and Hardening Law. Metals, 11(5), 793. https://doi.org/10.3390/met11050793







