A Short Review on the Finite Element Method for Asymmetric Rolling Processes
Abstract
1. Introduction
2. Finite Element Analysis Applied to Asymmetric Rolling Processes
- build the geometrical model;
- assign the material properties;
- define time steps;
- enforce boundary conditions;
- discretize the problem domain.
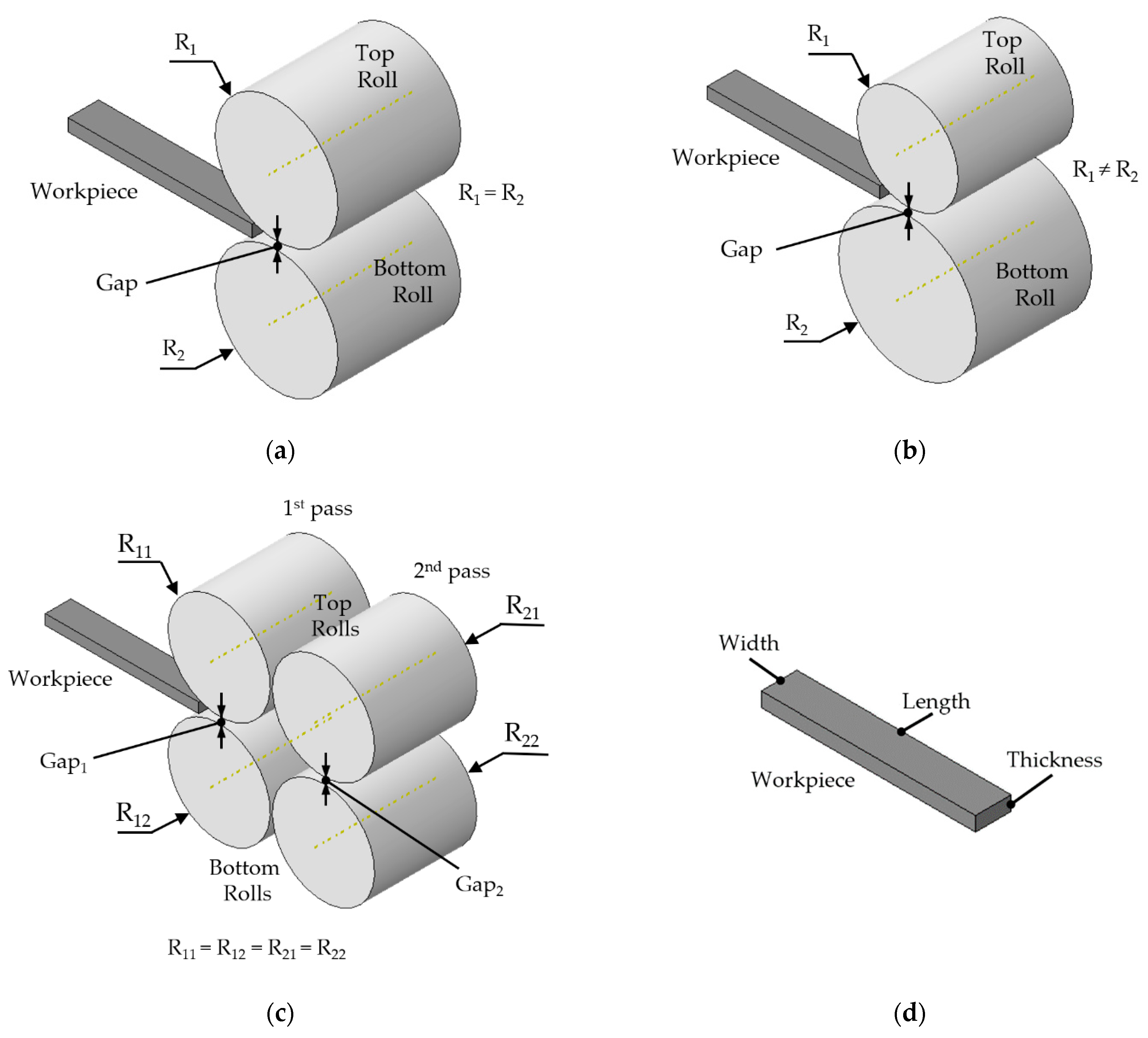
2.1. Build the Geometrical Model
2.2. Assign the Material Properties
2.3. Define Time Steps
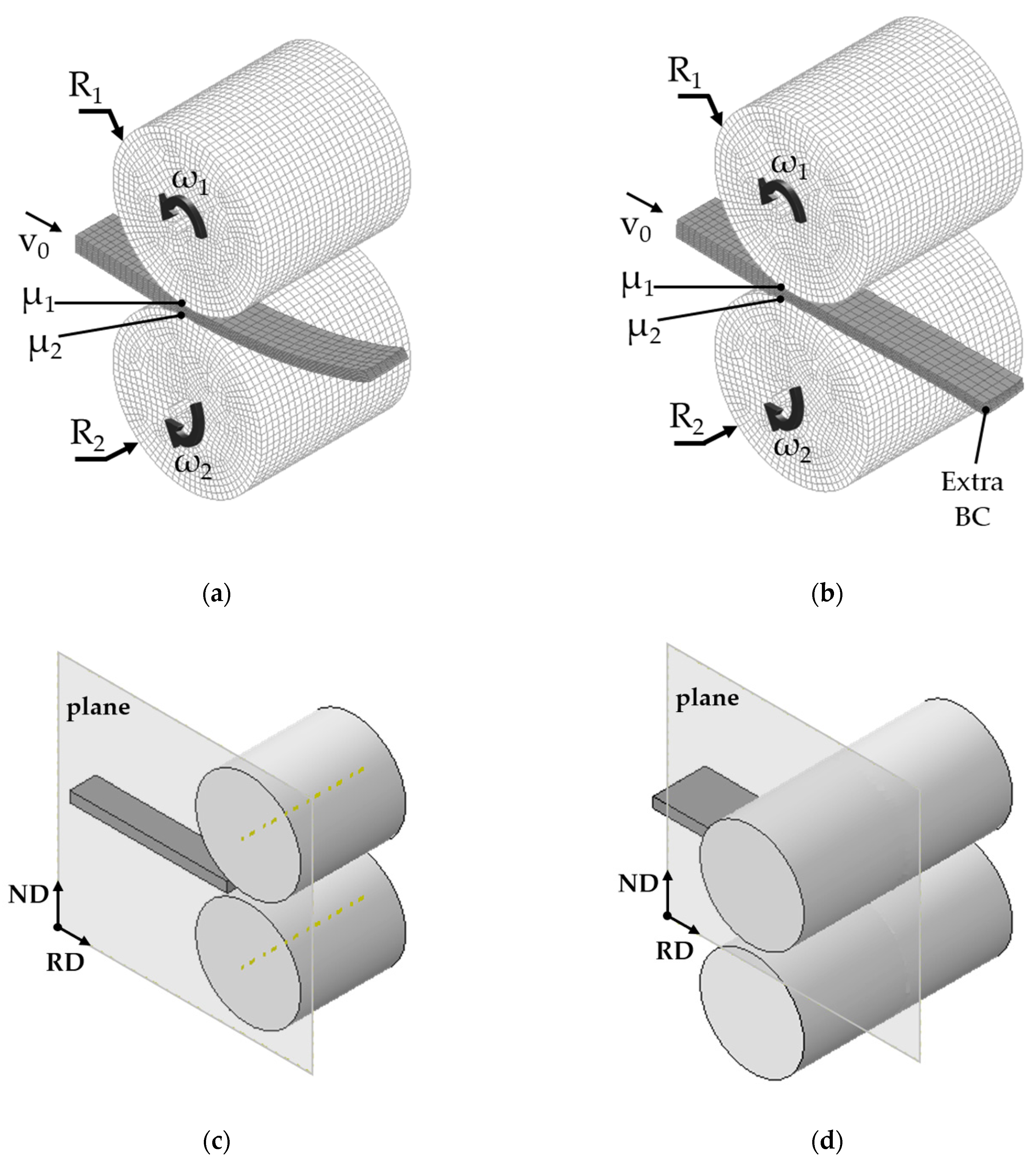
2.4. Enforce Boundary Conditions
2.5. Discretize the Problem Domain
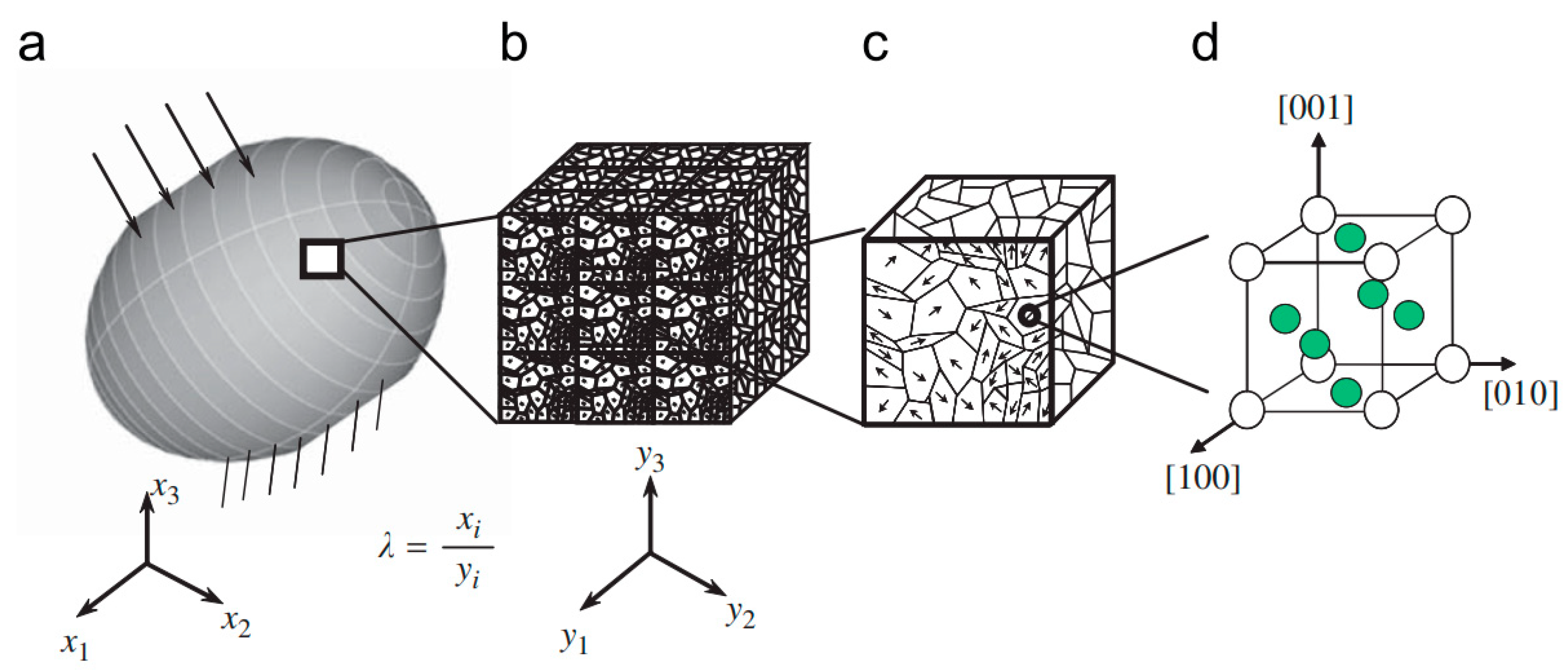
2.6. Crystallographic Models
2.6.1. Crystallographic Homogenized Model
2.6.2. Leffers-Wierzbanowski (LW) Model
2.6.3. ALAMEL Model
2.6.4. Visco-Plastic Self-Consistent (VPSC) Model
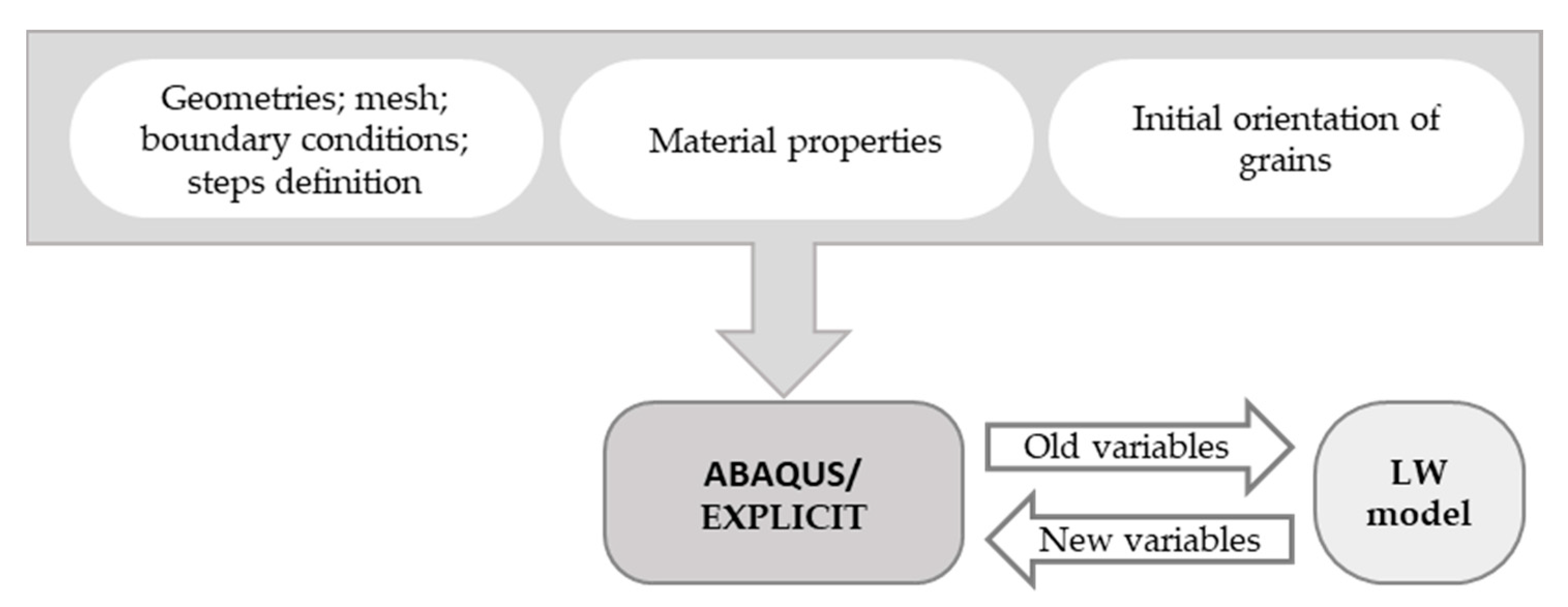
2.7. Simulation
2.8. Postprocessing
3. Summary and Final Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Shivpuri, R.; Chou, P.C.; Lau, C.W. Finite element investigation of curling in non-symmetric rolling of flat stock. Int. J. Mech. Sci. 1988, 30, 625–635. [Google Scholar] [CrossRef]
- Dyja, H.; Korczak, P.; Pilarczyk, J.W.; Grzybowski, J. Theoretical and experimental analysis of plates asymmetric rolling. J. Mater. Process. Tech. 1994, 45, 167–172. [Google Scholar] [CrossRef]
- Richelsen, A.B. Numerical analysis of asymmetric rolling accounting for differences in friction. J. Mater. Process. Tech. 1994, 45, 149–154. [Google Scholar] [CrossRef]
- Richelsen, A.B. Elastic-plastic analysis of the stress and strain distributions in asymmetric rolling. Int. J. Mech. Sci. 1997, 39, 1199–1211. [Google Scholar] [CrossRef]
- Lin, Z.C.; Shen, C.C. A three-dimensional finite element method for a nonisothermal aluminum flat strip rolling process. J. Mater. Eng. Perform. 1996, 5, 452–461. [Google Scholar] [CrossRef]
- Hwang, Y.M.; Chen, D.G.; Tzou, G.Y. Study on asymmetrical sheet rolling by the finite element method. J. Mech. 1999, 15, 149–155. [Google Scholar] [CrossRef]
- Knight, C.W.; Hardy, S.J.; Lees, A.W.; Brown, K.J. Investigations into the influence of asymmetric factors and rolling parameters on strip curvature during hot rolling. J. Mater. Process. Technol. 2003, 134, 180–189. [Google Scholar] [CrossRef]
- Lu, J.S.; Harrer, O.K.; Schwenzfeier, W.; Fischer, F.D. Analysis of the bending of the rolling material in asymmetrical sheet rolling. Int. J. Mech. Sci. 2000, 42, 49–61. [Google Scholar] [CrossRef]
- Lee, S.H.; Lee, D.N. Analysis of deformation textures of asymmetrically rolled steel sheets. Int. J. Mech. Sci. 2001, 43, 1997–2015. [Google Scholar] [CrossRef]
- Salimi, M.; Sassani, F. Modified slab analysis of asymmetrical plate rolling. Int. J. Mech. Sci. 2002, 44, 1999–2023. [Google Scholar] [CrossRef]
- Farhat-Nia, F.; Salimi, M.; Movahhedy, M.R. Elasto-plastic finite element simulation of asymmetrical plate rolling using an ALE approach. J. Mater. Process. Technol. 2006, 177, 525–529. [Google Scholar] [CrossRef]
- Akbari Mousavi, S.A.A.; Ebrahimi, S.M.; Madoliat, R. Three dimensional numerical analyses of asymmetric rolling. J. Mater. Process. Technol. 2007, 187. [Google Scholar] [CrossRef]
- Kim, J.K.; Jee, Y.K.; Huh, M.Y.; Jeong, H.T. Formation of textures and microstructures in asymmetrically cold rolled and subsequently annealed aluminum alloy 1100 sheets. J. Mater. Sci. 2004, 39, 5365–5369. [Google Scholar] [CrossRef]
- Kim, K.-H.H.; Lee, D.N.N. Analysis of deformation textures of asymmetrically rolled aluminum sheets. Acta Mater. 2001, 49, 2583–2595. [Google Scholar] [CrossRef]
- Tam, N.N.; Nakamura, Y.; Terao, T.; Kuramae, H.; Nakamachi, E.; Sakamoto, H.; Morimoto, H. Asymmetric rolling process simulations by using dynamic explicit crystallographic homogenized elasto/viscoplastic finite element method. Zair. Soc. Mater. Sci. Jpn. 2008, 57, 583–589. [Google Scholar] [CrossRef]
- Ji, Y.H.; Park, J.J. Development of severe plastic deformation by various asymmetric rolling processes. Mater. Sci. Eng. A 2009, 499, 14–17. [Google Scholar] [CrossRef]
- Sverdlik, M.; Pesin, A.; Pustovoytov, D.; Perekhozhikh, A. Numerical Research of Shear Strain in an Extreme Case of Asymmetric Rolling. In Advanced Materials Research; Trans Tech Publications Ltd.: Zurich, Switzerland, 2013; Volume 742, pp. 476–481. [Google Scholar]
- Hao, L.; Di, H.-s.; Gong, D.Y. Analysis of Sheet Curvature in Asymmetrical Cold Rolling. J. Iron Steel Res. Int. 2013, 20, 34–37. [Google Scholar] [CrossRef]
- Xie, H.B.; Manabe, K.; Jiang, Z.Y. A novel approach to investigate surface roughness evolution in asymmetric rolling based on three dimensional real surface. Finite Elem. Anal. Des. 2013, 74, 1–8. [Google Scholar] [CrossRef]
- Peng, L.; Lai, X.; Lee, H.J.; Song, J.H.; Ni, J. Friction behavior modeling and analysis in micro/meso scale metal forming process. Mater. Des. 2010, 31, 1953–1961. [Google Scholar] [CrossRef]
- Pesin, A.; Pustovoytov, D. Finite Element Simulation of Shear Strain During High-Ratio Differential Speed Rolling of Aluminum Alloy 5083. In Key Engineering Materials; Trans Tech Publications Ltd.: Zurich, Switzerland, 2016; Volume 716, pp. 700–707. [Google Scholar]
- Pesin, A.; Pustovoytov, D. Finite element simulation of extremely high shear strain during a single-pass asymmetric warm rolling of Al-6.2Mg-0.7Mn alloy sheets. Procedia Eng. 2017, 207. [Google Scholar] [CrossRef]
- Pustovoytov, D.; Pesin, A.; Biryukova, O. Finite element analysis of strain gradients in aluminium alloy sheets processed by asymmetric rolling. Procedia Manuf. 2018, 15, 129–136. [Google Scholar] [CrossRef]
- Pesin, A.; Pustovoytov, D.; Shveyova, T.; Vafin, R. Finite element simulation and comparison of a shear strain and equivalent strain during ECAP and asymmetric rolling. IOP Conf. Ser. Mater. Sci. Eng. 2018, 293. [Google Scholar] [CrossRef]
- Wroński, S.; Wierzbanowski, K.; Bacroix, B.; Chauveau, T.; Wróbel, M.; Rauch, A.; Montheillet, F.; Wroński, M. Texture heterogeneity of asymmetrically cold rolled low carbon steel. Arch. Met. Mater. 2009, 54, 89–102. [Google Scholar]
- Wroński, M.; Wierzbanowski, K.; Wróbel, M.; Wroński, S.; Bacroix, B. Effect of rolling asymmetry on selected properties of grade 2 titanium sheet. Met. Mater. Int. 2015, 21, 805–814. [Google Scholar] [CrossRef]
- Wronski, M.; Wierzbanowski, K.; Wronski, S.; Bacroix, B.; Lipinski, P. Experimental and finite element analysis of asymmetric rolling of 6061 aluminum alloy using two-scale elasto-plastic constitutive relation. Arch. Met. Mater. 2017, 62, 1991–1999. [Google Scholar] [CrossRef][Green Version]
- Nakamachi, E.; Kuramae, H.; Sakamoto, H.; Morimoto, H. Process metallurgy design of aluminum alloy sheet rolling by using two-scale finite element analysis and optimization algorithm. Int. J. Mech. Sci. 2010, 52, 146–157. [Google Scholar] [CrossRef]
- Kuramae, H.; Sakamoto, H.; Morimoto, H.; Nakamachi, E. Process metallurgy design for high-formability aluminum alloy sheet metal generation by using two-scale FEM. Procedia Eng. 2011, 10. [Google Scholar] [CrossRef]
- Tamimi, S.; Correia, J.P.; Lopes, A.B.; Ahzi, S.; Barlat, F.; Gracio, J.J. Asymmetric rolling of thin AA-5182 sheets: Modelling and experiments. Mater. Sci. Eng. A 2014, 603, 150–159. [Google Scholar] [CrossRef]
- Grácio, J.J.A.; Vincze, G.; Yoon, J.W.; Cardoso, R.P.R.; Rauch, E.F.; Barlat, F.G. Modeling the Effect of Asymmetric Rolling on Mechanical Properties of Al-Mg Alloys. Steel Res. Int. 2015, 86, 922–931. [Google Scholar] [CrossRef]
- Barlat, F.; Brem, J.C.; Yoon, J.W.; Chung, K.; Dick, R.E.; Lege, D.J.; Pourboghrat, F.; Choi, S.H.; Chu, E. Plane stress yield function for aluminum alloy sheets—Part 1: Theory. Int. J. Plast. 2003, 19, 1297–1319. [Google Scholar] [CrossRef]
- Marciniak, Z.; Kuczyński, K. Limit strains in the processes of stretch-forming sheet metal. Int. J. Mech. Sci. 1967, 9, 609–620. [Google Scholar] [CrossRef]
- Shore, D.; van Houtte, P.; Roose, D.; van Bael, A. Multiscale modelling of asymmetric rolling with an anisotropic constitutive law. Comptes Rendus Mecanique 2018, 346, 724–742. [Google Scholar] [CrossRef]
- Yekta, R.; Zohoor, H.; Motekallem, A. Analysis of asymmetric cold rolling using finite-element method for creating at sheet. Sci. Iran. 2018, 25, 3133–3140. [Google Scholar] [CrossRef]
- Hwang, Y.-M.; Tzou, G.-Y.I. Analytical and experimental study on asymmetrical sheet rolling. Int. J. Mech. Sci. 1997, 39, 289–303. [Google Scholar] [CrossRef]
- Qwamizadeh, M.; Kadkhodaei, M.; Salimi, M. Asymmetrical sheet rolling analysis and evaluation of developed curvature. Int. J. Adv. Manuf. Technol. 2012, 61, 227–235. [Google Scholar] [CrossRef]
- Feng, Y.; Liu, W.; Yang, T.; Du, F.; Sun, J. Theoretical and experimental analysis of the deformation zone and minimum thickness in single-roll-driven asymmetric ultrathin strip rolling. Int. J. Adv. Manuf. Technol. 2019, 104, 2925–2937. [Google Scholar] [CrossRef]
- Zanchetta, B.D.; da Silva, V.K.; Sordi, V.L.; Rubert, J.B.; Kliauga, A.M. Effect of asymmetric rolling under high friction coefficient on recrystallization texture and plastic anisotropy of AA1050 alloy. Trans. Nonferrous Met. Soc. China (Engl. Ed.) 2019, 29, 2262–2272. [Google Scholar] [CrossRef]
- Godoi, R.P.; Camilo Magalhães, D.C.; Avalos, M.; Bolmaro, R.E.; Sordi, V.L.; Kliauga, A.M. Microstructure, texture and interface integrity in sheets processed by Asymmetric Accumulative Roll-Bonding. Mater. Sci. Eng. A 2020, 771. [Google Scholar] [CrossRef]
- Kraner, J.; Fajfar, P.; Palkowski, H.; Kugler, G.; Godec, M.; Paulin, I. Microstructure and texture evolution with relation to mechanical properties of compared symmetrically and asymmetrically cold rolled aluminum alloy. Metals (Basel) 2020, 10, 156. [Google Scholar] [CrossRef]
- Zhang, T.; Li, L.; Lu, S.-H.; Gong, H.; Wu, Y.-X. Comparisons of Different Models on Dynamic Recrystallization of Plate during Asymmetrical Shear Rolling. Materials (Basel) 2018, 11, 151. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, Y.X.; Gong, H.; Shi, W.Z.; Jiang, F.M. Flow stress behaviour and constitutive model of 7055 aluminium alloy during hot plastic deformation. Mechanika 2016, 22, 359–365. [Google Scholar] [CrossRef]
- Vincze, G.; Simões, F.J.P.; Butuc, M.C. Asymmetrical Rolling of Aluminum Alloys and Steels: A Review. Metals (Basel) 2020, 10, 1126. [Google Scholar] [CrossRef]
- Kraner, J.; Smolar, T.; Volsak, D.; Cvahte, P.; Godec, M.; Paulin, I. A review of asymmetric rolling. Materiali in Tehnologije 2020, 54, 731–743. [Google Scholar] [CrossRef]
- Ji, Y.H.; Park, J.J.; Kim, W.J. Finite element analysis of severe deformation in Mg-3Al-1Zn sheets through differential-speed rolling with a high speed ratio. Mater. Sci. Eng. A 2007, 454, 570–574. [Google Scholar] [CrossRef]
- Kim, W.J.; Hwang, B.G.; Lee, M.J.; Park, Y.B. Effect of speed-ratio on microstructure, and mechanical properties of Mg-3Al-1Zn alloy, in differential speed rolling. J. Alloy. Compd. 2011, 509, 8510–8517. [Google Scholar] [CrossRef]
- Wronski, M.; Wierzbanowski, K.; Wronski, S.; Bacroix, B.; Lipinski, P. Texture variation in asymmetrically rolled titanium. Study by Finite Element Method with implemented crystalline model. Int. J. Mech. Sci. 2014, 87, 258–267. [Google Scholar] [CrossRef]
- Pesin, A.; Chukin, M.; Korchunov, A.; Pustovoytov, D. Finite element modeling of shear strain in asymmetric and symmetric rolling in multi roll calibers. Procedia Eng. 2014, 81, 2469–2474. [Google Scholar] [CrossRef]
- Park, J.J. Finite-element analysis of severe plastic deformation in differential-speed rolling. Comput. Mater. Sci. 2015, 100, 61–66. [Google Scholar] [CrossRef]
- Uniwersał, A.; Wróbel, M.; Wierzbanowski, K.; Wroński, S.; Wroński, M.; Kalemba-Rec, I.; Sak, T.; Bacroix, B. Microstructure, texture and mechanical characteristics of asymmetrically rolled polycrystalline copper. Mater. Charact. 2016, 118, 575–583. [Google Scholar] [CrossRef]
- Angella, G.; Esfandiar Jahromi, B.; Vedani, M. A comparison between equal channel angular pressing and asymmetric rolling of silver in the severe plastic deformation regime. Mater. Sci. Eng. A 2013, 559, 742–750. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Tieu, A.K.; Zhang, X.M.; Lu, C.; Sun, W.H. Finite element simulation of cold rolling of thin strip. J. Mater. Process. Technol. 2003, 140, 542–547. [Google Scholar] [CrossRef]
- Ren, Z.; Xiao, H.; Liu, X.; Wang, G. Experimental and theoretical analysis of roll flattening in the deformation zone for ultra-thin strip rolling. Ironmak. Steelmak. 2018, 45, 805–812. [Google Scholar] [CrossRef]
- Wronski, M.; Wierzbanowski, K.; Bacroix, B.; Lipinski, P. Asymmetric rolling textures of aluminium studied with crystalline model implemented into FEM. IOP Conf. Ser. Mater. Sci. Eng. 2015, 82. [Google Scholar] [CrossRef]
- Shore, D.; Kestens, L.A.I.; Sidor, J.; van Houtte, P.; van Bael, A. Process parameter influence on texture heterogeneity in asymmetric rolling of aluminium sheet alloys. Int. J. Mater. 2016, 11, 297–309. [Google Scholar] [CrossRef]
- Gudur, P.P.; Salunkhe, M.A.; Dixit, U.S. A theoretical study on the application of asymmetric rolling for the estimation of friction. Int. J. Mech. Sci. 2008, 50, 315–327. [Google Scholar] [CrossRef]
- Wanheim, T.; Bay, N. A model for friction in metal forming processes. CIRP Ann. Manuf. Technol. 1978, 27, 189–194. [Google Scholar]
- Nielsen, C.V.; Bay, N. Overview of friction modelling in metal forming processes. Procedia Eng. 2017, 207, 2257–2262. [Google Scholar] [CrossRef]
- Nakamachi, E.; Tam, N.N.; Morimoto, H. Multi-scale finite element analyses of sheet metals by using SEM-EBSD measured crystallographic RVE models. Int. J. Plast. 2007, 23, 450–489. [Google Scholar] [CrossRef]
- Leffers, T. Computer simulation of the plastic deformation in face-centred cubic polycrystals and the rolling texture derived. Phys. Status Solidi 1968, 25, 337–344. [Google Scholar] [CrossRef]
- Wierzbanowski, K.; Jura, J.; Haije, W.G.; Helmholdt, R.B. F.C.C. Rolling Texture Transitions in Relation to Constraint Relaxation. Cryst. Res. Technol. 1992, 27, 513–522. [Google Scholar] [CrossRef]
- Wierzbanowski, K.; Baczmański, A.; Lipiński, P.; Lodini, A. Elasto-plastic models of polycrystalline material deformation and their applications. Arch. Met. Mater. 2007, 52, 77–86. [Google Scholar]
- Wierzbanowski, K.; Wroński, M.; Leffers, T. F.C.C. Rolling Textures Reviewed in the Light of Quantitative Comparisons between Simulated and Experimental Textures. Crit. Rev. Solid State Mater. Sci. 2014, 39, 391–422. [Google Scholar] [CrossRef]
- Van Houtte, P.; Yerra, S.K.; van Bael, A. The Facet method: A hierarchical multilevel modelling scheme for anisotropic convex plastic potentials. Int. J. Plast. 2009, 25, 332–360. [Google Scholar] [CrossRef]
- Van Houtte, P.; Li, S.; Seefeldt, M.; Delannay, L. Deformation texture prediction: From the Taylor model to the advanced Lamel model. Int. J. Plast. 2005, 21, 589–624. [Google Scholar] [CrossRef]
- Taylor, G.I. Plastic Strain in Metals. J. Inst. Met. 1938, 62, 307–324. [Google Scholar]
- Bishop, J.F.W.; Hill, R. CXXVIII. A theoretical derivation of the plastic properties of a polycrystalline face-centred metal. Philos. Mag. J. Sci. Ser. 7 1951, 42, 1298–1307. [Google Scholar] [CrossRef]
- Molinari, A.; Canova, G.R.; Ahzi, S. A self consistent approach of the large deformation polycrystal viscoplasticity. Acta Met. 1987, 35, 2983–2994. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Tomé, C.N. A self-consistent anisotropic approach for the simulation of plastic deformation and texture development of polycrystals: Application to zirconium alloys. Acta Met. Mater. 1993, 41, 2611–2624. [Google Scholar] [CrossRef]
- Takajo, S.; Vogel, S.C.; Tomé, C.N. Viscoplastic self-consistent polycrystal modeling of texture evolution of ultra-low carbon steel during cold rolling. Model. Simul. Mater. Sci. Eng. 2019, 27, 045003. [Google Scholar] [CrossRef]
- Walde, T.; Riedel, H. Simulation of earing during deep drawing of magnesium alloy AZ31. Acta Mater. 2007, 55, 867–874. [Google Scholar] [CrossRef]
- Segurado, J.; Lebensohn, R.A.; Llorca, J.; Tomé, C.N. Multiscale modeling of plasticity based on embedding the viscoplastic self-consistent formulation in implicit finite elements. Int. J. Plast. 2012, 28, 124–140. [Google Scholar] [CrossRef]
- Galán, J.; Verleysen, P.; Lebensohn, R.A. An improved algorithm for the polycrystal viscoplastic self-consistent model and its integration with implicit finite element schemes. Model. Simul. Mater. Sci. Eng. 2014, 22. [Google Scholar] [CrossRef]
- Prakash, A.; Nöhring, W.G.; Lebensohn, R.A.; Höppel, H.W.; Bitzek, E. A multiscale simulation framework of the accumulative roll bonding process accounting for texture evolution. Mater. Sci. Eng. A 2015, 631, 104–119. [Google Scholar] [CrossRef]
- Dhinwal, S.S.; Toth, L.S. Unlocking deformation path in asymmetric rolling by texture simulation. Materials (Basel) 2020, 13, 101. [Google Scholar] [CrossRef]
- Xie, Q.; Eyckens, P.; Vegter, H.; Moerman, J.; van Bael, A.; van Houtte, P. Polycrystal plasticity models based on crystallographic and morphologic texture: Evaluation of predictions of plastic anisotropy and deformation texture. Mater. Sci. Eng. A 2013, 581, 66–72. [Google Scholar] [CrossRef]
| Geometrical Parameters | Boundary Conditions | Ref. No. | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Workpiece Dimensions (mm) 1 | Rolls Diameters (mm) 1 | Passes (No.) | Total Red. (%) 2 | Angular Velocities (rpm) 1 | Friction Coefficients | — | |||||
| Length | Width | Thickness | |||||||||
| 254 | 127/ 177.8 | 63.5 | 193.8 | 193.8 | single | 25 | var | var | 1 | 1 | [1] |
| — | — | 8–15 | 1000 | 1000 | multi (2) | — | var | var | 0.2 | 0.3 | [2] |
| 25.1 | 18.82 | 6.27 | 158.76 | 158.76 | single | 14.17 | 19.20 | 19.20 | — | — | [5] |
| 200 | var | 6/10 | 210/ 186 | 210/ 200 | single | 5:5:20/30 | 0.92/ 1.42 | 1/ 1.53 | 0.2/0.4/ 0.8/1.0 | 0.6 | [6] |
| — | — | 5/10 | var | var | single | 20:10:40 | var | var | 0.3 | 0.3 | [8] |
| — | — | 3.2 | 189/ 126 | 126 | multi (3) | 50 | var | var | 0.3 | 0.3 | [9] |
| — | — | 2 | 189 | 126 | multi | 80 | — | — | 0.4 | 0.4 | [14] |
| — | — | 206/ 54.2 | 1200 | 1200 | single | 10:10:40 | var | var | var | var | [7] |
| — | — | 4 | 128 | 128 | single | 37.5 | 18 | 12 | 0.2 | 0.2 | [13] |
| — | — | 5/10 | var | var | single | 12/25/40 | var | var | var | var | [11] |
| — | 80 | 2 | var | 210 | single | var | var | 28.65 | 0.15 | 0.15 | [12] |
| 36 | 0.4 | 6 | — | — | multi (3) | 83 | var | 0.2 | 0.2 | [15] | |
| — | — | 16 | var | 500 | single | 50 | var | 9.55 | var | 0.7 | [16] |
| 2.5 | 30 | 60 | 66 | 66 | single | 10–30 | 26.45 | 25.50 | 0.25 | 0.25 | [25] |
| 40 | — | 6 | 450 | 450 | multi (2) | 50 | var | var | — | — | [28] |
| 40 | — | 6 | 450 | 450 | multi (2) | 75 | 1080 | 2160 | 0.5 | 0.5 | [29] |
| — | — | 3 | 400 | 400 | single | 10:20:70/80 | var | 47.75 | 0.5 | 0.5 | [17] |
| — | — | 2 | var | 480 | single | 10/25/40 | 38.2 | 38.2 | 0.3 | 0.3 | [18] |
| 200 | var | 1.5/1.8/ 2.0 | 125 | 125 | single | 10/20 30 | var | var | 0.035 4 0.025 5 | 0.035 4 0.025 5 | [19] |
| 60 | — | 1.2 | 180 | 180 | multi | 50 | var | 2 | 0.05 | 0.15 | [30] |
| — | — | — | 180 | 180 | single | 36 | var | var | 0.1/0.4 | 0.1/0.4 | [55] |
| 25 | 20 | 2 | 200 | 200 | two | 75 | var | 0.95 | 0.3 | 0.3 | [21] |
| — | — | 2.9 | 180 | 180 | single | 36 | var | 10 | 0.1–0.4 | 0.1–0.4 | [27] |
| 50–100 | — | 1–8 | var | var | single | 10:10:60 | var | var | 0.3 | 0.3 | [22] |
| — | — | 1–8 | 50–500 | 50–500 | single | 10:10:60 | var | var | var | var | [23] |
| 40 | 40 | 1 | 500 | 500 | single | 60 | 3.82 | var | 0.1–0.4 | 0.1–0.4 | [24] |
| — | — | — | — | — | single | 20:10:40 | var | var | 0.4 | 0.4 | [34] |
| — | 100 | 2 | 100 | 120 | single | 10 | var | 50.6 | 0.359 | 0.359 | [35] |
| 50 | — | 0.2 | 80 | 270 | single | var | — | — | 0.2 | 0.2 | [38] |
| — | — | 7 | var | multi | 70 | 23 | 23 | — | — | [39] | |
| 35 | 20 | var | var | single | 50 | 24 | 24 | 0.9 | 0.9 | [40] | |
| 510 | 230 | 6.7 | 295 | 295 | single | 33/44 | var | var | 0.45 | 0.45 | [41] |
| — | — | 250 | 1000 | 1000 | single | 12/20 | 1 3 | 1.3 3 | 0.4 | 0.4 | [42] |
| Material | Temp. (°C) | (kg/m3) | E (GPa) | Constitutive Law | Crystal Plasticity Parameters 1 | Ref. No. | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n | C | ||||||||||
| Mild steel | 1200 | 6920 | — | — | n/a | n/a | n/a | n/a | n/a | [1] | |
| Low carbon steel | 1027 | — | — | — | n/a | n/a | n/a | n/a | n/a | [2] | |
| Aluminum | RT 420 | 2600 | 68.5 | 0.33 | — | n/a | n/a | n/a | n/a | n/a | [5] |
| Steel | RT | — | — | — | — | n/a | n/a | n/a | n/a | n/a | [6] |
| C15 | — | — | — | — | — | n/a | n/a | n/a | n/a | n/a | [8] |
| Steel | 700 | — | 110 | — | — | n/a | n/a | n/a | n/a | n/a | [9] |
| Aluminum | RT | — | — | — | — | — | — | — | — | [14] | |
| Low carbon steel | var | — | — | — | — | n/a | n/a | n/a | n/a | n/a | [7] |
| AA 1100 | RT | — | — | — | — | — | — | — | — | — | [13] |
| Aluminum | RT | — | 68 | 0.3 | n/a | n/a | n/a | n/a | n/a | [11] | |
| AA 1050P | RT | — | 69 | — | n/a | n/a | n/a | n/a | n/a | [12] | |
| AA 6022 | 250 | — | 70.2 | 0.3 | — | 16.4 | 0.26 | 24 | 6 | 0.004 | [15] |
| AISI-1015 | 1200 | — | — | — | n/a | n/a | n/a | n/a | n/a | [16] | |
| Low carbon steel | RT | — | 210 | 0.3 | — | — | — | — | — | — | [25] |
| AA 6022 | 250 | — | — | — | 16.5 | 0.26 | 22.5 | 5.6 | 0.005 | [28] | |
| AA 6022 | RT | — | — | — | 67.3 | 0.26 | 28.7 | 6 | 0.044 | [29] | |
| AA 6022 | 250 | — | — | — | 26.9 | 0.26 | 6.5 | 6 | 0.044 | [29] | |
| AISI-1045 | RT | — | — | — | — | n/a | n/a | n/a | n/a | n/a | [17] |
| Q235 | RT | — | 210 | — | n/a | n/a | n/a | n/a | n/a | [18] | |
| Steel | RT | 7850 | 117 | 0.3 | — | n/a | n/a | n/a | n/a | n/a | [19] |
| AA 182 | RT | 2700 | 68.1 | 0.3 | 55 | — | — | — | — | [30] | |
| AA 6061 | RT | — | — | — | — | — | — | — | — | — | [55] |
| AA 5083 | RT | — | — | — | — | n/a | n/a | n/a | n/a | n/a | [21] |
| AA 6061 | RT | 2700 | 70 | 0.34 | — | 70 | — | 390 | — | — | [27] |
| Al-6.2Mg-0.7Mn | 200 | 2700 | — | — | — | n/a | n/a | n/a | n/a | n/a | [22] |
| Al-6.2Mg-0.7Mn | 200 | 2700 | — | — | — | n/a | n/a | n/a | n/a | n/a | [23] |
| AA 5083 | RT | — | — | — | — | n/a | n/a | n/a | n/a | n/a | [24] |
| AA 6016-HR AA 1050-CR | (Hot) | — | — | — | — | — | — | — | — | [34] | |
| Aluminum | RT | 2710 | 70 | 0.3 | — | n/a | n/a | n/a | n/a | n/a | [35] |
| 9Cr2Mo | RT | — | 204 | 0.285 | — | n/a | n/a | n/a | n/a | n/a | [38] |
| AA 1050 | RT | — | 71 | — | n/a | n/a | n/a | n/a | n/a | [39] | |
| AA 1050 | 350 400 | — | — | — | — | n/a | n/a | n/a | n/a | n/a | [40] |
| AA 5454 | RT | 2690 | 70.5 | 0.33 | — | n/a | n/a | n/a | n/a | n/a | [41] |
| AA 7055 | 410 | — | — | — | (2) | — | — | — | — | — | [42] |
| Initial Orientation | Rotation | Orientation before the 2nd Pass |
|---|---|---|
| Case 1 | 0° (no rotation) | |
 | 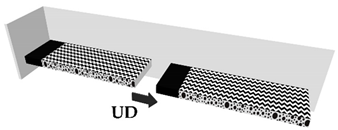 |  |
| Case 2 | 180° about the Transversal Direction | |
 | 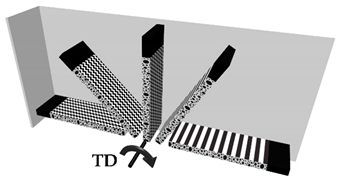 |  |
| Case 3 | 180° about the Rolling Direction | |
 |  |  |
| Case 4 | 180° about the Normal Direction | |
 | 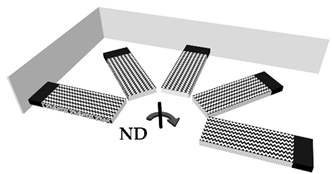 |  |
| Rolls Elements | Workpiece Elements | CP Grains 1 | Model | Software | Ref. No. | ||
|---|---|---|---|---|---|---|---|
| Type | No. | Type | No. | — | — | ||
| triangular | 90 | triangular | 1120 | n/a | Elastic-plastic FEM | DEFEL | [1] |
| — | — | — | — | n/a | Coupled FEM rigid-plastic with a general diffusion equation for the thermal phenomena in the deformation zone | — | [2] |
| — | — | — | — | n/a | Coupled thermo-elastic-plastic FEM | — | [5] |
| — | — | isoparametric | 500 | n/a | — | DEFORM | [6] |
| 2-node linear rigid | 4-node bilinear with reduced integration and hourglass control | — | n/a | Elastic-plastic FEM | — | [8] | |
| — | — | — | — | n/a | Elastic-plastic | — | [9] |
| — | — | — | — | — | Elastic-plastic FEM coupled with Taylor and the Renouward–Wintenberger theories | — | [14] |
| — | — | — | — | n/a | Elastic-plastic FEM | ABAQUS | [7] |
| — | — | — | — | — | Elastic-plastic FEM | — | [13] |
| — | — | 4-node quadrilateral | 800 | n/a | 2D elastic–plastic Arbitrary Lagrangian–Eulerian (ALE) | — | [11] |
| — | — | — | — | n/a | Elastic-plastic FEM | ABAQUS | [12] |
| — | — | — | 720 (1 × 144 × 5) | 19,440 (27 × 144 × 5) | Crystallographic homogenized FEM | — | [15] |
| — | — | — | — | n/a | Rigid-viscoplastic FEM method | DEFORM | [16] |
| — | — | — | — | 5000 | Elasto-plastic FEM coupled with LW model | ABAQUS | [25] |
| — | — | 8-node isoparametric solid | 800 (160 × 5) | 100,000 (125 × 160 × 5) | Crystallographic homogenized elasto-viscoplastic FEM | [28] | |
| — | — | — | 800 | 21,600 (27 × 800) | Crystallographic homogenized elasto-viscoplastic FEM and a discrete optimization method | [29] | |
| — | — | — | — | n/a | — | DEFORM | [17] |
| 2-node linear discrete rigid | — | 4-node bilinear reduced integration and hourglass control | — | n/a | Elastic-plastic | ABAQUS | [18] |
| 8-node solid (SOLID164) | — | 8-node solid (SOLID164) | 121,378 | n/a | Elastic-plastic | LS-DYNA | [19] |
| — | — | — | 9 elements in thickness | — | Elastic-plastic FEM coupled with VPSC | ABAQUS | [30] |
| — | — | 8-node brick element with reduced integration (C3D8R) | 128 (16 × 1 × 8) | — | FEM coupled LW model | ABAQUS | [55] |
| — | — | brick | 14,220 | n/a | Rigid-plastic | DEFORM 3D | [21] |
| — | — | 8-node brick element with reduced integration (C3D8R) | 128 | 19,200 (150 × 128) | FEM coupled LW model | ABAQUS | [27] |
| brick | 10,000 .. 12,000 | brick | 1000 .. 1200 | n/a | Rigid-plastic | DEFORM 2D | [22] |
| brick | 10,000 .. 12,000 | brick | 1000 .. 1200 | n/a | Rigid-plastic | DEFORM 2D | [23] |
| — | — | brick | 40,000 | n/a | Rigid-plastic | DEFORM 3D | [24] |
| — | — | — | 1000 .. 2500 | — | FACET/ALAMEL | ABAQUS + PYTHON | [34] |
| — | 11,368 | 4-node plane strain element | 28,000 | n/a | — | MSC.Marc | [38] |
| — | — | — | — | n/a | Elastic-plastic | DEFORM | [39] |
| — | — | — | — | n/a | Elastic-plastic | DEFORM 3D | [40] |
| — | — | — | — | n/a | — | ABAQUS | [41] |
| — | — | — | — | — | FEM coupled microstructure evolution model | — | [42] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Graça, A.; Vincze, G. A Short Review on the Finite Element Method for Asymmetric Rolling Processes. Metals 2021, 11, 762. https://doi.org/10.3390/met11050762
Graça A, Vincze G. A Short Review on the Finite Element Method for Asymmetric Rolling Processes. Metals. 2021; 11(5):762. https://doi.org/10.3390/met11050762
Chicago/Turabian StyleGraça, Ana, and Gabriela Vincze. 2021. "A Short Review on the Finite Element Method for Asymmetric Rolling Processes" Metals 11, no. 5: 762. https://doi.org/10.3390/met11050762
APA StyleGraça, A., & Vincze, G. (2021). A Short Review on the Finite Element Method for Asymmetric Rolling Processes. Metals, 11(5), 762. https://doi.org/10.3390/met11050762







