Behavior of Inelastic and Plastic Strains in Coarse-Grained Ti_49.3Ni_50.7(at%) Alloy Deformed in B2 States

Abstract

The regularities of the change in inelastic strain in coarse-grained samples of the Ti_49.3Ni_50.7 (at%) alloy are studied when the samples are given torsional strain in the state of the high-temperature B2 phase. During cooling and heating, the investigated samples underwent the B2–B19′ martensite transformation (MT); the temperature of the end of the reverse MT was A_f = 273 K. It was found that at the temperature of isothermal cycles “loading-unloading” A_f + 8 K, when the specimen is assigned a strain of 4%, the effect of superelasticity is observed. With an increase in the torsional strain, the shape memory effect is clearly manifested. It is assumed that the stabilization of the B19′ phase in unloaded samples is due to the appearance of dislocations during deformation due to high internal stresses at the interphase boundaries of the B2 phase and the martensite phase during MT. The appearance of dislocations during the loading of samples near the temperatures of forward and reverse MT can also be facilitated by the “softening” of the elastic moduli of the alloy in this temperature range. At a test temperature above A_f + 26 K, the superelasticity effect dominates in the studied samples.

1. Introduction

The significant interest in smart TiNi materials owes to the unique combination of their functional, strength, and plastic properties beneficial for engineering and medicine [1,2,3,4,5,6,7,8,9,10,11,12]. Their superelasticity (SE) and shape memory effect (SME) are provided by thermoelastic martensite transformations (MT) from a cubic B2 phase to a rhombohedral R or a monoclinic B19′ phase. When cooled and heated free of load or at low internal stress, such materials remain macroscopically invariant as their thermoelastic transformations result in a polyvariant system of self-accommodated martensite domains [4], but when exposed to external or oriented internal stresses, they display superelasticity and shape memory. Shape memory allows a material to accumulate reversible inelastic strains at T_d < M_f (where T_d is the deformation temperature and M_f is the martensite finish temperature on cooling) and to recover them at above A_f (which is the austenite finish temperature on heating). Superelasticity allows a material to change its macroscopic shape or linear dimensions through direct B2 → B19′ or B2 → R → B19′ transformations under external stress (tension, torsion, bending) at T > A_f and to take it back through inelastic strain recovery under subsequent isothermal unloading (because no martensite free of load can exist at this temperature). In both cases, the reversible inelastic strain can reach 6–8%. The inelastic strain, whether from SE or SME, depends largely on the crystallography limit of the recoverable strain whose value in TiNi-based alloys measures, on average, 11% [13,14,15].

However, reversible inelastic strains 1.5–2 times higher than the above limit have been found in TiNi-based alloys [16,17,18,19,20,21,22,23] after bending [15,16,17,18,20], torsion [20,21,22,23], and tension [19], with the total strain comprising an inelastic and a plastic component. For example, a reversible inelastic strain of up to 18% is attainable in Ti_49.3Ni_50.7 (at%) after torsion at T < M_f against a high (12%) plastic strain [23]. Its recovery is stepwise: via SE under unloading at T_d and via SME under further heating above the finish temperature of B19′ → B2 MT.

In one of the cited studies [16], Ti_49.3Ni_50.7 (at%) specimens differing in structure were bent to a total strain of 15% and were then kept constrained at 310 K (to prevent shape recovery), cooled to 77 K with keeping at this temperature for 30 s, and unloaded with further heating to room temperature. In nanocrystalline Ti_49.3Ni_50.7 (at%) (grain size 30–70 nm), the total strain was recovered completely so that 7.5% fell on SE and 7.5% on SME. In Ti_49.3Ni_50.7 (at%) with a mixed structure (nanocrystalline, subgrain), the strain recovery via SME was 14.8% against 0.2% of plastic strain, and in its specimens with microcrystalline structure (maximum grain size 10 µm), the SME value was 10% against up to 5% of plastic strain and zero SE.

In another study [17], Ti₅₀Ni₅₀ (at%) specimens annealed after cold drawing were bent at 5 K above A_f with further keeping at this temperature for 30 s, cooling in their constrained state to 273 K, and keeping at this temperature for 30 s. Thereafter, estimates of their strain recovery were taken under unloading (SE, including small elastic strain) and under further heating to 373 K (SME). The plastic strain is the residual one at 373 K. In Ti₅₀Ni₅₀ (at%) with a polygonized B2 substructure (annealing at 623 K for 1 h, subgrain size ≤ 200 nm), the strain recovery via SE and SME at a total strain of 18% measured 10.3% and 7.6%, respectively, against 0.1% of plastic strain; the total inelastic strain was 17.9%. In Ti₅₀Ni₅₀ (at%) with a polygonized B2 substructure comprising individual recrystallized grains of up to 3 μm (annealing at 723 K for 1 h), the strain recovery via SE and SME at the same total strain measured 7.2% and 8%, respectively, against 2.8% of plastic strain; the total inelastic strain reached 15.2%.

Thus, it is still unclear what conditions can bring the reversible inelastic strain in TiNi materials to above their theoretical limit. Clarifying this issue needs additional studies of TiNi alloys differing in chemical composition, structure (grain-subgrain size), and phase state. Here, we analyze the behavior of inelastic and plastic strains in coarse-grained Ti_49.3Ni_50.7 (at%) deformed at T_d > A_f.

2. Materials and Methods

The test material was Ti_49.3Ni_50.7 (at%) supplied as hot-swaged bars of diameter 30 mm (Matek-Sma Ltd., Moscow, Russia). The bars were spark cut into specimens (cross-sectional area ~1 mm², gage length ~10 mm), rinsed in ethanol, grinded with an abrasive and diamond paste, and electrolytically polished with plane stainless steel electrodes in a cold CH₃COOH/HClO₄ solution (75/25 vol%) at a voltage of 12–17 V for 10–15 s. For further structural analysis, they were chemically etched in a HNO₃/HF/H₂O mixture (14/4/82 vol%) for 15 s.

Their structure and phase state were analyzed on a DRON-7 diffractometer in Co-K_α radiation (Bourevestnik JSC, Saint-Petersburg, Russia) and on an AXIOVERT-200 MAT optical microscope (Carl Zeiss AG, Oberkochen, Germany). According to the analysis, the specimens at room temperature were in the state of a high-temperature B2 phase (CsCl superstructure) with less than 5 vol% of Ti₄Ni₂(O,N,C,H)_x. The average grain size was 53 ± 11 μm. The deformation-induced surface microrelief after torsion were studied by scanning electron microscopy LEO EVO 50XVP (Carl Zeiss AG, Oberkochen, Germany). These studies were conducted using the equipment of Nanotech shared Use Center of ISPMS SB RAS.

The temperatures and sequence of martensite transformations were determined by temperature resistometry (ρ(T) measurements). On cooling and heating, the specimens experienced martensite transformations B2 ↔ B19′. The start and finish temperatures of B2 → B19′ MT are M_S = 252 K, M_f = 223 K. The start and finish temperatures of B19′ → B2 MT are A_S = 258 K, A_f = 273 K.

The inelastic and plastic strains in the material were studied on an inverted torsion pendulum with an operating temperature of 573–120 K. The τ–γ dependences in isothermal loading–unloading cycles, and the inelastic strain recovery on further heating to 500 K (227 K above A_f) of unloaded specimens were obtained. In each cycle, the total strain γ_t was successively increased up to fracture. The temperature of loading–unloading cycles was 281, 299, 309, 315, and 339 K, i.e., T_d was above A_f and specimens were in the B2 state.

All components of the total strain γ_t were determined. The total strain is the sum of inelastic and plastic strains: γ_t = γ_SID + γ_pl. The total inelastic strain is γ_SID = γ_SE + γ_SME, where the summands stand for inelastic strains recovered via superelasticity, γ_SE, under isothermal unloading (including a small Hook strain of ~1.5%) and via shape memory, γ_SME, under further heating to complete shape recovery (via B19′ → B2 transformation). In more detail, the total inelastic strain has the form:

γ_SID = (γ_t − γ_r) + (γ_r − γ_pl) = γ_SE + γ_SME

(1)

where γ_r is the residual strain after isothermal unloading (295 K), and γ_t, γ_r, and γ_pl are equal to arctgS_t, arctgS_r, and arctgS_pl, with S_t = (rφ_t)/l; S_r = (rφ_r)/l; and S_pl = (rφ_pl)/l; having r and l for the specimen cross-section radius and gage length and φ_t, φ_r, and φ_pl for the torsion angles in radians after loading, unloading, and heating to 500 K, respectively. The plastic strain γ_pl is equal to the residual strain at 500 K. The γ_t, γ_r, γ_pl, γ_SE and γ_SME strains are presented in Figure 1. The measurement error for the quantities depended on the total strain, and at γ_t = 36.6%, it was Δγ_t = 0.3%, Δγ_SE = 0.4%, Δγ_SME = 0.4%, and Δγ_pl = 0.2%.

3. Results

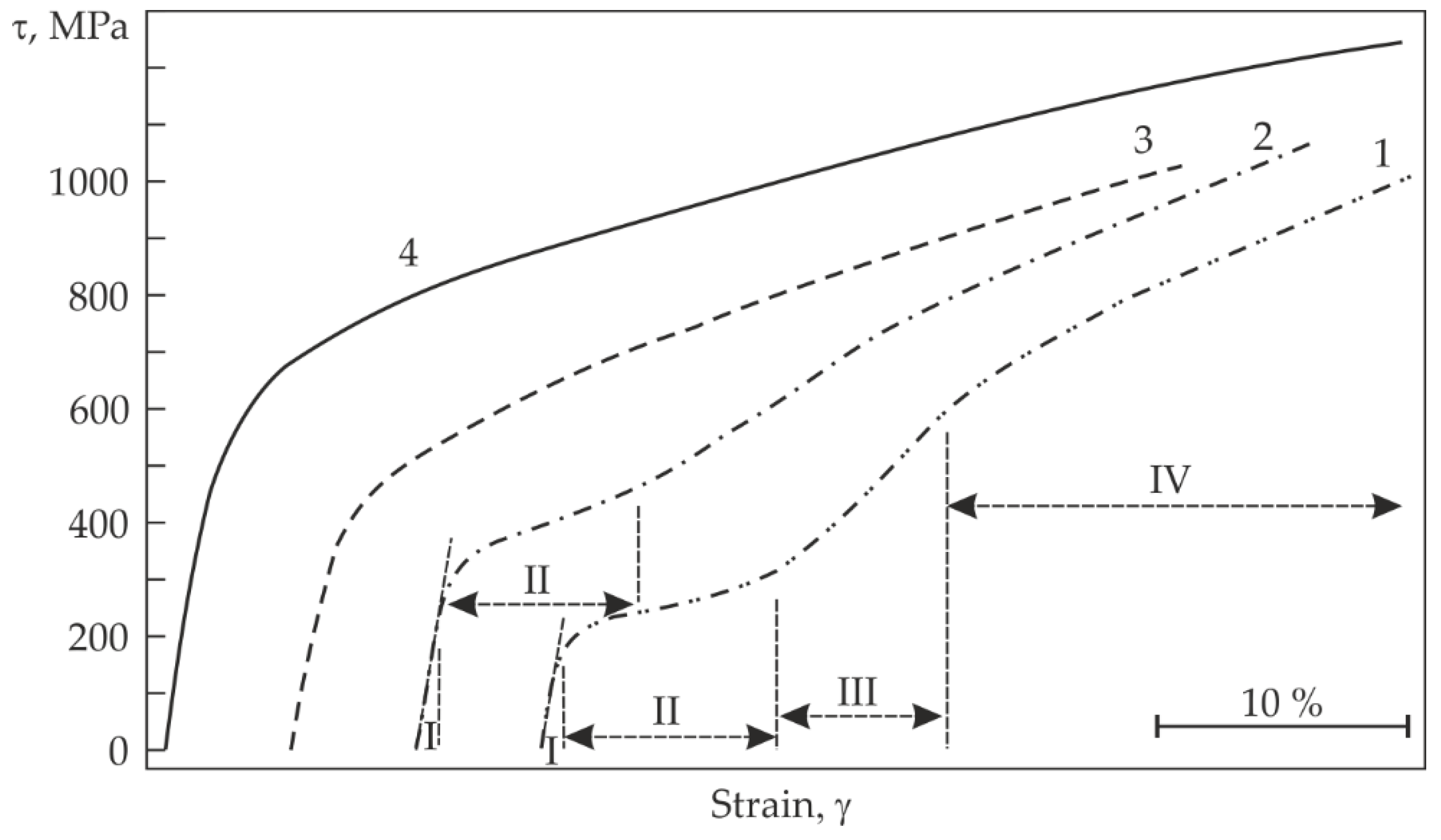
Figure 2 shows the τ–γ dependences of Ti_49.3Ni_50.7 (at%) in loading-unloading cycles at 281, 299, 309, and 339 K. As can be seen, the dependences at 281 and 299 K reveal four deformation stages. Stage I is quasi-elastic and its strain increases linearly as the applied stress is increased. At τ = τ_m (martensite shear stress), stage I passes into stage II, at which the strain increment is large while the external stress build-up is comparatively small. Stage II represents a so-called pseudo-yield plateau which ends, in our case, at about γ_t = 8%. Obviously, at 281 and 299 K (Figure 2, curves 1, 2), the pseudo-yield plateau results from the generation of B19′ martensite under loading [4,13]. Stage II is followed by stage III, at which γ_t increases almost linearly from 8% to 18–20% as τ is increased from ~450 to 800 MPa. Stage III represents strain hardening, which passes into active plastic flow at stage IV. From Figure 2, it is seen that when deformed at 309 K (curve 3) and 339 K (curve 4), the material shows no pseudo-yield plateau and its quasi-elastic stage passes directly into parabolic flow.

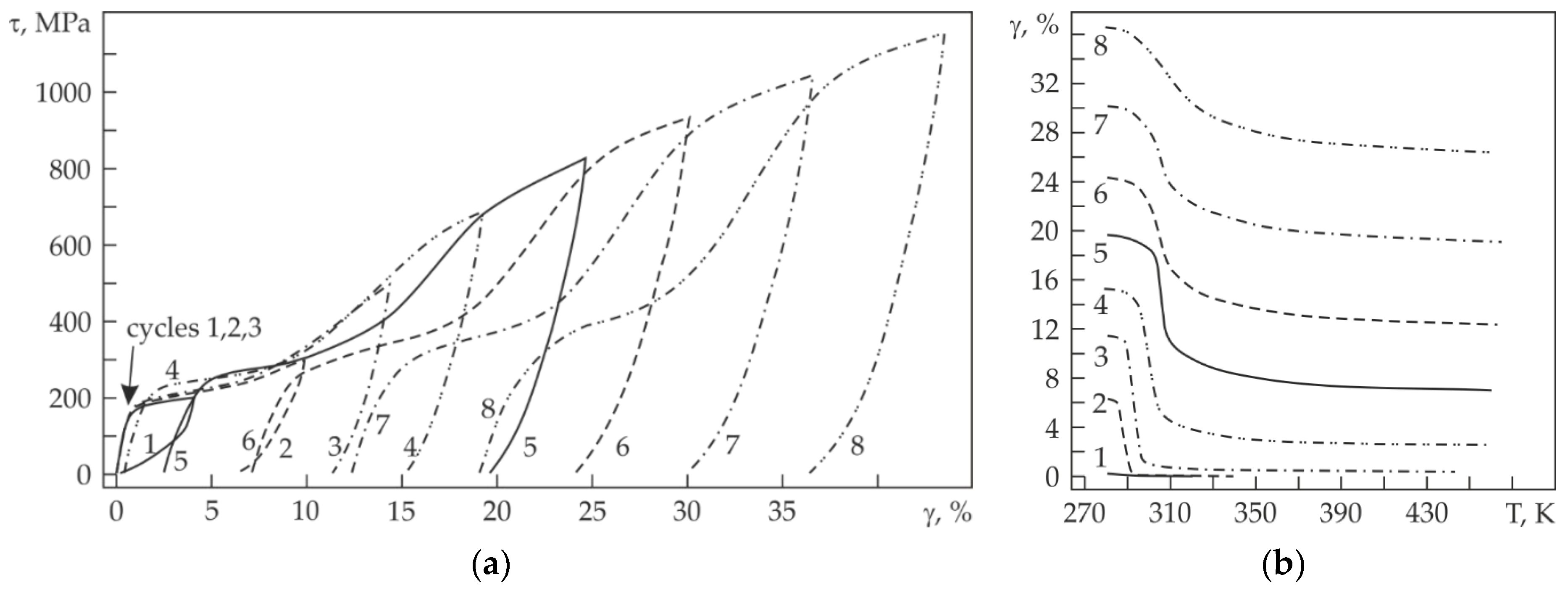
Figure 3 and Figure 4 show the τ−γ dependences of Ti_49.3Ni_50.7·(at%) in loading–unloading cycles with successively increasing γ_t and its inelastic strain recovery on further heating at different test temperatures. From Figure 3a, it is seen that as the number of loading–unloading cycles with T_d = 281 K is increased, the martensite shear stress τ_m grows and the extent of the pseudo-yield plateau first increases, then decreases (after the fifth cycle). It should be noted that the martensite shear stress τ_m increases from 180 MPa in the first loading–unloading cycle to 380 MPa in the seventh one. After the first loading–unloading cycle with γ_t = 4.1%, the strain recovery via superelasticity (under unloading) was 3.9%, and via shape memory (at heating), it was 0.2%. Although T_d was higher than A_f by about 8 K, the SE value in the next isothermal τ−γ cycles was low compared to γ_t. Even after the second cycle with γ_t = 9.9%, the SE value was γ_SE = 3.6% against γ_SME = 6.3% (Figure 3a), and no plastic component was detected within the measurement error. After the third cycle with γ_t = 14.4%, the SE and SME values were γ_SE = 3.0% and γ_SME = 11.0% against γ_pl = 0.4% (Figure 3b). As the number of loading–unloading–heating cycles was further increased, γ_SE increased monotonically. The γ_SME value first increased and then decreased, and γ_pl became larger (Figure 3b).

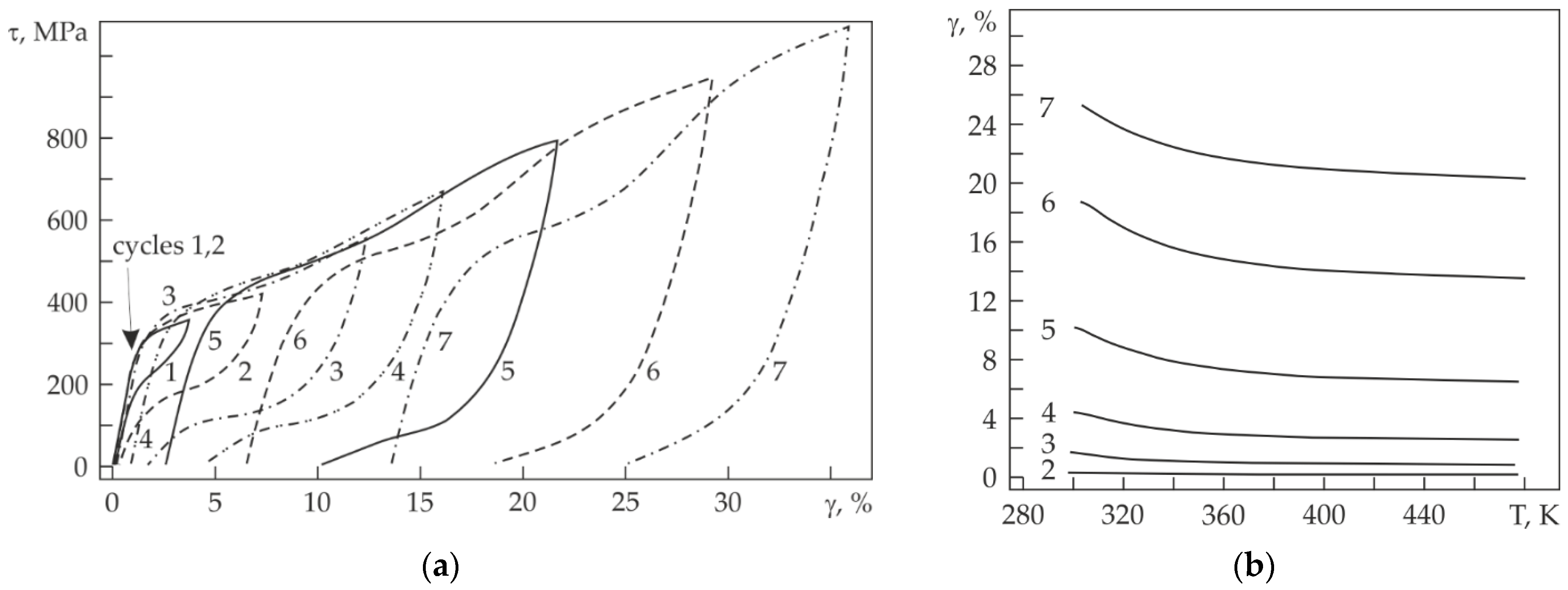
From Figure 4a it is seen that at T_d = 299 K (26 K above A_f), the first two loading–unloading cycles with increasing γ_t result in flag-shaped τ−γ dependences characteristic of superelasticity so that the total strain is fully recovered after unloading. It should be noted that all loading–unloading cycles at this temperature are dominated by the SE effect. After the first cycle with γ_t = 3.7%, γ_SE = 3.6%, and after the second cycle with γ_t = 7.3%, its value is γ_SE = 6.9%, i.e., almost the whole strain is recovered under unloading. After the third cycle, γ_SE is equal to about 10.6%, but some strain remains unrecovered under unloading. As the number of loading–unloading cycles as well as the total strain is further increased, γ_SE varies little. It should be noted that at T_d = 299 K, compared to T_d = 281 K, the SE effect is much more pronounced and the SME value γ_SME on heating is small (Figure 4b). It should also be noted that after the third loading–unloading cycle with up to γ_t = 12.3%, the strain is mostly inelastic and almost completely recovered via SE and SME under unloading and heating, respectively. However, in the next cycles, the plastic strain component steeply increases. Noteworthy also is that the pseudo-yield plateau at T_d = 299 K is poorly detectable in all loading–unloading cycles (Figure 4a).

Figure 5 shows the γ_t dependences of γ_SID, γ_SE, and γ_SME at different temperatures of isothermal τ−γ cycles. It is seen that at 281 K, γ_SME reaches 12.7% (Figure 5a). At the same time, the temperature interval of shape recovery is narrow on heating, spanning from 285 to 310 K (Figure 3b). Note that at all temperatures of isothermal loading–unloading cycles, except for T_d = 281 K, the γ_t dependences of γ_SID, γ_SE, and γ_SME are qualitatively similar: as γ_t is increased, these quantities first reach a maximum and then decrease. The γ_t strains at which γ_SID, γ_SE, and γ_SME reach their maximum values differ but fall on the stage of active plastic strain accumulation (Figure 5).

4. Discussion

Certainly, at first glance, it is rather strange that the total strain measuring about a mere 4.1% at 281 K (8 K above A_f) results in an SME of 0.2% (Figure 3b). With such a small total strain at 281 K, one would expect its complete recovery via SE after unloading [24]. Moreover, after the second loading–unloading cycle with γ_t = 9.9%, the SE value decreases to 3.6% against 3.9% after the first cycle, whereas the SME value increases from 0.2% in the first cycle to 6.3% in the second one (Figure 3b). Although no plastic strain is found in the second loading–unloading cycle, the rise of SME after the first and second cycles at 8 K above A_f is most likely due to the generation of dislocations at the interfaces of B2 and B19′ phases under internal stress, which results from their lattice misfit [25]. It has been known that as the temperature of TiNi-based alloys is decreased and brought to about M_S, their elastic constants C′ and C₄₄ decrease greatly [26,27,28], and the decrease in the elastic constants should decrease the martensite shear stress in this temperature range. It should be noted that at T_d > A_f in the temperature range of decreased elastic constants, the recovery of inelastic strains via SE at comparatively low external stresses can be incomplete due to the rise of small plastic strains lying within 0.3%. The stabilization of martensite B19′ caused by the development of plastic microdeformations as a result of the appearance of dislocations at small, specified strains in binary alloys with ~50 and 50.8 at% Ni was observed in [29,30,31]. The generation of lattice defects and, primarily, dislocations during plastic deformation and martensite transformations impedes the recovery of inelastic strains via SE and can even block this process. On heating after unloading, the recovery is contributed to by SME. Thus, it is reasonable to suggest that the rise of SME in the test material after the first and second loading–unloading cycles at 281 K, which is 8 K higher than A_f, is due to dislocation generation at comparatively low stresses. When the temperature is increased to 299 K, the strain recovery after the second cycle with γ_t = 7.2% measures 6.9% via SE and only 0.1% via SME against 0.2% of plastic strain (Figure 4 and Figure 5b). In addition, the analysis of experimental data shows that increasing T_d from 309 to 339 K leads to a decrease in γ_SE from 6% to 4% in isothermal cycles τ–γ with γ_t ≈ 7%. At the same time, the residual deformation increases from 1% to 3% after isothermal unloading of samples. Hence, the temperature interval of manifestation of superelasticity (4–7% and practically without residual deformation) is very narrow and localized from 281 K (A_f + 8 K) to 299 K (A_f + 26 K).

The fact that in loading–unloading cycles at T_d ≥ 309 K, the SE and the SME value decreases and the plastic component steeply increases, is explained by the deformation temperature approaching M_d, at which no B2 → B19′ transformation is possible in the material under applied stress. The higher the temperature of isothermal loading–unloading cycles, the lower the total inelastic strain γ_SID and the higher the plastic component γ_pl (Figure 5). In this work, we did not investigate the nature of the development of reversible and plastic strains during torsion of the samples (nonhomogeneous or homogeneous [32]). At the same time, it was shown in [31] that the plastic strain develops by dislocation sliding and twinning in an alloy of close composition (50.8 at% Ni) with an average grain size of 500 nm.

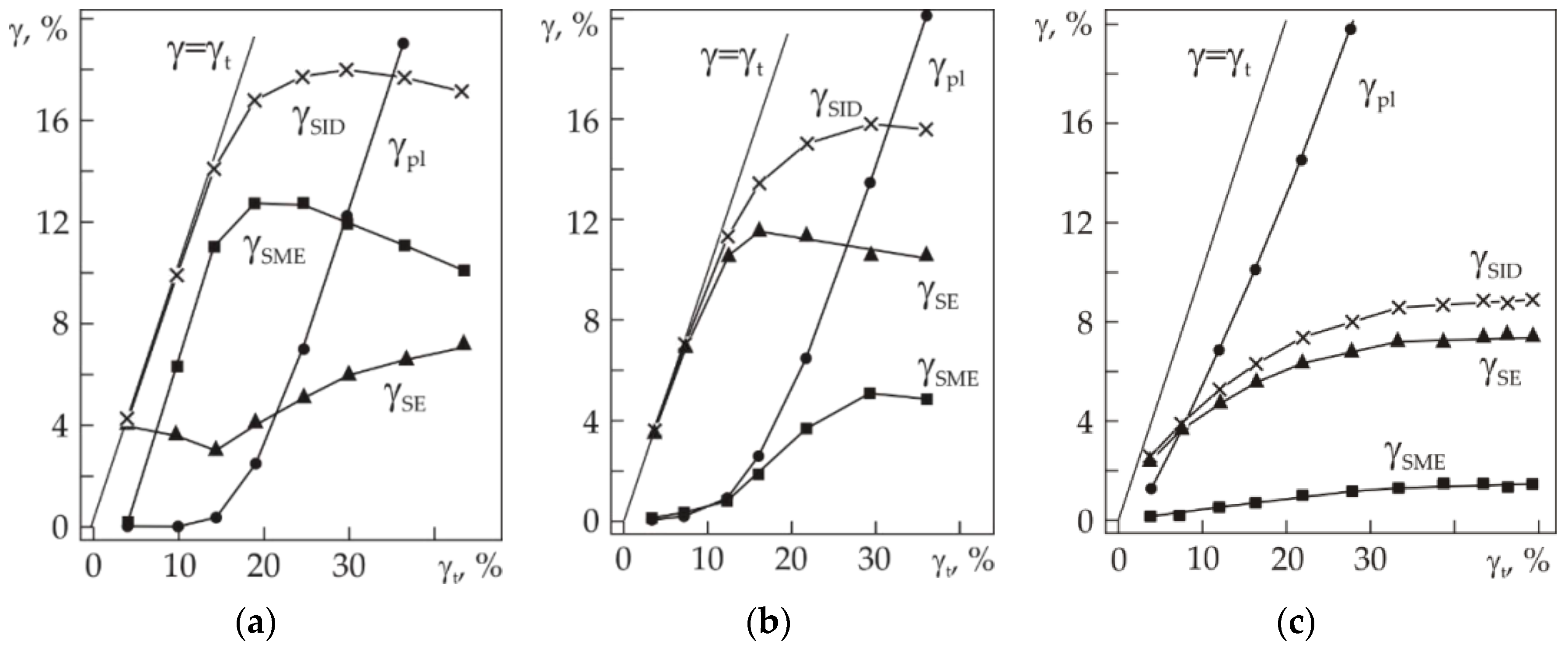
Plastic deformation accumulated during torsion causes the appearance of deformation microrelief on the original polished surface of the samples. Figure 6 shows the specimen surface microrelief after torsion at 299 K. Dependences of inelastic deformations γ_SE, γ_SME, γ_SID and plastic deformation γ_pl on a total γ_pl were presented in Figure 6. The surface microrelief image was obtained after the final cycle τ–γ with γ_t = 38%, heating the unloaded sample to 500 K and subsequent cooling to 299 K. The sample after cooling had a B2 phase structure. Plastic deformation γ_pl ≈ 20%, Figure 5c. Figure 6 clearly shows large deformation fragments with an intense microband structure within them. The average size of the large fragments, estimated from three similar images, is 46 ± 5 μm. This value correlates well with the average size of the original grains (53 ± 11 μm). Similar deformation fragments with sizes equal to those of the original grains arise as a result of mutual reversals and displacements of neighboring grains relative to each other during tensile plastic deformation of various materials not undergoing martensitic transformations: for example, aluminum-based alloy (Al 1100-0 [33], Al-Mg [34], AA-6022 [35]), AISI 1010 [36] steel, and others. At the same time, the formation of a fine microband structure within the fragments is due to the development of intra-grain plastic deformation processes by the mechanisms of dislocation sliding [29,31].

The maximum total reversible inelastic strain in torsion is γ_SID = 18% and is attained at 281 K (8 K higher than A_f) with γ_pl· = 12% against γ_t ≈ 30%. Interestingly, the same result is reported for Ti_49.3Ni_50.7 (at%) after torsion at T < M_f [23]: γ_SID = 18% with γ_pl = 12%. We think that this coincidence is not by chance but results from a certain common mechanism.

In conclusion, it should be noted that a direct comparison of inelastic and plastic strains obtained under torsion with similar strains obtained under compression, tension, or bending, and with the crystallography limit of martensitic strains at B19′ ↔ B2 MT, which is determined by compression-tension of the initial phase crystal lattice, is impossible. This is due to the difference in the deformation modes and the determination of the corresponding strains. In the first approximation, for a correct comparison of the total inelastic strain and plastic strain obtained in torsion with the results of studies of similar strains obtained in tension and bending and the crystallography limit of martensitic strain at B2 ↔ B19′ MT, equal to ~10% for the polycrystalline Ti_49.3Ni_50.7 (at%) alloy [14], it was the concept of equivalent true strain at different loading modes, used earlier in [20]. True tensile strain $e_1=\ln \left(1+\epsilon \right)$, where ε is the relative elongation. True torsional strain $e_2=S/\sqrt{3}$, where S = tgγ is the accumulated shear strain. Tensile strains ε_t, ε_r, ε_pl, corresponding to torsional strains γ_t, γ_r, γ_pl, can be obtained from the relation e₁ = e₂. Using these values of ε_t, ε_r, and ε_pl, the inelastic strains recovered by the realization of SE, ε_SE, and SME, ε_SME, and the total inelastic strain ε_SID can be determined. The tensile strains corresponding to torsion strains after loading at 281K (γ_SID· = 18%, γ_pl = 12%, γ_t· = 30%) are: ε_t = 19.6%, ε_SID· = 12.4%, ε_pl· = 7.2%. To take into account that both γ_SID and ε_SID include Hooke’s elastic strain, it can be concluded that the maximum reversible inelastic strain γ_SID during torsion approximately corresponds to the known crystallography limit of martensitic strain at B2 ↔ B19′ MT in our coarse-grained alloy samples with 50.7 at% Ni. This result corresponds to the data of [16,31]. When bending samples of alloy Ti_49.3Ni_50.7 (at%) with microcrystalline structure (grain size ≤ 10 μm), the maximum inelastic strain equal also to 10% was obtained [16]. It was shown in [31] that the maximum total recoverable inelastic strain ε_SID in σ-ε cycles during tension and the subsequent heating of unloaded binary alloy samples with 50.9 at% Ni and an average grain size of 500 nm is 13%, which is close to the maximum total inelastic strain in our coarse-grained alloy with 50.7 at% Ni. Thus, abnormally high inelastic strains (~18% [23] and ~15% [16] obtained under the bending of ultrafine-grained TiNi-based binary alloys) are not observed in the coarse-grained samples of binary alloy with 50.7 at% Ni.

5. Conclusions

It was found that the maximum value of the total inelastic torsional strain (γ_SID) of coarse-grained samples of Ti_49.3Ni_50.7 (at%) alloy, which was achieved in this work, is 18% and is observed with developed plastic deformation of about 12% (a total specified deformation γ_t ≈ 30%). It was shown that the maximum value of total inelastic strain γ_SID· = 18% obtained during torsion corresponds to the crystallographic limit of martensitic strain at B2 ↔ B19′ MT.

It was shown that very narrow temperature range of a bright manifestation of the superelasticity effect (4–7% and practically without the residual strain) in coarse-grained specimens of Ti_49.3Ni_50.7 (at%) alloy is from 281 K (A_f + 8 K) to 299 K (A_f + 26 K).

It is shown that in the temperature range from A_f + 8 K to A_f + 26 K, the maximum inelastic strain that can be obtained in coarse-grained samples of alloy Ti_49.3Ni_50.7 (at%) during torsion and can be returned completely as a superelasticity effect is 4–7%. When the external stress is increased in order to achieve a larger value of the superelasticity effect, the yield strength of the samples is exceeded. This leads to plastic strain of samples and hinders the return of inelastic strain in the form of superelasticity effect. This is the reason for the appearance and increase in SME when the γ_t total strain increases under torsion of samples at temperatures above A_f.