Prediction of Dimensional Changes of Low-Cost Metal Material Extrusion Fabricated Parts Using Machine Learning Techniques
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Equipment
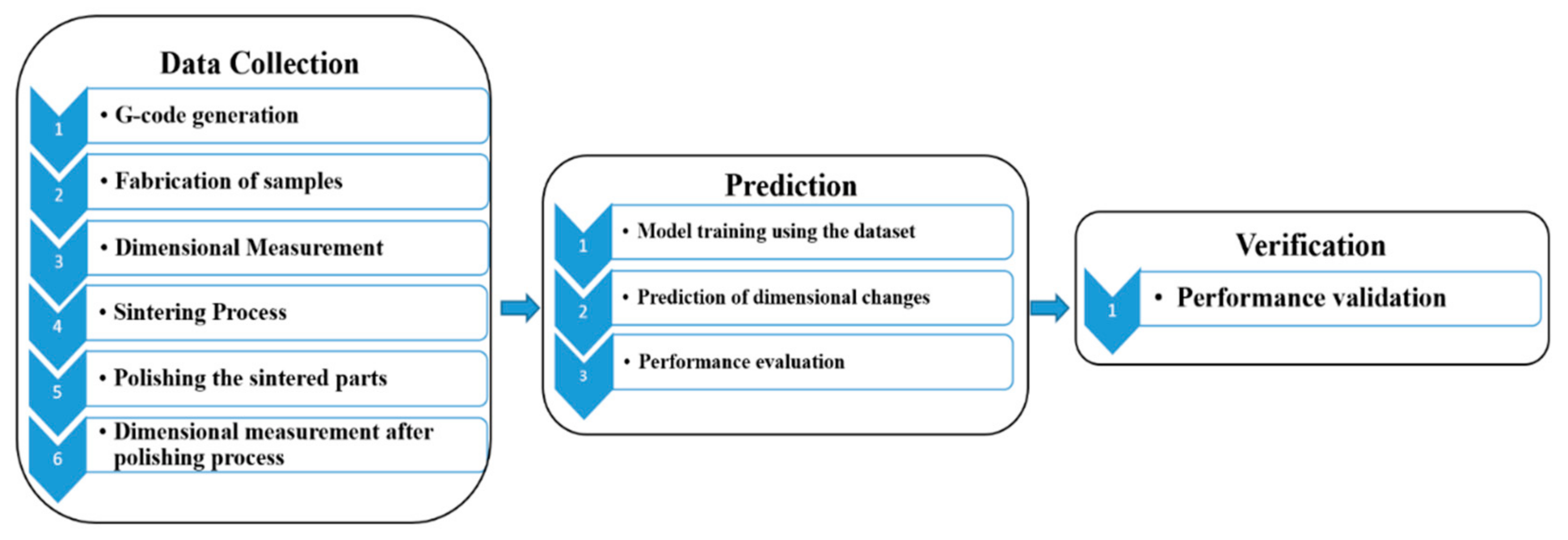
2.2. Process Workflow
2.3. Dataset Preparation
2.4. Prediction Algorithms
2.4.1. LR
2.4.2. LRI
RR × L RR × W RR × H NT × L NT × W NT × H PS × L PS × W PS × H]
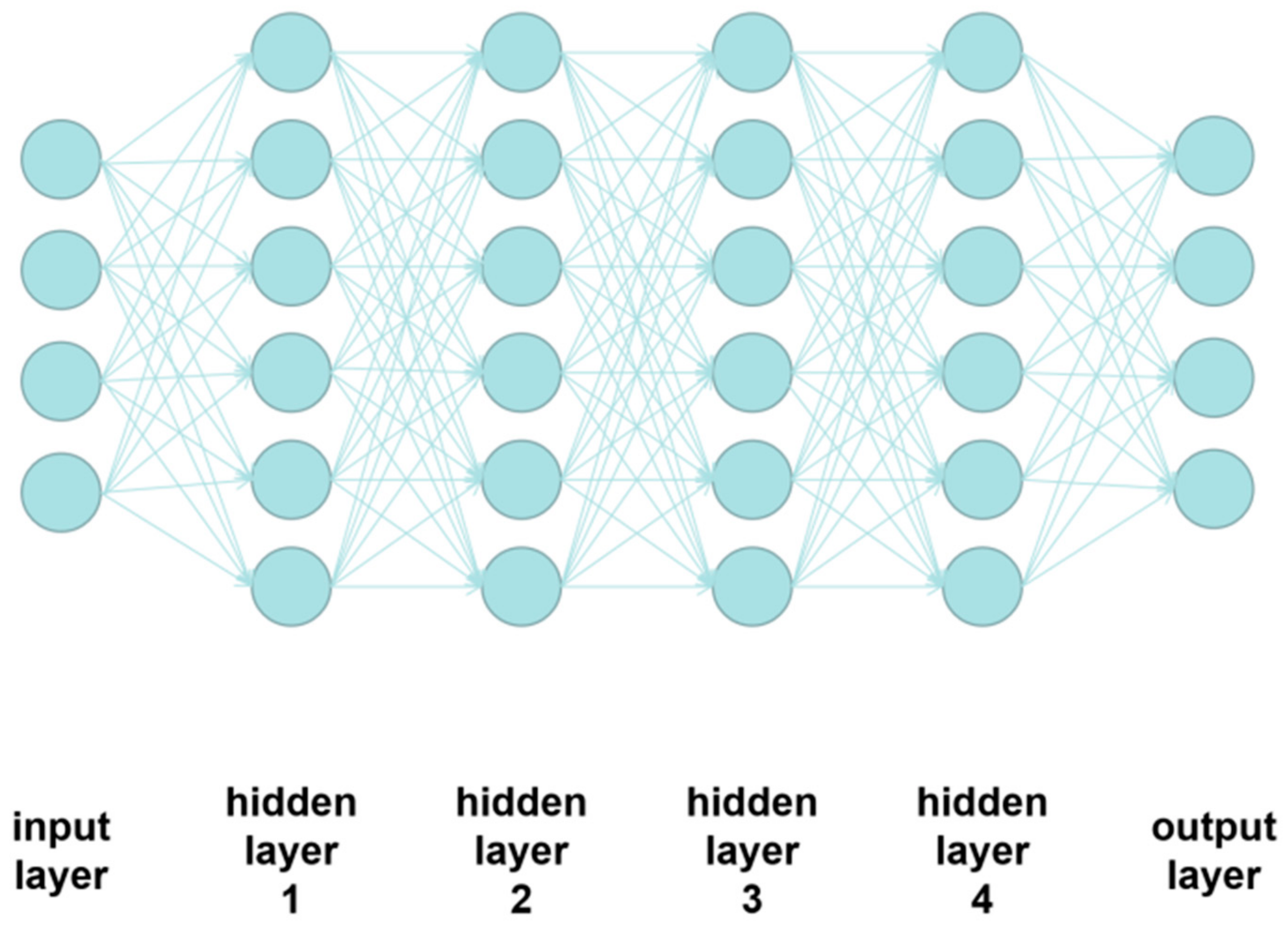
2.4.3. NN
3. Results and Discussions
3.1. Printing Accuracy
3.2. Analysis of Dimensional Variations of CAD and Sintered Samples
3.2.1. Results of Prediction by LR
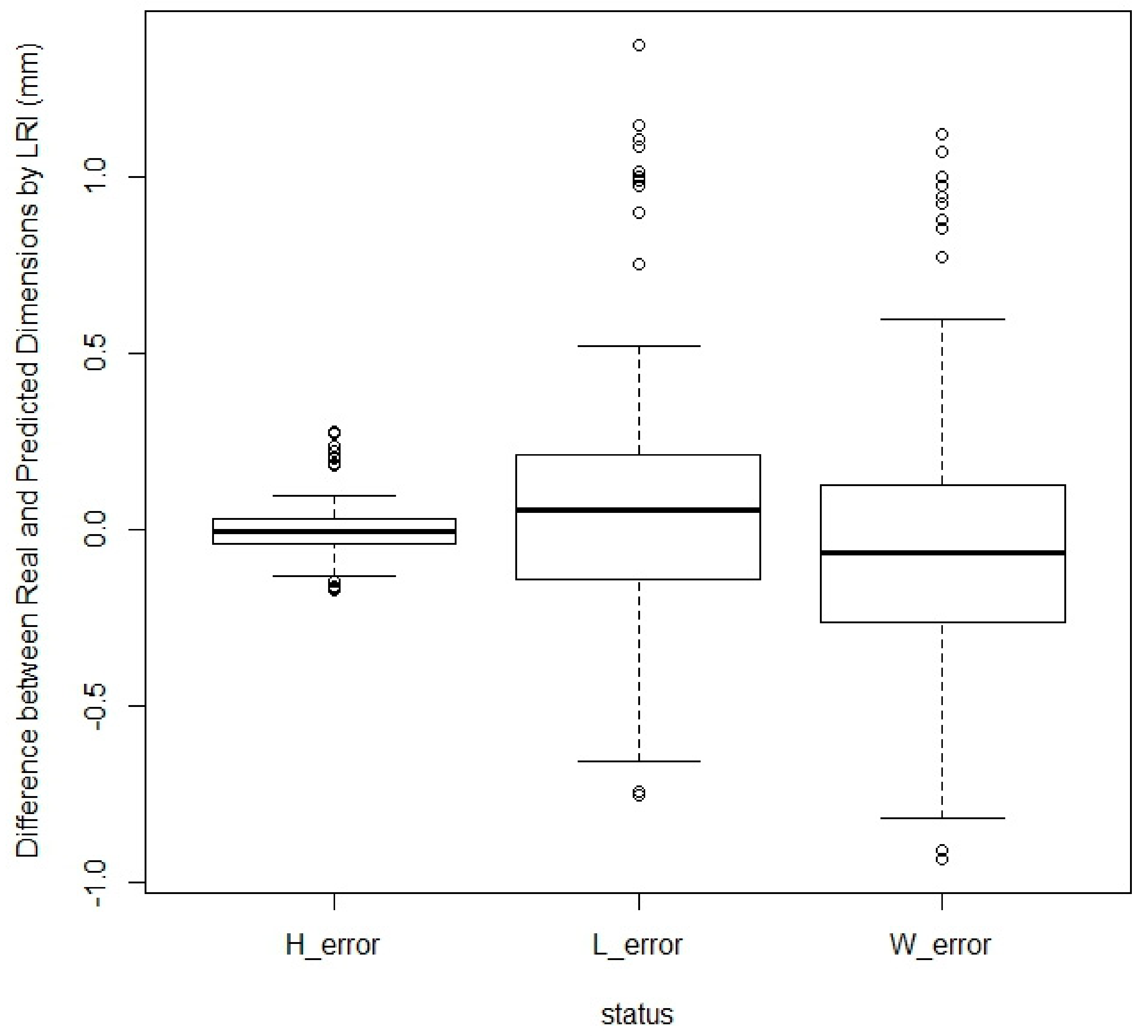
3.2.2. Results of Prediction by LRI
−28.133 0.787 −0.100 −0.386 0.119 −6.460 16.737 −1.964 2.305 −2.122 0.010]T + [−0.317]
−36.130 0.808 −0.108 −0.606 0.138 4.270 8.337 −4.605 0.917 −1.459 0.047]T + [−0.607]
−28.264 0.822 −0.132 −0.307 0.119 −7.583 20.620 −4.016 1.923 −2.281 0.290]T + [−0.431]
3.2.3. Results of Prediction by NN
4. Error Metrics
5. Verification
6. Conclusions
- The three types of algorithms behave differently in predicting CAD dimensions. NN has the smallest MSE (0.00228 in length, 0.0117 in width, and 0.0000878 in height) and, hence, will be the best algorithm to predict the initial CAD dimensions.
- Since both LRI and NN have smaller MSE than LR, which means that LRI and NN are more accurate than LR, these independent parameters have internal interactions.
- After verification, the errors between the real and target dimensions are negligible; the accuracy of the prediction by NN is acceptable.
- For NN that more hidden layers can be added to develop deep model that better capture complex behavioral patterns within the data leading to better prediction accuracy. Our results support this claim since the NN gave the best results.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Zhang, Z.; Fidan, I.; Allen, M. Detection of Material Extrusion In-Process Failures via Deep Learning. Inventions 2020, 5, 25. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.W.; Stucker, B. Additive Manufacturing Technologies; Springer: New York, NY, USA, 2014; Volume 17. [Google Scholar]
- Redwood, B. Additive Manufacturing Technologies: An Overview. Retrieved 16 April 2018. Available online: https://www.3dhubs.com/knowledge-base/additive-manufacturing-technologies-overview/ (accessed on 21 April 2021).
- Attaran, M. The rise of 3-D printing: The advantages of additive manufacturing over traditional manufacturing. Bus. Horiz. 2017, 60, 677–688. [Google Scholar] [CrossRef]
- Mohd, J.; Haleem, A. Additive manufacturing applications in medical cases: A literature based review. Alex. J. Med. 2018, 54, 411–422. [Google Scholar]
- Seyed Hamidreza, G.; Corker, J.; Fan, M. Additive manufacturing technology and its implementation in construction as an eco-innovative solution. Autom. Constr. 2018, 93, 1–11. [Google Scholar]
- Berger, R. Additive Manufacturing|Mechanical Engineering|Engineered Products/High Tech|Industrial Know-how|Expertise|Roland Berger. 2013. Available online: https://www.rolandberger.com/publications/publication_pdf/roland_berger_additive_manufacturing_1.pdf (accessed on 21 April 2021).
- Pinna, C.; Ramundo, L.; Sisca, F.G.; Angioletti, C.M.; Taisch, M.; Terzi, S. Additive Manufacturing applications within Food industry: An actual overview and future opportunities. In Proceedings of the 21st Summer School Francesco Turco, Naples, Italy, 13–15 September 2016. [Google Scholar]
- Gisario, A.; Kazarian, M.; Martina, F.; Mehrpouya, M. Metal additive manufacturing in the commercial aviation industry: A review. J. Manuf. Syst. 2019, 53, 124–149. [Google Scholar] [CrossRef]
- Gong, H.; Snelling, D.; Kardel, K.; Carrano, A. Comparison of Stainless Steel 316L Parts Made by FDM-and SLM-Based Additive Manufacturing Processes. JOM 2019, 71, 880–885. [Google Scholar] [CrossRef]
- Oxford English Dictionary. Edition on CD-ROM (v. 4.0); Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Liu, B.; Wang, Y.; Lin, Z.; Zhang, T. Creating metal parts by Fused Deposition Modeling and Sintering. Mater. Lett. 2020, 263, 127252. [Google Scholar] [CrossRef]
- Mohammadizadeh, M.; Lu, H.; Fidan, I.; Tantawi, K.; Gupta, A.; Hasanov, S.; Zhang, Z.; Alifui-Segbaya, F.; Rennie, A. Mechanical and Thermal Analyses of Metal-PLA Components Fabricated by Metal Material Extrusion. Inventions 2020, 5, 44. [Google Scholar] [CrossRef]
- German, R.M. Sintering Theory and Practice; Wiley-Interscience: Hoboken, NJ, USA, 1996. [Google Scholar]
- Burkhardt, C.; Freigassner, P.; Weber, O.; Imgrund, P.; Hampel, S. Fused filament fabrication (FFF) of 316L Green Parts for the MIM process. In European Congress and Exhibition on Powder Metallurgy, Proceedings of the European PM Conference Proceedings, Chantilly, France, 9–13 October 2016; The European Powder Metallurgy Association: Chantilly, France, 2016. [Google Scholar]
- Evren, Y.; Ersoy, K. Dimensional Accuracy and Mechanical Properties of Chopped Carbon Reinforced Polymers Produced by Material Extrusion Additive Manufacturing. Materials 2019, 12, 3885. [Google Scholar]
- Silva, D.N.; De Oliveira, M.G.; Meurer, E.; Meurer, M.I.; Da Silva, J.V.L.; Santa-Bárbara, A. Dimensional error in selective laser sintering and 3D-printing of models for craniomaxillary anatomy reconstruction. J. Cranio-Maxillofac. Surg. 2008, 36, 443–449. [Google Scholar] [CrossRef]
- Danilo, I.; Broilo, T.L.; Heitz, C.; de Oliveira, M.G.; de Oliveira, H.W.; Nobre, S.M.; Dos Santos Filho, J.H.; Silva, D.N. Dimensional error of selective laser sintering, three-dimensional printing and PolyJet™ models in the reproduction of mandibular anatomy. J. Cranio Maxillofac. Surg. 2009, 37, 167–173. [Google Scholar]
- Wang, Y.; Zhao, Y.F. Investigation of sintering shrinkage in binder jetting additive manufacturing process. Procedia Manuf. 2017, 10, 779–790. [Google Scholar] [CrossRef]
- Bustillo, A.; Pimenov, D.; Matuszewski, M.; Mikolajczyk, T. Using artificial intelligence models for the prediction of surface wear based on surface isotropy levels. Robot. Comput. Integr. Manuf. 2018, 53, 215–227. [Google Scholar] [CrossRef]
- Zhou, L.; Pan, S.; Wang, J.; Vasilakos, A.V. Machine learning on big data: Opportunities and challenges. Neurocomputing 2017, 237, 350–361. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, K.; Li, X.; Zhang, S.; Wu, Y.; Zhou, Y.; Meng, K.; Sun, C.; He, Q.; Fan, W.; et al. Sign-to-speech translation using machine-learning-assisted stretchable sensor arrays. Nat. Electron. 2020, 3, 571–578. [Google Scholar] [CrossRef]
- Nugrahaeni, R.A.; Mutijarsa, K. Comparative analysis of machine learning KNN, SVM, and random forests algorithm for facial expression classification. In Proceedings of the 2016 International Seminar on Application for Technology of Information and Communication (ISemantic), Piscataway, NJ, USA, 5–6 August 2016; IEEE: New York, NY, USA, 2016. [Google Scholar]
- Cammarota, G.; Ianiro, G.; Ahern, A.; Carbone, C.; Temko, A.; Claesson, M.J.; Gasbarrini, A.; Tortora, G. Gut microbiome, big data and machine learning to promote precision medicine for cancer. Nat. Rev. Gastroenterol. Hepatol. 2020, 1–14. [Google Scholar] [CrossRef]
- Bayraktar, Ö.; Uzun, G.; Çakiroğlu, R.; Guldas, A. Experimental study on the 3D-printed plastic parts and predicting the mechanical properties using artificial neural networks. Polym. Adv. Technol. 2017, 28, 1044–1051. [Google Scholar] [CrossRef]
- Hedberg, T.D., Jr.; Hartman, N.W.; Rosche, P.; Fischer, K. Identified research directions for using manufacturing knowledge earlier in the product life cycle. Int. J. Prod. Res. 2017, 55, 819–827. [Google Scholar] [CrossRef]
- Noriega, A.; Blanco, D.; Alvarez, B.J.; Garcia, A. Dimensional accuracy improvement of FDM square cross-section parts using artificial neural networks and an optimization algorithm. Int. J. Adv. Manuf. Technol. 2013, 69, 2301–2313. [Google Scholar] [CrossRef]
- The Virtual Foundary. Available online: https://shop.thevirtualfoundry.com/collections/metal-filaments/products/bronze-filamet?variant=12351189483603 (accessed on 21 April 2021).
- Ultimaker S5 PDF User Manuals. Available online: https://support.ultimaker.com/hc/en-us/articles/360011654419-Ultimaker-S5-PDF-user-manuals (accessed on 21 April 2021).
- MTI Corporation. Available online: https://www.mtixtl.com/1100CCompactMuffleFurnacewith30SegmentProgrammable-KSL-1100X-S-UL.aspx (accessed on 9 January 2021).
- iGaging. Available online: http://www.igaging.com/page73.html (accessed on 21 April 2021).
- Chen, J.; de Hoogh, K.; Gulliver, J.; Hoffmann, B.; Hertel, O.; Ketzel, M.; Bauwelinck, M.; van Donkelaar, A.; Hvidtfeldt, U.A.; Katsouyanni, K.; et al. A comparison of linear regression, regularization, and machine learning algorithms to develop Europe-wide spatial models of fine particles and nitrogen dioxide. Environ. Int. 2019, 130, 104934. [Google Scholar] [CrossRef]
- Uyanık, G.K.; Güler, N. A study on multiple linear regression analysis. Procedia Soc. Behav. Sci. 2013, 106, 234–240. [Google Scholar] [CrossRef]
- Hayes, A.F.; Montoya, A.K. A tutorial on testing, visualizing, and probing an interaction involving a multicategorical variable in linear regression analysis. Commun. Methods Meas. 2017, 11, 1–30. [Google Scholar] [CrossRef]
- Zhang, P.; Shen, H.; Zhai, H. Machine learning topological invariants with neural networks. Phys. Rev. Lett. 2018, 120, 066401. [Google Scholar] [CrossRef] [PubMed]
- Mao, H.; Han, S.; Pool, J.; Li, W.; Liu, X.; Wang, Y.; Dally, W.J. Exploring the regularity of sparse structure in convolutional neural networks. arXiv 2017, arXiv:1705.08922. [Google Scholar]
- Zhang, Z. Detection of the Additive Manufacturing In-Process Failures via Deep Learning. Master’s Thesis, Tennessee Technological University, Cookeville, TN, USA, 2019. [Google Scholar]
- Di Leo, G.; Sardanelli, F. Statistical significance: p value, 0.05 threshold, and applications to radiomics—Reasons for a conservative approach. Eur. Radiol. Exp. 2020, 4, 1–8. [Google Scholar]
- Cuadras, C.M. Increasing the correlations with the response variable may not increase the coefficient of determination: A PCA interpretation. In Multivariate Statistics and Matrices in Statistics; De Gruyter: Berlin, Germany, 2020; pp. 75–84. [Google Scholar]
- Nicolson, A.; Paliwal, K.K. Deep learning for minimum mean-square error approaches to speech enhancement. Speech Commun. 2019, 111, 44–55. [Google Scholar] [CrossRef]


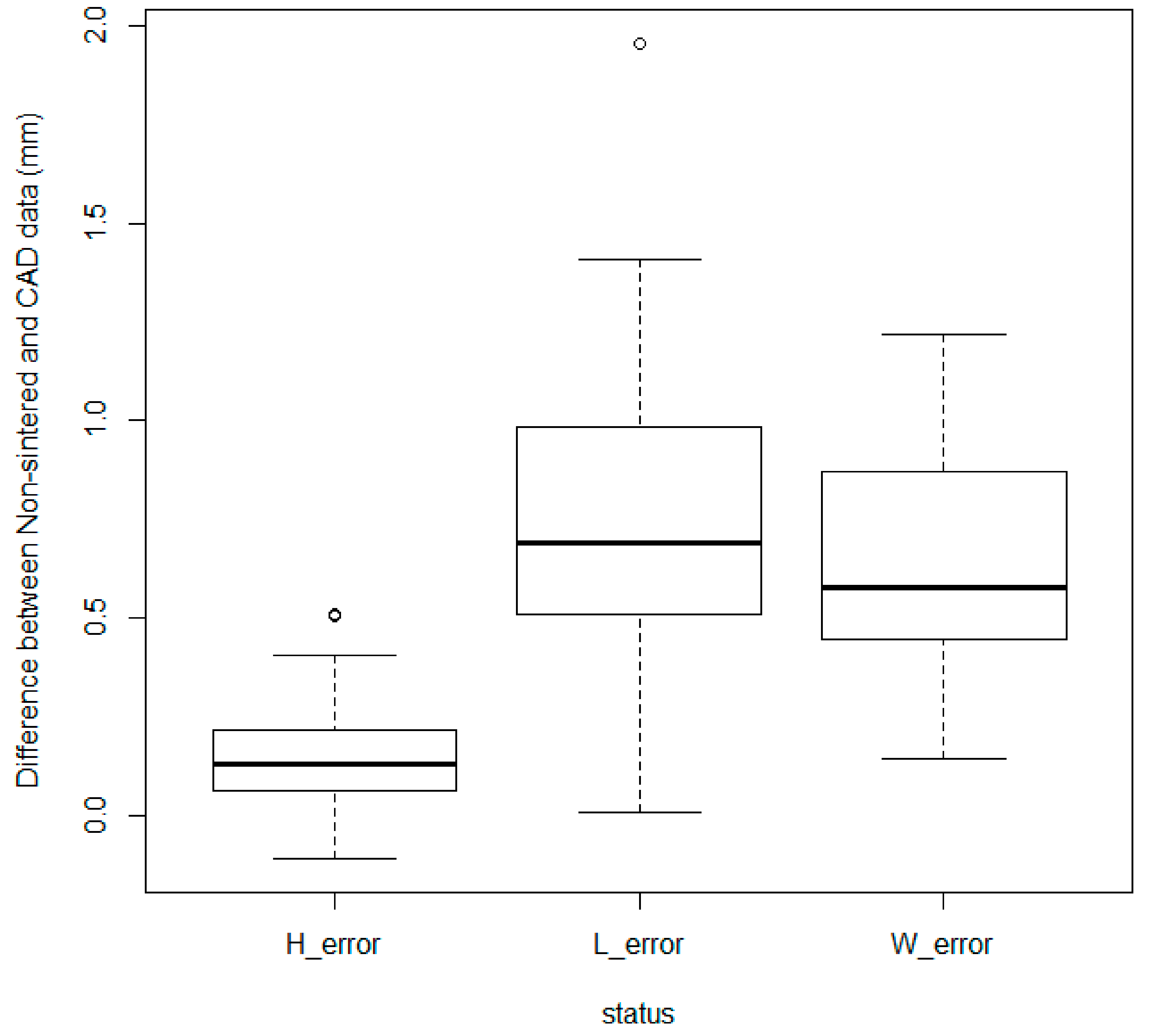


| Printing Parameters | Values | ||
|---|---|---|---|
| Layer Thickness (mm) | 0.1 | 0.2 | 0.3 |
| Nozzle Temperature (°C) | 220 | 230 | 240 |
| Printing Speed (mm/s) | 10 | 15 | 20 |
| Sintering Parameters | Values | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Layer Thickness (mm) | 0.1 | 0.2 | 0.3 | ||||||
| Sintering Temperature (°C) | 870 | 875 | 880 | 885 | 890 | 895 | 900 | ||
| Ramp Ratio (°C/min) | 2 | 3 | 4 | ||||||
| Printing Parameters | Sintering Parameters | Sample Type | Dimensions of the Sample | ||
|---|---|---|---|---|---|
| Length (mm) | Width (mm) | Height (mm) | |||
| 0.1 mm 240 °C 10 mm/s | 0.1 mm 870 °Ca 2 °C/mm | CAD | 20 | 15 | 6 |
| Non-sintered | 20.452 | 15.318 | 6.226 | ||
| Sintered | 18.787 | 13.922 | 5.236 | ||
| Number of hidden layers | 5 |
| Number of neurons in each hidden layer | 128 |
| Activation function at hidden layers | ReLU |
| Dimensions | Length | Width | Height |
|---|---|---|---|
| p-value | 2.99 × 10−8 | 1.097 × 10−4 | 1.272 × 10−6 |
| Method | R2 Value | ||
|---|---|---|---|
| Length | Width | Height | |
| LR | 0.891 | 0.921 | 0.885 |
| LRI | 0.989 | 0.995 | 0.999 |
| Method | Mean Square Error | ||
|---|---|---|---|
| Length (mm) | Width (mm) | Height (mm) | |
| LR | 0.269 | 0.183 | 0.0119 |
| LRI | 0.118 | 0.121 | 0.00532 |
| NN | 0.00228 | 0.0117 | 0.0000878 |
| Printing Parameter | Sintering Parameter | ||
|---|---|---|---|
| Layer Thickness (mm) | 0.3 | Layer Thickness (mm) | 0.3 |
| Nozzle Temperature (°C) | 220 | Sintering Temperature (°C) | 880 |
| Printing Speed (mm/s) | 15 | Ramp Ratio (°C/min) | 3 |
| Target Dimensions | Predicted CAD Dimensions | Final Dimensions after Sintering | |
|---|---|---|---|
| Length (mm) | 20 | 20.905 | 19.998 |
| Width (mm) | 15 | 15.394 | 14.996 |
| Height (mm) | 6 | 6.154 | 6.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Femi-Oyetoro, J.; Fidan, I.; Ismail, M.; Allen, M. Prediction of Dimensional Changes of Low-Cost Metal Material Extrusion Fabricated Parts Using Machine Learning Techniques. Metals 2021, 11, 690. https://doi.org/10.3390/met11050690
Zhang Z, Femi-Oyetoro J, Fidan I, Ismail M, Allen M. Prediction of Dimensional Changes of Low-Cost Metal Material Extrusion Fabricated Parts Using Machine Learning Techniques. Metals. 2021; 11(5):690. https://doi.org/10.3390/met11050690
Chicago/Turabian StyleZhang, Zhicheng, James Femi-Oyetoro, Ismail Fidan, Muhammad Ismail, and Michael Allen. 2021. "Prediction of Dimensional Changes of Low-Cost Metal Material Extrusion Fabricated Parts Using Machine Learning Techniques" Metals 11, no. 5: 690. https://doi.org/10.3390/met11050690
APA StyleZhang, Z., Femi-Oyetoro, J., Fidan, I., Ismail, M., & Allen, M. (2021). Prediction of Dimensional Changes of Low-Cost Metal Material Extrusion Fabricated Parts Using Machine Learning Techniques. Metals, 11(5), 690. https://doi.org/10.3390/met11050690








