Warpage Analysis and Control of Thin-Walled Structures Manufactured by Laser Powder Bed Fusion
Abstract
1. Introduction
2. Experimental Campaign
- Single-wall structures of different thicknesses and heights;
- Cylindrical structures of different diameters and heights;
- Square-section structures of several thicknesses;
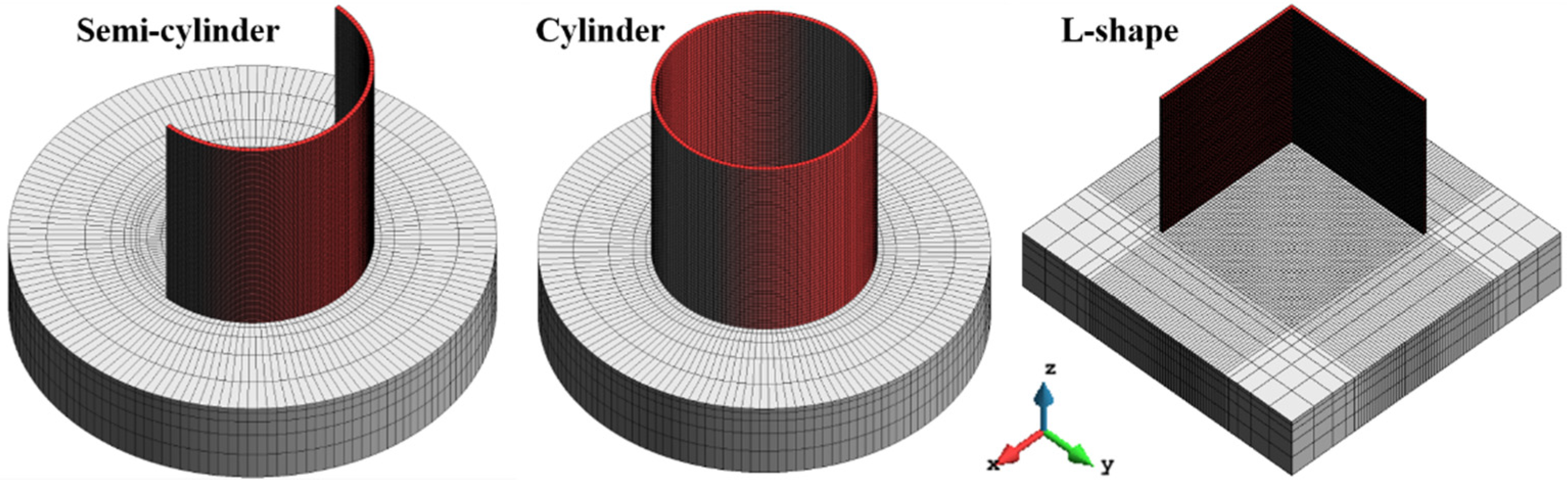
- Open-section structures (e.g., semi-cylinder, L-shape, etc.).
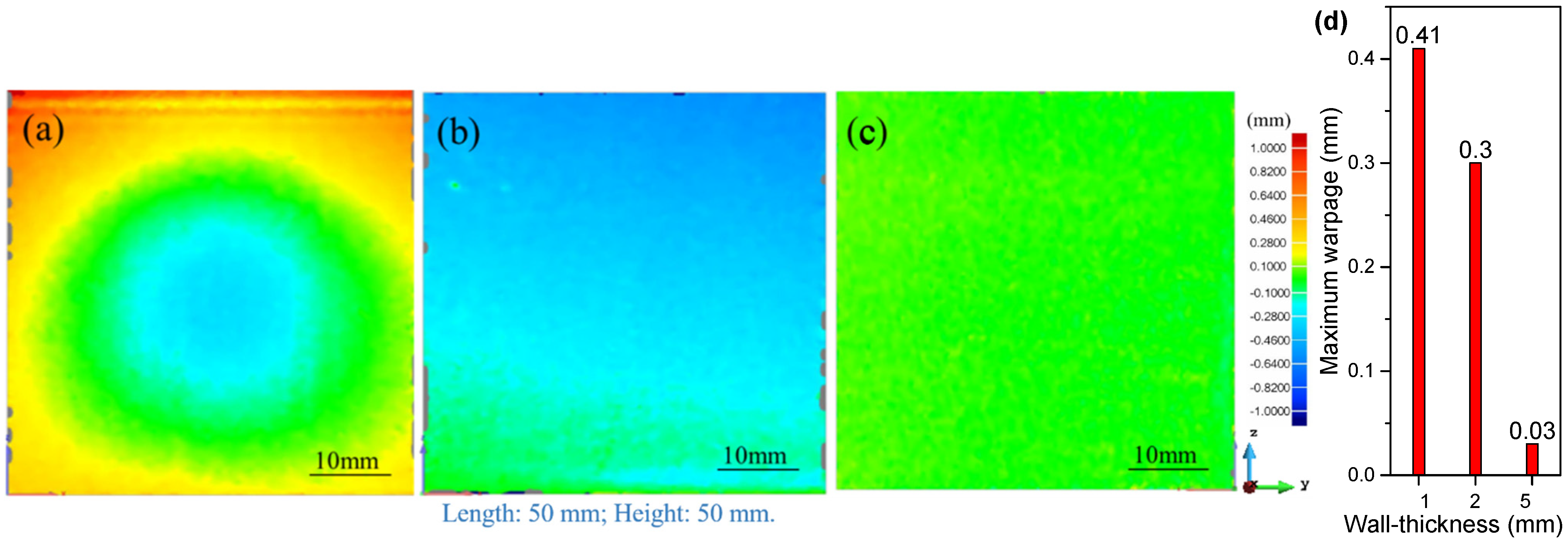
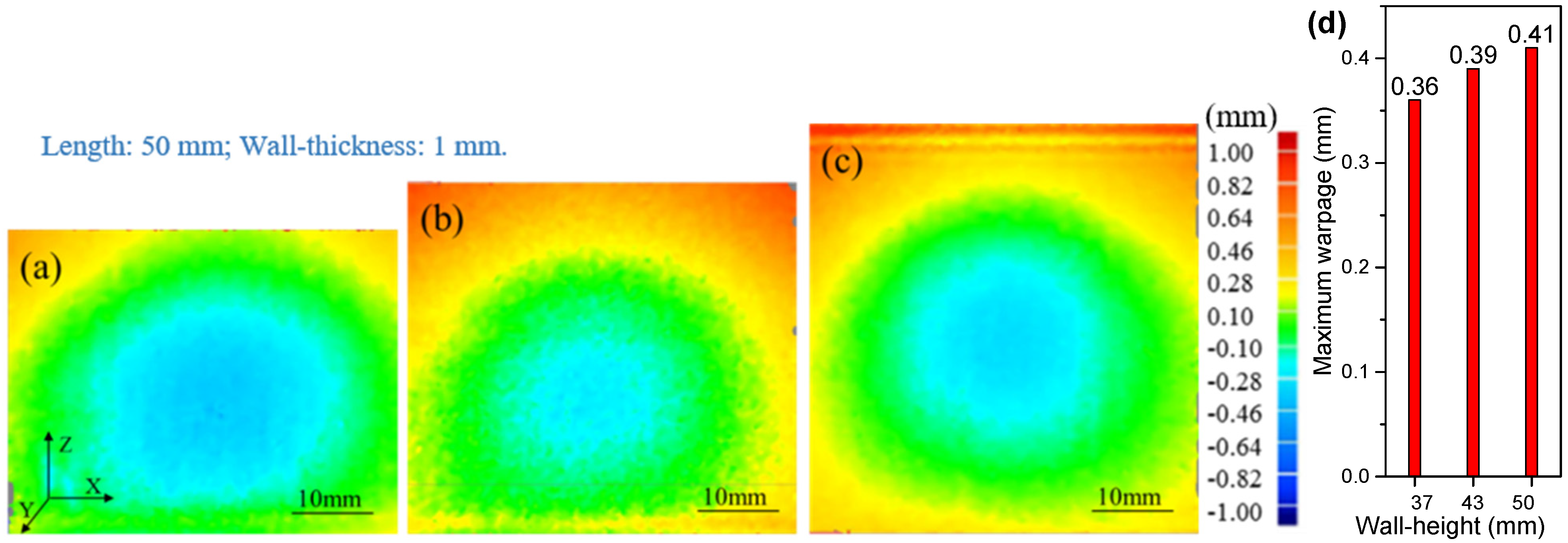
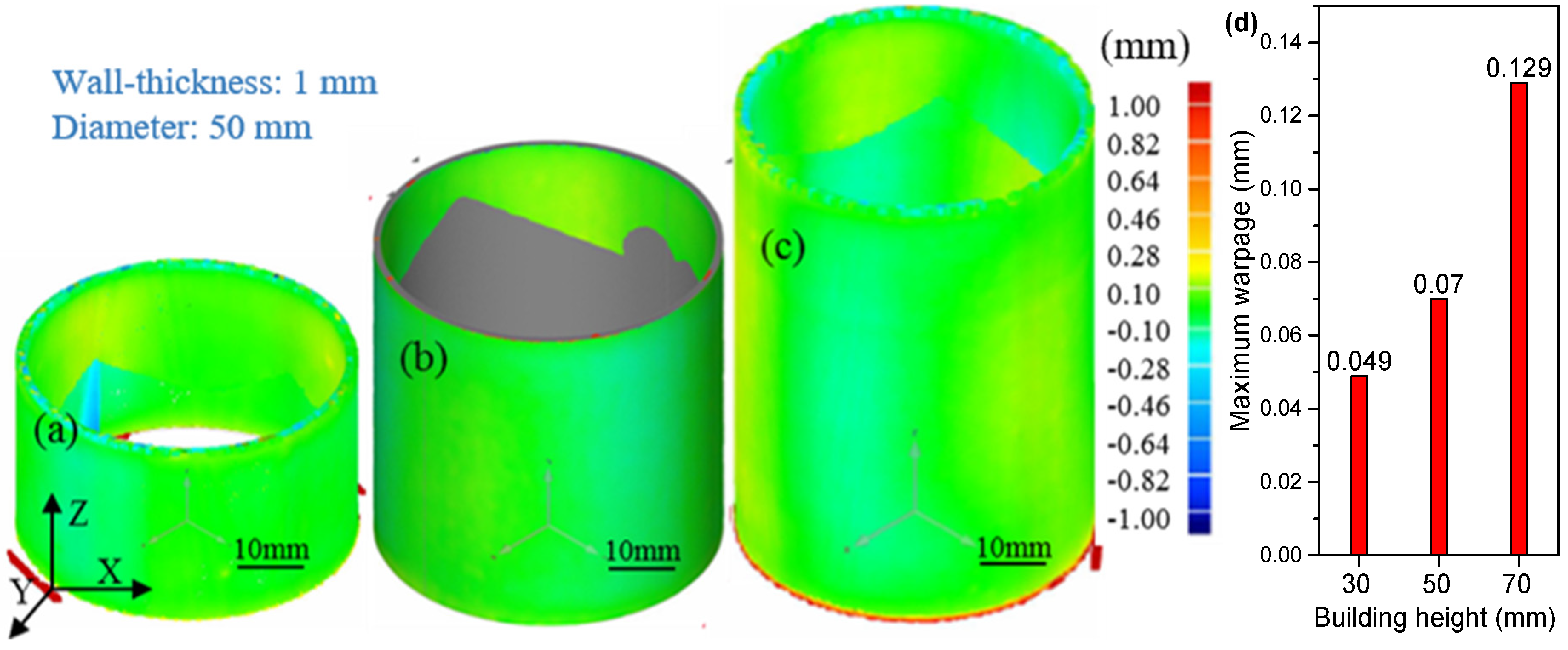
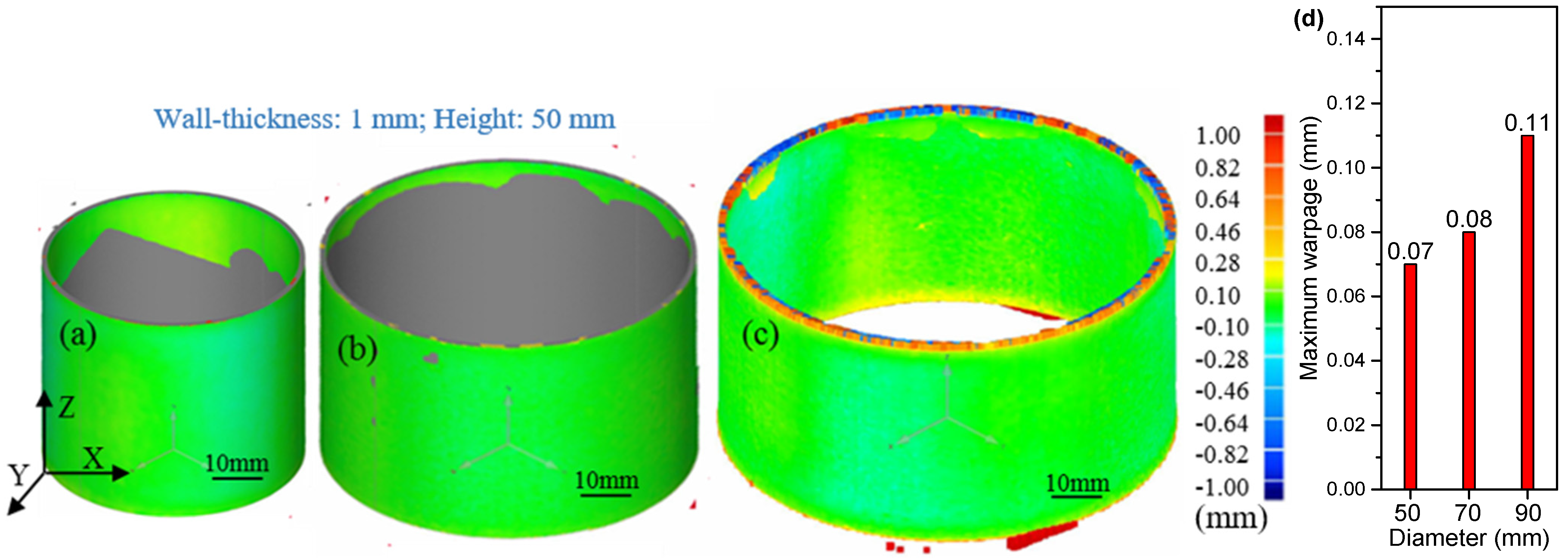
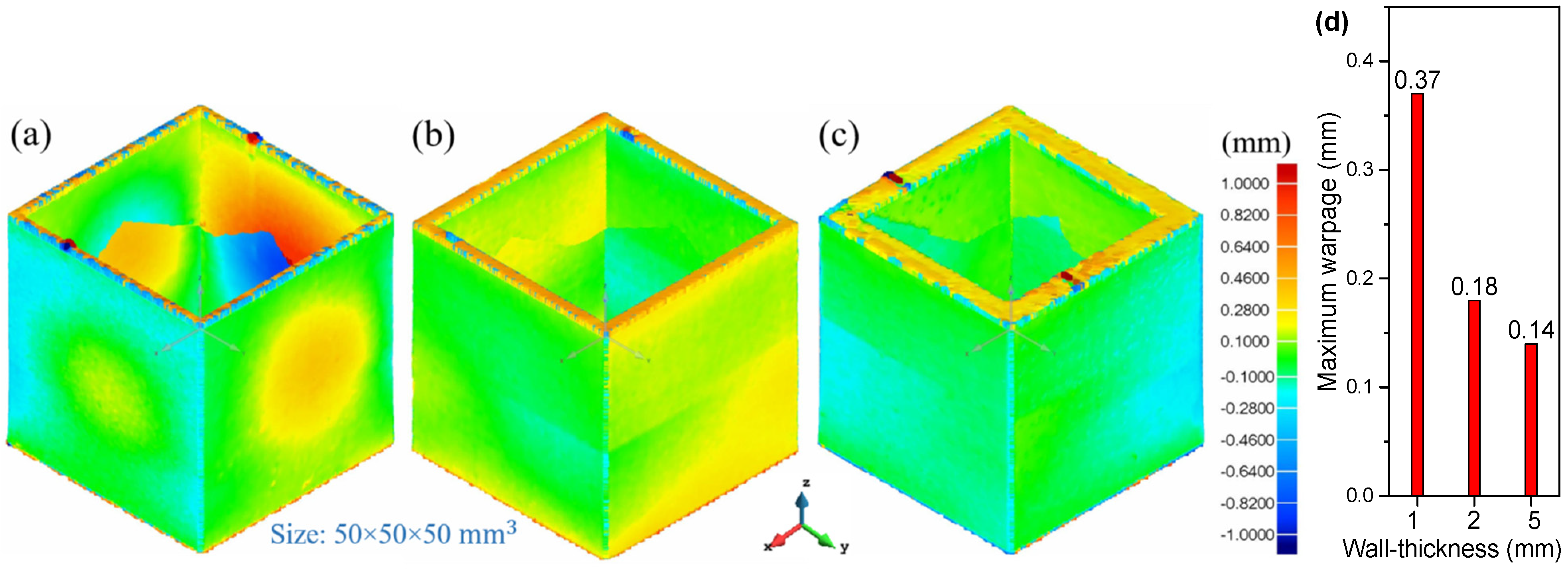
Scale Effect on the Part Warpage
3. Numerical Modeling
- Recoating: the baseplate is lowered to accommodate a new powder layer;
- Laser-scanning: the laser heat source generates a molten pool which follows a user-defined trajectory to selectively melt the powder bed consolidating the new layer comprising the AM build.
3.1. Mechanical Problem
3.2. Thermal Problem
3.3. Geometrical Models and FE Meshes
4. Calibration and Results
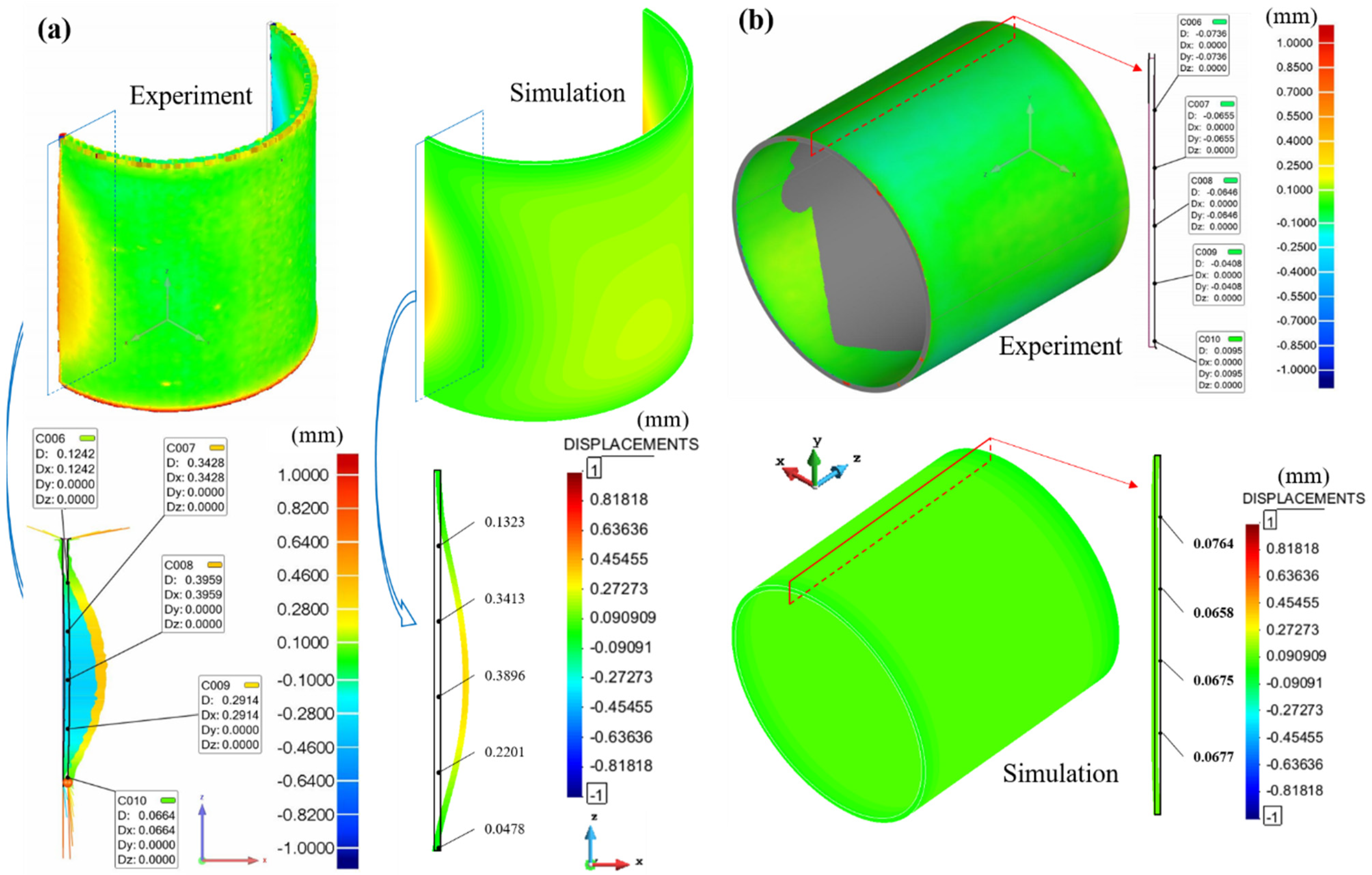
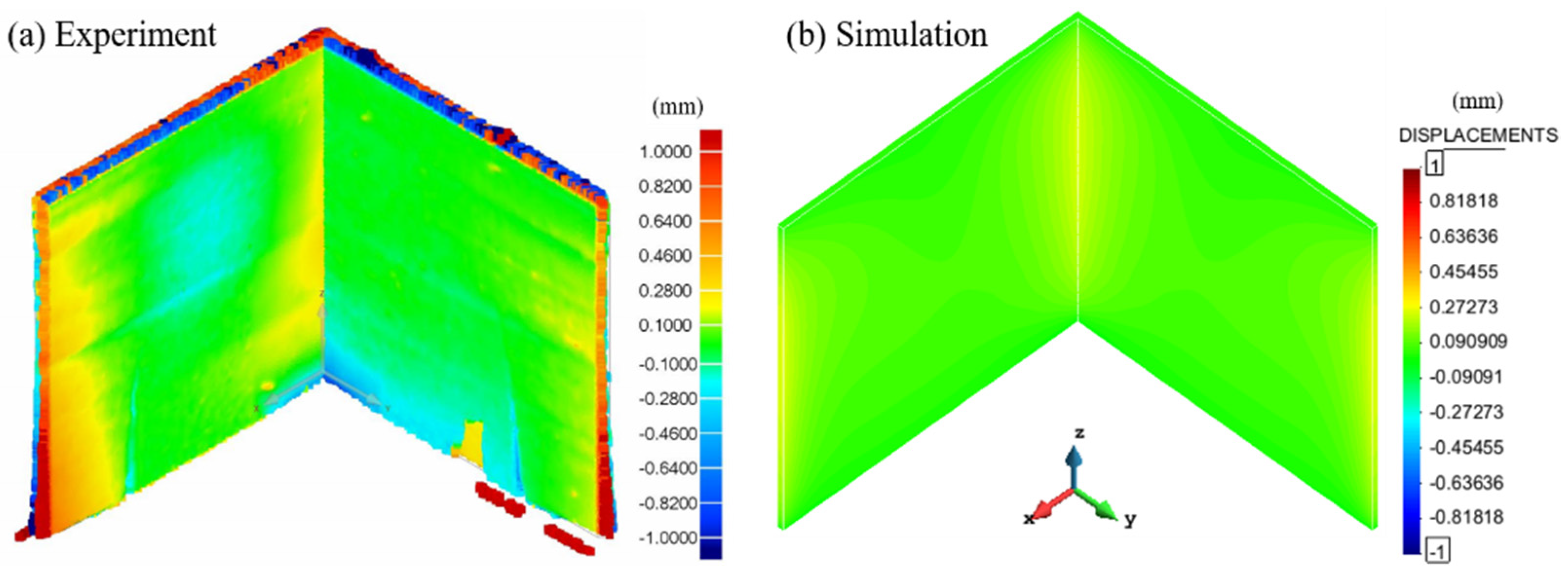
4.1. Calibration of the Numerical Model
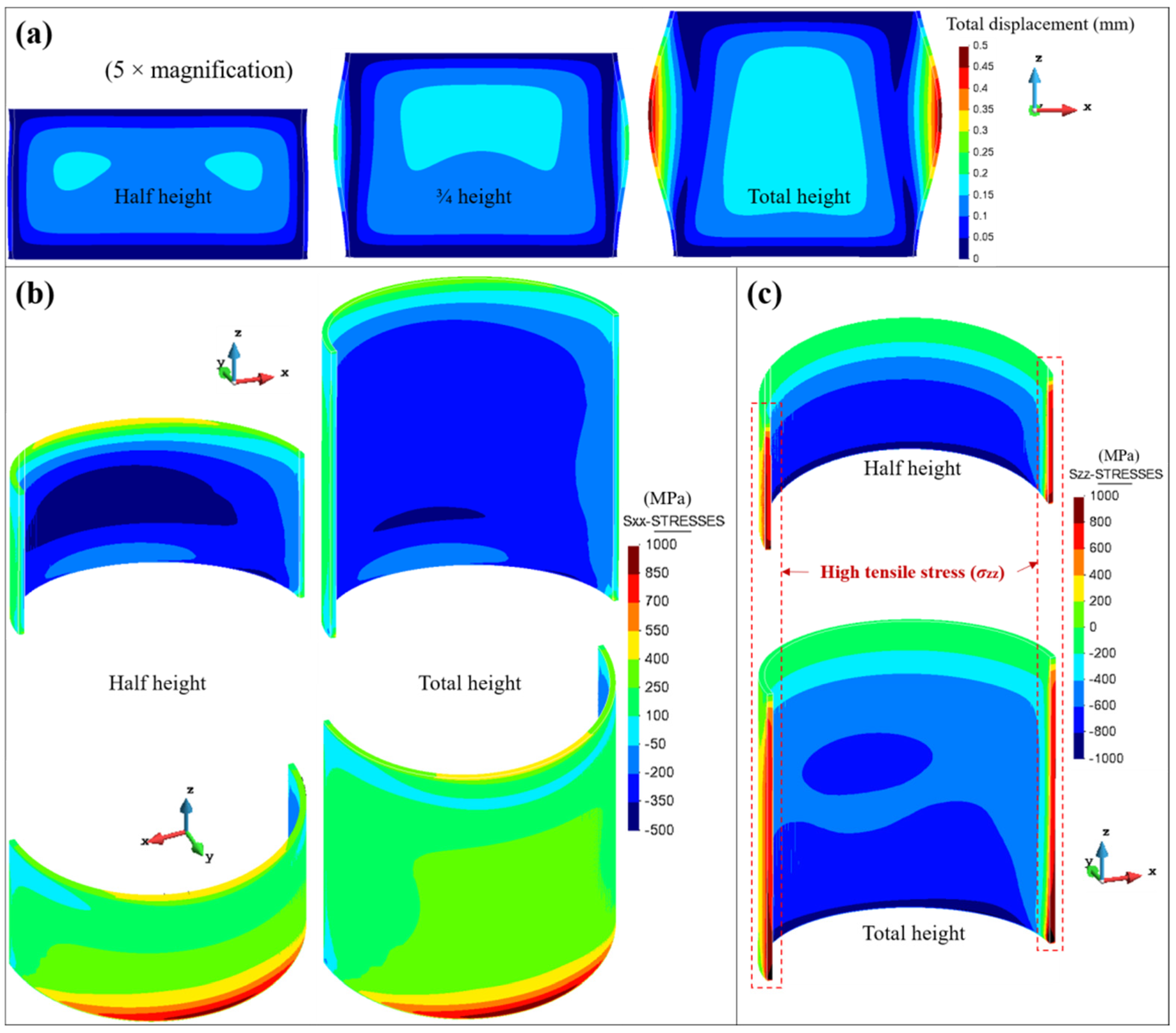
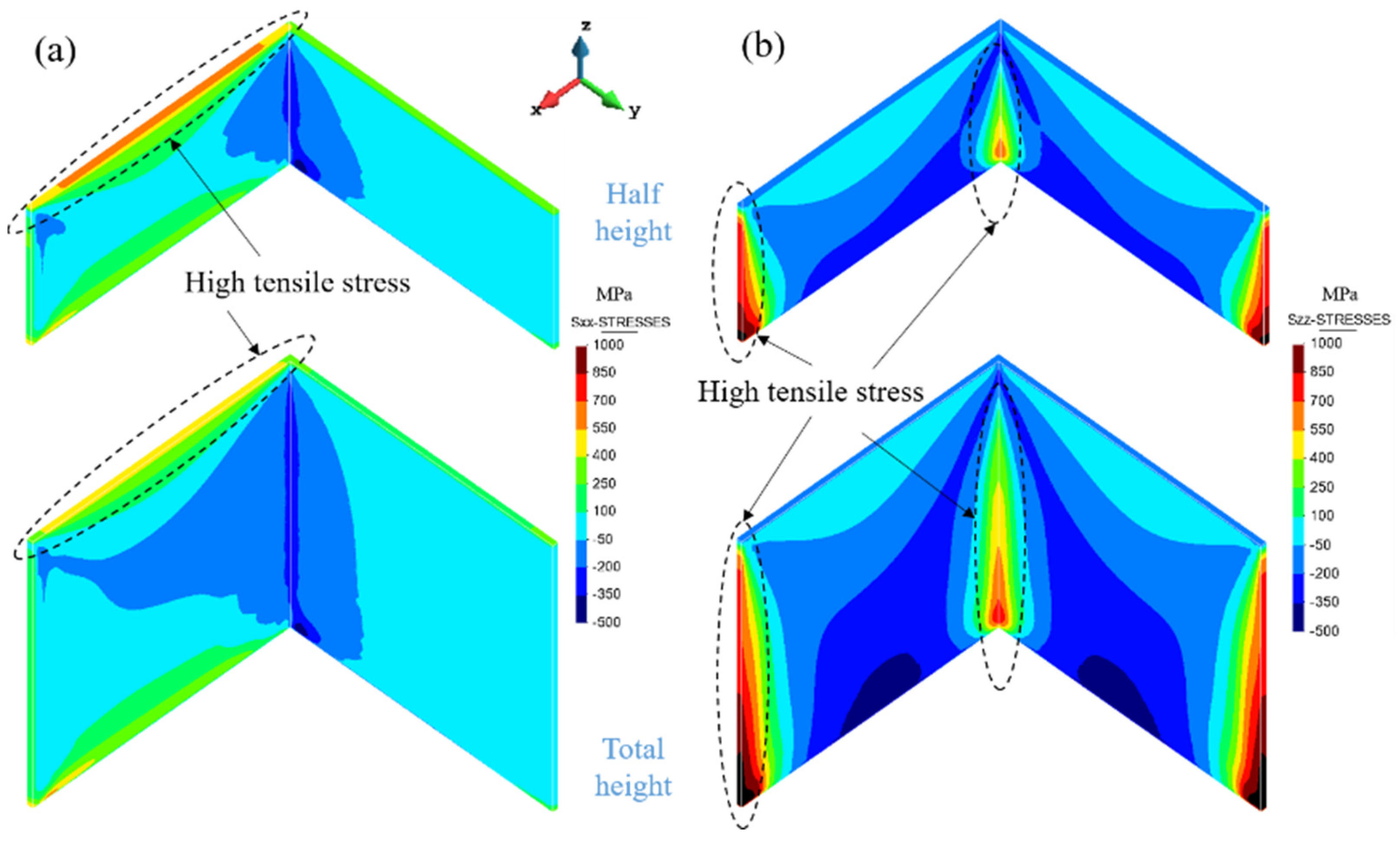
4.2. Results and Discussion on the Warpage Mechanism of the Thin-Walled Structures
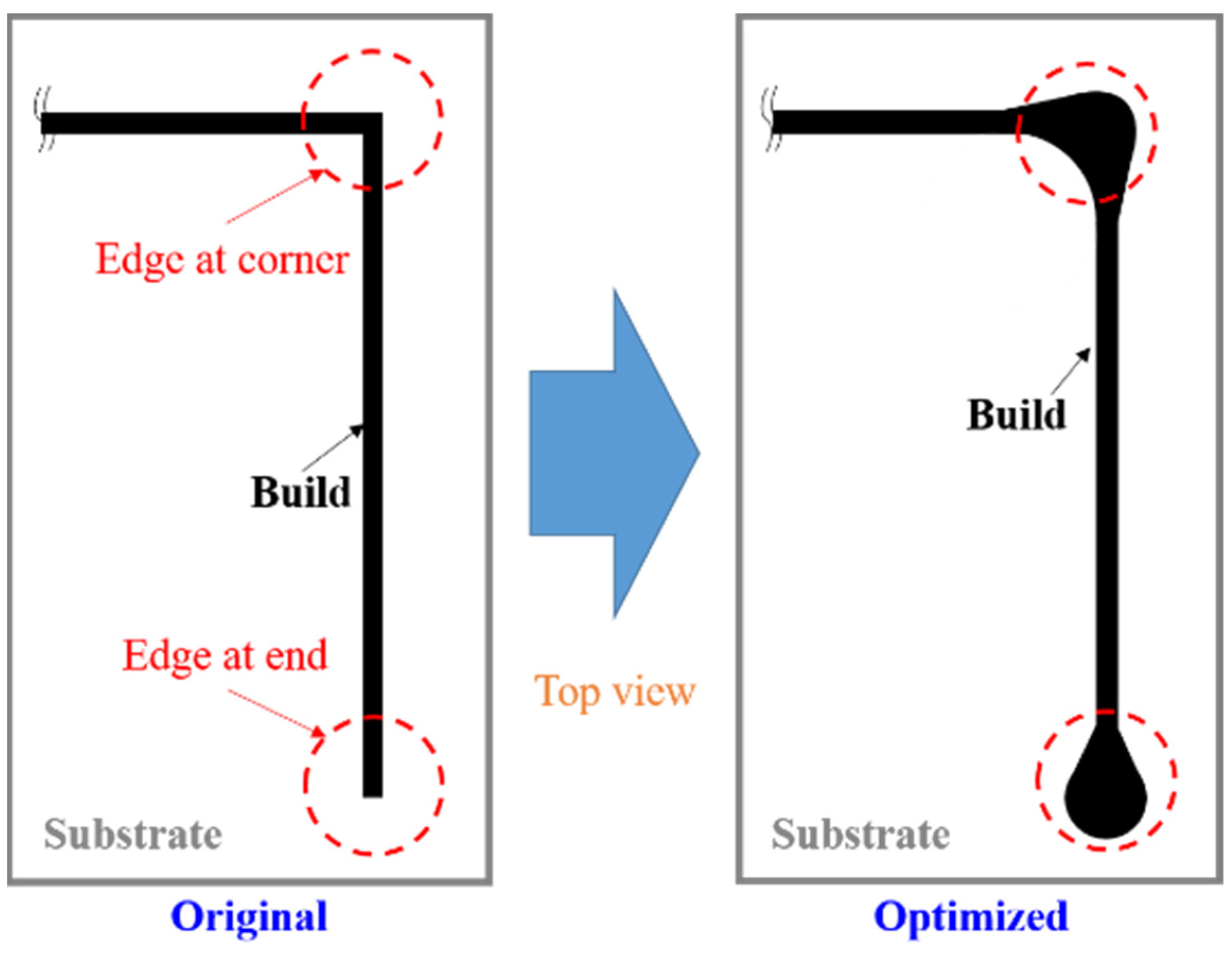
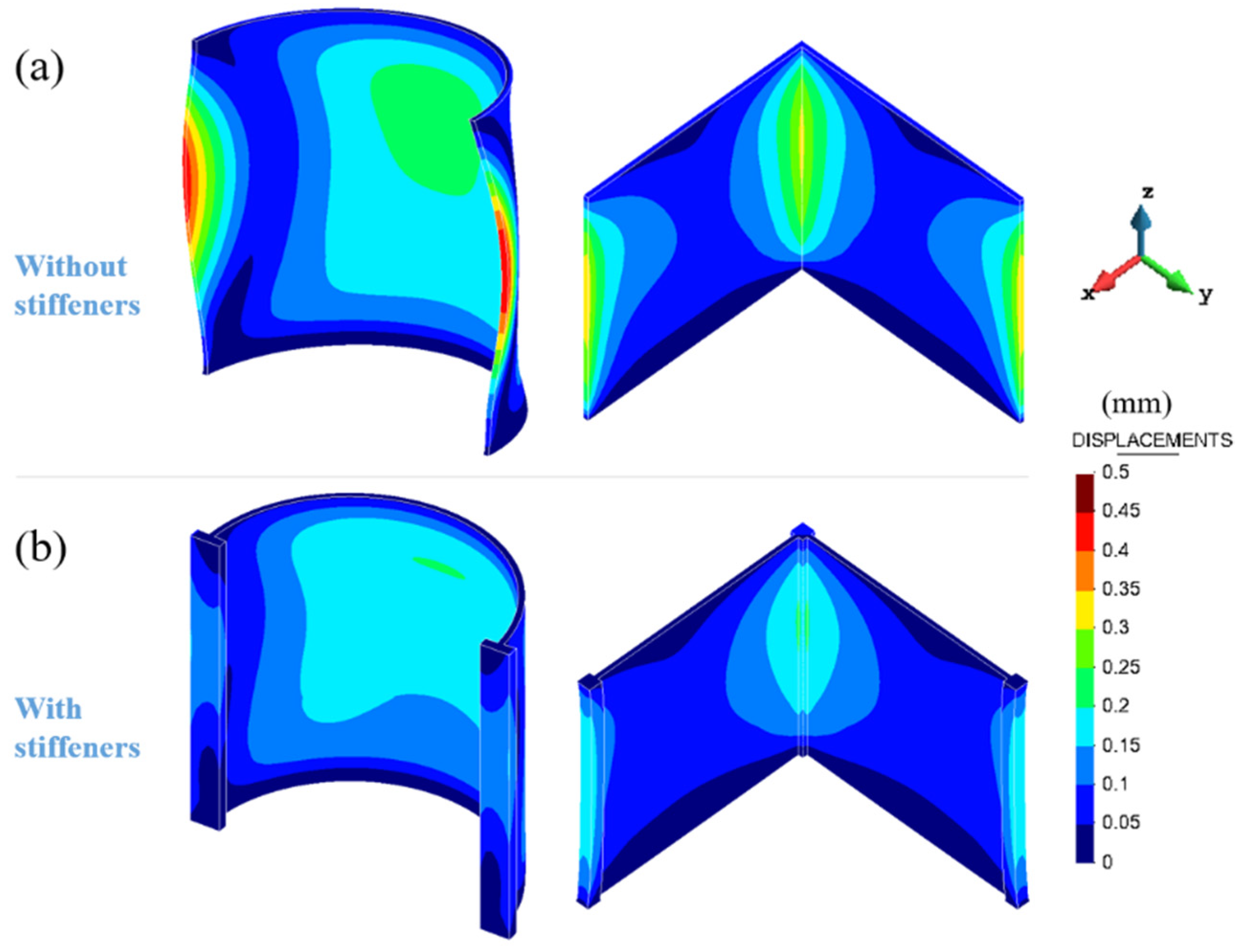
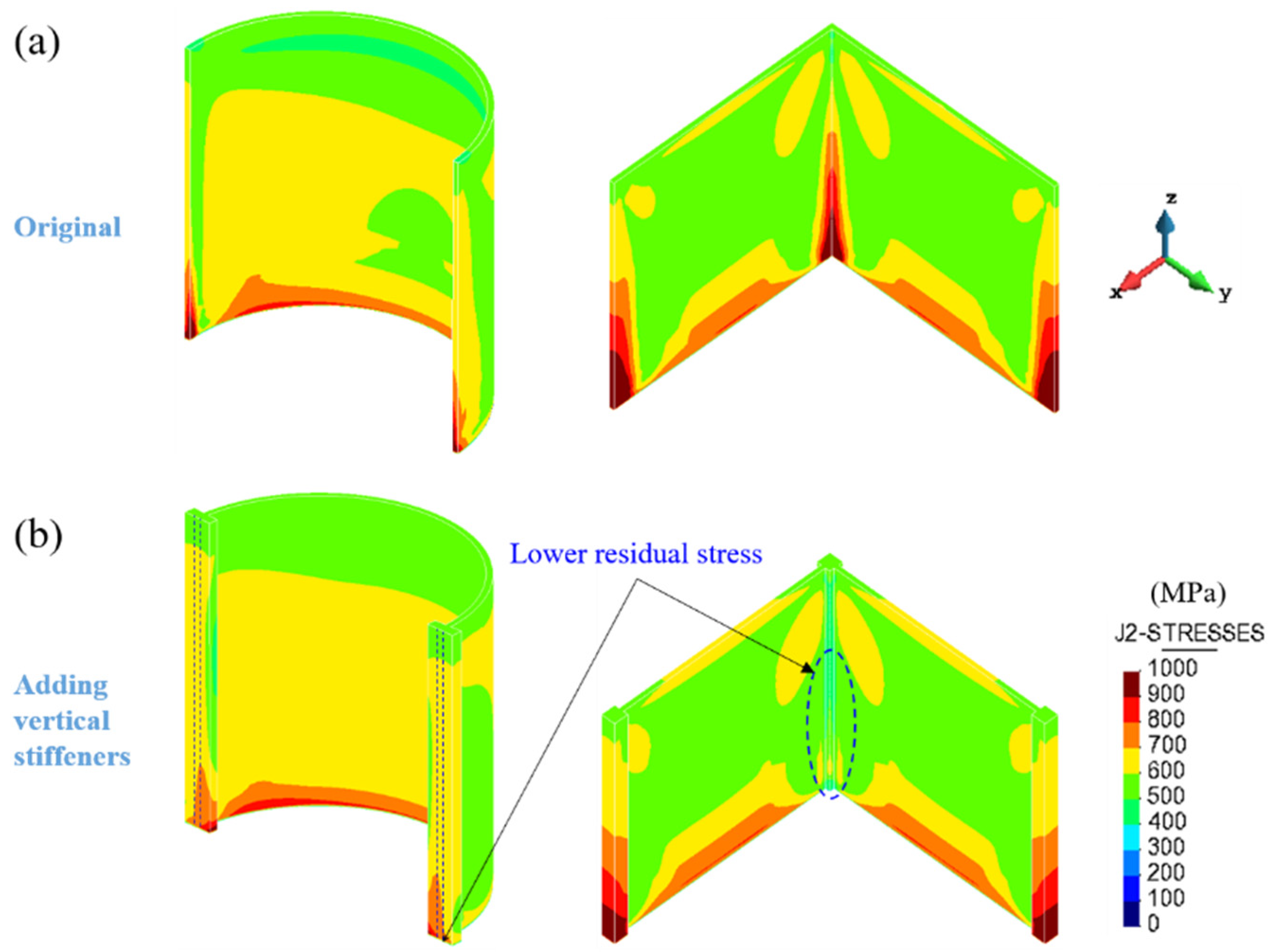
5. Structural Optimization for Warpage Control
6. Conclusions
- The wall thickness plays a significant role on the warpage of the final part. Thicker walled structures present reduced warpage.
- Increasing the build height as well as reducing the wall curvature causes larger warpage, as shown for the cylindrical structures.
- Open sections (e.g., semi-cylinder, L-shape, etc.) are more prone to warpage than closed ones (e.g., cylinder and square section) because of their reduced structural stiffness.
- The use of vertical stiffeners enables locally enhancing the structural stiffness of thin-walled structures, minimizing the residual warpage induced by the LPBF process.
- FE analysis of LPBF processes is a useful tool to analyse different thin-walled structures in order to predict the actual warpage. The developed FE model has been calibrated with experimental 3D-scanning images.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Herzog, D.; Seyda, V.; Wycisk, E.; Emmelmann, C. Additive manufacturing of metals. Acta Mater. 2016, 117, 371–392. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Lu, X.; Zhao, T.; Ji, X.; Hu, J.; Li, T.; Lin, X.; Huang, W. 3D printing well organized porous iron-nickel/ polyaniline nanocages multiscale supercapacitor. J. Alloys Compd. 2018, 760, 78–83. [Google Scholar] [CrossRef]
- Zheng, M.; Wei, L.; Chen, J.; Zhang, Q.; Zhong, C.; Lin, X.; Huang, W. A novel method for the molten pool and porosity formation modelling in selective laser melting. Int. J. Heat Mass Transf. 2019, 140, 1091–1105. [Google Scholar] [CrossRef]
- Lu, X.; Lin, X.; Chiumenti, M.; Cervera, M.; Li, J.; Ma, L.; Wei, L.; Hu, Y.; Huang, W. Finite element analysis and experimental validation of the thermomechanical behavior in Laser Laser Directed energy deposition of Ti-6Al-4V. Addit. Manuf. 2018, 21, 30–40. [Google Scholar]
- Cao, J.; Gharghouri, M.A.; Nash, P. Finite-element analysis and experimental validation of thermal residual stress and distortion in electron beam additive manufactured Ti-6Al-4V build plates. J. Mater. Process. Technol. 2016, 237, 409–419. [Google Scholar] [CrossRef]
- Lu, X.; Lin, X.; Chiumenti, M.; Cervera, M.; Hu, Y.; Ji, X.; Ma, L.; Yang, H.; Huang, W. Residual stress and distortion of rectangular and S-shaped Ti-6Al-4V parts by Directed Energy Deposition: Modelling and experimental calibration. Addit. Manuf. 2019, 26, 166–179. [Google Scholar] [CrossRef]
- Lu, X.; Lin, X.; Chiumenti, M.; Cervera, M.; Hu, Y.; Ji, X.; Ma, L.; Huang, W. In situ Measurements and Thermo-mechanical Simulation of Ti-6Al-4V Laser Laser Directed energy deposition Processes. Int. J. Mech. Sci. 2019, 153, 119–130. [Google Scholar] [CrossRef]
- Liu, Y.J.; Liu, Z.; Jiang, Y.; Wang, G.W.; Yang, Y.; Zhang, L.C. Gradient in microstructure and mechanical property of selective laser melted AlSi10Mg. J. Alloys Compd. 2018, 735, 1414–1421. [Google Scholar] [CrossRef]
- Fang, Z.C.; Wu, Z.L.; Huang, C.G.; Wu, C.W. Review on residual stress in selective laser melting additive manufacturing of alloy parts. Opt. Laser Technol. 2020, 129, 106283. [Google Scholar] [CrossRef]
- Lu, Y.; Wu, S.; Gan, Y.; Huang, T.; Yang, C.; Li, J.; Lin, J. Study on the microstructure, mechanical property and residual stress of SLM inconel-718 alloy manufactured by differing island scanning strategy. Opt. Laser Technol. 2015, 75, 197–206. [Google Scholar] [CrossRef]
- Zaeh, M.F.; Branner, G. Investigations on residual stresses and deformations in selective laser melting. Prod. Eng. 2009, 4, 35–45. [Google Scholar] [CrossRef]
- Vora, P.; Mumtaz, K.; Todd, I.; Hopkinson, N. AlSi12 in-situ alloy formation and residual stress reduction using anchorless selective laser melting. Addit. Manuf. 2015, 7, 12–19. [Google Scholar] [CrossRef]
- Lu, X.; Cervera, M.; Chiumenti, M.; Li, J.; Ji, X.; Zhang, G.; Lin, X. Modeling of the Effect of the Building Strategy on the Thermomechancial Response of Ti-6Al-4V Rectangular Parts Manufactured by Laser Directed Energy Deposition. Metals 2020, 10, 1643. [Google Scholar] [CrossRef]
- Yakout, M.; Elbestawi, M.; Veldhuis, S.; Nangle-Smith, S. Influence of thermal properties on residual stresses in SLM of aerospace alloys. Rapid Prototyp. J. 2020, 26, 213–222. [Google Scholar] [CrossRef]
- Chiumenti, M.; Neiva, E.; Salsi, E.; Cervera, M.; Badia, S.; Moya, J.; Chen, Z.; Lee, C.; Davies, C. Numerical modelling and experimental validation in Selective Laser Melting. Addit. Manuf. 2017, 18, 171–185. [Google Scholar] [CrossRef]
- Neiva, E.; Chiumenti, M.; Cervera, M.; Salsi, E.; Piscopo, G.; Badia, S.; Martín, A.F.; Chen, Z.; Lee, C.; Davies, C. Numerical modelling of heat transfer and experimental validation in powder-bed fusion with the virtual domain approximation. Finite Elem. Anal. Des. 2020, 168, 103343. [Google Scholar] [CrossRef]
- Lindgren, L.-E.; Lundbäck, A.; Malmelöv, A. Thermal stresses and computational welding mechanics. J. Therm. Stresses 2019, 42, 107–121. [Google Scholar] [CrossRef]
- Lundbäck, A.; Lindgren, L.-E. Modelling of metal deposition. Finite Elem. Anal. Des. 2011, 47, 1169–1177. [Google Scholar] [CrossRef]
- Williams, R.; Catrin, J.; Davies, M.; Hooper, P.A. A pragmatic part scale model for residual stress and distortion prediction in powder bed fusion. Addit. Manuf. 2018, 22, 416–425. [Google Scholar] [CrossRef]
- Baiges, J.; Chiumenti, M.; Moreira, C.A.; Cervera, M.; Codina, R. An Adaptive Finite Element strategy for the numerical simulation of Additive Manufacturing processes. Addit. Manuf. 2021, 37, 101650. [Google Scholar]
- Lu, X.; Chiumenti, M.; Cervera, M.; Li, J.; Lin, X.; Ma, L.; Zhang, G.; Liang, E. Substrate design to minimize residual stresses in Directed Energy Deposition AM processes. Mater. Des. 2021, 202, 109525. [Google Scholar] [CrossRef]
- Ramos, D.; Belblidia, F.; Sienz, J. New scanning strategy to reduce warpage in additive manufacturing. Addit. Manuf. 2019, 28, 554–564. [Google Scholar] [CrossRef]
- Levkulich, N.; Semiatin, S.; Gockel, J.; Middendorf, J.; Dewald, A.; Klingbeil, N. The effect of process parameters on residual stress evolution and distortion in the laser powder bed fusion of Ti-6Al-4V. Addit. Manuf. 2019, 28, 475–484. [Google Scholar] [CrossRef]
- Li, H.; Ramezani, M.; Chen, Z.; Singamneni, S. Effects of Process Parameters on Temperature and Stress Distributions During Selective Laser Melting of Ti-6Al-4V. Trans. Indian Inst. Met. 2019, 72, 3201–3214. [Google Scholar] [CrossRef]
- Afazov, S.; Denmark, W.A.; Toralles, B.L.; Holloway, A.; Yaghi, A. Distortion prediction and compensation in selective laser melting. Addit. Manuf. 2017, 17, 15–22. [Google Scholar] [CrossRef]
- Yaghi, A.; Ayvar-Soberanis, S.; Moturu, S.; Bilkhu, R.; Afazov, S. Design against distortion for additive manufacturing. Addit. Manuf. 2019, 27, 224–235. [Google Scholar] [CrossRef]
- Biegler, M.; Elsner, B.A.; Graf, B.; Rethmeier, M. Geometric distortion-compensation via transient numerical simulation for directed energy deposition additive manufacturing. Sci. Technol. Weld. Join. 2020, 25, 468–475. [Google Scholar] [CrossRef]
- Li, Z.; Xu, R.; Zhang, Z.; Kucukkoc, I. The influence of scan length on fabricating thin-walled components in selective laser melting. Int. J. Mach. Tools Manuf. 2018, 126, 1–12. [Google Scholar] [CrossRef]
- Chen, C.; Xiao, Z.; Zhu, H.; Zeng, X. Deformation and control method of thin-walled part during laser powder bed fusion of Ti–6Al–4V alloy. Int. J. Adv. Manuf. Technol. 2020, 110, 3467–3478. [Google Scholar] [CrossRef]
- Ahmed, A.; Majeed, A.; Atta, Z.; Jia, G. Dimensional Quality and Distortion Analysis of Thin-Walled Alloy Parts of AlSi10Mg Manufactured by Selective Laser Melting. J. Manuf. Mater. Process. 2019, 3, 51. [Google Scholar] [CrossRef]
- Setien, I.; Chiumenti, M.; Van Der Veen, S.; Sebastian, M.S.; Garciandía, F.; Echeverría, A. Empirical methodology to determine inherent strains in additive manufacturing. Comput. Math. Appl. 2019, 78, 2282–2295. [Google Scholar] [CrossRef]
- Chiumenti, M.; Lin, X.; Cervera, M.; Lei, W.; Zheng, Y.; Huang, W. Numerical simulation and experimental calibration of additive manufacturing by blown powder technology. Part I: Thermal analysis. Rapid Prototyp. J. 2017, 23, 448–463. [Google Scholar] [CrossRef]
- Chiumenti, M.; Cervera, M.; Salmi, A.; De Saracibar, C.A.; Dialami, N.; Matsui, K. Finite element modeling of multi-pass welding and shaped metal deposition processes. Comput. Methods Appl. Mech. Eng. 2010, 199, 2343–2359. [Google Scholar] [CrossRef]
- Chiumenti, M.; Cervera, M.; Dialami, N.; Wu, B.; Jinwei, L.; De Saracibar, C.A. Numerical modeling of the electron beam welding and its experimental validation. Finite Elem. Anal. Des. 2016, 121, 118–133. [Google Scholar] [CrossRef]
- Cervera, M.; de Saracibar, C.A.; Chiumenti, M. COMET: Coupled Mechanical and Thermal Analysis; Data Input Manual, Version 5.0, Technical Report IT-308; CIMNE: Barcelona, Spain, 2002. [Google Scholar]
- Dialami, N.; Cervera, M.; Chiumenti, M.; De Saracibar, C.A. A fast and accurate two-stage strategy to evaluate the effect of the pin tool profile on metal flow, torque and forces in friction stir welding. Int. J. Mech. Sci. 2017, 122, 215–227. [Google Scholar] [CrossRef]
- Ribó, R.; Pasenau, M.; Escolano, E.; Pérez, J.; Coll, A.; Melendo, A. GiD The Personal Pre and Postprocessor; Reference Manual; CIMNE: Barcelona, Spain, 2006. [Google Scholar]
- Zhang, W.; Tong, M.; Harrison, N.M. Resolution, energy and time dependency on layer scaling in finite element modelling of laser beam powder bed fusion additive manufacturing. Addit. Manuf. 2019, 28, 610–620. [Google Scholar] [CrossRef]
- Dunbar, A.J.; Denlinger, E.R.; Gouge, M.F.; Michaleris, P. Experimental validation of finite element modeling for laser powder bed fusion deformation. Addit. Manuf. 2016, 12, 108–120. [Google Scholar] [CrossRef]
- Yang, T.; Xie, D.; Yue, W.; Wang, S.; Rong, P.; Shen, L.; Zhao, J.; Wang, C. Distortion of Thin-Walled Structure Fabricated by Selective Laser Melting Based on Assumption of Constraining Force-Induced Distortion. Metals 2019, 9, 1281. [Google Scholar] [CrossRef]



| Al | V | O | H | N | C | Fe | Si | Ti |
|---|---|---|---|---|---|---|---|---|
| 6.28 | 3.90 | 0.098 | 0.002 | 0.020 | 0.008 | 0.022 | 0.026 | Balance |
| Laser Power (W) | Layer Thickness (µm) | Scan Speed (mm/s) | Hatch Spacing (µm) | Laser BeamDiameter (µm) |
|---|---|---|---|---|
| 200 | 30 | 1000 | 100 | 100 |
| Thin-Walled Parts | Dimensions | Number of FE Elements | Number of Nodes |
|---|---|---|---|
| Semi-cylindrical part | Φ50 mm × H50 mm | 21,606 | 37,618 |
| Cylindrical part | Φ50 mm × H50 mm | 34,632 | 63,336 |
| L-shaped part | L50 mm × W50 mm × H50 mm | 34,366 | 55,392 |
| Temperature (°C) | Density (kg/m3) | Specific Heat (J/(kg·°C)) | Thermal Conductivity (W/(m·°C)) | Poisson’s Ratio | Young’s Modulus (GPa) | Thermal Dilatancy (μm/m/ °C) | Yield Stress (MPa) |
|---|---|---|---|---|---|---|---|
| 20 | 4420 | 546 | 7 | 0.345 | 110 | 8.78 | 850 |
| 205 | 4395 | 584 | 8.75 | 0.35 | 100 | 10 | 630 |
| 500 | 4350 | 651 | 12.6 | 0.37 | 76 | 11.2 | 470 |
| 995 | 4282 | 753 | 22.7 | 0.43 | 15 | 12.3 | 13 |
| 1100 | 4267 | 641 | 19.3 | 0.43 | 5 | 12.4 | 5 |
| 1200 | 4252 | 660 | 21 | 0.43 | 4 | 12.42 | 1 |
| 1600 | 4198 | 732 | 25.8 | 0.43 | 1 | 12.5 | 0.5 |
| 1650 | 3886 | 831 | 35 | 0.43 | 0.1 | 12.5 | 0.1 |
| 2000 | 3818 | 831 | 35 | 0.43 | 0.01 | 12.5 | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Chiumenti, M.; Cervera, M.; Tan, H.; Lin, X.; Wang, S. Warpage Analysis and Control of Thin-Walled Structures Manufactured by Laser Powder Bed Fusion. Metals 2021, 11, 686. https://doi.org/10.3390/met11050686
Lu X, Chiumenti M, Cervera M, Tan H, Lin X, Wang S. Warpage Analysis and Control of Thin-Walled Structures Manufactured by Laser Powder Bed Fusion. Metals. 2021; 11(5):686. https://doi.org/10.3390/met11050686
Chicago/Turabian StyleLu, Xufei, Michele Chiumenti, Miguel Cervera, Hua Tan, Xin Lin, and Song Wang. 2021. "Warpage Analysis and Control of Thin-Walled Structures Manufactured by Laser Powder Bed Fusion" Metals 11, no. 5: 686. https://doi.org/10.3390/met11050686
APA StyleLu, X., Chiumenti, M., Cervera, M., Tan, H., Lin, X., & Wang, S. (2021). Warpage Analysis and Control of Thin-Walled Structures Manufactured by Laser Powder Bed Fusion. Metals, 11(5), 686. https://doi.org/10.3390/met11050686








