Deep Learning Sequence Methods in Multiphysics Modeling of Steel Solidification
Abstract
1. Introduction
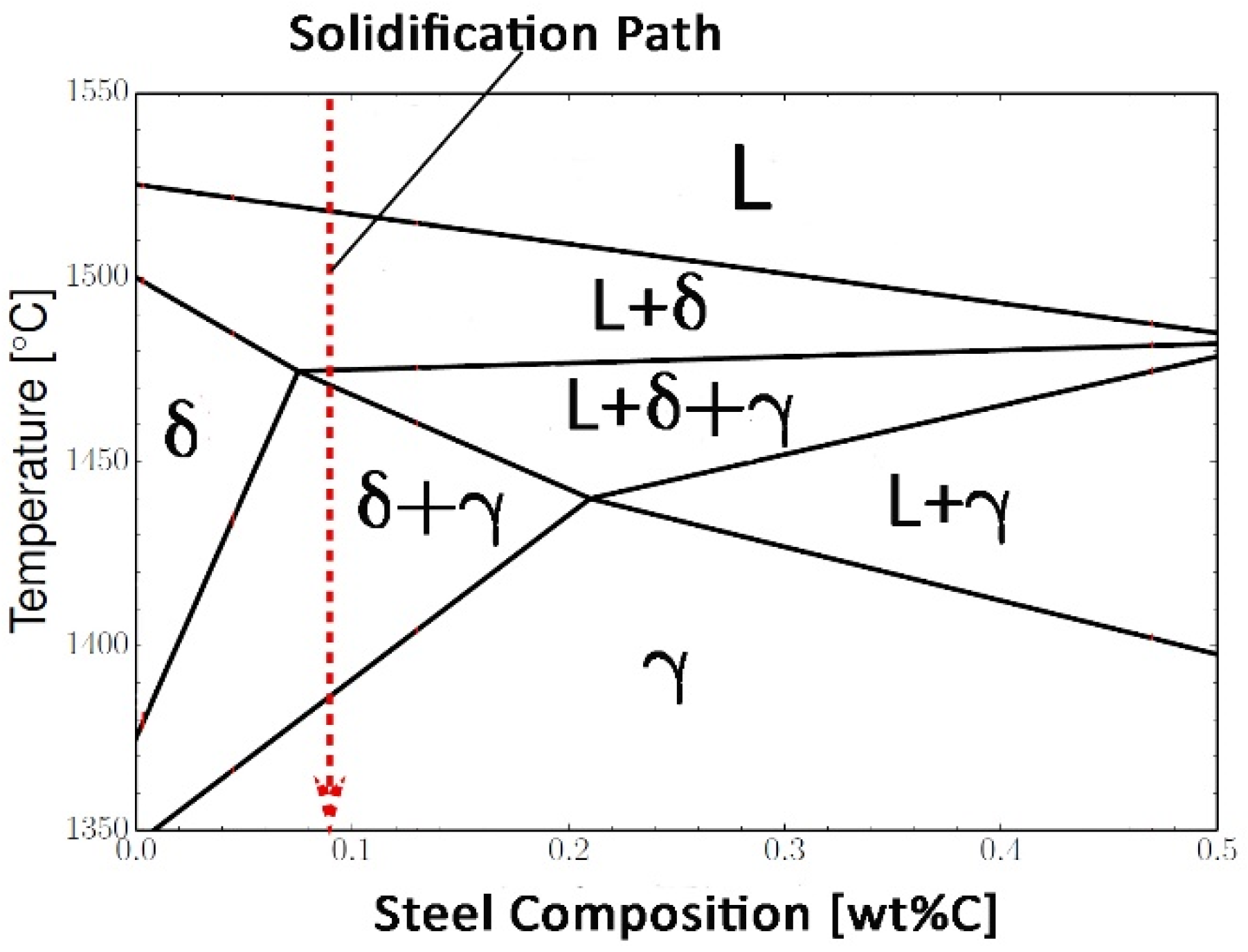
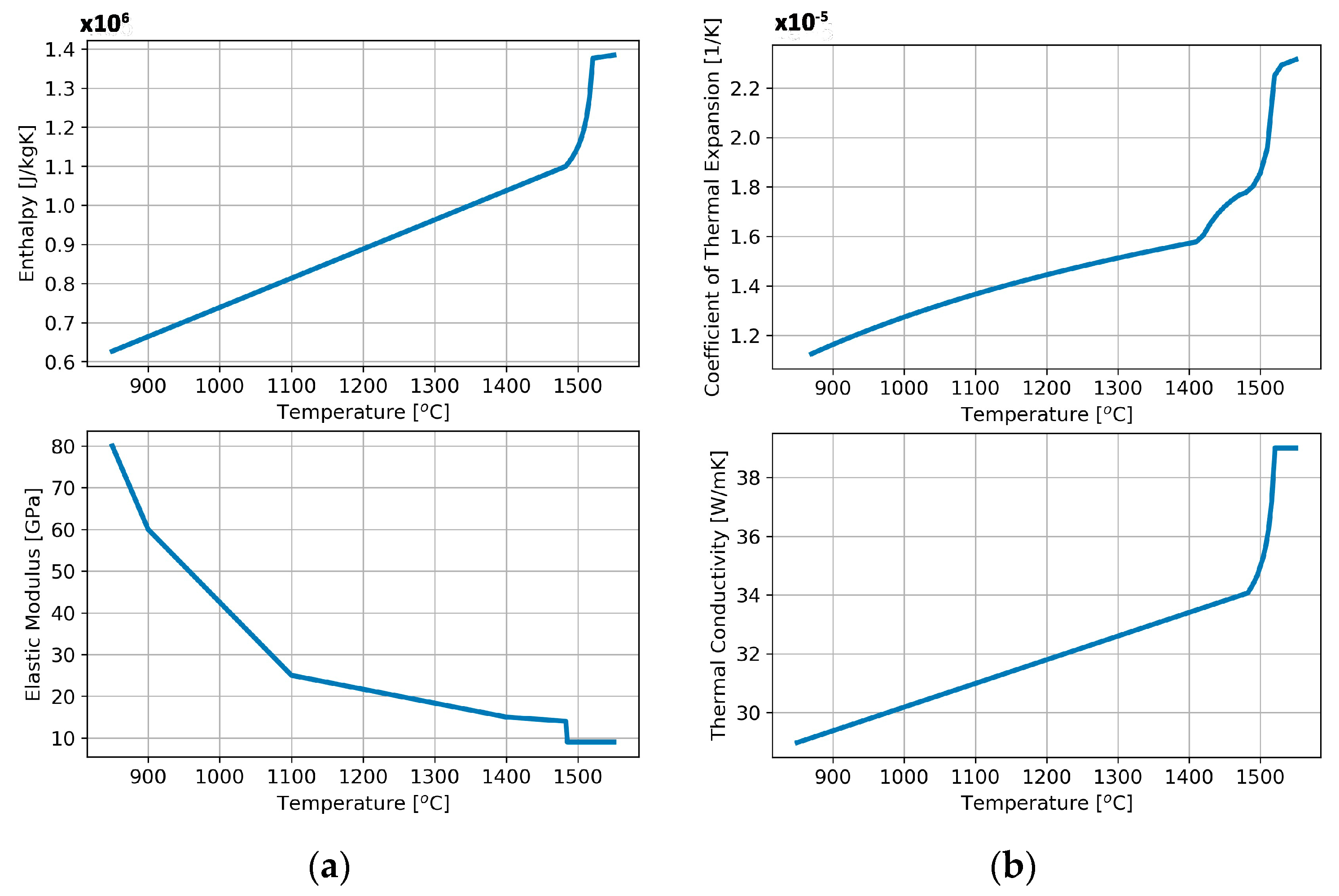
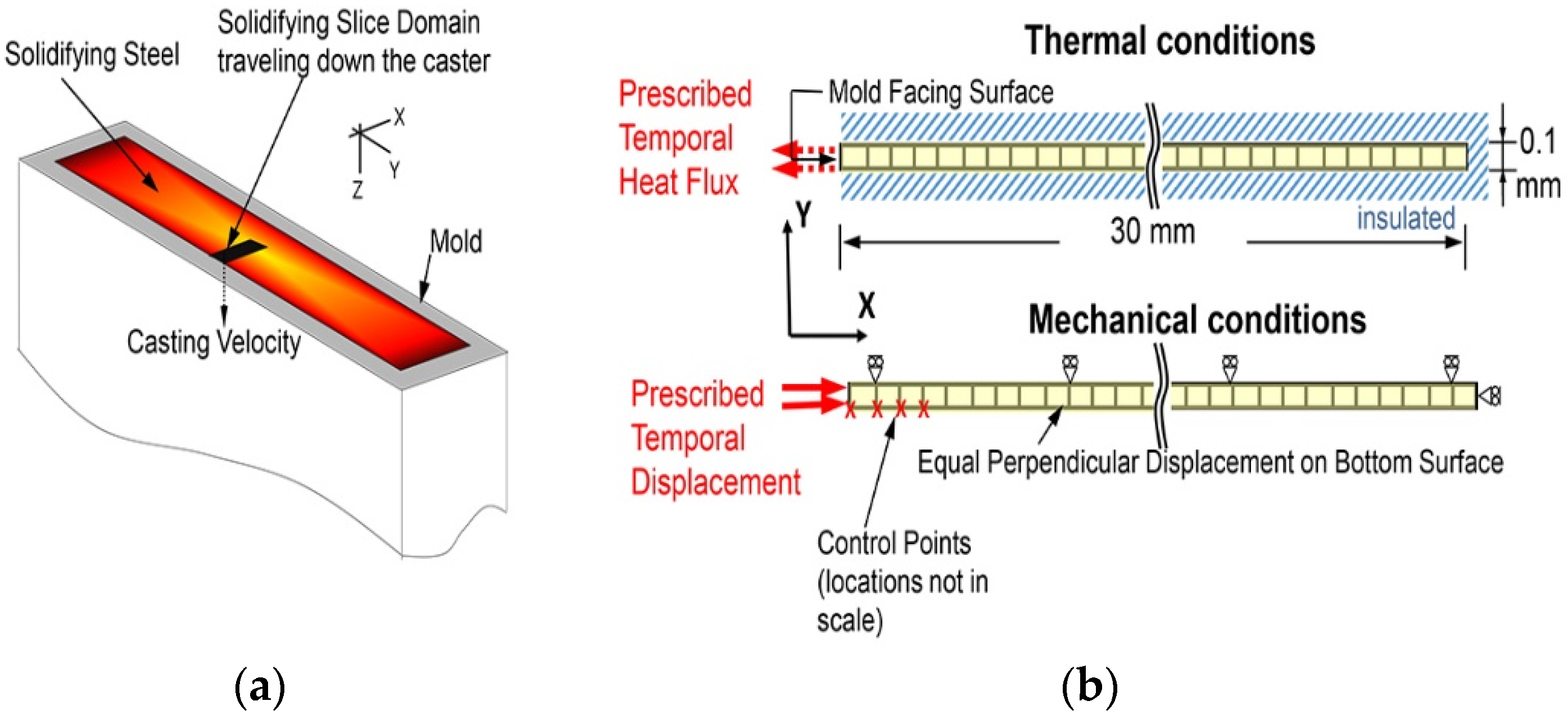
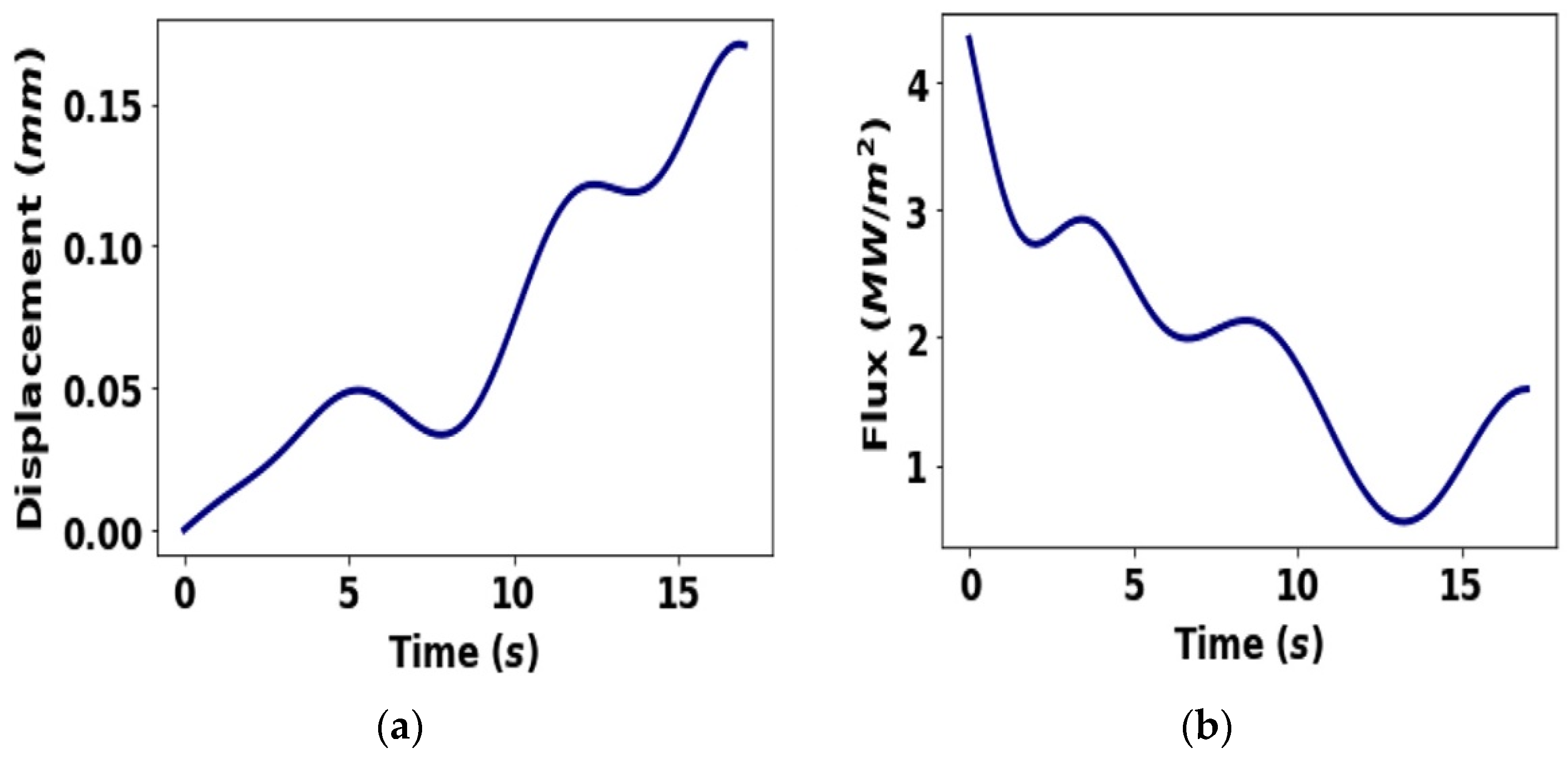
2. Thermo-Mechanical Model of Steel Solidification
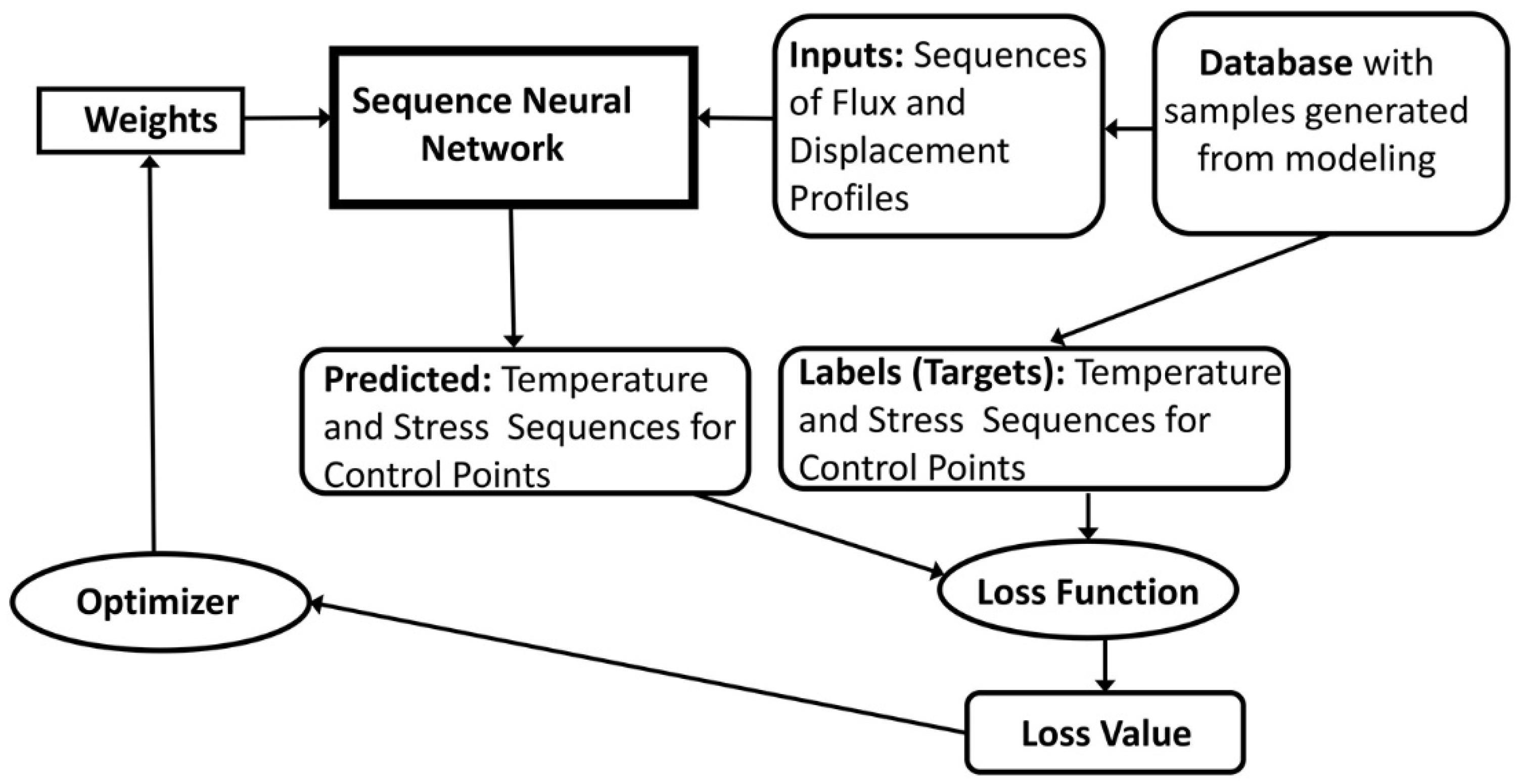
3. Deep Learning Models
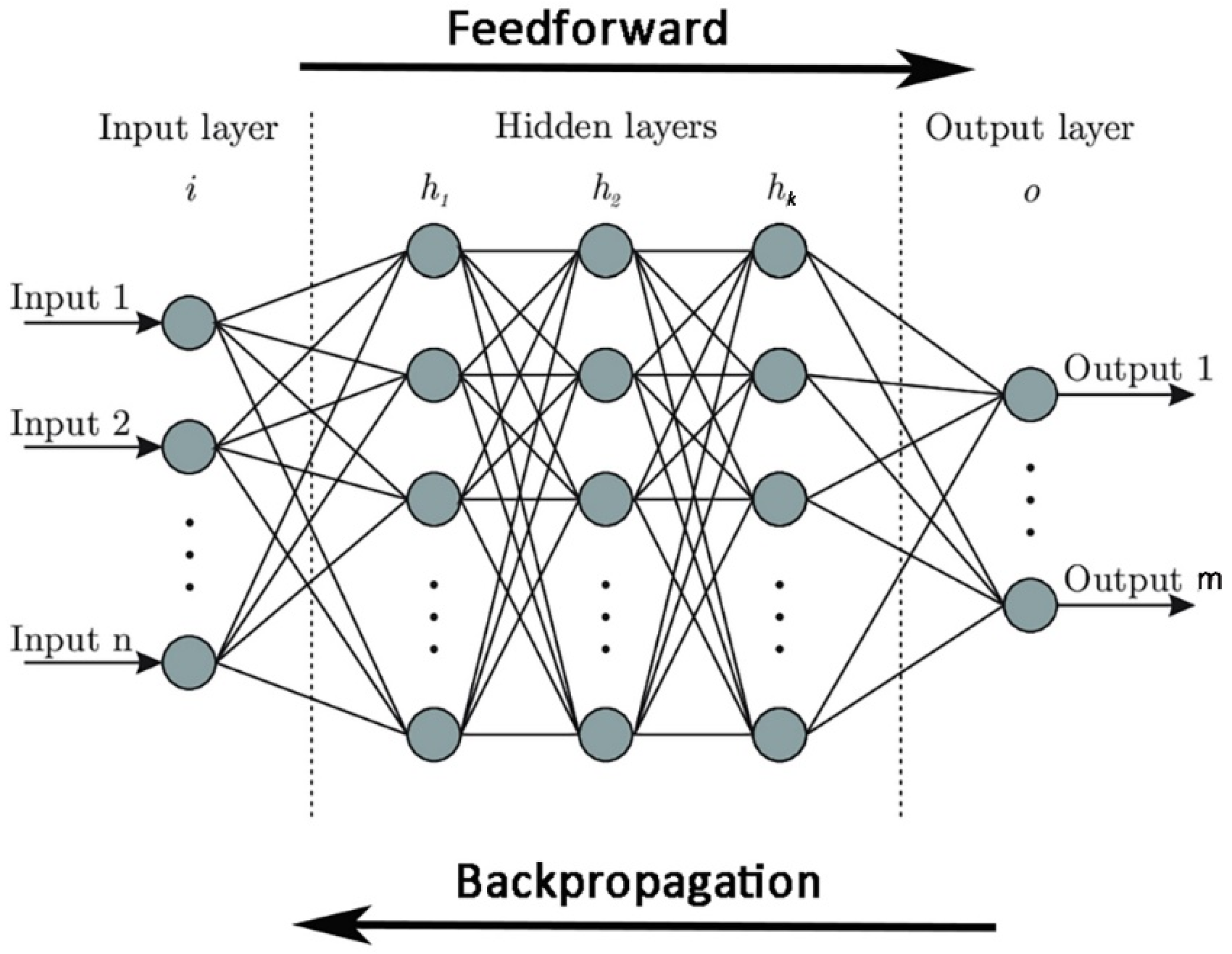
3.1. Dense Feedforward Neural Network
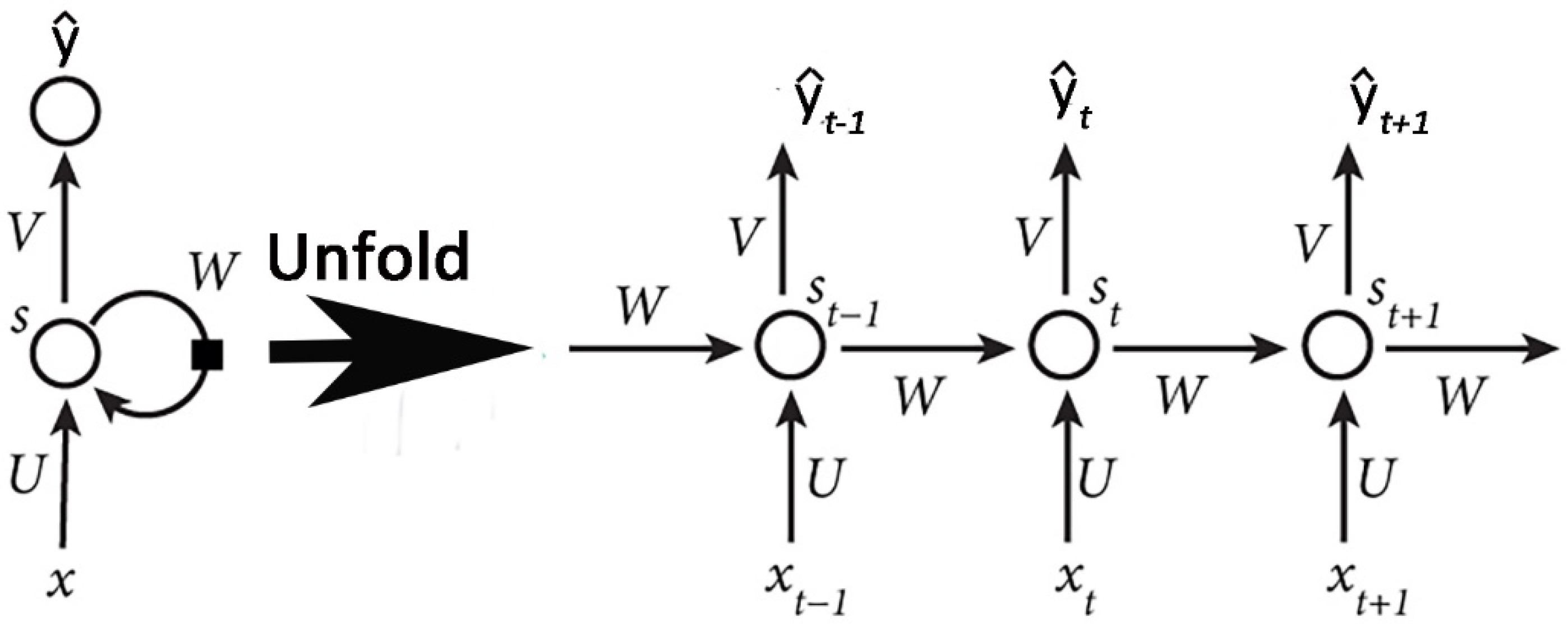
3.2. Recurrent Neural Networks
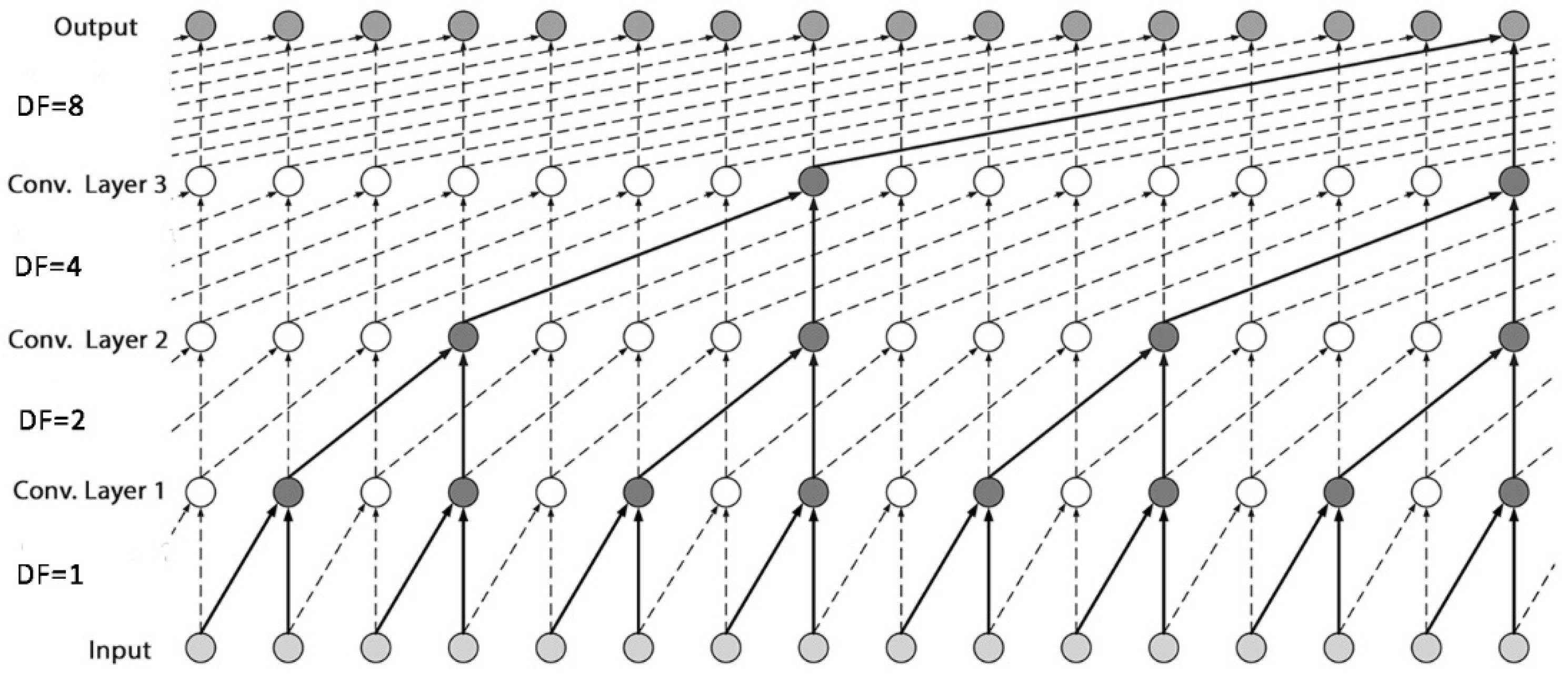
3.3. Temporal Convolutional Neural Network
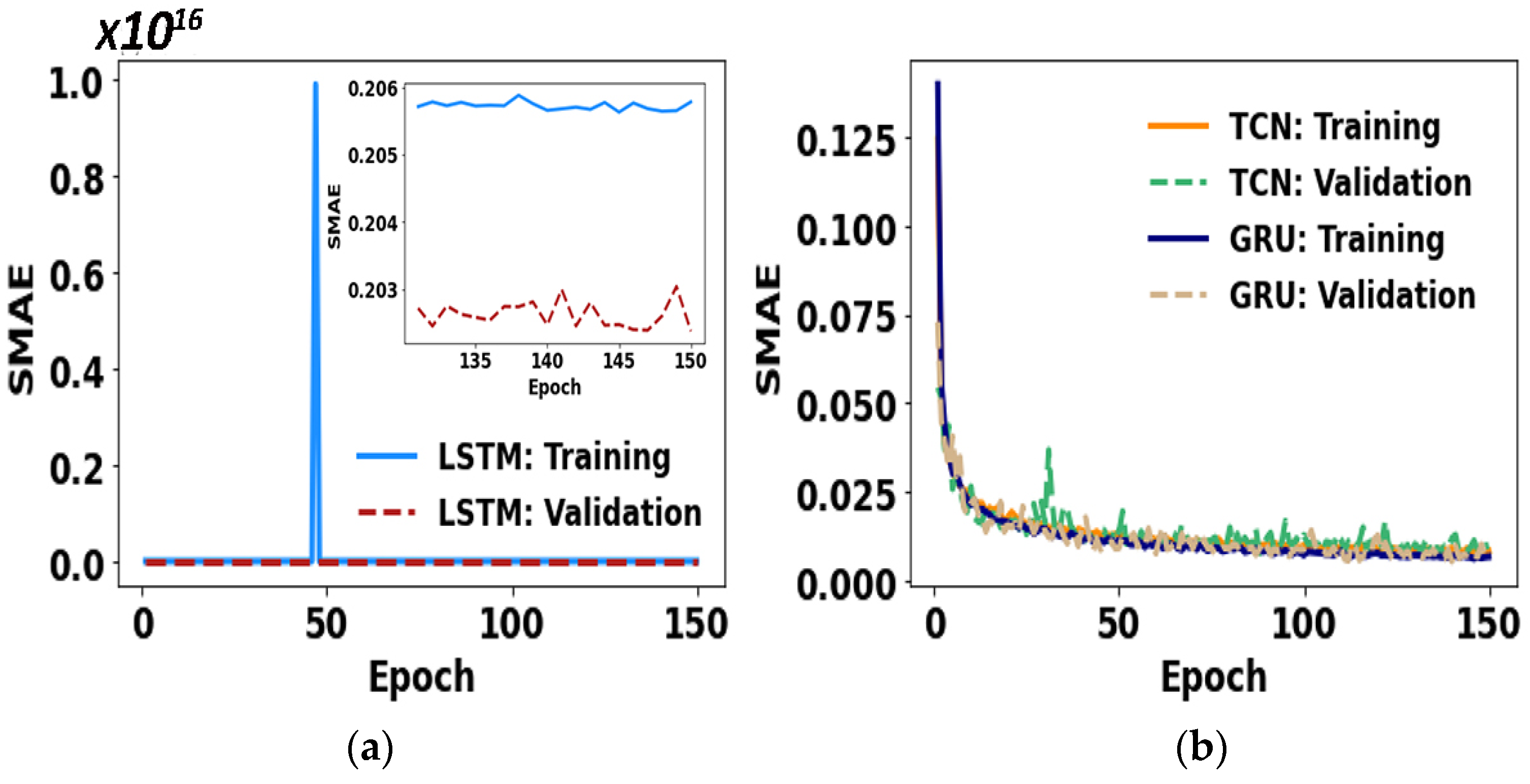
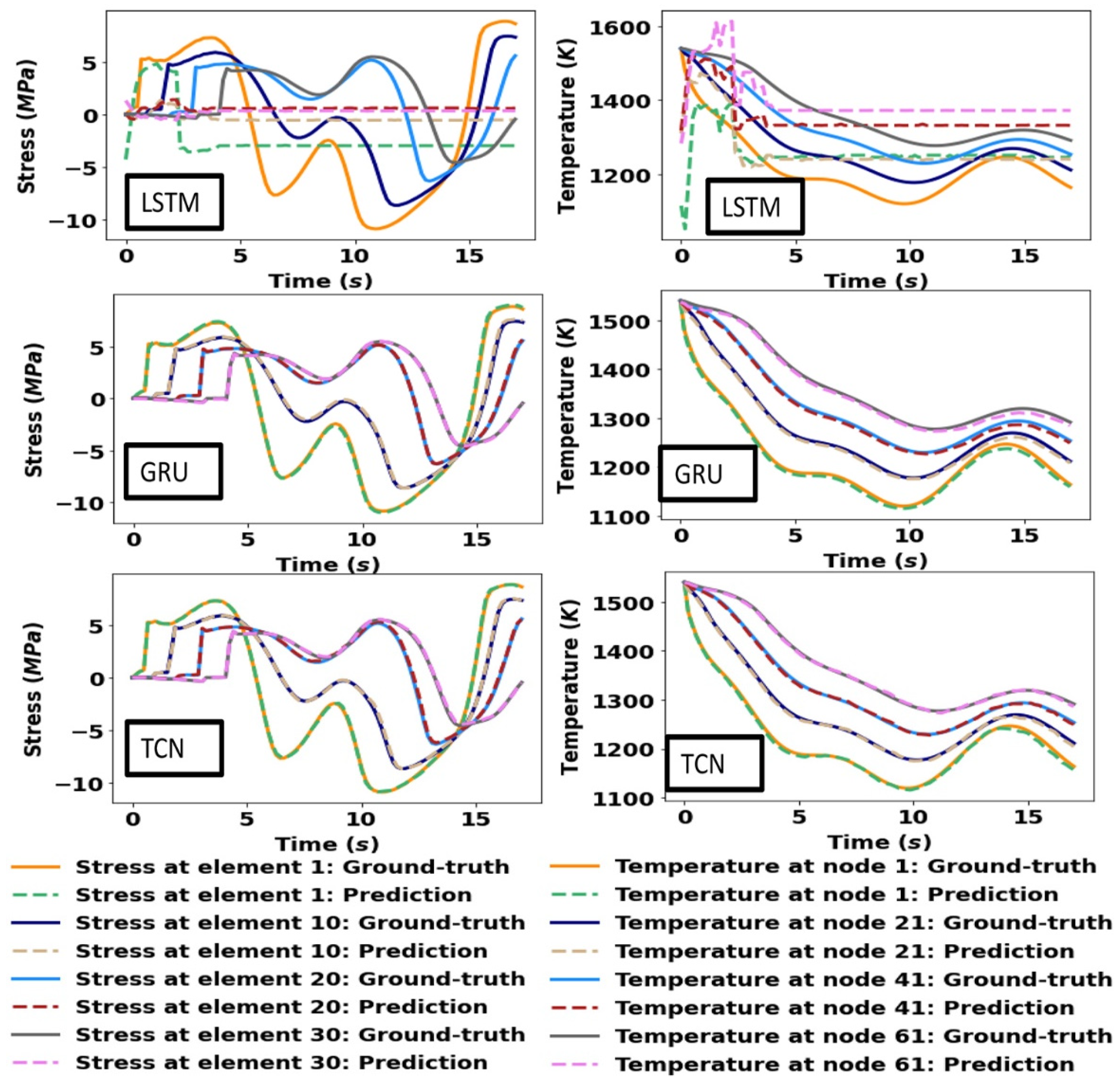
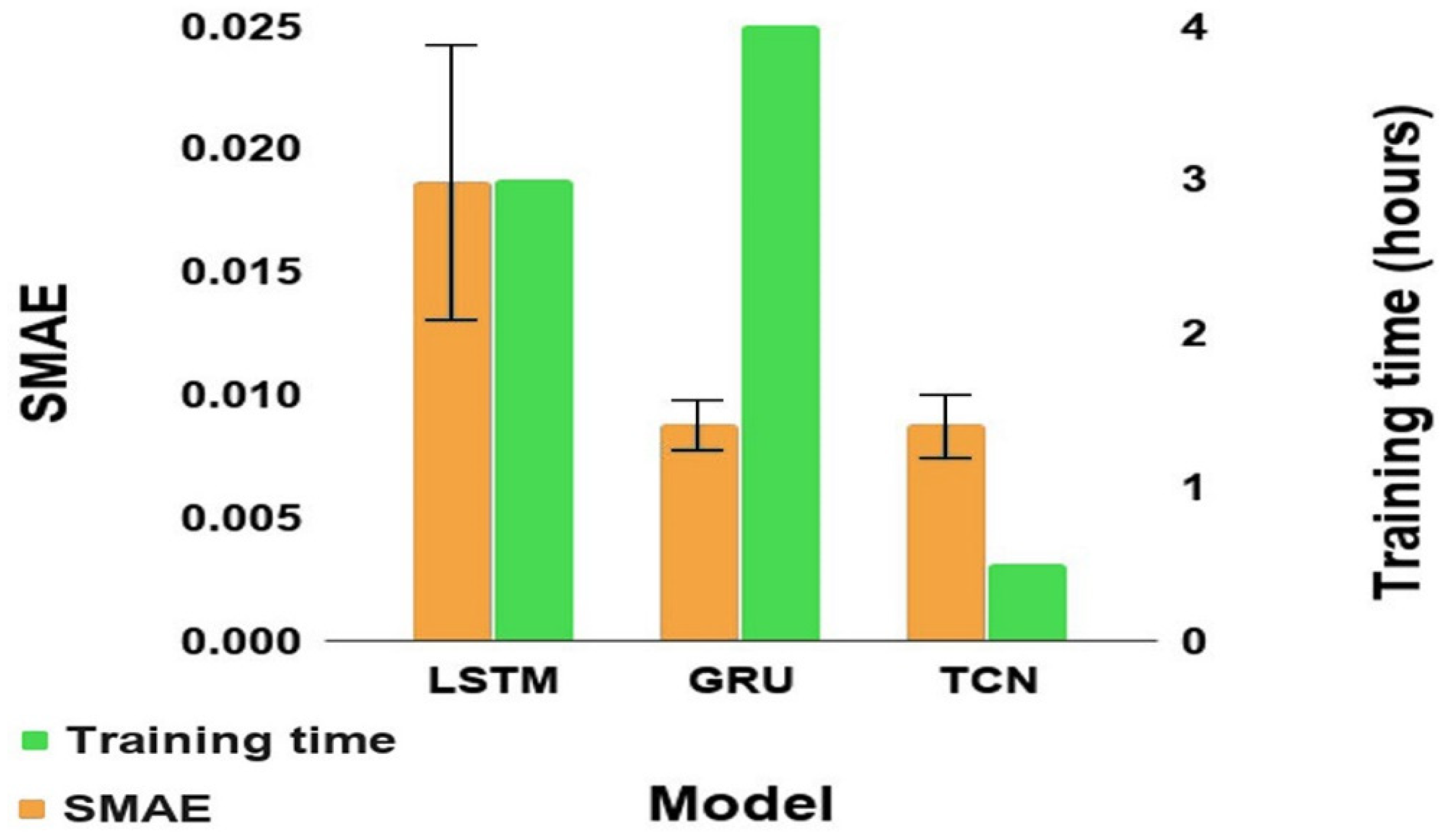
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, J.-E.; Yeo, T.-J.; Hwan, O.K.; Yoon, J.-K.; Yoon, U.-S. Prediction of cracks in continuously cast steel beam blank through fully coupled analysis of fluid flow, heat transfer, and deformation behavior of a solidifying shell. Metall. Mater. Trans. 2000, 31, 225–237. [Google Scholar] [CrossRef]
- Teskeredžić, A.; Demirdžić, I.; Muzaferija, S. Numerical method for heat transfer, fluid flow, and stress analysis in phase-change problems. Numer. Heat Transf. Part B Fundam. 2002, 42, 437–459. [Google Scholar] [CrossRef]
- Koric, S.; Thomas, B.G. Efficient thermo-mechanical model for solidification processes. Int. J. Numer. Methods Eng. 2006, 66, 1955–1989. [Google Scholar] [CrossRef]
- Li, C.; Thomas, B.G. Thermomechanical finite-element model of shell behavior in continuous casting of steel. Metall. Mater. Trans. B 2004, 35, 1151–1172. [Google Scholar] [CrossRef]
- Abaqus/Standard User’s Manual Version 2019; Simulia Dassault Systèmes: Providence, RI, USA, 2019.
- Koric, S.; Hibbeler, L.C.; Thomas, B.G. Explicit coupled thermo-mechanical finite element model of steel solidification. Int. J. Numer. Methods Eng. 2009, 78, 1–31. [Google Scholar] [CrossRef]
- Koric, S.; Thomas, B.G.; Voller, V.R. Enhanced Latent Heat Method to Incorporate Superheat Effects into Fixed-Grid Multiphysics Simulations. Numer. Heat Transf. Part B Fundam. 2010, 57, 396–413. [Google Scholar] [CrossRef]
- Koric, S.; Hibbeler, L.C.; Liu, R.; Thomas, B.G. Multiphysics Model of Metal Solidification on the Continuum Level. Numer. Heat Transf. Part B Fundam. 2010, 58, 371–392. [Google Scholar] [CrossRef]
- Zappulla, M.L.; Cho, S.-M.; Koric, S.; Lee, H.-J.; Kim, S.-H.; Thomas, B.G. Multiphysics modeling of continuous casting of stainless steel. J. Mater. Process. Technol. 2020, 278, 116469. [Google Scholar] [CrossRef]
- Zhang, S.; Guillemot, G.; Gandin, C.-A.; Bellet, M. A Partitioned Solution Algorithm for Concurrent Computation of Stress–Strain and Fluid Flow in Continuous Casting Process. Met. Mater. Trans. A 2021, 1–18. [Google Scholar] [CrossRef]
- Cai, L.; Wang, X.; Wei, J.; Yao, M.; Liu, Y. Element-Free Galerkin Method Modeling of Thermo-Elastic-Plastic Behavior for Continuous Casting Round Billet. Met. Mater. Trans. B 2021, 1–11. [Google Scholar] [CrossRef]
- Huitron, R.M.P.; Lopez, P.E.R.; Vuorinen, E.; Jentner, R.; Kärkkäinen, M.E. Converging criteria to characterize crack susceptibility in a micro-alloyed steel during continuous casting. Mater. Sci. Eng. A 2020, 772, 138691. [Google Scholar] [CrossRef]
- Li, G.; Ji, C.; Zhu, M. Prediction of Internal Crack Initiation in Continuously Cast Blooms. Met. Mater. Trans. B 2021, 1–15. [Google Scholar] [CrossRef]
- Rong, Q.; Wei, H.; Huang, X.; Bao, H. Predicting the effective thermal conductivity of composites from cross sections images using deep learning methods. Compos. Sci. Technol. 2019, 184, 107861. [Google Scholar] [CrossRef]
- Goli, E.; Vyas, S.; Koric, S.; Sobh, N.; Geubelle, P.H. ChemNet: A Deep Neural Network for Advanced Composites Manufacturing. J. Phys. Chem. B 2020, 124, 9428–9437. [Google Scholar] [CrossRef] [PubMed]
- Abueidda, D.W.; Koric, S.; Sobh, N.A. Topology optimization of 2D structures with nonlinearities using deep learning. Comput. Struct. 2020, 237, 106283. [Google Scholar] [CrossRef]
- Kollmann, H.T.; Abueidda, D.W.; Koric, S.; Guleryuz, E.; Sobh, N.A. Deep learning for topology optimization of 2D metamaterials. Mater. Design 2020, 196, 109098. [Google Scholar] [CrossRef]
- Spear, A.D.; Kalidindi, S.R.; Meredig, B.K.; Le Graverend, A.J.-B. Data driven materials investigations: The next frontier in understanding and predicting fatigue behavior. JOM 2018, 70, 1143–1146. [Google Scholar] [CrossRef]
- Mozafar, M.; Bostanabad, R.; Chen, W.; Ehmann, K.; Cao, J.; Bessa, M. Deep learning predicts path-dependent plasticity. Proc. Natl. Acad. Sci. USA 2019, 116, 26414–26420. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Koric, S.; Sobh, N.A.; Sehitoglu, H. Deep learning for plasticity and thermo-viscoplasticity. Int. J. Plast. 2021, 136, 102852. [Google Scholar] [CrossRef]
- Kozlowski, P.F.; Thomas, B.G.; Azzi, J.A.; Wang, H. Simple constitutive equations for steel at high temperature. Met. Mater. Trans. A 1992, 23, 903–918. [Google Scholar] [CrossRef]
- Zhu, H. Coupled Thermo-Mechanical Finite-Element Model with Application to Initial Solidification. Ph.D. Thesis, The University of Illinois at Urbana-Champaign, Urbana, IL, USA, May 1996. [Google Scholar]
- Fachinotti, V.D.; Le Corre, S.; Triolet, N.; Bobadilla, M.; Bellet, M. Two-phase thermo-mechanical and macrosegregation modelling of binary alloys solidification with emphasis on the secondary cooling stage of steel slab continuous casting processes. Int. J. Numer. Methods Eng. 2006, 67, 1341–1384. [Google Scholar] [CrossRef]
- Zhu, J.Z.; Guo, J.; Samonds, M.T. Numerical modeling of hot tearing formation in metal casting and its validations. Int. J. Numer. Methods Eng. 2011, 87, 289–308. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Represen-tations using RNN Encoder-Decoder for Statistical Machine Translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Pattanayak, S. Pro Deep Learning with TensorFlow, A Mathematical Approach to Advanced Artificial Intelligence in Python, 1st ed.; Apress Media LLC, Springer Media: New York, NY, USA, 2017; pp. 262–277. [Google Scholar]
- Alla, S.; Adari, S.K. Beginning Anomaly Detection Using Python-Based Deep Learning, 1st ed.; Apress Media LLC, Springer Media: New York, NY, USA, 2019; pp. 257–282. [Google Scholar]
- Keras, Chollet, François. Available online: https://github.com/keras-team/keras (accessed on 8 February 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koric, S.; Abueidda, D.W. Deep Learning Sequence Methods in Multiphysics Modeling of Steel Solidification. Metals 2021, 11, 494. https://doi.org/10.3390/met11030494
Koric S, Abueidda DW. Deep Learning Sequence Methods in Multiphysics Modeling of Steel Solidification. Metals. 2021; 11(3):494. https://doi.org/10.3390/met11030494
Chicago/Turabian StyleKoric, Seid, and Diab W. Abueidda. 2021. "Deep Learning Sequence Methods in Multiphysics Modeling of Steel Solidification" Metals 11, no. 3: 494. https://doi.org/10.3390/met11030494
APA StyleKoric, S., & Abueidda, D. W. (2021). Deep Learning Sequence Methods in Multiphysics Modeling of Steel Solidification. Metals, 11(3), 494. https://doi.org/10.3390/met11030494





