A Review of Damage, Void Evolution, and Fatigue Life Prediction Models
Abstract
1. Introduction
- Empirical models are established under a Newtonian mechanics framework (this also includes Hamiltonian and Lagrangian mechanics). Regardless of the different techniques used to characterize the damage evolution with equations and some parameters, it primarily relies on the test data curve to fit the empirical void/damage evolution function. Examples include the Gurson–Tvergaard–Needleman (GTN) model [2], Rice-Tracey model [3], Gunawardena model [4], the well-known, strain rate dependent Johnson-Cook (J-C) damage model [5], some micro-mechanism based damage models, and models using irreversible entropy as a metric with an empirical evolution function. These empirical models are popular for engineering applications due to their simplicity. Still, the identification of parameters is costly, time-consuming, and lacks any scientific basis due to a lack of physical and mathematical foundations [6].
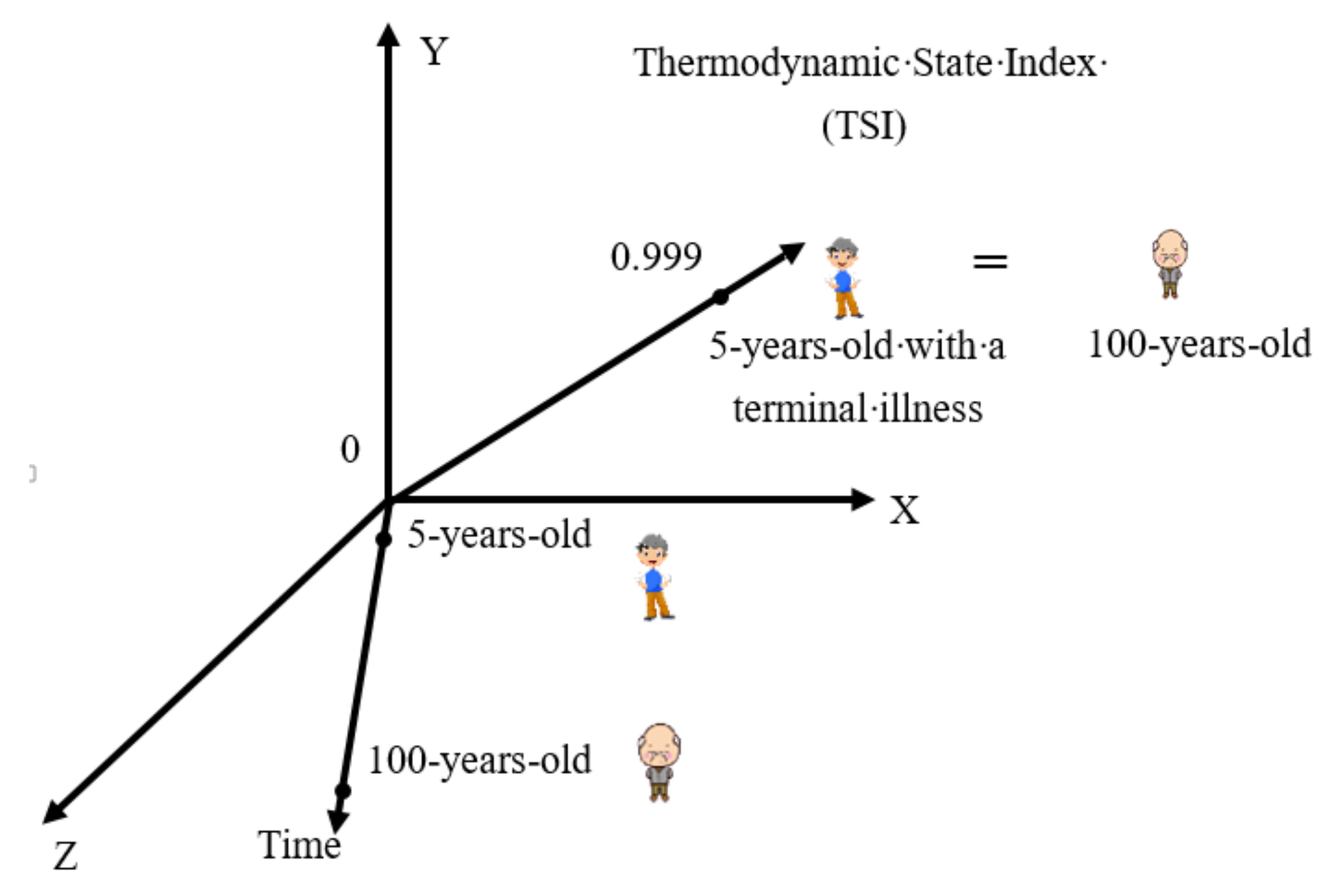
- The physics-based models, on the other hand, as the name suggests, are based on the physical foundations and do not require curve fitting empirical functions to test data. They can be classified under the framework of Unified Mechanics Theory (UMT), incorporating the second law of thermodynamics directly into Newton’s laws at the ab-initio level [7]. As a result, governing differential equations of any system automatically include energy loss, entropy generation, and the system’s degradation in a non-empirical way. The UMT based models are pure physics-based and do not need curve fitting to any test data for the evolution of void/damage. However, they do require deriving analytical thermodynamic fundamental equations of the material without curve fitting. Thermodynamic fundamental equation and the second law of thermodynamics controls the evolution of damage along the fifth axis (Thermodynamic State Index axis), according to Boltzmann equation.
2. Empirical Curve Fitting Models for Metals
2.1. Gurson–Tvergaard–Needleman (GTN) Model and Its Modified Form
2.2. Johnson-Cook (J-C) Type Models
2.3. Micro-Plasticity Models
2.4. Other Empirical Models for Metals
3. Empirical Curve Fitting Models for Non-Metallic Materials
3.1. Composite Materials
3.2. Laminates
3.3. Cement and Asphalt Mortar
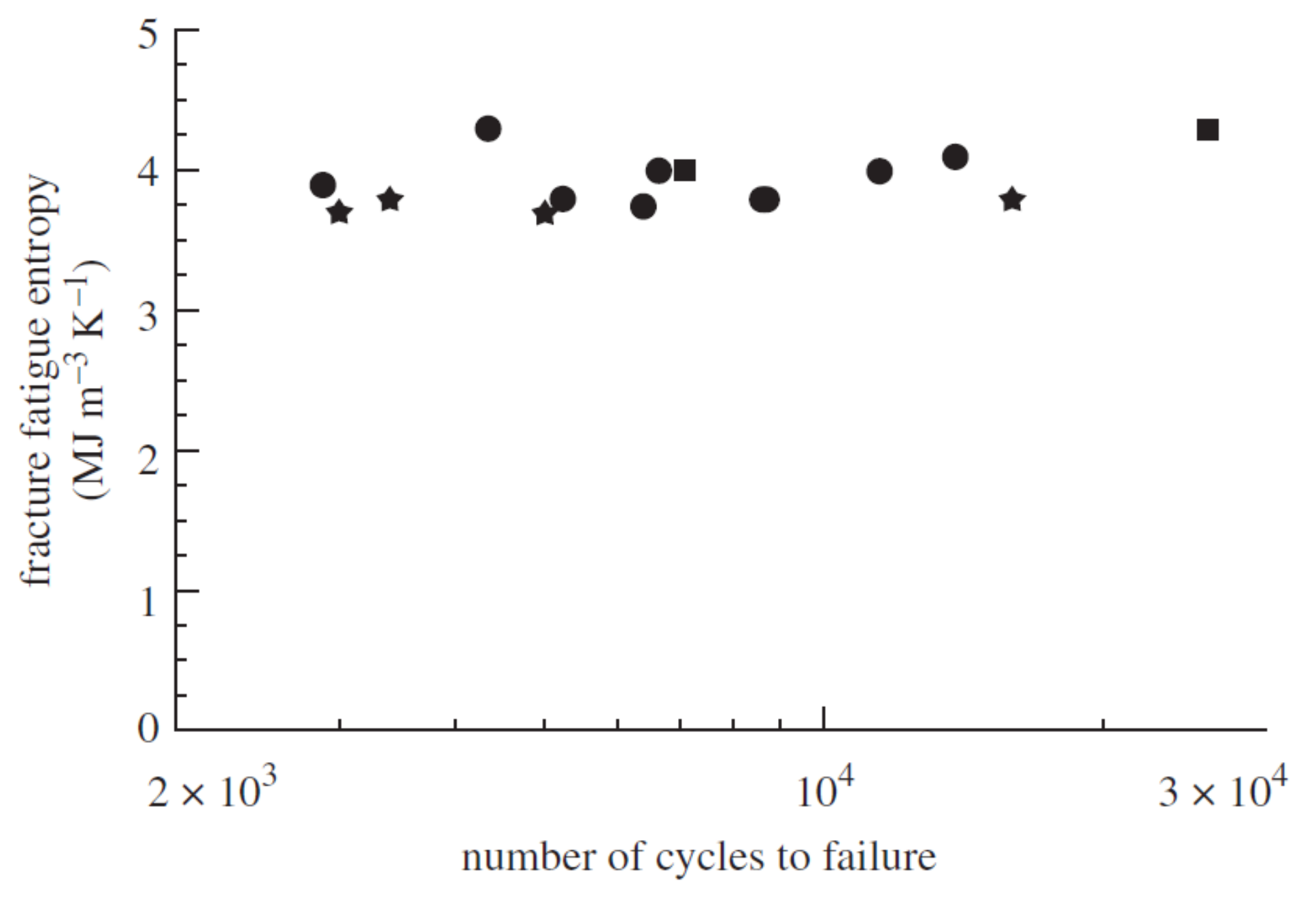
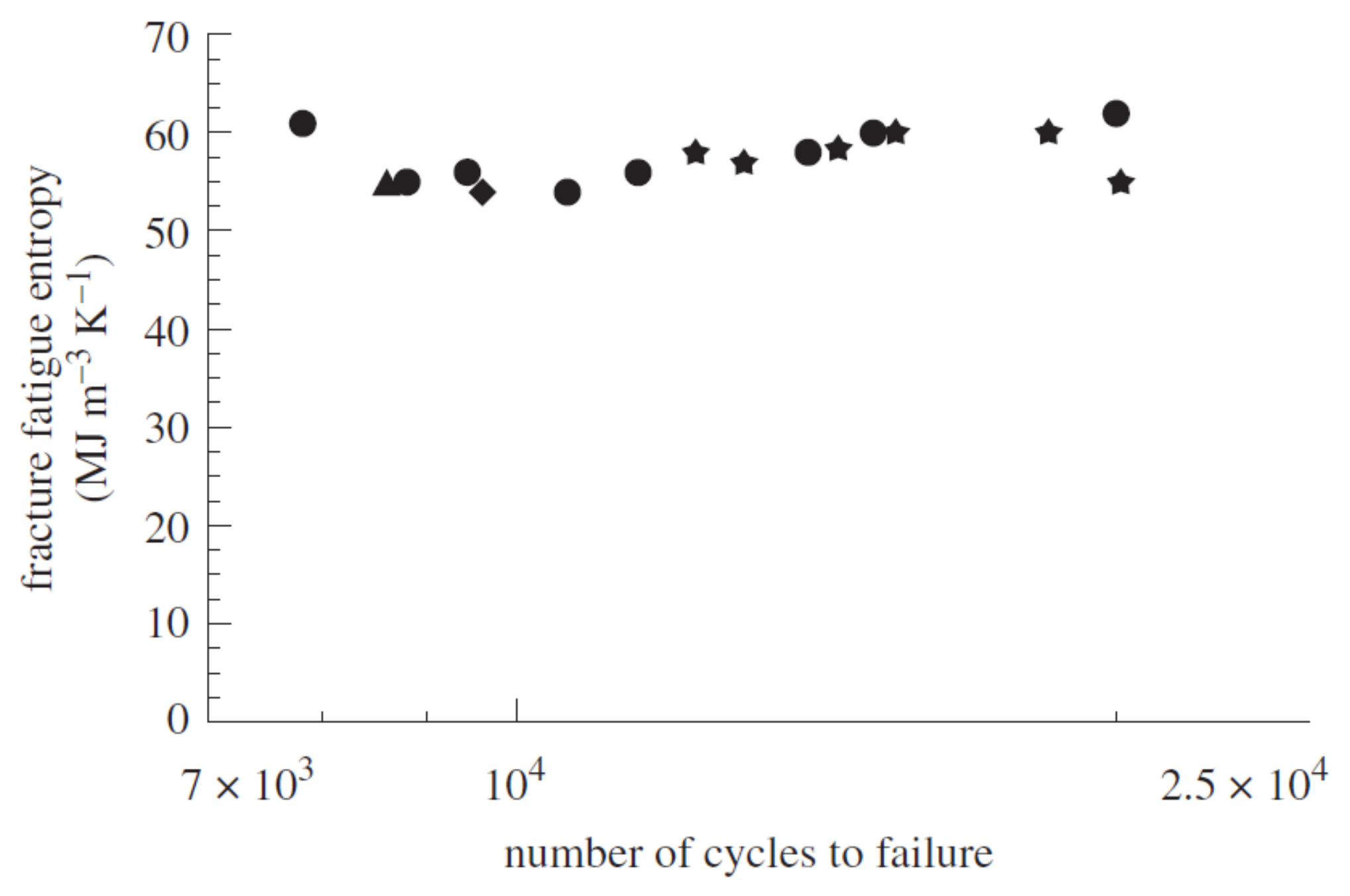
4. Entropy Based Models
4.1. Models Using Irreversible Entropy as a Metric with an Empirical Evolution Function
4.2. Physics Based Evolution Functions: Unified Mechanics Theory
5. Mechanical Treatment
5.1. Manufacturing Process
5.2. Surface Finishing
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Voyiadjis, G.; Palazotto, A.; Gao, X.-L. Modeling of metallic materials at high strain rates with continuum damage mechanics. Appl. Mech. Rev. 2002, 55, 481–493. [Google Scholar] [CrossRef]
- Gurson, A. Plastic Flow and Fracture Behavior of Ductile Materials Incorporating Void Nucleation, Growth, and Interaction. Ph.D. Thesis, Brown University, Providence, RI, USA, 1975. [Google Scholar]
- Boyer, J.-C.; Vidal-Salle, E.; Staub, C. A shear stress dependent ductile damage model. J. Mater. Process. Technol. 2002, 121, 87–93. [Google Scholar] [CrossRef]
- Weck, A.; Segurado, J.; Llorca, J.; Wilkinson, D.; Böhm, H. Numerical simulations of void linkage in model materials using a nonlocal ductile damage approximation. Int. J. Fract. 2007, 148, 205–219. [Google Scholar] [CrossRef][Green Version]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Rahimidehgolan, F.; Majzoobi, G.; Alinejad, F.; Sola, J.F. Determination of the Constants of GTN Damage Model Using Experiment, Polynomial Regression and Kriging Methods. Appl. Sci. 2017, 7, 1179. [Google Scholar] [CrossRef]
- Basaran, C. Introduction to Unified Mechanics Theory with Applications, 1st ed.; Springer Nature: Berlin/Heidelberg, Germany, 2021; ISBN 978-3-030-57772-8. [Google Scholar]
- Tvergaard, V.; Needleman, A. Analysis of the cup-cone fracture in a round tensile bar. Acta Met. 1984, 32, 157–169. [Google Scholar] [CrossRef]
- Xue, L. Constitutive modeling of void shearing effect in ductile fracture of porous materials. Eng. Fract. Mech. 2008, 75, 3343–3366. [Google Scholar] [CrossRef]
- Nahshon, K.; Hutchinson, J. Modification of the Gurson Model for shear failure. Eur. J. Mech. Solids 2008, 27, 1–17. [Google Scholar] [CrossRef]
- Zhou, J.; Gao, X.; Sobotka, J.C.; Webler, B.A.; Cockeram, B.V. On the extension of the Gurson-type porous plasticity models for prediction of ductile fracture under shear-dominated conditions. Int. J. Solids Struct. 2014, 51, 3273–3291. [Google Scholar] [CrossRef]
- Acharyya, S.; Dhar, S. A complete GTN model for prediction of ductile failure of pipe. J. Mater. Sci. 2008, 43, 1897–1909. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, C.; Varé, C. An extended GTN model for indentation-induced damage. Comput. Mater. Sci. 2017, 128, 229–235. [Google Scholar] [CrossRef]
- Jin, C.; Niu, J.; He, S.; Fu, C. Modeling thermal cycling induced micro-damage in aluminum welds: An extension of Gurson void nucleation model. Comput. Mater. Sci. 2008, 43, 1165–1171. [Google Scholar] [CrossRef]
- Linse, T.; Hütter, G.; Kuna, M. Simulation of crack propagation using a gradient-enriched ductile damage model based on dilatational strain. Eng. Fract. Mech. 2012, 95, 13–28. [Google Scholar] [CrossRef]
- Xu, F.; Zhao, S.D.; Han, X.L. Use of a modified Gurson model for the failure behaviour of the clinched joint on Al6061 sheet. Fatigue Fract. Eng. Mater. Struct. 2013, 37, 335–348. [Google Scholar] [CrossRef]
- Gatea, S.; Ou, H.; Lu, B.; McCartney, G. Modelling of ductile fracture in single point incremental forming using a modified GTN model. Eng. Fract. Mech. 2017, 186, 59–79. [Google Scholar] [CrossRef]
- Malcher, L.; Pires, F.A.; De Sá, J.C. An extended GTN model for ductile fracture under high and low stress triaxiality. Int. J. Plast. 2014, 54, 193–228. [Google Scholar] [CrossRef]
- Wang, S.; Chen, Z.; Dong, C. Tearing failure of ultra-thin sheet-metal involving size effect in blanking process: Analysis based on modified GTN model. Int. J. Mech. Sci. 2017, 133, 288–302. [Google Scholar] [CrossRef]
- Bambach, M.; Imran, M. Extended Gurson–Tvergaard–Needleman model for damage modeling and control in hot forming. CIRP Ann. 2019, 68, 249–252. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, Z.; Panicaud, B. Investigation of ductile damage during surface mechanical attrition treatment for TWIP steels using a dislocation density based viscoplasticity and damage models. Mech. Mater. 2019, 129, 279–289. [Google Scholar] [CrossRef]
- Bahrami, H.; Hoseini, S.; Voyiadjis, G.Z. Fracture investigation of the shape memory alloy using GTN model. Eng. Fract. Mech. 2019, 216, 106519. [Google Scholar] [CrossRef]
- Bahrami, H.; Hoseini, S.; Voyiadjis, G.Z. Fracture analysis of shape memory alloys in martensite and austenite phase based on the voids behavior. Mech. Mater. 2019, 137, 103119. [Google Scholar] [CrossRef]
- Boyd, J.; Lagoudas, D. A thermodynamical constitutive model for shape memory materials. Part I. The monolithic shape memory alloy. Int. J. Plast. 1996, 12, 805–842. [Google Scholar] [CrossRef]
- Bergström, J. Plasticity Models. Mech. Solid Polym. 2015, 353–369. [Google Scholar] [CrossRef]
- Zhang, Y.; Outeiro, J.; Mabrouki, T. On the Selection of Johnson-cook Constitutive Model Parameters for Ti-6Al-4V Using Three Types of Numerical Models of Orthogonal Cutting. Procedia CIRP 2015, 31, 112–117. [Google Scholar] [CrossRef]
- Li, F.; Qi, X.; Xiang, D. Finite Element Modeling of Crack Generation in Laser Shock Peening Processed Airfoils. Adv. Mater. Sci. Eng. 2014, 2014, 1–10. [Google Scholar] [CrossRef]
- Nam, H.-S.; Je, J.-H.; Han, J.-J.; Kim, Y.-J. Investigation of Crack Tip Stress and Strain Fields at Crack Initiation of A106 Gr. B Carbon Steels under High Strain Rates. Procedia Mater. Sci. 2014, 3, 764–771. [Google Scholar] [CrossRef][Green Version]
- Nam, H.-S.; Jeon, J.-Y.; Kim, J.-S.; Kim, Y.-J.; Kim, J.-W. A Strain Rate Dependent Computational Model of Ductile Damage for C(T) Specimen. Procedia Eng. 2015, 130, 861–867. [Google Scholar] [CrossRef][Green Version]
- Chen, H.; Zhang, J.; Yang, J.; Ye, F. Experimental Investigation into Corrosion Effect on Mechanical Properties of High Strength Steel Bars under Dynamic Loadings. Int. J. Corros. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Chen, G.; Ren, C.; Lu, L.; Ke, Z.; Qin, X.; Ge, X. Determination of ductile damage behaviors of high strain rate compression deformation for Ti-6Al-4V alloy using experimental-numerical combined approach. Eng. Fract. Mech. 2018, 200, 499–520. [Google Scholar] [CrossRef]
- Wang, J.; Hu, X.; Yuan, K.; Meng, W.; Li, P. Impact resistance prediction of superalloy honeycomb using modified Johnson–Cook constitutive model and fracture criterion. Int. J. Impact Eng. 2019, 131, 66–77. [Google Scholar] [CrossRef]
- Wang, X.; Hassani, M. Ultra-High Strain Rate Constitutive Modeling of Pure Titanium Using Particle Impact Test. J. Appl. Mech. 2020, 87. [Google Scholar] [CrossRef]
- Zerilli, F.J.; Armstrong, R.W. Dislocation-mechanics-based constitutive relations for material dynamics calculations. J. Appl. Phys. 1987, 61, 1816–1825. [Google Scholar] [CrossRef]
- Khan, A.S.; Suh, Y.S.; Kazmi, R. Quasi-static and dynamic loading responses and constitutive modeling of titanium alloys. Int. J. Plast. 2004, 20, 2233–2248. [Google Scholar] [CrossRef]
- Khan, A.S.; Kazmi, R.; Farrokh, B. Multiaxial and non-proportional loading responses, anisotropy and modeling of Ti–6Al–4V titanium alloy over wide ranges of strain rates and temperatures. Int. J. Plast. 2007, 23, 931–950. [Google Scholar] [CrossRef]
- Zhang, L.-H.; Pellegrino, A.; Petrinic, N. Dynamic necking of a near α titanium alloy at high strain rates: Experiments and modelling. Def. Technol. 2020. [Google Scholar] [CrossRef]
- Chiyatan, T.; Uthaisangsuk, V. Mechanical and fracture behavior of high strength steels under high strain rate deformation: Experiments and modelling. Mater. Sci. Eng. A 2020, 779, 139125. [Google Scholar] [CrossRef]
- Sung, J.H.; Kim, J.H.; Wagoner, R. A plastic constitutive equation incorporating strain, strain-rate, and temperature. Int. J. Plast. 2010, 26, 1746–1771. [Google Scholar] [CrossRef]
- Roth, C.C.; Mohr, D. Effect of strain rate on ductile fracture initiation in advanced high strength steel sheets: Experiments and modeling. Int. J. Plast. 2014, 56, 19–44. [Google Scholar] [CrossRef]
- Joós, B.; Duesbery, M.S. The Peierls Stress of Dislocations: An Analytic Formula. Phys. Rev. Lett. 1997, 78, 266–269. [Google Scholar] [CrossRef]
- Poole, W.; Embury, J.; Lloyd, D. Work hardening in aluminium alloys. Fund. Alum. Metal. 2011, 307–344. [Google Scholar] [CrossRef]
- Jeunechamps, P.-P.; Ponthot, J.-P. An efficient 3D implicit approach for the thermomechanical simulation of elastic-viscoplastic materials submitted to high strain rate and damage. Int. J. Numer. Methods Eng. 2013, 94, 920–960. [Google Scholar] [CrossRef]
- Perzyna, P. Fundamental Problems in Viscoplasticity. Adv. Appl. Mech. 1966, 9, 243–377. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, Z.; Liu, K.; Chen, G. Application of a material model based on the Johnson-Cook and Gurson-Tvergaard-Needleman model in ship collision and grounding simulations. Ocean Eng. 2020, 205, 106768. [Google Scholar] [CrossRef]
- Wan, V.; Cuddihy, M.; Jiang, J.; MacLachlan, D.; Dunne, F. An HR-EBSD and computational crystal plasticity investigation of microstructural stress distributions and fatigue hotspots in polycrystalline copper. Acta Mater. 2016, 115, 45–57. [Google Scholar] [CrossRef]
- Wilson, D.; Wan, W.; Dunne, F.P. Microstructurally-sensitive fatigue crack growth in HCP, BCC and FCC polycrystals. J. Mech. Phys. Solids 2019, 126, 204–225. [Google Scholar] [CrossRef]
- Bandyopadhyay, R.; Prithivirajan, V.; Peralta, A.D.; Sangid, M.D. Microstructure-sensitive critical plastic strain energy density criterion for fatigue life prediction across various loading regimes. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20190766. [Google Scholar] [CrossRef]
- Mughrabi, H. Cyclic slip irreversibility and fatigue life: A microstructure-based analysis. Acta Mater. 2013, 61, 1197–1203. [Google Scholar] [CrossRef]
- Ho, H.; Risbet, M.; Feaugas, X. A cyclic slip irreversibility based model for fatigue crack initiation of nickel base alloys. Int. J. Fatigue 2017, 102, 1–8. [Google Scholar] [CrossRef]
- Dondeti, P.; Paquet, D.; Ghosh, S. A rate-dependent homogenization based continuum plasticity-damage (HCPD) model for dendritic cast aluminum alloys. Eng. Fract. Mech. 2012, 89, 75–97. [Google Scholar] [CrossRef]
- Darras, B.M.; Abed, F.H.; Pervaiz, S.; Abdu-Latif, A. Analysis of damage in 5083 aluminum alloy deformed at different strainrates. Mater. Sci. Eng. A 2013, 568, 143–149. [Google Scholar] [CrossRef]
- Abed, F.; Abdul-Latif, A.; Yehia, A. Experimental Study on the Mechanical Behavior of EN08 Steel at Different Temperatures and Strain Rates. Metals 2018, 8, 736. [Google Scholar] [CrossRef]
- Khoei, A.; Eghbalian, M.; Azadi, H.; Saffar, H. Numerical simulation of ductile crack growth under cyclic and dynamic loading with a damage–viscoplasticity model. Eng. Fract. Mech. 2013, 99, 169–190. [Google Scholar] [CrossRef]
- Shojaei, A.; Voyiadjis, G.Z.; Tan, P. Viscoplastic constitutive theory for brittle to ductile damage in polycrystalline materials under dynamic loading. Int. J. Plast. 2013, 48, 125–151. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Y.; Yang, Z. Coupling damage and reliability model of low-cycle fatigue and high energy impact based on the local stress–strain approach. Chin. J. Aeronaut. 2014, 27, 846–855. [Google Scholar] [CrossRef]
- Carniel, T.; Muñoz-Rojas, P.; Vaz, M. A viscoelastic viscoplastic constitutive model including mechanical degradation: Uniaxial transient finite element formulation at finite strains and application to space truss structures. Appl. Math. Model. 2015, 39, 1725–1739. [Google Scholar] [CrossRef]
- Lemaitre, J. How to use damage mechanics. Nucl. Eng. Des. 1984, 80, 233–245. [Google Scholar] [CrossRef]
- Shen, F.; Voyiadjis, G.Z.; Hu, W.; Meng, Q. Analysis on the fatigue damage evolution of notched specimens with consideration of cyclic plasticity. Fatigue Fract. Eng. Mater. Struct. 2015, 38, 1194–1208. [Google Scholar] [CrossRef]
- Tang, B.; Bruschi, S.; Ghiotti, A.; Bariani, P. An improved damage evolution model to predict fracture of steel sheet at elevated temperature. J. Mater. Process. Technol. 2016, 228, 76–87. [Google Scholar] [CrossRef]
- Kachanov, L.M. On the creep rupture time. Otd. Teh. Nauki. 1958, 8, 26–31. [Google Scholar]
- Lemaitre, J.; Lippmann, H. A Course on Damage Mechanics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Wu, X.; Quan, G.; Sloss, C. Mechanism-Based Modeling for Low Cycle Fatigue of Cast Austenitic Steel. Met. Mater. Trans. A 2017, 48, 4058–4071. [Google Scholar] [CrossRef]
- Moelans, N.; Blanpain, B.; Wollants, P. An introduction to phase-field modeling of microstructure evolution. Calphad 2008, 32, 268–294. [Google Scholar] [CrossRef]
- Mozaffari, N.; Voyiadjis, G.Z. Phase field based nonlocal anisotropic damage mechanics model. Phys. D Nonlinear Phenom. 2015, 308, 11–25. [Google Scholar] [CrossRef]
- Mozaffari, N.; Voyiadjis, G.Z. Coupled gradient damage—Viscoplasticty model for ductile materials: Phase field approach. Int. J. Plast. 2016, 83, 55–73. [Google Scholar] [CrossRef]
- Badnava, H.; Etemadi, E.; Msekh, M.A. A Phase Field Model for Rate-Dependent Ductile Fracture. Metals 2017, 7, 180. [Google Scholar] [CrossRef]
- Perić, D. On a class of constitutive equations in viscoplasticity: Formulation and computational issues. Int. J. Numer. Methods Eng. 1993, 36, 1365–1393. [Google Scholar] [CrossRef]
- Schreiber, C.; Müller, R.; Kuhn, C. Phase field simulation of fatigue crack propagation under complex load situations. Arch. Appl. Mech. 2021, 91, 563–577. [Google Scholar] [CrossRef]
- Chu, D.; Li, X.; Liu, Z.; Cheng, J.; Wang, T.; Li, Z.; Zhuang, Z. A unified phase field damage model for modeling the brittle-ductile dynamic failure mode transition in metals. Eng. Fract. Mech. 2019, 212, 197–209. [Google Scholar] [CrossRef]
- Zhang, F.; Wu, L.; Wan, Y.; Gideon, R.K.; Gu, B.; Sun, B. Numerical modeling of the mechanical response of basalt plain woven composites under high strain rate compression. J. Reinf. Plast. Compos. 2014, 33, 1087–1104. [Google Scholar] [CrossRef]
- Alemi-Ardakani, M.; Milani, A.S.; Yannacopoulos, S. On Complexities of Impact Simulation of Fiber Reinforced Polymer Composites: A Simplified Modeling Framework. Sci. World J. 2014, 2014, 1–10. [Google Scholar] [CrossRef]
- Hashin, Z. Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Hashin, Z. Fatigue Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1981, 48, 846–852. [Google Scholar] [CrossRef]
- Chen, J.-F.; Morozov, E.V. A consistency elasto-viscoplastic damage model for progressive failure analysis of composite laminates subjected to various strain rate loadings. Compos. Struct. 2016, 148, 224–235. [Google Scholar] [CrossRef]
- Zaera, R.; Fernández-Sáez, J. An implicit consistent algorithm for the integration of thermoviscoplastic constitutive equations in adiabatic conditions and finite deformations. Int. J. Solids Struct. 2006, 43, 1594–1612. [Google Scholar] [CrossRef]
- Park, I.K.; Park, K.J.; Kim, S.J. Rate-dependent damage model for polymeric composites under in-plane shear dynamic loading. Comput. Mater. Sci. 2015, 96, 506–519. [Google Scholar] [CrossRef]
- Abu Seman, S.A.H.; Ahmad, R.; Akil, H.M. Meso-scale modelling and failure analysis of kenaf fiber reinforced composites under high strain rate compression loading. Compos. Part B Eng. 2019, 163, 403–412. [Google Scholar] [CrossRef]
- Alabdullah, M.; Ghoniem, N.M. A thermodynamics-based damage model for the non-linear mechanical behavior of SiC/SiC ceramic matrix composites in irradiation and thermal environments. Int. J. Damage Mech. 2020, 29, 1569–1599. [Google Scholar] [CrossRef]
- Morinière, F.; Alderliesten, R.; Benedictus, R. Modelling of impact damage and dynamics in fibre-metal laminates—A review. Int. J. Impact Eng. 2014, 67, 27–38. [Google Scholar] [CrossRef]
- Sitnikova, E.; Guan, Z.; Schleyer, G.; Cantwell, W. Modelling of perforation failure in fibre metal laminates subjected to high impulsive blast loading. Int. J. Solids Struct. 2014, 51, 3135–3146. [Google Scholar] [CrossRef]
- Fu, Q.; Xie, Y.; Long, G.; Niu, D.; Song, H.; Liu, X. Impact characterization and modelling of cement and asphalt mortar based on SHPB experiments. Int. J. Impact Eng. 2017, 106, 44–52. [Google Scholar] [CrossRef]
- Basaran, C.; Yan, C.-Y. A Thermodynamic Framework for Damage Mechanics of Solder Joints. J. Electron. Packag. 1998, 120, 379–384. [Google Scholar] [CrossRef]
- Basaran, C.; Chandaroy, R. Nonlinear Dynamic Analysis of Surface Mount Interconnects: Part I—Theory. J. Electron. Packag. 1999, 121, 8–11. [Google Scholar] [CrossRef]
- Basaran, C.; Chandaroy, R. Nonlinear Dynamic Analysis of Surface Mount Interconnects: Part II—Applications. J. Electron. Packag. 1999, 121, 12–17. [Google Scholar] [CrossRef][Green Version]
- Naderi, M.; Amiri, M.; Khonsari, M.M. On the thermodynamic entropy of fatigue fracture. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 423–438. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M. An experimental approach to low-cycle fatigue damage based on thermodynamic entropy. Int. J. Solids Struct. 2010, 47, 875–880. [Google Scholar] [CrossRef]
- Amiri, M.; Khonsari, M.M. On the Role of Entropy Generation in Processes Involving Fatigue. Entropy 2011, 14, 24–31. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M. Real-time fatigue life monitoring based on thermodynamic entropy. Struct. Health Monit. 2011, 10, 189–197. [Google Scholar] [CrossRef]
- Teng, Z.; Wu, H.; Boller, C.; Starke, P. Thermodynamic entropy as a marker of high-cycle fatigue damage accumulation: Example for normalized SAE 1045 steel. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 2854–2866. [Google Scholar] [CrossRef]
- Liakat, M.; Khonsari, M. On the anelasticity and fatigue fracture entropy in high-cycle metal fatigue. Mater. Des. 2015, 82, 18–27. [Google Scholar] [CrossRef]
- Ontiveros, V.; Amiri, M.; Kahirdeh, A.; Modarres, M. Thermodynamic entropy generation in the course of the fatigue crack initiation. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 423–434. [Google Scholar] [CrossRef]
- Guo, Q.; Zaïri, F.; Guo, X. An intrinsic dissipation model for high-cycle fatigue life prediction. Int. J. Mech. Sci. 2018, 140, 163–171. [Google Scholar] [CrossRef]
- Ribeiro, P.; Petit, J.; Gallimard, L. Experimental determination of entropy and exergy in low cycle fatigue. Int. J. Fatigue 2020, 136, 105333. [Google Scholar] [CrossRef]
- Idris, R.; Abdullah, S.; Thamburaja, P.; Omar, M.Z. Prediction of Fatigue Crack Growth Rate Based on Entropy Generation. Entropy 2019, 22, 9. [Google Scholar] [CrossRef] [PubMed]
- Osara, J.A.; Bryant, M.D. Thermodynamics of Fatigue: Degradation-Entropy Generation Methodology for System and Process Characterization and Failure Analysis. Entropy 2019, 21, 685. [Google Scholar] [CrossRef] [PubMed]
- Basaran, C.; Nie, S. An Irreversible Thermodynamics Theory for Damage Mechanics of Solids. Int. J. Damage Mech. 2004, 13, 205–223. [Google Scholar] [CrossRef]
- Sun, F.; Zhang, W.; Wang, N. A Copula Entropy Approach to Dependence Measurement for Multiple Degradation Processes. Entropy 2019, 21, 724. [Google Scholar] [CrossRef]
- Yun, H.; Modarres, M. Measures of Entropy to Characterize Fatigue Damage in Metallic Materials. Entropy 2019, 21, 804. [Google Scholar] [CrossRef]
- Young, C.; Subbarayan, G. Maximum Entropy Models for Fatigue Damage in Metals with Application to Low-Cycle Fatigue of Aluminum 2024-T351. Entropy 2019, 21, 967. [Google Scholar] [CrossRef]
- Wang, J.; Yao, Y. An Entropy-Based Failure Prediction Model for the Creep and Fatigue of Metallic Materials. Entropy 2019, 21, 1104. [Google Scholar] [CrossRef]
- Sosnovskiy, L.A.; Sherbakov, S.S. On the Development of Mechanothermodynamics as a New Branch of Physics. Entropy 2019, 21, 1188. [Google Scholar] [CrossRef]
- Bin Jamal, M.N.; Kumar, A.; Rao, C.L.; Basaran, C. Low Cycle Fatigue Life Prediction Using Unified Mechanics Theory in Ti-6Al-4V Alloys. Entropy 2019, 22, 24. [Google Scholar] [CrossRef]
- Chandaroy, R.; Basaran, C. Damage Mechanics of Surface Mount Technology Solder Joints under Concurrent Thermal and Dynamic Loading. J. Electron. Packag. 1999, 121, 61–68. [Google Scholar] [CrossRef]
- Basaran, C.; Chandaroy, R. Thermomechanical Analysis of Solder Joints under Thermal and Vibrational Loading. J. Electron. Packag. 2001, 124, 60–66. [Google Scholar] [CrossRef]
- Tang, H.; Basaran, C. Influence of Microstructure Coarsening on Thermomechanical Fatigue Behavior of Pb/Sn Eutectic Solder Joints. Int. J. Damage Mech. 2001, 10, 235–255. [Google Scholar] [CrossRef]
- Basaran, C.; Tang, H. Implementation of a Thermodynamic Framework for Damage Mechanics of Solder Interconnects in Microelectronics Packaging. Int. J. Damage Mech. 2002, 11, 87–108. [Google Scholar] [CrossRef]
- Tang, H.; Basaran, C. A Damage Mechanics-Based Fatigue Life Prediction Model for Solder Joints. J. Electron. Packag. 2003, 125, 120–125. [Google Scholar] [CrossRef]
- Gomez, J.; Basaran, C. A thermodynamics based damage mechanics constitutive model for low cycle fatigue analysis of microelectronics solder joints incorporating size effects. Int. J. Solids Struct. 2005, 42, 3744–3772. [Google Scholar] [CrossRef]
- Basaran, C.; Zhao, Y.; Tang, H.; Gomez, J. A Damage-Mechanics-Based Constitutive Model for Solder Joints. J. Electron. Packag. 2004, 127, 208–214. [Google Scholar] [CrossRef]
- Gomez, J.; Basaran, C. Nanoindentation of Pb/Sn solder alloys; experimental and finite element simulation results. Int. J. Solids Struct. 2006, 43, 1505–1527. [Google Scholar] [CrossRef]
- Gomez, J.; Basaran, C. Damage mechanics constitutive model for Pb/Sn solder joints incorporating nonlinear kinematic hardening and rate dependent effects using a return mapping integration algorithm. Mech. Mater. 2006, 38, 585–598. [Google Scholar] [CrossRef]
- Gomez, J.; Lin, M.; Basaran, C. Damage Mechanics Modeling of Concurrent Thermal and Vibration Loading on Electronics Packaging. Multidiscip. Model. Mater. Struct. 2006, 2, 309–326. [Google Scholar] [CrossRef]
- Temfack, T.; Basaran, C. Experimental verification of thermodynamic fatigue life prediction model using entropy as damage metric. Mater. Sci. Technol. 2015, 31, 1627–1632. [Google Scholar] [CrossRef]
- Jamal, M.N.; Rao, C.; Basaran, C. A unified mechanics theory-based model for temperature and strain rate dependent proportionality limit stress of mild steel. Mech. Mater. 2021, 155, 103762. [Google Scholar] [CrossRef]
- Bin Jamal, M.N.; Lee, H.; Rao, C.L.; Basaran, C. Dynamic Equilibrium Equations in Unified Mechanics Theory. Appl. Mech. 2021, 2, 5. [Google Scholar] [CrossRef]
- Lee, H.W.; Basaran, C. Predicting High Cycle Fatigue Life with Unified Mechanics Theory. Mech. Mater. 2021. (Submitted April 2021). [Google Scholar] [CrossRef]
- Egner, W.; Sulich, P.; Mroziński, S.; Egner, H. Modelling thermo-mechanical cyclic behavior of P91 steel. Int. J. Plast. 2020, 135, 102820. [Google Scholar] [CrossRef]
- Chaboche, J. A review of some plasticity and viscoplasticity constitutive theories. Int. J. Plast. 2008, 24, 1642–1693. [Google Scholar] [CrossRef]
- Basaran, C.; Lin, M.; Ye, H. A thermodynamic model for electrical current induced damage. Int. J. Solids Struct. 2003, 40, 7315–7327. [Google Scholar] [CrossRef]
- Lin, M.; Basaran, C. Electromigration induced stress analysis using fully coupled mechanical–diffusion equations with nonlinear material properties. Comput. Mater. Sci. 2005, 34, 82–98. [Google Scholar] [CrossRef]
- Basaran, C.; Lin, M. Damage mechanics of electromigration in microelectronics copper interconnects. Int. J. Mater. Struct. Integr. 2007, 1, 16. [Google Scholar] [CrossRef]
- Basaran, C.; Lin, M. Damage mechanics of electromigration induced failure. Mech. Mater. 2008, 40, 66–79. [Google Scholar] [CrossRef]
- Abdulhamid, M.F.; Li, S.; Basaran, C. Thermomigration in lead-free solder joints. Int. J. Mater. Struct. Integr. 2008, 2, 11. [Google Scholar] [CrossRef]
- Basaran, C.; Li, S.; Abdulhamid, M.F. Thermomigration induced degradation in solder alloys. J. Appl. Phys. 2008, 103, 123520. [Google Scholar] [CrossRef]
- Li, S.; Abdulhamid, M.F.; Basaran, C. Simulating Damage Mechanics of Electromigration and Thermomigration. Simulation 2008, 84, 391–401. [Google Scholar] [CrossRef]
- Li, S.; Basaran, C. A computational damage mechanics model for thermomigration. Mech. Mater. 2009, 41, 271–278. [Google Scholar] [CrossRef]
- Li, S.; Abdulhamid, M.F.; Basaran, C. Damage Mechanics of Low Temperature Electromigration and Thermomigration. IEEE Trans. Adv. Packag. 2009, 32, 478–485. [Google Scholar] [CrossRef]
- Abdulhamid, M.F.; Basaran, C.; Lai, Y.-S. Thermomigration Versus Electromigration in Microelectronics Solder Joints. IEEE Trans. Adv. Packag. 2009, 32, 627–635. [Google Scholar] [CrossRef]
- Basaran, C.; Abdulhamid, M.F. Low temperature electromigration and thermomigration in lead-free solder joints. Mech. Mater. 2009, 41, 1223–1241. [Google Scholar] [CrossRef]
- Yao, W.; Basaran, C. Electromigration analysis of solder joints under ac load: A mean time to failure model. J. Appl. Phys. 2012, 111, 063703. [Google Scholar] [CrossRef]
- Yao, W.; Basaran, C. Electromigration damage mechanics of lead-free solder joints under pulsed DC: A computational model. Comput. Mater. Sci. 2013, 71, 76–88. [Google Scholar] [CrossRef]
- Yao, W.; Basaran, C. Damage mechanics of electromigration and thermomigration in lead-free solder alloys under alternating current: An experimental study. Int. J. Damage Mech. 2013, 23, 203–221. [Google Scholar] [CrossRef]
- Yao, W.; Basaran, C. Computational damage mechanics of electromigration and thermomigration. J. Appl. Phys. 2013, 114, 103708. [Google Scholar] [CrossRef]
- Nie, S.; Basaran, C. A micromechanical model for effective elastic properties of particulate composites with imperfect interfacial bonds. Int. J. Solids Struct. 2005, 42, 4179–4191. [Google Scholar] [CrossRef]
- Basaran, C.; Nie, S. A thermodynamics based damage mechanics model for particulate composites. Int. J. Solids Struct. 2007, 44, 1099–1114. [Google Scholar] [CrossRef]
- Gunel, E.; Basaran, C. Damage characterization in non-isothermal stretching of acrylics. Part I: Theory. Mech. Mater. 2011, 43, 979–991. [Google Scholar] [CrossRef]
- Gunel, E.; Basaran, C. Damage characterization in non-isothermal stretching of acrylics. Part II: Experimental validation. Mech. Mater. 2011, 43, 992–1012. [Google Scholar] [CrossRef]
- Gunel, E.; Basaran, C. Influence of filler content and interphase properties on large deformation micromechanics of particle filled acrylics. Mech. Mater. 2013, 57, 134–146. [Google Scholar] [CrossRef]
- Xu, Z.; Dunleavey, J.; Antar, M.; Hood, R.; Soo, S.; Kucukturk, G.; Hyde, C.; Clare, A. The influence of shot peening on the fatigue response of Ti-6Al-4V surfaces subject to different machining processes. Int. J. Fatigue 2018, 111, 196–207. [Google Scholar] [CrossRef]
- Choi, Y. Influence of feed rate on surface integrity and fatigue performance of machined surfaces. Int. J. Fatigue 2015, 78, 46–52. [Google Scholar] [CrossRef]
- Choi, Y. Influence of rake angle on surface integrity and fatigue performance of machined surfaces. Int. J. Fatigue 2017, 94, 81–88. [Google Scholar] [CrossRef]
- Ayesta, I.; Izquierdo, B.; Flaño, O.; Sánchez, J.A.; Albizuri, J.; Avilés, R. Influence of the WEDM process on the fatigue behavior of Inconel® 718. Int. J. Fatigue 2016, 92, 220–233. [Google Scholar] [CrossRef]
- Bagehorn, S.; Wehr, J.; Maier, H. Application of mechanical surface finishing processes for roughness reduction and fatigue improvement of additively manufactured Ti-6Al-4V parts. Int. J. Fatigue 2017, 102, 135–142. [Google Scholar] [CrossRef]
- Suárez, A.; Veiga, F.; Polvorosa, R.; Artaza, T.; Holmberg, J.; De Lacalle, L.L.; Wretland, A. Surface integrity and fatigue of non-conventional machined Alloy 718. J. Manuf. Process. 2019, 48, 44–50. [Google Scholar] [CrossRef]
- Holmberg, J.; Wretland, A.; Hammersberg, P.; Berglund, J.; Suárez, A.; Beno, T. Surface integrity investigations for prediction of fatigue properties after machining of alloy 718. Int. J. Fatigue 2021, 144, 106059. [Google Scholar] [CrossRef]
- Obiukwu, O.; Grema, L.; Nwafor, M. The Effect of Surface Finish on the Low Cycle Fatigue of Low and Medium Carbon Steel. 2019. Available online: https://www.researchgate.net/publication/335240807 (accessed on 7 April 2021).
- Avilés, R.; Albizuri, J.; Rodríguez, A.; de Lacalle, L.L. Influence of low-plasticity ball burnishing on the high-cycle fatigue strength of medium carbon AISI 1045 steel. Int. J. Fatigue 2013, 55, 230–244. [Google Scholar] [CrossRef]
- Travieso-Rodriguez, J.A.; Gomez-Gras, G.; Dessein, G.; Carrillo, F.; Alexis, J.; Jorba-Peiro, J.; Aubazac, N. Effects of a ball-burnishing process assisted by vibrations in G10380 steel specimens. Int. J. Adv. Manuf. Technol. 2015, 81, 1757–1765. [Google Scholar] [CrossRef]
- Avilés, R.; Albizuri, J.; Ukar, E.; Lamikiz, A.; Avilés, A. Influence of laser polishing in an inert atmosphere on the high cycle fatigue strength of AISI 1045 steel. Int. J. Fatigue 2014, 68, 67–79. [Google Scholar] [CrossRef]
- Avilés, A.; Avilés, R.; Albizuri, J.; Pallarés-Santasmartas, L.; Rodríguez, A. Effect of shot-peening and low-plasticity burnishing on the high-cycle fatigue strength of DIN 34CrNiMo6 alloy steel. Int. J. Fatigue 2019, 119, 338–354. [Google Scholar] [CrossRef]
- Yu, H.; Li, F.; Wang, Z.; Zeng, X. Fatigue performances of selective laser melted Ti-6Al-4V alloy: Influence of surface finishing, hot isostatic pressing and heat treatments. Int. J. Fatigue 2019, 120, 175–183. [Google Scholar] [CrossRef]
- Rodriguez, A.; De Lacalle, L.N.L.; Pereira, O.; Fernandez, A.; Ayesta, I. Isotropic finishing of austempered iron casting cylindrical parts by roller burnishing. Int. J. Adv. Manuf. Technol. 2020, 110, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Tan, L.; Yao, C.; Zhang, D.; Ren, J.; Zhou, Z.; Zhang, J. Evolution of surface integrity and fatigue properties after milling, polishing, and shot peening of TC17 alloy blades. Int. J. Fatigue 2020, 136, 105630. [Google Scholar] [CrossRef]
- Kahlin, M.; Ansell, H.; Basu, D.; Kerwin, A.; Newton, L.; Smith, B.; Moverare, J. Improved fatigue strength of additively manufactured Ti6Al4V by surface post processing. Int. J. Fatigue 2020, 134, 105497. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.W.; Basaran, C. A Review of Damage, Void Evolution, and Fatigue Life Prediction Models. Metals 2021, 11, 609. https://doi.org/10.3390/met11040609
Lee HW, Basaran C. A Review of Damage, Void Evolution, and Fatigue Life Prediction Models. Metals. 2021; 11(4):609. https://doi.org/10.3390/met11040609
Chicago/Turabian StyleLee, Hsiao Wei, and Cemal Basaran. 2021. "A Review of Damage, Void Evolution, and Fatigue Life Prediction Models" Metals 11, no. 4: 609. https://doi.org/10.3390/met11040609
APA StyleLee, H. W., & Basaran, C. (2021). A Review of Damage, Void Evolution, and Fatigue Life Prediction Models. Metals, 11(4), 609. https://doi.org/10.3390/met11040609






