Determining Forming Limit Diagrams Using Sub-Sized Specimen Geometry and Comparing FLD Evaluation Methods
Abstract
1. Introduction
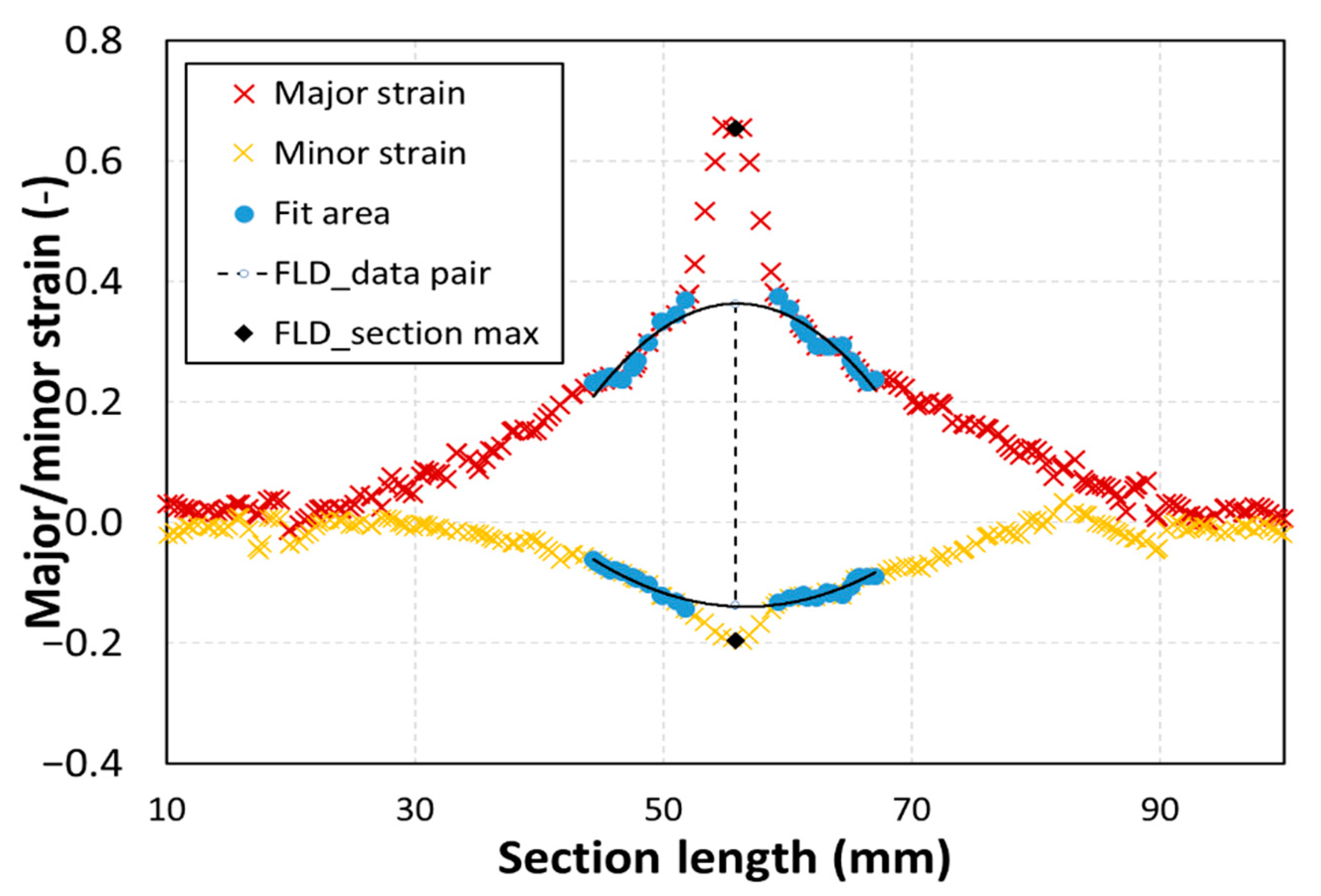
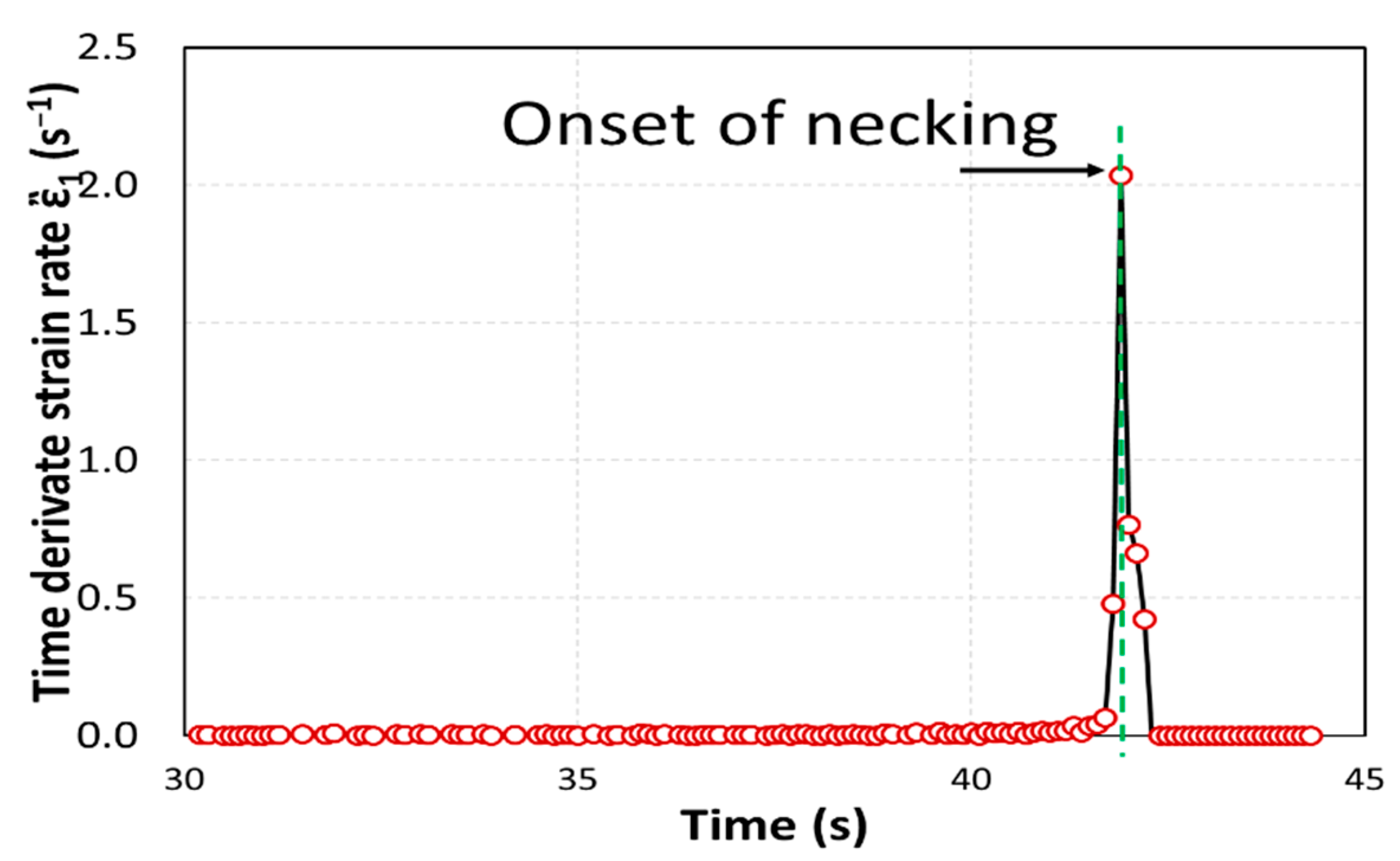
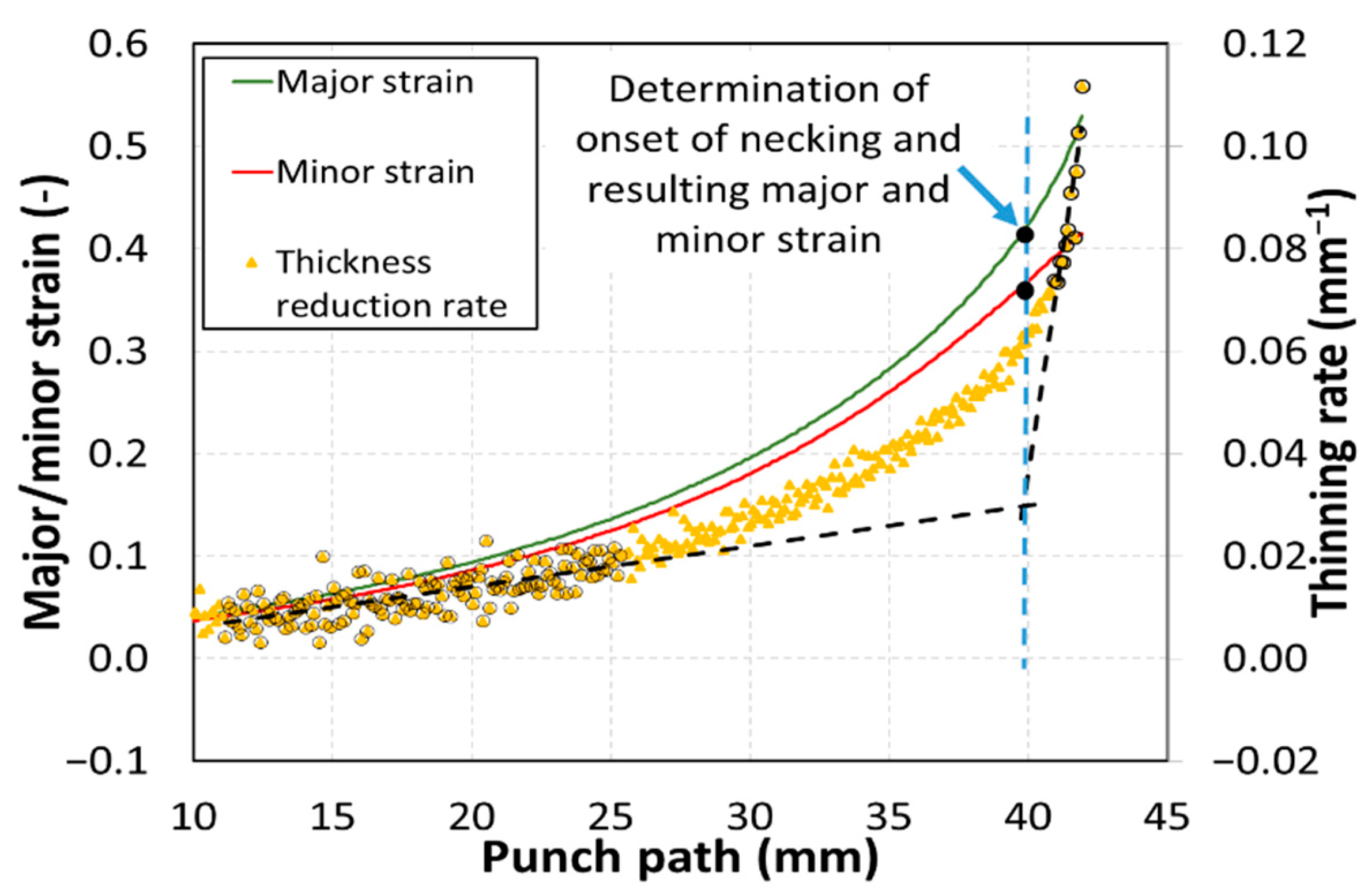
2. Materials and Methods
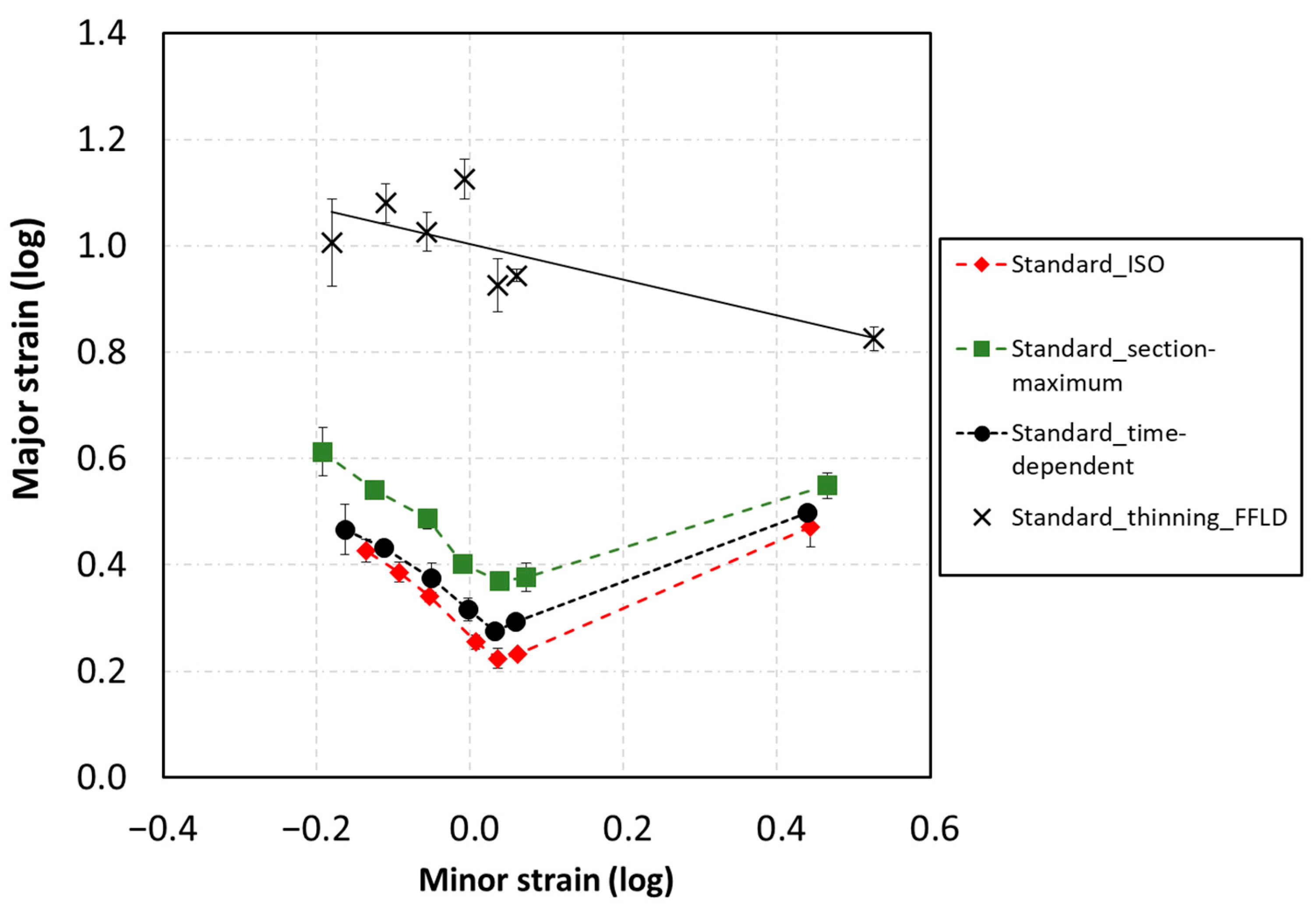
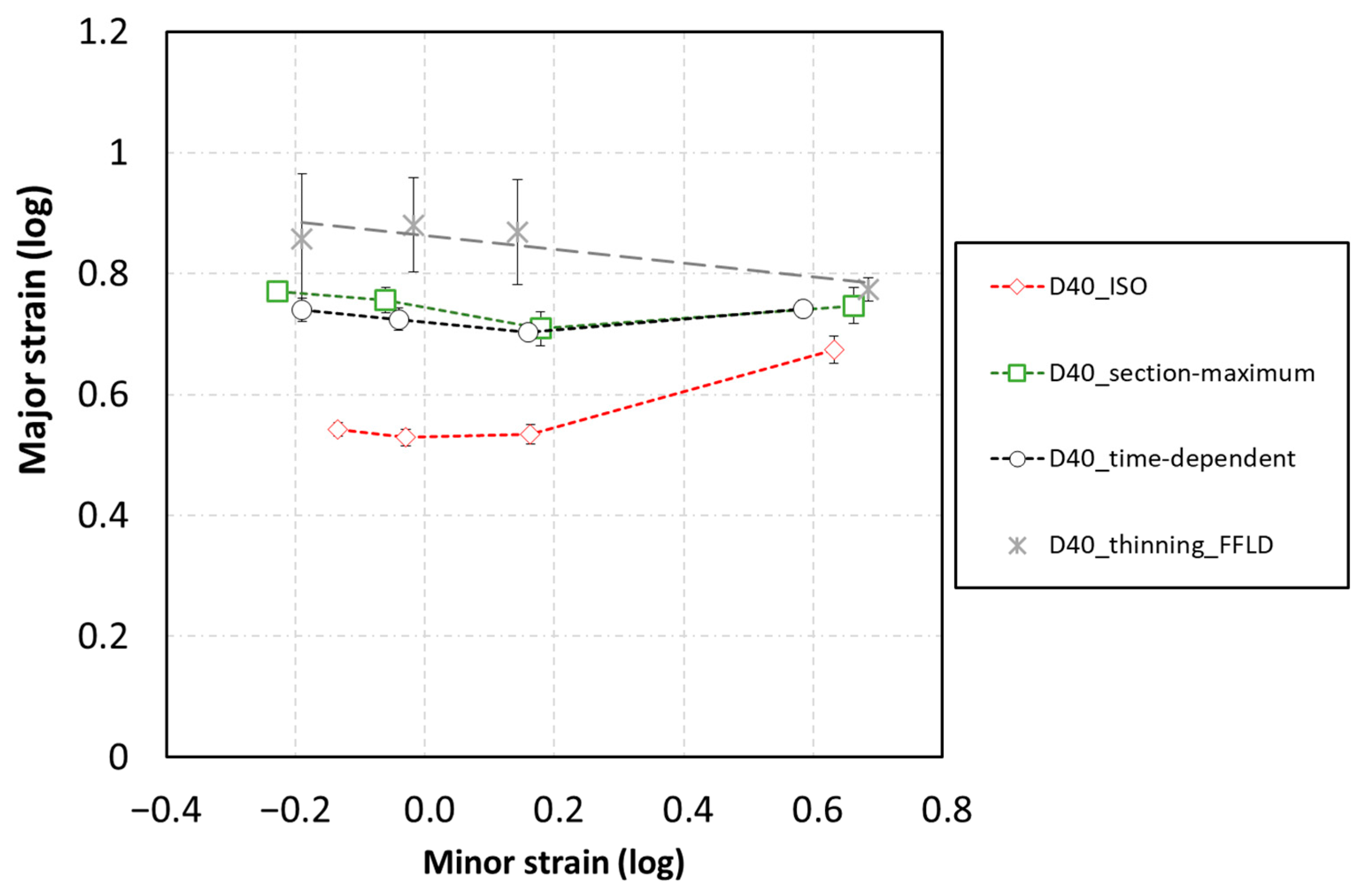
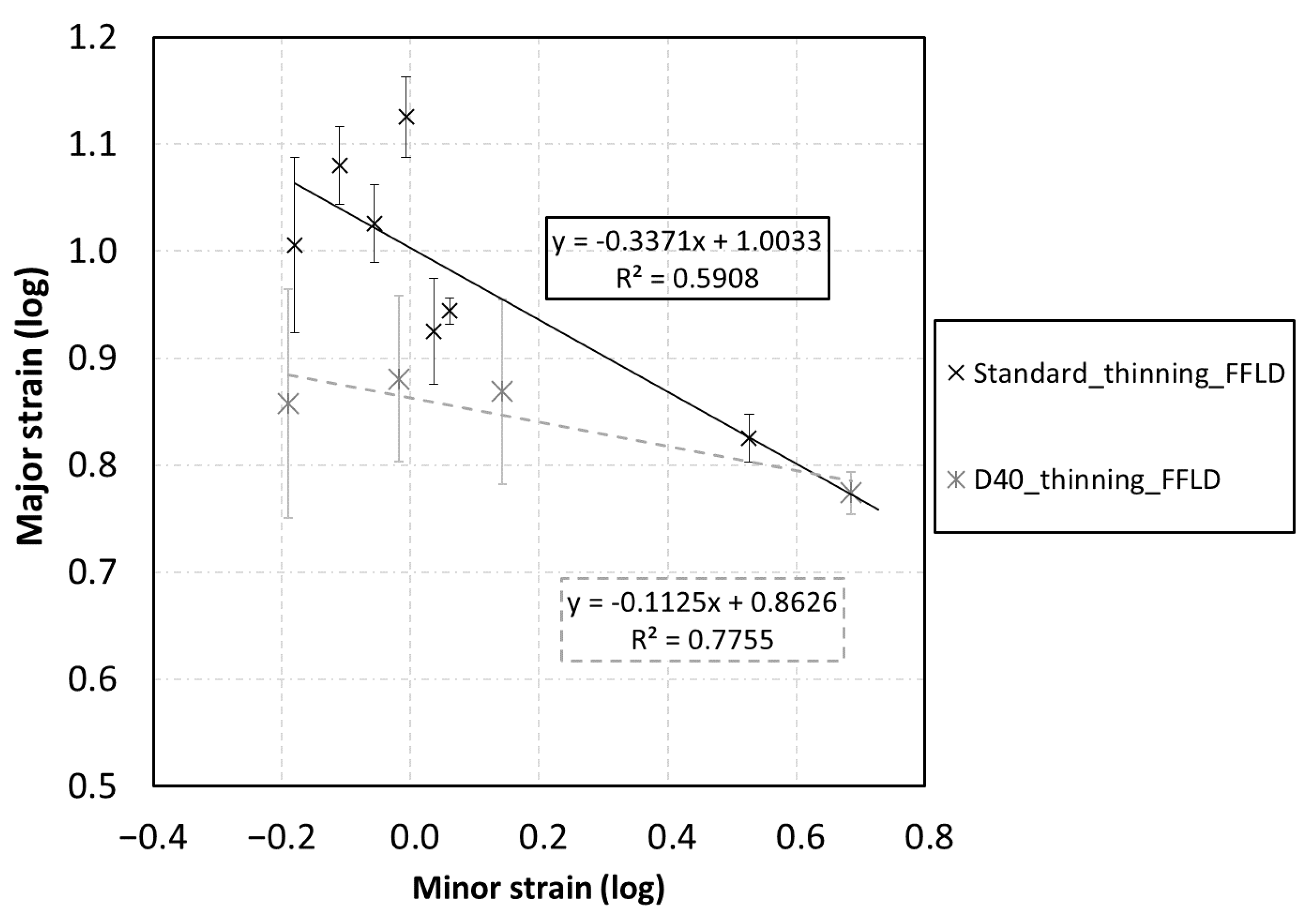
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- DIN ISO 12004-1:2008. Metallic Materials—Determination of Forming-Limit Curves for Sheet and Strip—Part 1: Measurement and Application of Forming-Limit Diagrams in the Press Shop; ISO: Geneva, Switzerland, 2008. [Google Scholar]
- DIN ISO 12004-2:2008. Metallic Materials—Sheet and Strip—Determination of Forming Limit Curves—Part 2: Determination of Forming Limit Curve in the Laboratory; ISO: Geneva, Switzerland, 2008. [Google Scholar]
- Gensamer, M. Strength and Ductility. Trans. ASM 1946, 36, 30–60. [Google Scholar] [CrossRef]
- Keeler, S.P.; Backofen, W.A. Plastic instability and fracture in sheets stretched over rigid punches. ASM Trans. Q. 1963, 56, 25–48. [Google Scholar]
- Goodwin, G.M. Applications of strain analysis to sheet metal forming in the press shop. Soc. Automot. Eng. 1968, 680093, 380–387. [Google Scholar]
- Marciniak, Z.; Kuczynski, K. Limit strains in the process of stretch—Forming sheets. Int. J. Mech. Sci. 1967, 9, 609–620. [Google Scholar] [CrossRef]
- Nakajima, K.; Kikuma, T.; Asaku, K. Study of the formability of steel sheet. Yawata Tech. Rep. 1968, 264, 8517–8530. [Google Scholar]
- Hašek, V. Untersuchung und theroretische Beschreibung wichtiger Einflussgrössen auf das Grenzformänderungschaubil. Blech Rohre Progile 1978, 25, 285–292. [Google Scholar]
- Geiger, M.; Merklein, M. Determination of forming limit diagrams—A new analysis method for characterization of material’s formability. CIRP Ann. 2003, 52, 213–216. [Google Scholar] [CrossRef]
- Ayachi, N.; Guermazi, N.; Pham, C.H.; Manach, P.-Y. Development of a Nakazima Test Suitable for Determining the Formability of Ultra-Thin Copper Sheets. Metals 2020, 10, 1163. [Google Scholar] [CrossRef]
- Gutierrez, J.E.; Noder, J.; Butcher, C. Experimental Characterization and Deterministic Prediction of In-Plane Formability of 3rd Generation Advanced High Strength Steels. Metals 2020, 10, 902. [Google Scholar] [CrossRef]
- Bayat, H.R.; Sarkar, S.; Anantharamaiah, B.; Italiano, F.; Bach, A.; Tharani, S.; Wulfinghoff, S.; Reese, S. Modeling of Forming Limit Bands for Strain-Based Failure-Analysis of Ultra-High-Strength Steels. Metals 2018, 8, 631. [Google Scholar] [CrossRef]
- Volk, W.; Hora, P. Evaluation of Experimental Forming Limit Curves and Investigation of Strain Rate Sensitivity for the Start of Local Necking. In Proceedings of the 8th International Conference and Workshop on Numerical Simulation of 3D Sheet Metal Forming Processes (NUMISHEET), Seoul, Korea, 21–26 August 2011; Chung, K., Han, H.N., Huh, H., Barlat, F., Lee, M.G., Eds.; AIP Conference Proceedings; Volume 1383, p. 99. [Google Scholar] [CrossRef]
- Hotz, W.; Merklein, M.; Kuppert, A.; Friebe, H.; Klein, M. Time dependent FLC determination—Comparison of different algorithms to detect the onset of unstable necking before fracture. Key Eng. Mater. 2012, 549, 397–404. [Google Scholar] [CrossRef]
- Farahnak, P.; Urbanek, M.; Konopik, P.; Dzugan, J. Influence of thickness reduction on forming limits of mild steel DC01. Int. J. Mater. Form. 2020, 13, 371–381. [Google Scholar] [CrossRef]
- Farahnak, P.; Prantl, A.; Dzugan, J.; Konopik, P.; Prochazka, R. Sheet necking prediction in forming limit diagrams with the anisotropy influence incorporation. In Proceedings of the 4th International Conference Recent Trends in Structural Materials, Pilsen, Czech Republic, 9–11 November 2016; IOP Conference Series-Materials Science and Engineering. Volume 179, p. 012023. [Google Scholar] [CrossRef]
- Gorji, M.; Berisha, B.; Hora, P.; Barlat, F. Modeling of localization and fracture phenomena in strain and stress space for sheet metal forming. Int. J. Mater. Form. 2016, 9, 573–584. [Google Scholar] [CrossRef]
- Grolleau, V.; Roth, C.C.; Lafilé, V.; Galpin, B.; Mohr, D. Loading of mini-Nakazima specimens with a dihedral punch: Determining the strain to fracture for plane strain tension through stretch-bending. Int. J. Mech. Sci. 2019, 152, 329–345. [Google Scholar] [CrossRef]
- Li, F.F.; Fu, M.W.; Lin, J.P.; Wang, X.N. Experimental and theoretical study on the hot forming limit of 22MnB5 steel. Int. J. Adv. Manuf. 2014, 71, 297–306. [Google Scholar] [CrossRef]
- Advanced High Strength Steel (AHSS). Application Guidelines, Volume 6, International Iron and Steel Institute, Committee on Automotive Applications; WorldAutoSteel: Middletown, OH, USA, 2006. [Google Scholar]
- Jiayue, L.; Junying, M.; Kaiyu, Q.; Jianping, L.; Fuqiang, L.; Leichao, L. Investigation on the effects of sheet thickness and deformation temperature on the forming limits of boron steel 22MnB5. Key Eng. Mater. 2011, 474–476, 993–997. [Google Scholar] [CrossRef]
- Turetta, A.; Bruschi, S.; Ghiotti, A. Investigation of 22MnB5 formability in hot stamping operations. J. Mater. Process. Technol. 2006, 177, 396–400. [Google Scholar] [CrossRef]
- Slota, J.; Jurčišin, M.; Spišák, E.; Šiser, M. Experimental flc determination of high strength steel sheet metal. AMS 2015, 21, 269–277. [Google Scholar] [CrossRef]
- Xu, Y.; Ji, Q.; Yang, G.; Bao, S.; Zhao, G.; Miao, X.; Mao, X. Effect of Cooling Path on Microstructures and Hardness of Hot-Stamped Steel. Metals 2020, 10, 1692. [Google Scholar] [CrossRef]
- GESTAMP, Hot Stamping. Available online: https://www.gestamp.com/What-we-do/Technologies (accessed on 26 January 2021).
- Affronti, E.; Merklein, M. Analysis of the bending effects and the biaxial pre-straining in sheet metal stretch forming processes for the determination of the forming limits. Int. J. Mech. Sci. 2018, 138–139, 295–309. [Google Scholar] [CrossRef]
- Konopik, P.; Dzugan, J.; Rund, M. Determination of fracture toughness in the upper shelf region using small sample test techniques. In Proceedings of the METAL 2015: 24th International Conference on Metallurgy and Materials, Brno, Czech Republic, 3–5 June 2015; pp. 710–715. [Google Scholar]
- Džugan, J.; Španiel, M.; Prantl, A.; Konopík, P.; Růžička, J.; Kuželka, J. Identification of ductile damage parameters for pressure vessel steel. Nucl. Eng. Des. 2018, 328, 372–380. [Google Scholar] [CrossRef]
- Jirková, H.; Rubešová, K.; Konopík, P.; Opatová, K. Effect of the Parameters of Semi-Solid Processing on the Elimination of Sharp-Edged Primary Chromium Carbides from Tool Steel. Metals 2018, 8, 713. [Google Scholar] [CrossRef]



| Chemical Composition—22MnB5 | ||||||||
|---|---|---|---|---|---|---|---|---|
| C | Si | Mn | P | S | Al | N | Cr | B |
| 0.25 | 0.4 | 1.35 | 0.023 | 0.01 | 0.08 | 0.01 | 0.25 | 0.004 |
| Mechanical Properties—22MnB5 | |
|---|---|
| Yield strength Rp0.2 | 382 ± 4 (MPa) |
| Ultimate tensile strength Rm | 549 ± 9 (MPa) |
| Uniform elongation Ag | 13 ± 0 (%) |
| Total elongation A20 | 23 ± 1 (%) |
| Hardness HV10 | 169 ± 2 (-) |
| Punch Diameter (mm) | 10 | 100 |
|---|---|---|
| Bending Effect (–) | 0.08 | 0.008 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rubešová, K.; Rund, M.; Rzepa, S.; Jirková, H.; Jeníček, Š.; Urbánek, M.; Kučerová, L.; Konopík, P. Determining Forming Limit Diagrams Using Sub-Sized Specimen Geometry and Comparing FLD Evaluation Methods. Metals 2021, 11, 484. https://doi.org/10.3390/met11030484
Rubešová K, Rund M, Rzepa S, Jirková H, Jeníček Š, Urbánek M, Kučerová L, Konopík P. Determining Forming Limit Diagrams Using Sub-Sized Specimen Geometry and Comparing FLD Evaluation Methods. Metals. 2021; 11(3):484. https://doi.org/10.3390/met11030484
Chicago/Turabian StyleRubešová, Kateřina, Martin Rund, Sylwia Rzepa, Hana Jirková, Štěpán Jeníček, Miroslav Urbánek, Ludmila Kučerová, and Pavel Konopík. 2021. "Determining Forming Limit Diagrams Using Sub-Sized Specimen Geometry and Comparing FLD Evaluation Methods" Metals 11, no. 3: 484. https://doi.org/10.3390/met11030484
APA StyleRubešová, K., Rund, M., Rzepa, S., Jirková, H., Jeníček, Š., Urbánek, M., Kučerová, L., & Konopík, P. (2021). Determining Forming Limit Diagrams Using Sub-Sized Specimen Geometry and Comparing FLD Evaluation Methods. Metals, 11(3), 484. https://doi.org/10.3390/met11030484







