Prediction of Microstructure Constituents’ Hardness after the Isothermal Decomposition of Austenite
Abstract
1. Introduction
2. Materials and Methods
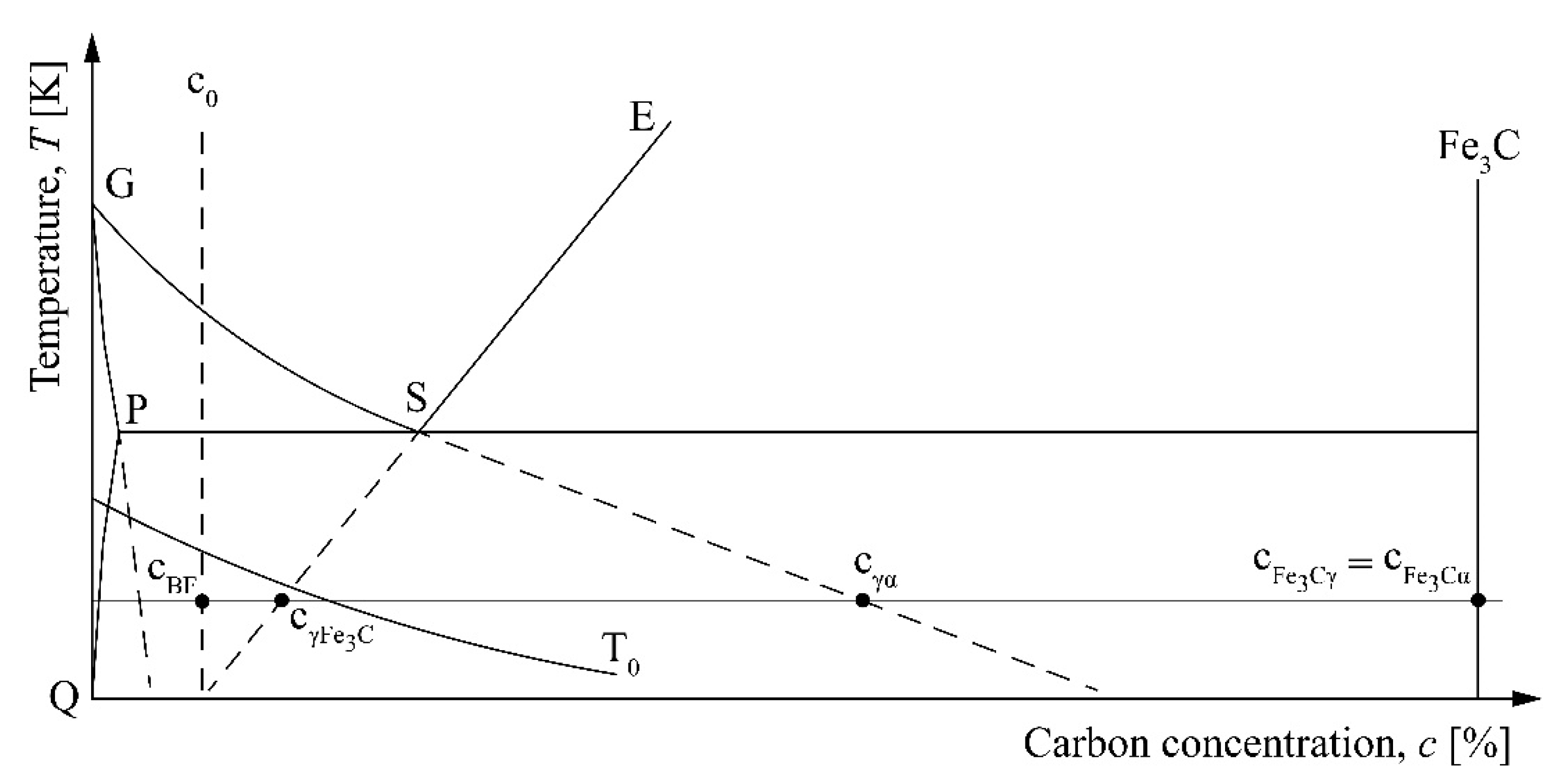
2.1. Methods for Estimation of Hardness of Microstructure Constituents
2.2. Materials
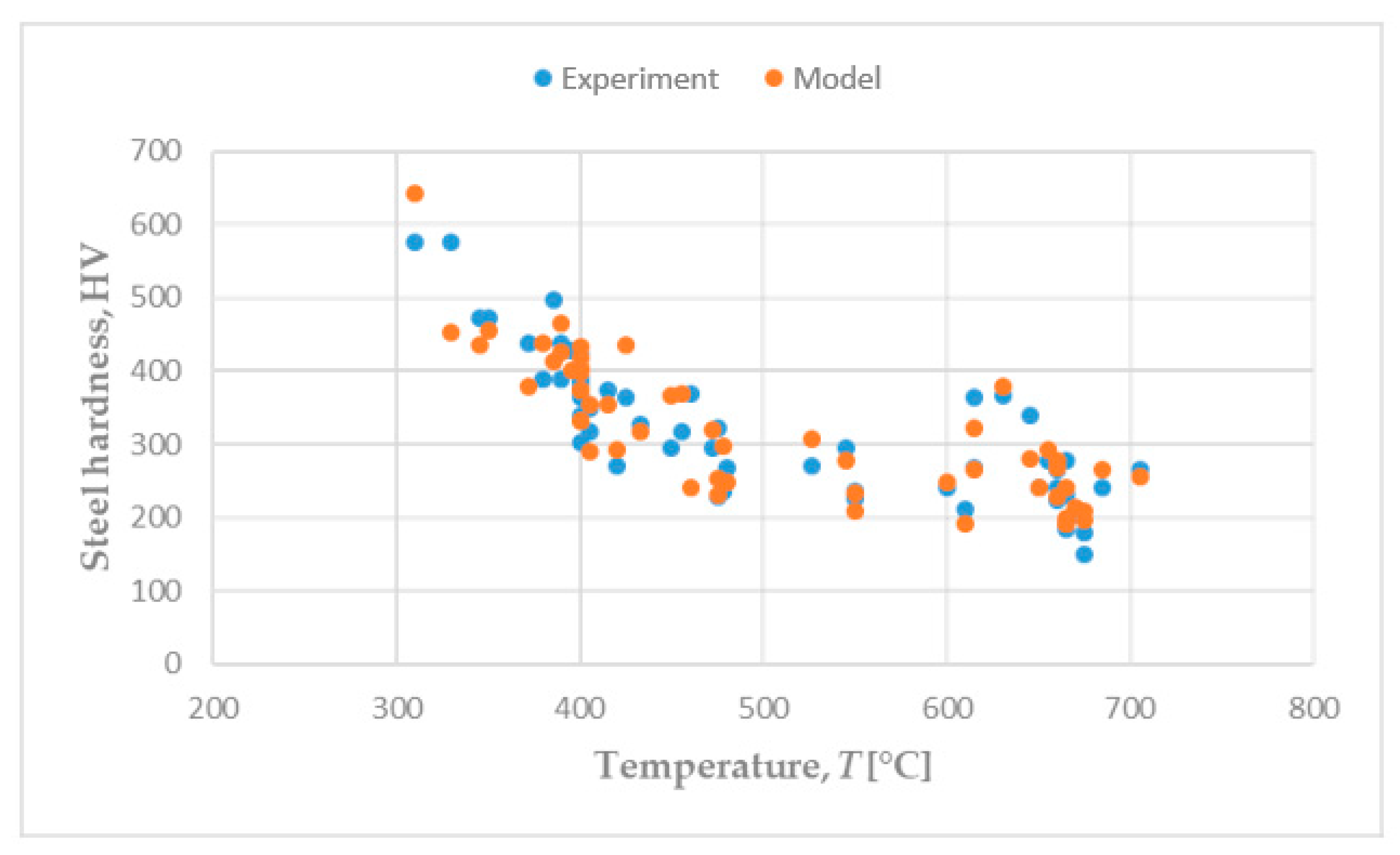
3. Results and Discussion
4. Conclusions
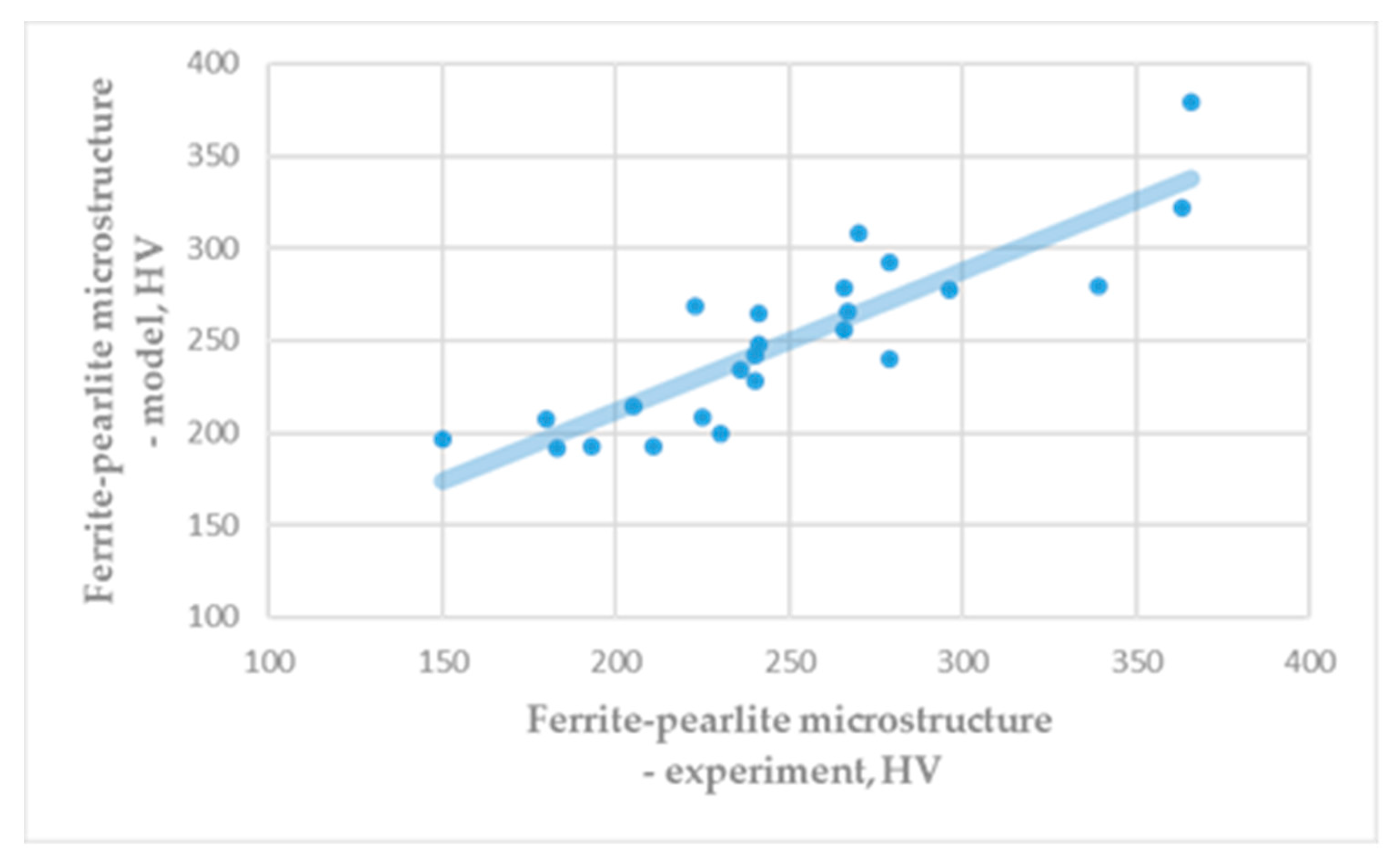
- The hardness of pearlite microstructure mostly depends on carbon content and interlamellar spacing of the pearlite. Hardness of ferrite and pearlite microstructure is function of volume fraction of pearlite and ferrite. Therefore, pearlite hardness depends on the carbon content in a steel and temperature of undercooling below Ae1 temperature.
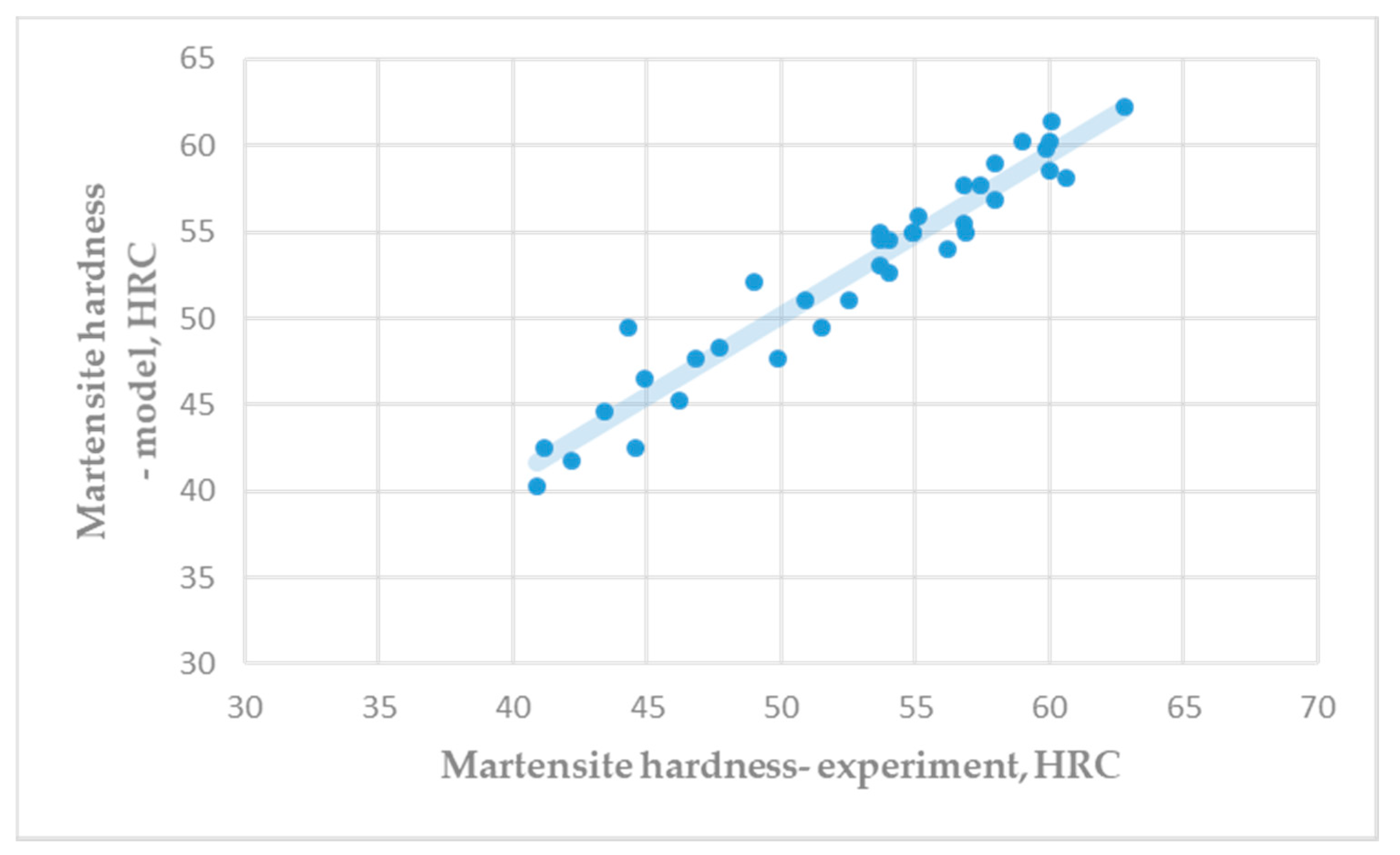
- The martensite hardness in hypoeutectoid steel commonly directly depends on the carbon content in a steel.
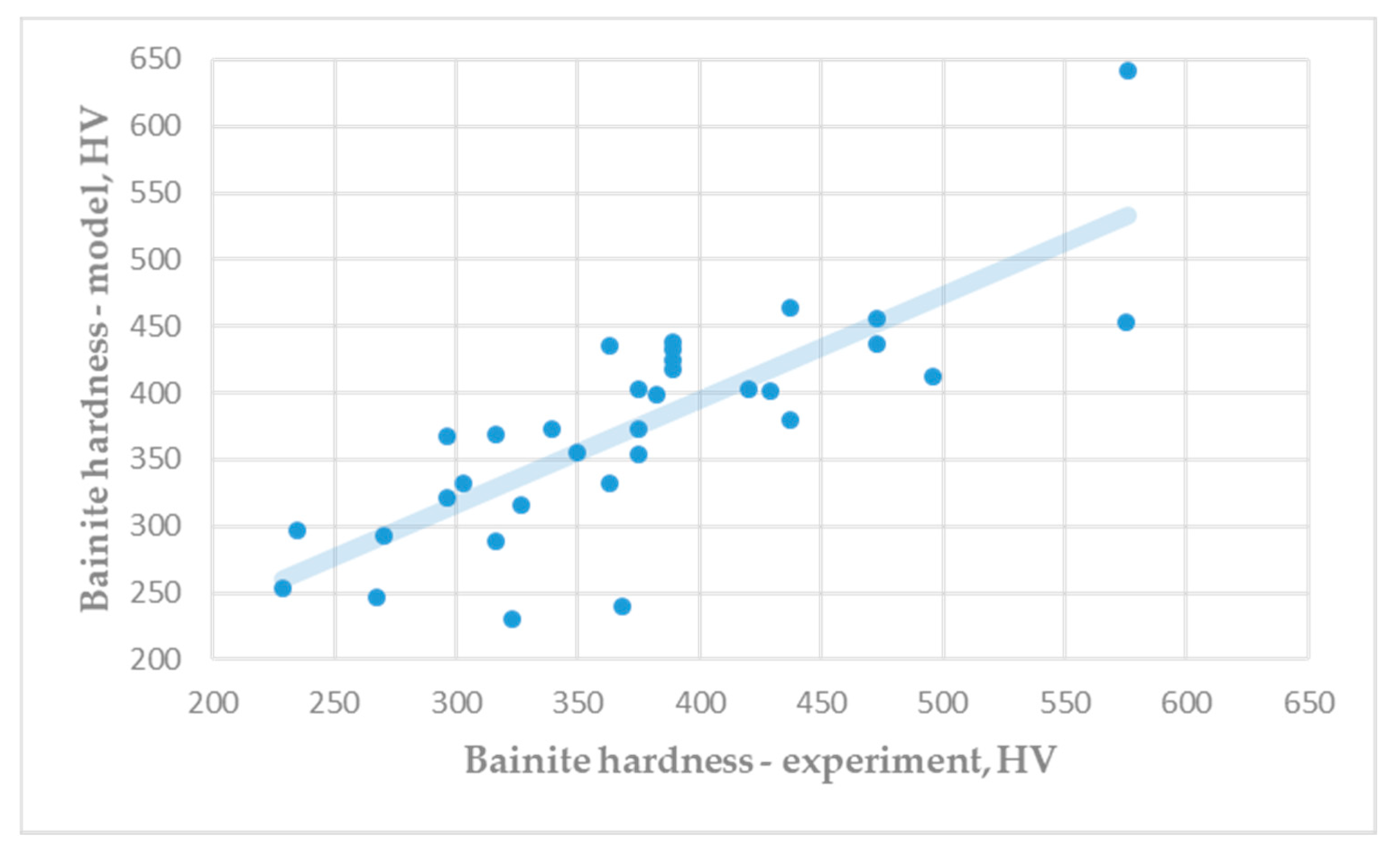
- Hardness of bainite depends on combination of the solid solution strengthening due to carbon, the effect of the dislocation cell structure, precipitation hardening by cementite, strengthening due to grain size refinement and strengthening due to particle spacing refinement. Hardening mechanism due to carbon, dislocation cell structure and precipitation hardening prevails at lower temperatures of austenite decompositions.
- The total hardness of steel can be estimated using the rule of mixture based on both fraction and hardness of microstructural components of steel.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Data No. | Ferrite-Pearlite Microstructure Hardness | Ferrite Content | Pearlite Content | Carbon Concentration in Steel | Temperature of Isothermal Transformation |
|---|---|---|---|---|---|
| HV | % | % | % | °C | |
| 1. | 266 | 0 | 100 | 0.43 | 705 |
| 2. | 241 | 1 | 99 | 0.44 | 685 |
| 3. | 150 | 60 | 40 | 0.22 | 675 |
| 4. | 180 | 60 | 40 | 0.30 | 675 |
| 5. | 205 | 30 | 70 | 0.30 | 670 |
| 6. | 193 | 80 | 20 | 0.13 | 665 |
| 7. | 183 | 70 | 30 | 0.16 | 665 |
| 8. | 230 | 70 | 30 | 0.24 | 665 |
| 9. | 279 | 5 | 95 | 0.36 | 665 |
| 10. | 240 | 30 | 70 | 0.35 | 660 |
| 11. | 223 | 5 | 95 | 0.44 | 660 |
| 12. | 266 | 5 | 95 | 0.47 | 660 |
| 13. | 279 | 2 | 98 | 0.50 | 655 |
| 14. | 240 | 20 | 80 | 0.38 | 650 |
| 15. | 339 | 7 | 93 | 0.47 | 645 |
| 16. | 366 | 3 | 97 | 0.73 | 630 |
| 17. | 267 | 15 | 85 | 0.43 | 615 |
| 18. | 363 | 0 | 100 | 0.55 | 615 |
| 19. | 211 | 70 | 30 | 0.16 | 610 |
| 20. | 241 | 20 | 80 | 0.38 | 600 |
| 21. | 225 | 75 | 25 | 0.30 | 550 |
| 22. | 236 | 60 | 40 | 0.43 | 550 |
| 23. | 296 | 15 | 85 | 0.44 | 545 |
| 24. | 270 | 2 | 98 | 0.48 | 526 |
| Data No. | Designation (DIN) | Chemical Composition, wt.% | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | Si | Mn | P | S | Al | Cr | Cu | Mo | Ni | V | ||
| 1. | Ck45 | 0.44 | 0.22 | 0.66 | 0.022 | 0.029 | - | 0.15 | - | - | - | 0.02 |
| 2. | 37MnSi5 | 0.34 | 1.11 | 1.23 | 0.022 | 0.012 | - | 0.19 | 0.17 | 0.04 | 0.18 | 0.03 |
| 3. | 0.38 | 1.05 | 1.14 | 0.035 | 0.019 | - | 0.23 | - | - | - | 0.02 | |
| 4. | 42MnV7 | 0.38 | 0.28 | 1.76 | 0.035 | 0.015 | - | 0.33 | 0.16 | 0.05 | 0.17 | 0.07 |
| 5. | 0.45 | 0.27 | 1.76 | 0.017 | 0.018 | - | 0.18 | 0.19 | <0.01 | 0.06 | 0.07 | |
| 6. | 34Cr4 | 0.30 | 0.21 | 0.57 | 0.015 | 0.018 | - | 0.90 | 0.25 | <0.01 | 0.06 | 0.01 |
| 7. | 0.37 | 0.35 | 0.68 | 0.027 | 0.020 | - | 1.06 | 0.17 | 0.02 | 0.18 | <0.01 | |
| 8. | 36Cr6 | 0.32 | 0.17 | 0.47 | 0.014 | 0.011 | - | 1.53 | 0.16 | 0.04 | 0.18 | <0.01 |
| 9. | 0.36 | 0.25 | 0.49 | 0.021 | 0.020 | - | 1.54 | 0.16 | 0.03 | 0.21 | <0.01 | |
| 10. | 41Cr4 | 0.44 | 0.22 | 0.80 | 0.030 | 0.023 | - | 1.04 | 0.17 | 0.04 | 0.26 | <0.01 |
| 11. | 25CrMo4 | 0.22 | 0.25 | 0.64 | 0.010 | 0.011 | - | 0.97 | 0.16 | 0.23 | 0.33 | <0.01 |
| 12. | 0.25 | 0.32 | 0.78 | 0.016 | 0.005 | - | 1.06 | 0.16 | 0.25 | 0.24 | <0.01 | |
| 13. | 34CrMo4 | 0.30 | 0.22 | 0.64 | 0.011 | 0.012 | - | 1.01 | 0.19 | 0.24 | 0.11 | <0.01 |
| 14. | 0.37 | 0.25 | 0.65 | 0.017 | 0.023 | - | 1.08 | 0.21 | 0.20 | 0.27 | <0.01 | |
| 15. | 50CrMo4 | 0.46 | 0.22 | 0.50 | 0.015 | 0.014 | - | 1.00 | 0.26 | 0.21 | 0.22 | <0.01 |
| 16. | 0.50 | 0.32 | 0.80 | 0.017 | 0.022 | - | 1.04 | 0.17 | 0.24 | 0.11 | <0.01 | |
| 17. | 0.51 | 0.25 | 0.67 | 0.012 | 0.011 | - | 1.05 | 0.17 | 0.25 | 0.39 | <0.01 | |
| 18. | 27MnCrV4 | 0.24 | 0.21 | 1.06 | 0.014 | 0.020 | - | 0.79 | 0.17 | 0.02 | 0.18 | 0.10 |
| 19. | 0.24 | 0.20 | 1.06 | 0.014 | 0.019 | - | 0.68 | 0.17 | 0.02 | 0.18 | 0.07 | |
| 20. | 0.27 | 0.20 | 1.12 | 0.022 | 0.017 | - | 0.90 | 0.20 | 0.01 | 0.13 | 0.06 | |
| 21. | 0.27 | 0.15 | 1.19 | 0.013 | 0.021 | - | 0.85 | 0.21 | 0.03 | 0.15 | 0.11 | |
| 22. | 0.33 | 0.24 | 1.17 | 0.021 | 0.018 | - | 0.85 | 0.22 | 0.02 | 0.07 | 0.08 | |
| 23. | 42CrV6 | 0.42 | 0.26 | 0.60 | 0.020 | 0.005 | - | 1.64 | 0.20 | <0.01 | 0.13 | 0.08 |
| 24. | 50CrV4 | 0.47 | 0.35 | 1.04 | 0.032 | 0.012 | - | 1.20 | 0.16 | 0.05 | 0.05 | 0.12 |
| 25. | 0.49 | 0.23 | 0.82 | 0.018 | 0.018 | - | 1.03 | 0.14 | 0.03 | 0.11 | 0.07 | |
| 26. | 0.53 | 0.27 | 0.93 | 0.029 | 0.013 | - | 0.98 | 0.20 | 0.05 | 0.33 | 0.07 | |
| 27. | 0.55 | 0.22 | 0.98 | 0.017 | 0.013 | - | 1.02 | 0.07 | - | 0.01 | 0.11 | |
| 28. | 0.3%C, 3% Ni | 0.30 | 0.32 | 0.51 | 0.011 | 0.007 | 0.032 | 0.07 | - | - | 3.03 | <0.01 |
| 29. | 16MnCr5 | 0.16 | 0.22 | 1.12 | 0.030 | 0.008 | 0.015 | 0.99 | 0.22 | 0.02 | 0.12 | 0.01 |
| 30. | 0.19 | 0.25 | 1.26 | 0.013 | 0.013 | 0.014 | 0.97 | - | - | <0.01 | - | |
| 31. | 71Si7 | 0.73 | 1.62 | 0.73 | 0.019 | 0.012 | - | 0.10 | 0.19 | - | 0.12 | 0.01 |
| 32. | 0,2%C, 1.2%Mn, 1%Cu, 0.6 Ni | 0.20 | 0.38 | 1.20 | 0.039 | 0.024 | - | 0.06 | 0.91 | - | 0.55 | - |
| 33. | 0.2%C, 1%Mn, 1%Cu, 0.25%Mo, 0.8%Ni | 0.19 | 0.38 | 1.12 | 0.037 | 0.036 | - | 0.28 | 0.98 | 0.27 | 0.79 | - |
| 34. | 0.15%C, 1.2%Cr, 0.25%Ni, 0.3%V | 0.15 | 0.48 | 0.67 | 0.044 | 0.024 | - | 1.20 | 0.18 | - | 0.25 | 0.31 |
| 35. | 0.45%C, 2%Mn | 0.48 | 0.28 | 1.98 | 0.020 | 0.011 | - | - | - | - | - | - |
| 36. | 0.45%C, 3.5%Cr | 0.43 | 0.14 | 0.04 | 0.015 | 0.012 | 0.14 | 3.52 | - | - | - | - |
| 37. | 15CrNi6 | 0.13 | 0.31 | 0.51 | 0.023 | 0.009 | 0.010 | 1.50 | 0.22 | 0.06 | 1.55 | <0.01 |
| 38. | 0.16 | 0.28 | 0.43 | 0.010 | 0.008 | 0.005 | 1.58 | 0.20 | 0.006 | 1.54 | <0.01 | |
| 39. | 18CrNi8 | 0.15 | 0.13 | 0.60 | 0.014 | 0.008 | 0.030 | 1.94 | 0.21 | 0.06 | 2.02 | <0.01 |
| 40. | 0.20 | 0.20 | 0.60 | 0.021 | 0.010 | 0.010 | 2.07 | 0.21 | 0.01 | 1.90 | 0.01 | |
| 41. | 42CrMo4 | 0.38 | 0.18 | 0.62 | 0.033 | 0.023 | - | 1.03 | 0.28 | 0.21 | 0.22 | <0.01 |
| 42. | 0.38 | 0.23 | 0.64 | 0.019 | 0.013 | - | 0.99 | 0.17 | 0.16 | 0.08 | <0.01 | |
| 43. | 0.39 | 0.15 | 0.50 | 0.013 | 0.014 | - | 0.97 | 0.19 | 0.19 | 0.20 | <0.01 | |
| 44. | 0.40 | 0.30 | 0.65 | 0.016 | 0.014 | - | 1.10 | 0.22 | 0.21 | 0.42 | <0.01 | |
| 45. | 0.44 | 0.28 | 0.67 | 0.025 | 0.024 | - | 1.07 | 0.21 | 0.15 | 0.22 | <0.01 | |
| Data No. | Designation (DIN) | Carbon Concentration in Steel | Martensite Microstructure Hardness |
|---|---|---|---|
| % | HRC | ||
| 1. | Ck45 | 0.44 | 56.8 |
| 2. | 37MnSi5 | 0.34 | 53.7 |
| 3. | 0.38 | 56.9 | |
| 4. | 42MnV7 | 0.38 | 54.9 |
| 5. | 0.45 | 60.6 | |
| 6. | 34Cr4 | 0.30 | 52.5 |
| 7. | 0.37 | 54.0 | |
| 8. | 36Cr6 | 0.32 | 49.0 |
| 9. | 0.36 | 56.2 | |
| 10. | 25CrMo4 | 0.22 | 44.9 |
| 11. | 0.25 | 47.7 | |
| 12. | 34CrMo4 | 0.30 | 50.9 |
| 13. | 0.37 | 53.7 | |
| 14. | 50CrMo4 | 0.46 | 60.0 |
| 15. | 0.50 | 59.0 | |
| 16. | 0.50 | 60.0 | |
| 17. | 27MnCrV4 | 0.24 | 46.8 |
| 18. | 0.24 | 49.9 | |
| 19. | 0.27 | 44.3 | |
| 20. | 0.27 | 51.5 | |
| 21. | 0.33 | 54.0 | |
| 22. | 42CrV6 | 0.42 | 58.0 |
| 23. | 50CrV4 | 0.47 | 58.0 |
| 24. | 0.49 | 59.9 | |
| 25. | 0.53 | 60.1 | |
| 26. | 0.55 | 62.8 | |
| 27. | 16MnCr5 | 0.16 | 41.2 |
| 28. | 0.19 | 43.4 | |
| 29. | 15CrNi6 | 0.13 | 40.9 |
| 30. | 0.16 | 44.6 | |
| 31. | 18CrNi8 | 0.15 | 42.2 |
| 32. | 0.20 | 46.2 | |
| 33. | 42CrMo4 | 0.38 | 53.7 |
| 34. | 0.38 | 54.9 | |
| 35. | 0.39 | 56.8 | |
| 36. | 0.40 | 55.1 | |
| 37. | 0.44 | 57.4 |
| Data No. | Designation (DIN) | Carbon Concentration in Steel | Temperature of Isothermal Transformation | Bainite Microstructure Hardness |
|---|---|---|---|---|
| % | °C | HV | ||
| 1. | Ck45 | 0.44 | 455 | 316 |
| 2. | 400 | 420 | ||
| 3. | 37MnSi5 | 0.38 | 400 | 375 |
| 4. | 42MnV7 | 0.43 | 450 | 296 |
| 5. | 400 | 382 | ||
| 6. | 345 | 473 | ||
| 7. | 34Cr4 | 0.35 | 472 | 296 |
| 8. | 405 | 350 | ||
| 9. | 41Cr4 | 0.44 | 400 | 375 |
| 10. | 36Cr6 | 0.36 | 415 | 375 |
| 11. | 372 | 437 | ||
| 12. | 25CrMo4 | 0.22 | 405 | 316 |
| 13. | 34CrMo4 | 0.30 | 478 | 235 |
| 14. | 433 | 327 | ||
| 15. | 400 | 363 | ||
| 16. | 50CrMo4 | 0.50 | 400 | 389 |
| 17. | 27MnCrV4 | 0.24 | 420 | 270 |
| 18. | 42CrV6 | 0.44 | 386 | 496 |
| 19. | 330 | 575 | ||
| 20. | 50CrV4 | 0.55 | 425 | 363 |
| 21. | 390 | 437 | ||
| 22. | 50CrV4 | 0.47 | 390 | 389 |
| 23. | 50CrV4 | 0.47 | 400 | 389 |
| 24. | 350 | 473 | ||
| 25. | 0.3%C, 3%Ni | 0.30 | 400 | 303 |
| 26. | 16MnCr5 | 0.16 | 460 | 368 |
| 27. | 71Si7 | 0.73 | 310 | 576 |
| 28. | 0.2%C, 1.2%Mn, 1%Cu, 0.6%Ni | 0.20 | 475 | 229 |
| 29. | 0.2%C, 1%Mn, 1%Cu, 0.25%Mo, 0.8%Ni | 0.19 | 480 | 267 |
| 30. | 0.15%C, 1.2%Cr, 0.25%Ni, 0.3%V | 0.15 | 475 | 323 |
| 31. | 0.45%C, 2%Mn | 0.48 | 380 | 389 |
| 32. | 0.45%C, 3.5%Cr | 0.43 | 395 | 429 |
| 33. | 42CrMo4 | 0.38 | 400 | 339 |
References
- Brooks, C.R. Principles of the Heat Treatment of Plain Carbon and Low-Alloy Steels; ASM International: Materials Park, OH, USA, 1996; pp. 87–128. [Google Scholar]
- Şimşir, C.; Gür, C.H. Simulation of Quenching. In Handbook of Thermal Process Modeling of Steels; Gür, C.H., Pan, J., Eds.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2009; pp. 341–425. [Google Scholar]
- Wang, Q.; Ye, Q.; Wang, Z.; Kan, L.; Wang, H. Thickness Effect on Microstructure, Strength, and Toughness of a Quenched and Tempered 178 mm Thickness Steel Plate. Metals 2020, 10, 572. [Google Scholar] [CrossRef]
- Wu, T.; Wu, R.; Liu, B.; Liang, W.; Ke, D. Enhancing the Mechanical Properties of a Hot Rolled High-Strength Steel Produced by Ultra-Fast Cooling and Q&P Process. Metals 2019, 9, 958. [Google Scholar] [CrossRef]
- Zhang, L.; Gong, D.; Li, Y.; Wang, X.; Ren, X.; Wang, E. Effect of Quenching Conditions on the Microstructure and Mechanical Properties of 51CrV4 Spring Steel. Metals 2018, 8, 1056. [Google Scholar] [CrossRef]
- Hannula, J.; Porter, D.; Kaijalainen, A.; Somani, M.; Kömi, J. Mechanical Properties of Direct-Quenched Ultra-High-Strength Steel Alloyed with Molybdenum and Niobium. Metals 2019, 9, 350. [Google Scholar] [CrossRef]
- Ritchie, R.O.; Knott, J.F. Mechanisms of fatigue crack growth in low alloy steel. Acta Metall. 1973, 21, 639–648. [Google Scholar] [CrossRef]
- Irving, P.E.; Kurzfeld, A. Measurements of intergranular failure produced during fatigue crack growth in quenched and tempered steels. Met. Sci. 1978, 12, 495–502. [Google Scholar] [CrossRef]
- Denis, S.; Archambault, P.; Gautier, E.; Simon, A.; Beck, G. Prediction of residual stress and distortion of ferrous and non-ferrous metals: Current status and future developments. J. Mater. Eng. Perform. 2002, 11, 92–102. [Google Scholar] [CrossRef]
- Hasan, M.F. Analysis of Mechanical Behavior and Microstructural Characteristics Change of ASTM A-36 Steel Applying Various Heat Treatment. J. Mater. Sci. Eng. 2016, 5. [Google Scholar] [CrossRef]
- Smoljan, B.; Iljkić, D.; Totten, G.E. Mathematical Modeling and Simulation of Hardness of Quenched and Tempered Steel. Metall. Mater. Trans. B 2015, 46, 2666–2673. [Google Scholar] [CrossRef]
- Cahoon, J.R.; Broughton, W.H.; Kutzak, A.R. The determination of yield strength from hardness measurements. Metall. Trans. 1971, 2, 1979–1983. [Google Scholar] [CrossRef]
- Bain, E.C. Functions of the Alloying Elements in Steel; American Society for Metals: Cleveland, OH, USA, 1939. [Google Scholar]
- Krauss, G. Steels: Heat Treatment and Processing Principles, 2nd ed.; ASM International: Materials Park, OH, USA, 1990; pp. 1–16. [Google Scholar]
- Sverdlin, A.V.; Ness, A.R. Fundamental Concepts in Steel Heat Treatment. In Steel Heat Treatment: Metallurgy and Technologies, 2nd ed.; Totten, G.E., Ed.; CRC Press, Tylor & Francis Group: Boca Raton, FL, USA, 2007; pp. 121–164. [Google Scholar]
- Colpaert, H. Metallography of Steel–Interpretation of Structure and the Effects of Processing; ASM International: Materials Park, OH, USA, 2018; pp. 193–352. [Google Scholar]
- Kurdjumow, G.; Sachs, G. Über den Mechanismus der Stahlhärtung. Zeitschrift für Physik 1930, 64, 325–343. [Google Scholar] [CrossRef]
- Nishiyama, Z. X-ray Investigation of the Mechanism of the Transformation from Face-Centred Cubic Lattice to Body-Centred Cubic. Sci. Rep. Tohoku Univ. 1934, 23, 637–664. [Google Scholar]
- Olson, G.B.; Cohen, M. A general mechanism of martensitic nucleation: Part II. FCC → BCC and other martensitic transformations. Metall. Trans. A 1976, 7, 1905–1914. [Google Scholar] [CrossRef]
- Christian, J.W. The Theory of Transformation in Metals and Alloys: Part 2, 3rd ed.; Pergamon Press, Elsevier Science: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Bhadeshia, H.K.D.H. Bainite in Steels: Transformations, Microstructure and Properties, 2nd ed.; IOM Communications: London, UK, 2001. [Google Scholar]
- Spies, H.-J. Mechanical Properties of Ferrous and Nonferrous Alloys after Quenching. In Quenching Theory and Technology, 2nd ed.; Liscic, B., Tensi, H.M., Canale, L.C.F., Totten, G.E., Eds.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2010; pp. 105–127. [Google Scholar]
- Qiu, Y.; Xin, R.; Luo, J.; Ma, Q. The Effects of Homogenizing and Quenching and Tempering Treatments on Crack Healing. Metals 2020, 10, 427. [Google Scholar] [CrossRef]
- De Moor, E.; Lacroix, S.; Clarke, A.J.; Penning, J.; Speer, J.G. Effect of Retained Austenite Stabilized via Quench and Partitioning on the Strain Hardening of Martensitic Steels. Metall. Mater. Trans. A 2008, 39, 2586–2595. [Google Scholar] [CrossRef]
- Abbasi, F.; Fletcher, A.J. Effect of transformation plasticity on generation of thermal stress and strain in quenched steel plates. Mater. Sci. Technol. 1985, 1, 830–837. [Google Scholar] [CrossRef]
- Sjöström, S. Interactions and constitutive models for calculating quench stresses in steel. Mater. Sci. Technol. 1985, 1, 823–829. [Google Scholar] [CrossRef]
- Tomita, Y. Effect of microstructure on plane-strain fracture toughness of AISI 4340 steel. Metall. Trans. A 1988, 19, 2513–2521. [Google Scholar] [CrossRef]
- Dieter, G.E. Mechanical Metallurgy, 2nd ed.; McGraw-Hill Series in Materials Science and Engineering; McGraw-Hill: Tokyo, Japan, 1976; pp. 232–235. [Google Scholar]
- Bowen, R.M. Theory of Mixture. Contin. Phys. 1976, 3, 2–129. [Google Scholar]
- Franceschi, M.; Pezzato, L.; Gennari, C.; Fabrizi, A.; Polyakova, M.; Konstantinov, D.; Brunelli, K.; Dabalà, M. Effect of Intercritical Annealing and Austempering on the Microstructure and Mechanical Properties of a High Silicon Manganese Steel. Metals 2020, 10, 1448. [Google Scholar] [CrossRef]
- Rose, A.; Hougardy, H. Atlas zur Wärmebehandlung der Stähle; Verlag Stahleisen: Düsseldorf, Germany, 1972. [Google Scholar]
| Ferrite, Equation (3) | Pearlite, Equation (1) | Martensite, Equation (5) | Bainite, Equation (8) | |||||
|---|---|---|---|---|---|---|---|---|
| aF | a0P | a1P | a2P | a0M | a1M | a0B | a1B | a2B |
| 83.50 | 116.34 | 279.61 | 8.63 | 19.51 | 57.58 | 26.35 | 1.02 | 0.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smokvina Hanza, S.; Smoljan, B.; Štic, L.; Hajdek, K. Prediction of Microstructure Constituents’ Hardness after the Isothermal Decomposition of Austenite. Metals 2021, 11, 180. https://doi.org/10.3390/met11020180
Smokvina Hanza S, Smoljan B, Štic L, Hajdek K. Prediction of Microstructure Constituents’ Hardness after the Isothermal Decomposition of Austenite. Metals. 2021; 11(2):180. https://doi.org/10.3390/met11020180
Chicago/Turabian StyleSmokvina Hanza, Sunčana, Božo Smoljan, Lovro Štic, and Krunoslav Hajdek. 2021. "Prediction of Microstructure Constituents’ Hardness after the Isothermal Decomposition of Austenite" Metals 11, no. 2: 180. https://doi.org/10.3390/met11020180
APA StyleSmokvina Hanza, S., Smoljan, B., Štic, L., & Hajdek, K. (2021). Prediction of Microstructure Constituents’ Hardness after the Isothermal Decomposition of Austenite. Metals, 11(2), 180. https://doi.org/10.3390/met11020180







