Effect of Low-Temperature Annealing on Creep Properties of AlSi10Mg Alloy Produced by Additive Manufacturing: Experiments and Modeling
Abstract
1. Introduction
1.1. AlSi10Mg Alloy Produced by Additive Manufacturing: Main Structural Features
- i.
- at a macroscopic level (100 μm–1 mm), the most noteworthy features are: (a) the high surface roughness resulting from the presence of melt pools; (b) the possible presence of porosities [7];
- ii.
- iii.
- at a microscopic level (10 nm–1 μm), the long cells are subdivided into equiaxed subcells, again with diameters of a few hundreds of nm, separated by a network of Si-rich eutectic regions. The eutectic regions are richer in Si [10] and contain densely spaced Si particles, the size and distribution of which can vary as a function of process parameters [7,8] or part size [9].
1.2. AlSi10Mg Alloy Produced by Additive Manufacturing: Effect of Stress Relieving/Low Temperature Annealing
- i.
- in some cases (see, for example data from [13]), the yield stress monotonically decreases with increasing annealing temperature. The phenomenon is quite correctly described by the model curves;
- ii.
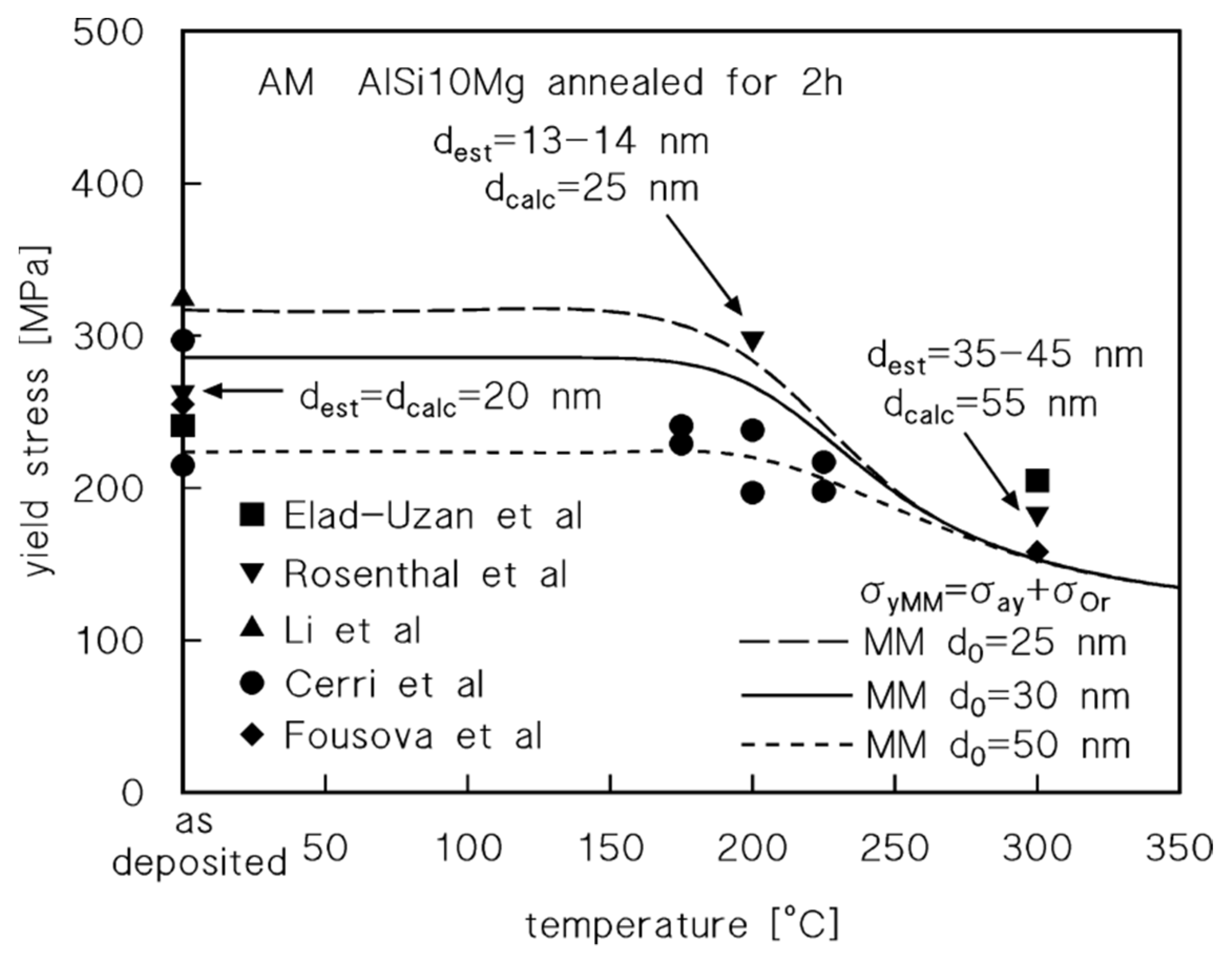
- in other cases (see data from [5] and evidence presented in [10]), precipitation of Si is not completed during the AM process. Thus, in the early stages of low-temperature annealing, an additional precipitation of fine Si particles results in an increase in yield stress. This secondary precipitation is not accounted for by the equations presented in Appendix A, since the model assumes that ripening starts immediately upon annealing. This fact is easily confirmed when comparing the estimated value of the Si crystallites (dest) [5] and the calculated value of Si particle size (Figure 1). The secondary precipitation results in a finer particle size than the one predicted by the ripening equations.
1.3. AlSi10Mg Alloy Produced by Additive Manufacturing: Creep Response
2. Materials and Methods
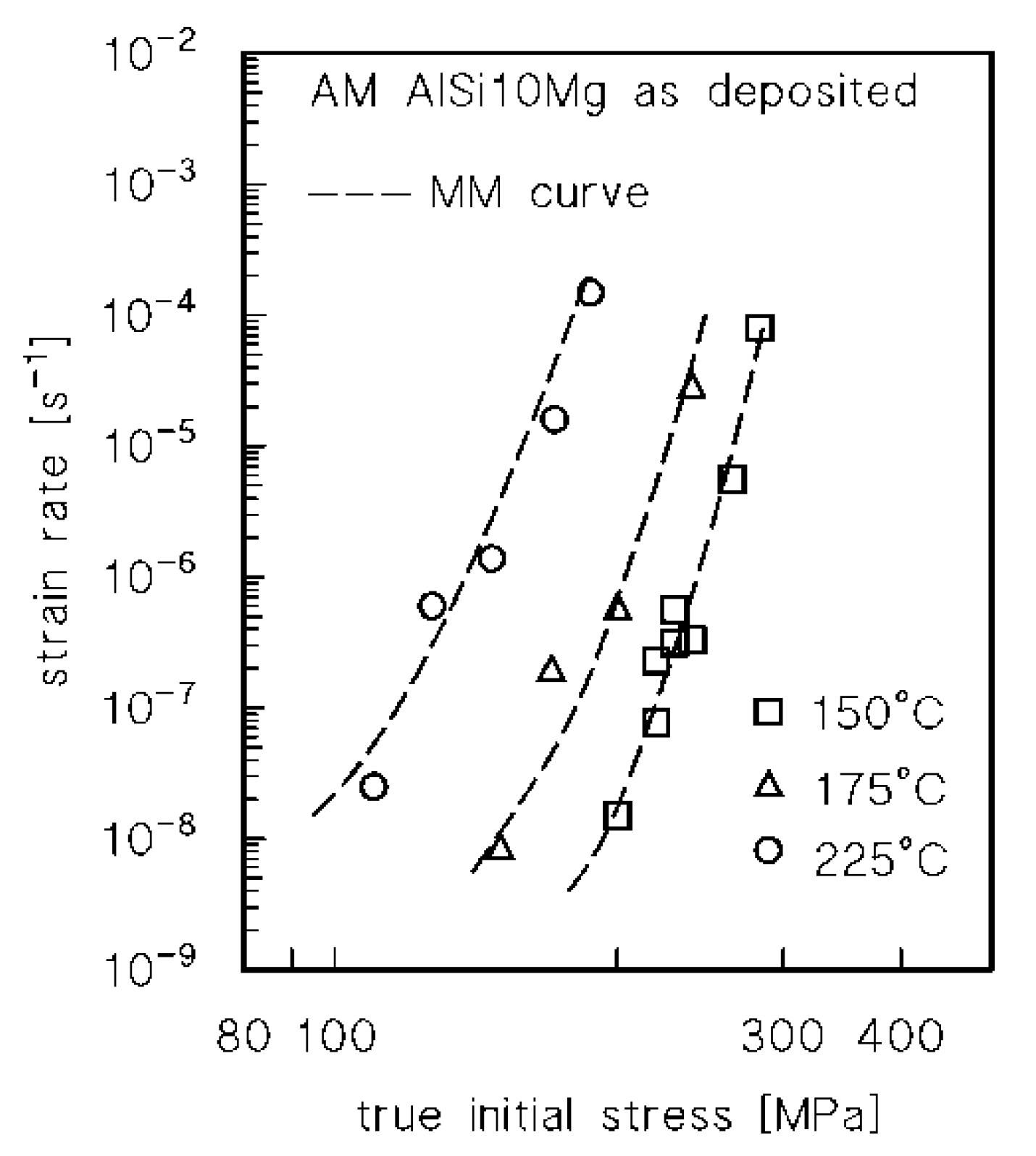
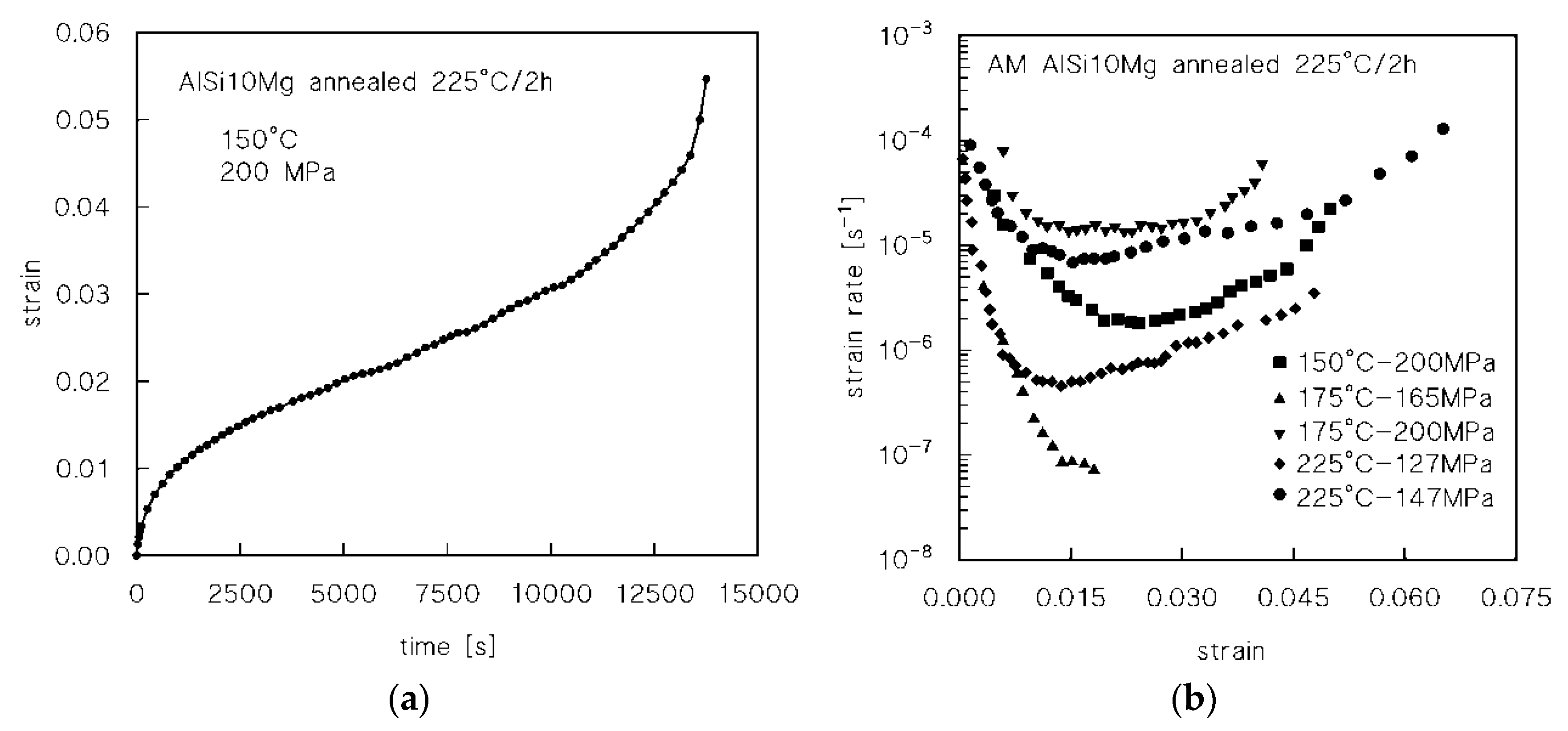
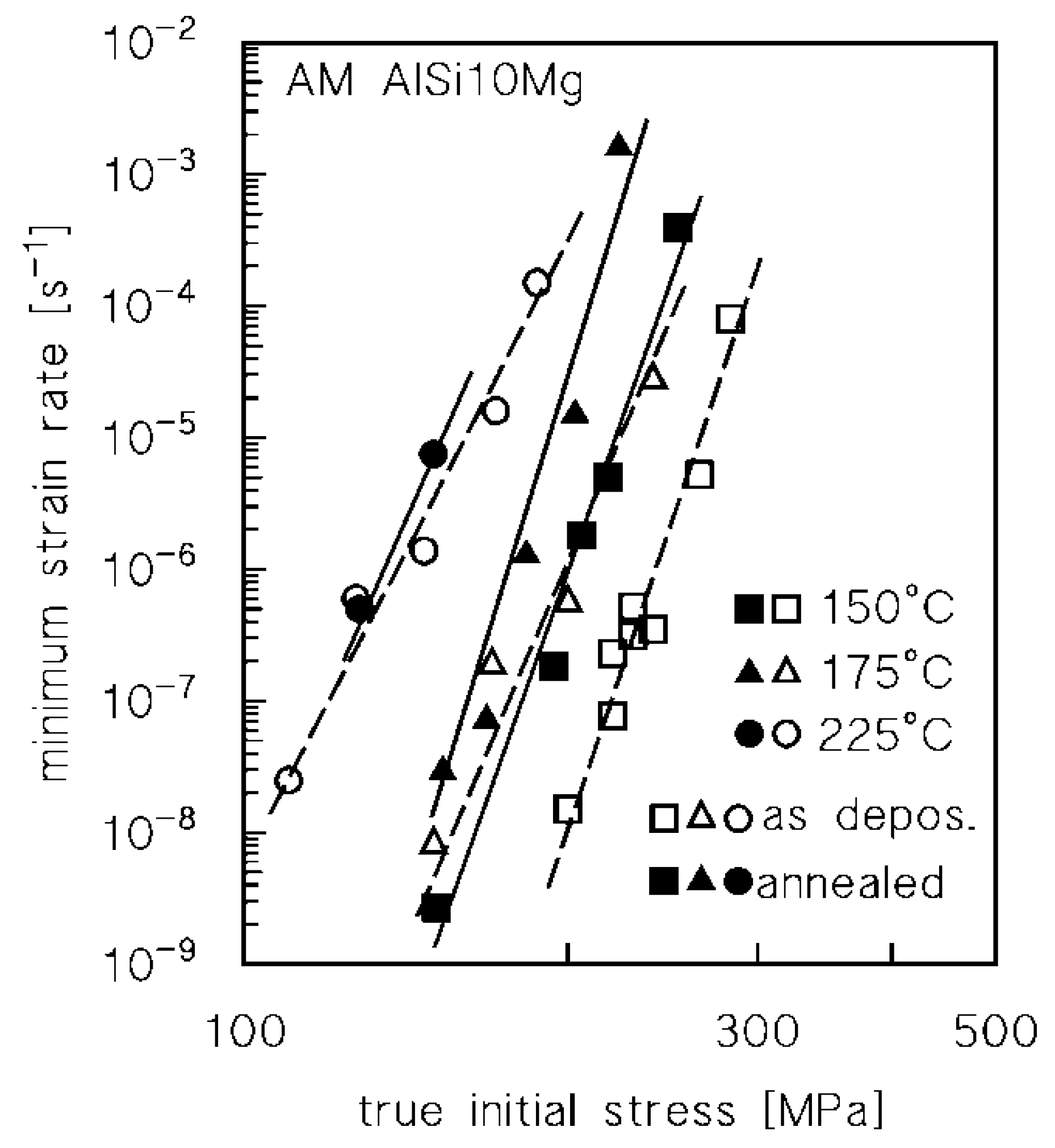
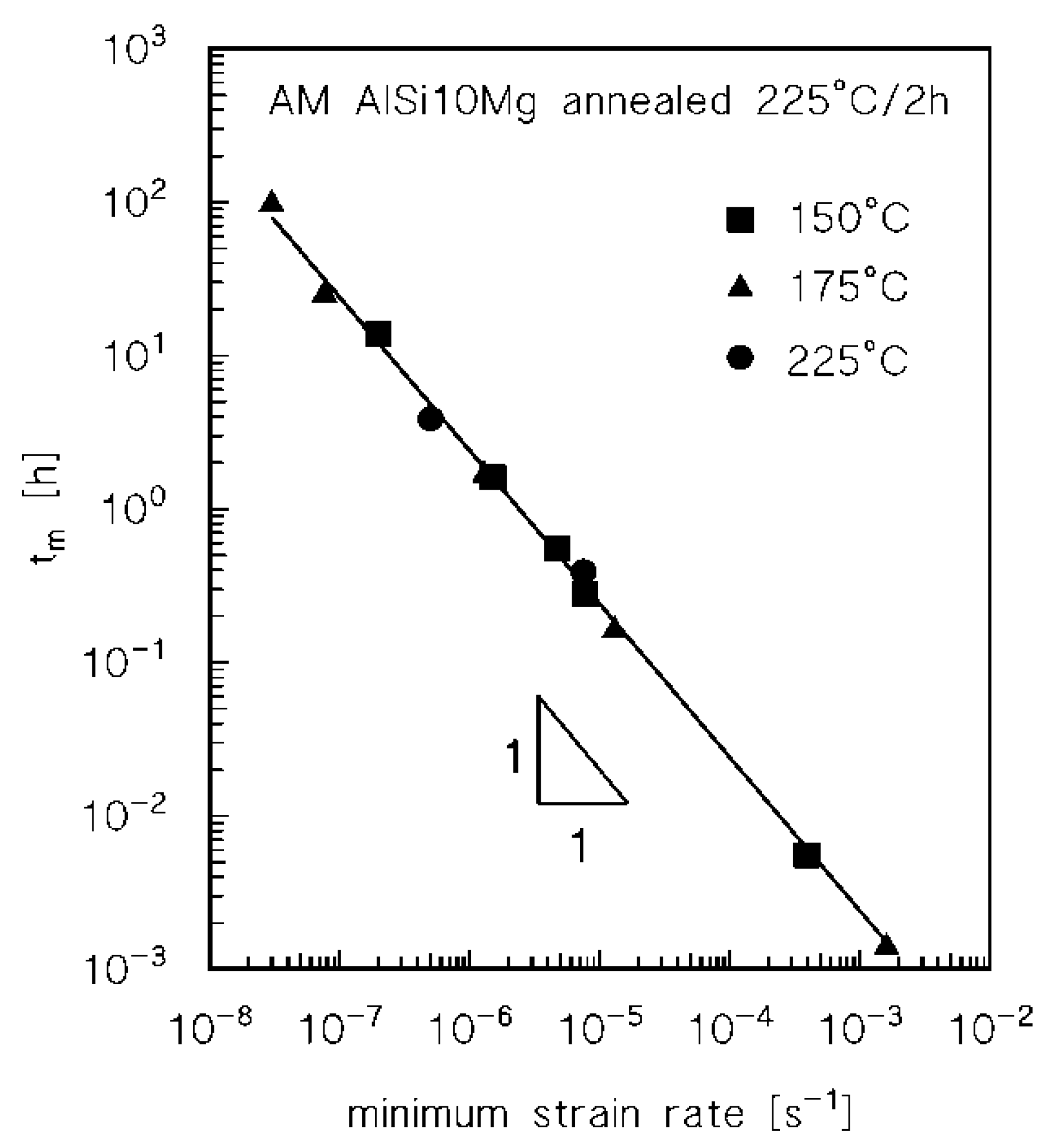
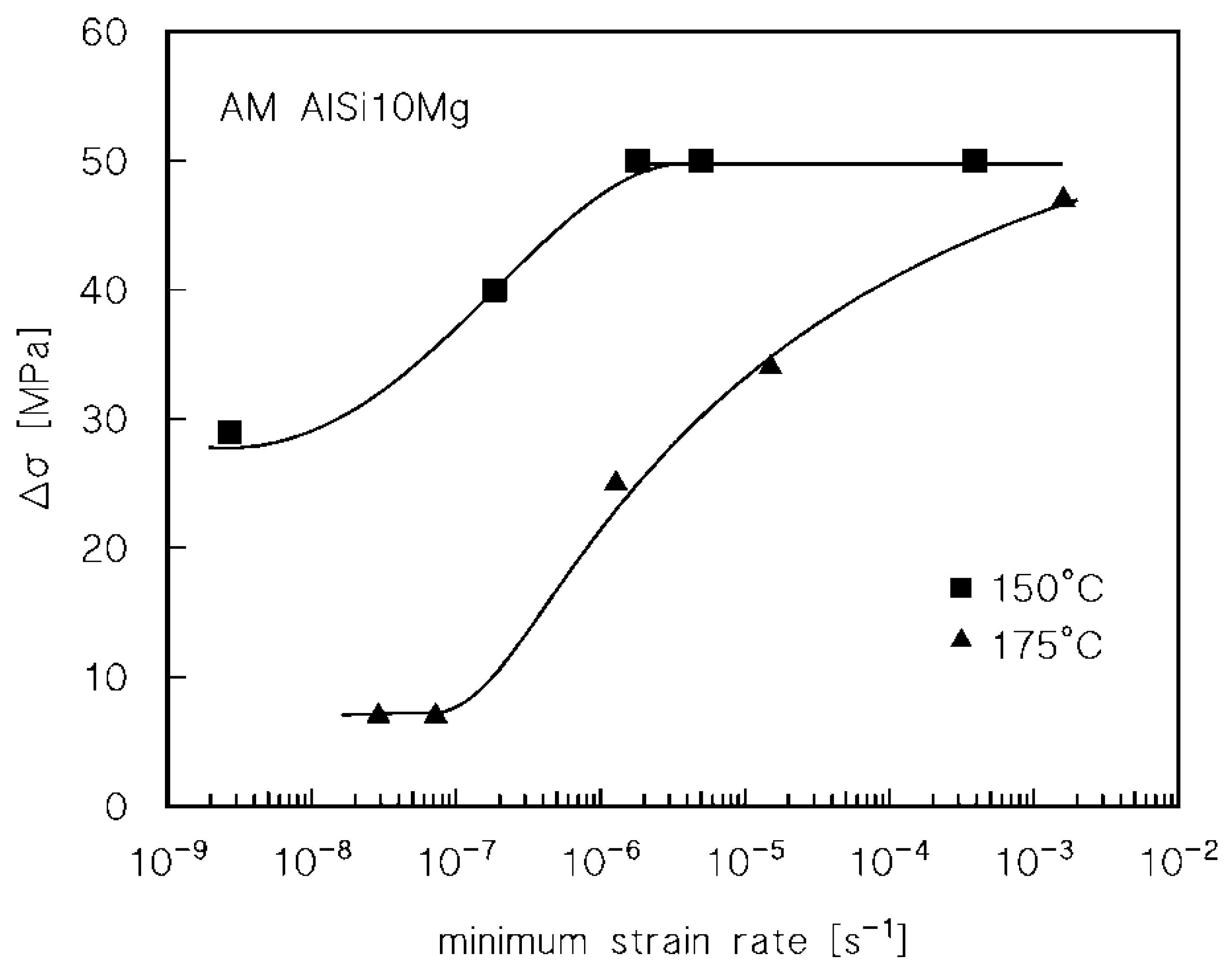
3. Results
4. Discussion
4.1. Analysis of the Effect of Low-Temperature Annealing on Creep Response
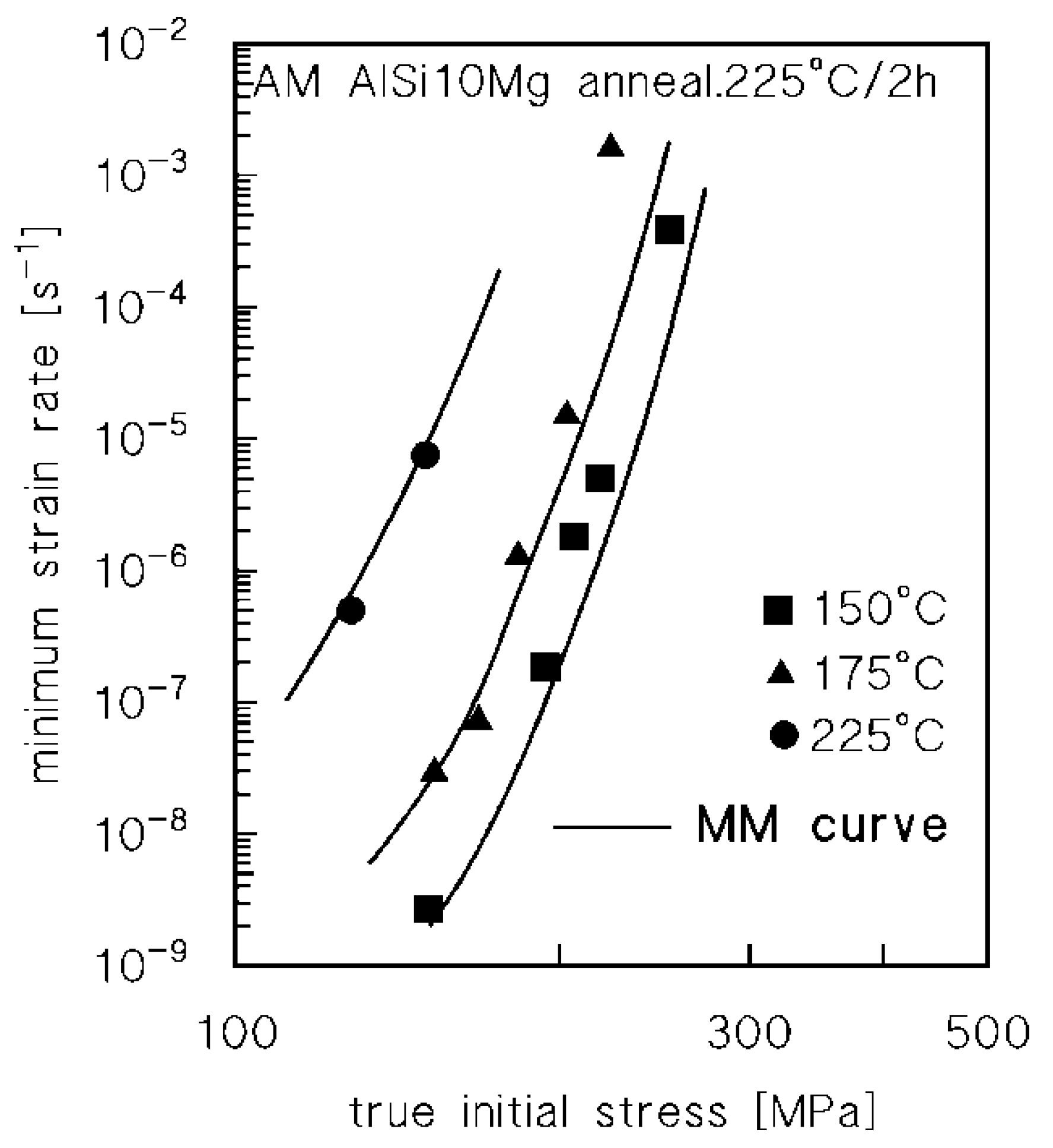
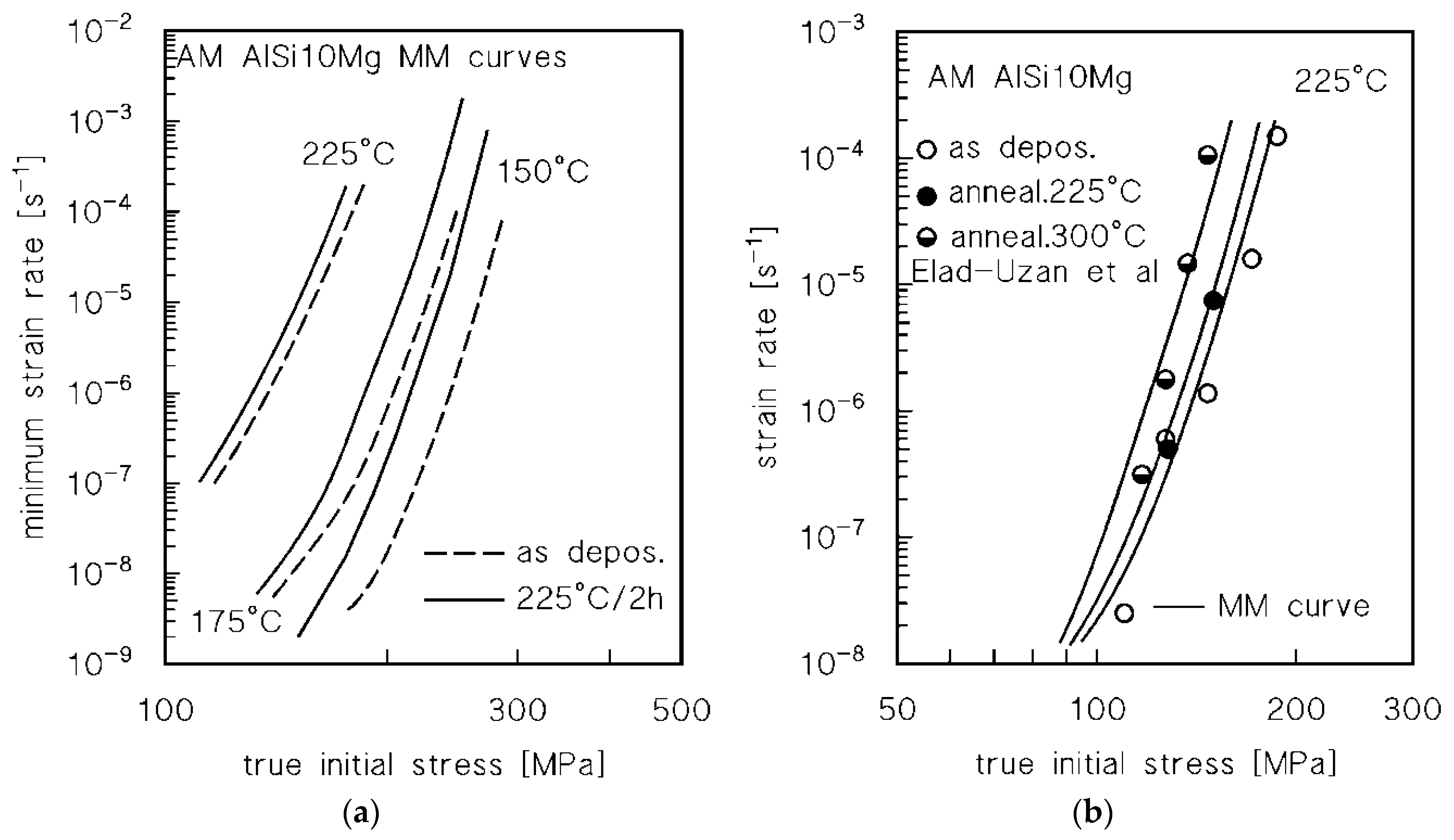
4.2. Modeling the Effect of Low-Temperature Annealing on Creep Response
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A


Appendix B
References
- Aboulkhair, N.T.; Simonelli, M.; Parry, L.; Ashcroft, I.; Tuck, C.; Hague, R. 3D printing of Aluminium alloys: Additive Manufacturing of Aluminium alloys using selective laser melting. Prog. Mater. Sci. 2019, 106, 100578. [Google Scholar] [CrossRef]
- Herzog, D.; Seyda, V.; Wycisk, E.; Emmelmann, C. Additive manufacturing of metals. Acta Mater. 2016, 117, 371–392. [Google Scholar] [CrossRef]
- Hebert, R.J. Viewpoint: Metallurgical aspects of powder bed metal additive manufacturing. J. Mater. Sci. 2016, 51, 1165–1175. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Rosenthal, I.; Shneck, R.; Stern, A. Heat treatment effect on the mechanical properties and fracture mechanism in AlSi10Mg fabricated by additive manufacturing selective laser melting process. Mater. Sci. Eng. A 2018, 729, 310–322. [Google Scholar] [CrossRef]
- Read, N.; Wang, W.; Essa, K.; Attallah, M.M. Selective laser melting of AlSi10Mg alloy: Process optimisation and mechanical properties development. Mater. Des. 2015, 65, 417–424. [Google Scholar] [CrossRef]
- Trevisan, F.; Calignano, F.; Lorusso, M.; Pakkanen, J.; Aversa, A.; Ambrosio, E.P.; Lombardi, M.; Fino, P.; Manfredi, D. On the selective laser melting (SLM) of the AlSi10Mg alloy: Process, microstructure, and mechanical properties. Materials 2017, 10, 76. [Google Scholar] [CrossRef]
- Wu, J.; Wang, X.Q.; Wang, W.; Attallah, M.M.; Loretto, M.H. Microstructure and strength of selectively laser melted AlSi10Mg. Acta Mater. 2016, 117, 311–320. [Google Scholar] [CrossRef]
- Takata, N.; Kodaira, H.; Suzuki, A.; Kobashi, M. Size dependence of microstructure of AlSi10Mg alloy fabricated by selective laser melting. Mater. Charact. 2018, 143, 18–26. [Google Scholar] [CrossRef]
- Fousová, M.; Dvorský, D.; Michalcová, A.; Vojtěch, D. Changes in the microstructure and mechanical properties of additively manufactured AlSi10Mg alloy after exposure to elevated temperatures. Mater. Charact. 2018, 137, 119–126. [Google Scholar] [CrossRef]
- Li, W.; Li, S.; Liu, J.; Zhang, A.; Zhou, Y.; Wei, Q.; Yan, C.; Shi, Y. Effect of heat treatment on AlSi10Mg alloy fabricated by selective laser melting: Microstructure evolution, mechanical properties and fracture mechanism. Mater. Sci. Eng. A 2016, 663, 116–125. [Google Scholar] [CrossRef]
- Uzan, N.E.; Shneck, R.; Yeheskel, O.; Frage, N. Fatigue of AlSi10Mg specimens fabricated by additive manufacturing selective laser melting (AM-SLM). Mater. Sci. Eng. A 2017, 704, 229–237. [Google Scholar] [CrossRef]
- Cerri, E.; Ghio, E. AlSi10Mg alloy produced by Selective Laser Melting: Relationships between Vickers microhardness, Rockwell hardness and mechanical properties. Metall. Ital. 2020, 7–8, 5–17. [Google Scholar]
- Paoletti, C.; Santecchia, E.; Cabibbo, M.; Cerri, E.; Spigarelli, S. Modelling the creep behavior of an AlSi10Mg alloy produced by additive manufacturing. Mater. Sci. Eng. A 2021, 140138. [Google Scholar] [CrossRef]
- Nix, W.D.; Ilschner, B. Mechanisms Controlling Creep of Single Phase Metals and Alloys; Haasen, P., Gerold, V., Kostorz, G., Eds.; Pergamon: Aachen, Germany, 1979; Volume 3, pp. 1503–1530. ISBN 978-1-4832-8412-5. [Google Scholar]
- Meier, M.; Blum, W. Modelling high temperature creep of academic and industrial materials using the composite model. Mater. Sci. Eng. A 1993, 164, 290–294. [Google Scholar] [CrossRef]
- Spigarelli, S. Constitutive equations in creep of Mg-Al alloys. Mater. Sci. Eng. A 2008, 492, 153–160. [Google Scholar] [CrossRef]
- Orowan, E. Dislocations in Metals; Cohen, M., Ed.; The Institute of Metals Division, the American Institute of Mining and Metallurgical Engineers: New York, NY, USA, 1954. [Google Scholar]
- Spigarelli, S.; Sandström, R. Basic creep modelling of Aluminium. Mater. Sci. Eng. A 2018, 711, 343–349. [Google Scholar] [CrossRef]
- Paoletti, C.; Regev, M.; Spigarelli, S. Modelling of creep in alloys strengthened by rod-shaped particles: Al-Cu-Mg age-hardenable alloys. Metals 2018, 8, 930. [Google Scholar] [CrossRef]
- Spigarelli, S.; Evangelista, E.; Cucchieri, S. Analysis of the creep response of an Al-17Si-4Cu-0.55Mg alloy. Mater. Sci. Eng. A 2004, 387–389, 702–705. [Google Scholar] [CrossRef]
- Uzan, N.E.; Shneck, R.; Yeheskel, O.; Frage, N. High-temperature mechanical properties of AlSi10Mg specimens fabricated by additive manufacturing using selective laser melting technologies (AM-SLM). Addit. Manuf. 2018, 24, 257–263. [Google Scholar] [CrossRef]
- Toschi, S. Optimization of a354 Al-Si-Cu-Mg alloy heat treatment: Effect on microstructure, hardness, and tensile properties of peak aged and overaged alloy. Metals 2018, 8, 961. [Google Scholar] [CrossRef]
- Salleh, M.S.; Omar, M.Z.; Syarif, J.; Alhawari, K.S.; Mohammed, M.N. Microstructure and mechanical properties of thixoformed A319 aluminium alloy. Mater. Des. 2014, 64, 142. [Google Scholar] [CrossRef]
- Buffington, F.S.; Cohen, M. Self-Diffusion in Alpha Iron Under Uniaxial Compressive Stress. JOM 1952, 4, 859–860. [Google Scholar] [CrossRef]
- Sandström, R. Basic model for primary and secondary creep in copper. Acta Mater. 2012, 60, 314–322. [Google Scholar] [CrossRef]
- Sandström, R. Influence of phosphorus on the tensile stress strain curves in copper. J. Nucl. Mater. 2016, 470, 290–296. [Google Scholar] [CrossRef]
- Sandström, R. The role of cell structure during creep of cold worked copper. Mater. Sci. Eng. A 2016, 674, 318–327. [Google Scholar] [CrossRef]
| Symbol | Meaning |
|---|---|
| σ | True applied stress (MPa) |
| Minimum creep rate (s−1) | |
| σ0 | Particle strengthening term (Orowan stress) (MPa) |
| α | Constant: 0.3 |
| m | Taylor factor: 3.06 |
| R | Gas constant: 8.314 (J mol−1K−1) |
| G | Shear modulus: 30,220–16 T (MPa) |
| b | Burgers vector: 2.47 × 10−10 (m) |
| ρ | Dislocation density (m−2) |
| σρ | Dislocation hardening term: =αmGbρ1/2 (MPa) |
| τl | Dislocation line tension: =0.5Gb2 (N) |
| Rmax | Maximum strength at the testing temperature [MPa) |
| k | Boltzmann constant = 1.38 × 10−23 (J K−1) |
| D0L | Pre-exponential factor in the Arrhenius equation describing the temperature dependence of the vacancy diffusion coefficient: 8.3 × 10−6 (m2s−1) [19] |
| QL | Activation energy in the Arrhenius equation describing the temperature dependence of the vacancy diffusion coefficient: 122 (kJ mol−1) [19] |
| Uss | Energy necessary for Si (and Mg) atoms still in solid solution to jump in and out of the atmospheres that spontaneously form around dislocations; previous calculations gave values close to 10–15 kJ mol−1 for Mg [20]. For the sake of simplicity, here Uss is assumed to be 10 (kJ mol−1) |
| RUTSa | Room temperature tensile strength of an alloy with the same impurity level, similar content of elements in solid solution and coarse intergranular intermetallics, in the absence of fine Si particles, here roughly estimated to be 115 (MPa) |
| L | Surface-to-surface interparticle spacing (m) |
| GT, GRT | Shear modulus at the testing temperature and at 25 °C, respectively (MPa) |
| Mcg | Temperature dependent dislocation mobility |
| d0 | Initial dimension of Si particles |
| dest | Experimental estimate of the size of Si particles at time t |
| dcalc | Calculated value of the size of Si particles at time t |
| σyi | Yield stress |
| σa | Yield stress of an alloy containing 0.5% Mg but no Si particles |
| σOri | Orowan stress in the i-region (i = H,S) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paoletti, C.; Cerri, E.; Ghio, E.; Santecchia, E.; Cabibbo, M.; Spigarelli, S. Effect of Low-Temperature Annealing on Creep Properties of AlSi10Mg Alloy Produced by Additive Manufacturing: Experiments and Modeling. Metals 2021, 11, 179. https://doi.org/10.3390/met11020179
Paoletti C, Cerri E, Ghio E, Santecchia E, Cabibbo M, Spigarelli S. Effect of Low-Temperature Annealing on Creep Properties of AlSi10Mg Alloy Produced by Additive Manufacturing: Experiments and Modeling. Metals. 2021; 11(2):179. https://doi.org/10.3390/met11020179
Chicago/Turabian StylePaoletti, Chiara, Emanuela Cerri, Emanuele Ghio, Eleonora Santecchia, Marcello Cabibbo, and Stefano Spigarelli. 2021. "Effect of Low-Temperature Annealing on Creep Properties of AlSi10Mg Alloy Produced by Additive Manufacturing: Experiments and Modeling" Metals 11, no. 2: 179. https://doi.org/10.3390/met11020179
APA StylePaoletti, C., Cerri, E., Ghio, E., Santecchia, E., Cabibbo, M., & Spigarelli, S. (2021). Effect of Low-Temperature Annealing on Creep Properties of AlSi10Mg Alloy Produced by Additive Manufacturing: Experiments and Modeling. Metals, 11(2), 179. https://doi.org/10.3390/met11020179










