Experimental and Numerical Investigations of In Situ Alloying during Powder Bed Fusion of Metals Using a Laser Beam
Abstract
:1. Introduction and State of the Art
1.1. Problem Statement
1.2. Approach
2. Numerical Modeling of the In Situ Alloying
Alloy Species Transport
3. Experiments
3.1. Experimental Setup
3.1.1. Calibration of the Thermographic Imaging System
3.1.2. Experimental Approach
3.2. Simulation Setup
4. Results and Discussion
5. Conclusions and Outlook
- The powder blends consisting of 316L and AlSi10Mg were successfully simplified with an Fe-Al system using curve-fitted material parameters.
- The simulation results were validated with a novel experimental setup. High-speed thermographic imaging provided validation data of the melt pool cross-section on a small spatial scale. The global validation quantity was the melt pool length. For both simulation and experiment, the same trend of increasing melt pool dimensions with higher amounts of additives was found.
- The simulation results show a good agreement with the experimental SEM-EDS results for the concentration profile of a single AlSi10Mg powder particle.
- The presented framework is a suitable basis for the simulation of in situ alloying during PBF-LB/M.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| 316L | Property | Temperature Range | Value | Units | References |
|---|---|---|---|---|---|
| Solidus temperature | − | 1633 | K | [42] | |
| Liquidus temperature | − | 1683 | K | [42] | |
| Boiling temperature | − | 3073 | K | [43] | |
| k | Thermal conductivity | [44] | |||
| [44] | |||||
| [44] | |||||
| H | Specific enthalpy | [45] | |||
| −374,150.00 + | [45] | ||||
| −8,181,263.00 + | [45] | ||||
| −336,177.97 + | [45] | ||||
| c | Specific heat capacity | 492 | [42] | ||
| 736 | [42] | ||||
| Dynamic viscosity | [46] | ||||
| Surface tension coefficient | 1.82 | [47] | |||
| [47] | |||||
| M | Molar mass | - | |||
| a | Absorptivity | 0.4 | − | [43] |
| AlSi10Mg | Property | Temperature Range | Value | Units | References |
|---|---|---|---|---|---|
| Solidus temperature | − | 816 | K | [48] | |
| Liquidus temperature | − | 853 | K | [48] | |
| Boiling temperature | − | 2737 | K | [49] | |
| k | Thermal conductivity | 155 | [50] | ||
| 120 | [51] | ||||
| H | Specific enthalpy | − 230,136.36 + | [42] | ||
| −8,243,682.40 + | [42] | ||||
| 140,209.01 + | [42] | ||||
| c | Specific heat capacity | 920 | [52] | ||
| 1050 | [51] | ||||
| Dynamic viscosity | [53] | ||||
| Surface tension coefficient | 0.88 | [54] | |||
| M | Molar mass | - | |||
| a | Absorptivity | 0.09 | − | [55] |
References
- Wohlers, T.; Campbell, I.; Diegel, O.; Huff, R.; Kowen, J. Wohlers Report 2020: 3D Printing and Additive Manufacturing State of the Industry; Wohlers Associates: Fort Collins, CO, USA, 2020. [Google Scholar]
- Duan, R.; Li, S.; Cai, B.; Tao, Z.; Zhu, W.; Ren, F.; Attallah, M. In situ alloying based laser powder bed fusion processing of βTi–Mo alloy to fabricate functionally graded composites. Compos. Part B Eng. 2021, 222, 109059. [Google Scholar] [CrossRef]
- Gorsse, S.; Hutchinson, C.; Gouné, M.; Banerjee, R. Additive manufacturing of metals: A brief review of the characteristic microstructures and properties of steels, Ti-6Al-4V and high-entropy alloys. Sci. Technol. Adv. Mater. 2017, 18, 584–610. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.; Fezzaa, K.; Cunningham, R.W.; Wen, H.; de Carlo, F.; Chen, L.; Rollett, A.D.; Sun, T. Real-time monitoring of laser powder bed fusion process using high-speed X-ray imaging and diffraction. Sci. Rep. 2017, 7, 3602. [Google Scholar] [CrossRef]
- Martin, A.A.; Calta, N.P.; Hammons, J.A.; Khairallah, S.A.; Nielsen, M.H.; Shuttlesworth, R.M.; Sinclair, N.; Matthews, M.J.; Jeffries, J.R.; Willey, T.M.; et al. Ultrafast dynamics of laser-metal interactions in additive manufacturing alloys captured by in situ X-ray imaging. Mater. Today Adv. 2019, 1, 100002. [Google Scholar] [CrossRef]
- Montero-Sistiaga, M.L.; Mertens, R.; Vrancken, B.; Wang, X.; Van Hooreweder, B.; Kruth, J.P.; Van Humbeeck, J. Changing the alloy composition of Al7075 for better processability by selective laser melting. J. Mater. Process. Technol. 2016, 238, 437–445. [Google Scholar] [CrossRef]
- Wimmer, A.; Kolb, C.G.; Assi, M.; Favre, J.; Bachmann, A.; Fraczkiewicz, A.; Zaeh, M.F. Investigations on the influence of adapted metal-based alloys on the process of laser beam melting. J. Laser Appl. 2020, 32, 022029. [Google Scholar] [CrossRef]
- Keene, B.J. Review of data for the surface tension of pure metals. Int. Mater. Rev. 1993, 38, 157–192. [Google Scholar] [CrossRef]
- Labudovic, M.; Hu, D.; Kovacevic, R. A three dimensional model for direct laser metal powder deposition and rapid prototyping. Journal of materials science. J. Mater. Sci. 2003, 38, 35–49. [Google Scholar] [CrossRef]
- Wimmer, A.; Hofstaetter, F.; Jugert, C.; Wudy, K.; Zaeh, M.F. In situ alloying: Investigation of the melt pool stability during powder bed fusion of metals using a laser beam in a novel experimental set-up. Prog. Addit. Manuf. 2021, 1–9. [Google Scholar] [CrossRef]
- Sun, Z.; Chueh, Y.H.; Li, L. Multiphase mesoscopic simulation of multiple and functionally gradient materials laser powder bed fusion additive manufacturing processes. Addit. Manuf. 2020, 35, 101448. [Google Scholar] [CrossRef]
- Otto, A.; Koch, H.; Leitz, K.H.; Schmidt, M. Numerical Simulations - A Versatile Approach for Better Understanding Dynamics in Laser Material Processing. Phys. Procedia 2011, 12, 11–20. [Google Scholar] [CrossRef] [Green Version]
- Koch, H.; Leitz, K.H.; Otto, A.; Schmidt, M. Laser deep penetration welding simulation based on a wavelength dependent absorption model. Phys. Procedia 2010, 5, 309–315. [Google Scholar] [CrossRef] [Green Version]
- Gürtler, F.J.; Karg, M.; Leitz, K.H.; Schmidt, M. Simulation of Laser Beam Melting of Steel Powders using the Three-Dimensional Volume of Fluid Method. Phys. Procedia 2013, 41, 881–886. [Google Scholar] [CrossRef] [Green Version]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013. [Google Scholar] [CrossRef]
- Ye, T.; Pan, D.; Huang, C.; Liu, M. Smoothed particle hydrodynamics (SPH) for complex fluid flows: Recent developments in methodology and applications. Phys. Fluids 2019, 31, 011301. [Google Scholar]
- Incardona, P.; Leo, A.; Zaluzhnyi, Y.; Ramaswamy, R.; Sbalzarini, I.F. OpenFPM: A scalable open framework for particle and particle-mesh codes on parallel computers. Comput. Phys. Commun. 2019, 241, 155–177. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Crespo, A.J.; Gómez-Gesteira, M. Optimization strategies for CPU and GPU implementations of a smoothed particle hydrodynamics method. Comput. Phys. Commun. 2013, 184, 617–627. [Google Scholar] [CrossRef]
- Russell, M.A.; Souto-Iglesias, A.; Zohdi, T.I. Numerical simulation of Laser Fusion Additive Manufacturing processes using the SPH method. Comput. Methods Appl. Mech. Eng. 2018, 341, 163–187. [Google Scholar] [CrossRef]
- Weirather, J.; Rozov, V.; Wille, M.; Schuler, P.; Seidel, C.; Adams, N.A.; Zaeh, M.F. A Smoothed Particle Hydrodynamics Model for Laser Beam Melting of Ni-based Alloy 718. Comput. Math. Appl. 2019, 78, 2377–2394. [Google Scholar] [CrossRef]
- Tong, M.; Browne, D.J. An incompressible multi-phase smoothed particle hydrodynamics (SPH) method for modelling thermocapillary flow. Int. J. Heat Mass Transf. 2014, 73, 284–292. [Google Scholar] [CrossRef]
- Hu, X.; Adams, N. A constant-density approach for incompressible multi-phase SPH. J. Comput. Phys. 2009, 228, 2082–2091. [Google Scholar] [CrossRef]
- Sun, P.; Colagrossi, A.; Marrone, S.; Zhang, A. The δplus-SPH model: Simple procedures for a further improvement of the SPH scheme. Comput. Methods Appl. Mech. Eng. 2017, 315, 25–49. [Google Scholar] [CrossRef]
- Hu, X.Y.; Adams, N.A. A multi-phase SPH method for macroscopic and mesoscopic flows. J. Comput. Phys. 2006, 213, 844–861. [Google Scholar] [CrossRef]
- Adami, S.; Hu, X.Y.; Adams, N.A. A transport-velocity formulation for smoothed particle hydrodynamics. J. Comput. Phys. 2013, 241, 292–307. [Google Scholar] [CrossRef]
- Cleary, P.W.; Prakash, M.; Ha, J. Novel applications of smoothed particle hydrodynamics (SPH) in metal forming. J. Mater. Process. Technol. 2006, 177, 41–48. [Google Scholar] [CrossRef]
- Cleary, P.W. Extension of SPH to predict feeding, freezing and defect creation in low pressure die casting. Appl. Math. Model. 2010, 34, 3189–3201. [Google Scholar] [CrossRef]
- Adami, S.; Hu, X.; Adams, N. A generalized wall boundary condition for smoothed particle hydrodynamics. J. Comput. Phys. 2012, 231, 7057–7075. [Google Scholar] [CrossRef]
- Valizadeh, A.; Monaghan, J.J. A study of solid wall models for weakly compressible SPH. J. Comput. Phys. 2015, 300, 5–19. [Google Scholar] [CrossRef]
- Adami, S.; Hu, X.Y.; Adams, N.A. A conservative SPH method for surfactant dynamics. J. Comput. Phys. 2010, 229, 1909–1926. [Google Scholar] [CrossRef]
- Cleary, P.W.; Monaghan, J.J. Conduction Modelling Using Smoothed Particle Hydrodynamics. J. Comput. Phys. 1999, 148, 227–264. [Google Scholar] [CrossRef]
- Balogh, Z.; Schmitz, G. Diffusion in Metals and Alloys. In Physical Metallurgy; Elsevier: Amsterdam, The Netherlands, 2014; pp. 387–559. [Google Scholar] [CrossRef]
- Fick, A. Ueber Diffusion. Ann. Der Phys. Und Chem. 1855, 170, 59–86. [Google Scholar] [CrossRef]
- Aristodemo, F.; Federico, I.; Veltri, P.; Panizzo, A. Two-phase SPH modelling of advective diffusion processes. Environ. Fluid Mech. 2010, 10, 451–470. [Google Scholar] [CrossRef]
- Morris, J.P.; Fox, P.J.; Zhu, Y. Modeling Low Reynolds Number Incompressible Flows Using SPH. J. Comput. Phys. 1997, 136, 214–226. [Google Scholar] [CrossRef]
- Oikawa, H. Review on Lattice Diffusion of Substitutional Impurities in Iron. A Summary Report. 1982. Available online: http://inaba.nims.go.jp/diff/DIF_Oikawa/Table.html (accessed on 10 October 2021).
- Bruna-Rosso, C.; Demir, A.G.; Previtali, B. Selective laser melting finite element modeling: Validation with high-speed imaging and lack of fusion defects prediction. Mater. Des. 2018, 156, 143–153. [Google Scholar] [CrossRef] [Green Version]
- Khairallah, S.; Anderson, A. Mesoscopic simulation model of selective laser melting of stainless steel powder. J. Mater. Process. Technol. 2014, 214, 2627–2636. [Google Scholar] [CrossRef]
- Wimmer, A.; Lehmann, M.; Schuler, A.; Zaeh, M.F. Analysis of the phase transformation of AlSi10Mg during Laser Powder Bed Fusion. Procedia CIRP 2020, 94, 177–181. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, Y.; Chen, J. Numerical simulation of random packing of spherical particles for powder-based additive manufacturing. J. Manuf. Sci. Eng. 2009, 131, 031004. [Google Scholar] [CrossRef]
- Mills, K.C. Recommended Values of Thermophysical Properties for Selected Commercial Alloys; Woodhead: Cambridge, UK, 2002. [Google Scholar]
- Trapp, J.; Rubenchik, A.M.; Guss, G.; Matthews, M.J. In situ absorptivity measurements of metallic powders during laser powder-bed fusion additive manufacturing. Appl. Mater. Today 2017, 9, 341–349. [Google Scholar] [CrossRef]
- Valencia, J.J.; Quested, P.N. Thermophysical Properties. In Metals Process Simulation; ASM International: Almere, The Netherland, 2010. [Google Scholar] [CrossRef] [Green Version]
- Pichler, P.; Simonds, B.J.; Sowards, J.W.; Pottlacher, G. Measurements of thermophysical properties of solid and liquid NIST SRM 316L stainless steel. J. Mater. Sci. 2020, 55, 4081–4093. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, C.S. Thermophysical Properties of Stainless Steels; Argonne National Lab.: Lemont, IL, USA, 1975. [Google Scholar] [CrossRef]
- Fukuyama, H.; Higashi, H.; Yamano, H. Thermophysical Properties of Molten Stainless Steel Containing 5 mass % B4C. Nucl. Technol. 2019, 205, 1154–1163. [Google Scholar] [CrossRef] [Green Version]
- Vončina, M.; Mrvar, P.; Medved, J. Thermodynamic Analysis of AlSi10Mg Alloy. Mater. Geoenviron. 2006, 52, 621–633. [Google Scholar]
- Renishaw plc. Aluminium Powder ALSi10Mg—Safety Data Sheet (SDS); Tech. Rep; Renishaw plc: Gloucestershire, UK, 2018. [Google Scholar]
- Li, Y.; Gu, D. Parametric analysis of thermal behavior during selective laser melting additive manufacturing of aluminum alloy powder. Mater. Des. 2014, 63, 856–867. [Google Scholar] [CrossRef]
- Wei, P.; Wei, Z.; Chen, Z.; He, Y.; Du, J. Thermal behavior in single track during selective laser melting of AlSi10Mg powder. Appl. Phys. A 2017, 123, 1–13. [Google Scholar] [CrossRef]
- EOS. EOS Aluminium AlSi10Mg—Material Data Sheet; Tech. Rep.; EOS GmbH-Electro Optical Systems: Bavaria, Germany, 2014. [Google Scholar]
- Paradis, P.F.; Ishikawa, T. Surface Tension and Viscosity Measurements of Liquid and Undercooled Alumina by Containerless Techniques. Jpn. J. Appl. Phys. 2005, 44, 5082–5085. [Google Scholar] [CrossRef]
- Chen, L.; Li, H.; Liu, S.; Shen, S.; Zhang, T.; Huang, Y.; Zhang, G.; Zhang, Y.; He, B.; Yang, C. Simulation of surface deformation control during selective laser melting of AlSi10Mg powder using an external magnetic field. AIP Adv. 2019, 9, 045012. [Google Scholar] [CrossRef]
- Louvis, E.; Fox, P.; Sutcliffe, C.J. Selective laser melting of aluminium components. J. Mater. Process. Technol. 2011, 211, 275–284. [Google Scholar] [CrossRef]
- Fürstenau, J.P.; Wessels, H.; Weißenfels, C.; Wriggers, P. Generating virtual process maps of SLM using powder-scale SPH simulations. Comput. Part. Mech. 2019, 7, 655–677. [Google Scholar] [CrossRef]
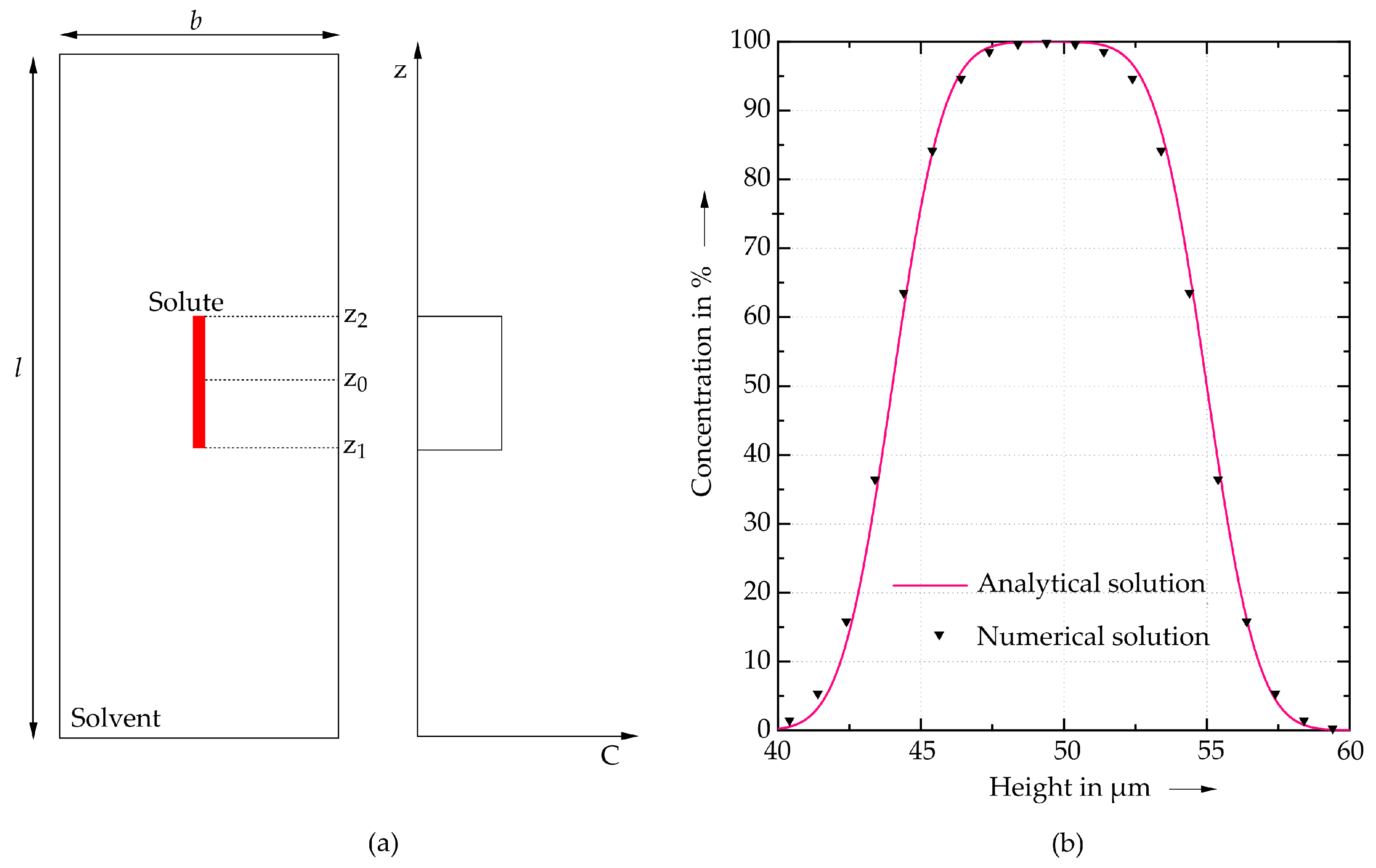


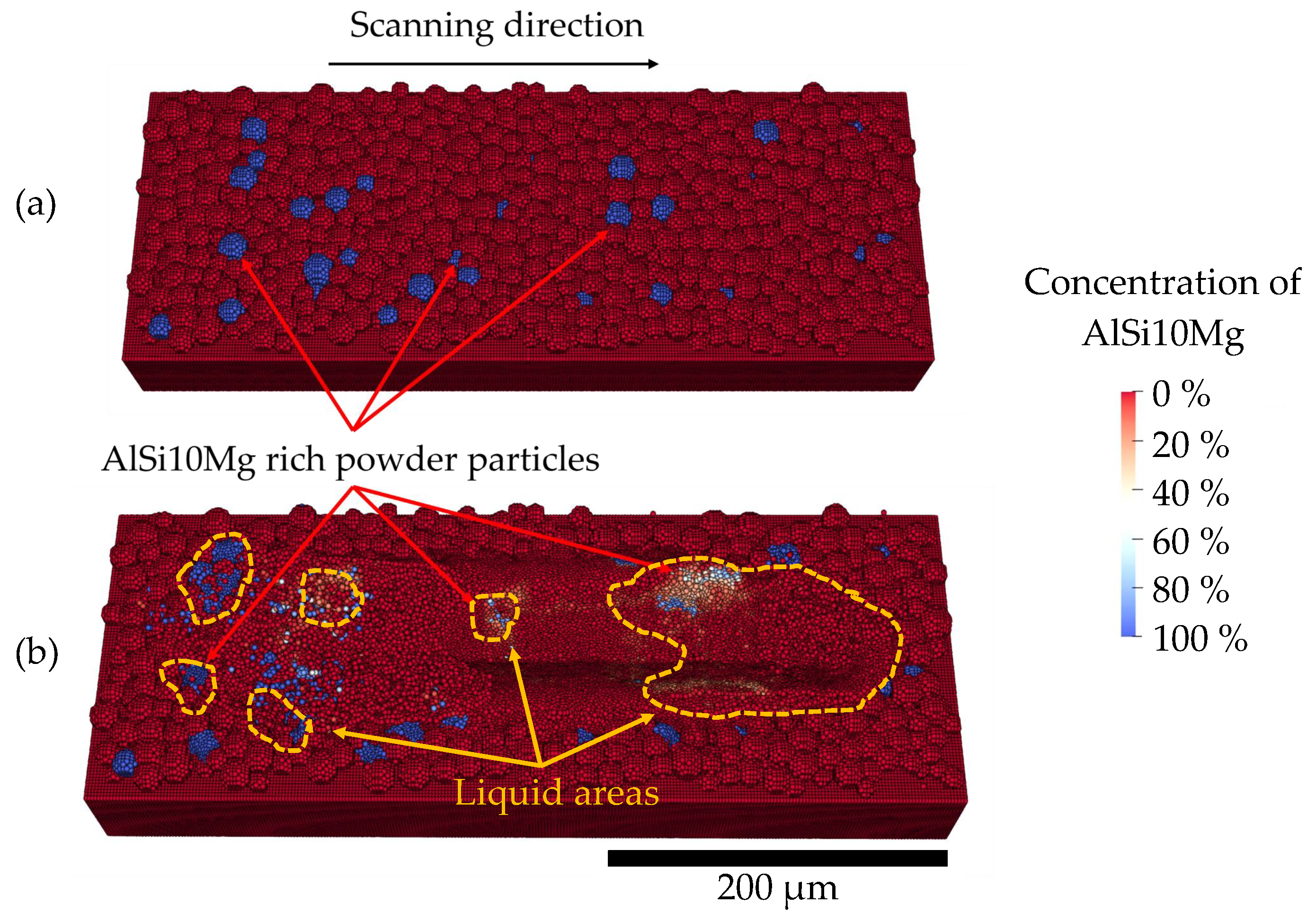
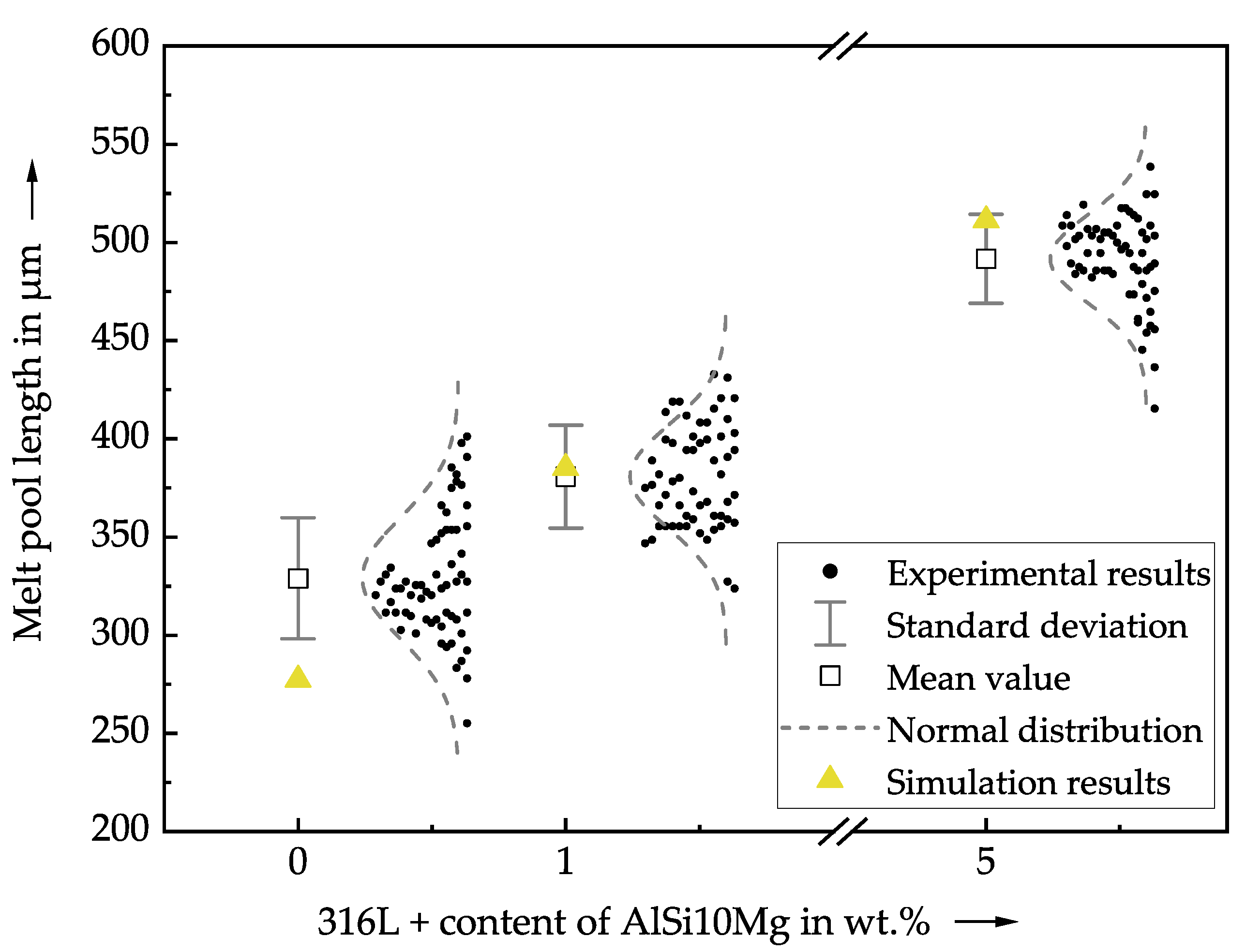

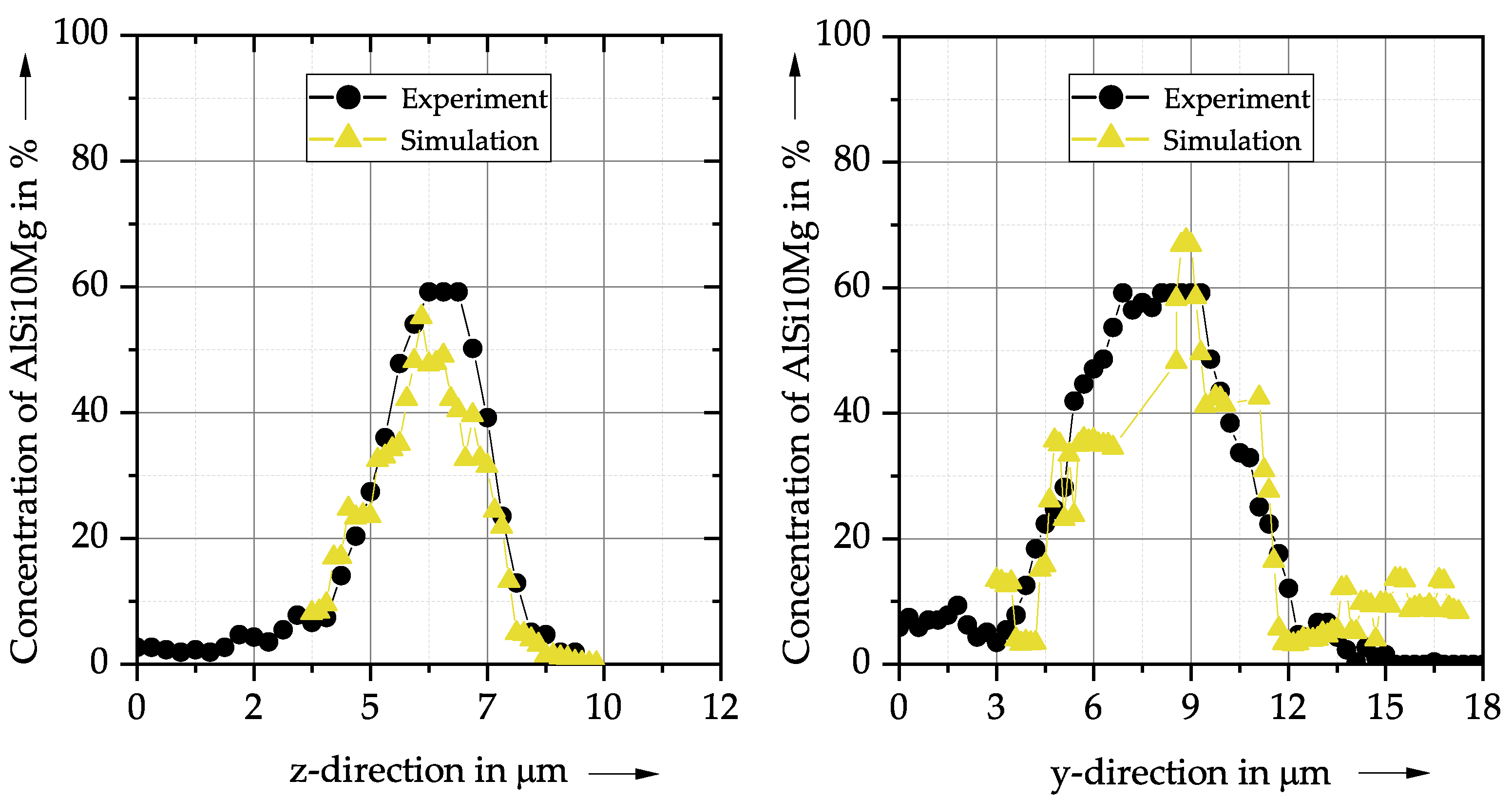
| Symbol | Property | Value | Unit |
|---|---|---|---|
| l | Height of the domain (z-direction) | 100 | µm |
| b | Width of the domain (x-direction) | 40 | µm |
| Position of the stripe in x-direction | 20 | µm | |
| Position of the stripe in z-direction | 44 | µm | |
| Position of the stripe in z-direction | 55 | µm | |
| Solute concentration | 100 | % | |
| Solvent concentration | 0 | % | |
| Solute density | 1000 | ||
| Solvent density | 1000 | ||
| Diffusivity | |||
| Particle size | 1 | µm |
| Symbol | Property | Value | Unit |
|---|---|---|---|
| d | Powder layer thickness | 20 | µm |
| - | Amount of AlSi10Mg additives in the powder blend | 0 | wt.% |
| 1 | wt.% | ||
| 5 | wt.% | ||
| P | Laser power | 175 | |
| r | Laser beam radius | 40 | µm |
| Laser beam velocity | 0.375 |
| Symbol | Property | Value | Unit |
|---|---|---|---|
| Reference density | 7763 | kg/m | |
| - | Kernel type | Quintic spline | - |
| Particle spacing | 2.0 | µm | |
| g | Gravity | 9.81 | m/s |
| t | Exposure time ( = 0.375 m/s) | s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wimmer, A.; Yalvac, B.; Zoeller, C.; Hofstaetter, F.; Adami, S.; Adams, N.A.; Zaeh, M.F. Experimental and Numerical Investigations of In Situ Alloying during Powder Bed Fusion of Metals Using a Laser Beam. Metals 2021, 11, 1842. https://doi.org/10.3390/met11111842
Wimmer A, Yalvac B, Zoeller C, Hofstaetter F, Adami S, Adams NA, Zaeh MF. Experimental and Numerical Investigations of In Situ Alloying during Powder Bed Fusion of Metals Using a Laser Beam. Metals. 2021; 11(11):1842. https://doi.org/10.3390/met11111842
Chicago/Turabian StyleWimmer, Andreas, Baturay Yalvac, Christopher Zoeller, Fabian Hofstaetter, Stefan Adami, Nikolaus A. Adams, and Michael F. Zaeh. 2021. "Experimental and Numerical Investigations of In Situ Alloying during Powder Bed Fusion of Metals Using a Laser Beam" Metals 11, no. 11: 1842. https://doi.org/10.3390/met11111842
APA StyleWimmer, A., Yalvac, B., Zoeller, C., Hofstaetter, F., Adami, S., Adams, N. A., & Zaeh, M. F. (2021). Experimental and Numerical Investigations of In Situ Alloying during Powder Bed Fusion of Metals Using a Laser Beam. Metals, 11(11), 1842. https://doi.org/10.3390/met11111842






