Abstract
A model-based system for real-time monitoring and operational support has been developed for the Composition Adjustment by Sealed argon-bubbling with Oxygen Blowing (CAS-OB) process. The model of the system is based on a previously developed dynamic model using first principles, i.e., mass and energy balances, reaction kinetics, and thermodynamics. Adaptive estimation of state variables has been implemented using a Kalman filter to ensure that the model is able to correct for deviations between measured and calculated temperatures in real-time operation. The estimation technique reduces the standard deviation of the predicted end temperature from 19.5 °C to 5.5 °C in a data series with more than 1000 heats. The system also includes an endpoint optimisation, which calculates the amount of scrap or oxygen to be added to achieve the target temperature at the end of the heat. The model has been implemented in the Cybernetica® CENIT™ framework. The overall model can be regarded as a hybrid digital twin, where a first principles model is adapted in real time using process measurements. The system also includes user interfaces for operators where process predictions can be followed, and suggested optimised inputs are presented. The system has been deployed at two refining stations at SSAB Europe OY in Raahe, Finland. The optimized suggestions for oxygen and scrap are presented to the operators in the graphical user interface. A projected temperature profile is calculated into the near future using the planned operational procedure as well as the projected temperature profile using optimised inputs. Both profiles are displayed in the user interface. Based on these trajectories, the operator can decide on whether to follow the nominal trajectory, or the recommendation from the optimisation This will help the operators make better decisions, which in turn reduces the number of rejected heats in the CAS-OB process.
1. Introduction
Composition Adjustment by Sealed argon-bubbling with Oxygen Blowing (CAS-OB) is a secondary steelmaking process step used for alloying and temperature control. The CAS-OB-process was developed by Nippon Steel Corporation to improve on existing refining and alloying stations. The CAS-OB process provides a buffer station in the secondary steelmaking area where chemical composition and steel temperature can be adjusted as well as homogenized in a controlled manner.
The main component of the CAS-OB design is a refractory lined ladle with a porous plug for gas bubbling in the bottom. The operation of the process is accomplished through the use of three items: (1) a refractory bell on top of the ladle, which can be used to contain an inert atmosphere of argon or the chemical reaction between oxygen and aluminium, (2) supply of argon gas, and (3) a water-cooled oxygen lance. These functional items form the heart of the process (Figure 1).
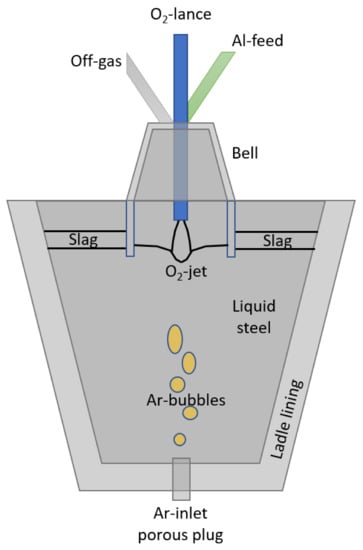
Figure 1.
Illustration of the CAS-OB process.
Molten steel from a primary steelmaking process (Basic Oxygen Furnace, BOF) is initially poured into a ladle. The ladle consists of a steel casing with a refractory brick layer on the inside. The refractory layer provides insulation and is resistant to the corrosive environment of the steel bath, having a high temperature of around 1600 °C. During treatment, steel components will react with added oxygen to form a slag phase. Additions in form of oxides will also dissolve into the slag phase. Typical slag components are FeO, SiO, MgO, AlO, and CaO. In the CAS-OB-process, the slag phase takes part in the reactions and protects the molten steel from the atmosphere and works as an insulating layer.
The CAS-OB process is designed to create an inert atmosphere above the steel to allow the addition of alloys without contact with atmospheric oxygen or an oxide slag. This is accomplished by first creating a slag free area (known as an eye) at the surface of the molten steel by the introduction of argon into the steel through a porous plug at the bottom of the ladle. Argon bubbles reaching the surface of the steel push aside the slag layer on top of the ladle, creating a slag free area. The amount of argon flow required to produce the required size of eye on top of the ladle varies with the condition of the porous plug, the depth of slag on top of the ladle, and the fluidity of the slag. Once the eye is created, the refractory bell can be lowered into the slag free area.
The bell provides a protected environment for adding alloying materials, where the steel surface is open, but still protected from contact with the surrounding atmosphere. This also ensures that the amount of absorbed nitrogen can be kept at a low level. The argon bubbling also provides stirring for homogenizing temperature and composition of the steel [1,2,3,4].
2. Materials and Methods
The numerical model used for describing the dynamic behaviour of the CAS-OB process is based on previous work by Rotevatn et al. [5] and Järvinen [2]. In recent years, CAS-OB model updates have have been reported by Sulasalmi et al. [6], Visuri et al. [7], and Kärnä et al. [8]. The latter have done a comprehensive work on utilizing computational fluid dynamics (CFD) calculations to develop an improved model of the CAS-OB. Industrial trials using a pyrometer were also made and measurements applied for validation of temperature development in the model. The model developed in this work consists of a set of ordinary differential equations describing the mass and energy balance of the process, including component balances, main reactions, and thermodynamics. The approach in this work is to provide a model that is as simple as possible to describe the main process dynamics, focusing primarily on temperature development, in order to obtain fast enough real-time calculation for optimization of the industrial process. The model used in this work is the same as the one presented in Rotevatn et al. [5], but with the addition of a stirring-dependent heat transfer coefficient for the convective heat transfer between the metal and the ladle wall. In addition, considerable work has been done in preparing the model for online signals, process measurements, and material and product analyses.
2.1. Control Volumes and State-Space Variables
The model is formulated as a continuous state space model, which also contains an integrator providing a time discrete state vector. The model has control volumes where the masses of each species and the temperature are calculated for each time step. These control volumes include liquid steel in the bulk of the vessel, free surface on the top of the metal inside the bell, and the slag phase at the top of the metal. The model also includes states describing the temperature distribution through the refractories in the ladle and the bell.
2.1.1. Liquid Steel Phases
The liquid steel is divided into two control volumes, (1) the main bulk volume of the treatment ladle and (2) the free surface. The modeled metal components are the same as for the two control volumes: Al, Si, Mn, Fe, C, P, S, Nb, V, Ni, Ti, B, Ca, N, Cr, Cu, and Mo. For each of the metal components, a time dynamic component balance is calculated, based on material flows and reaction rates. The main control volume in the model comprises the main bulk of the metal in the ladle, typically about 90% of the total mass, whereas the rest, typically 10%, is assumed to be part of the free surface control volume.
There is an exchange of mass between the main bulk control volume and the free surface. The amount of exchange is varying with degree of bubbling in the process. Higher volumes of stirring gas will increase the flow of material exchange between the two control volumes.
Material additions as well as the oxygen blowing are assumed to enter the free surface control volume. Added materials are heated up from ambient temperature to the free surface temperature and are assumed to melt instantly into the free surface. The energy required is taken from the free surface control volume. For numerical stability and accuracy, this assumption means that the additions should not be too large compared to the mass and available energy in the free surface control volume. If larger and energy demanding material additions are applied, the model dimensions, calculation intervals, or equation solver should be adjusted accordingly. Both the free surface and the main bulk are assumed to be liquid at all times during a treatment batch.
2.1.2. Slag Phase
The slag phase is floating on top of the hot metal. The slag is assumed to be in contact with the hot metal and chemical components in the slag will interact with the metal through interface reactions between hot metal and slag. In the model, it is assumed here that there is no contact between the free surface control volume and slag. The following chemical components are assumed present in the slag phase: AlO, SiO, MnO, FeO, MgO, TiO, PO, CaO. The slag is assumed to be liquid at all times during a batch treatment.
2.1.3. Gas Phase
In the model, it is assumed that there is no gas phase inside the liquid hot metal. This is a simplification that has been done to save computation time. The aim of this model is to be able to track the main dynamics of the process during a treatment. The gas dynamics of bubbles inside the hot metal is in this respect considered to be much faster than the component balances and the temperature. The bubbling gas is argon which is inert to reactions. In the cases where oxygen heating is applied, the oxygen is assumed to react instantly with metal components forming oxides that are subsequently reacting further, where the slag–metal equilibrium will decide the reaction potentials.
2.1.4. Ladle
The ladle refractory is modeled as a number of equally thick shells from the inside in contact with the hot metal to the outside in contact with the steel casing, which in turn is in contact with the surrounding air. The number of refractory shell is configurable but typically a value of five shells is applied. This means that there are in total six control volumes describing the temperature profile of the ladle refractory and steel shell. The ladle only has equations describing the heat evolution. No chemical reactions or mass balance equations are included. Refractory wear can be modeled by adjusting refractory thickness between heats. Consumed refractory is not assumed to influence slag composition in single heats.
2.1.5. Bell
Similarly, as for the ladle, the bell is divided into refractory shells and steel casing. Typically, six control volumes are applied. On the inside of the bell, the refractory is in contact with the gas phase and also exposed to radiation from the free surface. Through the shells and to the steel casing, heat is transferred by conduction. From the steel casing, heat is lost to the surrounding air by convection, as well as radiation.
2.2. Chemical Reactions
2.2.1. Dissolution of Added Material
Added metallic material, such as aluminium, is assumed to melt instantaneously into the free surface control volume:
Dissolution of other metallic additions is modeled similarly.
Added oxides are assumed to melt instantaneously into the slag phase:
Dissolution of other non-metallic additions are modeled similarly.
Instantaneous dissolution of additions is a simplification and approximation. The additions are assumed to be small in sizing and amounts for the dissolution to be fast, such that the introduced temporary error in mass and energy balance will be negligible with respect to the required accuracy for the industrial application of the model.
Solid phase from added materials is denoted (s), chemical components in the free surface volume, a liquid phase, is denoted (f), gas phase is denoted (g), while liquid hot metal is denoted by underline, and liquid slag phase by parentheses.
2.2.2. Free Surface Reactions
Furthermore, the metallic components including dissolved carbon are assumed to react with added oxygen. All free surface reactions involving oxygen are assumed to be irreversible:
All of these reactions are assumed to be irreversible reactions, driven far to the right. The reaction rates are calculated based on the activities of the reacting species and calculated thermochemical equilibrium. The available oxygen is distributed according to an oxygen yield factor and individual reaction rates. The oxygen available to take part in reactions are given by , where is the molar flow of oxygen from the lance. The oxygen yield factor, , should be a number between 0 and 1.
As an example, the nominal reaction rate for (R2) is given by:
where is the thermochemical equilibrium constant.
The total reaction rate of (R2)–(R6) is limited by the available oxygen:
which leads to the following actual reaction rates:
With these reaction rates, the reactions will compete for the oxygen based on thermochemical terms, yet only consuming the available oxygen.
2.2.3. Slag-Metal Interface Reactions
On the interface between slag and free surface equilibrium reactions are assumed to take place:
2.3. Heat Transfer
The refractory layer of the bell typically has a radial temperature gradient, where heat conduction transports heat from the hot inside to the cooler outside of the bell. Heat is transferred by heat convection from the gas phase inside the bell to the inside of the bell. Radiation takes place between the hot free surface area and the inside of the bell. From the steel cap to the surrounding air, heat is transferred by convection, as well as a term for radiation losses to the surroundings.
Similarly, in the ladle refractory, heat transfer is assumed to take place by convection from the hot metal to the inner refractory layer. Heat is further transferred by conduction through the refractories to the steel cap. From the steel cap, heat is lost by radiation to the surroundings, as well as through heat convection to the air.
The varying heat convection from the hot metal to the inner refractory layer due to flow conditions in the hot metal and free surface control volumes inside the ladle has a substantial impact on the energy balance. The internal exchange of mass between the free surface and the bulk hot metal is influenced strongly by stirring gas and oxygen blowing.
Heat is also transferred by convection between slag and hot metal, and between free surface and hot metal. The free surface and hot metal are also mixed by the stirring, which provides a substantial exchange of heat and mass between the two control volumes.
2.4. Mass and Energy Balances
A list of symbols used in the mathematical description and equations is provided in Abbreviation.
2.4.1. Free Surface
The added aluminium is assumed to melt as soon as it enters the free surface control volume. Reactions are consuming aluminium in this control volume, and stirring will mix the materials between hot metal and the free surface:
where is the sum of the representative aluminium part of metallic additions. is the net mass of aluminium being exchanged between the liquid hot metal and the free surface control volumes due to mixing.
where is the sum of the representative silicon part of metallic additions. is the net mass of aluminium being exchanged between the liquid hot metal and the free surface control volumes due to mixing.
In general, for all components in the free surface, we can write:
where is the net sum of reactions where component i takes part, weighted by the stoichiometric factor for the component.
The mixing is assumed to preserve the total mass, so the amount of liquid going into the free surface from the hot metal is the same as the amount going from the free surface into the hot metal. Therefore, the net flow for each component will be given by the chemical composition difference between the two control volumes and the composition in each control volume:
where are the components in the free surface and hot metal.
2.4.2. Liquid Steel
The energy balance for the liquid main bulk results in the following differential equation describing the temperature:
where
The terms , , and are describing heat convection between the phases main bulk, free surface, inner ladle and slag, determined by the temperature difference between the neighbouring phases, the interface areas and the heat transfer coefficients . The flows are assumed equal.
2.4.3. Gas Phase
The gas phase is defined primarily to account for CO-gas produced in the process. The component balance is given as:
where is the molar mass of CO(g) and is the molar rate of reaction.
where is a time constant for the gas dynamics.
The gas temperature is calculated as an algebraic relation:
where is the mass flow of argon being purged from the bottom of the ladle.
The reason for simplifying the gas temperature calculation is to avoid unnecessary complex equations that would cause stiffness to system and slow down the calculation speed.
2.4.4. Model Summary
The model consists of 61 ordinary differential equations describing the chemistry and temperature of the CAS-OB process. A total of 222 parameters and constants describe physical properties of materials, geometrical data of the system, etc. In the industrial implementation, there are 50 input variables, providing information on added materials, gas bubbling and oxygen blowing. Forty-three measurements are implemented, including slag and metal analysis and temperatures. Many of the measurements are not available during online operation, but data are often available after end of treatment. The logged data can be used for offline validation and improvements of the process model.
2.5. Recursive Parameter and State Estimation
In the CAS-OB process, there are considerable uncertainties related to the initial conditions before heat. The hot metal arriving from the BOF process has an end of BOF treatment temperature measurement. Occasionally, additional materials are added to adjust composition after BOF treatment and before CAS-OB treatment. Waiting time between the processes may vary. Refractory wear and net heat loss may vary between vessels. The initial ladle temperature is also unknown. These factors introduce uncertainties to the initial temperature of the CAS-OB process. To mitigate this issue, recursive estimation of ladle state in general and specifically ladle temperature has been introduced.
Estimation is implemented using an augmented and extended Kalman filter [9,10]. The metal temperature is typically measured three times during the treatment: once in the beginning of the heat, once midway through the heat, and once towards the end of the heat.
2.6. Real-Time Optimization
Real-time optimization is implemented using the nonlinear model predictive control schema similar to the method described by Maciejowski [11]. Two applications are implemented: (1) a monitoring application calculating the predicted result of the heat based on current and planned inputs. (2) an optimizing application where the desired end-point temperature and the delivery time to the subsequent continuous caster is specified. Based on this specification, the application optimizes the inputs of scrap metal addition and oxygen blowing such that the targets are met. The suggested optimized inputs are presented to the operator through the user interface.
The real-time optimization is repeated every five seconds, and new predictions and optimized inputs are calculated.
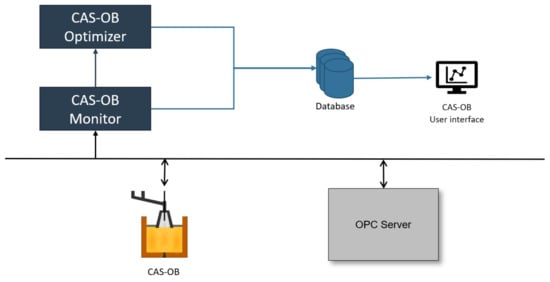
Figure 2.
Real-time application configuration at SSAB.
3. Results
The monitoring and control application has been installed on two CAS-OB refining stations at SSAB Europe OY’s Raahe plant with a configuration as illustrated in Figure 2. The application has been running in real-time operation since 2019 and validation of the results taken place over time by process engineers and recently also by process operators. Process data have been logged over the last two years, and the model agreement with process data studied based on a large set of data from this period.
3.1. Model Agreement with Process Data
An early version of the model was presented by Rotevatn [5] where model validation was also a part of the work. The model was in reasonable agreement with most of the chemical elements in the metal and slag. Not surprisingly, when studying the validation results, the slag components in general had the largest deviation. This is natural as the mass of slag is smaller and even moderate variations in metal components to be refined may have a larger impact on the resulting slag composition. Industrially, getting a representative sample of slag for analysis can also be more challenging.
The main use of this application has been in temperature control. The application optimizes the use scrap metal additions and the use of additional oxygen for reheating. Therefore, the main focus in this work has been on validation of the metal temperature. In Figure 3, a histogram of the prediction error of the end temperature is shown for a total of 1031 heats collected over a period of one month. The wider distribution curve in dark blue color shows the histogram for the prediction error for the end temperature using ballistic simulation. This corresponds to the nominal model accuracy. The standard deviation is 19.5 C and a bias of 3.1 C. The required specification for the application to give added value to the operation is approximately 10 C.
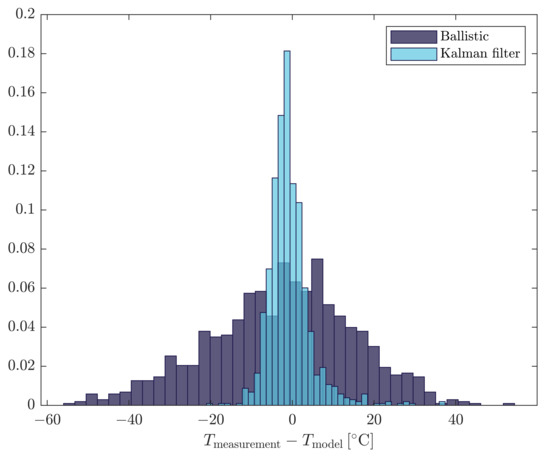
Figure 3.
Histogram showing improvement of prediction errors by estimation on the final temperature estimates in the heat.
3.2. Recursive Estimation
In Figure 3, the effect of estimation on the final temperature is also illustrated. When applying the implemented Kalman-filtering, the standard deviation of prediction errors is reduced to 5.5 C with a bias of 2.2 C. The result is now well within the required specifications for the process improvements.
Figure 4 shows how the Kalman-filtering is adjusting the temperature estimates. In particular, the first measurement is very important since the initial temperature of the CAS-OB ladle is uncertain. After being adjusted by the first temperature measurement, the model is able to follow the remaining course of the process with high accuracy. This includes the following process events such as material additions and reheating by oxygen.
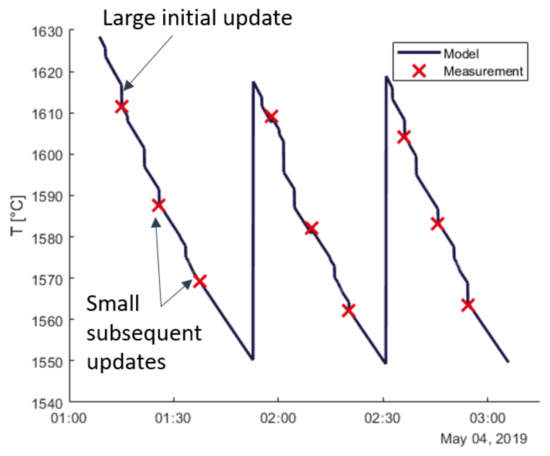
Figure 4.
Temperature evolution and estimation improvement during the course of the heat.
3.3. Industrial Use and Application
The user interface has been developed in cooperation between SSAB Europe OY’s engineers and operators, providing a suggestion for operators to reheat or add cooling scrap to meet the accurate target window of time and temperature for the so-called hook time. The hook time is the time when the refining ladle should be “hooked up” for transport to the casting station. Typically, the end of heat temperature from the CAS-OB station should be a few degrees higher than the specified temperature for casting to obtain optimal steel quality.
In the user interface (Figure 5), the vertical line represents the present time, and data to the left are historical values, while future model predictions are shown to the right. There are two predicted temperature curves; the dark line represents the prediction if the heat continues with the current plan for the heat. The light green curve shows the predicted temperature if the recommended optimized input is applied. The orange line shows that the target temperature has been specified for the hook time. In the historical data to the left, temperature measurements can also be seen as light blue crosses, while the target point for the previous heat is shown as an orange cross. The recommended amount and timing of oxygen reheating, aluminium and scrap metal additions are presented for the operators.
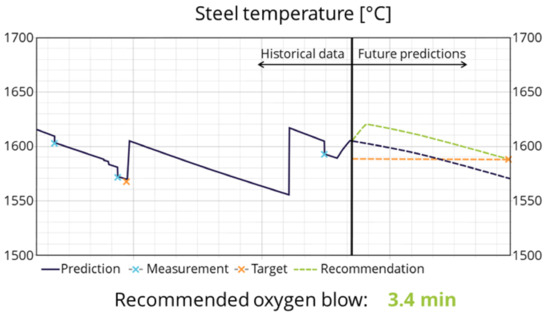
Figure 5.
User interface for temperature control.
4. Conclusions
A monitoring and control application for temperature control of the CAS-OB secondary steelmaking process has been developed and tested industrially during the Morse project. The application is based on a first-principles model of the process, which provides a good problem structure. Since the model, provided with available input data, is not accurate enough for online use, an estimator is provided in the form of a Kalman filter. The estimator utilizes the available measurements to adjust the model in real time. The overall model may be regarded as a hybrid digital twin, utilizing the best of two worlds; the structure of first principles and the flexibility of a data driven approach. This hybrid twin is combined with a nonlinear model predictive control algorithm which is applied to optimize amount and timing of process inputs. The optimized inputs are presented to process operators along with the currently used heating profile, thus providing an operator support system for process control.
Author Contributions
Conceptualization, S.O.W., T.R. and K.L.; methodology, S.O.W., K.L. and T.R. ; software, K.L. and T.R.; validation, S.O., A.B. and K.L.; formal analysis, K.L., T.R. and S.O.; investigation, S.O. and K.L.; resources, A.B. and S.O.W.; data curation, S.O.; writing—original draft preparation, S.O.W.; writing—review and editing, S.O.W.; visualization, K.L.; supervision, A.B. and S.O.W.; project administration, A.B. and S.O.W.; funding acquisition, A.B. and S.O.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Commission, Directorate-General for Research and Innovation, through the project ”Model-based optimisation for efficient use of resources and energy” (MORSE), Grant No. 768652. https://www.spire2030.eu/morse, accessed on 27 September 2021.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors acknowledge the assistance by Timo Veijola during the early validation phases of the online system.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BOF | Basic Oxygen Furnace | |
| CAS-OB | Composition Adjustment by Sealed | |
| argon-bubbling with Oxygen Blowing | ||
| CFD | Computational Fluid Dynamics | |
| MPC | Model Predictive Control | |
| NMPC | Nonlinear Model Predictive Control | |
| Symbol | Description | Unit |
| Mass of component i | kg | |
| Concentration of component i | mass fraction | |
| Specific molar mass of component i | kg/kmol | |
| Mass flow of component i | kg/s | |
| Reaction rate of reaction j | kmol/s | |
| Temperature of control volume k | K | |
| Heat transfer between control volumes k and l | W | |
| Heat capacity of component or control volume | J/(kg K) | |
| Surface area of k | m | |
| Heat transfer coefficient for k | W/(m K) | |
| Subscript notation | ||
| f | Free surface control volume | |
| L | Liquid control volume | |
| Inner section of Ladle control volume | ||
| Inner section of Bell control volume | ||
| s | Slag control volume | |
| f–L | From Free surface to Liquid control volumes | |
| L–f | From Liquid to Free surface control volumes | |
| Material addition |
References
- Ollila, S.; Syrjänen, A.; Robey, R. Commissioning and Initial Results from New Twin CAS-OB Plant at Ruukki, Raahe Steel Works. In Proceedings of the 6th European Oxygen Steelmaking Conference (EOSC), Stockholm, Sweden, 7–9 September 2011; pp. 170–183. [Google Scholar]
- Järvinen, M.; Kärnä, A.; Ollila, S.; Fabritius, T. A novel approach for numerical modeling of the CAS-OB process. In Proceedings of the Scanmet IV, Luleå, Sweden, 10–13 June 2012; pp. 79–88. [Google Scholar]
- Fruehan, R.J. (Ed.) The Making, Shaping and Treating of Steel; The AISE Steel Foundation: Pittsburgh, PA, USA, 1998; ISBN 0-930767-02-0. [Google Scholar]
- Ghosh, A. Secondary Steelmaking, Principles and Applications; CRC Press: Boca Raton, FL, USA, 2001; ISBN 978-0-849-30264-0. [Google Scholar]
- Rotevatn, T.; Wasbø, S.; Järvinen, M.; Fabritius, T.; Ollila, S.; Hammervold, A.; Blasio, C.D. A Model of the CAS-OB Process for Online Applications. In Proceedings of the Preprints of the IFAC 4th Workshop on Mining, Minerals and Metal Processing, Oulu, Finland; 2015. [Google Scholar]
- Sulasalmi, P.; Visuri, V.V.; Kärnä, A.; Järvinen, M.; Ollila, S.; Fabritius, T. A Mathematical Model for the Reduction Stage of the CAS-OB Process. Metall. Trans. B 2016, 47, 3544–3556. [Google Scholar] [CrossRef]
- Visuri, V.V.; Järvinen, M.; Pääskylä, K.; Kärnä, A.; Sulasalmi, P.; DeBlasio, C.; Ollila, S.; Fabritius, T. Preliminary Validation of a Numerical Model for the CAS-OB Process. In Proceedings of the 7th European Oxygen Steelmaking Conference (EOSC), Třinec, Czech Republic, 9–11 September 2014. [Google Scholar]
- Kärnä, A.; Järvinen, M.; Sulasalmi, P.; Visuri, V.V.; Ollila, S.; Fabritius, T. An Improved Model for the Heat-Up Stage of the CAS-OB Process: Development and Validation. Steel Res. Int. 2018, 89, 1800141-16. [Google Scholar] [CrossRef]
- Schei, T.S. On-line estimation for process control and optimization applications. J. Process. Control 2008, 18, 821–828. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; Wiley: Hoboken, NJ, USA, 2006; ISBN 978-0-471-70858-2. [Google Scholar]
- Maciejowski, J.M. Predictive Control With Constraints; Prentice Hall: Boston, MA, USA, 2002; ISBN 978-0-201-39823-6. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).