Effect of the Surface Roughness of Tungsten on the Sputtering Yield under Helium Irradiation: A Molecular Dynamics Study
Abstract
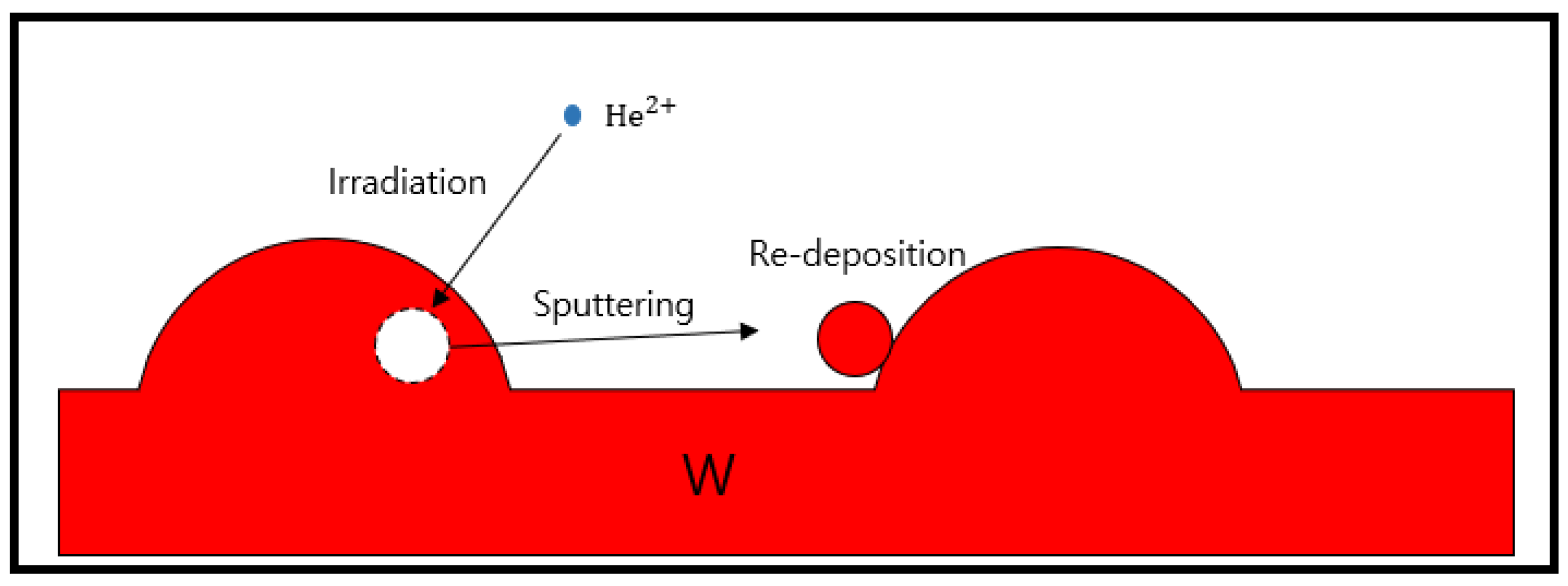
1. Introduction
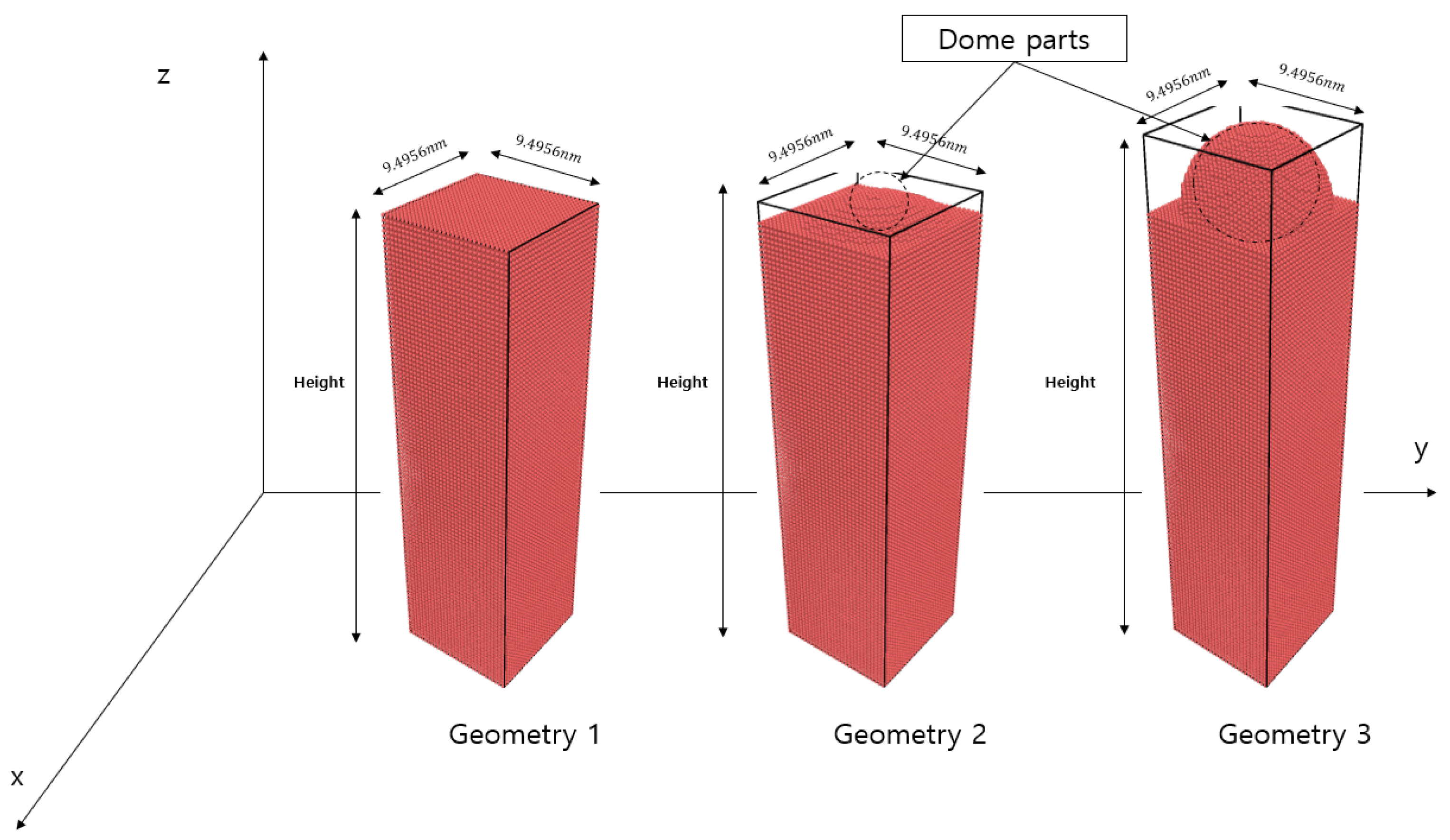
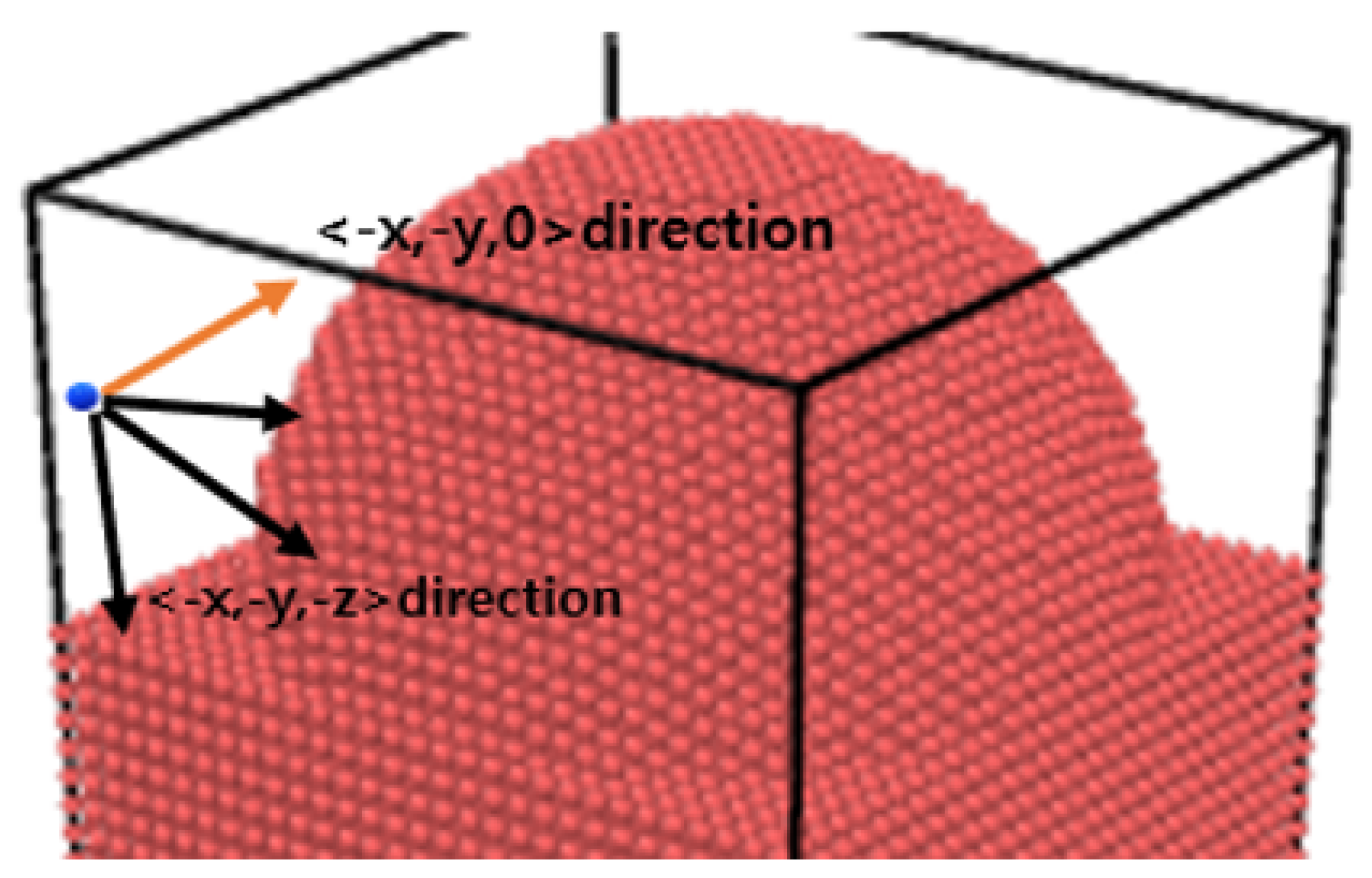
2. Simulation Method
- The system has a width of 9.4956 nm × 9.4956 nm and the height varies throughout the COD;
- x-y directions of the system adopt periodic boundary conditions;
- A He ion was irradiated every ps until 500 ps. The total number of the He ions is the same in our simulations;
- He ions are irradiated to a random position by a random function. However, each geometry has the same coordinate where ions are irradiated;
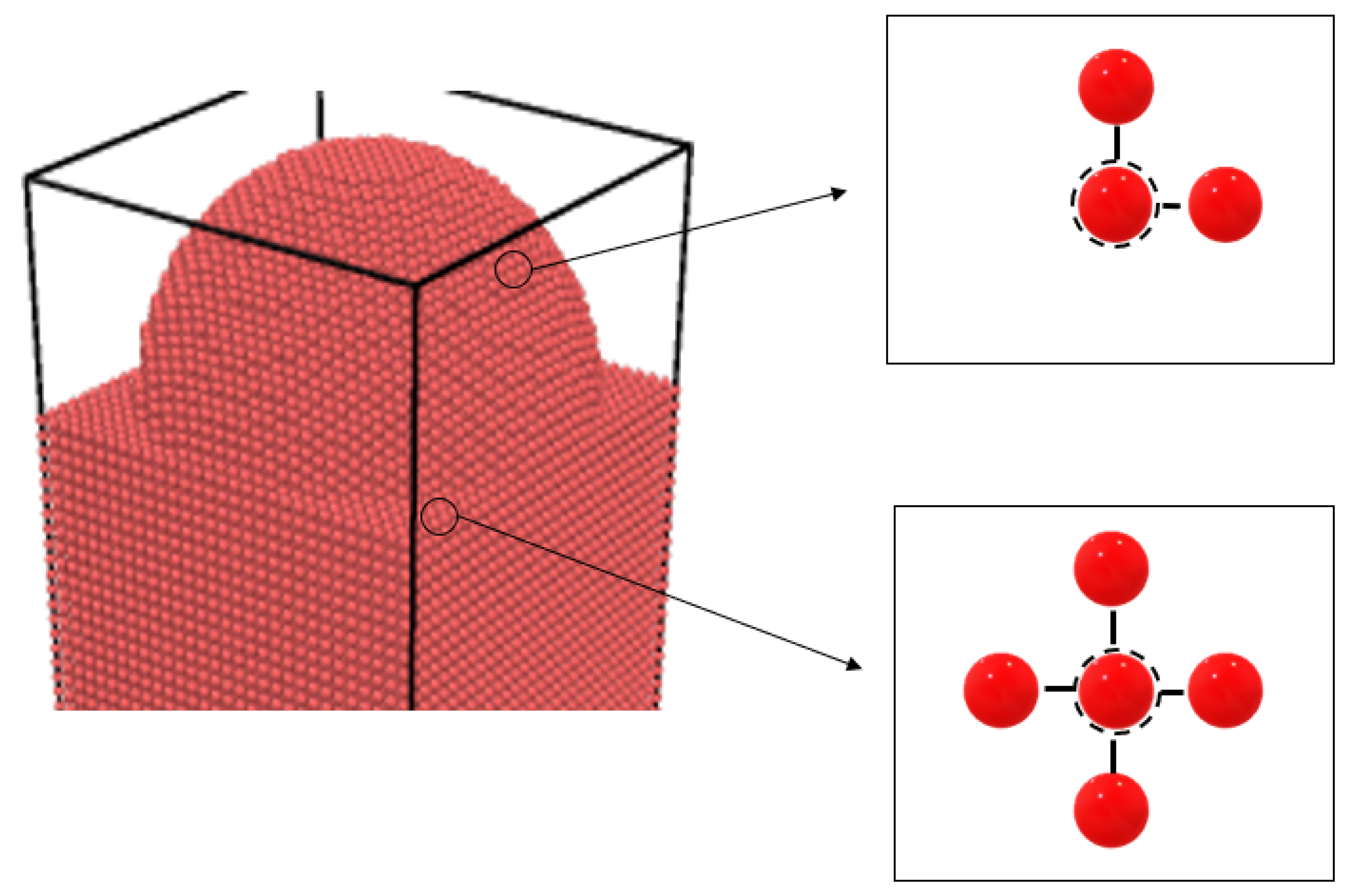
- When CN (coordination number) = 0, the tungsten atoms are assumed to be sputtered. CN is defined as the number of tungsten particles adjacent to the tungsten particle. Thus, CN = 0 means that there are no other tungsten particles near the tungsten particle. It indicates that the tungsten particles with CN = 0 are sputtered particles.
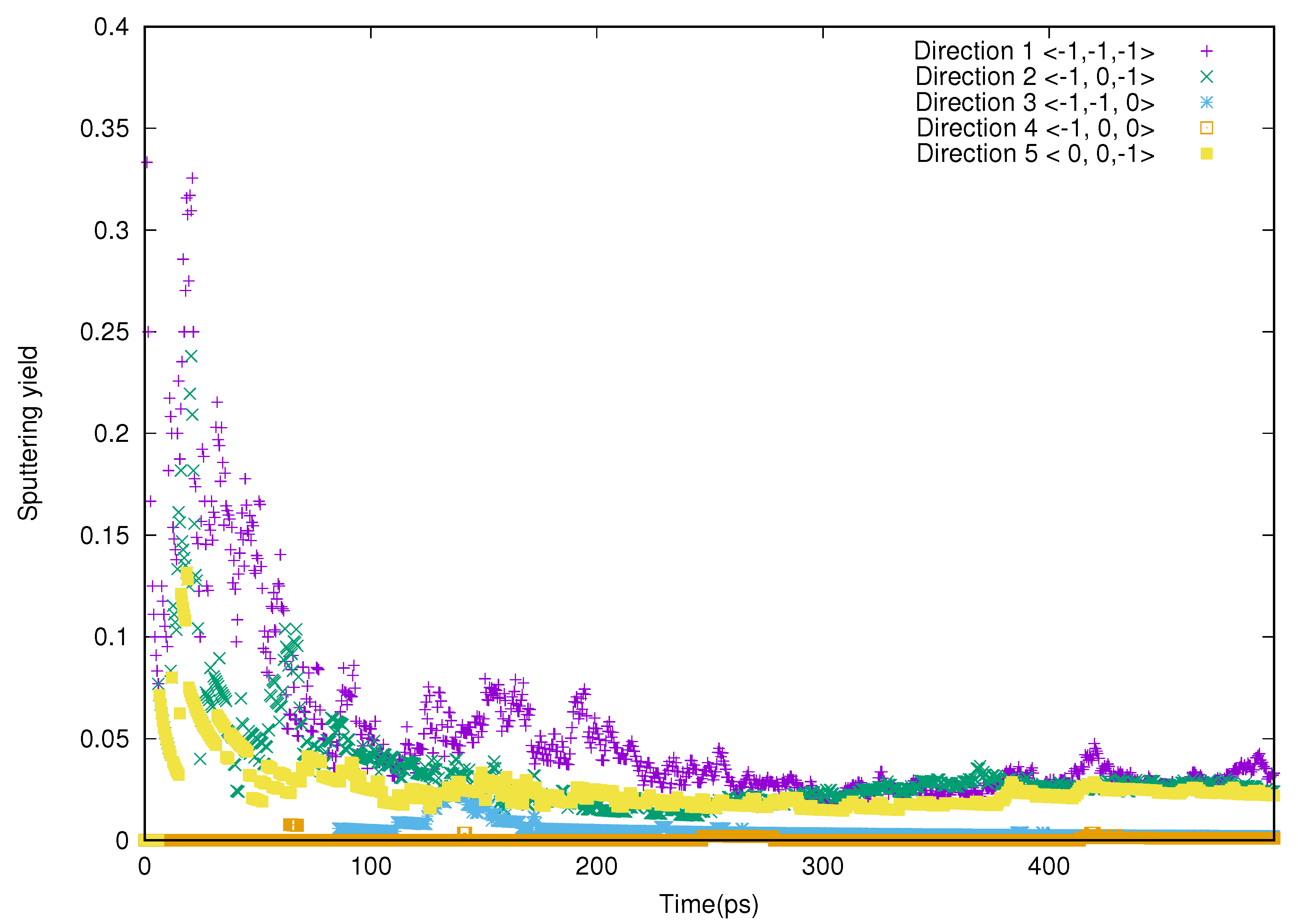
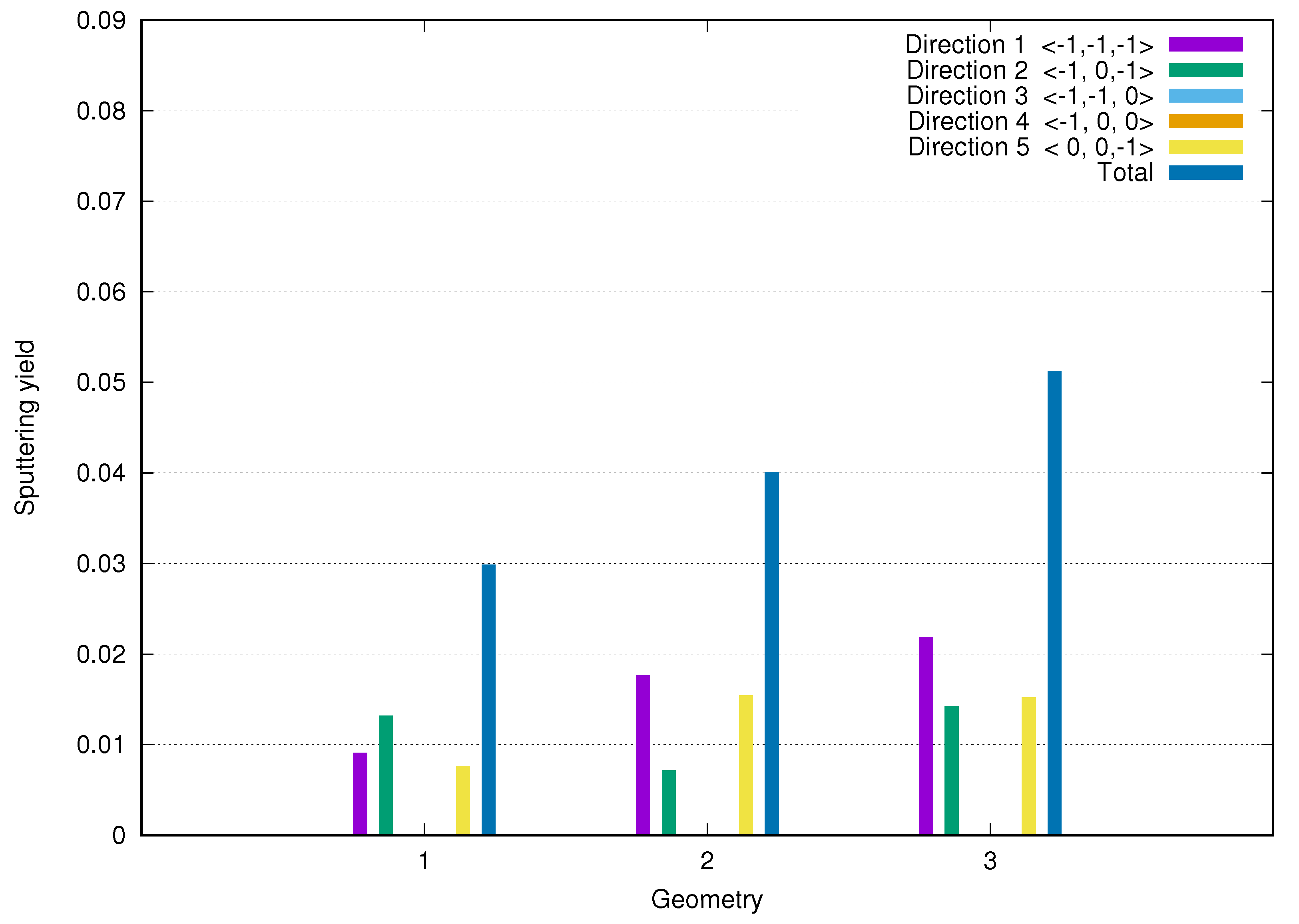
| Incident Direction | Vector |
| Direction 1 | <, , > |
| Direction 2 | <, 0, > |
| Direction 3 | <, , 0> |
| Direction 4 | <, 0, 0> |
| Direction 5 | <0, 0, > |
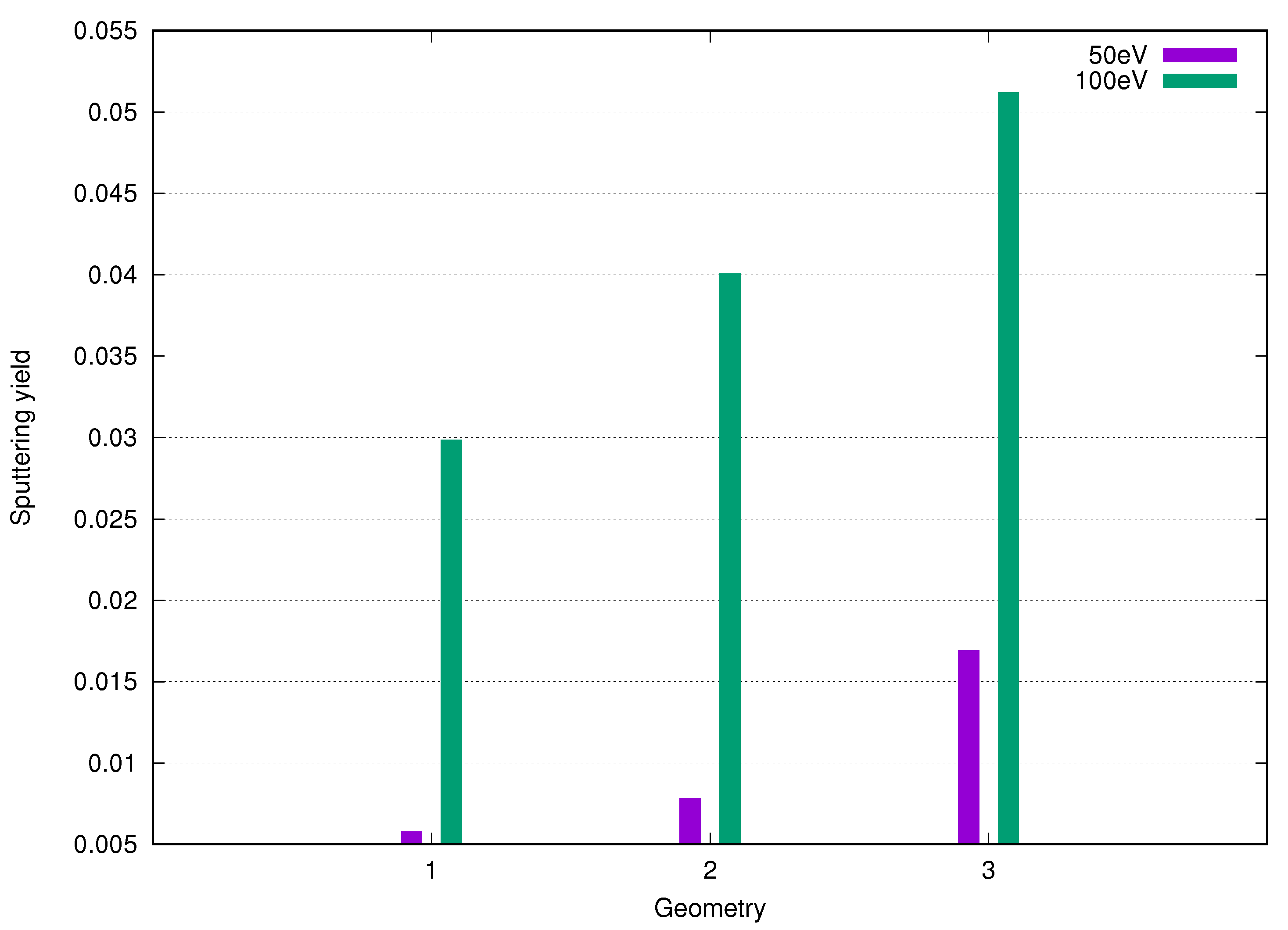
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kammash, T.; Ragheb, M.M.; Higgins, T.J. Fusion reactor physics, principles and technology. IEEE Trans. Nucl. Sci. 1976, 23, 1304–1306. [Google Scholar] [CrossRef]
- Miyamoto, K. Plasma Physics for Nuclear Fusion; MIT Press: Cambridge, MA, USA, 1980. [Google Scholar]
- Guo, H.; Matthews, G.; Coffey, I.; Erents, S.; Groth, M.; Harbour, P.; Von Hellermann, M.; Hillis, D.; Hogan, J.; Horton, L.; et al. Effects of divertor geometry and chemical sputtering on impurity behaviour and plasma performance in JET. Nucl. Fusion 2000, 40, 379. [Google Scholar] [CrossRef][Green Version]
- Kwon, T.H.; Park, S.; Ha, J.M.; Youn, Y.S. Study on sputtering yield of tungsten with different particle sizes: Surface roughness dependence. Nucl. Eng. Technol. 2021, 53, 1939–1941. [Google Scholar] [CrossRef]
- Sigmund, P. Sputtering by ion bombardment theoretical concepts. In Sputtering by Particle Bombardment I; Springer: Berlin/Heidelberg, Germany, 1981; pp. 9–71. [Google Scholar]
- Roth, J. Sputtering of limiter and divertor materials. J. Nucl. Mater. 1990, 176, 132–141. [Google Scholar] [CrossRef]
- Vörtler, K.; Björkas, C.; Nordlund, K. The effect of plasma impurities on the sputtering of tungsten carbide. J. Phys. Condens. Matter 2011, 23, 085002. [Google Scholar] [CrossRef] [PubMed]
- Hirooka, Y.; Bourham, M.; Brooks, J.; Causey, R.; Chevalier, G.; Conn, R.; Eddy, W.; Gilligan, J.; Khandagle, M.; Ra, Y. Evaluation of tungsten as a plasma-facing material for steady state magnetic fusion devices. J. Nucl. Mater. 1992, 196, 149–158. [Google Scholar] [CrossRef]
- Wielunska, B.; Mayer, M.; Schwarz-Selinger, T.; Sand, A.; Jacob, W. Deuterium retention in tungsten irradiated by different ions. Nucl. Fusion 2020, 60, 096002. [Google Scholar] [CrossRef]
- Rieth, M.; Doerner, R.; Hasegawa, A.; Ueda, Y.; Wirtz, M. Behavior of tungsten under irradiation and plasma interaction. J. Nucl. Mater. 2019, 519, 334–368. [Google Scholar] [CrossRef]
- Xie, H.; Ding, R.; Kirschner, A.; Chen, J.; Ding, F.; Mao, H.; Feng, W.; Borodin, D.; Wang, L. ERO modelling of tungsten erosion and re-deposition in EAST L mode discharges. Phys. Plasmas 2017, 24, 092512. [Google Scholar] [CrossRef]
- Nishijima, D.; Baldwin, M.; Doerner, R.; Yu, J. Sputtering properties of tungsten ‘fuzzy’surfaces. J. Nucl. Mater. 2011, 415, S96–S99. [Google Scholar] [CrossRef]
- Neu, R.; Dux, R.; Kallenbach, A.; Pütterich, T.; Balden, M.; Fuchs, J.; Herrmann, A.; Maggi, C.; O’Mullane, M.; Pugno, R.; et al. Tungsten: An option for divertor and main chamber plasma facing components in future fusion devices. Nucl. Fusion 2005, 45, 209. [Google Scholar] [CrossRef]
- Chankin, A.; Coster, D.; Dux, R. Monte Carlo simulations of tungsten redeposition at the divertor target. Plasma Phys. Control. Fusion 2014, 56, 025003. [Google Scholar] [CrossRef]
- Nakamura, H.; Saito, S.; Ito, A.M.; Takayama, A. Tungsten-Surface-Structure Dependence of Sputtering Yield for a Noble Gas. Plasma Fusion Res. 2016, 11, 2401080. [Google Scholar] [CrossRef]
- Van Rooij, G.; Coenen, J.; Aho-Mantila, L.; Brezinsek, S.; Clever, M.; Dux, R.; Groth, M.; Krieger, K.; Marsen, S.; Matthews, G.; et al. Tungsten divertor erosion in all metal devices: Lessons from the ITER like wall of JET. J. Nucl. Mater. 2013, 438, S42–S47. [Google Scholar] [CrossRef]
- Krieger, K.; Maier, H.; Neu, R.; Team, A.U. Conclusions about the use of tungsten in the divertor of ASDEX Upgrade. J. Nucl. Mater. 1999, 266, 207–216. [Google Scholar] [CrossRef]
- Herrmann, A.; Greuner, H.; Jaksic, N.; Böswirth, B.; Reimold, F.; Scarabosio, A.; Vorbrugg, S.; Wischmeier, M. Design and concept validation of the new solid tungsten divertor for ASDEX Upgrade. Fusion Eng. Des. 2013, 88, 577–580. [Google Scholar] [CrossRef][Green Version]
- Kreter, A.; Brezinsek, S.; Hirai, T.; Kirschner, A.; Krieger, K.; Mayer, M.; Philipps, V.; Pospieszczyk, A.; Samm, U.; Schmitz, O.; et al. Effect of surface roughness and substrate material on carbon erosion and deposition in the TEXTOR tokamak. Plasma Phys. Control. Fusion 2008, 50, 095008. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Short, M.P.; Ding, Z.; Zeng, Z.; Li, J. Ion radiation albedo effect: Influence of surface roughness on ion implantation and sputtering of materials. Nucl. Fusion 2016, 57, 016038. [Google Scholar] [CrossRef]
- Beck, D. A new interatomic potential function for helium. Mol. Phys. 1968, 14, 311–315. [Google Scholar] [CrossRef]
- Ackland, G.J.; Thetford, R. An improved N-body semi-empirical model for body-centred cubic transition metals. Philos. Mag. A 1987, 56, 15–30. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Biersack, J.P. The stopping and range of ions in matter. In Treatise on Heavy-Ion Science; Springer: Berlin/Heidelberg, Germany, 1985; pp. 93–129. [Google Scholar]
- Juslin, N.; Wirth, B. Interatomic potentials for simulation of He bubble formation in W. J. Nucl. Mater. 2013, 432, 61–66. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Kwon, J.; Chang, K. Effect of the Surface Roughness of Tungsten on the Sputtering Yield under Helium Irradiation: A Molecular Dynamics Study. Metals 2021, 11, 1532. https://doi.org/10.3390/met11101532
Kim H, Kwon J, Chang K. Effect of the Surface Roughness of Tungsten on the Sputtering Yield under Helium Irradiation: A Molecular Dynamics Study. Metals. 2021; 11(10):1532. https://doi.org/10.3390/met11101532
Chicago/Turabian StyleKim, Hyeonho, Joongseok Kwon, and Kunok Chang. 2021. "Effect of the Surface Roughness of Tungsten on the Sputtering Yield under Helium Irradiation: A Molecular Dynamics Study" Metals 11, no. 10: 1532. https://doi.org/10.3390/met11101532
APA StyleKim, H., Kwon, J., & Chang, K. (2021). Effect of the Surface Roughness of Tungsten on the Sputtering Yield under Helium Irradiation: A Molecular Dynamics Study. Metals, 11(10), 1532. https://doi.org/10.3390/met11101532





