A Systematic Review of Structural Reliability Methods for Deformation and Fatigue Analysis of Offshore Jacket Structures
Abstract
1. Introduction
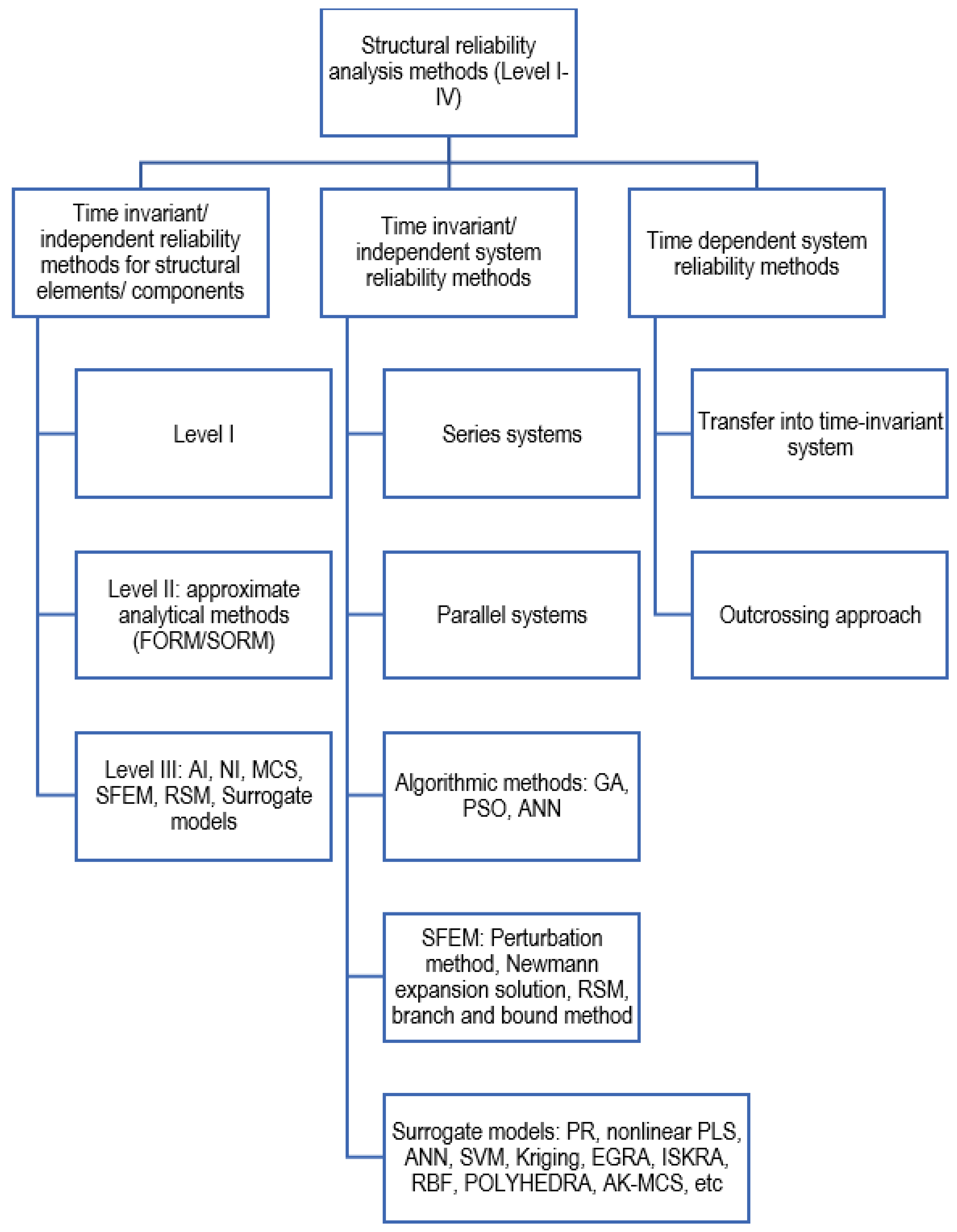
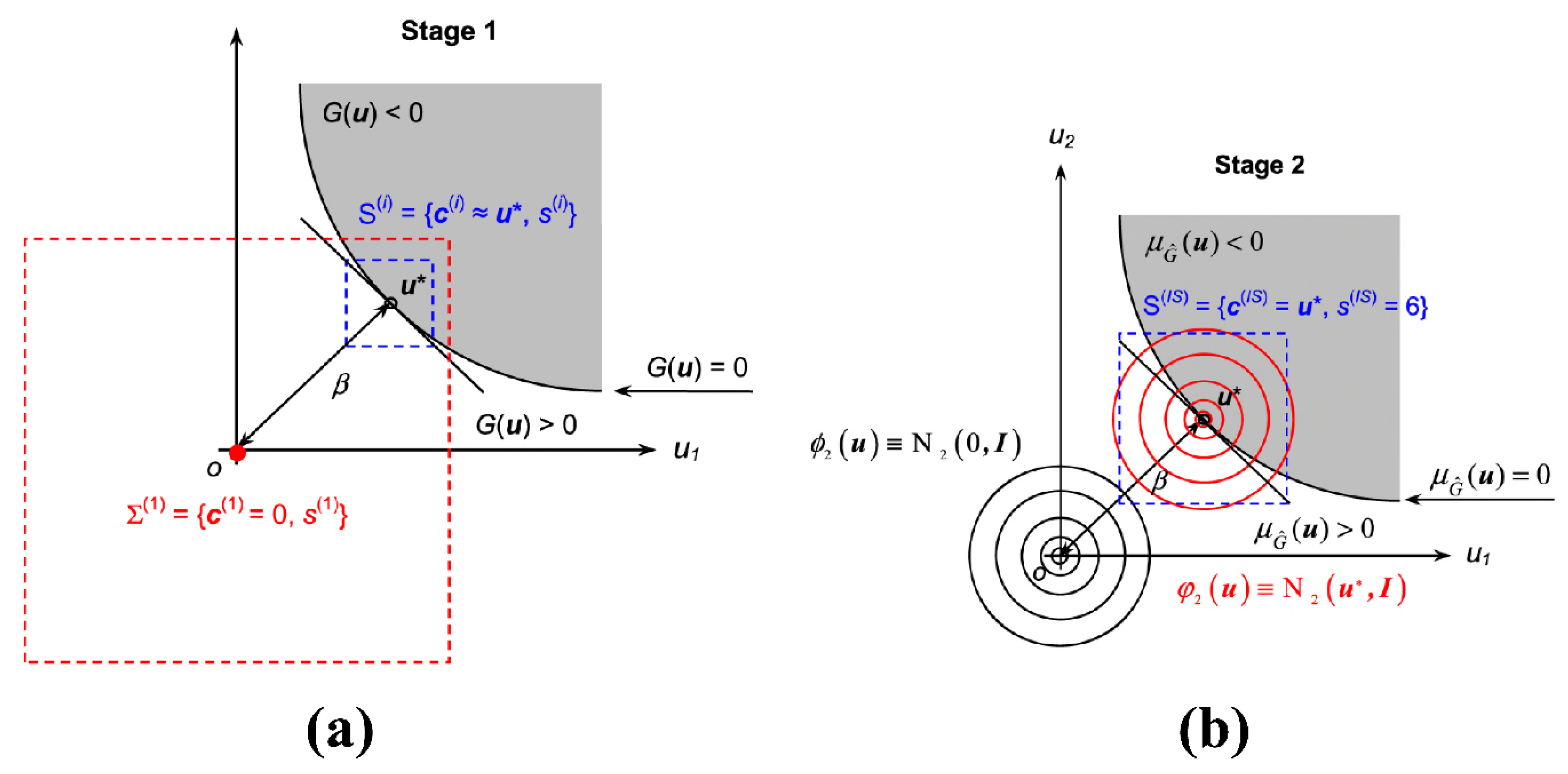
2. Level III Analytical Structural Reliability Analysis Methods
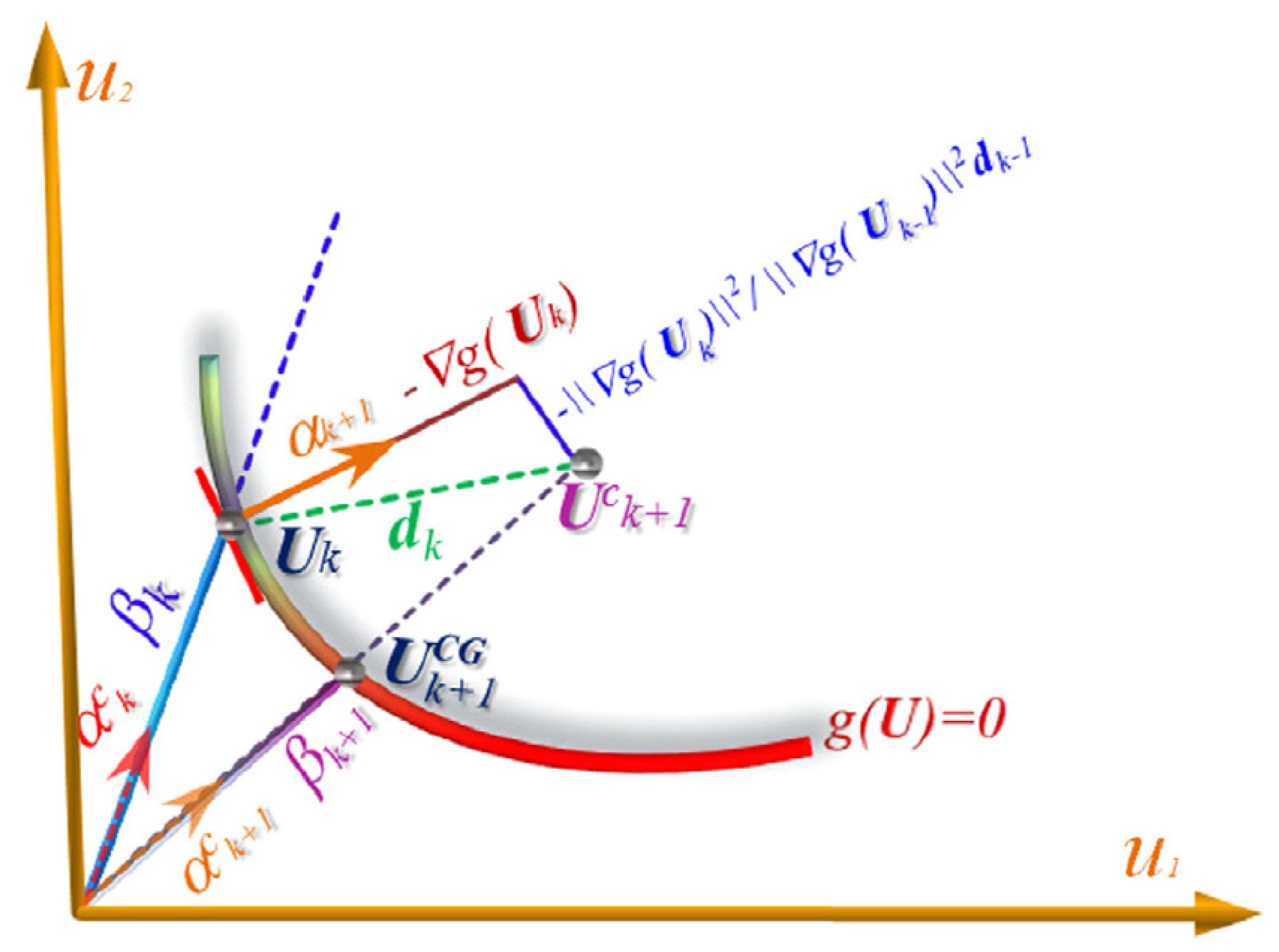
2.1. First-Order Reliability Method (FORM)
- (1)
- Define the PF for the corresponding LS, e.g., ultimate limit state (ULS), serviceability limit state (SLS), fatigue limits state (FLS), etc.
- (2)
- Let the mean value point be the initial design point, i.e., , and evaluate the gradients of the LSF at this design point, where represents the element in the vector of the iteration and is the mean value of the element.
- (3)
- Compute the initial RI, adopting the mean-value approach, i.e., and its direction cosine .
- (4)
- Calculate a new design point and function value, as well as gradients at this new design point.
- (5)
- Compute the RI and direction cosine using Equations (4) and (5) respectively.
2.2. Second-Order Reliability Method (SORM)
3. Level III (Direct) Reliability Methods
4. Advanced Approximation Modeling Methods
4.1. Response Surface Method
4.2. Surrogate Models (SMs)
4.2.1. Kriging Incorporated with FORM
4.2.2. Kriging Incorporated with IS/SS
4.2.3. Efficient Global Reliability Analysis (EGRA)
4.2.4. Sequential Kriging Reliability Analysis (SKRA)
4.2.5. Support Vector Approach
4.2.6. Artificial Neural Network Approach
4.2.7. Radial Basis Function Approach
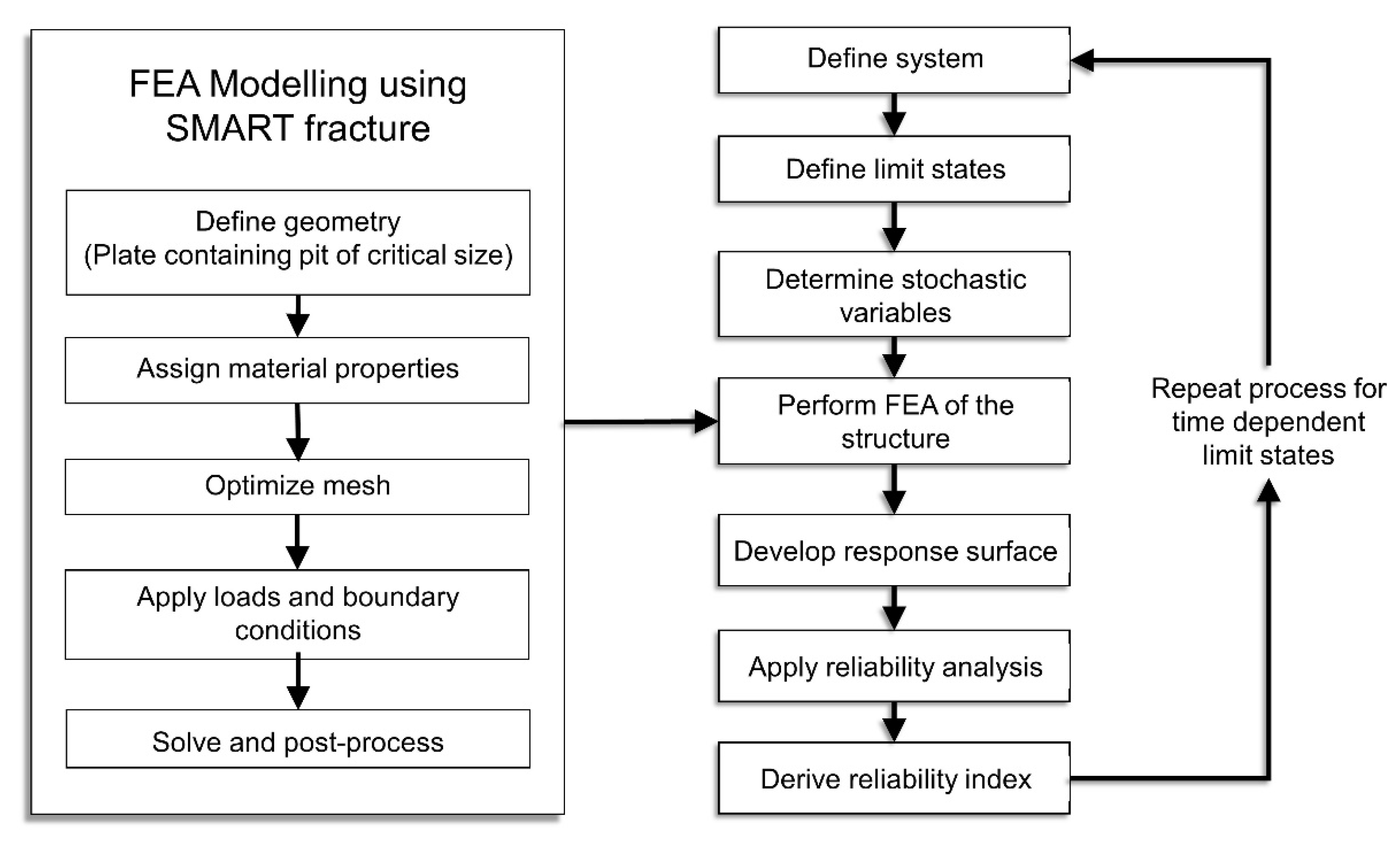
5. Probabilistic Fatigue and Fracture Mechanics Approaches
6. Other Methods and Applications
6.1. Stochastic Finite Element Method (SFEM)
6.2. Reliability Analysis of Systems
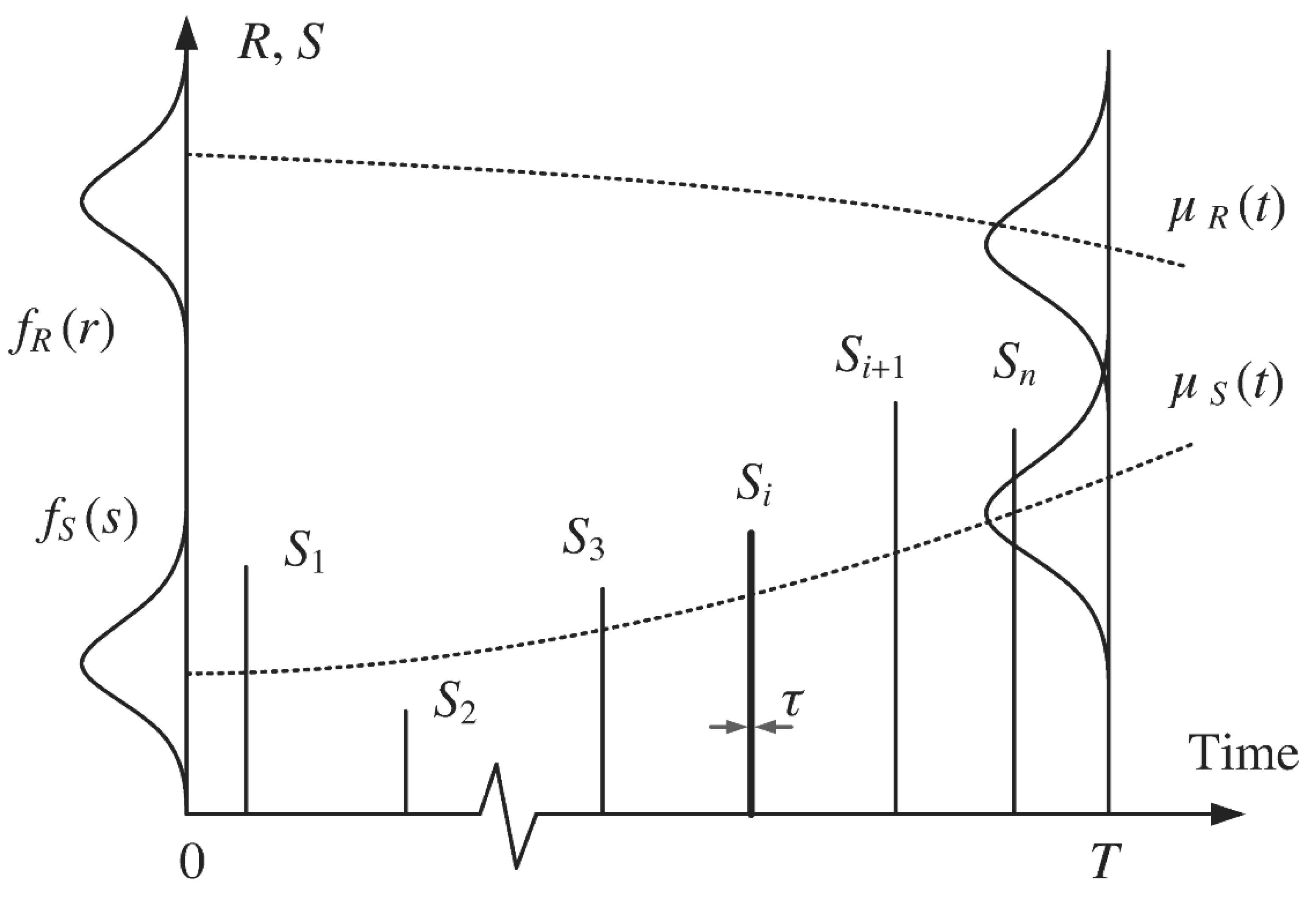
6.3. Time-Variant Reliability of Systems
7. Critical Discussion
8. Conclusions
- The FORM was improved by the development of the conjugate search direction, finite-based Armijo search direction method, Hybrid Relaxed HL–RF, stability transformation method (STM) with chaos feedback control, STM with chaos feedback control, and STM with chaotic conjugate search direction, among others. The combination of Maximum Entropy Fitting Method and the FORM was applied to problems of implicit LSFs. The SORM is an improvement on the FORM, to provide solutions to highly non-linear LSFs. A new SORM for RA was developed using the SAP in order to overcome some of the issues inherent in the traditional SORM.
- The MCS method was improved by the development of interval MC method, which combines simulation process with interval analysis, new MC-based methods involving the use of brute force MCS methods for complicated structural systems, IMC-IFEM, merging IS with directional simulation, etc. Improvements in variance reduction techniques were achieved, such as the development of interval importance sampling (IS) method, which applies the IS technique and imprecise probability, and the LHS-based quasi-random polar sampling technique.
- The advanced approximation modeling methods include the well-established Response Surface Models/Method (RSM) and the Surrogate Models (SM) as well as the Stochastic RSM (SRSM). The SRSM is a model for the RA of complex systems with low Probability of Failure (POF) for which approximate methods are inaccurate and for which Monte Carlo Simulation (MCS) is too computationally intensive. The efficiency of the RSMs developed for implicit LSFs studied herein include the Collocation Based SRSM, novel SRSM combining FEA, MPR, and FORM/SORM, incorporating the SRSM with Saddle point approximation (SPA), among others. Examples of SM include the Kriging, Adaptive Kriging, EGRA, Support vector machines, ANN, RBF, etc. These can be combined with conventional reliability methods for problems of implicit LSFs. Kriging and Adaptive Kriging interpolation models were combined with the FORM, Line sampling, IS, SS, MCS, etc.
- This study focused specifically on the probabilistic fatigue and fracture mechanics approaches because the fatigue limit state in most cases is the design-driving criterion for structural components of offshore jacket structures. Consequently, the SRA of structures considering pitting-corrosion fatigue phenomenon was identified as particularly of note and is recommended as an area open to further investigation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Analytical integration |
| AK-IS | active learning kriging with importance sampling |
| AK-MCS | Active learning kriging with Monte Carlo simulation |
| ALM | Active learning methods |
| ANN | Artificial neural networks |
| ASCE | American Society of Civil Engineers |
| ASME | American Society of Mechanical Engineers |
| ASVM | Adaptive support vector machine |
| BM | Bending moment |
| CDF | Cumulative density function |
| CGF | Cumulant generating function |
| CM | Computational models |
| CSRSM | Collocation-based stochastic response surface method |
| DNV | Det Norske Veritas |
| DoE | Design of experiment |
| EGRA | Efficient global reliability analysis |
| FAL | Finite-based Armijo line search direction |
| FCG | Fatigue crack growth |
| FEA | Finite element analysis |
| FEM | Finite element method |
| FLS | Fatigue limit state |
| FM | Fracture mechanics |
| FORM | First-order reliability method |
| FR | Fletcher and Reeves method |
| FRA | Fatigue reliability analysis |
| GA | Genetic algorithm |
| HL | Hasofer and Lind method |
| HL–RF | Hasofer Lind–Rackwitz Fiessler method |
| HRHL–RF | Hybrid relaxed Hasofer Lind–Rackwitz Fiessler method |
| HSAC | Hybrid self-adaptive conjugate |
| ICE | Institution of Civil Engineers |
| IFEM | Interval finite element method |
| IMC | Interval Monte Carlo simulation |
| IS | Importance sampling |
| ISKRA | Improved sequential kriging reliability analysis |
| ISO | International Organisation for Standardisation |
| KIM | Kriging interpolation model |
| KL | Karhunen–Leove expansion |
| LCoE | Levelized cost of energy |
| LEFM | Linear-elastic fracture mechanics |
| LHS | Latin hypercube sampling |
| LIF | Least improvement function |
| LS | Limit state(s) |
| LSF | Limit state function |
| LSS | Limit state surface |
| MC | Monte Carlo |
| MCMC | Markov Chain Monte Carlo |
| MCS | Monte-Carlo simulation |
| MEM | Maximum entropy fitting method |
| MFEM | Multi-scale finite element method |
| MLS | Moving least square |
| MM | Meta-model(s) |
| MPP | Most probable failure point |
| MPR | Multivariate (quadratic) polynomial regression |
| MVFOSM | Mean value first-order second moment method |
| NF | Number of fitting points |
| NI | Numerical integration |
| OWT | Offshore wind turbine |
| PCE | Polynomial chaos expansion |
| PC-Kriging | Polynomial chaos-kriging |
| Probability density function | |
| PF | Performance function |
| PLS | Partial least squares |
| PMA | Performance measure approach |
| POF | Probability of failure |
| PSMFEM | Perturbation-based stochastic multi-scale finite element method |
| RA | Reliability analysis/assessment |
| RBF | Radial basis function |
| RBO | Reliability-based optimization |
| RHL–RF | Relaxed Hasofer Lind–Rackwitz Fiessler method |
| RI | Reliability index |
| RS | Response surface |
| RSM | Response surface method/model |
| SAC | Self-adaptive conjugate |
| SFEM | Stochastic finite element method |
| SGFEM | Stochastic Galerkin FEM |
| SHM | Structural health monitoring |
| SKRA | Sequential kriging reliability Analysis |
| SLS | Serviceability limit state |
| SM | Surrogate modelling |
| SORM | Second-Order reliability method |
| SPA | Saddle point approximation |
| SR | Structural reliability |
| SRA | Structural reliability assessment |
| SRBDO | System reliability-based design optimization |
| SRE | Structural reliability evaluation |
| SRSM | Stochastic response surface method |
| SS | Subset simulation |
| SSFEM | Spectral stochastic finite element Method |
| STM | Stability Transformation Method |
| SVM | Support vector machines |
| SVR | Support vector regression |
| T-D | Time-dependent |
| T-I | Time-independent/time-invariant |
| T-V | Time-variant |
| ULS | Ultimate limit state |
| Nomenclature | |
| Density function | |
| POF | |
| Random variable | |
| Regression coefficients for a quadratic regression | |
| The joint PDF of the random variables | |
| Limit-state function | |
| Realization of the random variable | |
| Direction cosine | |
| Mean of random variables | |
| Standard deviation of random variables | |
| Cumulative density function of the standard normal distribution | |
| Density function of standard normal distribution | |
| Failure domain identifier | |
| Number of samples | |
| Probability function | |
| Standard normal form of variables | |
| Vector | |
| Target coefficient of variation of failure probability | |
| n-dimensional random vector | |
| Reliability/safety index | |
References
- Leimeister, M.; Kolios, A. A review of reliability-based methods for risk analysis and their application in the offshore wind industry. Renew. Sustain. Energy Rev. 2018, 91, 1065–1076. [Google Scholar] [CrossRef]
- Shittu, A.A.; Mehmanparast, A.; Shafiee, M.; Kolios, A.; Hart, P.; Pilario, K.E. Structural Reliability Assessment of Offshore Wind Turbine Support Structures Subjected to Pitting Corrosion-Fatigue: A Damage Tolerance Modelling Approach. Wind Energy 2020, 23, 2004–2026. [Google Scholar] [CrossRef]
- Shittu, A.A.; Mehmanparast, A.; Wang, L.; Salonitis, K.; Kolios, A. Comparative Study of Structural Reliability Assessment Methods for Offshore Wind Turbine Jacket Support Structures. Appl. Sci. 2020, 10, 860. [Google Scholar] [CrossRef]
- Shittu, A.A. Structural Reliability Assessment of Complex Offshore Structures Based on Non-Intrusive Stochastic Methods; Cranfield University: Bedford, UK, 2020. [Google Scholar]
- Melchers, R.; Andre, T. Structural Reliability Analysis and Prediction, 3rd ed.; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Choi, S.-K.; Grandhi, R.; Canfield, R. Reliability-Based Structural Design; Springer: New York, NY, USA, 2006. [Google Scholar]
- Kolios, A. A multi-Configuration Approach to Reliability Based Structural Integrity Assessment for Ultimate Strength; Cranfield University: Cranfield, UK, 2010. [Google Scholar]
- Vrouwenvelder, T.; Karadeniz, H. Overview of structural reliability methods. In Safety and Reliability of Industrial Products, Systems and Structures; Soares, G.C., Ed.; Taylor & Francis Group: San Francisco, CA, USA, 2010; pp. 181–189. ISBN 9780415663922. [Google Scholar]
- Karadeniz, H. Review of Structural Reliability Methods with Applicability in Practice. In Proceedings of the the Sixteenth (2006) International Offshore and Polar Engineering Conference, San Francisco, CA, USA, 28 May–2 June 2006; The International Society of Offshore and Polar Engineers: San Francisco, CA, USA, 2006; pp. 393–402. [Google Scholar]
- Ditlevsen, O.; Madsen, H.O. Structural Reliability Methods; Wiley: New York, NY, USA, 2007; ISBN 0471960861. [Google Scholar]
- Li, Q.; Wang, C.; Ellingwood, B.R. Time-dependent reliability of aging structures in the presence of non-stationary loads and degradation. Struct. Saf. 2015, 52, 132–141. [Google Scholar] [CrossRef]
- Li, G.; Lu, Z.; Li, L.; Ren, B. Aleatory and epistemic uncertainties analysis based on non-probabilistic reliability and its kriging solution. Appl. Math. Model. 2016, 40, 5703–5716. [Google Scholar] [CrossRef]
- Wei, P.; Song, J.; Bi, S.; Broggi, M.; Beer, M.; Lu, Z.; Yue, Z. Non-intrusive stochastic analysis with parameterized imprecise probability models: II. Reliability and rare events analysis. Mech. Syst. Signal Process. 2019, 126, 227–247. [Google Scholar] [CrossRef]
- Huang, C.; El Hami, A.; Radi, B. Overview of Structural Reliability Analysis Methods—Part III: Global Reliability Methods. Incert. Fiabilité des Systèmes Multiphysiques 2016, 17, 1–10. [Google Scholar] [CrossRef]
- Huang, C.; El Hami, A.; Radi, B. Overview of Structural Reliability Analysis Methods—Part I: Local Reliability Methods. Incert. Fiabilité des Systèmes Multiphysiques 2017, 17, 1–10. [Google Scholar] [CrossRef]
- Nowak, A.S.; Collins, K.R. Reliability of Structures, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Breitung, K. 40 years FORM: Some new aspects? Probabilistic Eng. Mech. 2015, 42, 71–77. [Google Scholar] [CrossRef]
- Shi, P.; Mahadevan, S. Damage tolerance approach for probabilistic pitting corrosion fatigue life prediction. Eng. Fract. Mech. 2001, 68, 1493–1507. [Google Scholar] [CrossRef]
- Ayyub, B.M.; McCuen, R.H. Probability, Statistics, and Reliability for Engineers and Scientists, 3rd ed.; Taylor and Francis Group: Boca Raton, FL, USA, 2011; ISBN 9781439895337. [Google Scholar]
- Low, B.K.; Tang, W.H. Efficient Spreadsheet Algorithm for First-Order Reliability Method. J. Eng. Mech. 2007, 133, 1378–1387. [Google Scholar] [CrossRef]
- Keshtegar, B.; Chakraborty, S. A hybrid self-adaptive conjugate first order reliability method for robust structural reliability analysis. Appl. Math. Model. 2018, 53, 319–332. [Google Scholar] [CrossRef]
- Keshtegar, B.; Meng, Z. A hybrid relaxed first-order reliability method for efficient structural reliability analysis. Struct. Saf. 2017, 66, 84–93. [Google Scholar] [CrossRef]
- Keshtegar, B.; Chakraborty, S. An efficient-robust structural reliability method by adaptive finite-step length based on Armijo line search. Reliab. Eng. Syst. Saf. 2018, 172, 195–206. [Google Scholar] [CrossRef]
- Yang, D. Chaos control for numerical instability of first order reliability method. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 3131–3141. [Google Scholar] [CrossRef]
- Keshtegar, B. Chaotic conjugate stability transformation method for structural reliability analysis. Comput. Methods Appl. Mech. Eng. 2016, 310, 866–885. [Google Scholar] [CrossRef]
- Pedroso, D.M. FORM reliability analysis using a parallel evolutionary algorithm. Struct. Saf. 2017, 65, 84–99. [Google Scholar] [CrossRef]
- Shi, X.; Teixeira, A.P.; Zhang, J.; Soares, C.G. Structural reliability analysis based on probabilistic response modelling using the Maximum Entropy Method. Eng. Struct. 2014, 70, 106–116. [Google Scholar] [CrossRef]
- Rackwitz, R. Reliability analysis—A review and some perspectives. Struct. Saf. 2001, 23, 365–395. [Google Scholar] [CrossRef]
- Huang, X.; Li, Y.; Zhang, Y.; Zhang, X. A new direct second-order reliability analysis method. Appl. Math. Model. 2018, 55, 68–80. [Google Scholar] [CrossRef]
- Karadeniz, H. Stochastic Analysis of Offshore Steel Structures; Springer: London, UK, 2013; ISBN 9781849961899. [Google Scholar]
- Cardoso, J.B.; de Almeida, J.R.; Dias, J.M.; Coelho, P.G. Structural reliability analysis using Monte Carlo simulation and neural networks. Adv. Eng. Softw. 2008, 39, 505–513. [Google Scholar] [CrossRef]
- Zhang, H.; Mullen, R.L.; Muhanna, R.L. Interval Monte Carlo methods for structural reliability. Struct. Saf. 2010, 32, 183–190. [Google Scholar] [CrossRef]
- Naess, A.; Leira, B.J.; Batsevych, O. Reliability analysis of large structural systems. Probabilistic Eng. Mech. 2012, 28, 164–168. [Google Scholar] [CrossRef]
- Gaspar, B.; Naess, A.; Leira, B.J.; Soares, C.G. System reliability analysis by monte carlo based method and finite element structural models. J. Offshore Mech. Arct. Eng. 2014, 136, 1–9. [Google Scholar] [CrossRef]
- Jahani, E.; Muhanna, R.L.; Shayanfar, M.A.; Barkhordari, M.A. Reliability assessment with fuzzy random variables using interval monte carlo simulation. Comput. Civ. Infrastruct. Eng. 2014, 29, 208–220. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, H.; Wang, W. A support vector density-based importance sampling for reliability assessment. Reliab. Eng. Syst. Saf. 2012, 106, 86–93. [Google Scholar] [CrossRef]
- Shayanfar, M.A.; Barkhordari, M.A.; Barkhori, M.; Barkhori, M. An adaptive directional importance sampling method for structural reliability analysis. Struct. Saf. 2018, 70, 14–20. [Google Scholar] [CrossRef]
- Zhang, H. Interval importance sampling method for finite element-based structural reliability assessment under parameter uncertainties. Struct. Saf. 2012, 38, 1–10. [Google Scholar] [CrossRef]
- Reh, S.; Beley, J.D.; Mukherjee, S.; Khor, E.H. Probabilistic finite element analysis using ANSYS. Struct. Saf. 2006, 28, 17–43. [Google Scholar] [CrossRef]
- Papaioannou, I.; Betz, W.; Zwirglmaier, K.; Straub, D. MCMC algorithms for Subset Simulation. Probabilistic Eng. Mech. 2015, 41, 89–103. [Google Scholar] [CrossRef]
- Schneider, R.; Thöns, S.; Straub, D. Reliability analysis and updating of deteriorating systems with subset simulation. Struct. Saf. 2017, 64, 20–36. [Google Scholar] [CrossRef]
- Bucher, C.; Most, T. A comparison of approximate response functions in structural reliability analysis. Probabilistic Eng. Mech. 2008, 23, 154–163. [Google Scholar] [CrossRef]
- Salonitis, K.; Kolios, A. Reliability assessment of cutting tool life based on surrogate approximation methods. Int. J. Adv. Manuf. Technol. 2014, 71, 1197–1208. [Google Scholar] [CrossRef]
- Kolios, A.; Di Maio, L.F.; Wang, L.; Cui, L.; Sheng, Q. Reliability assessment of point-absorber wave energy converters. Ocean Eng. 2018, 163, 40–50. [Google Scholar] [CrossRef]
- Salonitis, K.; Kolios, A. Force-based reliability estimation of remaining cutting tool life in titanium milling. Int. J. Adv. Manuf. Technol. 2020, 106, 3321–3333. [Google Scholar] [CrossRef]
- Kolios, A.J.; Brennan, F. Reliability Deterioration of Offshore/Marine Steel Structures due to Effects of Corrosion. In Proceedings of the Asranet 2012, London, UK, 2–4 July 2012; p. 10. [Google Scholar]
- Ivanhoe, R.O.; Wang, L.; Kolios, A. Generic framework for reliability assessment of offshore wind turbine jacket support structures under stochastic and time dependent variables. Ocean Eng. 2020, 216, 107691. [Google Scholar] [CrossRef]
- Wang, L.; Kolios, A. A generic framework for reliability assessment of offshore wind turbine monopiles considering soil-solid interaction and harsh marine environments. In Proceedings of the Progress in the Analysis and Design of Marine Structures-Proceedings of the 6th International Conference on Marine Structures, MARSTRUCT 2017, Lisbon, Portugal, 8–10 May 2017; pp. 931–938. [Google Scholar]
- Kolios, A.; Wang, L. Advanced reliability assessment of offshore wind turbine monopiles by combining reliability analysis method and SHM/CM technology. In Proceedings of the 28th International Ocean and Polar Engineering Conference, Sapporo, Japan, 1–15 June 2018; pp. 1412–1419. [Google Scholar]
- Huang, X.; Liu, Y.; Zhang, Y.; Zhang, X. Reliability analysis of structures using stochastic response surface method and saddlepoint approximation. Struct. Multidiscip. Optim. 2017, 55, 2003–2012. [Google Scholar] [CrossRef]
- Gavin, H.P.; Yau, S.C. High-order limit state functions in the response surface method for structural reliability analysis. Struct. Saf. 2008, 30, 162–179. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, S.G. Reliability analysis of offshore wind turbine support structures under extreme ocean environmental loads. Renew. Energy 2015, 79, 161–166. [Google Scholar] [CrossRef]
- Rücker, W.; Faber, M.H. Support Structure Reliability of Offshore Wind Turbines Utilizing an Adaptive Response Surface Method. In Proceedings of the ASME 2010 29th International Conference on Ocean Offshore Arctic Engineering, Shanghai, China, 1–6 June 2010. [Google Scholar] [CrossRef]
- Wen, Z.; Pei, H.; Liu, H.; Yue, Z. A Sequential Kriging reliability analysis method with characteristics of adaptive sampling regions and parallelizability. Reliab. Eng. Syst. Saf. 2016, 153, 170–179. [Google Scholar] [CrossRef]
- Gaspar, B.; Teixeira, A.P.; Guedes Soares, C. Adaptive surrogate model with active refinement combining Kriging and a trust region method. Reliab. Eng. Syst. Saf. 2017, 165, 277–291. [Google Scholar] [CrossRef]
- Bichon, B.J. Efficient Surrogate Modeling for Reliability Analysis and Design; Vanderbilt University: Vanderbilt, TN, USA, 2010. [Google Scholar]
- Richmond, M.; Sobey, A.; Pandit, R.; Kolios, A. Stochastic assessment of aerodynamics within offshore wind farms based on machine-learning. Renew. Energy 2020, 161, 650–661. [Google Scholar] [CrossRef]
- Zhao, H.; Yue, Z.; Liu, Y.; Gao, Z.; Zhang, Y. An efficient reliability method combining adaptive importance sampling and Kriging metamodel. Appl. Math. Model. 2015, 39, 1853–1866. [Google Scholar] [CrossRef]
- Cadini, F.; Santos, F.; Zio, E. An improved adaptive kriging-based importance technique for sampling multiple failure regions of low probability. Reliab. Eng. Syst. Saf. 2014, 131, 109–117. [Google Scholar] [CrossRef]
- Huang, X.; Chen, J.; Zhu, H. Assessing small failure probabilities by AK–SS: An active learning method combining Kriging and Subset Simulation. Struct. Saf. 2016, 59, 86–95. [Google Scholar] [CrossRef]
- Bichon, B.J.; Eldred, M.S.; Swiler, L.P.; Mahadevan, S.; McFarland, J.M. Efficient Global Reliability Analysis for Nonlinear Implicit Performance Functions. AIAA J. 2008, 46, 2459–2468. [Google Scholar] [CrossRef]
- Pan, Q.; Dias, D. An efficient reliability method combining adaptive Support Vector Machine and Monte Carlo Simulation. Struct. Saf. 2017, 67, 85–95. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, B.; Wang, W. A multiwavelet support vector regression method for efficient reliability assessment. Reliab. Eng. Syst. Saf. 2015, 136, 132–139. [Google Scholar] [CrossRef]
- Chojaczyk, A.A.; Teixeira, A.P.; Neves, L.C.; Cardoso, J.B.; Guedes Soares, C. Review and application of Artificial Neural Networks models in reliability analysis of steel structures. Struct. Saf. 2015, 52, 78–89. [Google Scholar] [CrossRef]
- Gomes, H.M.; Awruch, A.M. Comparison of response surface and neural network with other methods for structural reliability analysis. Struct. Saf. 2004, 26, 49–67. [Google Scholar] [CrossRef]
- Nie, J.; Ellingwood, B.R. Finite element-based structural reliability assessment using efficient directional simulation. J. Eng. Mech. 2005, 131, 259–267. [Google Scholar] [CrossRef]
- Sundar, V.S.; Shields, M.D. Surrogate-enhanced stochastic search algorithms to identify implicitly defined functions for reliability analysis. Struct. Saf. 2016, 62, 1–11. [Google Scholar] [CrossRef]
- Zhang, H.; Ellingwood, B.R.; Rasmussen, K.J.R. System reliabilities in steel structural frame design by inelastic analysis. Eng. Struct. 2014, 81, 341–348. [Google Scholar] [CrossRef]
- DNV-OS-C101 Design of Offshore Steel Structures, General (LRFD Method); National Association of Corrosion Engineers: Huston, TX, USA, 2015.
- Mehmanparast, A.; Taylor, J.; Brennan, F.; Tavares, I. Experimental investigation of mechanical and fracture properties of offshore wind monopile weldments: SLIC interlaboratory test results. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 2485–2501. [Google Scholar] [CrossRef]
- Mehmanparast, A.; Brennan, F.; Tavares, I. Fatigue crack growth rates for offshore wind monopile weldments in air and seawater: SLIC inter-laboratory test results. Mater. Des. 2017, 114, 494–504. [Google Scholar] [CrossRef]
- Igwemezie, V.; Mehmanparast, A. Waveform and frequency effects on corrosion-fatigue crack growth behaviour in modern marine steels. Int. J. Fatigue 2020, 134, 105484. [Google Scholar] [CrossRef]
- Igwemezie, V.; Dirisu, P.; Mehmanparast, A. Critical assessment of the fatigue crack growth rate sensitivity to material microstructure in ferrite-pearlite steels in air and marine environment. Mater. Sci. Eng. A 2019, 754, 750–765. [Google Scholar] [CrossRef]
- Igwemezie, V.; Mehmanparast, A.; Kolios, A. Current trend in offshore wind energy sector and material requirements for fatigue resistance improvement in large wind turbine support structures–A review. Renew. Sustain. Energy Rev. 2019, 101, 181–196. [Google Scholar] [CrossRef]
- Igwemezie, V.; Mehmanparast, A.; Kolios, A. Materials selection for XL wind turbine support structures: A corrosion-fatigue perspective. Mar. Struct. 2018, 61, 381–397. [Google Scholar] [CrossRef]
- Jacob, A.; Mehmanparast, A.; D’Urzo, R.; Kelleher, J. Experimental and numerical investigation of residual stress effects on fatigue crack growth behaviour of S355 steel weldments. Int. J. Fatigue 2019, 128, 105196. [Google Scholar] [CrossRef]
- Jacob, A.; Oliveira, J.; Mehmanparast, A.; Hosseinzadeh, F.; Kelleher, J.; Berto, F. Residual stress measurements in offshore wind monopile weldments using neutron diffraction technique and contour method. Theor. Appl. Fract. Mech. 2018, 96, 418–427. [Google Scholar] [CrossRef]
- Bocher, M.; Mehmanparast, A.; Braithwaite, J.; Shafiee, M. New shape function solutions for fracture mechanics analysis of offshore wind turbine monopile foundations. Ocean Eng. 2018, 160, 264–275. [Google Scholar] [CrossRef]
- Khajeian, A.; Mahmoudi, A.H.; Mehmanparast, A. Shot peening effects on residual stresses redistribution of offshore wind monopile multi-pass weldments. Mar. Struct. 2019, 66, 106–120. [Google Scholar] [CrossRef]
- Aldosary, M.; Wang, J.; Li, C. Structural reliability and stochastic finite element methods: State-of-the-art review and evidence-based comparison. Eng. Comput. 2018, 35, 2165–2214. [Google Scholar] [CrossRef]
- Li, Y.-J.; Huang, B.; Li, C.-Q. Hybrid perturbation-Galerkin methods for structural reliability analysis. Probabilistic Eng. Mech. 2017, 48, 59–67. [Google Scholar] [CrossRef]
- Feng, J.; Wu, D.; Gao, W.; Li, G. Hybrid uncertain natural frequency analysis for structures with random and interval fields. Comput. Methods Appl. Mech. Eng. 2018, 328, 365–389. [Google Scholar] [CrossRef]
- Papadopoulos, V.; Papadrakakis, M.; Deodatis, G. Analysis of mean and mean square response of general linear stochastic finite element systems. Comput. Methods Appl. Mech. Eng. 2006, 195, 5454–5471. [Google Scholar] [CrossRef]
- Gong, C.; Zhou, W. Improvement of equivalent component approach for reliability analyses of series systems. Struct. Saf. 2017, 68, 65–72. [Google Scholar] [CrossRef]
- Zhang, H.; Shayan, S.; Rasmussen, K.J.R.; Ellingwood, B.R. System-based design of planar steel frames, I: Reliability framework. J. Constr. Steel Res. 2016, 123, 135–143. [Google Scholar] [CrossRef]
- Gong, C.; Frangopol, D.M. An efficient time-dependent reliability method. Struct. Saf. 2019, 81, 101864. [Google Scholar] [CrossRef]
- Yang, D.Y.; Teng, J.G.; Frangopol, D.M. Cross-entropy-based adaptive importance sampling for time-dependent reliability analysis of deteriorating structures. Struct. Saf. 2017, 66, 38–50. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: New York, NY, USA, 1999. [Google Scholar]
- Jiang, Z.; Hu, W.; Dong, W.; Gao, Z.; Ren, Z. Structural reliability analysis of wind turbines: A review. Energies 2017, 10, 2099. [Google Scholar] [CrossRef]
- Shittu, A.A.; Mehmanparast, A.; Pilario, K.E.; Hart, P.; Kolios, A.J. Comparative study between SN and fracture mechanics approach on reliability assessment of offshore wind turbine jacket foundations. 2020. under review. [Google Scholar]
- Dong, W.; Moan, T.; Gao, Z. Fatigue reliability analysis of the jacket support structure for offshore wind turbine considering the effect of corrosion and inspection. Reliab. Eng. Syst. Saf. 2012, 106, 11–27. [Google Scholar] [CrossRef]
- Yeter, B.; Garbatov, Y.; Soares, C.G. Fatigue reliability of an offshore wind turbine supporting structure accounting for inspection and repair. In Analysis and Design of Marine Structures; Soares, G., Shenoi, E., Eds.; Taylor & Francis Group: London, UK, 2015; pp. 737–747. [Google Scholar]
- Yeter, B.; Garbatov, Y.; Soares, C.G. Reliability of Offshore Wind Turbine Support Structures Subjected to Extreme Wave-Induced Loads and Defects. In Proceedings of the ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 14–18 June 2016. [Google Scholar]
- Yeter, B.; Garbatov, Y.; Guedes Soares, C. System reliability of a jacket offshore wind turbine subjected to fatigue. In Proceedings of the 5th International Conference on Marine Structures, MARSTRUCT, Lisbon, Portugal, 25–27 March 2017; pp. 939–950. [Google Scholar]
- Gholizad, A.; Golafshani, A.A.; Akrami, V. Structural reliability of offshore platforms considering fatigue damage and different failure scenarios. Ocean Eng. 2012, 46, 1–8. [Google Scholar] [CrossRef]
- Ayala-uraga, E.; Moan, T. Fatigue reliability-based assessment of welded joints applying consistent fracture mechanics formulations. Int. J. Fatigue 2007, 29, 444–456. [Google Scholar] [CrossRef]
- Ziegler, L.; Muskulus, M. Comparing a fracture mechanics model to the SN-curve approach for jacket-supported offshore wind turbines: Challenges and opportunities for lifetime prediction. In Proceedings of the ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering, OMAE2016, Busan, Korea, 19–24 June 2016; American Society of Mechanical Engineers (ASME): Busan, Korea, 2016; pp. 1–10. [Google Scholar]

| Method | Capabilities | Limitations | |
|---|---|---|---|
| First Order Reliability Method (FORM) | Mean Value First Order Second Moment Reliability Method |
| The applicability range of this method is diminished as a result of the following reasons:
|
| Hasofer and Lind Method | FORM approximation gives adequate outcome when the function is nearly linear close to the MPP, and the LSS has only one minimal distance point. |
| |
| Hasofer and Lind-Rackwitz Fiessler Method | Widely used approximate analytical method since it provides a good balance between efficiency and accuracy in realistic engineering RA. |
| |
| Second-Order Reliability Method | Ideal for cases where the LSS has large or irregular curvatures (high non-linearity), the POF estimated by FORM, using the RI , can produce inaccurate and unreliable results. By introducing second-order Taylor series expansions (or other polynomials), this drawback may be overcome. |
| |
| Method | Capabilities | Limitations | ||
|---|---|---|---|---|
| Analytical Integration | Ideal for simple failure surface |
| ||
| Numerical Integration | Standard routines are found in most computer systems | Not always feasible, owing to the growth-off errors and excessive computational times | ||
| Crude Monte Carlo Simulation Technique (MCS) | Most versatile, clear, and well understood exact method available Requires no partial derivative of LSF; therefore, the method can be used for implicit LSF. |
| ||
| Variance Reduction Techniques | MCS with Importance Sampling Technique |
|
| |
| Adaptive Sampling |
| Application of the directional sampling and adaptive sampling is limited to a moderate number of random variables | ||
| Conditional Expectation Techniques | Directional Simulation |
| The technique is not very efficient for one or a few planar LS. | |
| Axis Orthogonal Simulation Technique | Is recommended for convex failure sets | They typically require a large number of response function evaluations, which makes them impractical if the response function is expensive to evaluate. | ||
| Design Point Simulation | Makes use of the FORM design point which makes it less cumbersome in the search for the POF | |||
| Subset Simulation |
|
| ||
| Method | Capabilities | Limitations | ||
|---|---|---|---|---|
| Parallel System | A parallel system fails when all the links (potential failure modes) fail. The most consistent function of the parallel system is for modelling the sequential failure of components in a single failure path leading to structural failure | Redundant members are introduced which introduces a computationally intensive procedure | ||
| Series System | Ideal for pipelines | Failure of one component leads to failure of the system | ||
| Stochastic Finite Element Method | Perturbation Method | The perturbation techniques are desirable owing to their efficiency in terms of computation times and accuracy | Too mathematically intensive | |
| Neumann Expansion Solution |
| Determining the covariance matrix among all elements of the fluctuation part of the stiffness matrix involves prohibitively high computational effort. | ||
| Response Surface Method |
|
| ||
| Branch and Bound Method | Are useful for the elastic-plastic analysis of frame structures where effects of plasticity like the formation of plastic hinges give sharp changes in the stiffness behavior | Its application is limited | ||
| Surrogate Models/Response Surface Model/Meta-Models | Polynomial Regression Models | The most widely used due to their simple formulations and implementation |
| |
| Approaches Based on: | Radial Basis Function |
| Computationally efficient but at the expense of accuracy | |
| Local Interpolation Model (Polyhedra) |
| It is an approximate method | ||
| Artificial Neural Network |
|
| ||
| Support vector Machine | In comparison to ANNs, SVM employs the theory of minimizing the structure risk to avoid the problems of excessive study, calamity data, local minimum value etc. | Its implementation involves high computational efforts, and sufficient model sparsity cannot be guaranteed. | ||
| Moving Least Squares |
|
| ||
| Kriging Models |
| Significantly more complex compared to polynomial regression models | ||
| Method | Capabilities | Limitations | ||
|---|---|---|---|---|
| Stochastic Expansion | Non-Intrusive | Stochastic Response Surface Method |
| It is widely used in chemical Engineering. Its application in Structural Engineering is still burgeoning. |
| Intrusive | Spectral Stochastic FEM | Gives more reliable results |
| |
| Time variant reliability Methods |
| Practical application of T-V reliability methodology appears rather limited, partially because only very few computer codes are available | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shittu, A.A.; Kolios, A.; Mehmanparast, A. A Systematic Review of Structural Reliability Methods for Deformation and Fatigue Analysis of Offshore Jacket Structures. Metals 2021, 11, 50. https://doi.org/10.3390/met11010050
Shittu AA, Kolios A, Mehmanparast A. A Systematic Review of Structural Reliability Methods for Deformation and Fatigue Analysis of Offshore Jacket Structures. Metals. 2021; 11(1):50. https://doi.org/10.3390/met11010050
Chicago/Turabian StyleShittu, Abdulhakim Adeoye, Athanasios Kolios, and Ali Mehmanparast. 2021. "A Systematic Review of Structural Reliability Methods for Deformation and Fatigue Analysis of Offshore Jacket Structures" Metals 11, no. 1: 50. https://doi.org/10.3390/met11010050
APA StyleShittu, A. A., Kolios, A., & Mehmanparast, A. (2021). A Systematic Review of Structural Reliability Methods for Deformation and Fatigue Analysis of Offshore Jacket Structures. Metals, 11(1), 50. https://doi.org/10.3390/met11010050