Thermomechanical Simulations of Residual Stresses and Distortion in Electron Beam Melting with Experimental Validation for Ti-6Al-4V
Abstract
1. Introduction
2. Materials and Methods
2.1. Finite Element Modeling
2.1.1. Material Properties
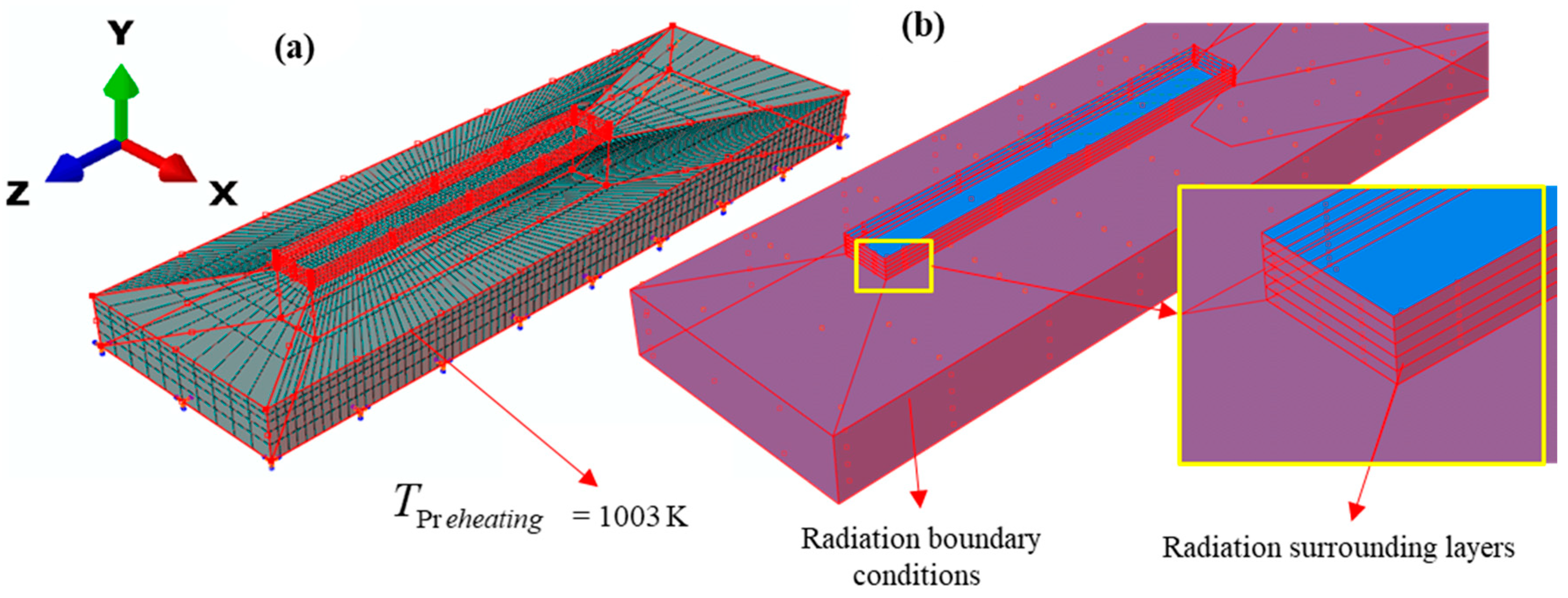
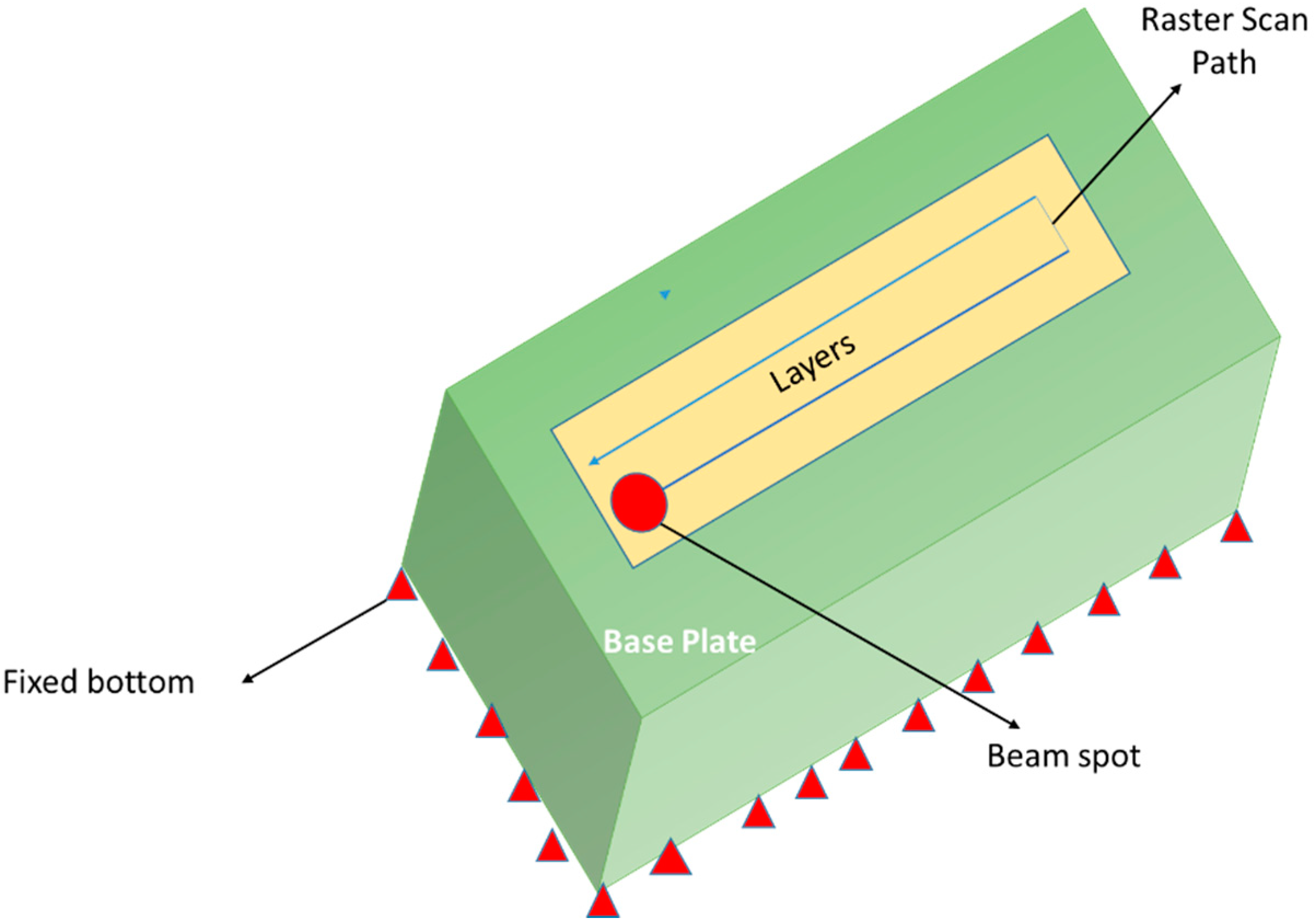
2.1.2. Initial and Boundary Conditions
2.1.3. Electron Beam Modeling
2.2. Contact
- ○
- The deformation effect will be transferred from one layer to another layer through the tied nodes.
- ○
- Heat degree of freedom will be transferred from one layer to another through the tied nodes.
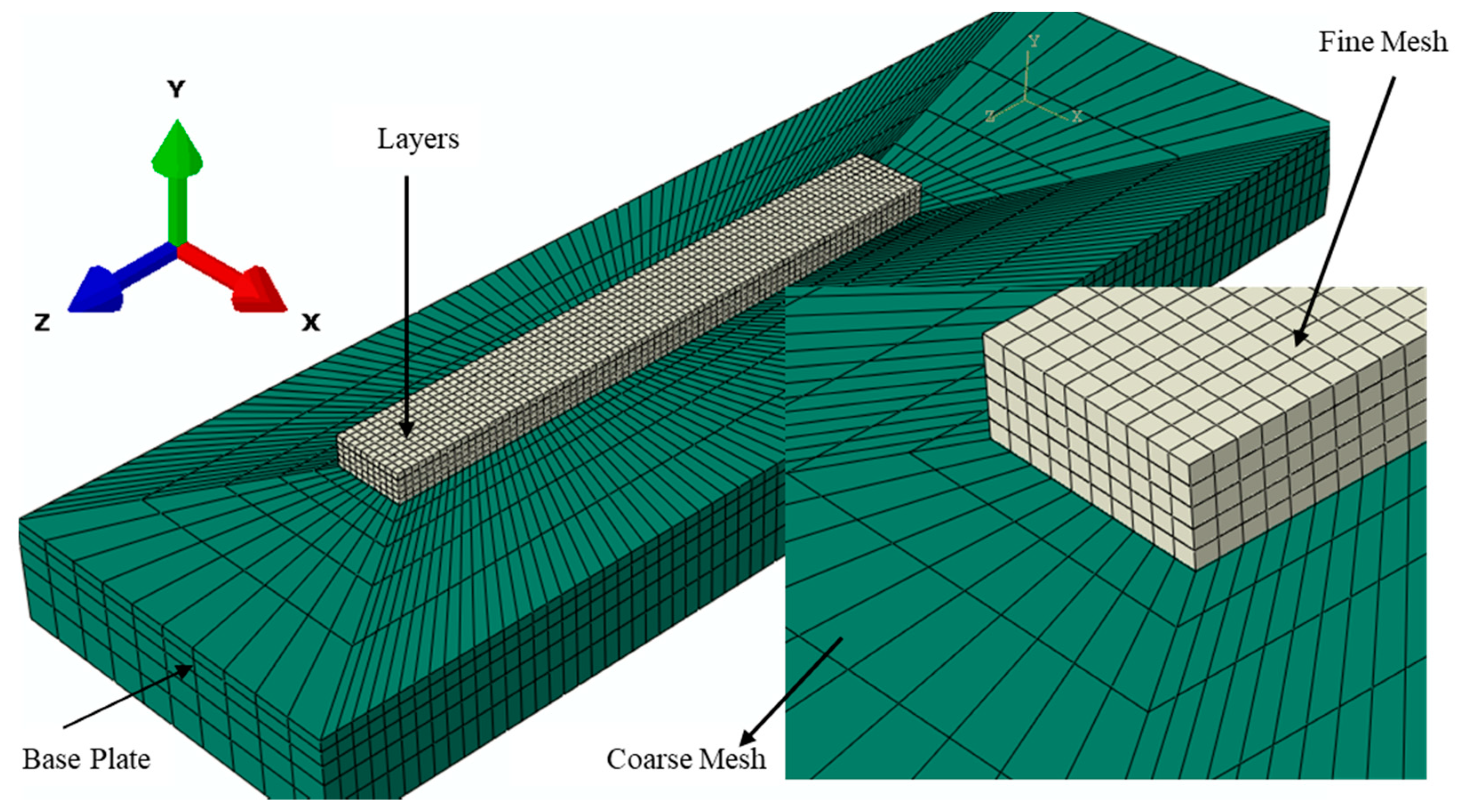
2.3. FE Mesh
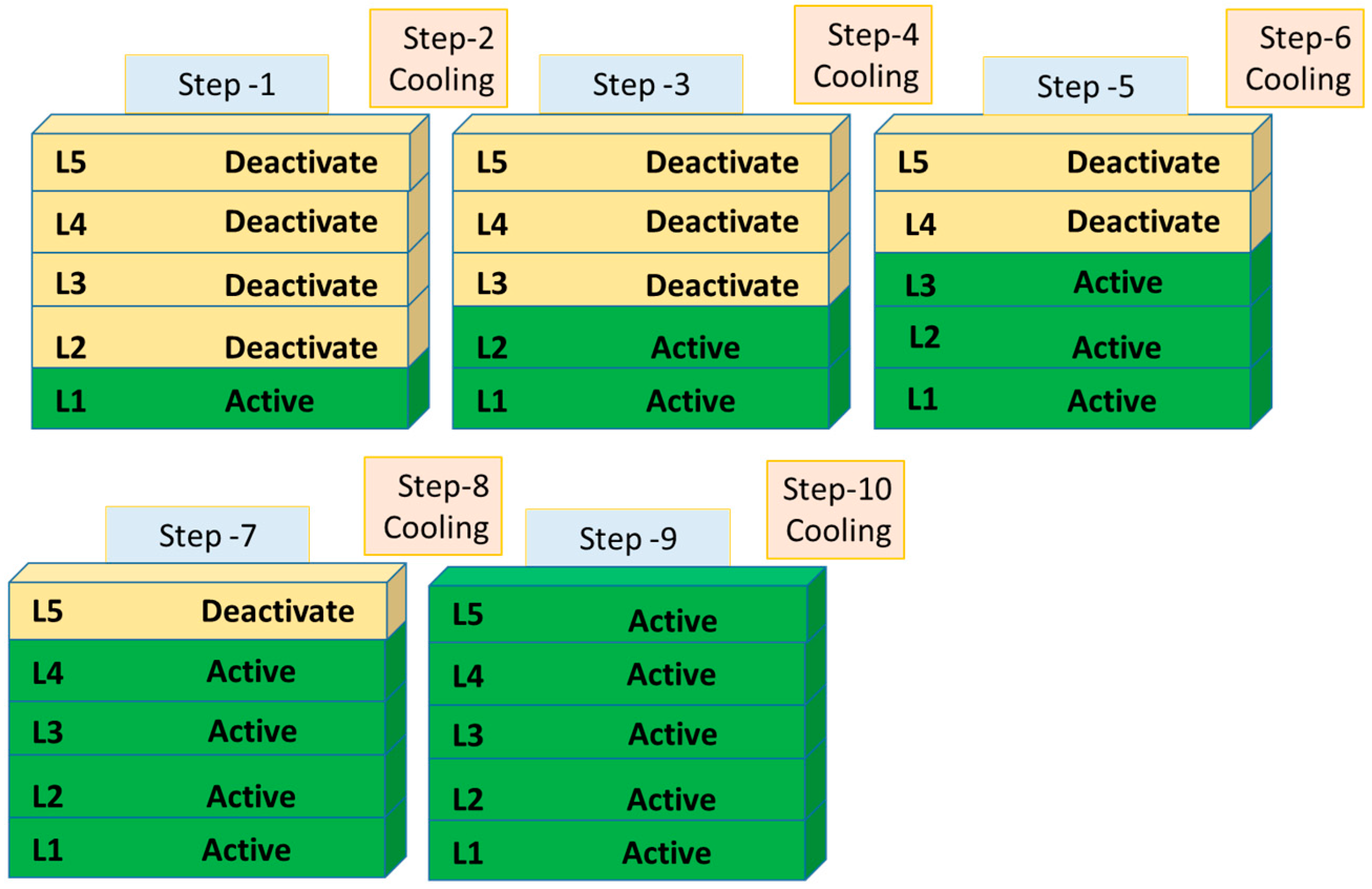
2.4. Powder Addition in a Layer by Layer Fashion
2.5. Fabrication of the Thin-Walled EBM Parts
3. Results and Discussion
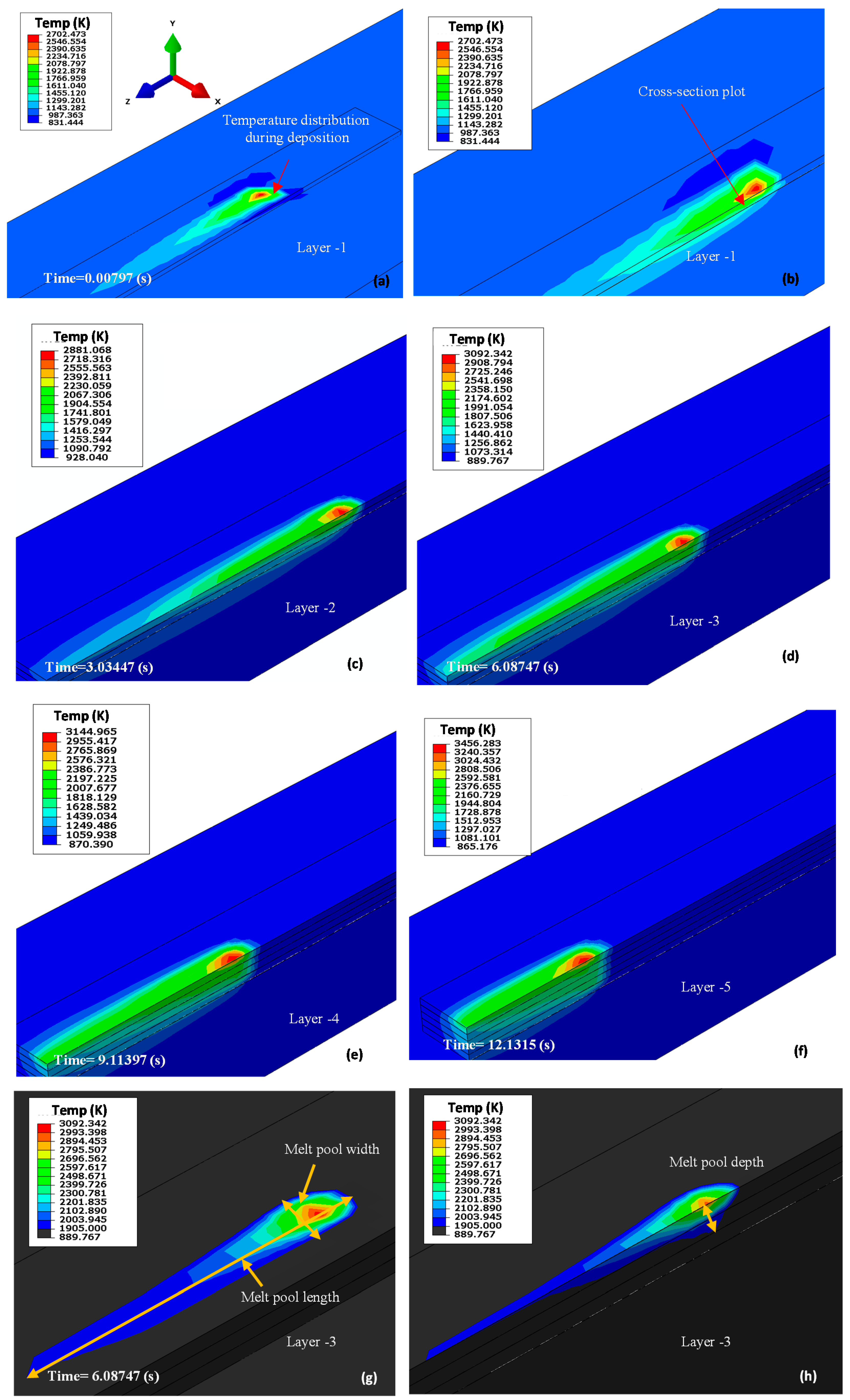
3.1. Temperature Field
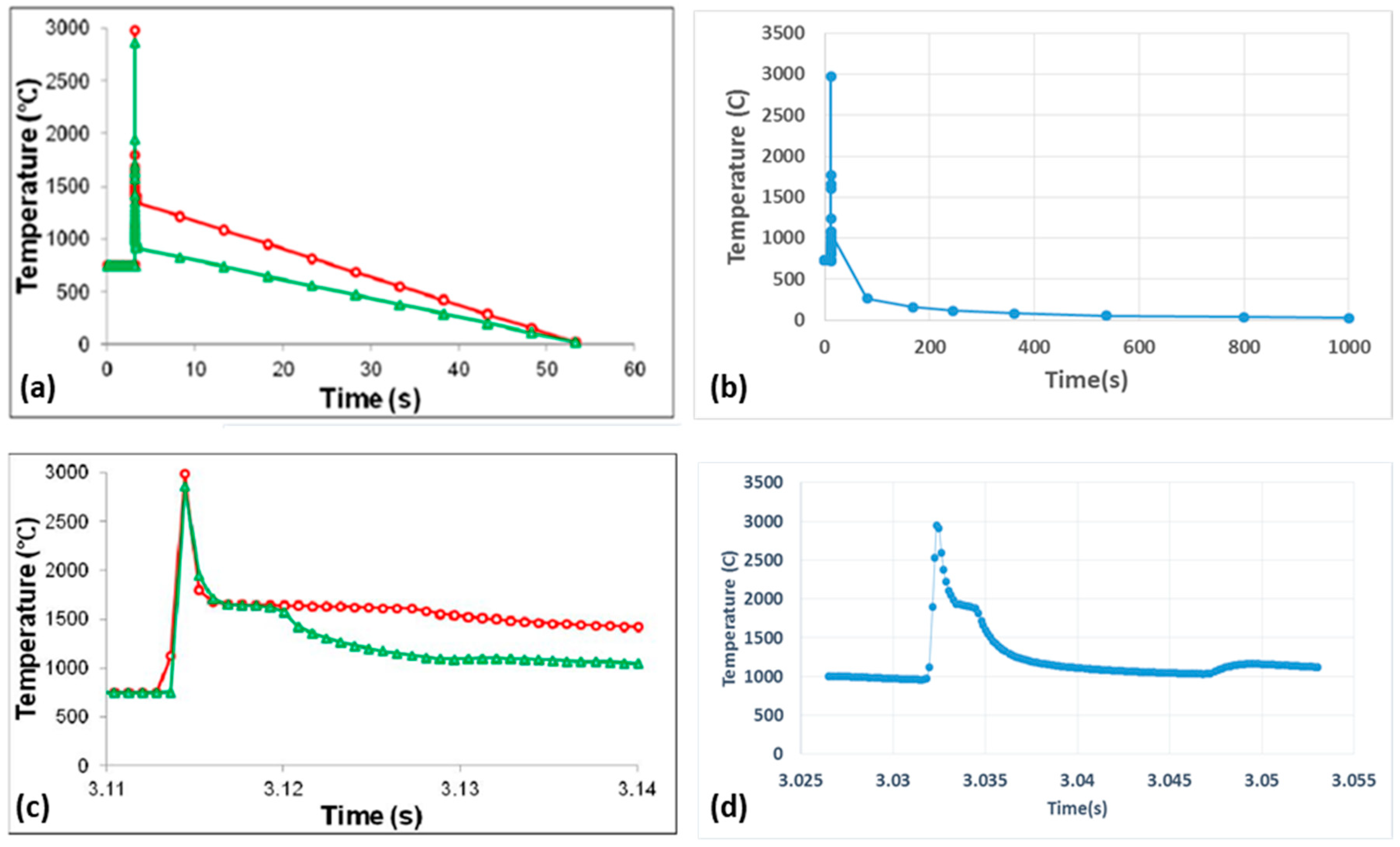
3.1.1. Temperature Gradient
3.1.2. Model Validation
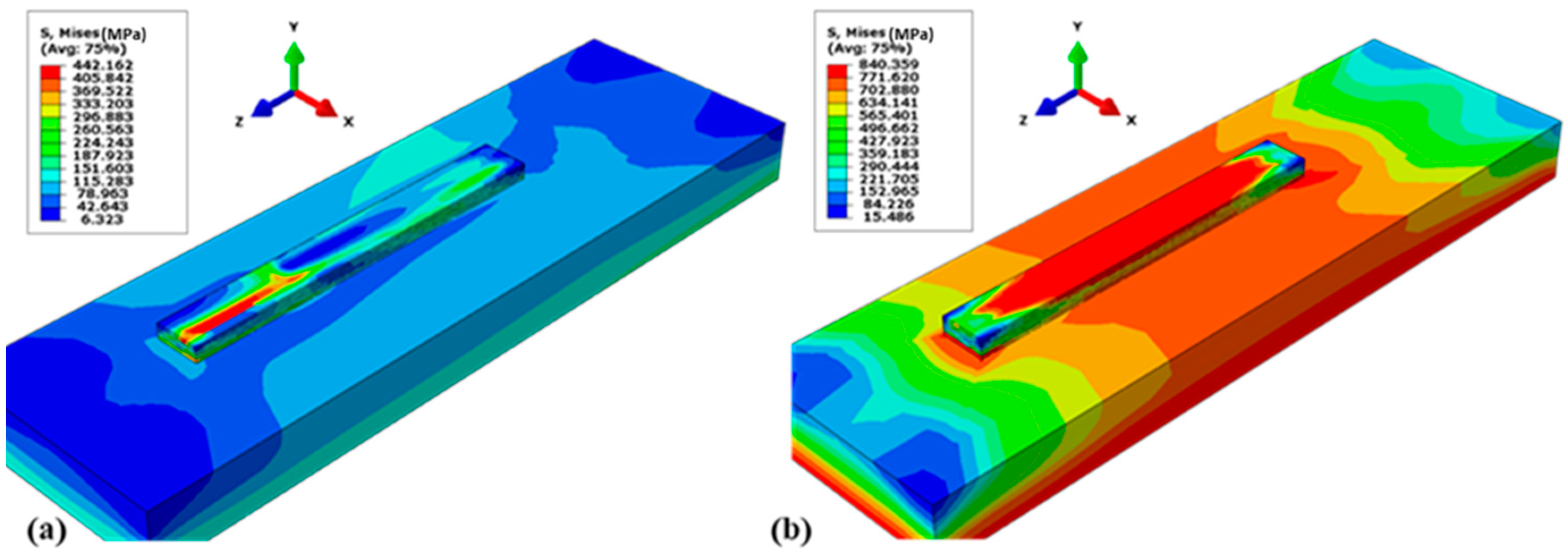
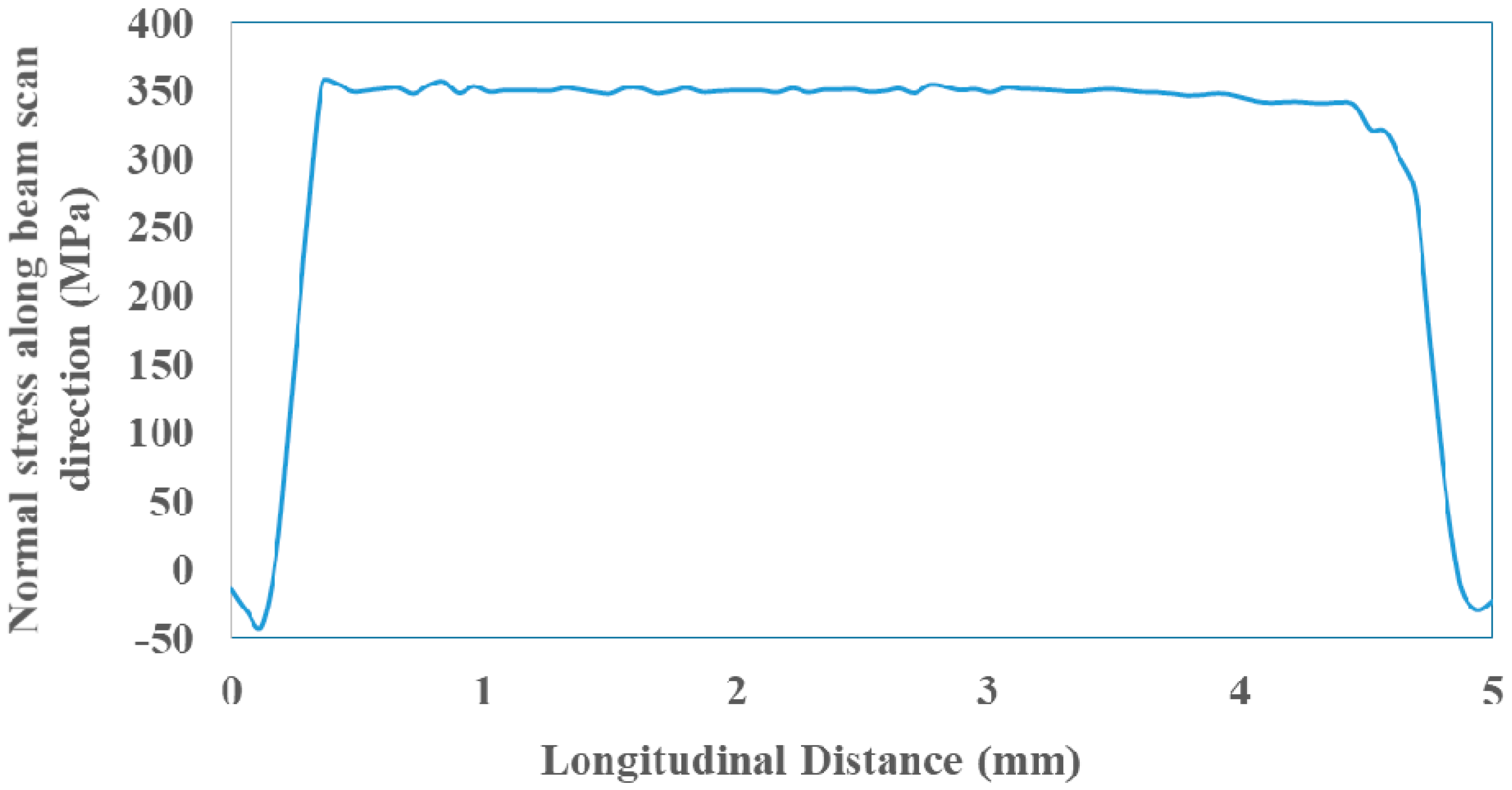
3.2. Residual Stresses
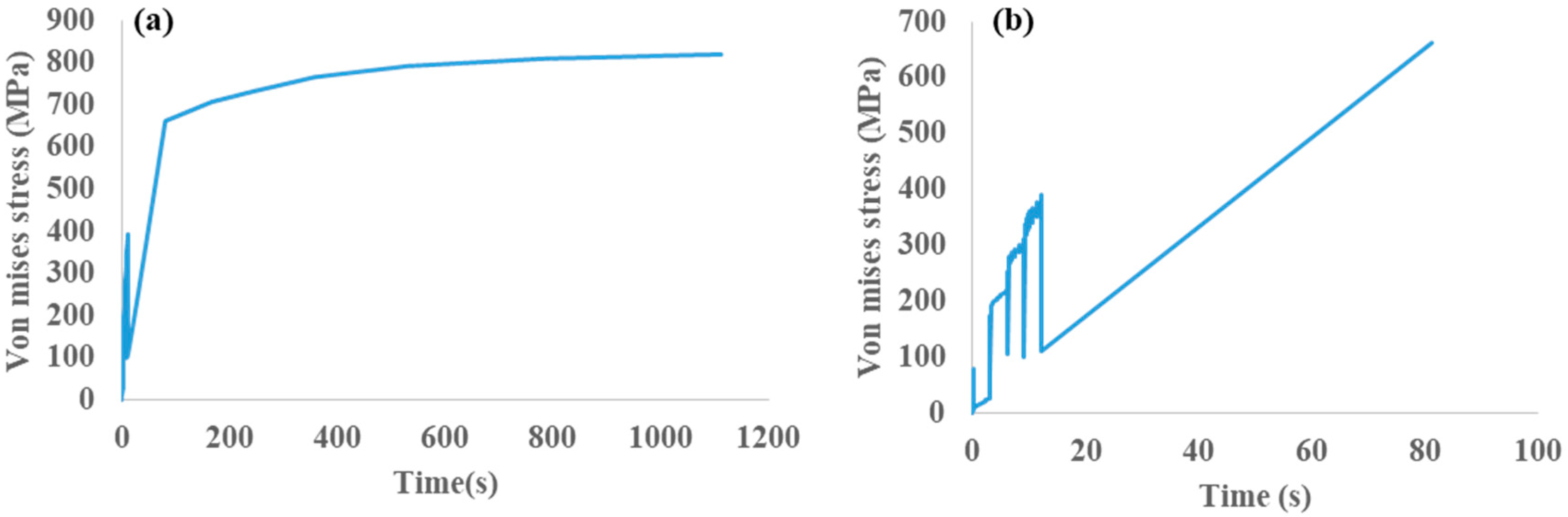
3.2.1. Instantaneous Stress
3.2.2. Model Results Versus Reported Results
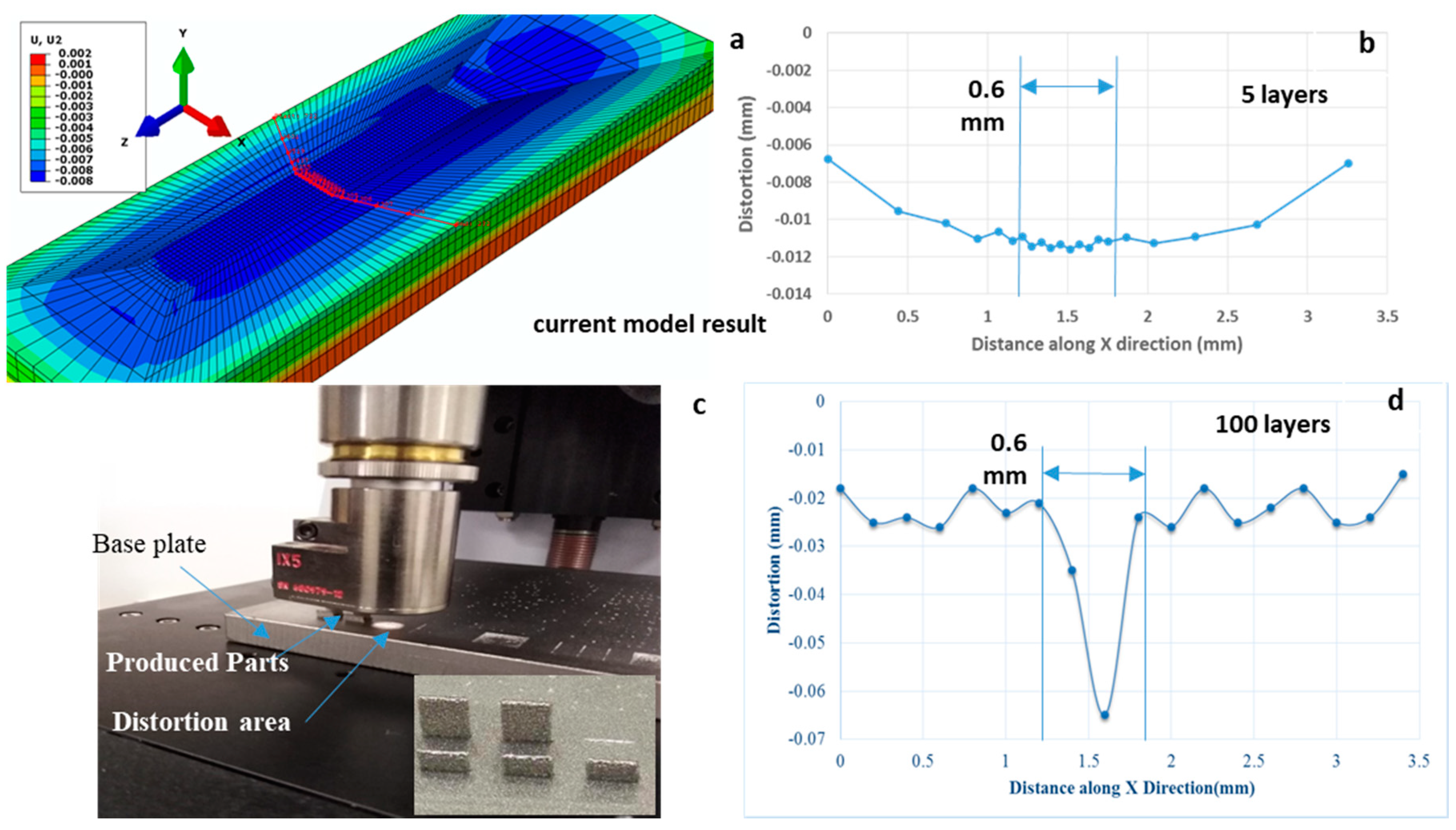
3.3. Thermal Distortion
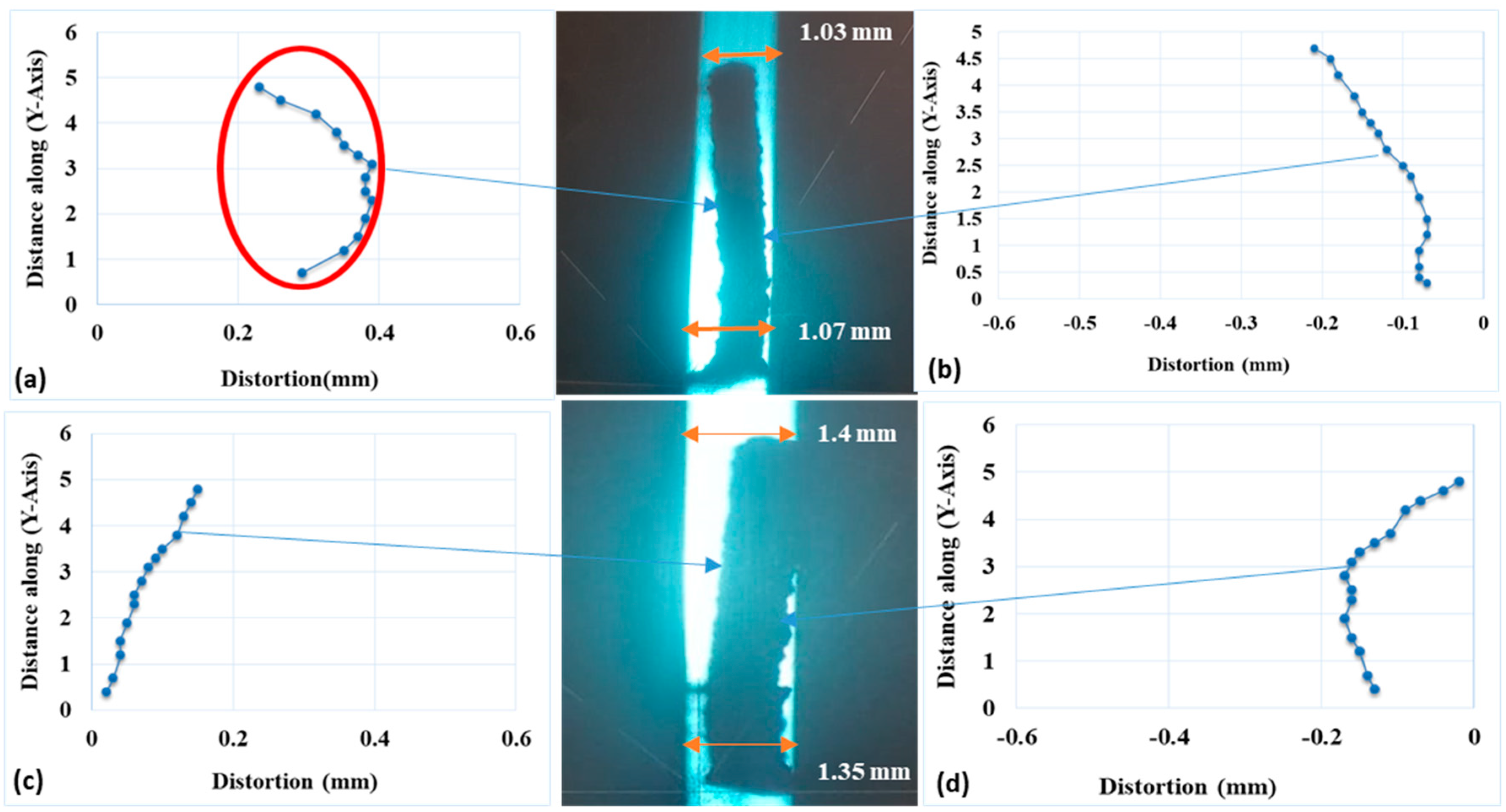
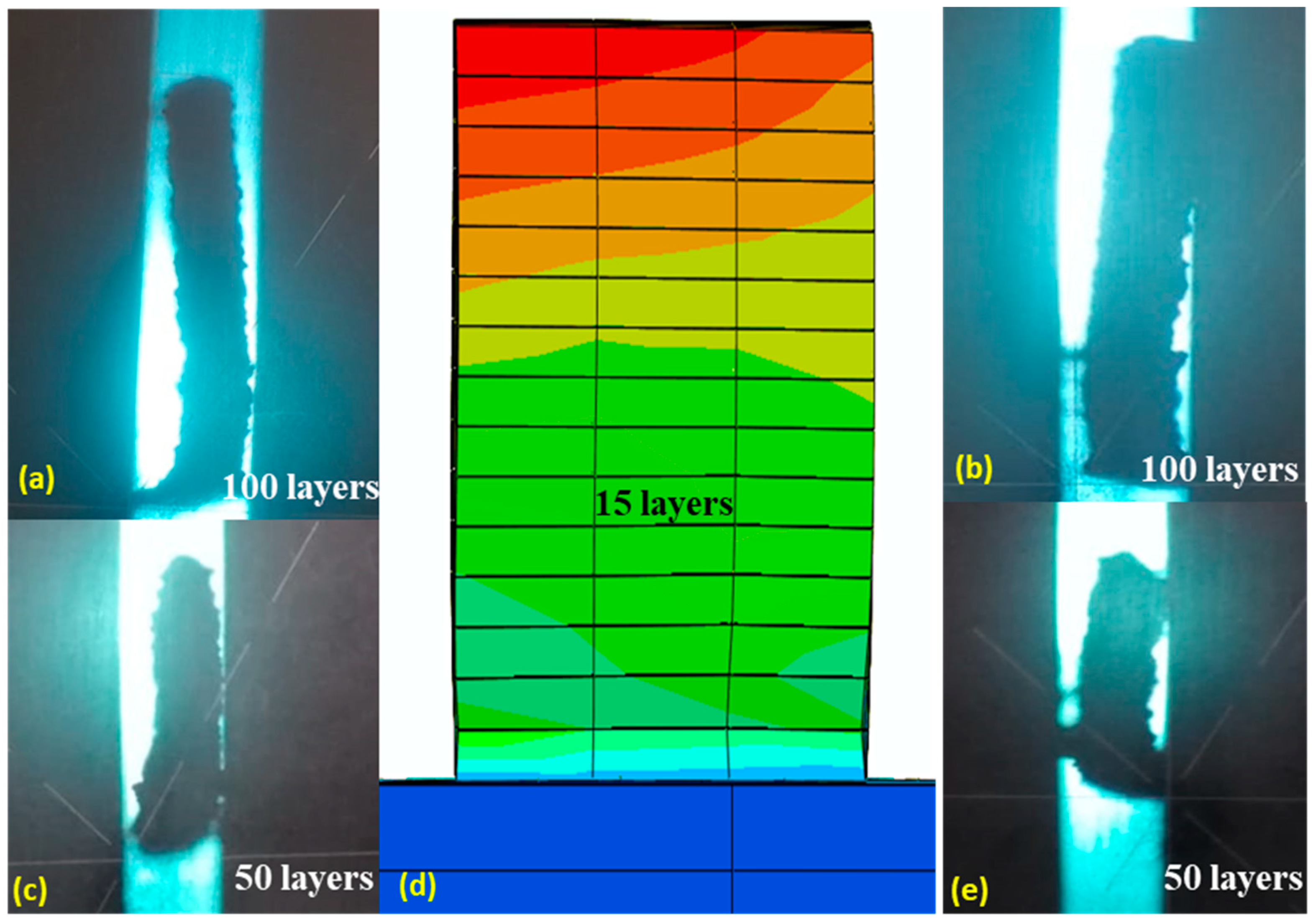
3.4. Experimental Validation
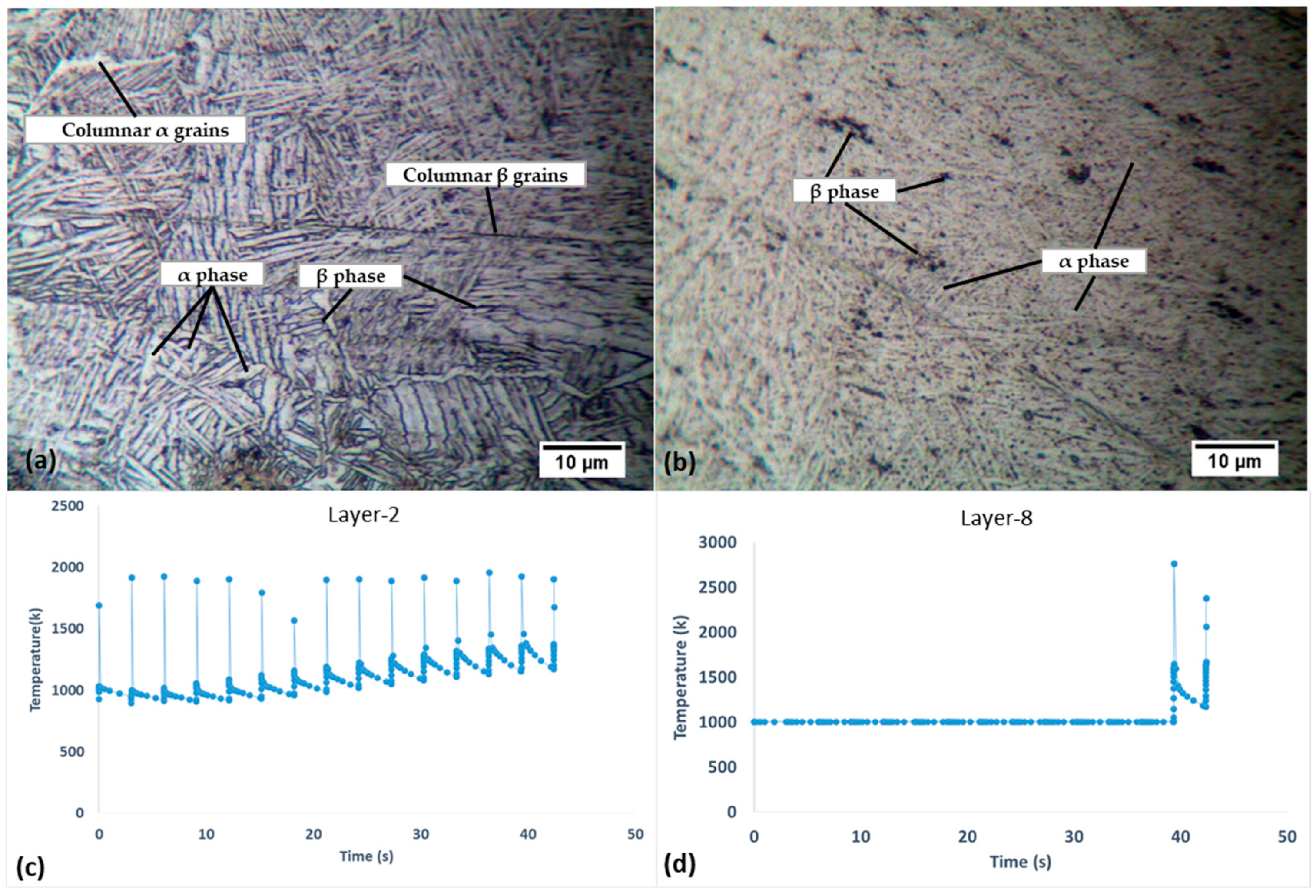
3.5. Microstructure Evolution
4. The Effects of Different Electron Beam Parameters
4.1. The Effect of Scan Speed on the EBM Process
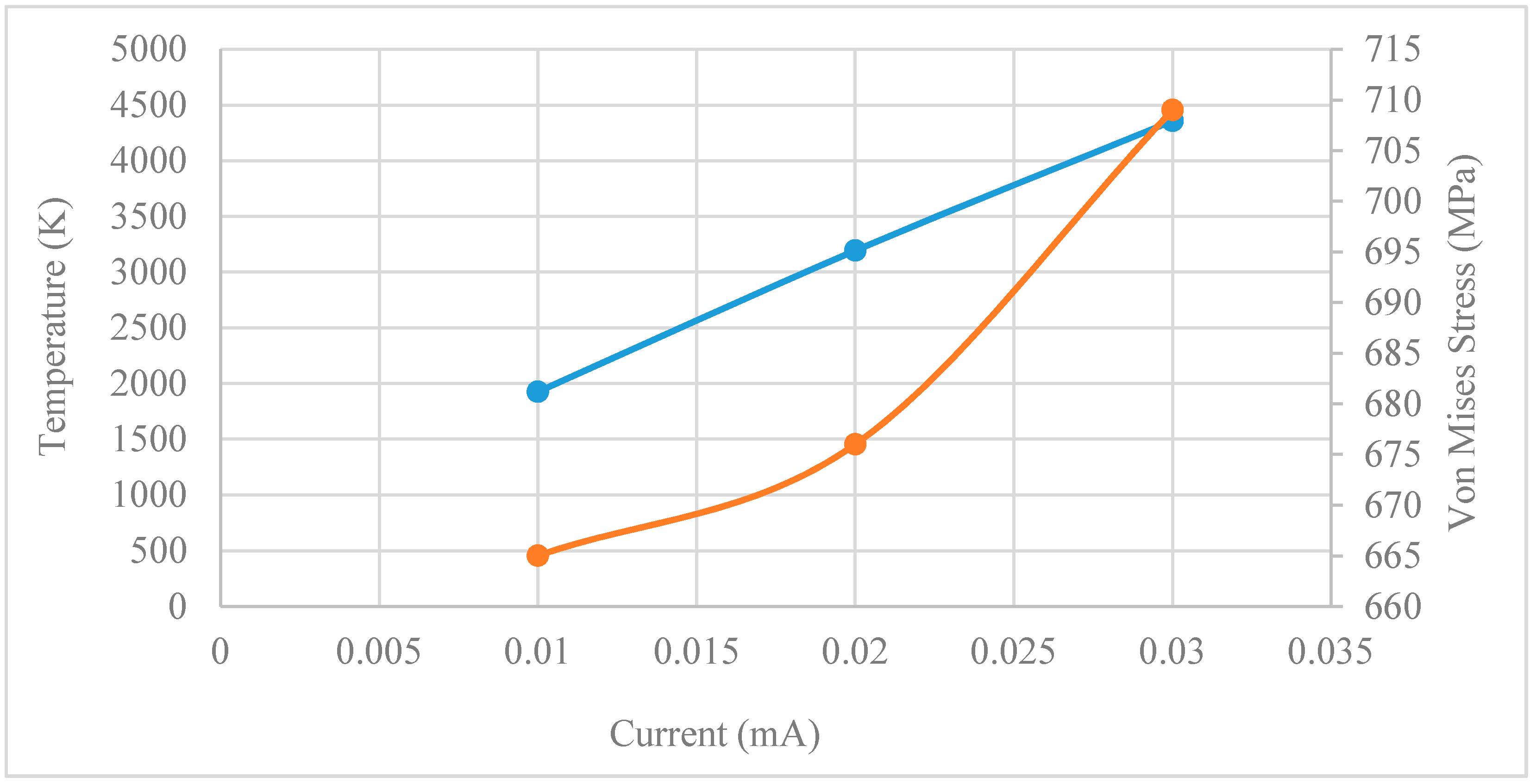
4.2. The Effect of Current on the EBM Process
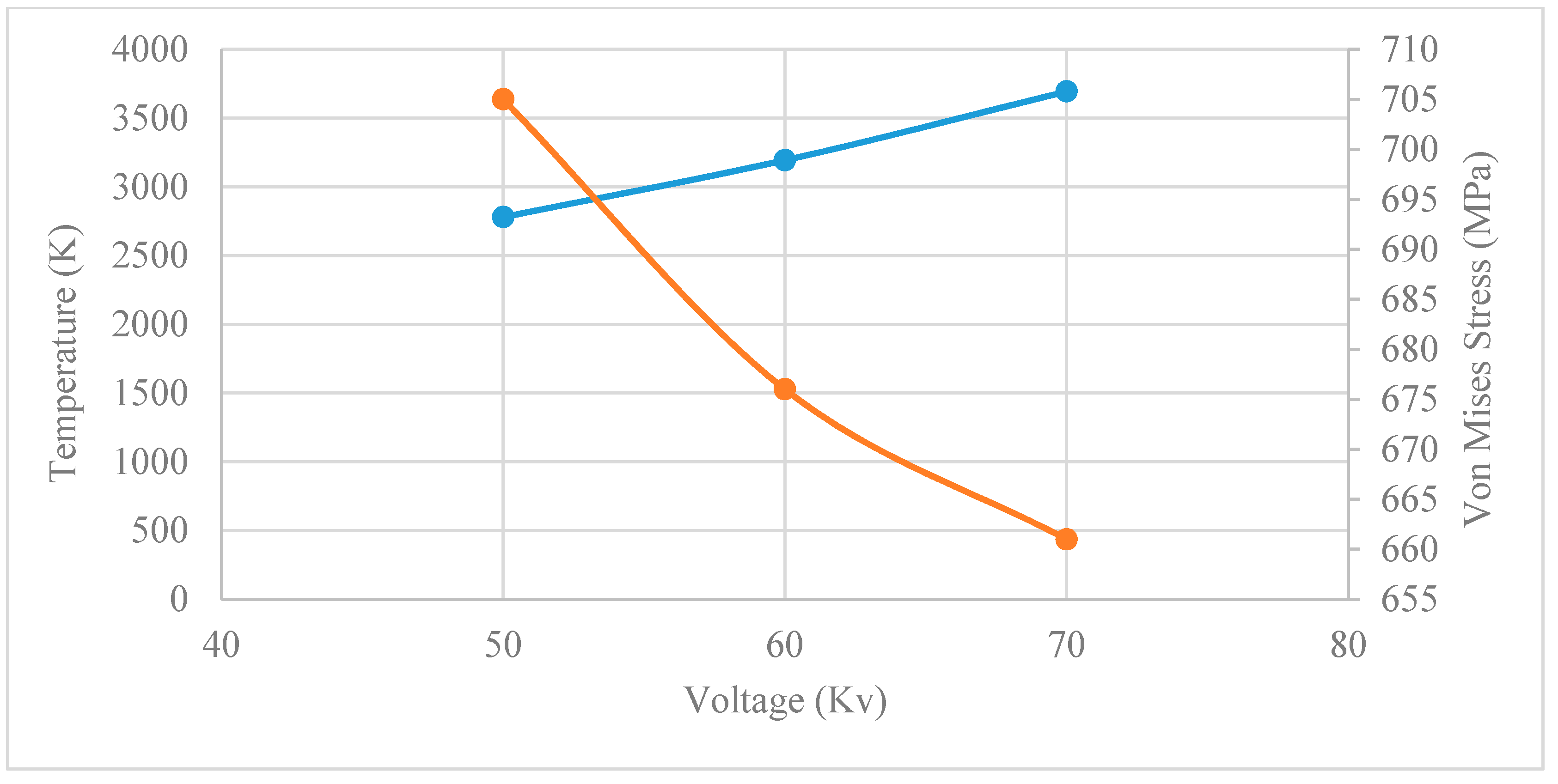
4.3. The Effect of Voltage on the EBM Process
5. Conclusions
- ○
- The FEA can predict the thermomechanical behavior of products fabricated by the electron beam melting process or similar processes with localized heat sources such as laser sintering, laser cladding, and welding.
- ○
- During the deposition of layers with EBM, high residual stresses resulted after final cooling, i.e., the stresses in the deposited layers increased with cooling due to thermal contraction. It is highly recommended to validate the FE residual stress results by conducting the experimental observations and measurements as well.
- ○
- The distortion in the EBM produced parts was experimentally measured. The experimental results showed that the overall distortion was independent of the part height produced. The simulated pattern of the distortion in the results from the FE model was found to be in close agreement with the experimental data.
- ○
- The maximum predicted temperatures and the temperature profiles were found to be in close agreement with the reported experimental and simulated results.
- ○
- An increase in scan speed leads to a decrease in temperature.
- ○
- An increase in scan speed leads to an increase in the residual stresses within the part produced by EBM.
- ○
- An increase in current leads to a rise in temperature of the electron beam melting process.
- ○
- A decrease in current leads to a reduction in the residual stresses within the part produced by EBM.
- ○
- An increase in voltage leads to a rise in the temperature of the electron beam melting process.
- ○
- An increase in voltage leads to lower residual stresses within the part produced by EBM.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ameen, W.; Al-Ahmari, A.; Mohammed, M.K. Self-supporting overhang structures produced by additive manufacturing through electron beam melting. Int. J. Adv. Manuf. Technol. 2019, 104, 2215–2232. [Google Scholar] [CrossRef]
- Ameen, W.; Al-Ahmari, A.; Mohammed, M.; Mian, S. Manufacturability of overhanging holes using electron beam melting. Metals 2018, 8, 397. [Google Scholar] [CrossRef]
- Schwerdtfeger, J.; Heinl, P.; Singer, R.; Körner, C. Auxetic cellular structures through selective electron-beam melting. Phys. Status Solidi B 2010, 247, 269–272. [Google Scholar] [CrossRef]
- Yu, P.; Qian, M.; Tomus, D.; Brice, C.A.; Schaffer, G.B.; Muddle, B.C. Electron beam processing of aluminium alloys. In Materials Science Forum; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2009; Volume 618, pp. 621–626. [Google Scholar]
- Cormier, D.; Harrysson, O.; West, H. Characterization of H13 steel produced via electron beam melting. Rapid Prototyp. J. 2004, 10, 35–41. [Google Scholar] [CrossRef]
- Gaytan, S.M.; Murr, L.E.; Martinez, E.; Martinez, J.L.; Machado, B.I.; Ramirez, D.A.; Medina, F.; Collins, S.; Wicker, R.B. Comparison of microstructures and mechanical properties for solid and mesh cobalt-base alloy prototypes fabricated by electron beam melting. Metall. Mater. Trans. A 2010, 41, 3216–3227. [Google Scholar] [CrossRef]
- Parthasarathy, J.; Starly, B.; Raman, S.; Christensen, A. Mechanical evaluation of porous titanium (Ti6Al4V) structures with electron beam melting (EBM). J. Mech. Behav. Biomed. Mater. 2010, 3, 249–259. [Google Scholar] [CrossRef]
- Leyens, C.; Peters, M. Titanium and Titanium Alloys: Fundamentals and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Liu, W.; Li, L.; Kochhar, A. A method for assessing geometrical errors in layered manufacturing. Part 1: Error interaction and transfer mechanisms. Int. J. Adv. Manuf. Technol. 1998, 14, 637–643. [Google Scholar] [CrossRef]
- Lim, G.; Lau, K.; Cheng, W.; Chiang, Z.; Krishnan, M.; Ardi, D. Residual Stresses in Ti-6Al-4V Parts Manufactured by Direct Metal Laser Sintering and Electron Beam Melting. Brit. Soc. Strain Meas. 2017, 71, 348–353. [Google Scholar]
- Weman, K. Welding Processes Handbook; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Denlinger, E.R.; Heigel, J.C.; Michaleris, P. Residual stress and distortion modeling of electron beam direct manufacturing Ti-6Al-4V. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 1803–1813. [Google Scholar] [CrossRef]
- Cheng, B.; Chou, K. Thermal stresses associated with part overhang geometry in electron beam additive manufacturing: Process parameter effects. Proc. Annu. Int. Solid Free. Fabr. Symp. 2014, 25, 1076. [Google Scholar]
- Shen, N.; Chou, K. Thermal modeling of electron beam additive manufacturing process: Powder sintering effects. In Proceedings of the ASME 2012 International Manufacturing Science and Engineering Conference Collocated with the 40th North American Manufacturing Research Conference and in participation with the International Conference on Tribology Materials and Processing, Notre Dame, IN, USA, 4–8 June 2012; pp. 287–295. [Google Scholar]
- Cao, J.; Gharghouri, M.A.; Nash, P. Finite-element analysis and experimental validation of thermal residual stress and distortion in electron beam additive manufactured Ti-6Al-4V build plates. J. Mater. Process. Technol. 2016, 237, 409–419. [Google Scholar] [CrossRef]
- Umer, U.; Ameen, W.; Abidi, M.H.; Moiduddin, K.; Alkhalefah, H.; Alkahtani, M.; Al-Ahmari, A. Modeling the Effect of Different Support Structures in Electron Beam Melting of Titanium Alloy Using Finite Element Models. Metals 2019, 9, 806. [Google Scholar] [CrossRef]
- Algardh, J.K.; Horn, T.; West, H.; Aman, R.; Snis, A.; Engqvist, H.; Lausmaa, J.; Harrysson, O. Thickness dependency of mechanical properties for thin-walled titanium parts manufactured by Electron Beam Melting (EBM)®. Addit. Manuf. 2016, 12, 45–50. [Google Scholar] [CrossRef]
- Isaev, A.; Grechishnikov, V.; Pivkin, P.; Ilyukhin, Y.; Kozochkin, M.; Peretyagin, P. Structure and machinability of thin-walled parts made of titanium alloy powder using electron beam melting technology. J. Silic. Based Compos. Mater. 2016, 68, 46. [Google Scholar]
- Cormier, D.; West, H.; Harrysson, O.; Knowlson, K. Characterization of Thin Walled Ti-6Al-4V Components Reduced via Electron Beam Melting 440. In Proceedings of the 2004 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 4 August 2004. [Google Scholar]
- Everhart, W.; Dinardo, J.; Barr, C. The effect of scan length on the structure and mechanical properties of electron beam-melted Ti-6Al-4V. Metall. Mater. Trans. A 2017, 48, 697–705. [Google Scholar] [CrossRef]
- Fu, C.; Guo, Y. 3-dimensional finite element modeling of selective laser melting Ti-6Al-4V alloy. In Proceedings of the 25th Annual International Solid Freeform Fabrication Symposium, Tuscaloosa, AL, USA, 4 August 2014; pp. 1129–1144. [Google Scholar]
- Boivineau, M.; Cagran, C.; Doytier, D.; Eyraud, V.; Nadal, M.H.; Wilthan, B.; Pottlacher, G. Thermophysical properties of solid and liquid Ti-6Al-4V (TA6V) alloy. Int. J. Thermophys. 2006, 27, 507–529. [Google Scholar] [CrossRef]
- Liu, S.; Shin, Y.C. Additive manufacturing of Ti6Al4V alloy: A review. Mater. Des. 2019, 164, 107552. [Google Scholar] [CrossRef]
- Abbes, B.; Anedaf, T.; Abbes, F.; Li, Y. Direct energy deposition metamodeling using a meshless method. Eng. Comput. 2020. [Google Scholar] [CrossRef]
- Ahmed, S.H.; Mian, A. Influence of material property variation on computationally calculated melt pool temperature during laser melting process. Metals 2019, 9, 456. [Google Scholar] [CrossRef]
- Seyedian, C.M.; Haghpanahi, M.; Sedighi, M. Investigation of the Effect of Clamping on Residual Stresses and Distortions in Butt-Welded Plates; Scientia Iranica. Transaction B: Mechanical Engineering: Tehran, Iran, 2010. [Google Scholar]
- Ameen, W.; Al-Ahmari, A.; Mohammed, M.; Abdulhameed, O.; Umer, U.; Moiduddin, K. Design, finite element analysis (FEA), and fabrication of custom titanium alloy cranial implant using electron beam melting additive manufacturing. Adv. Prod. Eng. Manag. 2018, 13, 267–278. [Google Scholar] [CrossRef]
- Gong, X.; Cheng, B.; Price, S.; Chou, K. Powder-bed electron-beam-melting additive manufacturing: Powder characterization, process simulation and metrology. In Proceedings of the Early Career Technical Conference, Birmingham, AL, USA, 2–3 November 2013; pp. 55–66. [Google Scholar]
- Cheng, B.; Lu, P.; Chou, K. Thermomechanical investigation of overhang fabrications in electron beam additive manufacturing. In Proceedings of the ASME 2014 International Manufacturing Science and Engineering Conference Collocated with the JSME 2014 International Conference on Materials and Processing and the 42nd North American Manufacturing Research Conference, Detroit, MI, USA, 9–13 June 2014. [Google Scholar]
- He, J.; Li, D.; Jiang, W.; Ke, L.; Qin, G.; Ye, Y.; Qin, Q.; Qiu, D. The Martensitic Transformation and Mechanical Properties of Ti6Al4V Prepared via Selective Laser Melting. Materials 2019, 12, 321. [Google Scholar] [CrossRef] [PubMed]
- Shen, N.; Chou, K. Thermomechanical investigation of overhang fabrications in electron beam additive manufacturing. In Proceedings of the International Manufacturing Science and Engineering Conference, Detroit, MI, USA, 9–13 June 2014; p. V002T02A024. [Google Scholar]
- Shen, N.; Chou, K. Numerical thermal analysis in electron beam additive manufacturing with preheating effects. In Proceedings of the 23rd solid freeform fabrication symposium, Tuscaloosa, AL, USA, 6 August 2012; pp. 774–784. [Google Scholar]
- Guo, Q.; Zhao, C.; Qu, M.; Xiong, L.; Escano, L.I.; Hojjatzadeh, S.M.; Parab, N.D.; Fezzaa, K.; Everhart, W.; Sun, T.; et al. In-situ characterization and quantification of melt pool variation under constant input energy density in laser powder bed fusion additive manufacturing process. Addit. Manuf. 2019, 28, 600–609. [Google Scholar] [CrossRef]
- Cezairliyan, A.; Miiller, A. Melting point, normal spectral emittance/at the melting point/, and electrical resistivity/above 1900 K/ of titanium by a pulse heating method. J. Res. 1977, 82, 119–122. [Google Scholar] [CrossRef]
- Raghavan, S.; Nai, M.L.S.; Wang, P.; Sin, W.J.; Li, T.; Wei, J. Heat treatment of electron beam melted (EBM) Ti-6Al-4V: Microstructure to mechanical property correlations. Rapid Prototyp. J. 2018, 24, 774–783. [Google Scholar] [CrossRef]
- Singh, A.P.; Yang, F.; Torrens, R.; Gabbitas, B. Heat Treatment, Impact Properties, and Fracture Behaviour of Ti-6Al-4V Alloy Produced by Powder Compact Extrusion. Materials 2019, 12, 3824. [Google Scholar] [CrossRef]
- Gong, H.; Rafi, K.; Starr, T.; Stucker, B. The effects of processing parameters on defect regularity in Ti-6Al-4V parts fabricated by selective laser melting and electron beam melting. In Proceedings of the 24th Annual International Solid Freeform Fabrication Symposium—An Additive Manufacturing Conference, Austin, TX, USA, 12 August 2013; pp. 424–439. [Google Scholar]











| Temperature (K) | Density (kg/m3) | Heat Capacity (J/(kg K)) | Thermal Conductivity (W/(m K)) | Thermal Expansion Coefficient (m/(m K)) | Yield Strength (MPa) | Young’s Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|---|
| 273 | 0.0079 | 462 | 0.0146 | 265 | 198.5 | 0.294 | |
| 373 | 0.00788 | 496 | 0.0151 | 218 | 193 | 0.295 | |
| 473 | 0.00783 | 512 | 0.0161 | 186 | 185 | 0.301 | |
| 573 | 0.00779 | 525 | 0.0179 | 170 | 176 | 0.31 | |
| 673 | 0.00775 | 540 | 0.018 | 155 | 167 | 0.318 | |
| 873 | 0.00766 | 577 | 0.0208 | 149 | 159 | 0.326 | |
| 1073 | 0.00756 | 604 | 0.0239 | 91 | 151 | 0.333 | |
| 1473 | 0.00737 | 676 | 0.0322 | 25 | 60 | 0.339 | |
| 1573 | 0.00732 | 692 | 0.0337 | 21 | 20 | 0.342 | |
| 1773 | 0.00732 | 935 | 0.12 | 10 | 10 | 0.388 |
| Temperature (K) | Density (kg/m3) | Heat Capacity (J/(kg K)) | Thermal Conductivity (W/(m K)) Solid | Thermal Conductivity (W/(m K)) Powder [21] | Thermal Expansion Coefficient (m/(m K)) | Yield Strength (MPa) | Young’s Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|---|---|
| 293 | 4420 | 546 | 7 | 0.2 | 850 | 102 | 0.345 | |
| 400 | 4402 | 567 | 7.8 | - | 720 | 101 | 0.35 | |
| 500 | 4391 | 591 | 8.9 | - | 680 | 95 | 0.355 | |
| 600 | 4376 | 611 | 10.5 | - | 630 | 91 | 0.36 | |
| 700 | 4361 | 636 | 11.7 | - | 590 | 85 | 0.365 | |
| 800 | 4345 | 656 | 13 | - | 540 | 80 | 0.37 | |
| 900 | 4331 | 679 | 14.5 | - | 490 | 75 | 0.375 | |
| 1000 | 4319 | 699 | 16.2 | - | 450 | 70 | 0.385 | |
| 1100 | 4303 | 719 | 18.4 | - | 400 | 65 | 0.395 | |
| 1200 | 4289 | 733 | 20.1 | - | 360 | 60 | 0.405 | |
| 1300 | 4278 | 647 | 19.7 | - | 315 | 35 | 0.43 | |
| 1400 | 4264 | 664 | 21.7 | - | 268 | 20 | 0.43 | |
| 1950 | 4189 | 790 | 72 | 28.3 | 20 | 10 | 0.43 |
| Layer | Phase | Step | Description | Time (s) | Total Time (s) |
|---|---|---|---|---|---|
| Complete model | Preheating | Initial | Preheating phase for the whole model at 1003k | 0 | 0 |
| L1 | Melting | 1 | Electron beam scanning along X-Z direction | 0.0265 | 0.0265 |
| Cooling | 2 | Transformation of material from powder to solid-state then cooling phase | 3 | 3.0265 | |
| L2 | Melting | 3 | Activation of layer-2 and scanning of electron beam along X-Z direction | 0.0265 | 3.0795 |
| Cooling | 4 | Transformation of material from powder to solid-state then cooling phase | 3 | 6.0795 | |
| L3 | Melting | 5 | Activation of layer-3 and scanning of electron beam along X-Z direction | 0.0265 | 6.106 |
| Cooling | 6 | Transformation of material from powder to solid-state then cooling phase | 3 | 9.106 | |
| L4 | Melting | 7 | Activation of layer-4 and scanning of electron beam along X-Z direction | 0.0265 | 9.1325 |
| Cooling | 8 | Transformation of material from powder to solid-state then cooling phase | 3 | 12.1325 | |
| L5 | Melting | 9 | Activation of the next layer and scanning of electron beam along X-Z direction | 0.0265 | 12.159 |
| Cooling | 10 | Transformation of material from powder to solid-state then cooling phase | 1100 | 112.16 | |
| Total time | 1112.16 | ||||
| Parameters | Values |
|---|---|
| Electron beam diameter, Φ (mm) | 0.3 |
| Scan speed, v (mm/s) | 400 |
| Acceleration voltage, U (kV) | 60 |
| Beam current, Ib (mA) | 0.002 |
| Powder layer thickness, tlayer (mm) | 0.05 |
| Beam penetration depth, dP (mm) | 0.05 |
| Preheat temperature, Tpreheat (k) | 1003 |
| Parameter | Level-1 | Level-2 | Level-3 |
|---|---|---|---|
| Speed (mm/s) | 300 | 400 | 500 |
| Current (mA) | 0.002 | 0.002 | 0.002 |
| Voltage (kV) | 60 | 60 | 60 |
| Parameter | Level-1 | Level-2 | Level-3 |
|---|---|---|---|
| Speed (mm/s) | 400 | 400 | 400 |
| Current (mA) | 0.001 | 0.002 | 0.003 |
| Voltage (kV) | 60 | 60 | 60 |
| Parameter | Level-1 | Level-2 | Level-3 |
|---|---|---|---|
| Speed (mm/s) | 400 | 400 | 400 |
| Current (mA) | 0.002 | 0.002 | 0.002 |
| Voltage (kV) | 50 | 60 | 70 k |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
M. Abdullah, F.; Anwar, S.; Al-Ahmari, A. Thermomechanical Simulations of Residual Stresses and Distortion in Electron Beam Melting with Experimental Validation for Ti-6Al-4V. Metals 2020, 10, 1151. https://doi.org/10.3390/met10091151
M. Abdullah F, Anwar S, Al-Ahmari A. Thermomechanical Simulations of Residual Stresses and Distortion in Electron Beam Melting with Experimental Validation for Ti-6Al-4V. Metals. 2020; 10(9):1151. https://doi.org/10.3390/met10091151
Chicago/Turabian StyleM. Abdullah, Fawaz, Saqib Anwar, and Abdulrahman Al-Ahmari. 2020. "Thermomechanical Simulations of Residual Stresses and Distortion in Electron Beam Melting with Experimental Validation for Ti-6Al-4V" Metals 10, no. 9: 1151. https://doi.org/10.3390/met10091151
APA StyleM. Abdullah, F., Anwar, S., & Al-Ahmari, A. (2020). Thermomechanical Simulations of Residual Stresses and Distortion in Electron Beam Melting with Experimental Validation for Ti-6Al-4V. Metals, 10(9), 1151. https://doi.org/10.3390/met10091151







