Circumferential Material Flow in the Hydroforming of Overlapping Blanks
Abstract
1. Introduction
2. Materials and Methods
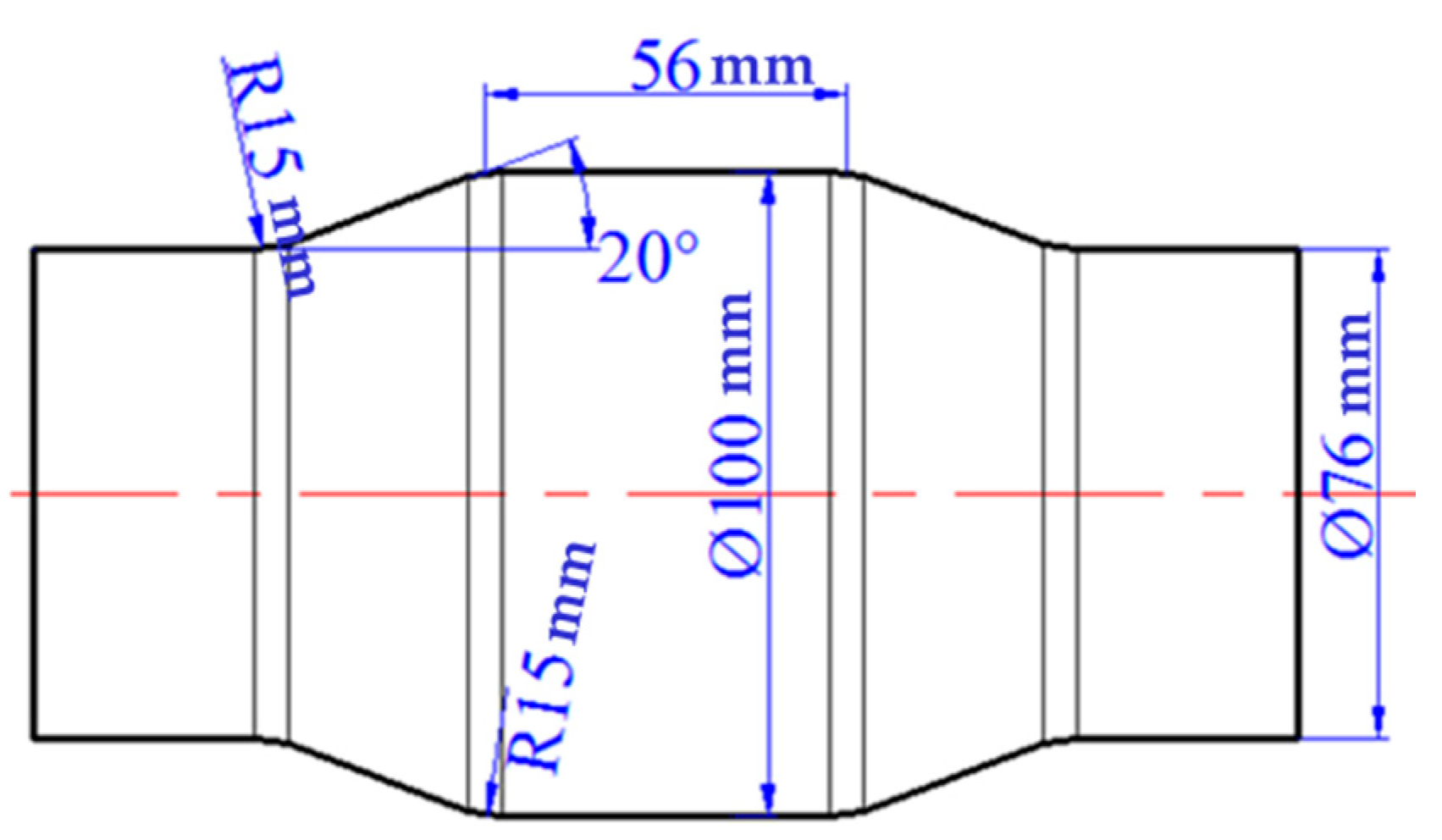
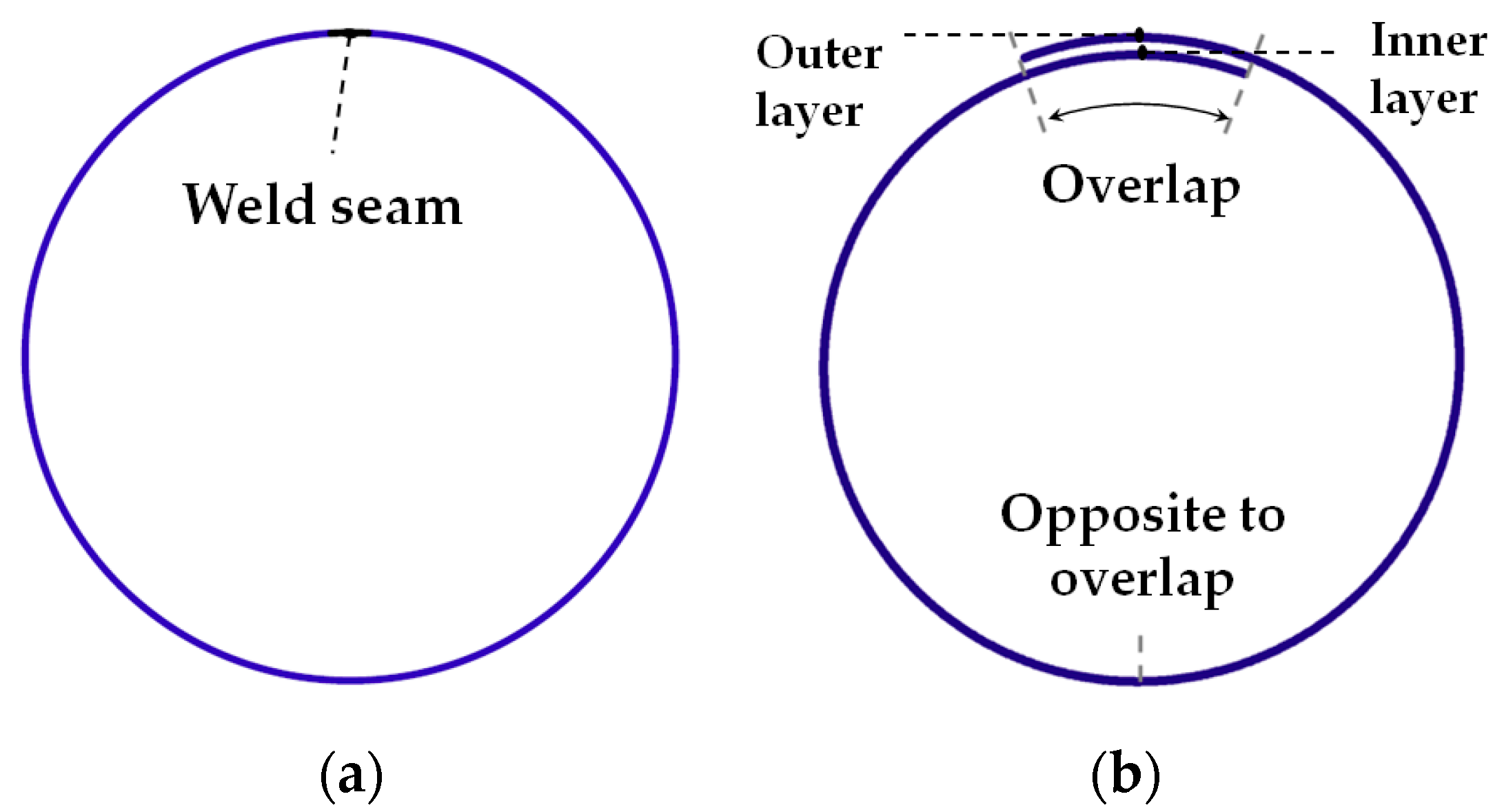
2.1. Samples and Material
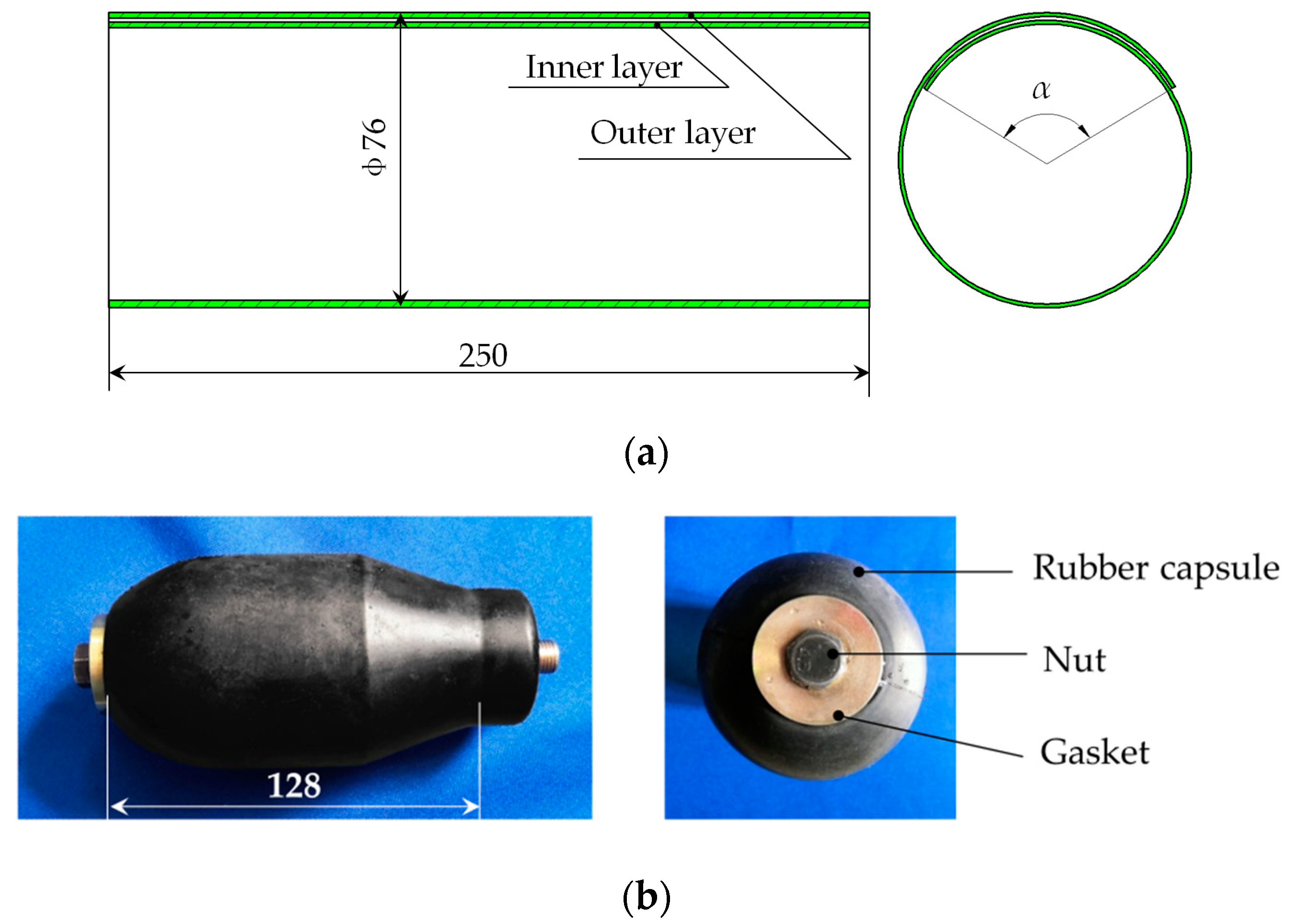
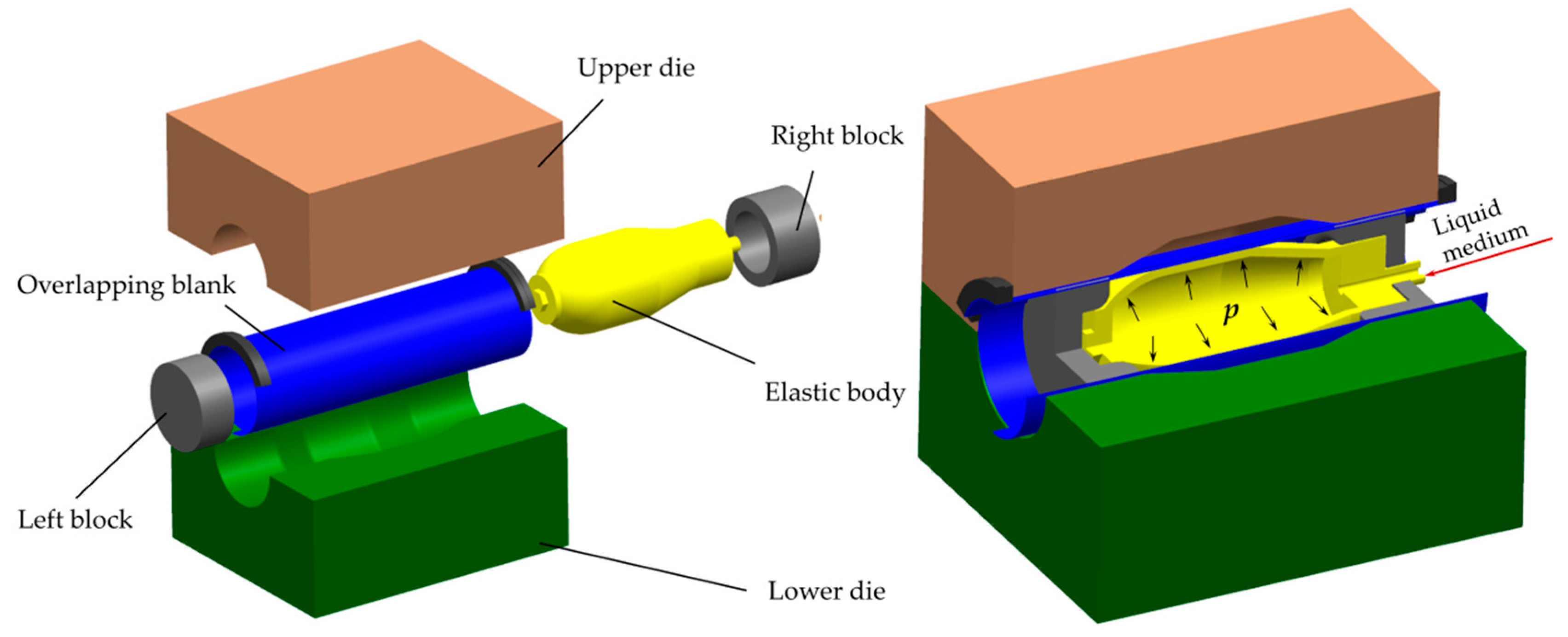
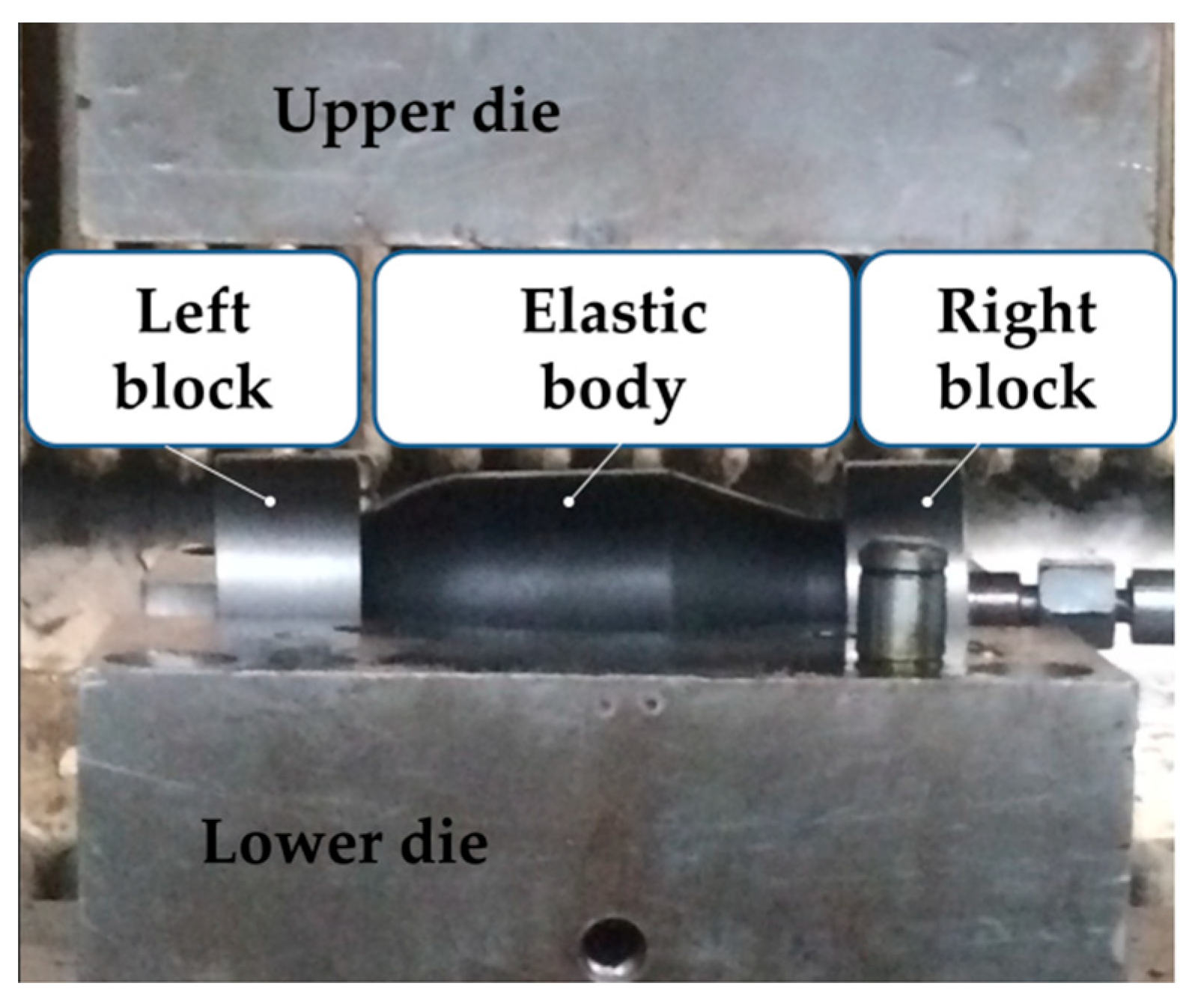
2.2. Experimental Setup
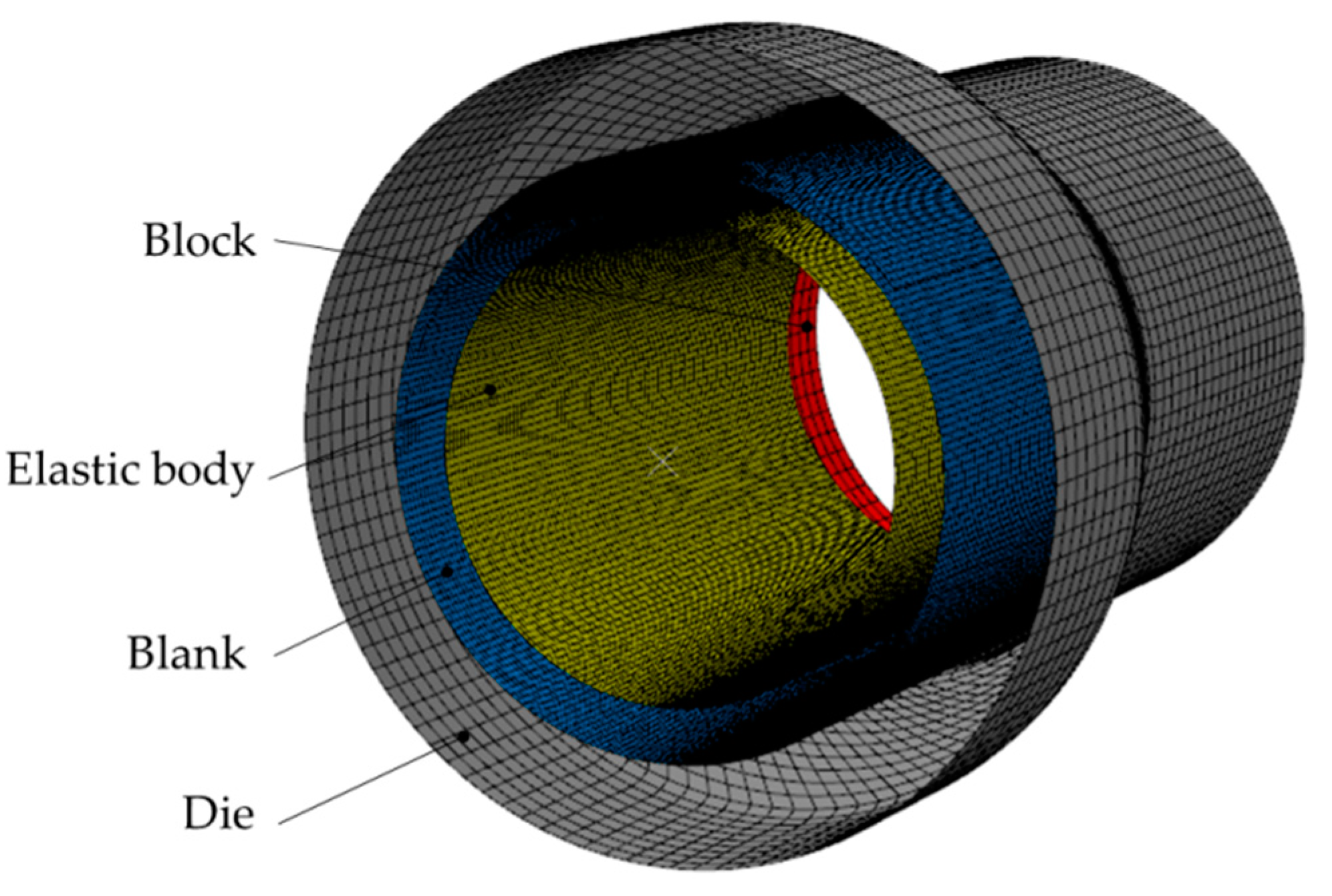
2.3. Finite Element Model
2.4. Boundary Conditions
3. Results
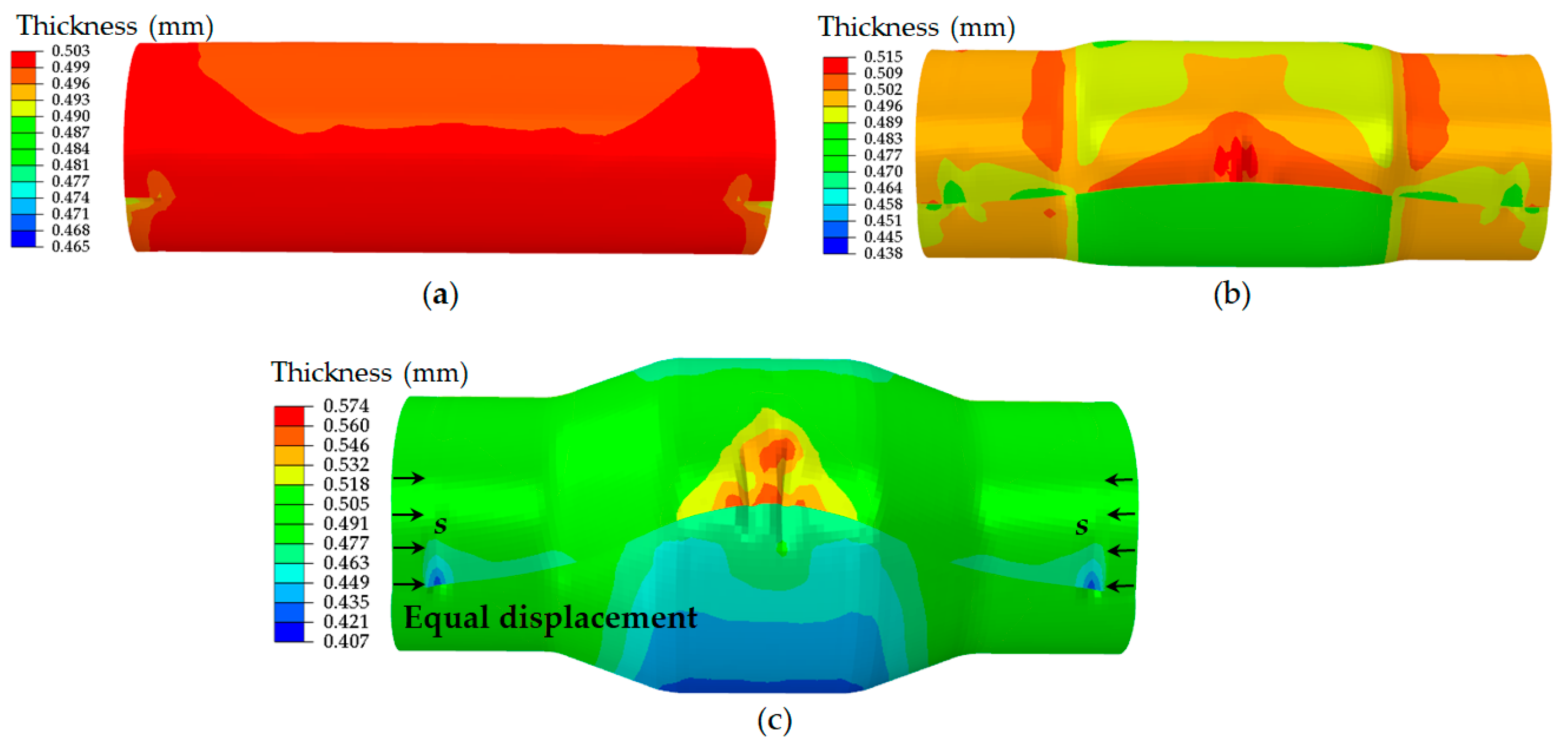
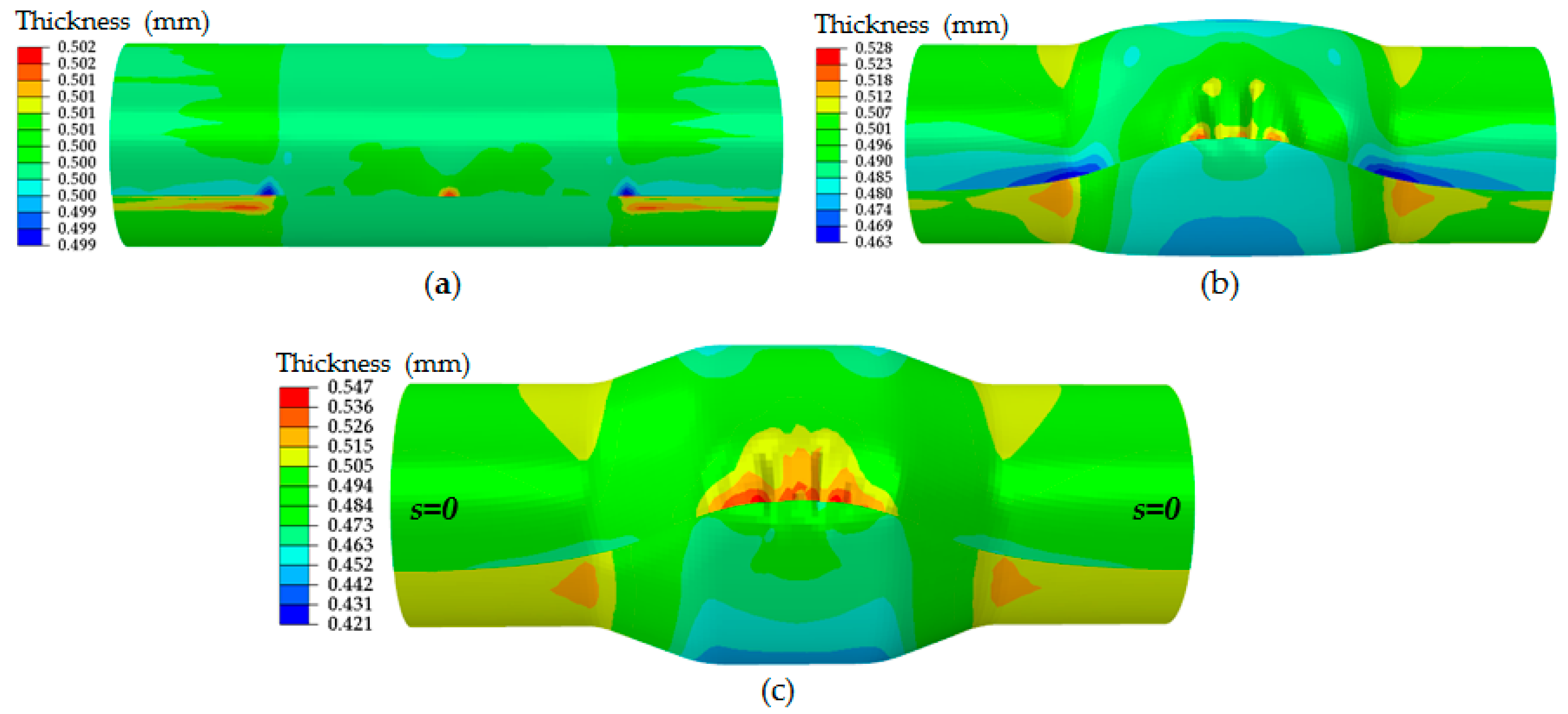
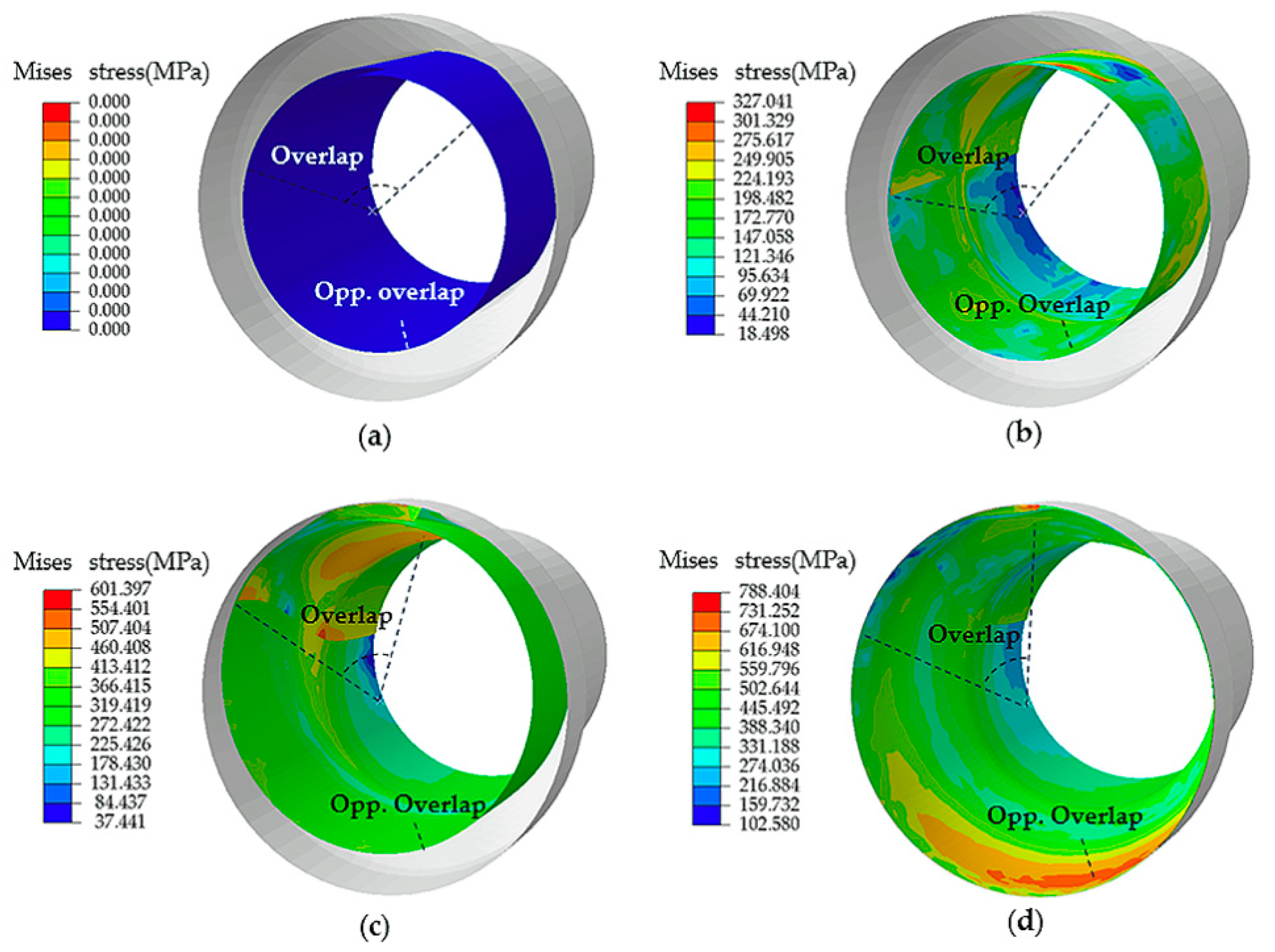
3.1. Effect of Boundary Conditions on Wrinkling Defects
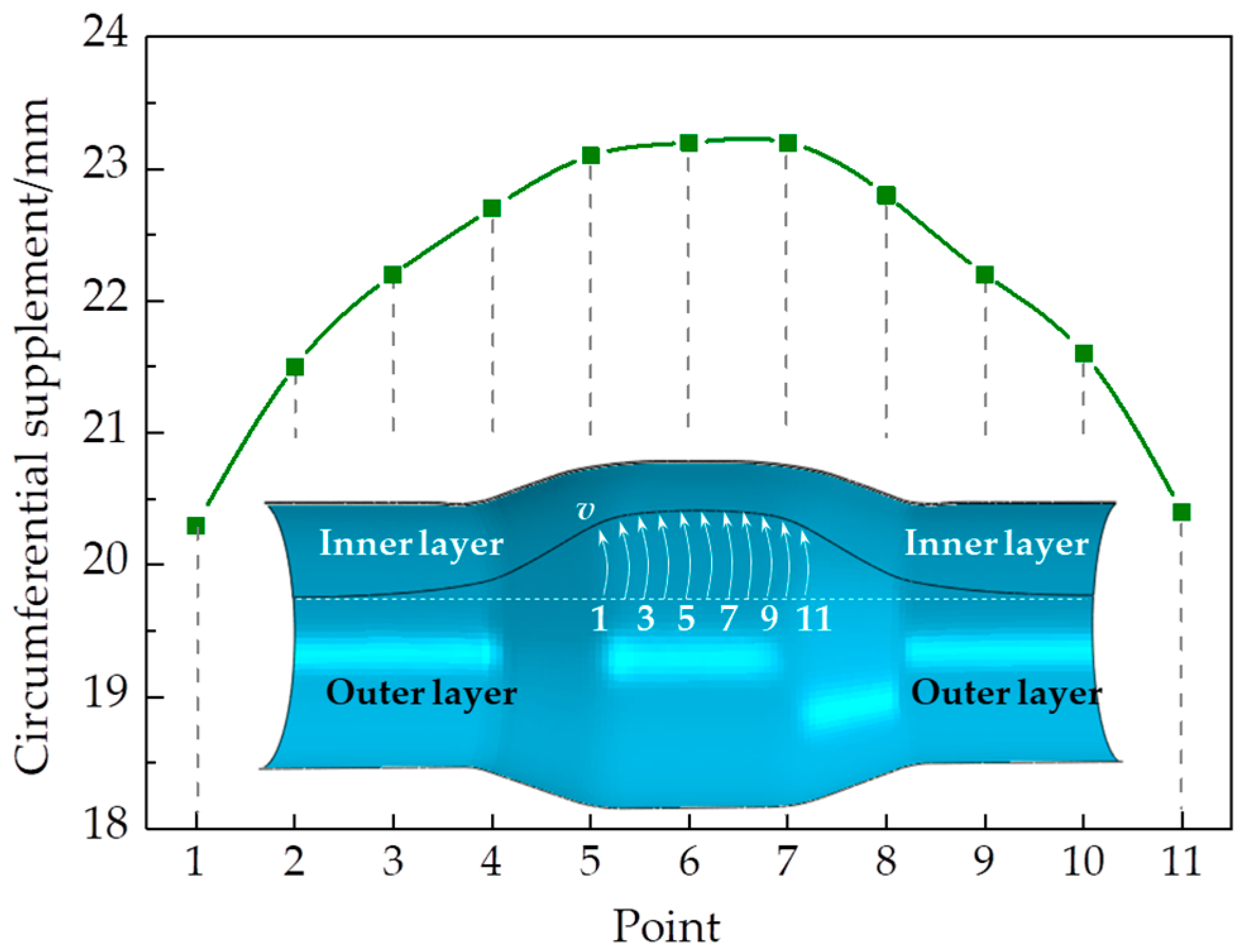
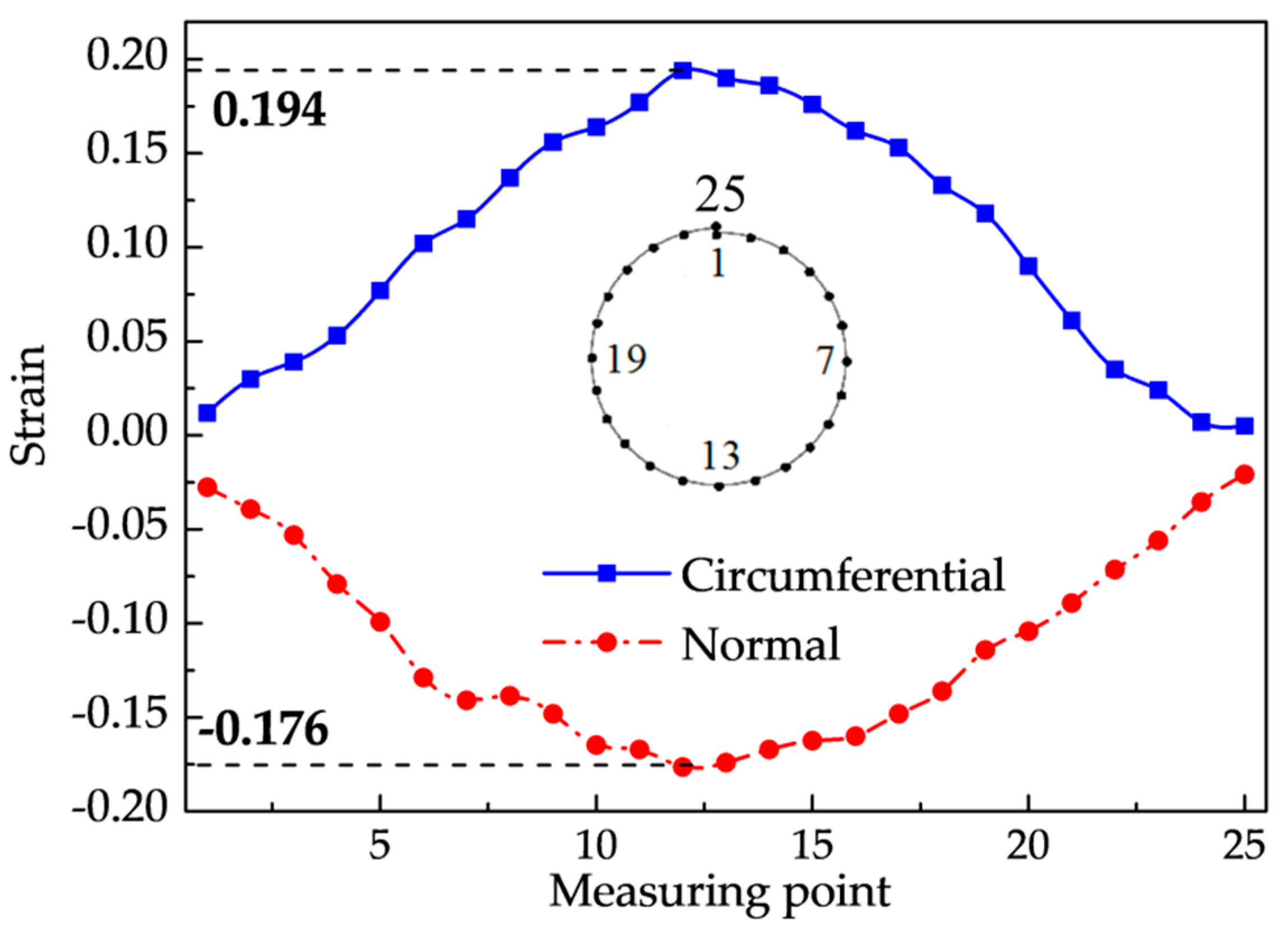
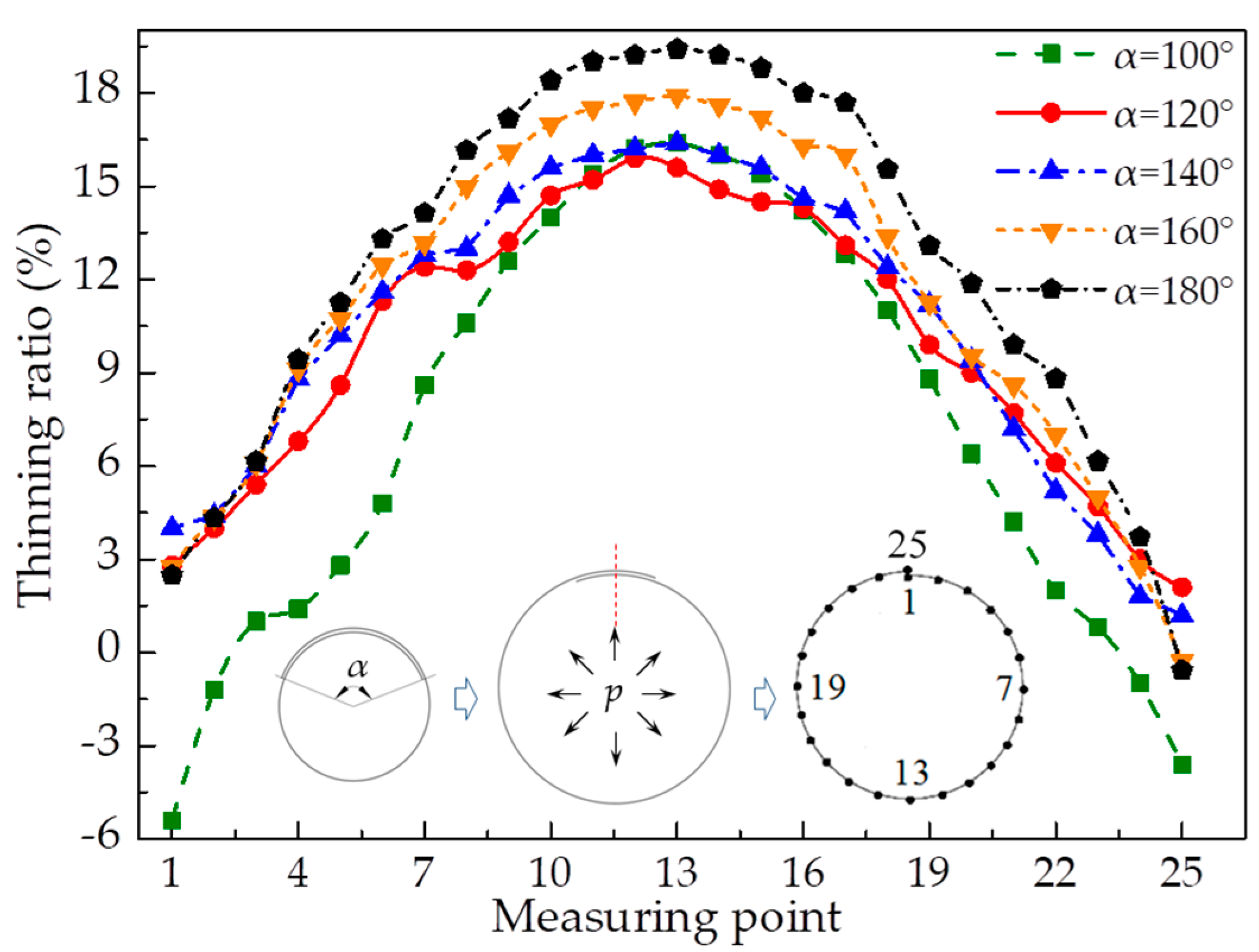
3.2. Material Flow Along the Circumferential Direction
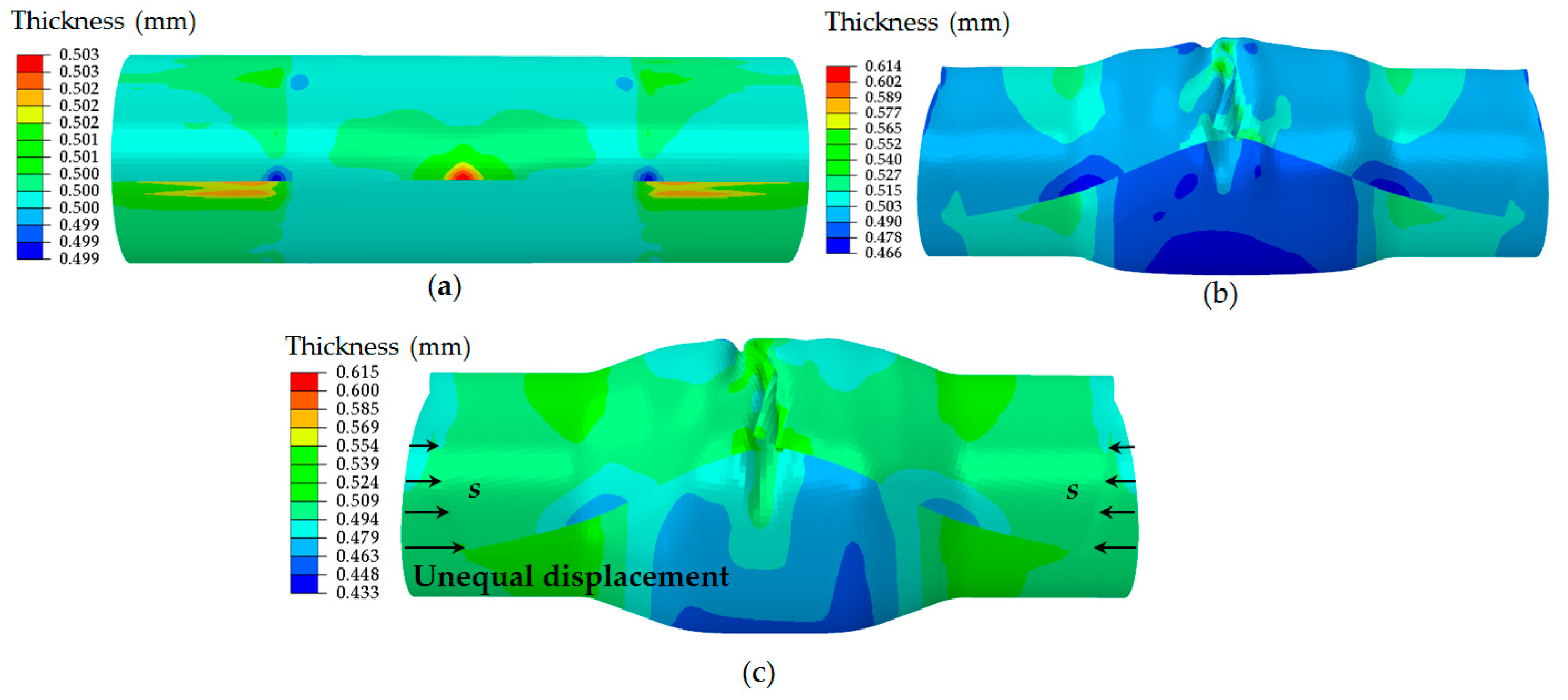
3.3. Thickness Distribution
4. Discussion
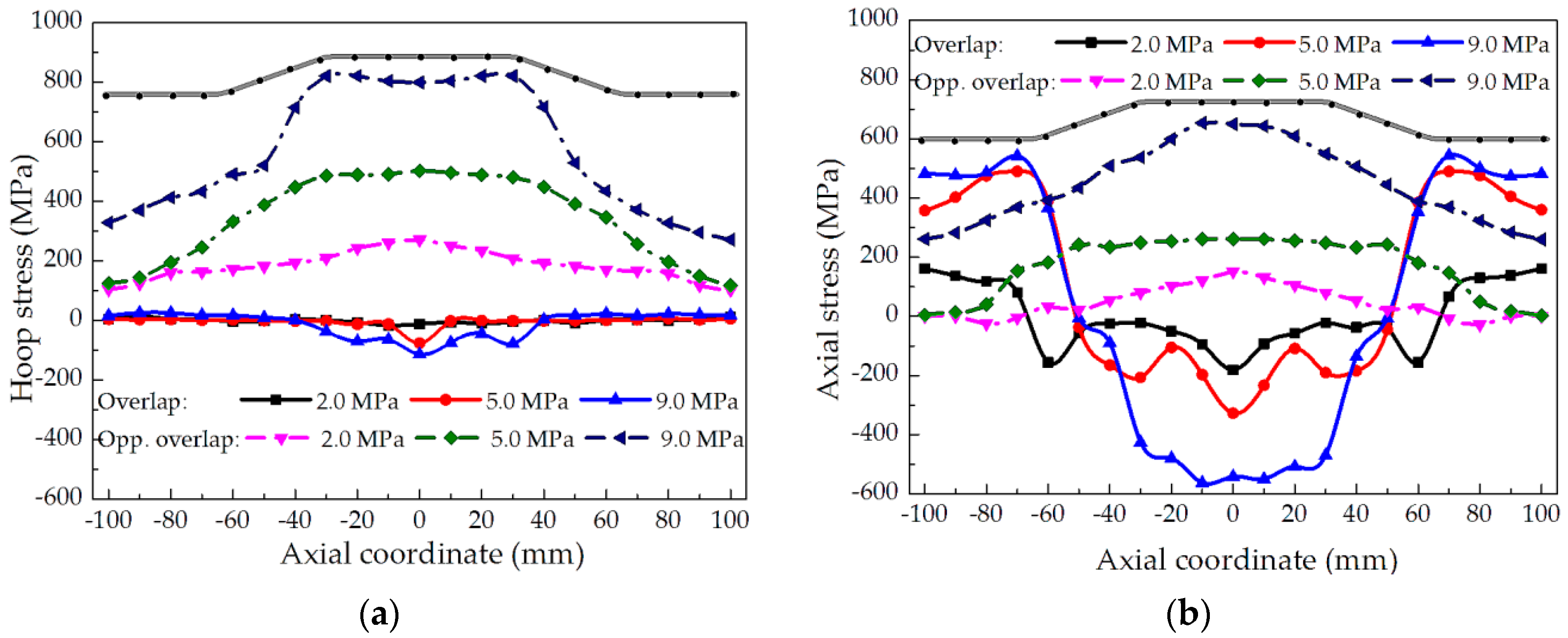
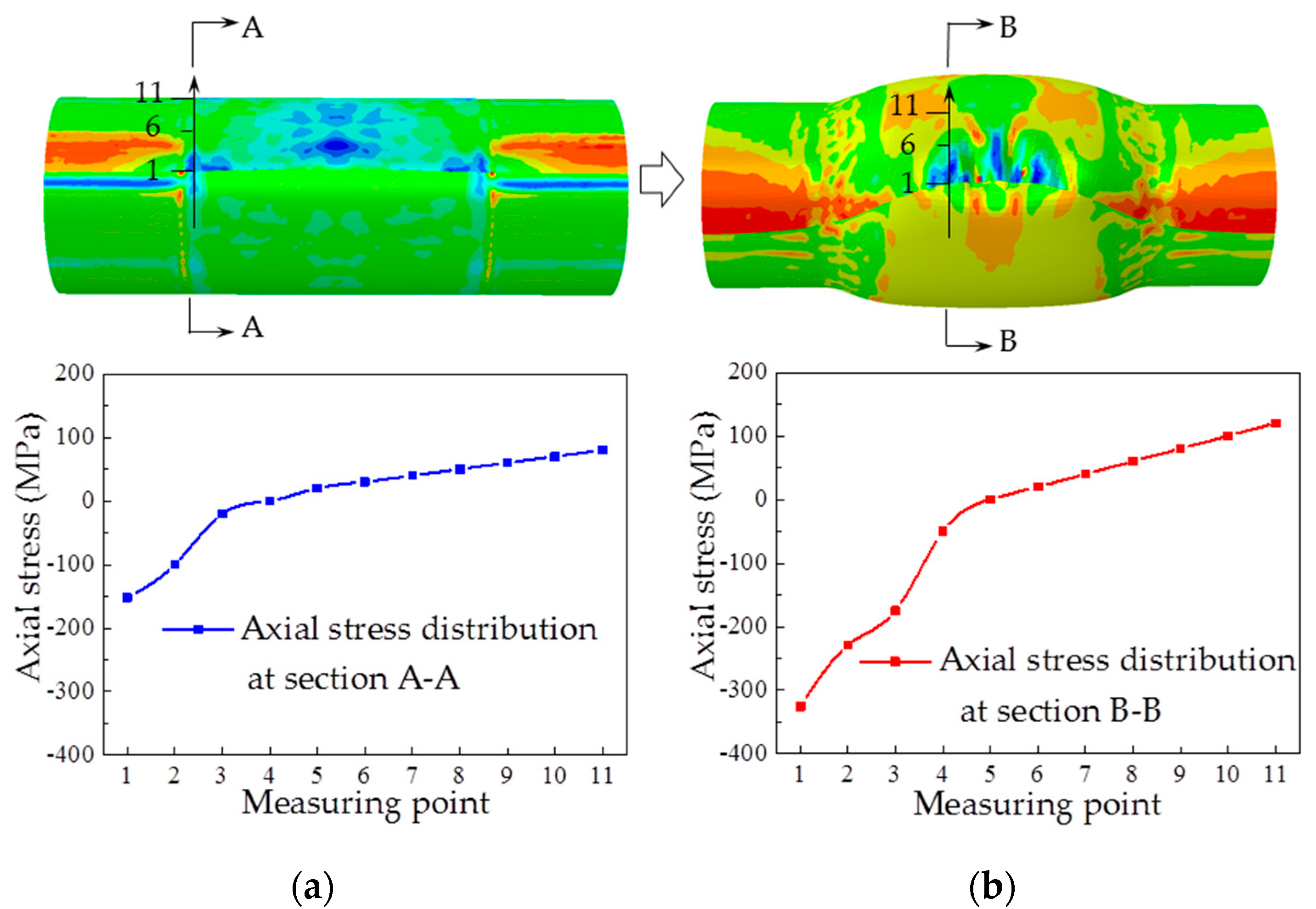
4.1. Stress and Strain Analysis
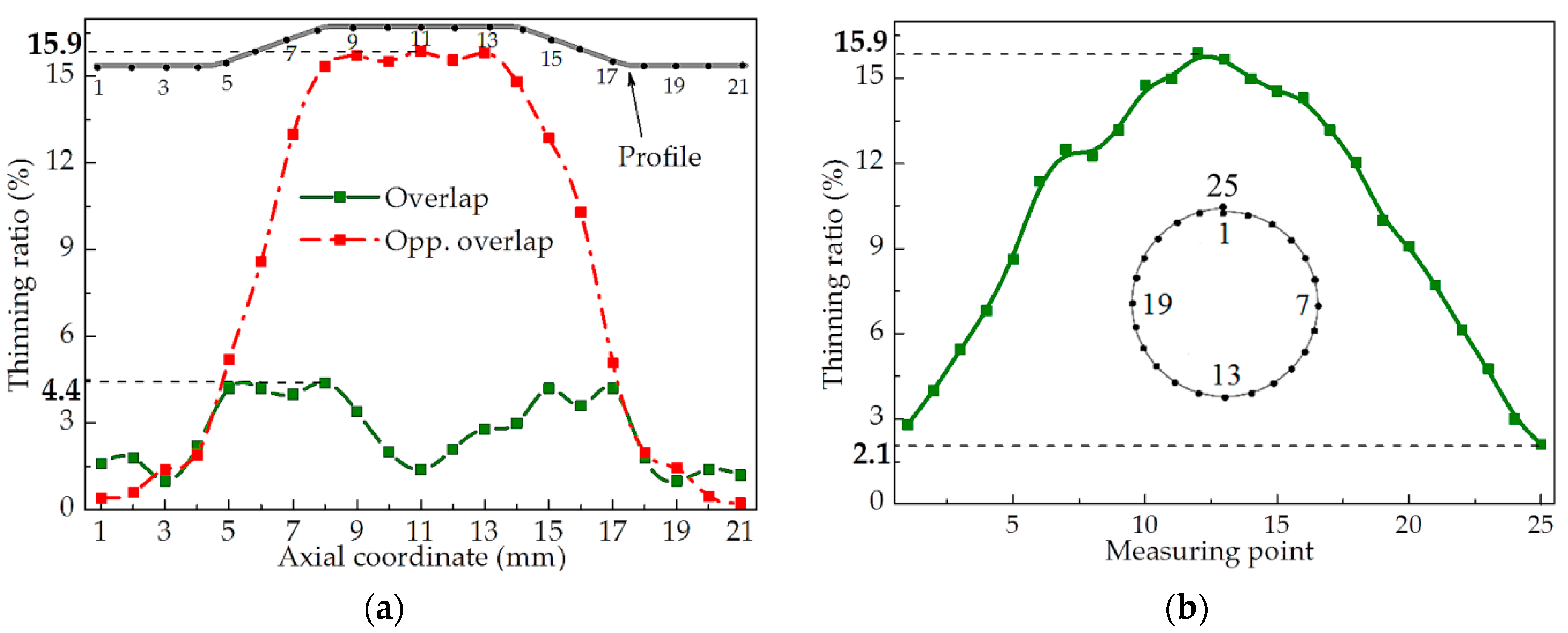
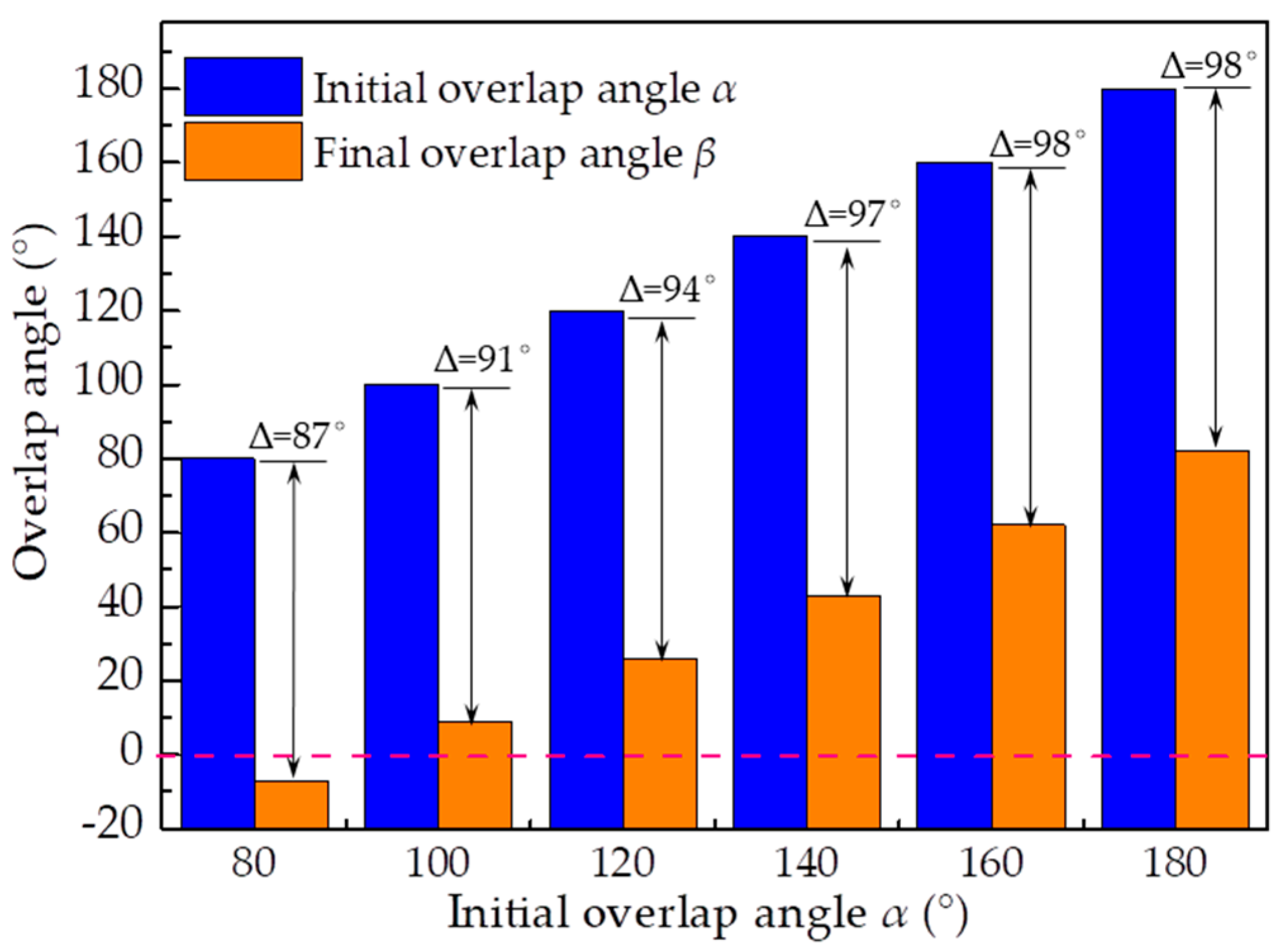
4.2. Variation of the Overlap Angle
4.3. Effect of the Overlap Angle on the Thickness Distribution
5. Conclusions
- (1)
- The effect of boundary conditions: free ends, tied ends and axial constraint ends, on wrinkling defects at the overlap was studied. Wrinkling defects can be weakened when the blank with axial constraint ends was used.
- (2)
- Wrinkling defects occurred at the edge of the overlap owing to the compressive axial stress. Furthermore, a bending deformation was observed through the stress analysis.
- (3)
- The deformation of the blank at the overlap initiated at a low pressure that was nearly half of the yield pressure for tube bugling. The contact sequence to the die cavity of the blank was the overlap at first, then the inner layer of overlap, and the opposite side to the overlap at last.
- (4)
- The circumferential material flow was obtained when axial constraints were applied to avoid the influence of the axial material flow. The profile was concave at the edge of the overlap due to the circumferential material flow. The peak value is located at the middle cross-section.
- (5)
- The variation of the overlap angle increased with the initial overlap angle increasing but the improvement of the thickness distribution did not. An optimal thickness distribution was obtained when the initial angle was 120° for the hydroforming of the variable-diameter part with an expansion of 31.6%.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Saboori, M.; Champliaud, H.; Gholipour, J.; Gakwaya, J.; Savoie, A.; Wanjara, P. Evaluating the flow stress of aerospace alloys for tube hydroforming process by free expansion testing. Int. J. Adv. Manuf. Technol. 2014, 72, 1275–1286. [Google Scholar] [CrossRef]
- Cristina, C.; Sánchez-Amaya, J.; Francisco, C.; Juan, V.M.; Javier, B. Springback estimation in the hydroforming process of UNS A92024-T3 aluminum alloy by FEM simulations. Metals 2018, 8, 404. [Google Scholar]
- Hartl, C. Review on advances in metal micro-tube forming. Metals 2019, 9, 542. [Google Scholar] [CrossRef]
- Aue-U-Lan, Y.; Ngaile, G.; Altan, T. Optimizing tube hydroforming using process simulation and experimental verification. J. Mater. Process. Technol. 2004, 146, 137–143. [Google Scholar] [CrossRef]
- Yuan, S.J.; Han, C.; Wang, X.S. Hydroforming of automotive structural components with rectangular-sections. Int. J. Mach. Tools. Manuf. 2006, 46, 1201–1206. [Google Scholar] [CrossRef]
- Kim, C.I.; Yang, S.H.; Kim, Y.S. Analysis of forming limit in tube hydroforming. J. Mech. Sci. Technol. 2013, 27, 3817–3823. [Google Scholar] [CrossRef]
- He, Z.B.; Wang, Z.B.; Lin, Y.L.; Fan, X.B. Hot deformation behavior of a 2024 aluminum alloy sheet and its modeling by Fields-Backofen model considering strain rate evolution. Metals 2019, 9, 243. [Google Scholar] [CrossRef]
- Manabe, K.I.; Amino, M. Effects of process parameters and material properties on deformation process in tube hydroforming. J. Mater. Process. Technol. 2002, 123, 285–291. [Google Scholar] [CrossRef]
- Sadlowska, H.; Kocanda, A. On the problem of material properties in numerical simulation of tube hydroforming. Arch. Civ. Mech. Eng. 2010, 10, 77–83. [Google Scholar] [CrossRef]
- Ngaile, G.; Jaeger, S.; Altan, T. Lubrication in tube hydroforming (THF) Part II. Performance evaluation of lubricants using LDH test and pear-shaped tube expansion test. J. Mater. Process. Technol. 2004, 146, 116–123. [Google Scholar] [CrossRef]
- Fiorentino, A.; Ceretti, E.; Giardini, C. Tube hydroforming compression test for friction estimation-numerical inverse method, application, and analysis. Int. J. Adv. Manuf. Technol. 2013, 64, 695–705. [Google Scholar] [CrossRef]
- Korkolis, Y.P.; Kyriakides, S. Hydroforming of anisotropic aluminum tubes: Part II analysis. Int. J. Mech. Sci. 2011, 53, 83–90. [Google Scholar] [CrossRef]
- Ben Abdessalem, A.; El-Hami, A. Global sensitivity analysis and multi-objective optimization of loading path in tube hydroforming process based on metamodelling techniques. Int. J. Adv. Manuf. Technol. 2014, 71, 753–773. [Google Scholar] [CrossRef]
- Yuan, S.J.; Wang, X.S.; Liu, G.; Wang, Z.R. Control and use of wrinkles in tube hydroforming. J. Mater. Process. Technol. 2007, 182, 6–11. [Google Scholar] [CrossRef]
- Han, C.; Liu, Q.; Lu, H.; Gao, G.L.; Xie, W.C.; Yuan, S.J. Thickness improvement in hydroforming of a variable diameter tubular component by using wrinkles and preforms. Int. J. Adv. Manuf. Technol. 2018, 99, 2993–3003. [Google Scholar] [CrossRef]
- Wang, X.S.; Cui, X.L.; Yuan, S.J. Research on flattening behavior of wrinkled 5a02 aluminum alloy tubes under internal pressure. Int. J. Adv. Manuf. Technol. 2016, 87, 1159–1167. [Google Scholar] [CrossRef]
- Feng, H.; Han, C. Study on wrinkling behavior in hydroforming of large diameter thin-walled tube through local constraints. Int. J. Adv. Manuf. Technol. 2018, 99, 1329–1340. [Google Scholar] [CrossRef]
- Han, C.; Feng, H. A new method for hydroforming of thin-walled spherical parts using overlapping tubular blanks. Int. J. Adv. Manuf. Technol. 2020, 106, 1543–1552. [Google Scholar] [CrossRef]
- Han, C.; Feng, H. A new method for hydroforming of a variable-diameter part with partially overlapping tubular blanks. In Proceedings of the 9th International Conference on Tube Hydroforming, Kaohsuing, Taiwan, 18–21 November 2019; pp. 146–152. [Google Scholar]
- Sasso, M.; Palmieri, G.; Chiappini, G.; Amodio, D. Characterization of hyperelastic rubber-like materials by biaxial and uniaxial stretching tests based on optical methods. Polym. Test. 2008, 27, 995–1004. [Google Scholar] [CrossRef]
- Mooney, M. A theory of large elastic deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Koubaa, S.; Belhassen, L.; Wali, M.; Dammak, F. Numerical investigation of the forming capability of bulge process by using rubber as a forming medium. Int. J. Adv. Manuf. Technol. 2017, 92, 1839–1848. [Google Scholar] [CrossRef]
- Koc, M.; Altan, T. Prediction of forming limits and parameter in the tube hydroforming process. Int. J. Mach. Tools. Manuf. 2002, 42, 123–138. [Google Scholar] [CrossRef]
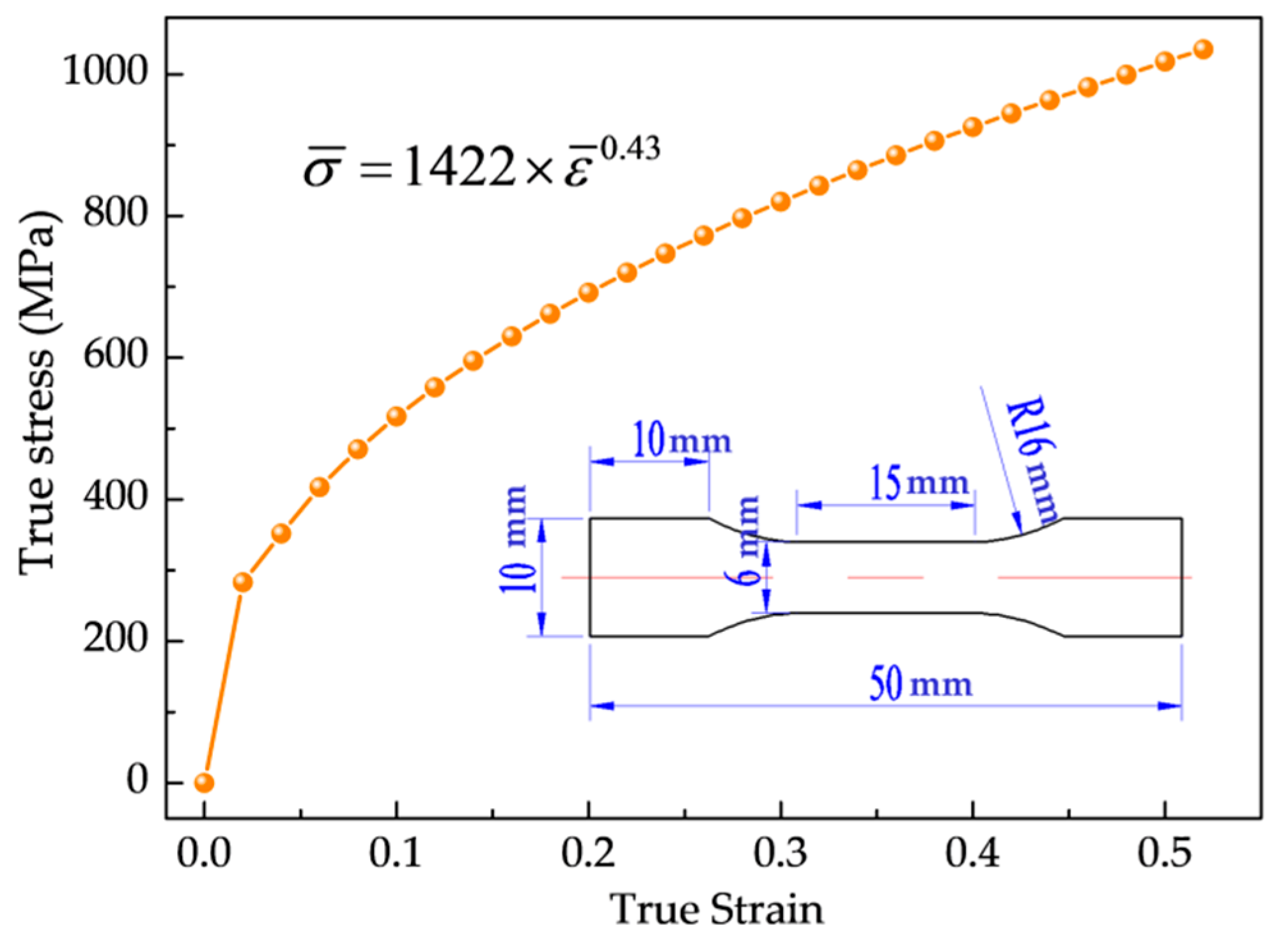



| Elastic Modulus E (GPa) | Yield Strength σs (MPa) | Ultimate Strength σb (MPa) | Elongation δ (%) |
|---|---|---|---|
| 208 | 287 | 903 | 52.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, C.; Feng, H. Circumferential Material Flow in the Hydroforming of Overlapping Blanks. Metals 2020, 10, 864. https://doi.org/10.3390/met10070864
Han C, Feng H. Circumferential Material Flow in the Hydroforming of Overlapping Blanks. Metals. 2020; 10(7):864. https://doi.org/10.3390/met10070864
Chicago/Turabian StyleHan, Cong, and Hao Feng. 2020. "Circumferential Material Flow in the Hydroforming of Overlapping Blanks" Metals 10, no. 7: 864. https://doi.org/10.3390/met10070864
APA StyleHan, C., & Feng, H. (2020). Circumferential Material Flow in the Hydroforming of Overlapping Blanks. Metals, 10(7), 864. https://doi.org/10.3390/met10070864




