Modelling and Experimental Validation of the Porosity Effect on the Behaviour of Nano-Crystalline Materials
Abstract
1. Introduction
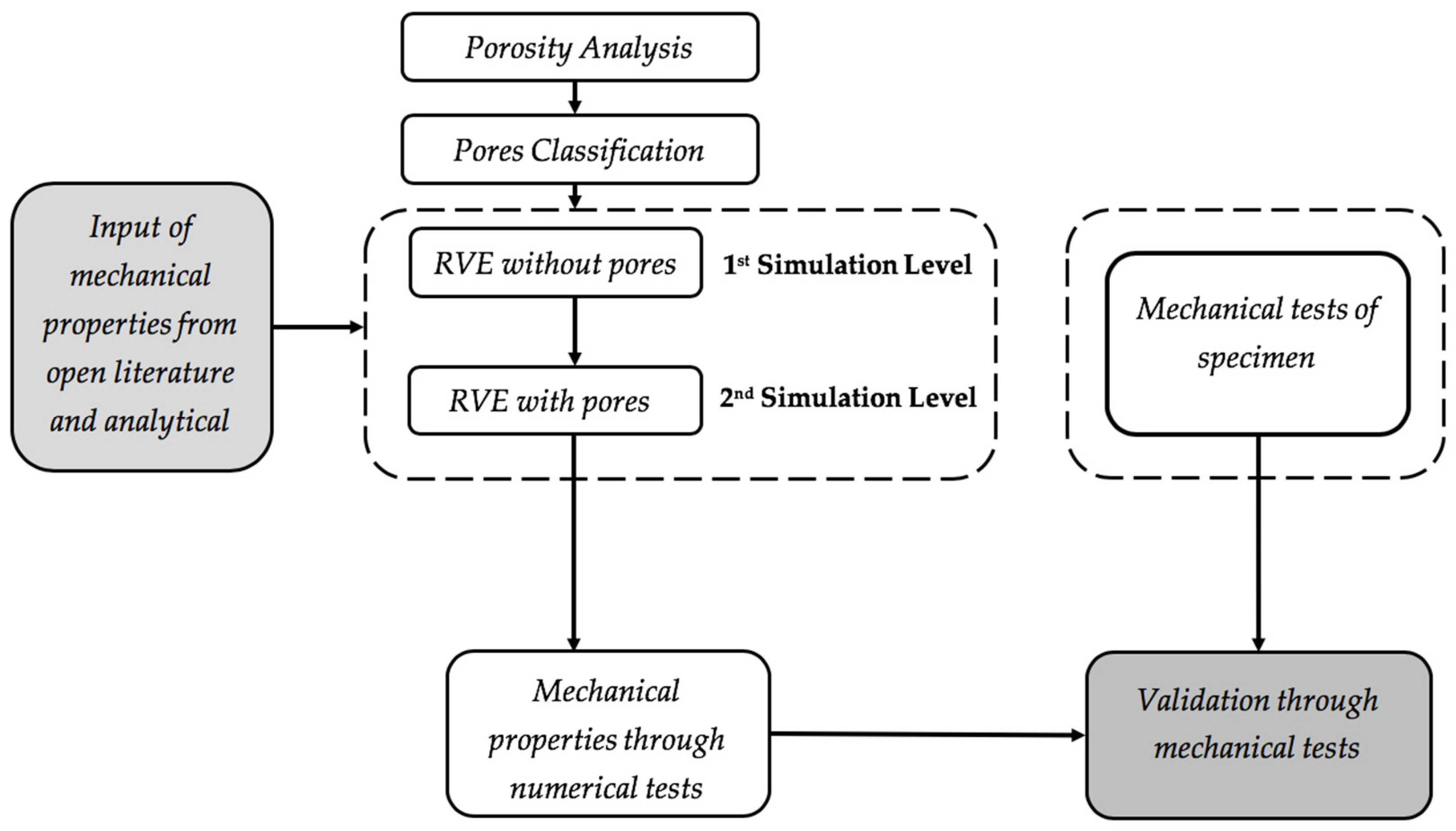
2. Methodology
3. Experimental Procedure
3.1. Materials
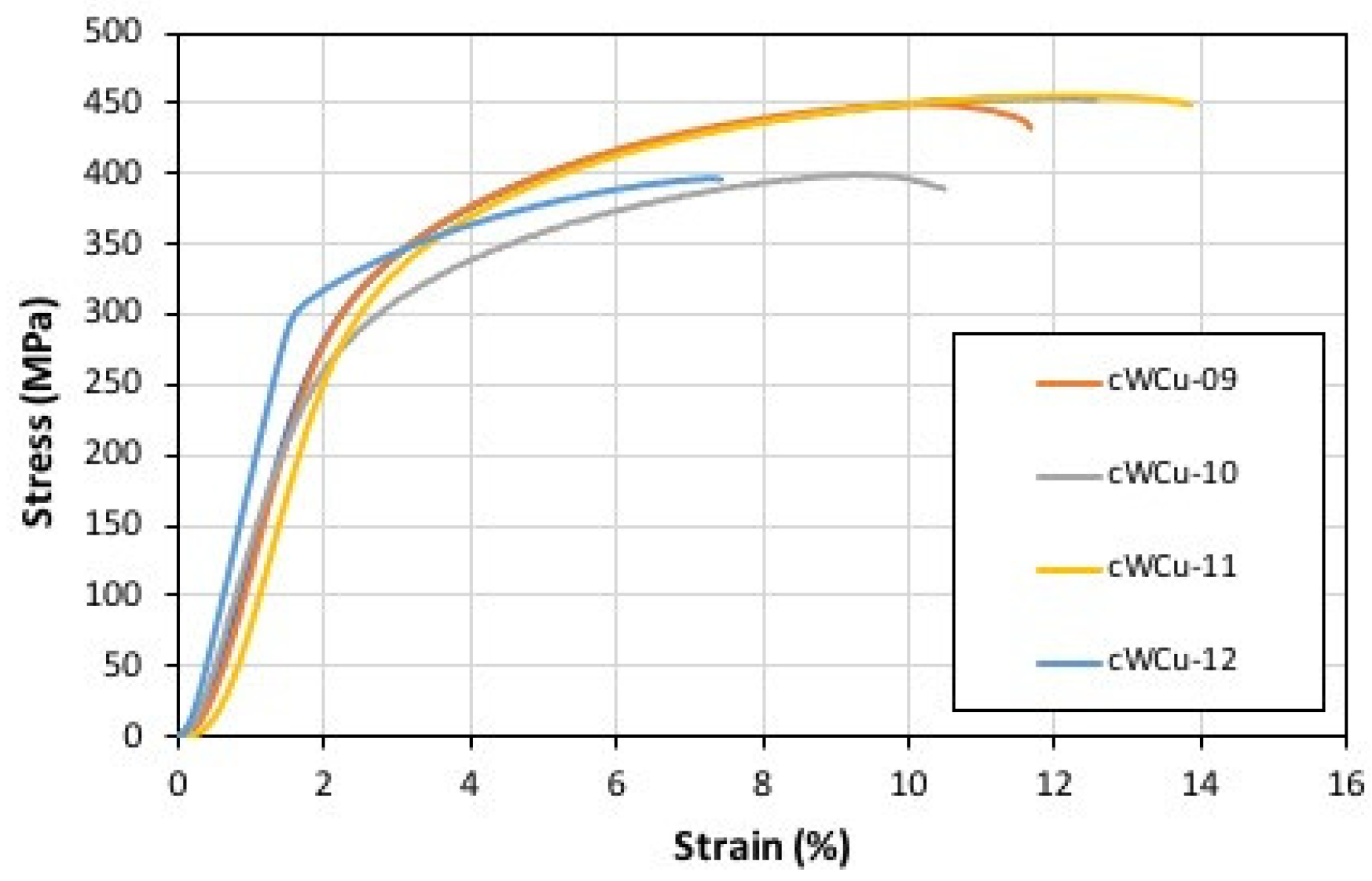
3.2. Compression Testing of the cW-Cu and W-Cu Samples
4. Numerical Model
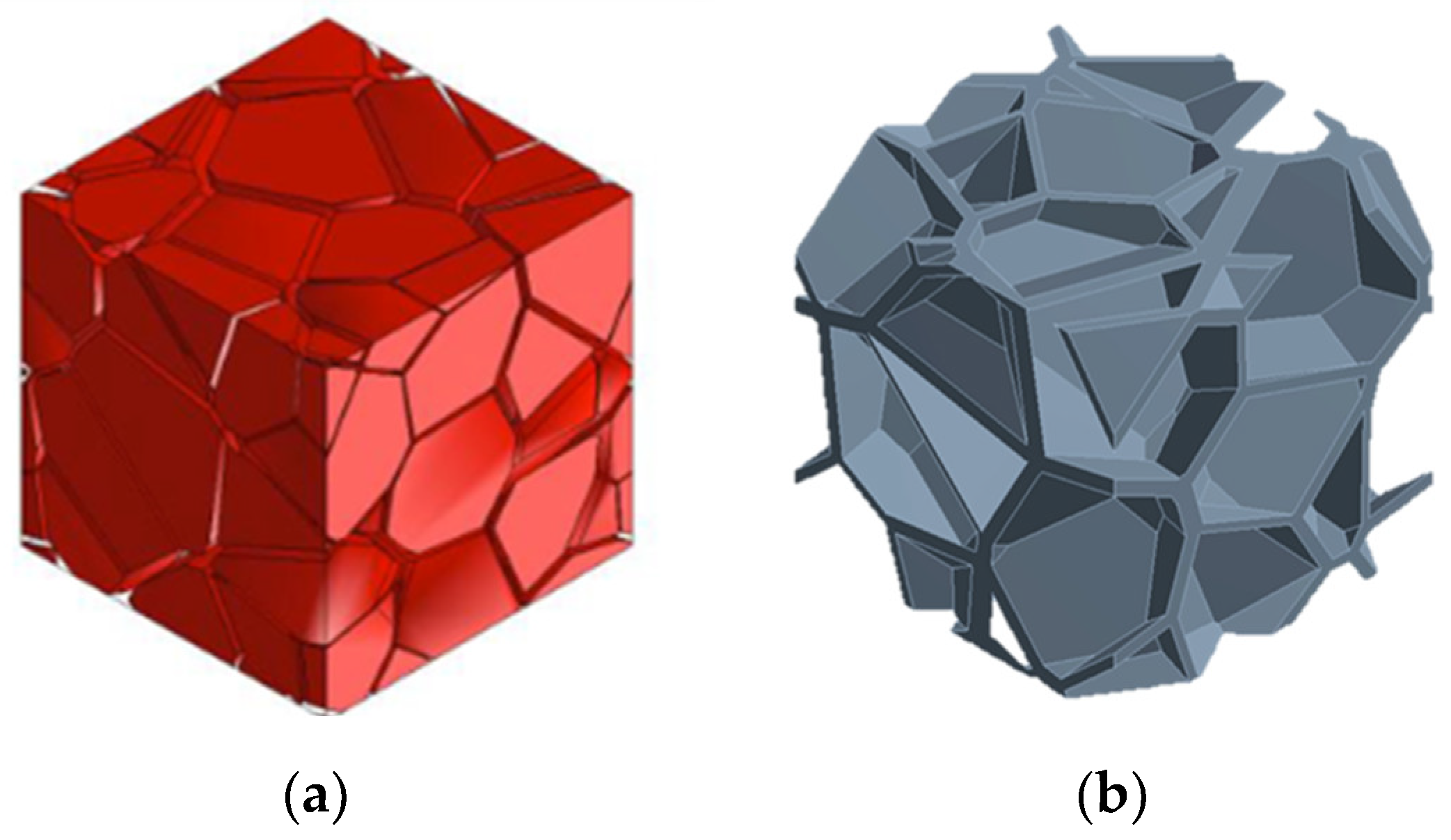
4.1. Porosity Classification
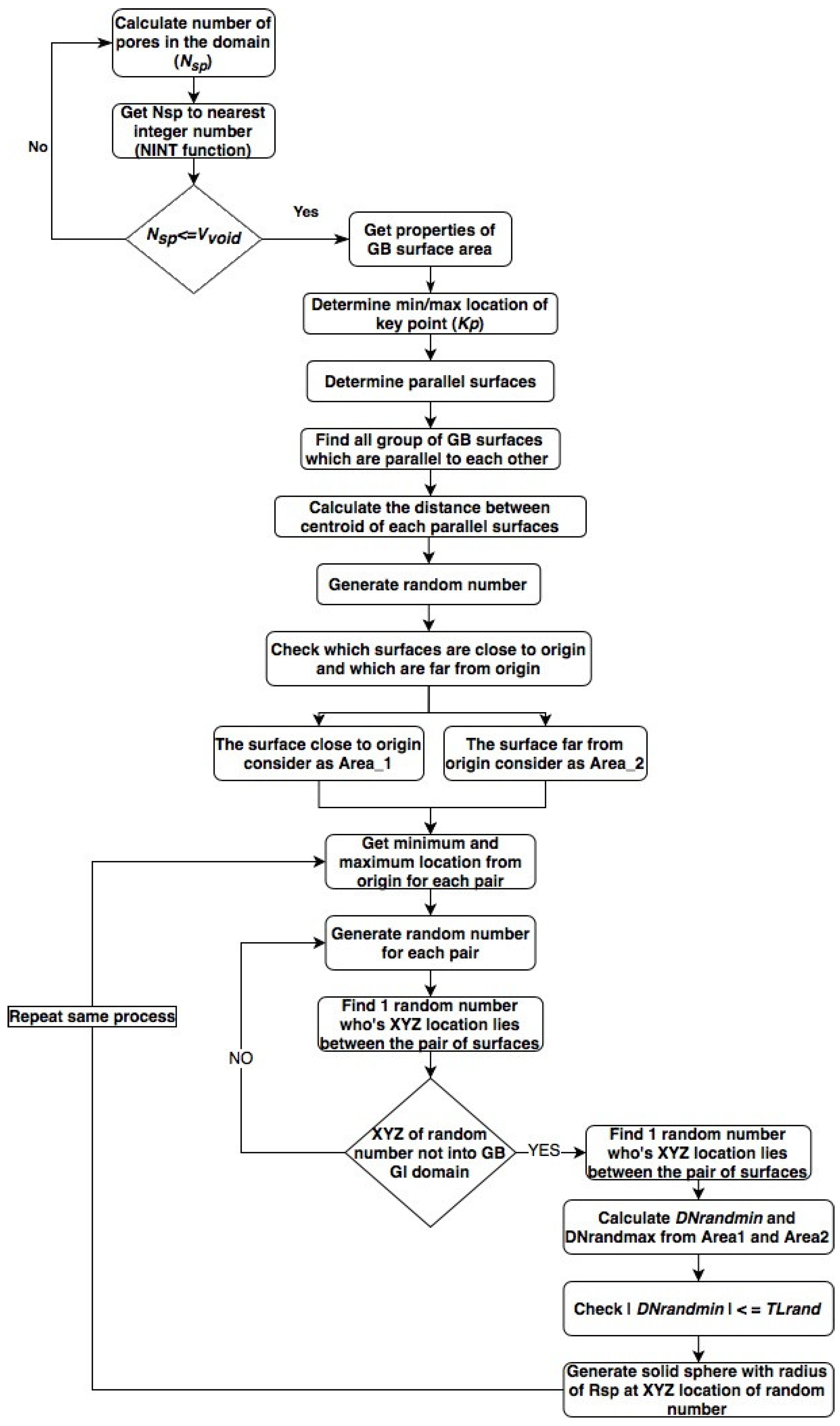
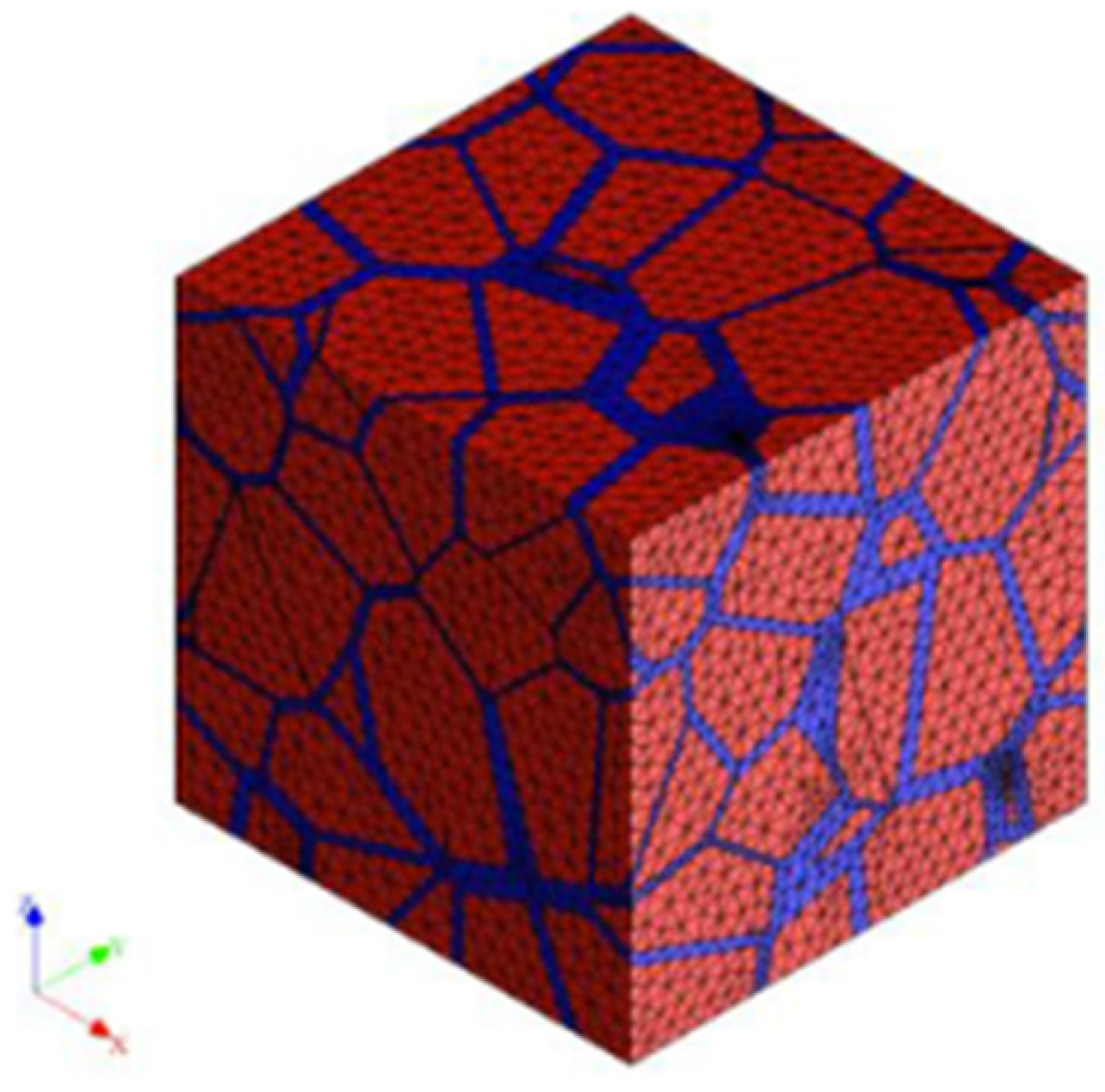
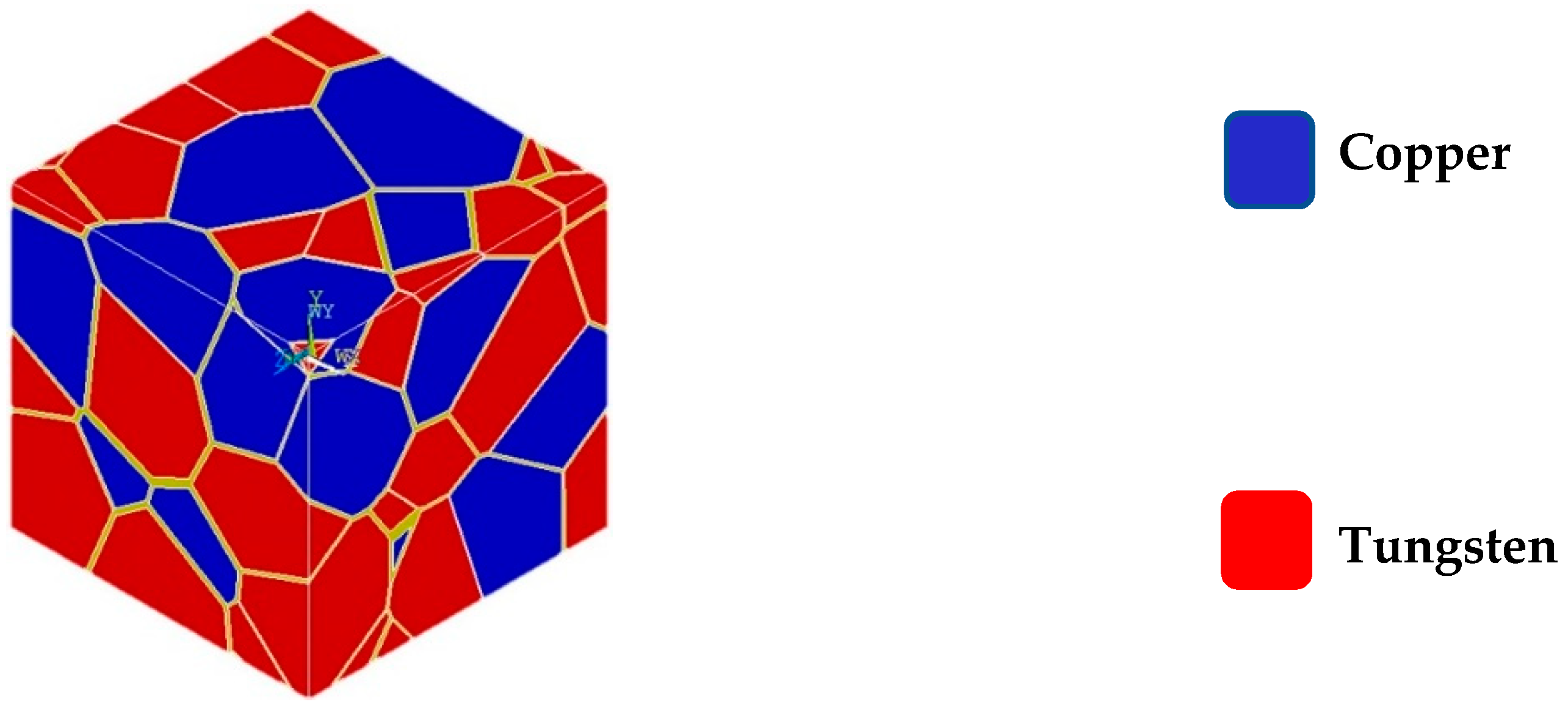
4.2. The RVE
- 1.
- Calculate number of pores in the domain bywhere Vtotal is the total volume (volume of all grains + grain boundary), poros is the porosity percentage, Vvoid is the total porous empty volume, Rsp is the radius of the spherical porous hole and Nsp is the number of porous holes in the domain
- 2.
- Get Nsp as the nearest whole integer number (NINT function in ANSYS APDL) (ANSYS Inc., Canonsburg, PA, USA) [27] and then recheck that total volume of all porous is not greater than Vvoid.
- 3.
- Get the properties of the surface area of GB
- Calculate the area of each surface of GB
- Calculate normal of each area
- Determine min/max location of key point (Kp) from the origin and its associated Kp number for each area (GB surface)
- 4.
- Determine parallel Surface
- d.
- Check whether GB surface lies on the boundary of a cube or not from its max/min centroid location
- e.
- Find all groups of GB surfaces (excluding boundary surfaces) who’s normal vectors are parallel to each other.
- f.
- Calculate the distance between the centroid of each parallel surface and find the pair of surfaces which has minimum centroid distance.
- 5.
- Generate a random number
- g.
- For each pair, calculate distance from the origin of global coordinate (0,0,0) to the centroid of both the surfaces. In order to check which surface is close to the origin and which surfaces are far from the origin. The surface close to the origin is considered as Area 1 and the surface far from the origin is considered as Area 2.
- h.
- From the previously calculated min/max kp location, get the minimum and maximum location from the origin for each pair. This will define a small cubical space covered by a pair of surfaces in the GB and GI domain. Size of that cubical space will be xmin-xmax, ymin-ymax and zmin-zmax.
- i.
- Generate 500 (randsize) random numbers within the range of that cubical space for each pair.
- j.
- Find a minimum of one random number who’s XYZ location lies in between the pair of surfaces (Area 1 and Area 2)
- First, check that XYZ location of random number does not lie on the boundary of GB and GI domain
- Calculate the normal distance (DNrandmin) of the random number from Area 1 and similarly the normal distance (DNrandmax) from Area 2
- Recalculate the distance (Dcentmin) between the centroid of Area 1 and Area 2
- Check the XYZ location of the random number is greater than the location of Kp (xcent1, ycent1, zcent1) of Area 1 that is close to the origin (0,0,0) and the XYZ location is less than Kp (xcent2, ycent2, zcent2) of Area 1 that is far from the origin. By doing so, it is decided whether the random number lies inside the cubical space of area pair, not on the boundary of area pair.
- Considering GB as imported solid bodies, it is assumed that normal of all surfaces will be in an outward direction. Hence, the normal direction of both the surfaces of each pair will be in opposition to each other’s direction. Now check the location of the random number with respect to the normal direction of Area 1 and Area 2. If the normal vector from Area 1 to the XYZ location of the random number has the same direction as the normal vector of Area 1, then the previously calculated normal distance DNrandmin will be positive, otherwise, it will be negative. Therefore, check that normal distance DNrandmin of the random number is greater than 0 and DNrandmax is less than 0.
- Further, check that sum of the absolute value of the normal distance of a random number from Area 1 and Area 2 is not greater than the centroidal distance (Dcentmin). This confirms if the random number perfectly comes in between the pair of areas (Area 1 and Area 2)
- In order to make sure that random number does not lie very close to Area 1 or Area 2, check that the absolute value of DNrandmin is greater than tolerance TLdrand. Tolerance is nothing but 5% of Dcentmin. This is the optional condition.
- k.
- Repeat the same process. The total number of random numbers (Nsp) is found.
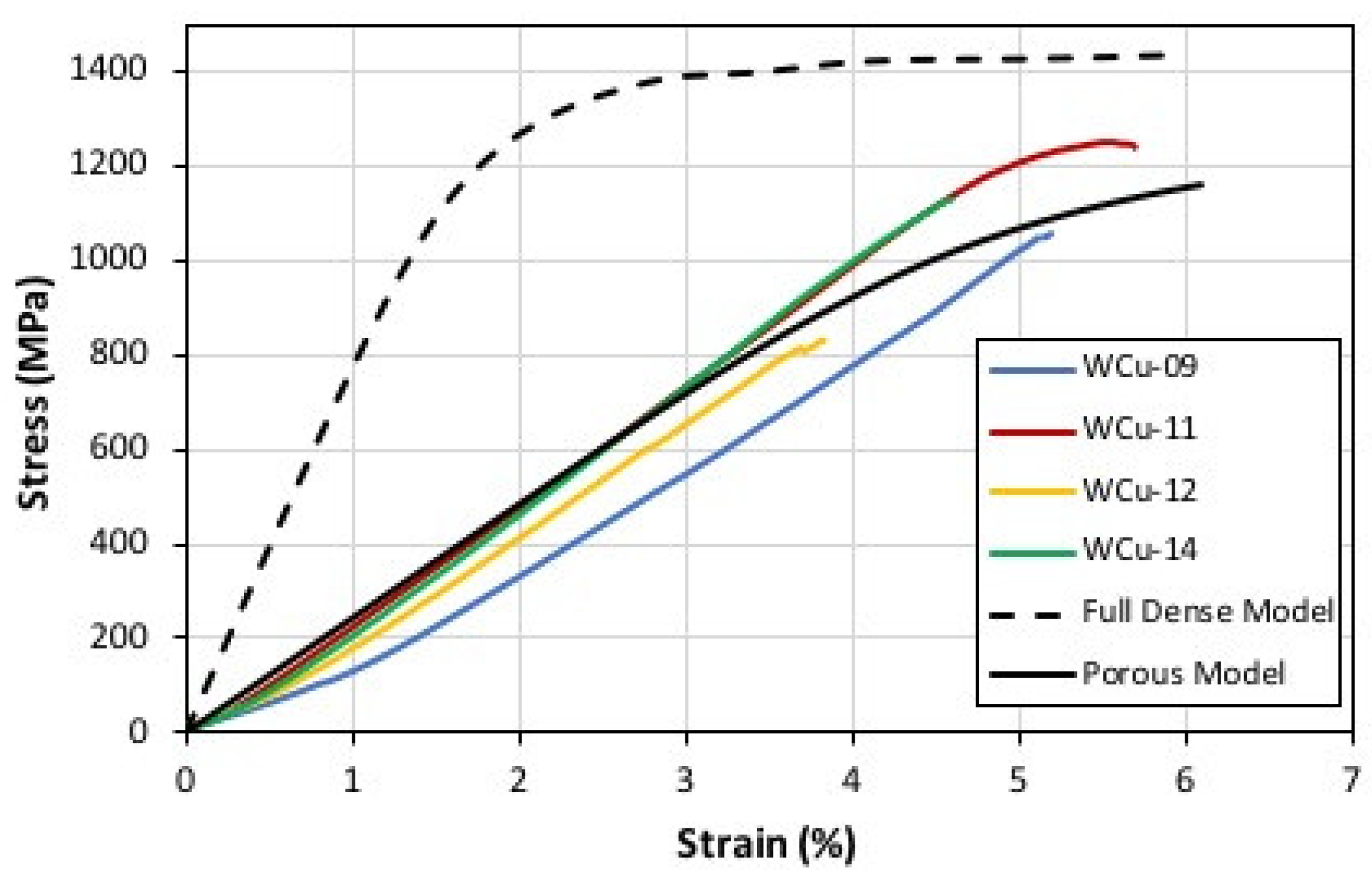
5. Comparison of Numerical and Experimental Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gleiter, H. Nanocrystalline materials. Prog. Mater. Sci. 1989, 33, 223–315. [Google Scholar] [CrossRef]
- Gleiter, H. Nanostructured materials: Basic concepts and microstructure. Acta Mater. 2000, 48, 1–29. [Google Scholar] [CrossRef]
- Suryanarayana, C. Nanocrystalline materials. Int. Mater. Rev. 1995, 40, 41–64. [Google Scholar] [CrossRef]
- Hibbard, G.; Erb, U.; Aust, K.; Klement, U.; Palumbo, G. Thermal Stability of Nanostructured Electrodeposits. J. Metastable Nanocryst. Mater. 2002, 13, 387–396. [Google Scholar]
- Groza, J. Nanostructured Materials. Mater. Today 2002, 5, 55. [Google Scholar]
- Lowe, T.; Valiev, R. Producing nanoscale microstructures through severe plastic deformation. JOM 2000, 52, 27–28. [Google Scholar] [CrossRef]
- Valiev, R.; Islamgaliev, R.; Alexandrov, I. Bulk nanostructured materials from severe plastic deformation. Progress Mater. Sci. 2000, 45, 103–189. [Google Scholar] [CrossRef]
- El-Atwani, O.; Hinks, J.; Greaves, G.; Allain, J.; Maloy, S. Grain size threshold for enhanced irradiation resistance in nanocrystalline and ultrafine tungsten. Mater. Res. Lett. 2017, 5, 343–349. [Google Scholar] [CrossRef]
- El-Atwani, O.; Esquivel, E.; Aydogan, E.; Martinez, E.; Baldwin, J.; Li, M.; Uberuaga, B.; Maloy, S. Unprecedented irradiation resistance of nanocrystalline tungsten with equiaxed nanocrystalline grains to dislocation loop accumulation. Acta Mater. 2019, 165, 118–128. [Google Scholar] [CrossRef]
- Lennon, A.; Ramesh, K. The thermoviscoplastic response of polycrystalline tungsten in compression. Mater. Sci. Eng. A 2000, 276, 9–21. [Google Scholar] [CrossRef]
- Dümmer, T.; Lasalvia, J.; Ravichandran, G.; Meyers, M. Effect of strain rate on plastic flow and failure in polycrystalline tungsten. Acta Mater. 1998, 46, 6267–6290. [Google Scholar] [CrossRef]
- Lassner, E.; Schubert, W. Tungsten: Properties, Chemistry, Technology of the Element, Alloys, and Chemical Compounds, 1st ed.; Kluwer Academic/Plenum Publishers: New York, NY, USA, 1999. [Google Scholar]
- Gumbsch, P. Controlling Factors for the Brittle-to-Ductile Transition in Tungsten Single Crystals. Science 1998, 282, 1293–1295. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Jiao, T.; Ramesh, K.; Ma, E.; Kecskes, L.; Magness, L.; Dowding, R.; Kazykhanov, V.; Valiev, R. Mechanical behavior and dynamic failure of high-strength ultrafine grained tungsten under uniaxial compression. Acta Mater. 2006, 54, 77–87. [Google Scholar] [CrossRef]
- Raghu, T.; Sundaresan, R.; Ramakrishnan, P.; Rama Mohan, T. Synthesis of nanocrystalline copper–tungsten alloys by mechanical alloying. Mater. Sci. Eng. A 2001, 304–306, 438–441. [Google Scholar] [CrossRef]
- Raghu, T.; Sundaresan, R.; Ramakrishnan, P.; Mohan, T. Synthesis of nanocrystalline copper–tungsten alloys by mechanical alloying. In Proceedings of the International Symposium on Metastable, Mechanically Alloyed and Nanostructured Materials (ISMANAM), Rome, Italy, 20–24 May 1996. [Google Scholar]
- Bachurin, D. Influence of voids distribution on the deformation behavior of nanocrystalline palladium. Solid State Commun. 2018, 275, 43–47. [Google Scholar] [CrossRef]
- Tserpes, K.; Stamopoulos, A.; Pantelakis, S. A numerical methodology for simulating the mechanical behavior of CFRP laminates containing pores using X-ray computed tomography data. Compos. Part B Eng. 2016, 102, 122–133. [Google Scholar] [CrossRef]
- Shen, T.; Dai, Y.; Lee, Y. Microstructure and tensile properties of tungsten at elevated temperatures. J. Nucl. Mater. 2016, 468, 348–354. [Google Scholar] [CrossRef]
- Meyers, M.; Mishra, A.; Benson, D. Mechanical properties of nanocrystalline materials. Prog. Mater. Sci. 2006, 51, 427–556. [Google Scholar] [CrossRef]
- Ma, E.; Zhu, T. Towards strength–ductility synergy through the design of heterogeneous nanostructures in metals. Mater. Today 2017, 20, 323–331. [Google Scholar] [CrossRef]
- Sanders, P.; Eastman, J.; Weertman, J. Pore distributions in nanocrystalline metals from small-angle neutron scattering. Acta Mater. 1998, 46, 4195–4202. [Google Scholar] [CrossRef]
- Agnew, S.; Elliott, B.; Youngdahl, C.; Hemker, K.; Weertman, J. Microstructure and mechanical behavior of nanocrystalline metals. Mater. Sci. Eng. A 2000, 285, 391–396. [Google Scholar] [CrossRef]
- Bazios, P.; Tserpes, K.; Pantelakis, S. Numerical Computation of Material Properties of Nanocrystalline Materials Utilizing Three-Dimensional Voronoi Models. Metals 2019, 9, 202. [Google Scholar] [CrossRef]
- Van Swygenhoven, H.; Farkas, D.; Caro, A. Grain-boundary structures in polycrystalline metals at the nanoscale. Phys. Rev. B 2000, 62, 831–838. [Google Scholar] [CrossRef]
- Birringer, R. Nanocrystalline materials. Mater. Sci. Eng. A 1989, 117, 33–43. [Google Scholar] [CrossRef]
- ANSYS, Inc. Release 11.0 Documentation for ANSYS; ANSYS Inc.: Canonsburg, PA, USA, 2006. [Google Scholar]
- Pierard, O.; LLorca, J.; Segurado, J.; Doghri, I. Micromechanics of particle-reinforced elasto-viscoplastic composites: Finite element simulations versus affine homogenization. Int. J. Plast. 2007, 23, 1041–1060. [Google Scholar] [CrossRef]
- Majewski, M.; Holobut, P.; Kursa, M.; Kowalczyk-Gajewska, K. Packing and size effects in elastic-plastic particulate composites: Micromechanical modelling and numerical verification. Int. J. Eng. Sci. 2020, 151, 103271. [Google Scholar] [CrossRef]
- Dobosz, R.; Lewandowska, M.; Kurzydlowski, K. The effect of grain size diversity on the flow stress of nanocrystalline metals by finite-element modelling. Scr. Mater. 2012, 67, 408–411. [Google Scholar] [CrossRef]
- Online Materials Information Resource—MatWeb. Available online: http://www.matweb.com/ (accessed on 23 October 2018).
- Callister, W.; Rethwisch, D. Materials Science and Engineering; John Wiley and Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Cordero, Z.; Knight, B.; Schuh, C. Six decades of the Hall–Petch effect—A survey of grain-size strengthening studies on pure metals. Int. Mater. Rev. 2016, 61, 495–512. [Google Scholar] [CrossRef]
- Volpp, T.; Göring, E.; Kuschke, W.; Arzt, E. Grain size determination and limits to Hall-Petch behavior in nanocrystalline NiAl powders. Nanostruct. Mater. 1997, 8, 855–865. [Google Scholar] [CrossRef]
- Diehl, J. Verfestigungskurven und Oberflächenerscheinungen. Z. Met. 1956, 47, 331–343. [Google Scholar]
- Nieh, T.; Wadsworth, J. Hall-petch relation in nanocrystalline solids. Scr. Metall. Mater. 1991, 25, 955–958. [Google Scholar] [CrossRef]
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1948, 193, 281–297. [Google Scholar]
- Farrell, K.; Schaffhauser, A.; Stiegler, J. Recrystallization, grain growth and the ductile-brittle transition in tungsten sheet. J. Less Common Met. 1967, 13, 141–155. [Google Scholar] [CrossRef]




| Material | Diameter (mm) | Height (mm) | Mass (g) | Theoretical Density (g/cm3) | Calculated Relative Density (%) |
|---|---|---|---|---|---|
| W-Cu | 13.08–13.11 | 25.1 | 45.12–46.53 | 14.95 | 89.04–92.25 |
| cW-Cu | 13.08–13.14 | 24.72–25.16 | 44.92–46.14 | 88.84–92.04 |
| Step | Status | W | Cu |
|---|---|---|---|
| Composition (wt%) | 74% | 26% | |
| 1 | As-received powder size (nm) | 1300 ± 300 | 279 ± 62 |
| 2 | Cold pressed powder size (nm) | 1011 ± 225 | 74 ± 55 |
| 3 | HIP grain size (nm) | 113 ± 25 | 45 ± 25 |
| 4 | Grain size after 36 h annealing (nm) | 206 ± 70 | 247 ± 55 |
| Step | Status | W | Cu |
|---|---|---|---|
| - | Composition (wt%) | 73.67% | 26.33% |
| 1 | Milled powder size (nm) | 30 ± 15 | 6 ± 5 |
| 2 | Cold pressed powder size (nm) | 16 ± 4 | 8 ± 3 |
| 3 | HIP grain size (nm) | 95 ± 60 | 31 ± 7 |
| 4 | Grain size after 36h annealing (nm) | 187 ± 65 | 108 ± 24 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bazios, P.; Tserpes, K.; Pantelakis, S. Modelling and Experimental Validation of the Porosity Effect on the Behaviour of Nano-Crystalline Materials. Metals 2020, 10, 821. https://doi.org/10.3390/met10060821
Bazios P, Tserpes K, Pantelakis S. Modelling and Experimental Validation of the Porosity Effect on the Behaviour of Nano-Crystalline Materials. Metals. 2020; 10(6):821. https://doi.org/10.3390/met10060821
Chicago/Turabian StyleBazios, Panagiotis, Konstantinos Tserpes, and Spiros Pantelakis. 2020. "Modelling and Experimental Validation of the Porosity Effect on the Behaviour of Nano-Crystalline Materials" Metals 10, no. 6: 821. https://doi.org/10.3390/met10060821
APA StyleBazios, P., Tserpes, K., & Pantelakis, S. (2020). Modelling and Experimental Validation of the Porosity Effect on the Behaviour of Nano-Crystalline Materials. Metals, 10(6), 821. https://doi.org/10.3390/met10060821






