Recovery of Diamond and Cobalt Powders from Polycrystalline Drawing Die Blanks via Ultrasound Assisted Leaching Process—Part 2: Kinetics and Mechanisms
Abstract
:Part 1: Experimental Design and Efficiencies
1. Introduction
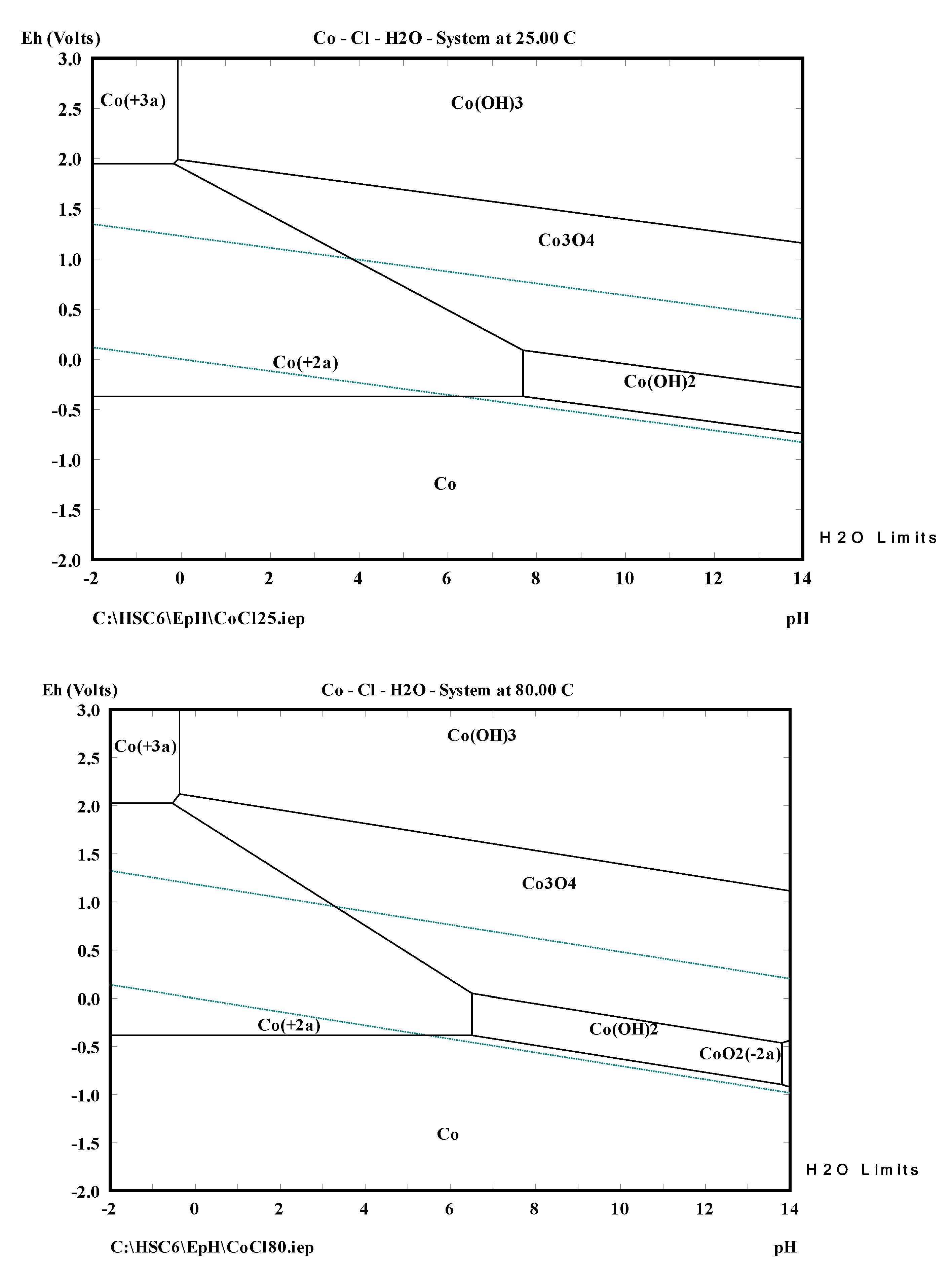
2. Thermochemistry of Cobalt Leaching
3. Experiment
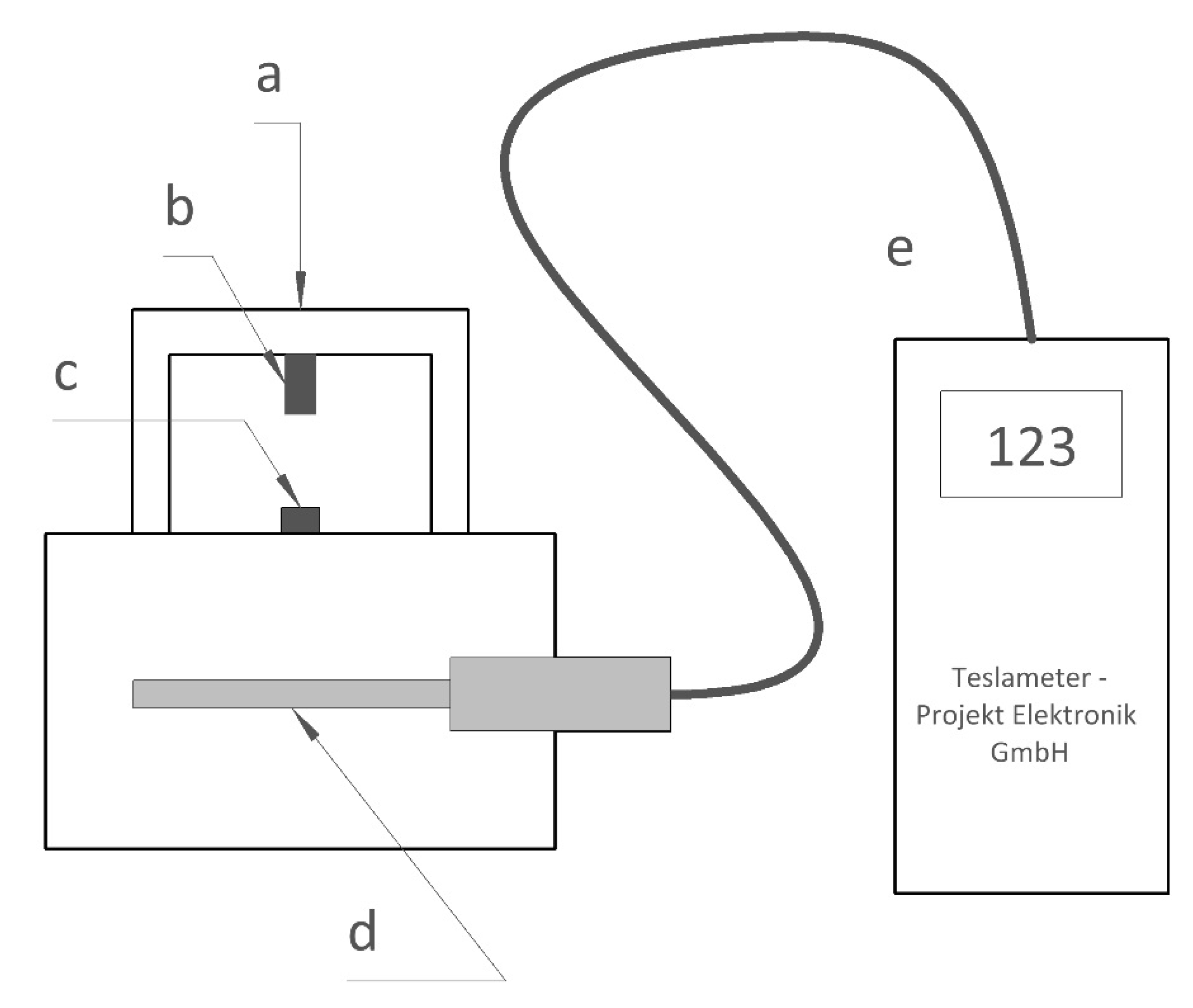
3.1. Changes in Magnetic Properties of the PCD
3.2. Preparation of Samples
3.3. Increase of Co Content in Solution
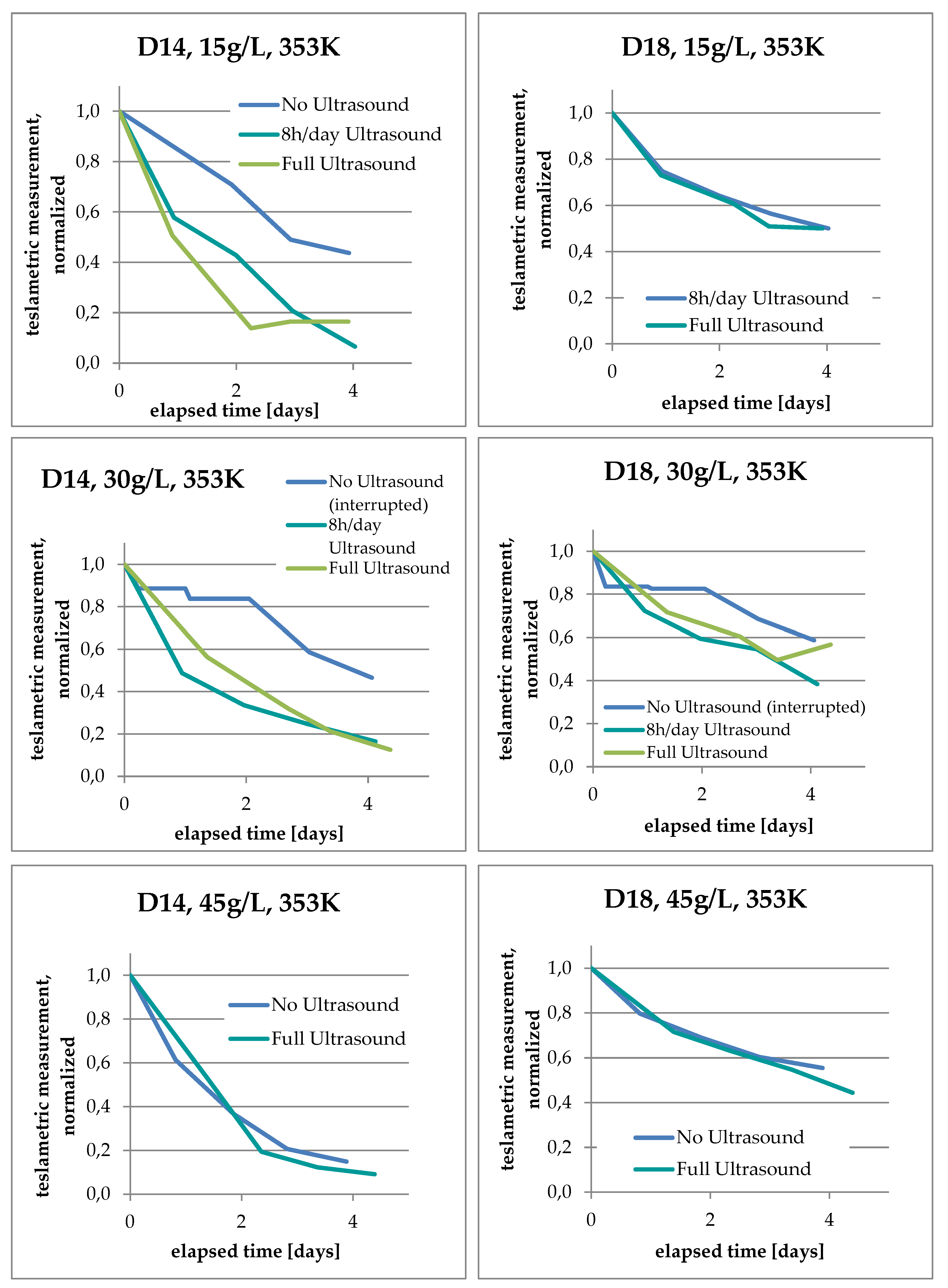
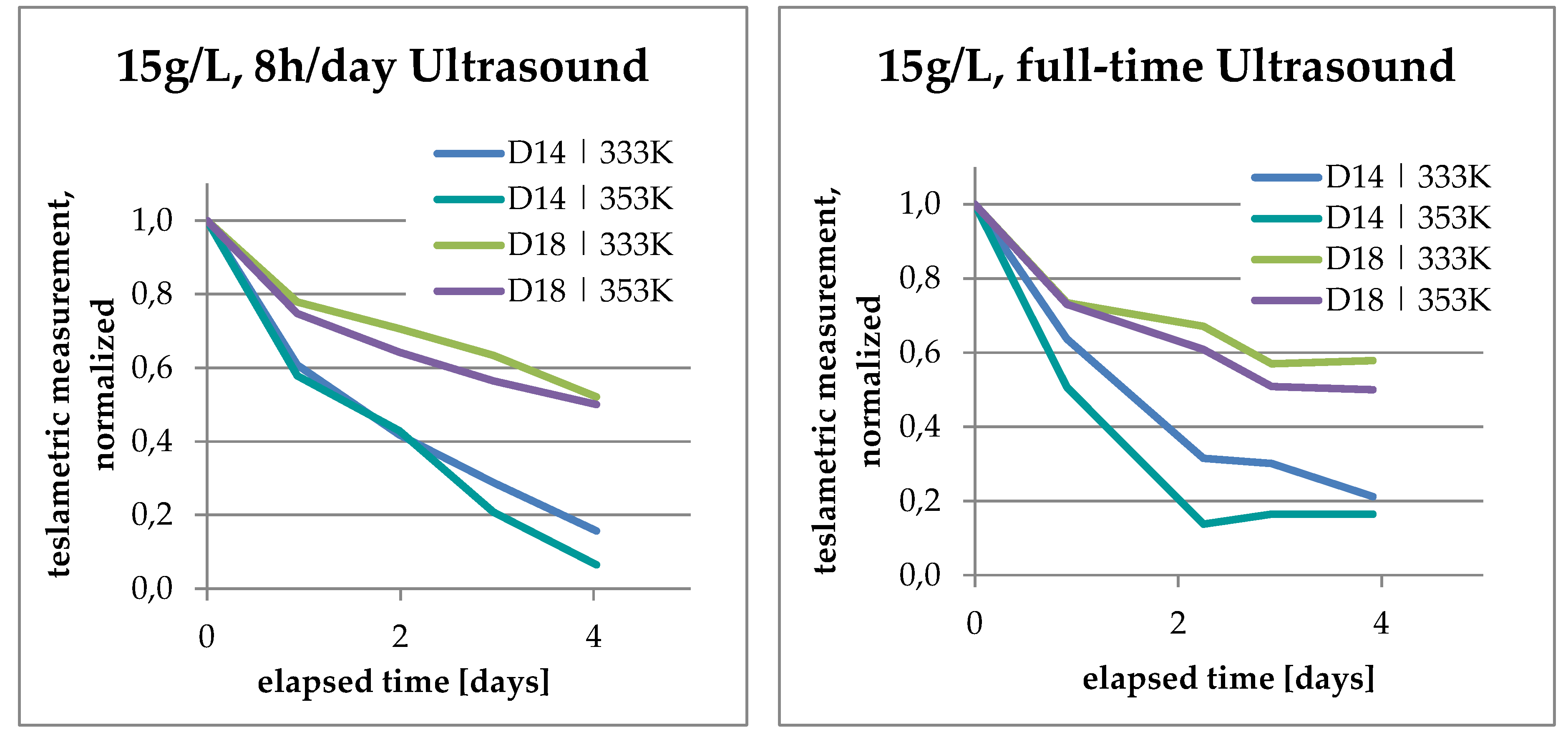
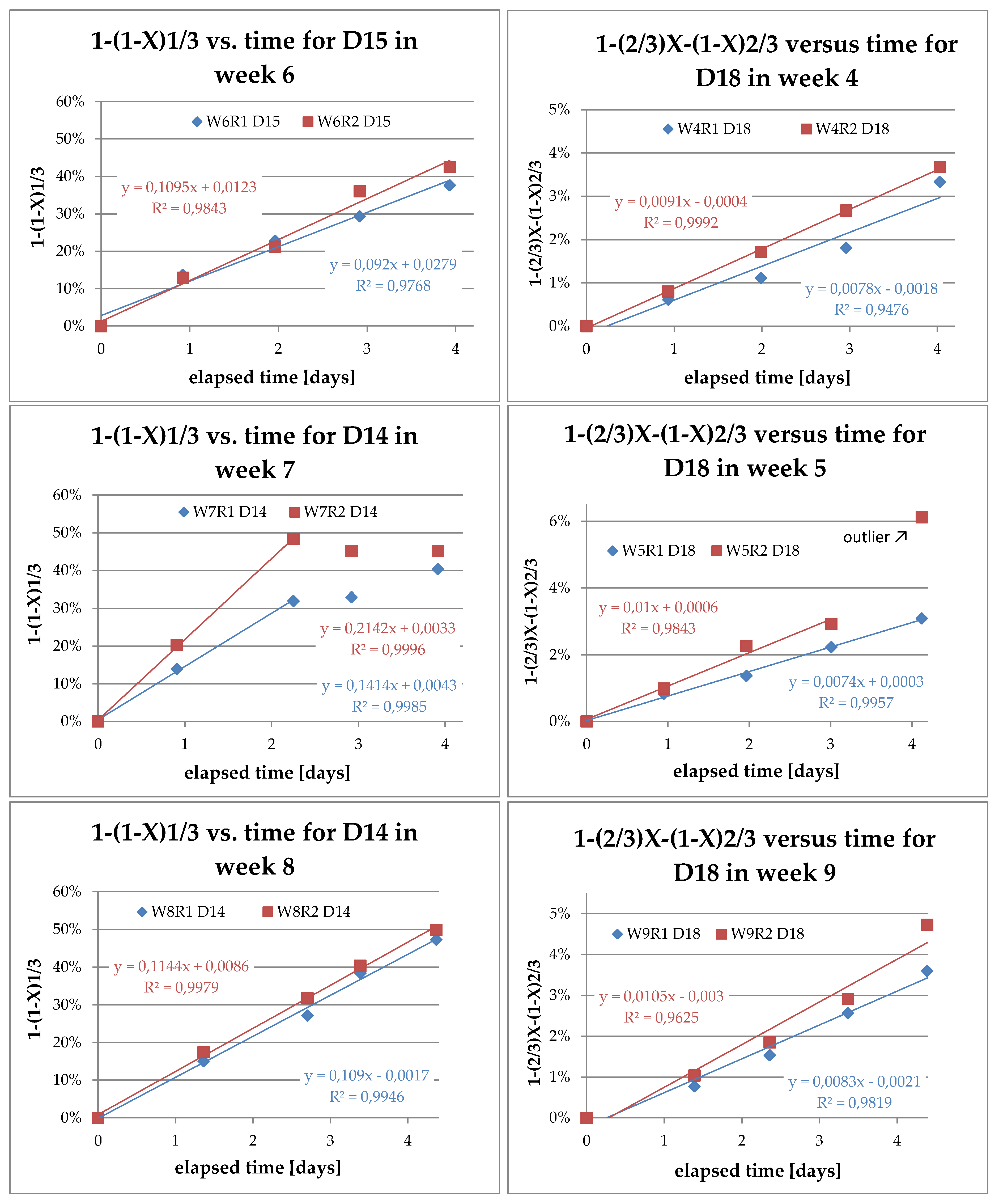
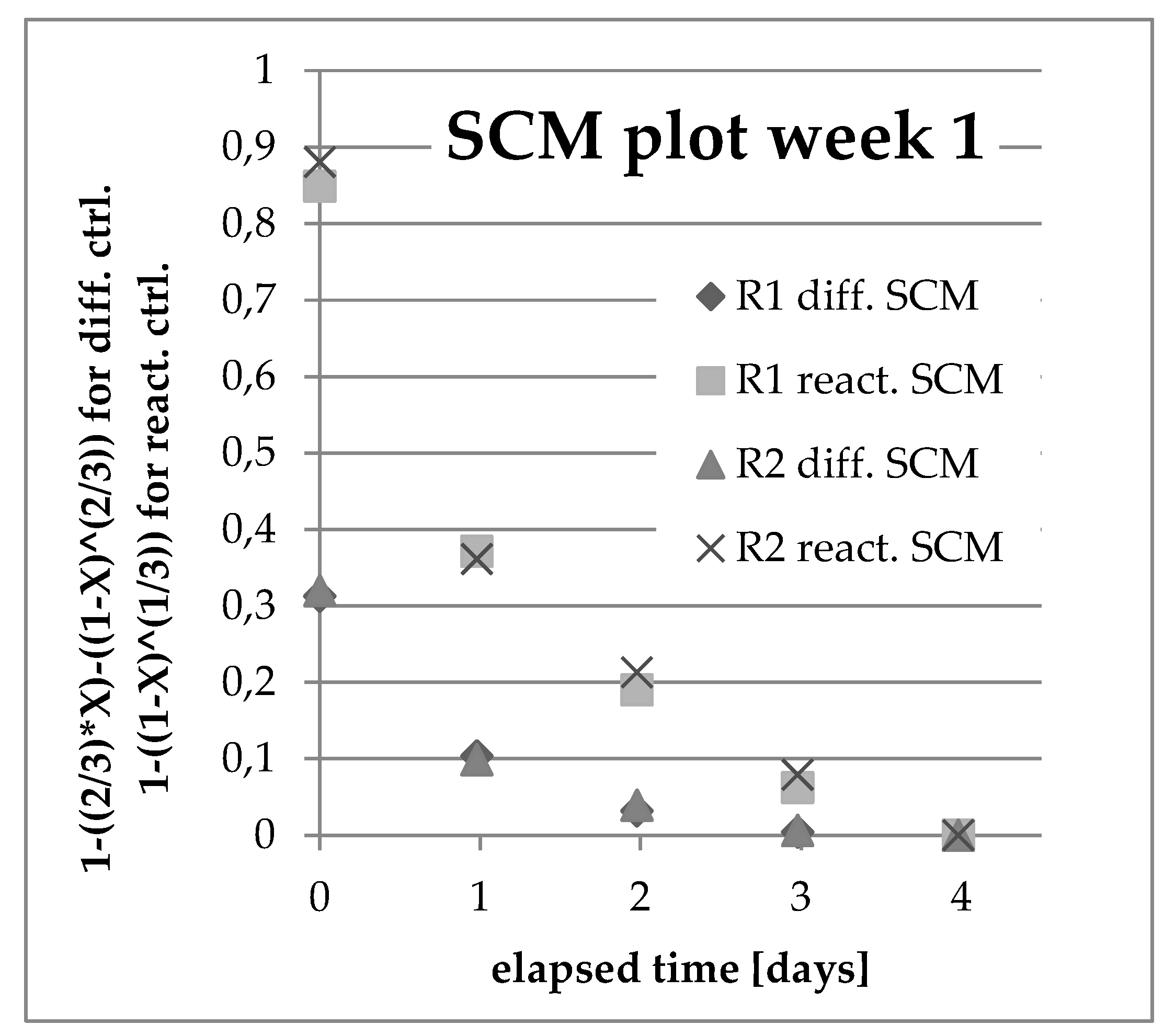
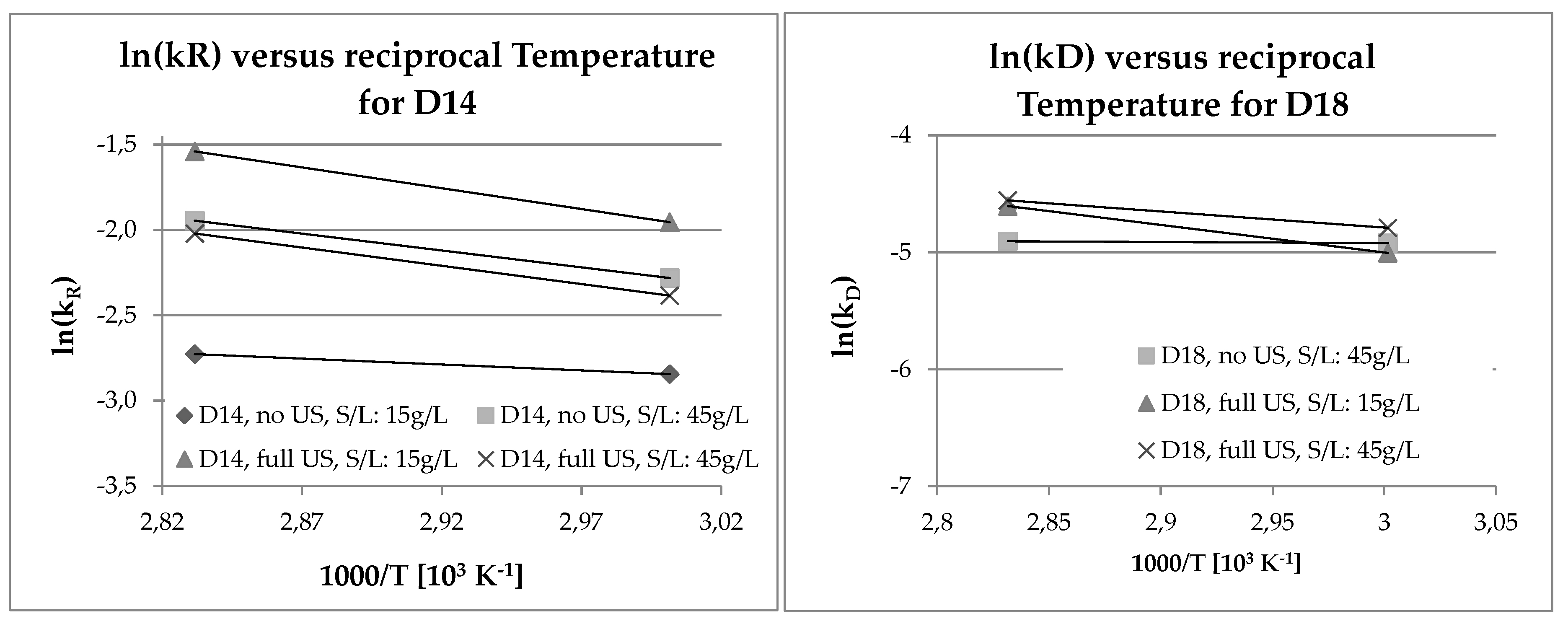
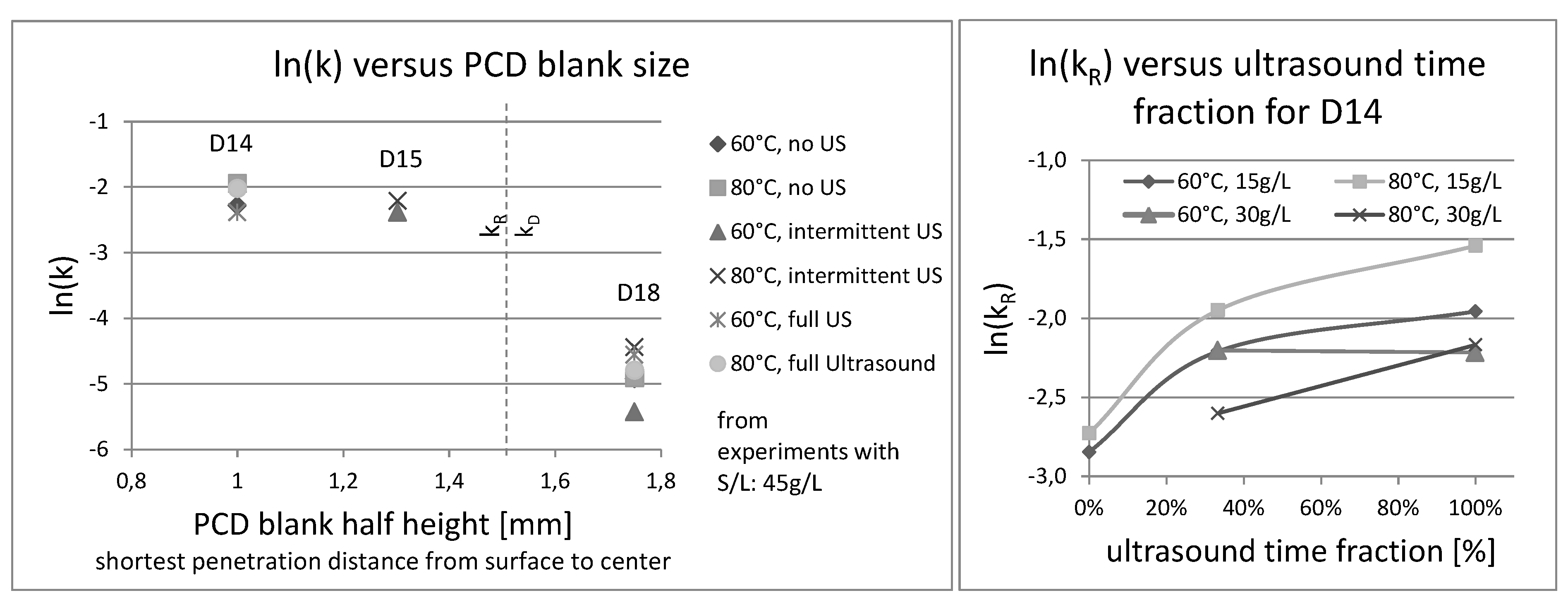
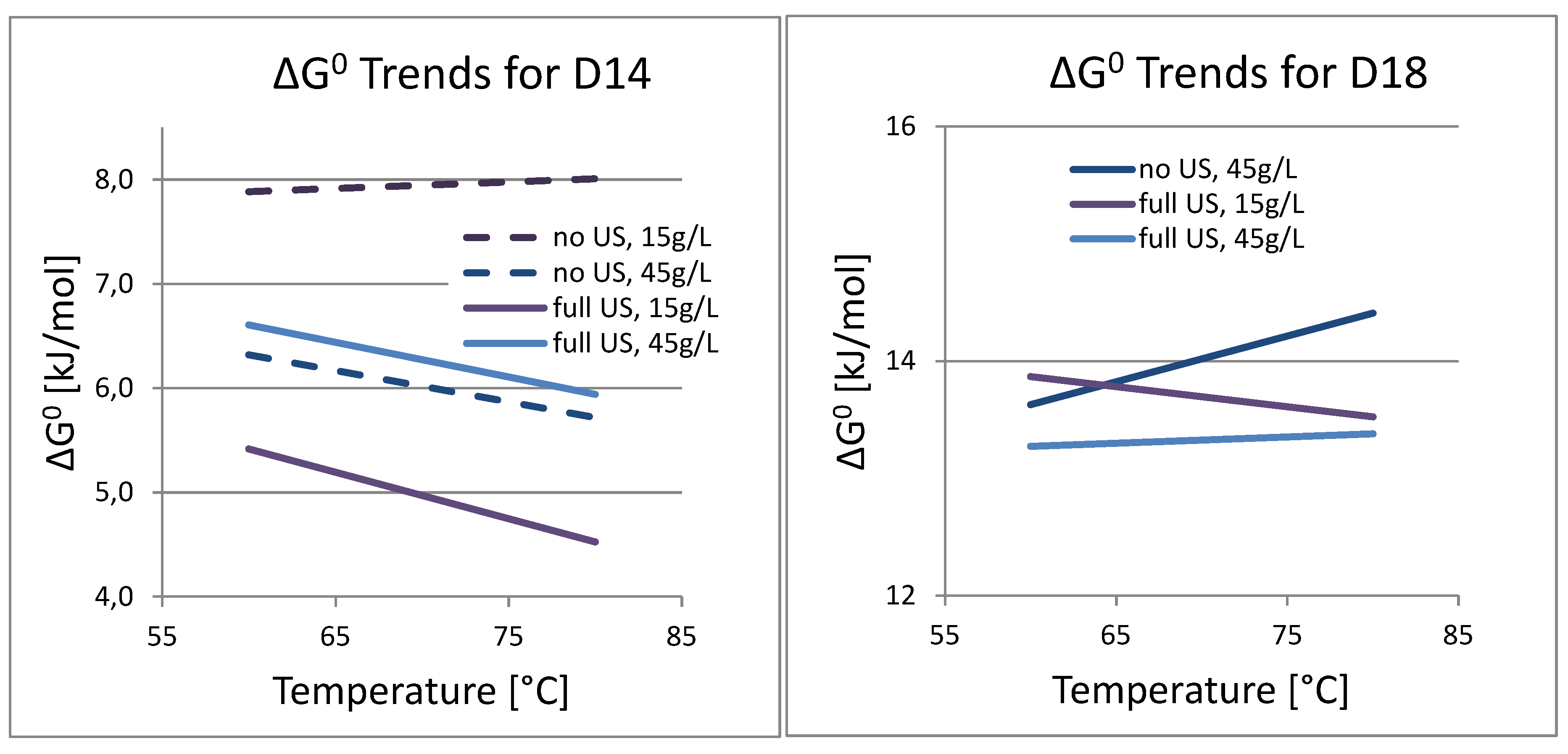
3.4. Analysis of Kinetics and Thermochemistry of Cobalt Dissolution
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dekempeneer, E.; Jacobs, R.; Smeets, J.; Meneve, J.; Eersels, L.; Blanpain, B.; Roos, J.; Oostra, D.J. Rf plasma-assisted chemical vapour deposition of diamond-like carbon: Physical and mechanical properties. Thin Solid Films 1992, 217, 56–61. [Google Scholar] [CrossRef]
- General Electric Research Laboratory. Man-made diamonds. Nature 1955, 176, 50–56. [Google Scholar]
- Bovenkerk, H.P.; Bundy, F.P.; Hall, H.T.; Strong, H.M.; Wentorf, R.H., Jr. Preparation of Diamond. Nature 1959, 184, 1094–1098. [Google Scholar] [CrossRef]
- Strong, H.M.; Chrenko, R.M. Diamond growth rates and physical properties of laboratory-made diamond. J. Phys. Chem. 1971, 75, 838–1843. [Google Scholar] [CrossRef]
- Lavoisier, A.L. Elements of Chemistry, in a New Systematic Order. Containing All the Modern Discoveries. In Dover Histories and Classics of Science; Dover Publications: New York, NY, USA, 1965. [Google Scholar]
- Massucci, M.; Clegg, S.L.; Brimblecombe, P. Equilibrium Partial Pressures, Thermodynamic Properties of Aqueous and Solid Phases, and Cl2 Production from Aqueous HCl and HNO3 and Their Mixtures. J. Phys. Chem. A 1999, 21, 4209–4226. [Google Scholar] [CrossRef]
- Baghalha, M.; Khosravian, G.H.; Mortaheb, H.R. Kinetics of platinum extraction from spent reforming catalysts in aqua-regia solutions. Hydrometallurgy 2009, 95, 247–253. [Google Scholar] [CrossRef]
- Huang, J.H.; Kargl-Simard, C.; Oliazadeh, M.; Alfantazi, A.M. pH-Controlled precipitation of cobalt and molybdenum from industrial waste effluents of a cobalt electrodeposition process. Hydrometallurgy 2004, 75, 77–90. [Google Scholar] [CrossRef]
- Moskalyk, R.R.; Alfantazi, A.M. Nickel laterite processing and electrowinning practice. Miner. Eng. 2002, 15, 593–605. [Google Scholar]
- Olanipekun, E.O. Kinetics of leaching laterite. Int. J. Miner. Process. 2000, 60, 9–14. [Google Scholar] [CrossRef]
- De Graaf, J.E. The treatment of lateritic nickel ores—A further study of the caron process and other possible improvements. Part, I. Effect of reduction conditions. Hydrometallurgy 1979, 5, 47–65. [Google Scholar] [CrossRef]
- Chang, J.; Zhang, E.-D.; Zhang, L.-B.; Peng, J.-H.; Zhou, J.-W.; Srinivasakannan, C.; Yang, C.-J. A comparison of ultrasound-augmented and conventional leaching of silver from sintering dust using acidic thiourea. Ultrason. Sonochem. 2017, 34, 222–231. [Google Scholar] [CrossRef] [PubMed]
- Wen, C.Y. Noncatalytic heterogeneous solid-fluid reaction models. Ind. Eng. Chem. 1968, 9, 34–54. [Google Scholar] [CrossRef]
- Khawam, A.; Flanagan, D.R. Solid state kinetic models- Basics and Mathematical Fundamentals. J. Phys. Chem. B 2006, 110, 17315–17328. [Google Scholar] [CrossRef] [PubMed]
- Wedler, G. Lehrbuch der Physikalischen Chemie; Wiley-VCH: Weinheim, Germany, 2010. [Google Scholar]
- Han, K.N.; Meng, X. The Leaching Behavior of Nickel and Cobalt from Metals and Ores—A review. Extr. Metall. Copp. Nickel Cobalt 1993, 1, 709–733. [Google Scholar]
- Kiessling, F.; Gürmen, S.; Stopic, S.; Friedrich, B. Advances in synthesis of metallic powders using ultrasound assisted leaching process from polycrystalline diamond blanks—Process design, (First part). Metals 2020, in press. [Google Scholar]
- Grénnman, H.; Salmi, T.Y.; Murzin, D. Solid-liquid reaction kinetics—Experimental aspects and model development. Rev. Chem. Eng. 2011, 27, 53–77. [Google Scholar] [CrossRef]
- Han, K.N.; Lawson, F. Leaching behavior of cobalt in acid solutions. J. Less Common. Metals 1974, 38, 19–29. [Google Scholar] [CrossRef]


| Content (Weight %) | C | O | Fe | Co |
|---|---|---|---|---|
| Spectrum 1 | 86.81 | 12.94 | - | 0.25 |
| Spectrum 2 | 88.31 | 10.42 | 0.21 | 1.05 |
| Spectrum 3 | 89.35 | 10.32 | - | 0.34 |
| Spectrum 4 | 87.41 | 10.78 | 0.14 | 1.67 |
| Max. | 89.35 | 12.94 | 0.21 | 1.67 |
| Min. | 86.81 | 10.32 | 0.00 | 0.25 |
| Blank Type | Symbol | Diameter [mm] | Height [mm] | Weight [g] | Volume [mm3] | Surface Area [mm2] | Surface/Volume [mm−1] |
|---|---|---|---|---|---|---|---|
| Mant® MSD-14-005 | D14 | 4.05 ± 0.09 | 2.00 ± 0.04 | 0.099 | 25.71 ± 1.40 | 51.14 ± 1.97 | 1.99 (+0.20|−0.18) |
| Mant® MSD-15-005 | D15 | 5.2 | 2.5 | 0.241 | 53.093 | 83.315 | 1.569 |
| Mant® MSD-18-005 | D18 | 5.22 ± 0.02 | 3.50 ± 0.02 | 0.299 | 74.90 ± 0.77 | 100.22 ± 0.68 | 1.338 (±0.023) |
| ID | TBath [K] | PCD Type | Leaching Time [h/d] in the Presence of Ultrasound | S/L [g/L] |
|---|---|---|---|---|
| W1R1 | 333 | D14 | 0 | 15 |
| W1R2 | 353 | D14 | 0 | 15 |
| W2R1 | 333 | D14 + D18 | 0 | 30 |
| W2R2 | 353 | D14 + D18 | 0 | 30 |
| W3R1 | 333 | D14 + D18 | 0 | 45 |
| W3R2 | 353 | D14 + D18 | 0 | 45 |
| W4R1 | 333 | D14 + D18 | 8 h/d | 15 |
| W4R2 | 353 | D14 + D18 | 8 h/d | 15 |
| W5R1 | 333 | D14 + D18 | 8 h/d | 30 |
| W5R2 | 353 | D14 + D18 | 8 h/d | 30 |
| W6R1 | 333 | D15 + D18 | 8 h/d | 45 |
| W6R2 | 353 | D15 + D18 | 8h/d | 45 |
| W7R1 | 333 | D14 + D18 | 24 h/d | 15 |
| W7R2 | 353 | D14 + D18 | 24 h/d | 15 |
| W8R1 | 333 | D14 + D18 | 24 h/d | 30 |
| W8R2 | 353 | D14 + D18 | 24 h/d | 30 |
| W9R1 | 333 | D14 + D18 | 24 h/d | 45 |
| W9R2 | 353 | D14 + D18 | 24 h/d | 45 |
| Week No. | PCD Type | δln(k) = ln(k353K) − ln(k333K) | δ/T = (1/353K) − (1/333K) | RIdeal [J*K−1*mol−1] | EA = −RIdeal*(δln(k)/(δ/T)) |
|---|---|---|---|---|---|
| 1 | D14 | 0.1183566 | −0.000170142 | 8.314 | 5783.8 |
| 3 | D14 | 0.3347918 | −0.000170142 | 8.314 | 16360.5 |
| 7 | D14 | 0.4153174 | −0.000170142 | 8.314 | 20295.6 |
| 9 | D14 | 0.3621971 | −0.000170142 | 8.314 | 17699.8 |
| 3 | D18 | 0.0136057 | −0.000170142 | 8.314 | 664.9 |
| 7 | D18 | 0.4004776 | −0.000170142 | 8.314 | 19570.4 |
| 9 | D18 | −0.2351197 | −0.000170142 | 8.314 | 11489.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kießling, F.; Stopic, S.; Gürmen, S.; Friedrich, B. Recovery of Diamond and Cobalt Powders from Polycrystalline Drawing Die Blanks via Ultrasound Assisted Leaching Process—Part 2: Kinetics and Mechanisms. Metals 2020, 10, 741. https://doi.org/10.3390/met10060741
Kießling F, Stopic S, Gürmen S, Friedrich B. Recovery of Diamond and Cobalt Powders from Polycrystalline Drawing Die Blanks via Ultrasound Assisted Leaching Process—Part 2: Kinetics and Mechanisms. Metals. 2020; 10(6):741. https://doi.org/10.3390/met10060741
Chicago/Turabian StyleKießling, Ferdinand, Srecko Stopic, Sebahattin Gürmen, and Bernd Friedrich. 2020. "Recovery of Diamond and Cobalt Powders from Polycrystalline Drawing Die Blanks via Ultrasound Assisted Leaching Process—Part 2: Kinetics and Mechanisms" Metals 10, no. 6: 741. https://doi.org/10.3390/met10060741
APA StyleKießling, F., Stopic, S., Gürmen, S., & Friedrich, B. (2020). Recovery of Diamond and Cobalt Powders from Polycrystalline Drawing Die Blanks via Ultrasound Assisted Leaching Process—Part 2: Kinetics and Mechanisms. Metals, 10(6), 741. https://doi.org/10.3390/met10060741







