Oblique/Curved Tube Necking Formed by Synchronous Multipass Spinning
Abstract
1. Introduction
2. Calculation of Roller Position
- (1)
- Calculation of the roller contact position with the product with the target shape.
- (2)
- Interpolation of the blank shape and the target shape along the normalized paths.
2.1. Calculation of Roller–Product Contact Position
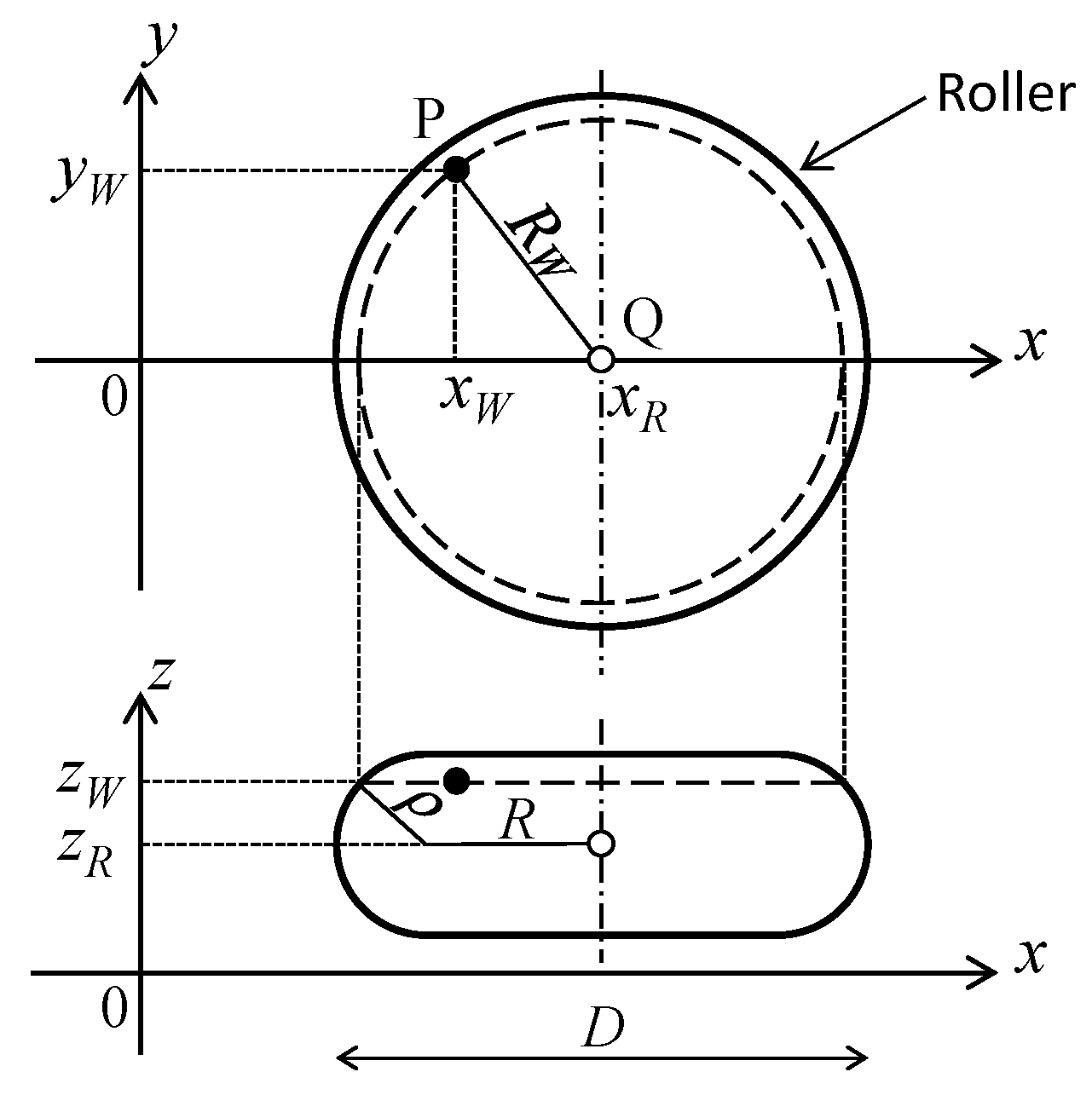
2.1.1. Expression of Target Shape and Roller Shape
2.1.2. Search of Contact Position
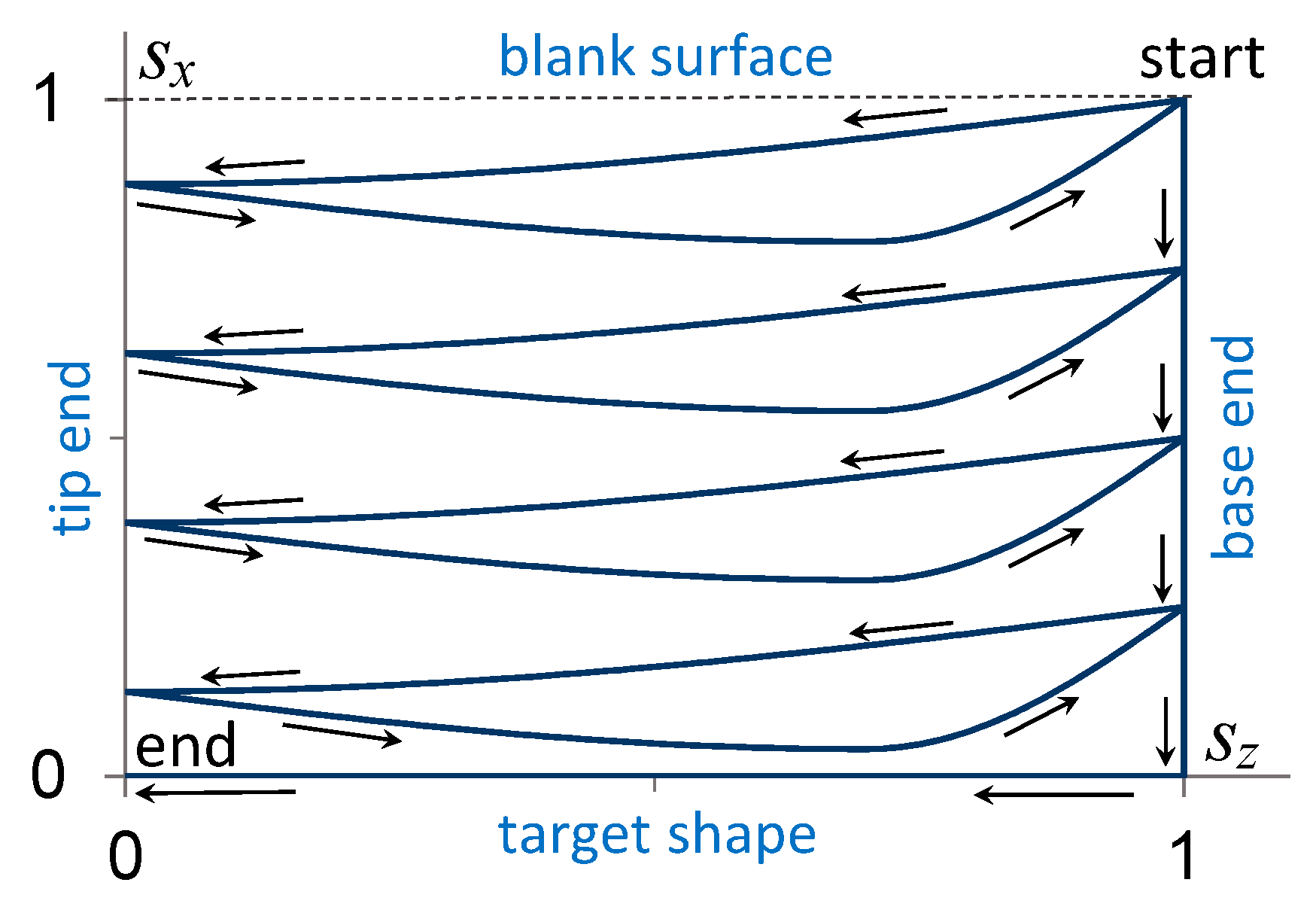
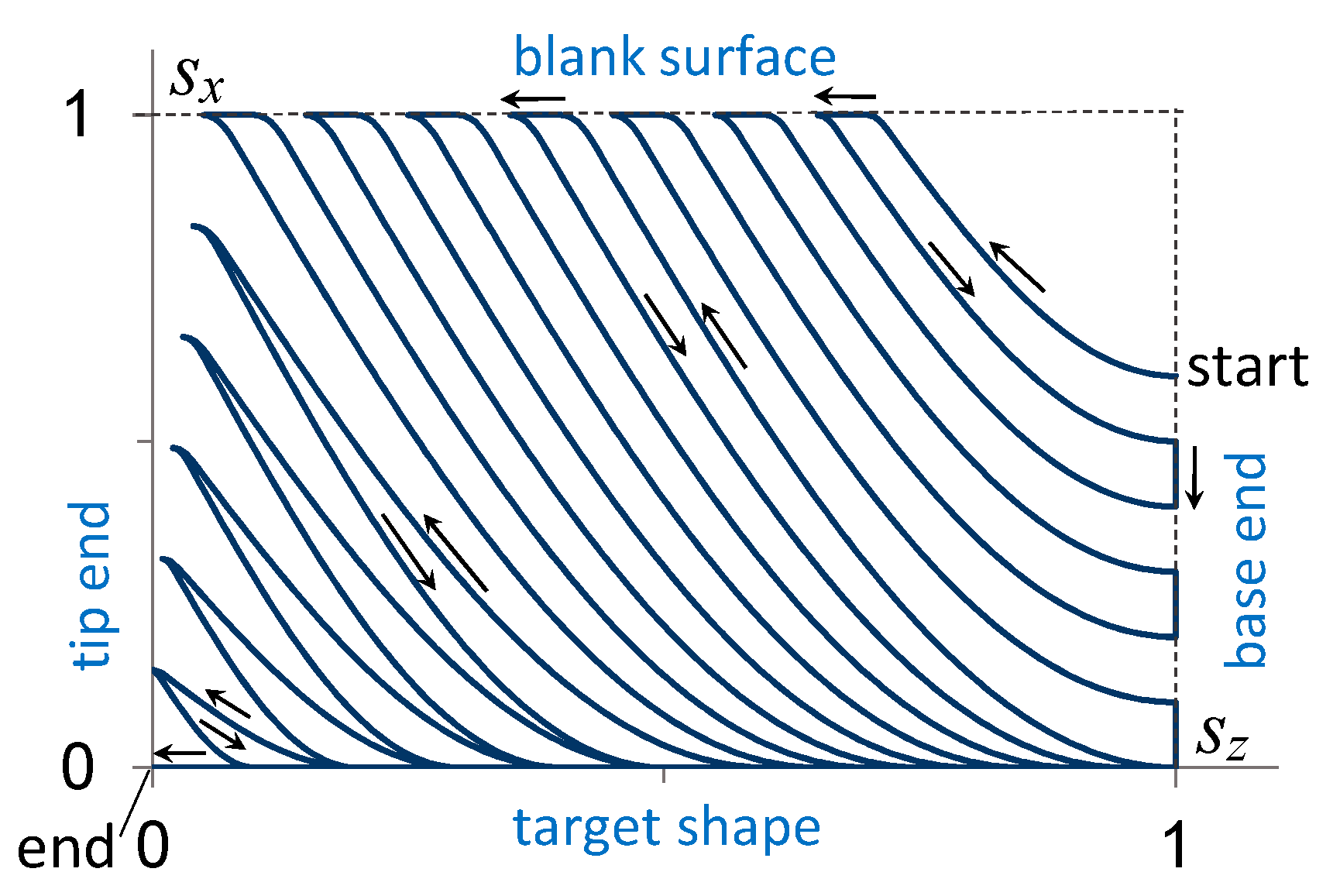
2.2. Interpolation of Roller Position
3. Forming Experiments
3.1. Experimental Setup
3.2. Target Shape
3.3. Multiple Tool Paths
3.4. Mearsurement of Products
4. Results and Discussion
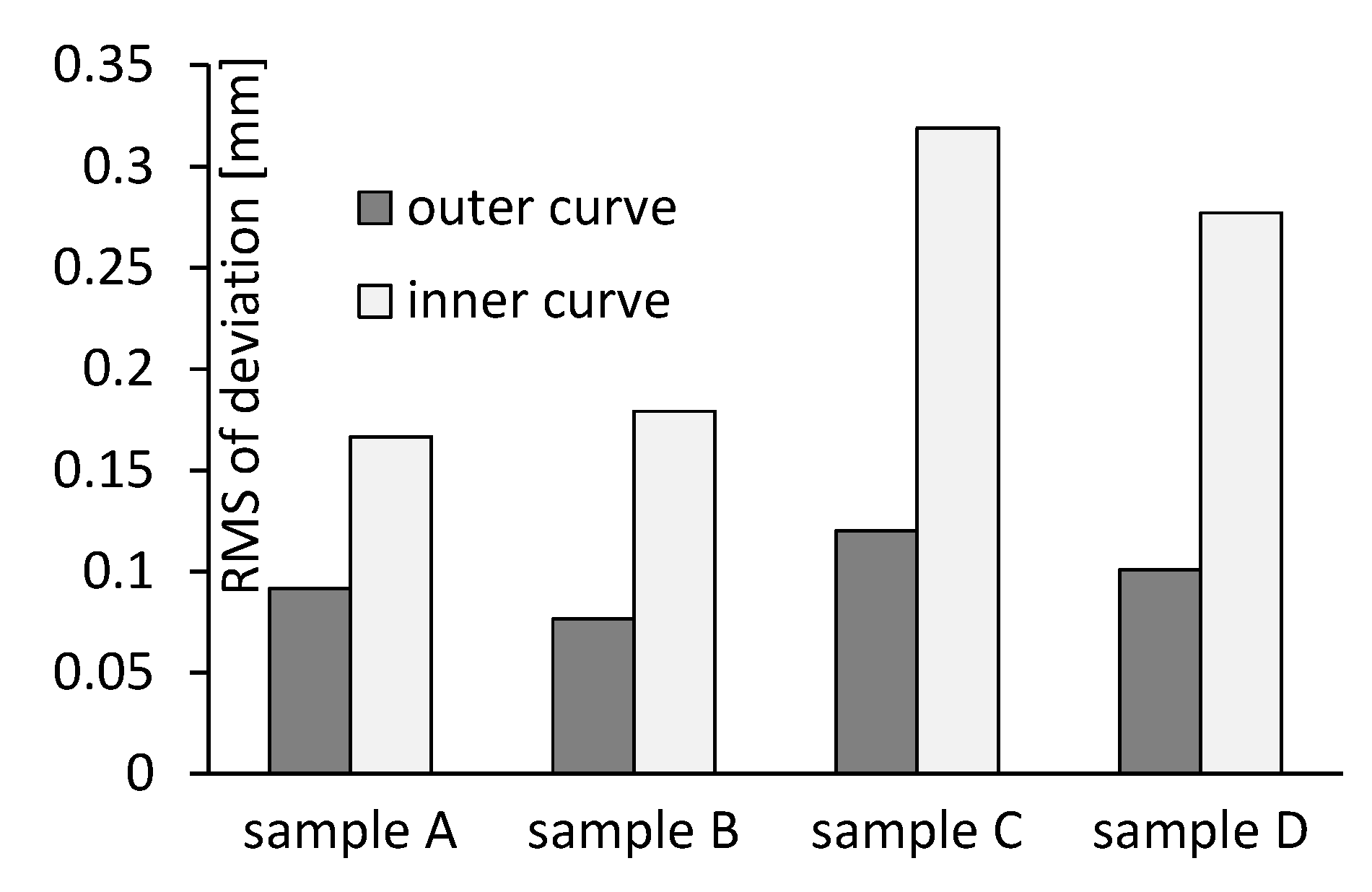
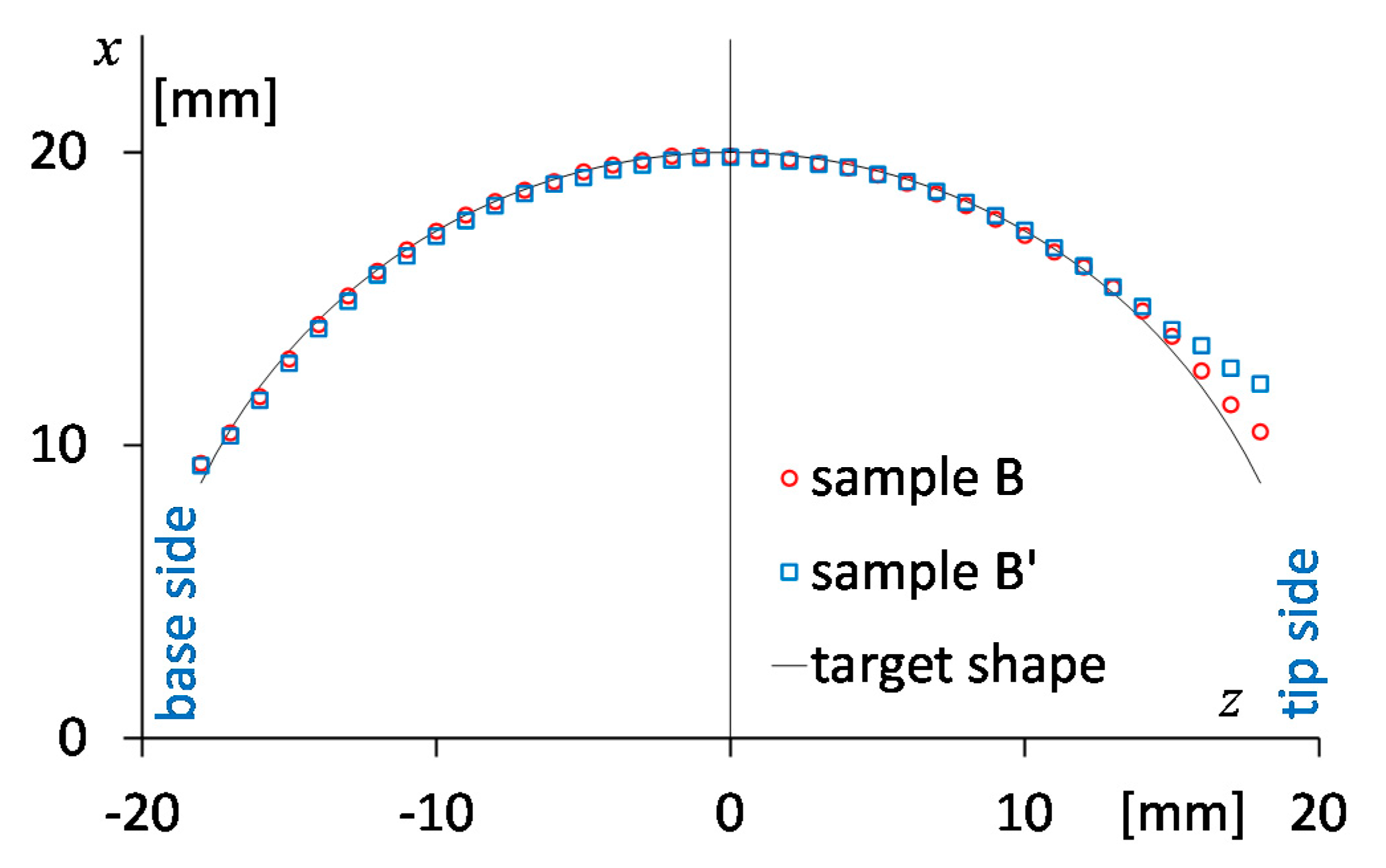
4.1. Dimensional Accuracy
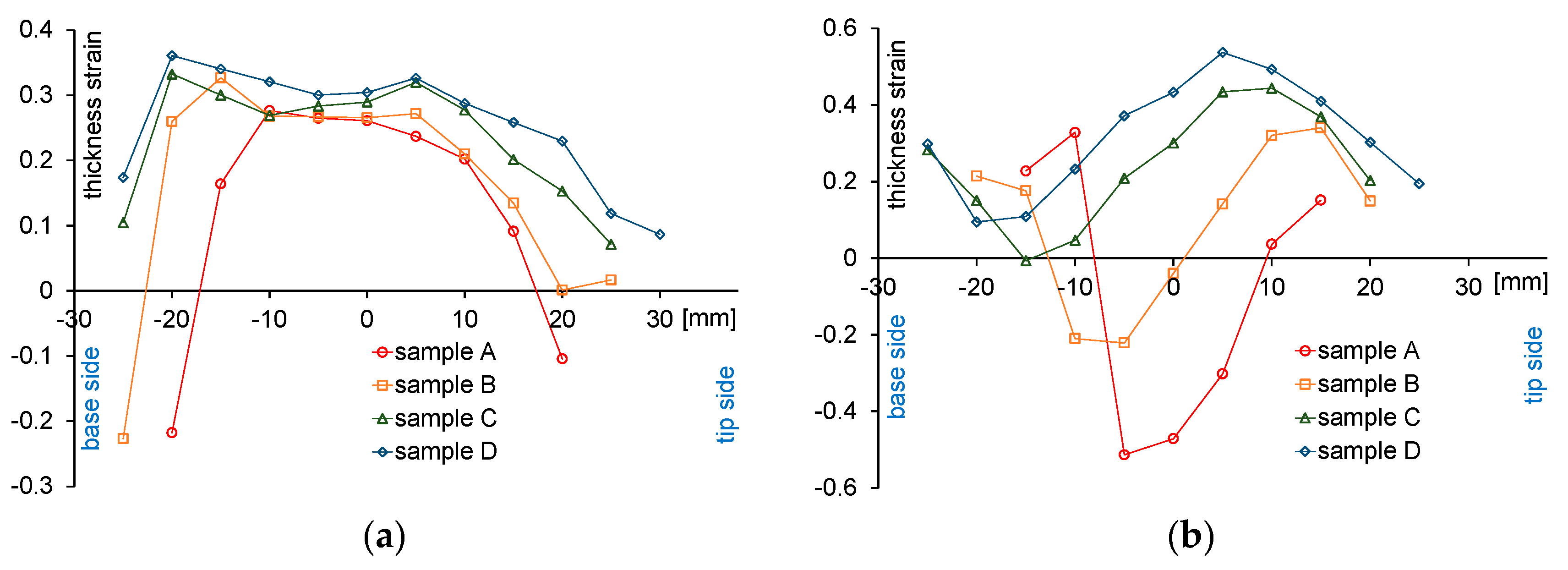
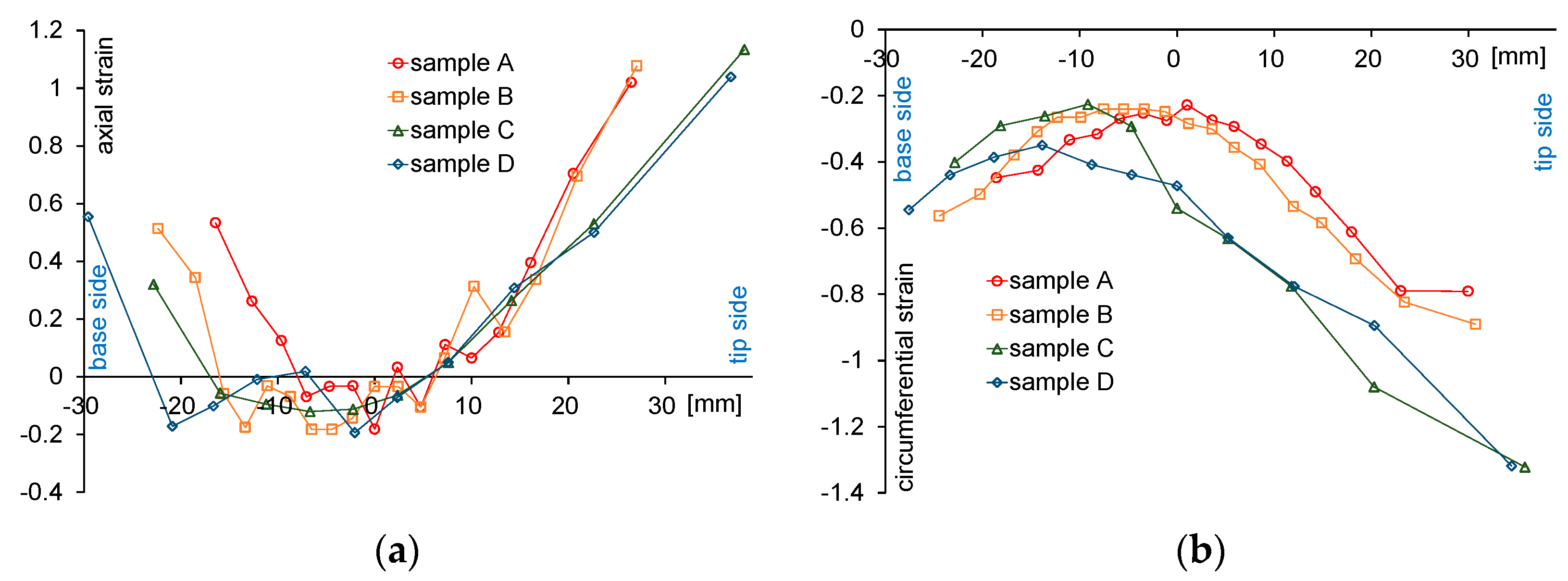
4.2. Strain Distribution
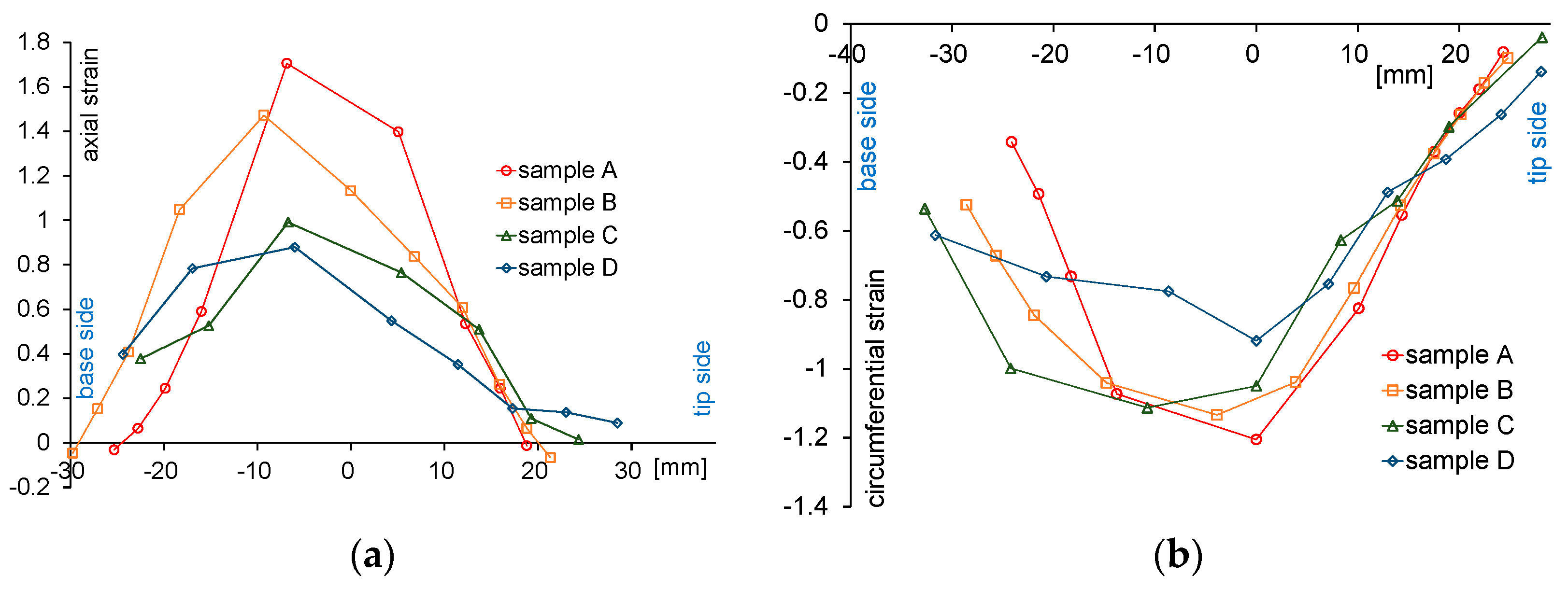
4.3. Effect of Normalized Paths
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Music, O.; Allwood, J.M.; Kawai, K. A review of the mechanics of metal spinning. J. Mater. Process. Technol. 2010, 219, 3–23. [Google Scholar] [CrossRef]
- Xia, Q.; Xiao, G.; Long, H.; Cheng, X.; Sheng, X. A review of process advancement of novel metal spinning. Int. J. Mach. Tools Manuf. 2014, 85, 100–121. [Google Scholar] [CrossRef]
- Irie, T. Method and Apparatus for Forming a Processed Portion of a Workpiece. U.S. Patent US6223993B1, 22 May 2001. [Google Scholar]
- Xia, Q.; Cheng, X.; Hu, Y.; Ruan, F. Finite element simulation and experimental investigation on the forming forces of 3D non-axisymmetrical tubes spinning. Int. J. Mech. Sci. 2006, 48, 726–735. [Google Scholar] [CrossRef]
- Xia, Q.; Cheng, X.; Long, H.; Ruan, F. Finite element analysis and experimental investigation on deformation mechanism of non-axisymmetric tube spinning. Int. J. Adv. Manuf. Technol. 2012, 59, 263–272. [Google Scholar] [CrossRef]
- Amano, T.; Tamura, K. The study of an elliptical cone spinning by the trial equipment. In Proceedings of the 3rd International Conference on Rotary Metalworking Processes, Kyoto, Japan, 8–10 September 1984; pp. 213–224. [Google Scholar]
- Xia, Q.; Lai, Z.; Zhan, X.; Cheng, X. Research on Spinning Method of Hollow Part with Triangle Arc-Type Cross Section Based on Profiling Driving. Steel Res. Int. 2010, 81, 994–998. [Google Scholar] [CrossRef]
- Shimizu, I. Asymmetric forming of aluminum sheets by synchronous spinning. J. Mater. Process. Technol. 2010, 210, 585–592. [Google Scholar] [CrossRef]
- Arai, H.; Okazaki, I.; Fujimura, S. Synchronized metal spinning of non-axisymmetric tubes. In Proceedings of the 56th Japanese Joint Conference for the Technology of Plasticity, Naha, Japan, 18–20 November 2005; pp. 687–688. (In Japanese). [Google Scholar]
- Härtel, S.; Laue, R. An optimization approach in non-circular spinning. J. Mater. Process. Technol. 2016, 229, 417–430. [Google Scholar] [CrossRef]
- Sugita, Y.; Arai, H. Formability in synchronous multipass spinning using simple pass set. J. Mater. Process. Technol. 2015, 217, 336–344. [Google Scholar] [CrossRef]
- Music, O.; Allwood, J.M. Flexible asymmetric spinning. CIRP Ann. Manuf. Technol. 2011, 60, 319–322. [Google Scholar] [CrossRef]
- Russo, I.; Cleaver, C.; Allwood, J.M.; Loukaides, E. The influence of part asymmetry on the achievable forming height in multi-pass spinning. J. Mater. Process. Technol. 2020, 275, 116350. [Google Scholar] [CrossRef]
- Sekiguchi, A.; Arai, H. Synchronous die-less spinning of curved products. Steel Res. Int. 2010, 81, 1010–1013. [Google Scholar] [CrossRef]
- Han, Z.; Xu, Q.; Jia, Z.; Li, X. Experimental research on oblique cone die-less shear spinning. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2017, 231, 1182–1189. [Google Scholar] [CrossRef]
- Sekiguchi, A.; Arai, H. Development of oblique metal spinning with force control. In Proceedings of the 2010 International Symposium on Flexible Automation, Tokyo, Japan, 12–14 July 2010; pp. 1863–1869. [Google Scholar]
- Arai, H.; Kanazawa, T. Synchronous multipass spinning of oblique-bottom shape. J. Mater. Process. Technol. 2018, 260, 66–76. [Google Scholar] [CrossRef]
- Xiao, Y.; Han, Z.; Zhou, S.; Jia, Z. Asymmetric spinning for offset blanks. Int. J. Adv. Manuf. Technol. 2020, 107, 2433–2448. [Google Scholar] [CrossRef]
- Xiao, Y.; Han, Z.; Fan, Z.; Jia, Z. A study of asymmetric multi-pass spinning for angled-flange cylinder. J. Mater. Process. Technol. 2018, 256, 202–215. [Google Scholar] [CrossRef]
- Arai, H. NC programming for oblique/curved tube necking using synchronous multipass spinning. In Proceedings of the 2015 Japanese Spring Conference for the Technology of Plasticity, Yokohama, Japan, 29–31 May 2015; pp. 171–172. (In Japanese). [Google Scholar]
- Arai, H. Noncircular tube spinning based on three-dimensional CAD model. Int. J. Mach. Tools Manuf. 2019, 144. [Google Scholar] [CrossRef]




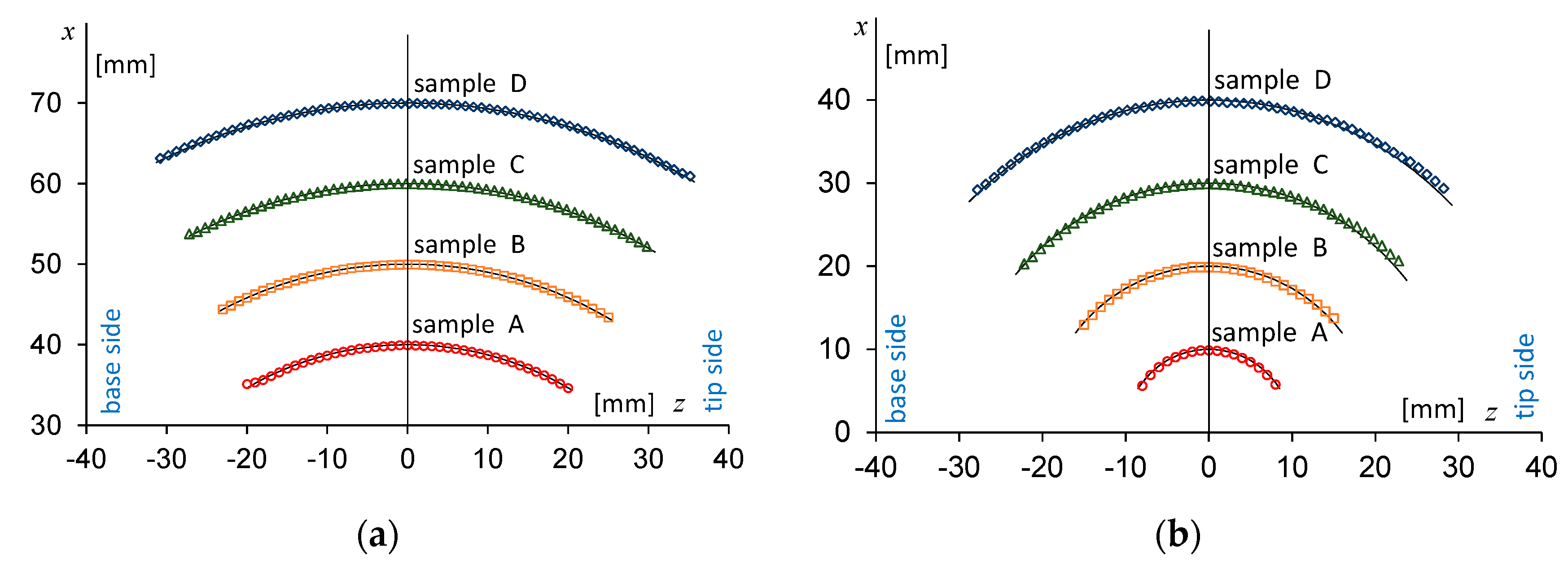
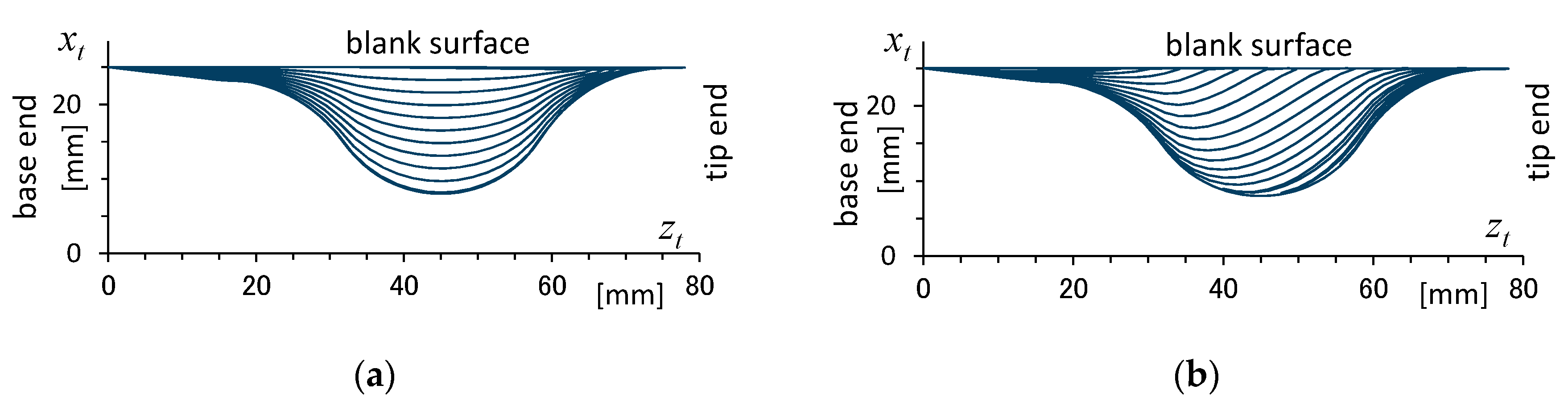
| Sample Type | Average Radius (mm) | Offset from Axis (mm) | Out of Roundness (mm) |
|---|---|---|---|
| A | 15.046 | 6.893 | 0.096 |
| B | 15.063 | 6.945 | 0.082 |
| C | 15.047 | 6.859 | 0.129 |
| D | 15.045 | 6.917 | 0.068 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arai, H.; Gondo, S. Oblique/Curved Tube Necking Formed by Synchronous Multipass Spinning. Metals 2020, 10, 733. https://doi.org/10.3390/met10060733
Arai H, Gondo S. Oblique/Curved Tube Necking Formed by Synchronous Multipass Spinning. Metals. 2020; 10(6):733. https://doi.org/10.3390/met10060733
Chicago/Turabian StyleArai, Hirohiko, and Shiori Gondo. 2020. "Oblique/Curved Tube Necking Formed by Synchronous Multipass Spinning" Metals 10, no. 6: 733. https://doi.org/10.3390/met10060733
APA StyleArai, H., & Gondo, S. (2020). Oblique/Curved Tube Necking Formed by Synchronous Multipass Spinning. Metals, 10(6), 733. https://doi.org/10.3390/met10060733





