Relation between Crystal Structure and Transition Temperature of Superconducting Metals and Alloys
Abstract
1. Introduction
2. Outline of the Model
- (i)
- The distance x is no longer related to the doping distance as in the case of HTSc, but corresponds to an atomic distance similar to the PiB approach applied in [31].
- (ii)
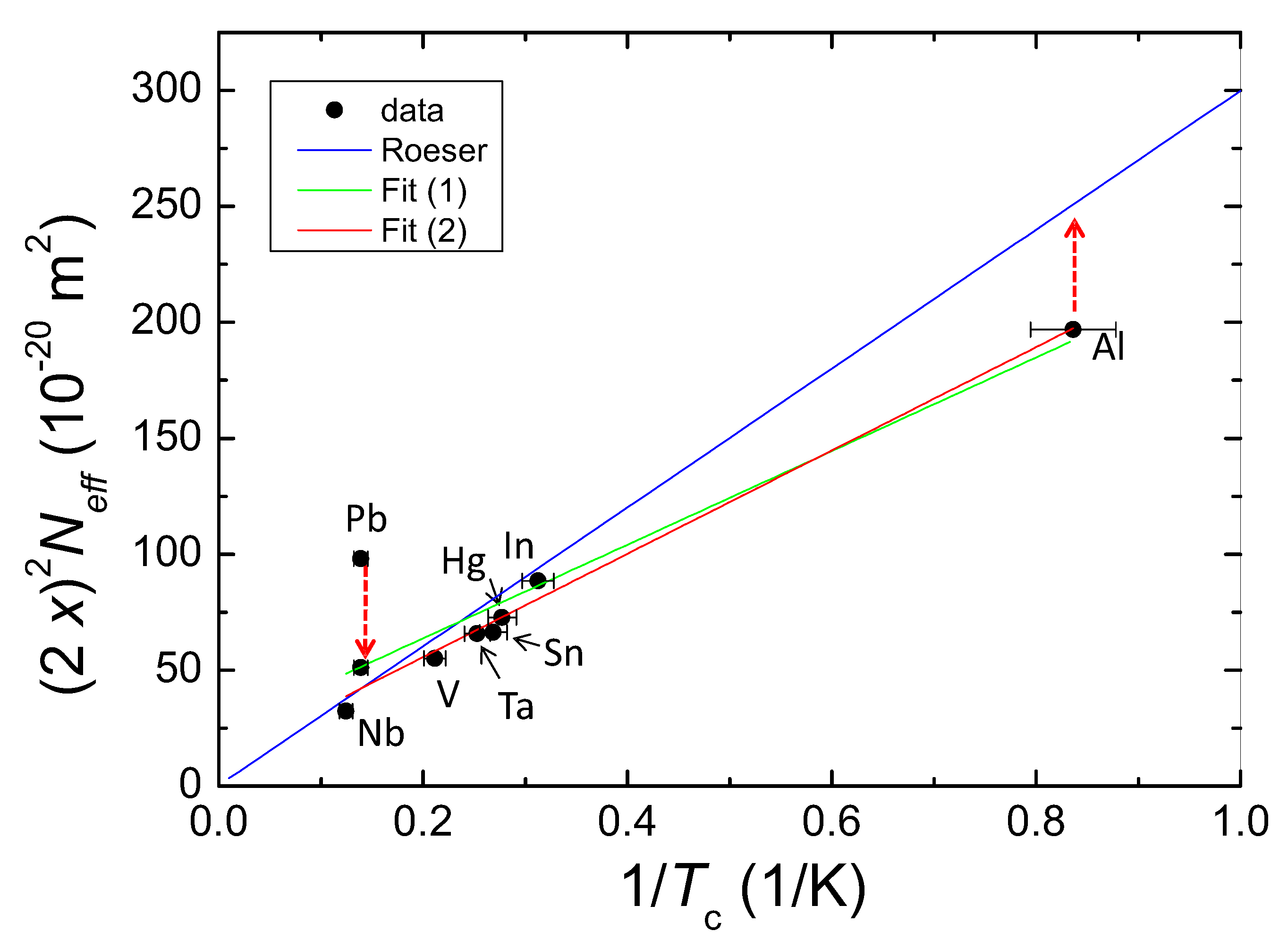
- In all calculations of the various HTSc materials, was set equal to 2 ( electron mass). In the case of metallic superconductors, turns out to be much higher. As the charge carriers in the metallic superconductors are always Cooper pairs formed by electrons or by holes, we introduce here the abbreviation, , not to be confused with used in the band structure calculations. In a first approximation, is found to correspond closely to the mass of a proton (). A justification for this is given in the diagrams of Figures 9 and 10 below, where such a high mass is needed to unify the data of the HTSc and the metallic superconductors. Thus, the charge carrier mass is then expressed in terms of in all further calculations.
- (iii)
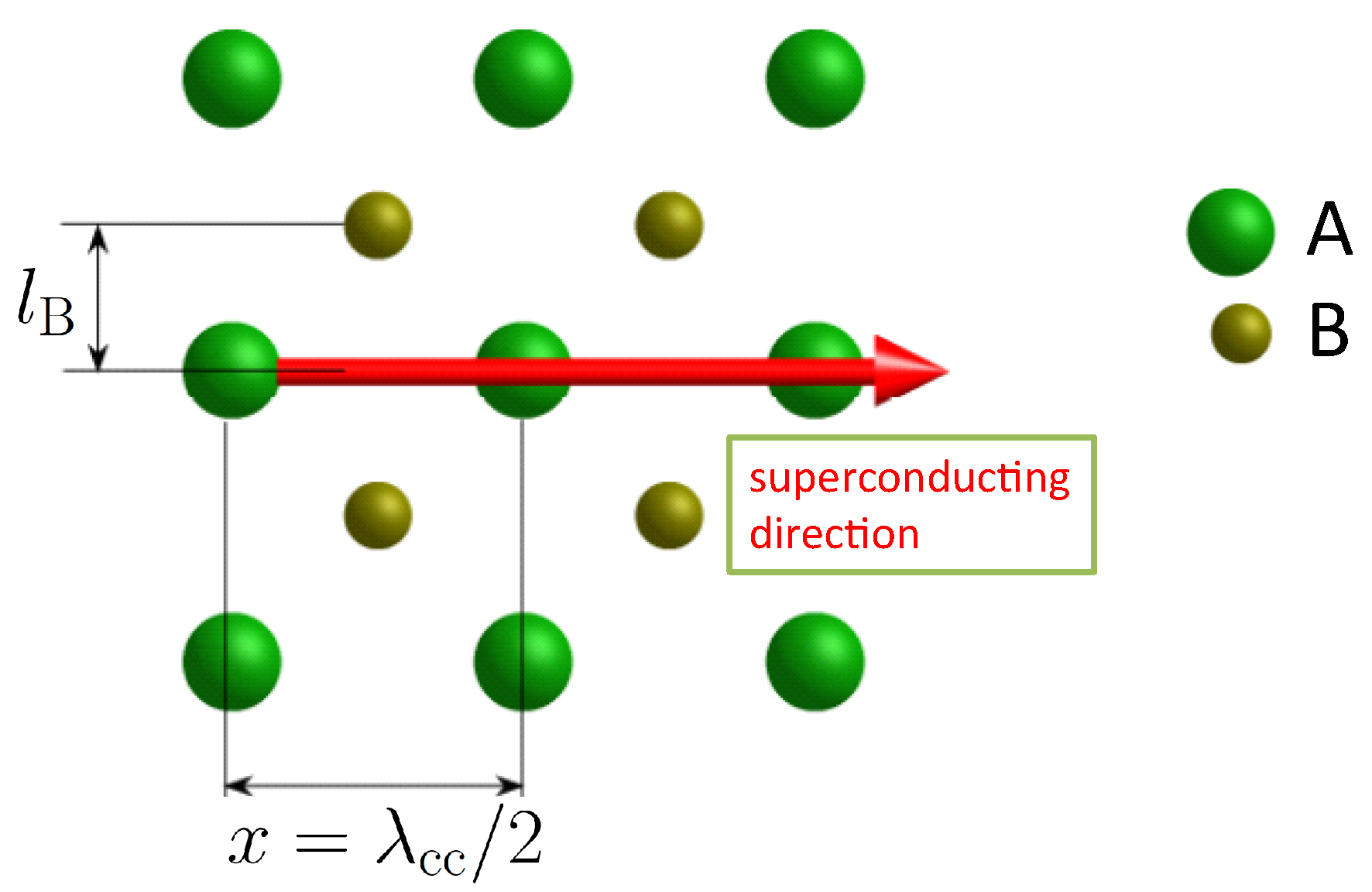
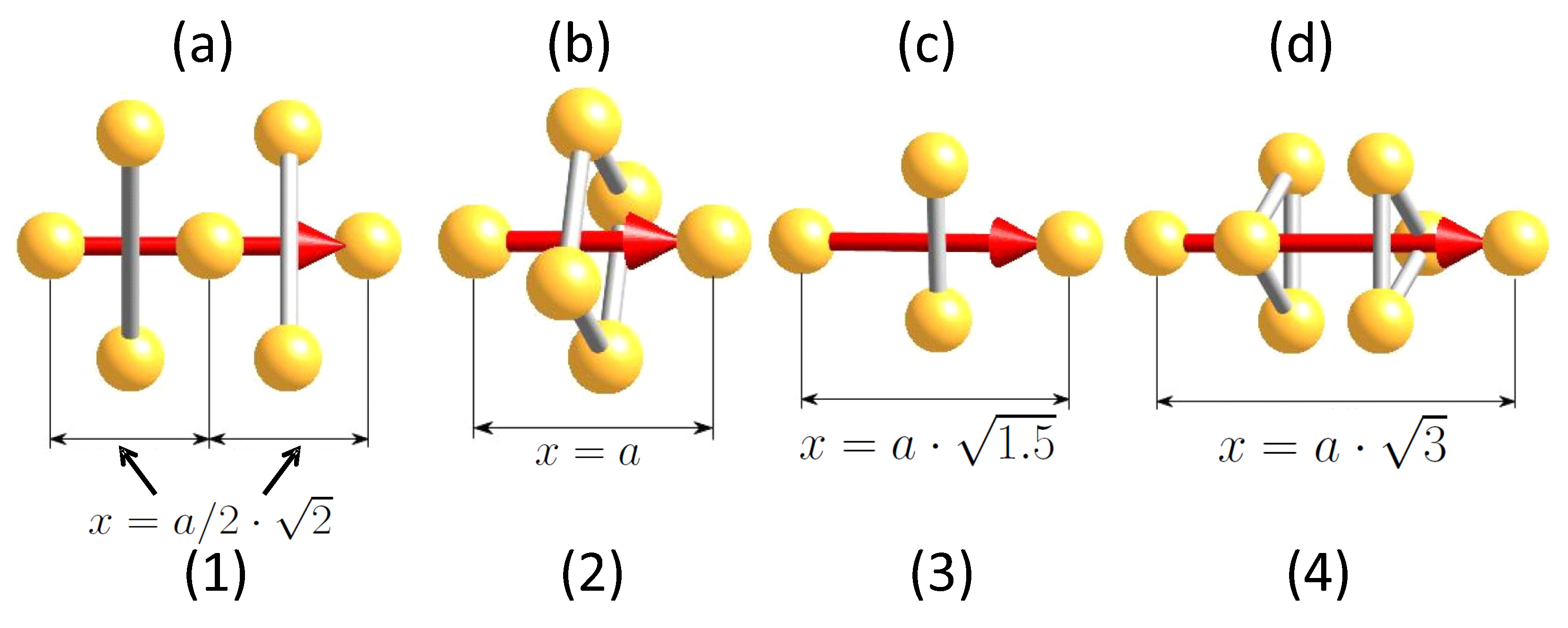
- There are more correction factors required besides setting 1 as described before. This is required to account for the more complex crystal structures. Atoms close to a superconducting direction may have an influence on the moving charge carriers via the phonon interaction. Therefore, the number of atoms passed within a unit cell is counted. This correction is added to the charge carrier mass via:with giving the number of charge carriers, the number of near, passed atoms and is the proton mass. One can introduce then a new first correction factor via , so . In case there are no (near) passed atoms, then 1. As the symmetry plays an important role for our considerations, the passed atoms must be symmetrically arranged, otherwise the charge carriers would be not in phase due to the unsymmetric forces. In turn, this implies that superconductivity cannot exist in directions with unsymmetrically arranged passed atoms. To test the influence of the passed atoms, we define a relation (see Figure 1). l is the perpendicular distance to the direction of the moving charge carriers. If 0.5, we assume that the passed atoms have an influence on the superconductivity. This relation is, therefore, very important in the following calculations of .
- (iv)
- Another correction is necessary for anisotropic superconductivity, which can even lead to so-called multimode superconductivity as in the case of MgB. This correction factor will be named , giving a relation between the specific directions, R. Here, it is important to note that it becomes possible to calculate a transition temperature for each direction separately, which does not need to be equal to the “total” transition temperature of the entire system. In this way, there will be an equation system to be solved. Further details of this will be presented when discussing the calculation of the A15 superconductors and MgB.
- (1)
- Which crystal directions are able to carry the charge carrier wave, and how many of them exist for a given crystal structure?
- (2)
- How large is the interatomic distance in such an atomic chain?
- (3)
- How many symmetric passages are possible, or formulated differently, how many partners for the phonon interaction exist for the charge carriers?
- (4)
- How large is the distance of the passed atoms to have an influence on the charge carrier mass?
- (5)
- Which atom is the main carrier of superconductivity, or does superconductivity only exist in a combination?
- (6)
- How many electrons are involved in superconductivity?
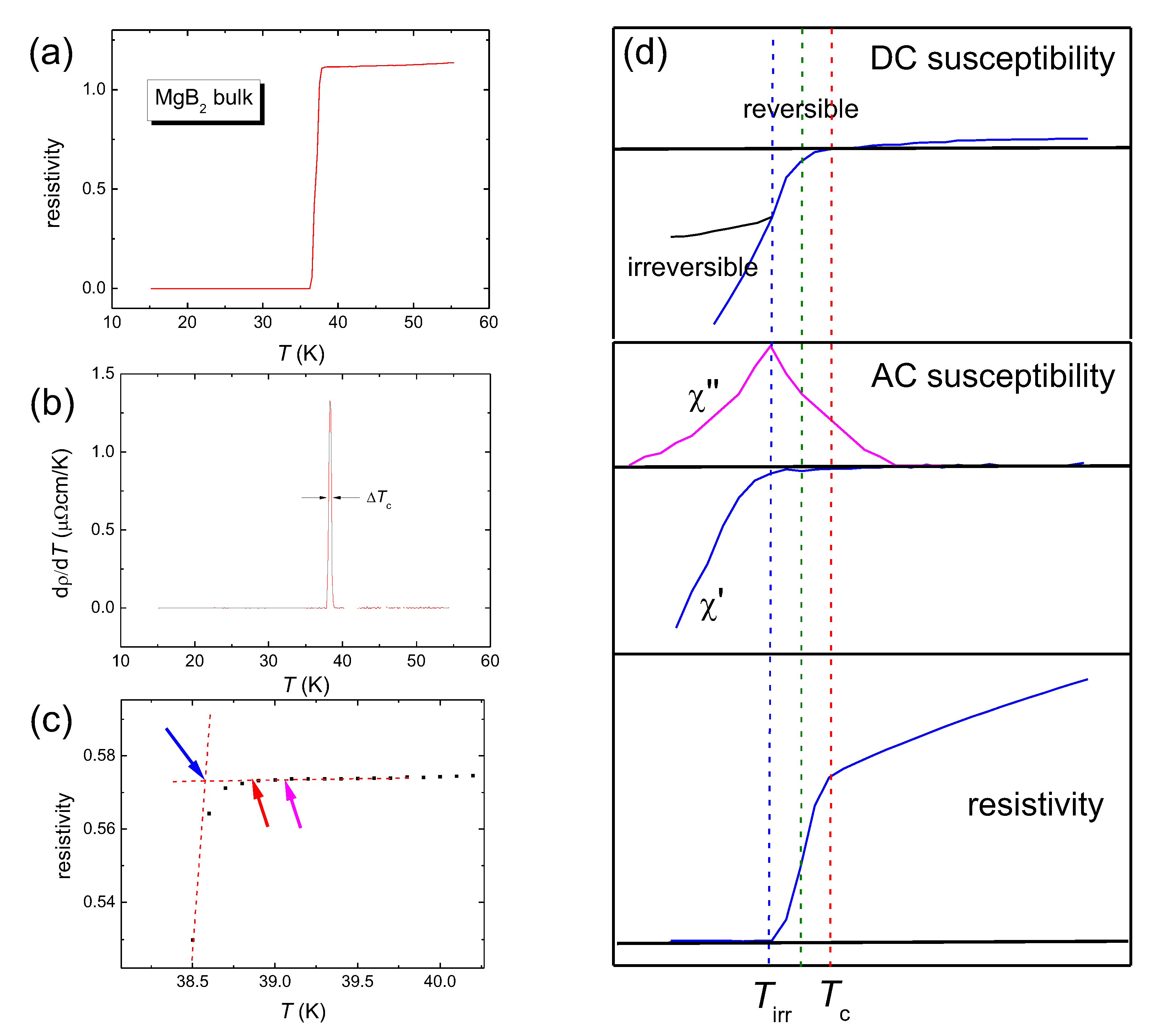
3. Experimental Procedures
4. Results of the Calculations and Discussion
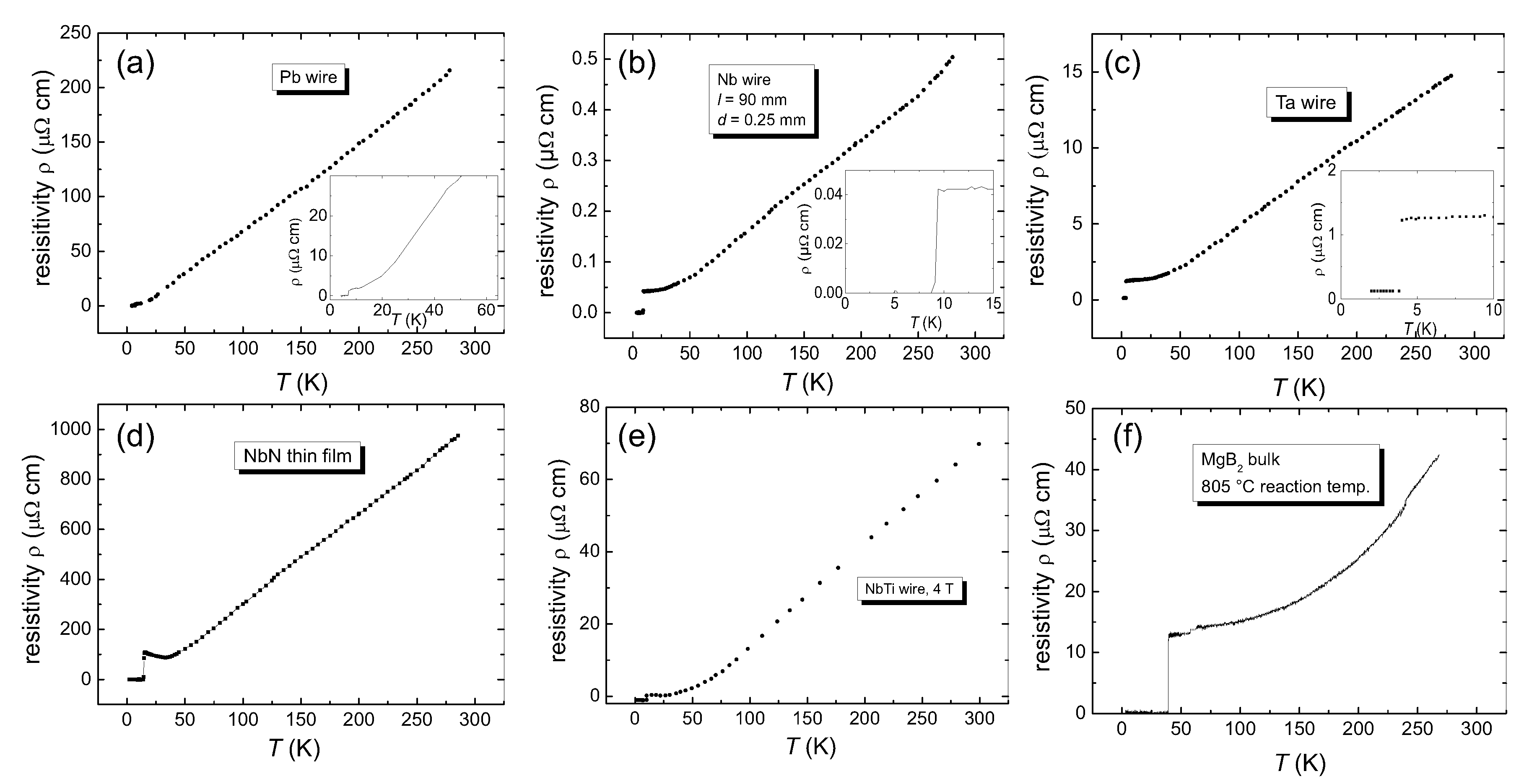
4.1. Lead
- Direction (1) is the diagonal in one crystal face. This length is . However, the next atom is located in the center of the diagonal, so .
- Direction (2) along the edge of the unit cell. This length corresponds directly to the lattice constant, so .
- Direction (3). There is a highly periodic connection between an atom at the edge of the unit cell with an atom located in the middle of a not directly neighboring face. This can be calculated as .
- Direction (4) is given by the diagonal in space. This length can be calculated as .
4.2. Aluminum
4.3. Sn
- Direction (1) along the edge of the unit cell with 0.318 nm. There are no near atoms to be considered.
- Direction (2) along the spatial diagonal with 0.442 nm. Again, no near atoms have to be taken into account.
4.4. Nb and V
- Direction (1) along the edge of the unit cell with 0.33 nm,
- Direction (2) along the face diagonal with 0.4667 nm and
- Direction (3) along the space diagonal with 0.2858 nm.
- Direction (1) 0.303 nm,
- Direction (2) 0.4285 nm and
- Direction (3) along the space diagonal with 0.2624 nm.
4.5. NbN
4.6. NbTi
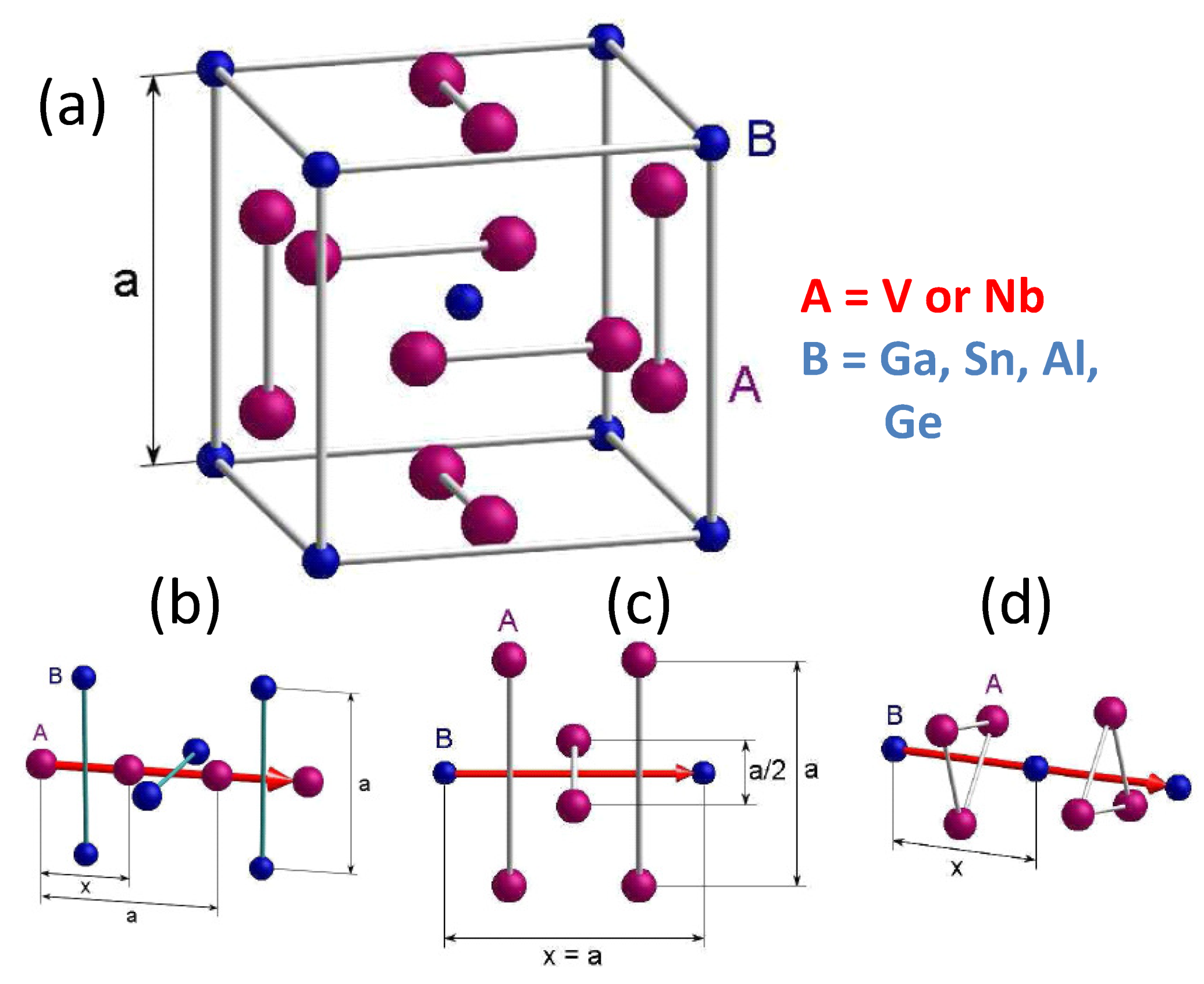
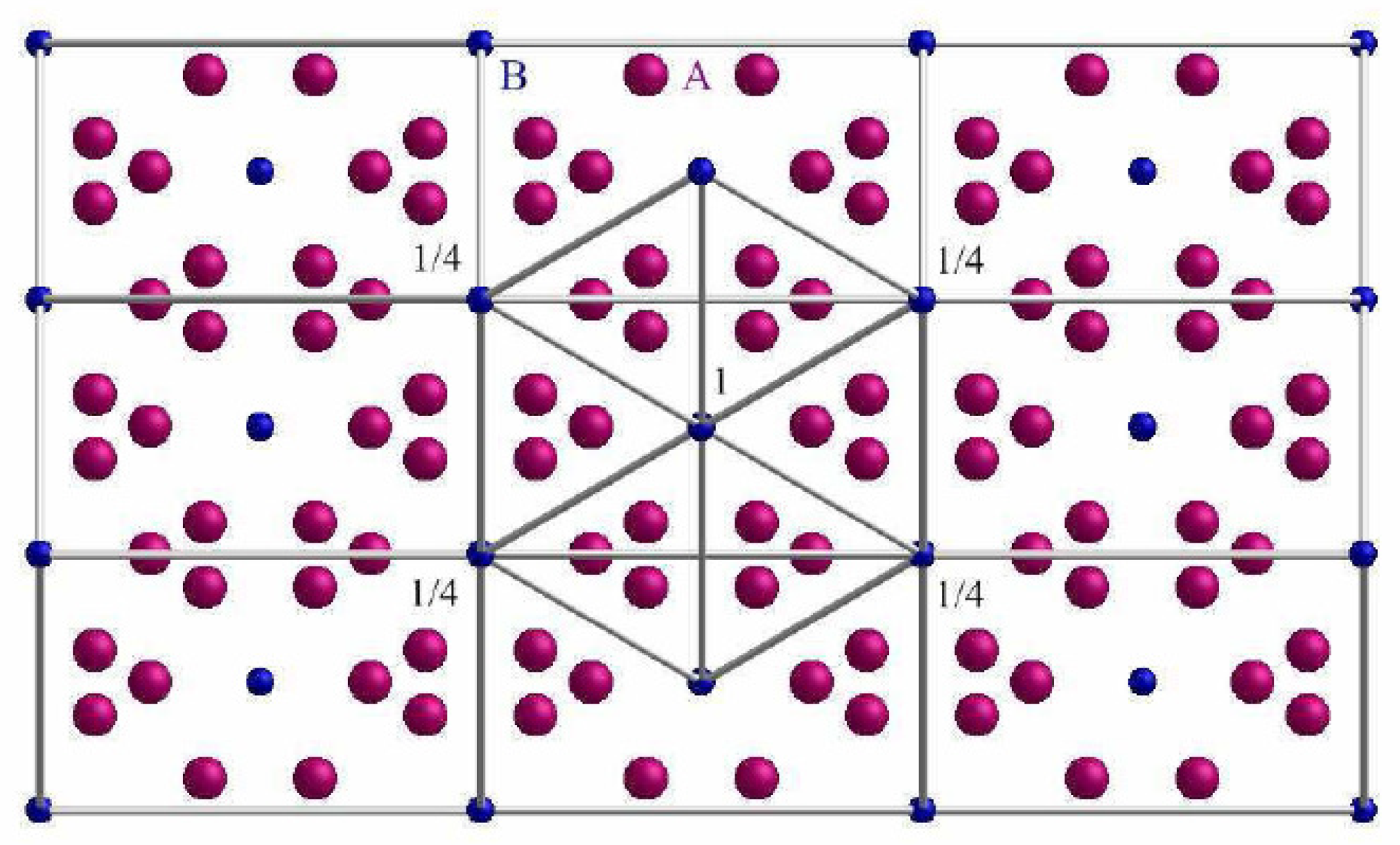
4.7. A15 Superconductors
- Direction (1) along the A-A atoms following the faces of the unit cell (b). The distance between the A atoms is . In this direction, two B atoms will be passed, which have a distance of . The relation 1, which is much larger than , so an influence can be excluded.
- Direction (2) along the B-B atoms following the faces of the unit cell (c). The distance between the B atoms is . Two A atoms will be passed, which have a distance of , so there will be an influence. Further, there are four more atoms at a distance of . The relation 1/2, but these atoms are not located in the main direction, so that an influence of them can be excluded.
- Direction (3) along the B-B atoms following the space diagonal in the unit cell (d). The distance between the B atoms is . There are three A atoms being passed, which have a distance of . The relation is , so that there is certainly an influence of these atoms, which must be taken into account.
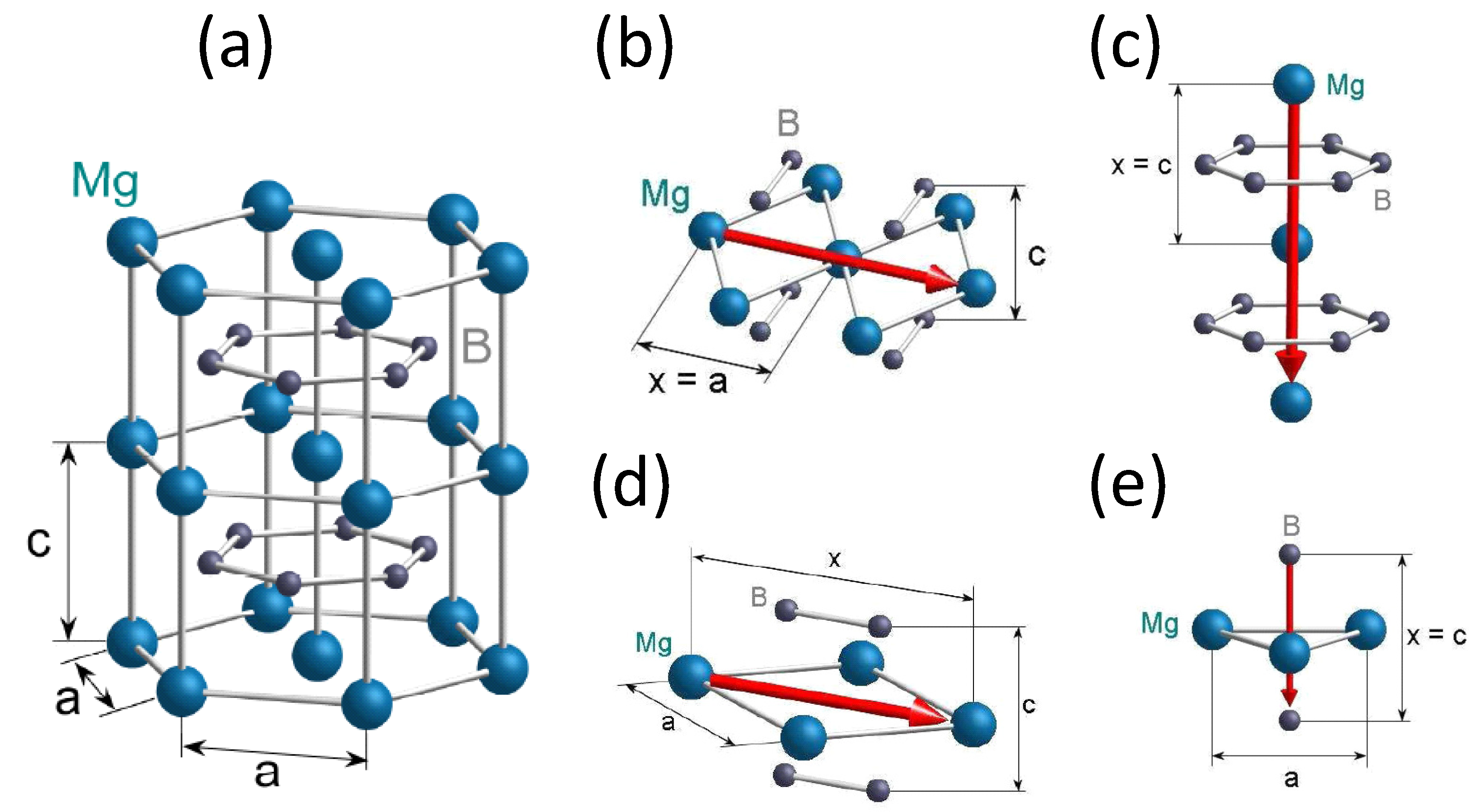
4.8. MgB
- Direction (1) along the Mg-Mg atoms within the Mg plane (b): The distance between the Mg atoms is 0.3047 nm. The charge carriers along this direction will pass 4 B atoms, 2 from the layer below and 2 from the layer above. Furthermore, two Mg atoms from the same layer are passed as well. The distances are 0.192 nm (B) with 0.630 and 0.264 nm with the relation 0.866. Thus, the distances to the neighboring atoms are too big to have an influence on the superconductivity.
- Direction (2) along the Mg-Mg atoms within the Mg layer (c): The distance between the Mg atoms is 0.528 nm. The passed atoms are the same as in Direction (1), but the distances are different: 0.171 ( 0.324) and 0.152 nm with 0.288 nm. All distance ratios are smaller than 0.5, so all six atoms have an influence.
- Direction (3) along the Mg-Mg atoms in the c direction (d): The distance between the Mg atoms is 0.3421 nm. In this direction, a hexagon of B atoms is passed. The corresponding distance is 0.176 nm, and the relation 0.514, which is close to 0.5.
- Direction (4): along the B-B atoms in the c direction (e). The distance between the boron atoms is 0.3421 nm. In this direction, three Mg atoms arranged in a triangle are passed, which have the same short distance to the main direction. The distance between the Mg atoms and the charge carrier direction is 0.176 nm, where h denotes the height of the triangle. The relation 0.514, so an influence on the charge carriers is proposed.
5. Discussion
- (1)
- Will it be possible to analyze also the change of when applying pressure to the material?
- (2)
- Is it possible to find an explanation to the dependence on the sample thickness of thin films?
- (3)
- Can we make predictions concerning new superconductor materials?
6. Outlook
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Gutton, M. Annales de Chimie et de Physique; V. Masson: Paris, France, 1816. [Google Scholar]
- Onnes, H.K. Part I.—Laboratory methods of liquefaction. On the lowest temperature yet obtained. Trans. Faraday Soc. 1922, 18, 145–174. [Google Scholar] [CrossRef]
- van Delft, D.; Kes, P.H. The discovery of superconductivity. Phys. Today 2010, 63, 38–43. [Google Scholar] [CrossRef]
- Matthias, B.T.; Geballe, T.H.; Geller, S.; Corenzwit, E. Superconductivity of Nb3Sn. Phys. Rev. 1954, 95, 1435. [Google Scholar] [CrossRef]
- Nagamatsu, J.; Nakagawa, N.; Muranaka, T.; Zenitani, Y.; Akimitsu, J. Superconductivity at 39 K in magnesium diboride. Nature 2001, 410, 63–64. [Google Scholar] [CrossRef] [PubMed]
- Bednorz, J.G.; Müller, K.A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. B Condens. Matter 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Chu, C.W.; Hor, P.H.; Meng, R.L.; Gao, L.; Huang, Z.J.; Wang, Y.Q. Evidence for superconductivity above 40 K in the La-Ba-Cu-O compound system. Phys. Rev. Lett. 1987, 58, 405–407. [Google Scholar] [CrossRef]
- Wu, M.K. Superconductivity at 93 K in a new mixed-phase Y-Ba-Cu-O compound system at ambient pressure. Phys. Rev. Lett. 1987, 58, 908–910. [Google Scholar] [CrossRef]
- Gao, L. Superconductivity up to 164 K in HgBa2Cam-1CumO2+2+δ (m= 1, 2, and 3) under quasihydrostatic pressures. Phys. Rev. B 1994, 50, 4260–4263. [Google Scholar] [CrossRef]
- Drozdov, A.P.; Eremets, M.I.; Troyan, I.A.; Ksenofontov, V.; Shylin, S.I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73–76. [Google Scholar] [CrossRef]
- Drozdov, A.P.; Kong, P.P.; Minkov, V.S.; Besedin, S.P.; Kuzovnikov, M.A.; Mozaffari, S.; Balicas, L.; Balakirev, F.F.; Graf, D.E.; Prakapenka, V.B.; et al. Superconductivity at 250 K in lanthanum hydride under high pressures. Nature 2019, 569, 528–533. [Google Scholar] [CrossRef]
- Somayazulu, M.; Ahart, M.; Mishra, A.K.; Geballe, Z.M.; Baldini, M.; Meng, Y.; Struzhkin, V.V.; Hemley, R.J. Evidence for Superconductivity above 260 K in Lanthanum Superhydride at Megabar Pressures. Phys. Rev. Lett. 2019, 122, 027001. [Google Scholar] [CrossRef]
- Savitskii, E.M.; Baron, V.V.; Efimov, Y.V.; Bychkova, M.I.; Myzenkova, L.F. Superconducting Materials, 1st ed.; Plenum Press: New York, NY, USA; London, UK, 1973. [Google Scholar]
- Poole, C.P. (Ed.) Handbook of Superconductivity, 1st ed.; Elsever: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Matthias, B.T. Chapter V Superconductivity in the Periodic System. Prog. Low Temp. Phys. 1957, 2, 138–150. [Google Scholar] [CrossRef]
- Matthias, B.T.; Geballe, T.H.; Compton, V.B. Superconductivity. Rev. Mod. Phys. 1963, 35, 1. [Google Scholar] [CrossRef]
- Conder, K. A second life of the Matthias’ rules. Supercond. Sci. Technol. 2016, 29, 080502. [Google Scholar] [CrossRef]
- Kinjo, T.; Kajino, S.; Nishio, T.; Kawashima, K.; Yanagi, Y.; Hase, I.; Yanagisawa, T.; Ishida, S.; Kito, H.; Takeshita, N.; et al. Superconductivity in LaBi3 with AuCu3-type structure. Supercond. Sci. Technol. 2016, 29, 03LT02. [Google Scholar] [CrossRef]
- McMillan, W.L. Transition Temperature of Strong-Coupled Superconductors. Phys. Rev. 1968, 167, 331–334. [Google Scholar] [CrossRef]
- Seiden, P.E. Calculation of the Superconducting Transition Temperature. Phys. Rev. 1968, 168, 403–408. [Google Scholar] [CrossRef]
- Allen, P.B.; Cohen, M.L. Pseudopotential Calculation of the Mass Enhancement and Superconducting Transition Temperature of Simple Metals. Phys. Rev. 1969, 187, 525–538. [Google Scholar] [CrossRef]
- Kessel, W. On a general formula for the transition temperature of superconductors. Z. Naturforsch. 1974, 29a, 445–451. [Google Scholar] [CrossRef]
- Haufe, U.; Kerker, G.; Bennemann, K.H. Calculation of the superconducting transition temperature Tc for metals with phonon-anomalies. Solid State Commun. 1975, 17, 321–325. [Google Scholar] [CrossRef]
- Nowotny, H.; Hittmair, O. Calculation of the transition temperature Tc of superconductors. Phys. Stat. Solidi (B) 1979, 91, 647–656. [Google Scholar] [CrossRef]
- Arita, R.; Koretsune, T.; Sakai, S.; Akashi, R.; Nomura, Y.; Sano, W. Nonempirical Calculation of Superconducting Transition Temperatures in Light-Element Superconductors. Adv. Mater. 2017, 29, 1602421. [Google Scholar] [CrossRef] [PubMed]
- Roeser, H.P.; Haslam, D.T.; Hetflleisch, F.; Lopez, J.S.; von Schoenermark, M.F.; Stepper, M.; Huber, F.M.; Nikoghosyan, A.S. Electron transport in nanostructures: A key to high temperature superconductivity? Acta Astronaut. 2010, 67, 546–552. [Google Scholar] [CrossRef]
- Roeser, H.P.; Hetfleisch, F.; Huber, F.M.; Stepper, M.; von Schoenermark, M.F.; Moritz, A.; Nikoghosyan, A.S. A link between critical transition temperature and the structure of superconducting YBa2Cu3O7-δ. Acta Astronautica 2008, 62, 733–736. [Google Scholar] [CrossRef]
- Roeser, H.P.; Haslam, D.T.; Lopez, J.S.; Stepper, M.; von Schoenermark, M.F.; Huber, F.M.; Nikoghosyan, A.S. Electronic energy levels in high temperature superconductors. J. Supercond. Novel Mag. 2011, 24, 1443–1451. [Google Scholar] [CrossRef]
- Huber, F.; Roeser, H.P.; von Schoenermark, M.F. A correlation between Tc of Fe based HT Superconductors and the crystal superlattice constants of the doping element positions. J. Phys. Soc. Jpn. 2008, 77 (Suppl. C), 142–144. [Google Scholar] [CrossRef][Green Version]
- Rohlf, J.W. Modern Physics from α to Z0; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Roeser, H.P.; Haslam, D.T.; Lopez, J.S.; Stepper, M.; von Schoenermark, M.F.; Huber, F.M.; Nikoghosyan, A.S. Correlation between transition temperature and crystal structure of niobium, vanadium, tantalum and mercury superconductors. Acta Astronaut. 2010, 67, 1333–1336. [Google Scholar] [CrossRef]
- Moritz, A. Calculation of the Transition Temperature of One-Component-Superconductors. Master’s Thesis, Institute of Space Systems, University of Stuttgart, Stuttgart, Germany, 2009. (In German). [Google Scholar]
- Stepper, M. Calculation of the Transition Temperature of Two-Component-Superconductors. Master’s Thesis, Institute of Space Systems, University of Stuttgart, Stuttgart, Germany, (In German). 2008. [Google Scholar]
- ICDD. ICDD PDF Data Base; ICDD: Newtown Square, PA, USA, 2019. [Google Scholar]
- Materials Project Database V2019.05. Available online: https://materialsproject.org/ (accessed on 12 December 2019).
- Wördenweber, R. Mechanism of vortex motion in high temperature superconductors. Rep. Prog. Phys. 1999, 62, 187–236. [Google Scholar] [CrossRef]
- Koblischka, M.R. Magnetic Properties of High-Temperature Superconductors; Alpha Science International Ltd.: Oxford, UK, 2009; ISBN 978-1-84265-149-0. [Google Scholar]
- Pradhan, A.K.; Muralidhar, M.; Koblischka, M.R.; Murakami, M.; Nakao, K.; Koshizuka, N. Flux pinning in melt-processed ternary (Nd–Eu–Gd)Ba2Cu3Oy superconductors with Gd2BaCuO5 addition. J. Appl. Phys. 1999, 86, 5705–5711. [Google Scholar] [CrossRef]
- Chen, D.X.; Goldfarb, R.B. Kim model for magnetization of type-II superconductors. J. Appl. Phys. 1989, 66, 2489–2500. [Google Scholar] [CrossRef]
- Skumryev, V.; Koblischka, M.R.; Kronmüller, H. Sample size dependence of the AC-susceptibility of sintered YBa2Cu3O7-δ superconductors. Phys. C 1991, 184, 332–340. [Google Scholar] [CrossRef]
- Karwoth, T.; Furutani, K.; Koblischka, M.R.; Zeng, X.L.; Wiederhold, A.; Muralidhar, M.; Murakami, M.; Hartmann, U. Electrotransport and magnetic measurements on bulk FeSe superconductors. J. Phys. Conf. Ser. 2018, 1054, 012018. [Google Scholar] [CrossRef]
- Karwoth, T. Electronic Transport Measurements on Electrospun High-Tc Fibers. Master’s Thesis, Saarland University, Saarbrücken, Germany, 2016. [Google Scholar]
- Prozorov, R.; Shantsev, D.V.; Mints, R.G. Collapse of the critical state in superconducting niobium. Phys. Rev. B 2006, 74, 220511. [Google Scholar] [CrossRef]
- Pust, L.; Wenger, L.E.; Koblischka, M.R. Detailed investigation of the superconducting transition of niobium disks exhibiting the paramagnetic Meissner effect. Phys. Rev. B 1998, 58, 14191–14194. [Google Scholar] [CrossRef]
- Pust, L.; Wenger, L.E.; Koblischka, M.R. Details of the Superconducting Phase Transition in Nb showing the Paramagnetic Meissner Effect. Phys. Stat. Solidi (B) 1999, 212, R13–R14. [Google Scholar] [CrossRef]
- Wenger, L.E.; Pust, L.; Koblischka, M.R. Investigation of the paramgnetic Meissner effect on Nb disks. Phys. B 2000, 284–288, 797–798. [Google Scholar] [CrossRef]
- Hauser, J.J.; Theuerer, H.C. Superconducting Tantalum films. Rev. Mod. Phys. 1964, 36, 80–83. [Google Scholar] [CrossRef]
- Joshi, L.M.; Verma, A.; Gupta, A.; Rout, P.K.; Husale, S.; Budhani, R.C. Superconduting properties of NbN film, bridge and meanders. AIP Adv. 2018, 8, 055305. [Google Scholar] [CrossRef]
- Grawatsch, K. Grundlegende Untersuchungen über die Einsatzmöglichkeiten Supraleitender Schalter in der Kryogenen Energietechnik. Ph.D. Thesis, Zentralbibliothek d. Kernforschungsanlage, Jülich, Germany, 1974. [Google Scholar]
- Wiederhold, A.; Koblischka, M.R.; Inoue, K.; Muralidhar, M.; Murakami, M.; Hartmann, U. Electric transport measurements on bulk, polycrystalline MgB2 samples prepared at various reaction temperatures. J. Phys. Conf. Ser. 2016, 695, 012004. [Google Scholar] [CrossRef]
- Koblischka-Veneva, A.; Koblischka, M.R.; Schmauch, J.; Inoue, K.; Muralidhar, M.; Berger, K.; Noudem, J. EBSD analysis of MgB2 bulk superconductors. Supercond. Sci. Technol. 2016, 29, 044007. [Google Scholar] [CrossRef]
- Yamamoto, A.; Shimoyama, J.; Kishio, K.; Matsushita, T. Limiting factors of normal-state conductivity in superconducting MgB2: An application of mean-field theory for a site percolation problem. Supercond. Sci. Technol. 2007, 20, 658–666. [Google Scholar] [CrossRef]
- Ivry, Y.; Kim, C.-S.; Dane, A.E.; De Fazio, D.; McCaughan, A.N.; Sunter, K.A.; Zhao, Q.; Berggren, K.K. Universal scaling of the critical temperature for thin films near the superconducting-to-insulating transition. Phys. Rev. B 2014, 90, 214515. [Google Scholar] [CrossRef]
- Aschermann, G.; Friedrich, E.; Justi, E.; Kramer, J. Superconductive connections with extremely high cracking temperatures (NbH and NbN). Phys. Z. 1941, 42, 349–360. [Google Scholar]
- Guard, R.W.; Savage, J.W.; Swarthout, D.G. Constitution of a portion of the niobium (columbium)-nitrogen system. Trans. Met. Soc. AIME 1967, 239, 643–649. [Google Scholar]
- Brauer, G.; Kirner, H. Drucksynthese von Niobnitriden und von δ-NbN. Z. Anorg. Allg. Chem. 1964, 328, 34–43. [Google Scholar] [CrossRef]
- Geibel, C.; Rietschel, H.; Junod, A.; Pelizzone, M.; Müller, J. Electronic properties, phono densities of states and superconductivity in Nb1-xNx. J. Phys. F Met. Phys. 1985, 15, 405–416. [Google Scholar] [CrossRef]
- Roedhammer, P.; Gmelin, E.; Weber, W.; Remeika, J.P. Observation of phonon anomalies in NbxN1-x alloys. Phys. Rev. B 1977, 15, 711–717. [Google Scholar] [CrossRef]
- Meyer, O.; Friedland, E.; Scheerer, B. Superconductivity of niobium nitride single-crystals after implantation of carbon and nitrogen. Solid State Commun. 1981, 39, 1217–1221. [Google Scholar] [CrossRef]
- Bauer, H.; Saur, E.J.; Schweitzer, D.G. Effect of thermal-neutron irradiations on superconductivity of B-1 compounds doped with B-10 and U-235. J. Low Temp. Phys. 1975, 19, 189–200. [Google Scholar] [CrossRef]
- Pessall, N.; Gold, R.E.; Johansen, H.A. A study of superconductivity in interstitial compounds. J. Hys. Chem. Solids 1968, 29, 19–38. [Google Scholar] [CrossRef]
- Geballe, T.H.; Matthias, B.T.; Remeika, J.P.; Clogston, A.M.; Compton, V.B.; Maita, J.P.; Williams, H.J. High temperature SP-band superconductors. Phys. Phys. Fiz. 1966, 2, 293–310. [Google Scholar] [CrossRef]
- Horn, G.; Saur, E. Preparation and superconductive properties of niobium nitride and niobium nitride with admixtures of titanium, zirconium and tantalum. Z. Phys. 1968, 210, 70–79. [Google Scholar] [CrossRef]
- Rögener, H. Zur Supraleitung des Niobnitrids. Z. Phys. 1952, 132, 446–467. [Google Scholar] [CrossRef]
- Hechler, K.; Horn, G.; Otto, G.; Saur, E. Measurements of critical data for some type II superconductors and comparison with theory. J. Low Temp. Phys. 1969, 1, 29–43. [Google Scholar] [CrossRef]
- Glowacki, B.A. Development of Nb based conductors. In Frontiers of Superconducting Materials; Narlikar, A.V., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 697–738. [Google Scholar]
- Seeber, B. (Ed.) Handbook of Applied Superconductivity; IOP Publishing: Bristol, UK, 1999. [Google Scholar]
- Cardwell, D.A.; Ginley, D.S. (Eds.) Handbook of Superconducting Materials; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Hillmann, H. Interaction of metallurgical treatment and flux pinning of NbTi superconductors. Supercond. Sci. Technol. 1999, 12, 348–355. [Google Scholar] [CrossRef]
- Hutchinson, T.S.; Ocampo, G.; Carpenter, G.J.C. Crystal structure and morphology in commercial NbTi (46.5 wt.-% Ti) superconducing fibers. Scr. Metall. 1985, 19, 635–638. [Google Scholar] [CrossRef]
- Steele, M.C.; Hein, R.A. Superconductivity of Titanium. Phys. Rev. 1953, 92, 243–247. [Google Scholar] [CrossRef]
- Gajda, D. Analysis Method of High-Field Pinning Centers in NbTi Wires and MgB2 Wires. J. Low Temp. Phys. 2019, 194, 166–182. [Google Scholar] [CrossRef]
- Shimizu, J.; Tonooka, K.; Yoshida, Y.; Furuse, M.; Takashima, H. Growth and superconductivity of niobium titanium alloy thin films on strontium titanate (001) single crystal substrates for superconducting joints. Sci. Rep. 2018, 8, 15135. [Google Scholar] [CrossRef]
- Lee, P.J. Abridged Metallurgy of Ductile Alloy Superconductors. Wiley Encyclopedia of Electrical and Electronics Engineering. 1999, Volume 24. Available online: http://fs.magnet.fsu.edu/~lee/asc/pdf_papers/589.pdf (accessed on 12 December 2019).
- Cooley, L.; Lee, P.J.; Larbalestier, D.C. Processing of Low Tc Conductors. In Handbook of Superconducting Materials; Seeber, B., Ed.; Institute of Physics Publishing: Bristol, UK, 2003; pp. 603–639. [Google Scholar]
- Meingast, C.; Larbalestier, D.C. Quantitative description of a very high critical current-density Nb-Ti superconductor during its final optimization strain. 2. Flux pinning mechanism. J. Appl. Phys. 1989, 66, 5971–5983. [Google Scholar] [CrossRef]
- Hardy, G.F.; Hulm, J.K. The Superconductivity of Some Transition Metal Compounds. Phys. Rev. 1954, 93, 1004–1016. [Google Scholar] [CrossRef]
- Hulm, J.K.; Matthias, B.T. High-field, high-current superconductors. Science 1980, 208, 881–887. [Google Scholar] [CrossRef] [PubMed]
- Stewart, G.A. Superconductivity in the A15 structure. Phys. C 2015, 514, 28–35. [Google Scholar] [CrossRef]
- Matthias, B.T.; Geballe, T.H.; Longinotti, L.D.; Corenzwit, E.; Hull, G.W.; Willens, R.H.; Maita, J.P. Superconductivity at 20 degrees Kelvin. Science 1967, 156, 645–646. [Google Scholar] [CrossRef] [PubMed]
- Webb, G.W.; Vieland, L.J.; Miller, R.E.; Wicklund, A. Superconductivity above 20 degrees K in stoichiometric Nb3Ga. Solid State Commun. 1971, 9, 1769–1773. [Google Scholar] [CrossRef]
- Gavaler, J.R.; Janocko, M.A.; Jones, C.K. Preparation and properties of high Tc Nb-Ge thin films. J. Appl. Phys. 1974, 45, 3009–3012. [Google Scholar] [CrossRef]
- Testardi, L.R.; Wernick, J.H.; Royer, W.A. Superconductivity with onset above 23 K in Nb-Ge sputtered films. Solid State Commun. 1974, 15, 1–4. [Google Scholar] [CrossRef]
- Stewart, G.A.; Newkirk, L.A.; Valencia, F.A. Impurity stabilized A15 Nb3Nb—A new superconductor. Phys. Rev. B 1980, 21, 5055–5064. [Google Scholar] [CrossRef]
- Ballarino, A.; Hopkins, S.C.; Simon, C.; Bordini, B.; Richter, D.; Tommasini, D.; Bottura, L.; Benedikt, M.; Sugano, M.; Ogitsu, T.; et al. The CERN FCC Conductor Development Program: A Worldwide Effort for the Future Generation of High-Field Magnets. IEEE Trans. Appl. Supercond. 2019, 29, 6000709. [Google Scholar] [CrossRef]
- Kawashima, S.; Kawarada, T.; Kato, H.; Murakami, Y.; Sugano, M.; Oguro, H.; Awaji, S. Development of a High Current Density Distributed Tin Method Nb3Sn Wire. IEEE Trans. Appl. Supercond. 2020, 30, 6000105. [Google Scholar] [CrossRef]
- Hishinuma, Y.; Taniguchi, H.; Kikuchi, A. Development of the internal matrix reinforcement bronze processed Nb3Sn multicore wires using Cu-Sn-In ternary alloy matrix for fusion magnet application. Fusion Eng. Des. 2019, 148, 111269. [Google Scholar] [CrossRef]
- Testardi, L.R. Structural instability and superconductivity in A-15 compounds. Rev. Mod. Phys. 1975, 47, 637–648. [Google Scholar] [CrossRef]
- Sayeed, M.N.; Pudasaini, U.; Reece, C.E.; Eremeev, G.; Elsayed-Ali, H.E. Structural and superconducting properties of Nb3Sn films grown by multilayer sequential magnetron sputtering. J. Alloys Compd. 2019, 800, 272–278. [Google Scholar] [CrossRef]
- Ho, K.M.; Pickett, W.E.; Cohen, M.L. Electronic properties of Nb3Ge and Nb3Al from self-consistent pseudopotentials. II. Bonding, electronic charge distributions, and structural transformation. Phys. Rev. B 1979, 19, 1751–1761. [Google Scholar] [CrossRef]
- Lowrey, W.H. Hall effect in V3Si. J. Less-Common Met. 1979, 58, 99–100. [Google Scholar] [CrossRef]
- Huang, C.C.; Goldman, A.M.; Toth, L.E. Specific heat of a transforming V3Si crystal. Solid State Commun. 1980, 33, 581–584. [Google Scholar] [CrossRef]
- Foner, S.; McNiff, E.J., Jr.; Webb, G.W.; Vieland, L.J.; Miller, R.E.; Wicklund, A. Upper critical fields of NbxGa1-x—binary high temperature superconductor. Phys. Lett. 1972, 38A, 323–324. [Google Scholar] [CrossRef]
- Guritanu, V.; Goldacker, W.; Bouquet, F.; Wang, Y.; Lortz, R.; Goll, G.; Junod, A. Specific heat of Nb3Sn: The case for a second energy gap. Phys. Rev. B 2004, 70, 184526. [Google Scholar] [CrossRef]
- Junod, A.; Jorda, J.L.; Pelizzone, M.; Muller, J. Specific heat and magnetic susceptibility of nearly stoichiometric and homogeneous Nb3Al. Phys. Rev. B 1984, 29, 1189–1198. [Google Scholar] [CrossRef]
- Webb, G.W.; Matthias, B.T. Influence of composition on superconducting transition temperature of alloys with A-15 structure. Solid State Commun. 1977, 21, 193–194. [Google Scholar] [CrossRef]
- Vereshchagin, L.F.; Savitskii, E.M.; Evdokimova, V.V.; Novokshenov, V.I.; Petrenko, V.G. Effect of high pressures and temperatures on superconducting properties of compound Nb3Ge with A-15 structure. JETP Lett. 1976, 24, 193–194. [Google Scholar]
- Buzea, C.; Yamashita, T. Review of the superconducting properties of MgB2. Supercond. Sci. Technol. 2001, 14, R115–R146. [Google Scholar] [CrossRef]
- Muranaka, T.; Akimitsu, J. Superconductivity in MgB2. Z. Kristallogr. 2011, 226, 385–394. [Google Scholar] [CrossRef]
- Kurmaev, E.Z.; Lyakhovskaya, I.I.; Kortus, J.; Moewes, A.; Miyata, N.; Demeter, M.; Neumann, M.; Yanagihara, M.; Watanabe, M.; Muranaka, T.; et al. Electronic structure of MgB2: X-ray emission and absorption studies. Phys. Rev. B 2002, 65, 134509. [Google Scholar] [CrossRef]
- Kortus, J.; Mazin, I.I.; Belashchenko, K.D.; Antropov, V.P.; Boyer, L.L. Superconductivity of Metallic Boron in MgB2. Phys. Rev. Lett. 2001, 86, 4656–4659. [Google Scholar] [CrossRef]
- Belashchenko, K.D.; van Schilfgaarde, M.; Antropov, V.P. Coexistence of covalent and metallic bonding in the boron intercalation superconductor MgB2. Phys. Rev. B 2001, 64, 092503. [Google Scholar] [CrossRef]
- Das, S.K.; Bedar, A.; Kannan, A.; Jasuja, K. Aqueous dispersions of few-layer-thick chemically modified magnesium diboride nanosheets by ultrasonication assisted exfoliation. Sci. Rep. 2015, 5, 10522. [Google Scholar] [CrossRef]
- Souma, S.; Machida, Y.; Sato, T.; Takahashi, T.; Matsui, H.; Wang, S.-C.; Ding, H.; Kaminski, A.; Campuzano, J.C.; Sasaki, S.; et al. The origin of multiple superconducting gaps in MgB2. Nature 2003, 423, 65–67. [Google Scholar] [CrossRef]
- Pallecchi, I.; Ferrando, V.; Galleani D’Agliano, E.; Marré, D.; Monni, M.; Putti, M.; Tarantini, C.; Gatti, F.; Aebersold, H.U.; Lehmann, E.; et al. Magnetoresistivity as a probe of disorder in the π and σ bands of MgB2. Phys. Rev. B 2005, 72, 184512, Erratum in 2006, 73, 029901. [Google Scholar] [CrossRef]
- Gonnelli, R.S.; Daghero, D.; Ummarino, G.A.; Stepanov, V.A.; Jun, J.; Kazakov, S.M.; Karpinski, J. Direct Evidence for Two-Band Superconductivity in MgB2 Single Crystals from Directional Point-Contact Spectroscopy in Magnetic Fields. Phys. Rev. Lett. 2002, 89, 247004. [Google Scholar] [CrossRef]
- Dolgov, O.V.; Gonnelli, R.S.; Ummarino, G.A.; Golubov, A.A.; Shulga, S.V.; Kortus, J.J. Extraction of the electron-phonon interaction from tunneling data in the multigap superconductor MgB2. Phys. Rev. B 2003, 68, 132503. [Google Scholar] [CrossRef]
- Gonnelli, R.S.; Daghero, D.; Ummarino, G.A.; Stepanov, V.A.; Jun, J.; Kazakov, S.M.; Karpinski, J. Independent determination of the two gaps by directional point-contact spectroscopy in MgB2 single crystals. Supercond. Sci. Technol. 2003, 16, 171–175. [Google Scholar] [CrossRef][Green Version]
- Daghero, D.; Gonnelli, R.S.; Ummarino, G.A.; Calzolari, A.; Dellarocca, V.; Stepanov, V.A.; Kazakov, S.M.; Jun, J.; Karpinski, J. Effect of the magnetic field on the gaps of MgB2: A directional point-contact study. J. Phys. Chem. Solids 2006, 67, 424–427. [Google Scholar] [CrossRef]
- Silva-Guillen, J.A.; Noat, Y.; Cren, T.; Sacks, W.; Canadell, E.; Ordejon, P. Tunneling and electronic structure of the two-gap superconductor MgB2. Phys. Rev. B 2015, 92, 064514. [Google Scholar] [CrossRef]
- Choi, H.J.; Roundy, D.; Sun, H.; Cohen, M.L.; Louie, S.G. The Origin of the Anomalous Superconducting Properties of MgB2. Nature 2002, 418, 758–760. [Google Scholar] [CrossRef]
- Moshchalkov, V.; Menghini, M.; Nishio, T.; Chen, Q.H.; Silhanek, A.V.; Dao, V.H.; Chibotaru, L.F.; Zhigadlo, N.D.; Karpinski, J. Type-1.5 Superconductivity. Phys. Rev. Lett. 2009, 102, 117001. [Google Scholar] [CrossRef]
- Roth, S. Theoretical Investigation of One-Component-Superconductors and their Relationship between Transition Temperature and Ionization Energy, Crystal Parameters and Further Parameters. Ph.D. Thesis, Institute of Space Systems, University of Stuttgart, Stuttgart, Germany, 2018. (In German). [Google Scholar]
- Gou, H.; Dubrovinskaia, N.; Bykova, E.; Tsirlin, A.A.; Kasinathan, D.; Schnelle, W.; Richter, A.; Merlini, M.; Hanfland, M.; Abakumov, A.M.; et al. Discovery of a Superhard Iron Tetraboride Superconductor. Phys. Rev. Lett. 2013, 111, 157002. [Google Scholar] [CrossRef]
- Stanev, V.; Oses, C.; Kusne, A.G.; Rodriguez, E.; Paglione, J.; Curtarolo, S.; Takeuchi, I. Machine learning modeling of superconducting critical temperature. NPJ Comput. Mater. 2018, 4, 29. [Google Scholar] [CrossRef]
- Matsumoto, K.; Horide, T. An acceleration search method of higher Tc superconductors by a machine learning algorithm. Appl. Phys. Express 2019, 12, 073003. [Google Scholar] [CrossRef]
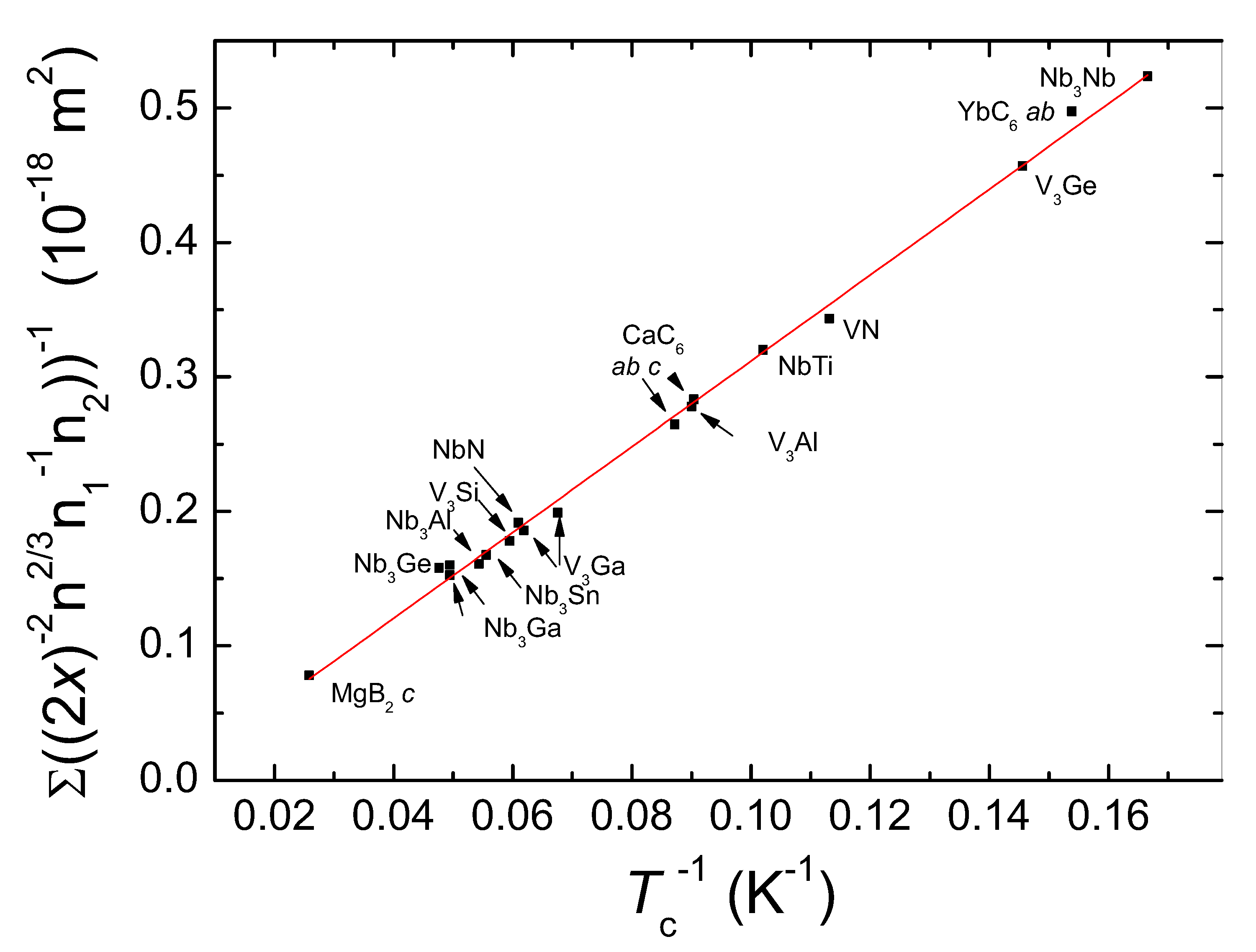
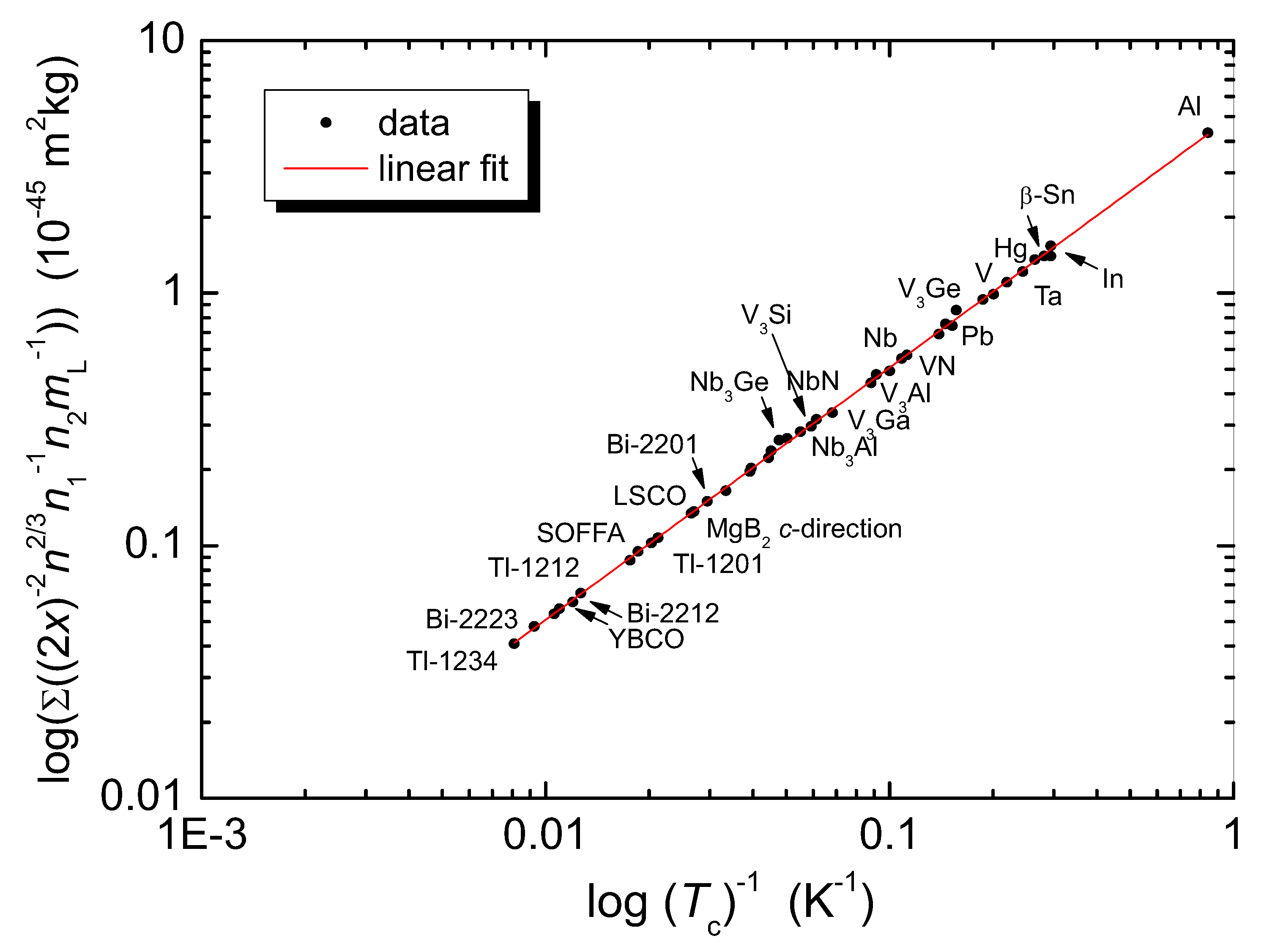
| Direction | x (10 m) | (2x) (10 m) | () | [10 J] |
|---|---|---|---|---|
| 1 | 3.5 | 4.9 | 4 | 6.69 |
| 2 | 4.95 | 9.8 | 1 | 13.4 |
| 3 | 6.06 | 14.7 | 2 | 4.46 |
| 4 | 8.58 | 29.4 | 2/3 | 6.69 |
| Direction | x (10 m) | (2x) (10 m) | () | (10 J) |
|---|---|---|---|---|
| 1 | 2.86 | 3.28 | 13 | 3.08 |
| 2 | 4.05 | 6.56 | 13/4 | 6.16 |
| 3 | 4.96 | 9.84 | 13/2 | 2.05 |
| 4 | 7.01 | 19.7 | 13/6 | 3.08 |
| (nm) | x (nm) | (meV) | (K) | |||
|---|---|---|---|---|---|---|
| 0.436 | 0.308 | 1 | 2 | 0.5 | 4.31 | 15.92 |
| 0.4393 | 0.311 | 1 | 2 | 0.5 | 4.24 | 15.68 |
| Compound | (nm) | (exp) (K) | x (nm) | (meV) | (K) | (meV) | (K) |
|---|---|---|---|---|---|---|---|
| VSi | 0.472 | 16.8 | 0.2360 (1) | 1.839 | 6.79 | 4.597 | 16.98 |
| [91] | 0.4720 (2) | 0.460 | 1.70 | ||||
| [92] | 0.4088 (3) | 0.919 | 3.39 | ||||
| NbGa | 0.5165 | 20.2 | 0.2584 (1) | 3.071 | 11.34 | 5.375 | 19.86 |
| [93] | 0.5165 (2) | 0.384 | 1.42 | ||||
| 0.4473 (3) | 0.768 | 2.84 | |||||
| NbSn | 0.529 | 18.05 | 0.2645 (1) | 2.927 | 10.81 | 4.879 | 18.02 |
| [94] | 0.5290 (2) | 0.488 | 1.80 | ||||
| 0.4581 (3) | 0.976 | 3.60 | |||||
| NbAl | 0.518 | 18.4 | 0.2590 (1) | 3.053 | 11.28 | 5.089 | 18.8 |
| [95] | 0.5180 (2) | 0.509 | 1.88 | ||||
| [96] | 0.4486 (3) | 1.018 | 3.76 | ||||
| NbGe | 0.5135 | 19.7 | 0.2568 (1) | 3.107 | 11.48 | 5.179 | 19.13 |
| [97] | 0.5135 (2) | 0.518 | 1.91 | ||||
| 0.4447 (3) | 1.036 | 3.83 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koblischka, M.R.; Roth, S.; Koblischka-Veneva, A.; Karwoth, T.; Wiederhold, A.; Zeng, X.L.; Fasoulas, S.; Murakami, M. Relation between Crystal Structure and Transition Temperature of Superconducting Metals and Alloys. Metals 2020, 10, 158. https://doi.org/10.3390/met10020158
Koblischka MR, Roth S, Koblischka-Veneva A, Karwoth T, Wiederhold A, Zeng XL, Fasoulas S, Murakami M. Relation between Crystal Structure and Transition Temperature of Superconducting Metals and Alloys. Metals. 2020; 10(2):158. https://doi.org/10.3390/met10020158
Chicago/Turabian StyleKoblischka, Michael Rudolf, Susanne Roth, Anjela Koblischka-Veneva, Thomas Karwoth, Alex Wiederhold, Xian Lin Zeng, Stefanos Fasoulas, and Masato Murakami. 2020. "Relation between Crystal Structure and Transition Temperature of Superconducting Metals and Alloys" Metals 10, no. 2: 158. https://doi.org/10.3390/met10020158
APA StyleKoblischka, M. R., Roth, S., Koblischka-Veneva, A., Karwoth, T., Wiederhold, A., Zeng, X. L., Fasoulas, S., & Murakami, M. (2020). Relation between Crystal Structure and Transition Temperature of Superconducting Metals and Alloys. Metals, 10(2), 158. https://doi.org/10.3390/met10020158





