Magnetic Field Generated during Electric Current-Assisted Sintering: From Health and Safety Issues to Lorentz Force Effects
Abstract
1. Magnetic Field Effects in Electromagnetic Processing of Materials (EPM)
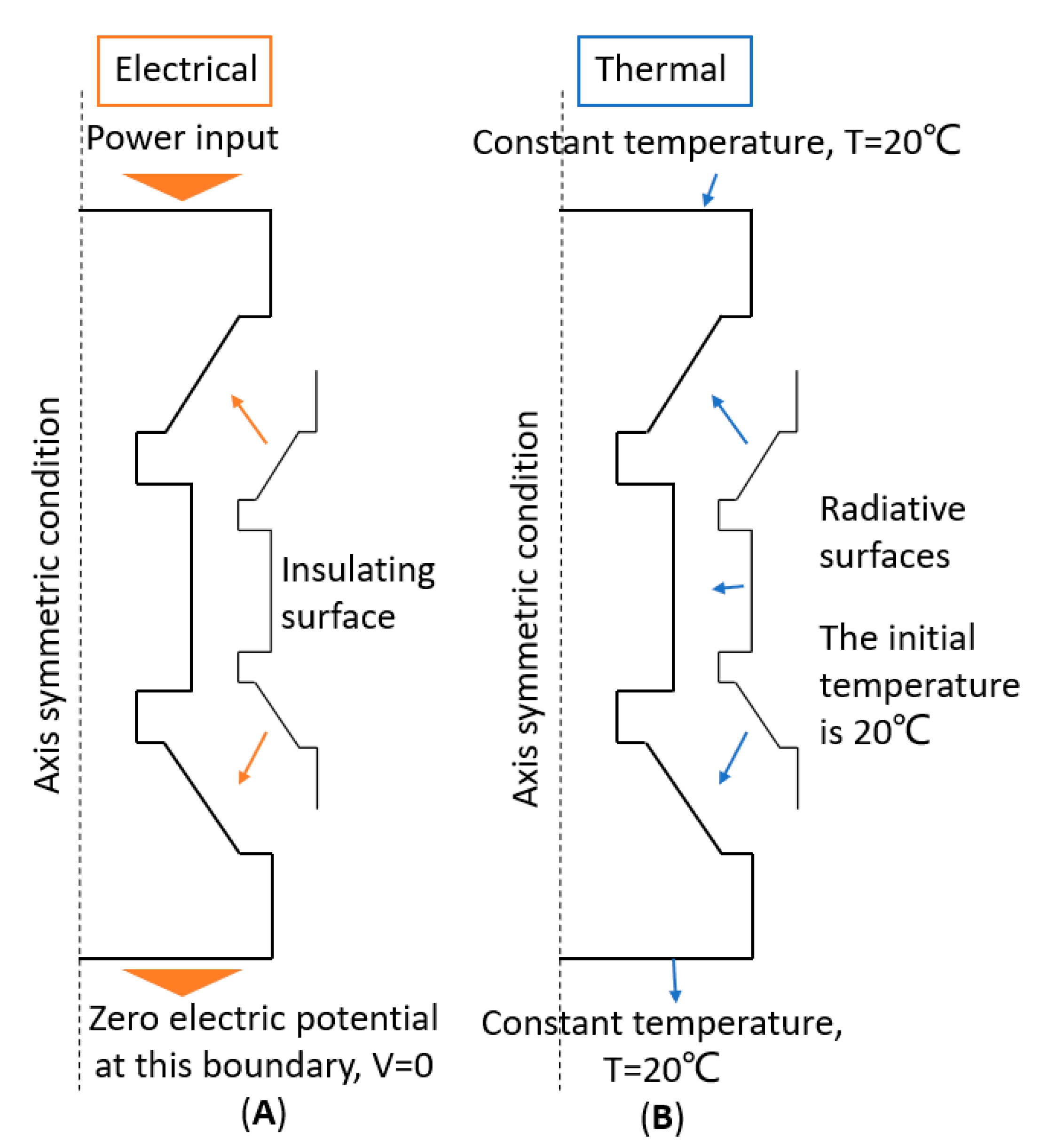
2. The Combined Experimental/Computational Methodology
3. Health Effects and Safe Distance for the Operators
4. Magnetic Field Distribution during SPS of Different Materials: Electrical Conductivity and Magnetic Permeability Effects
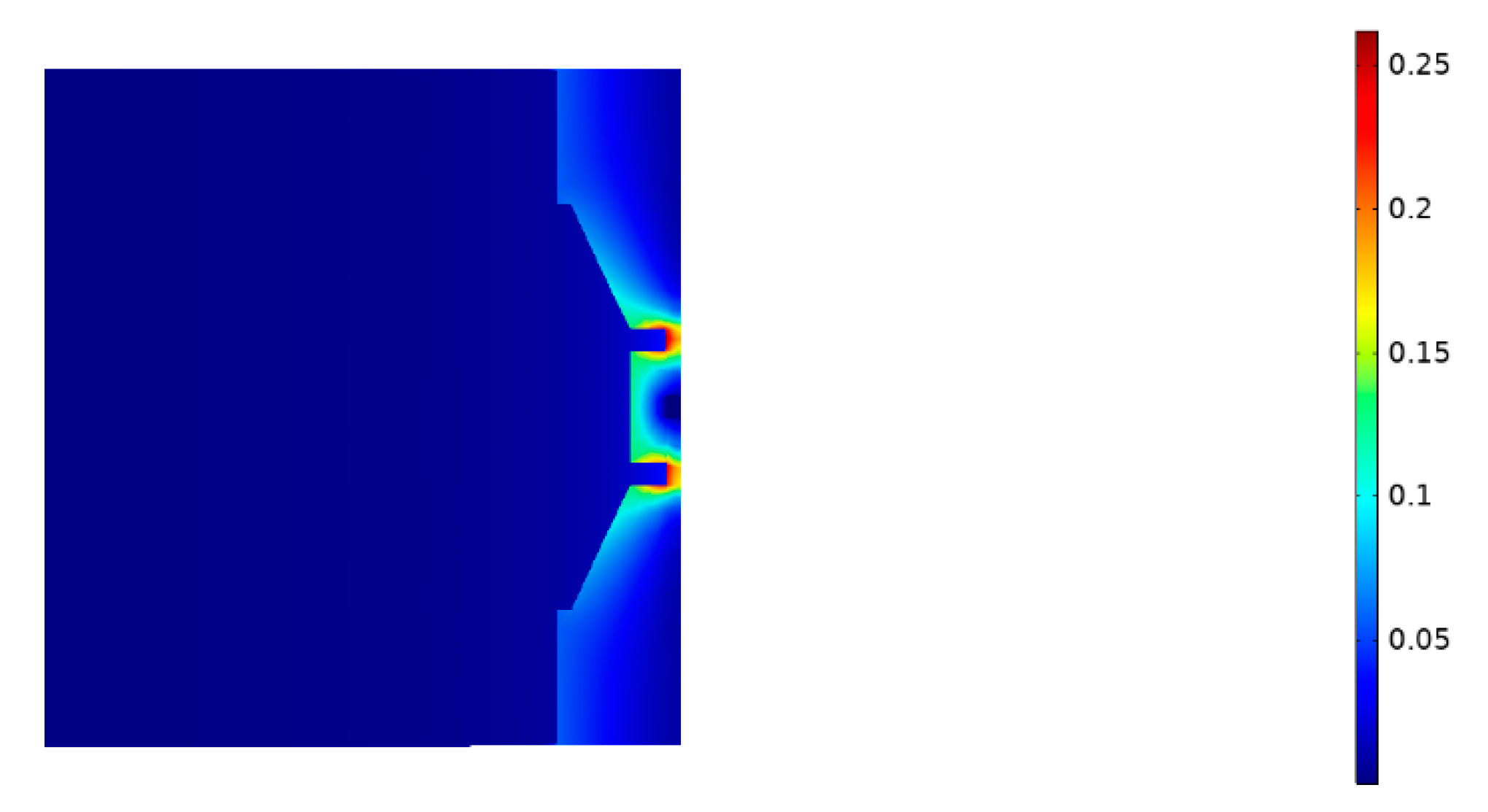
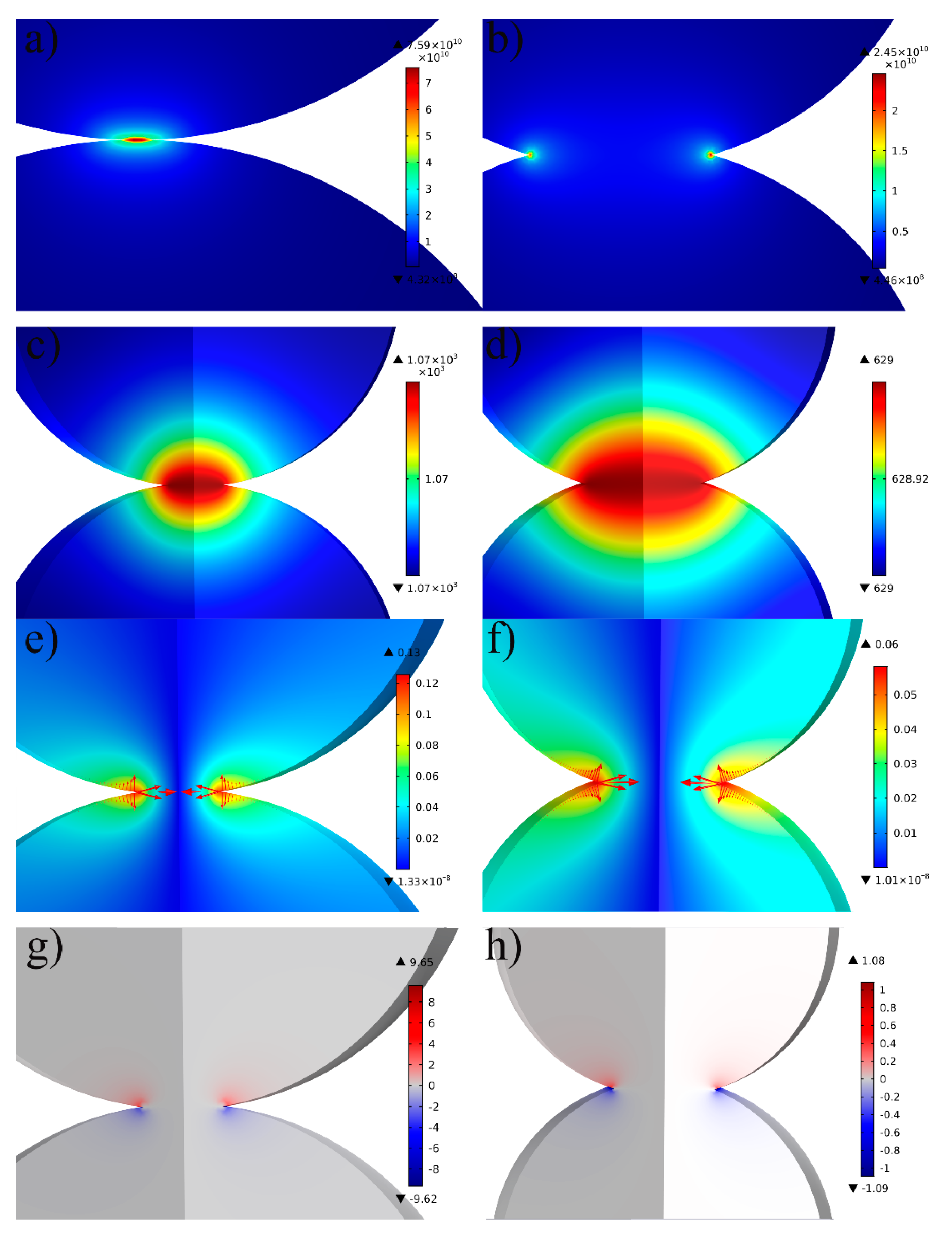
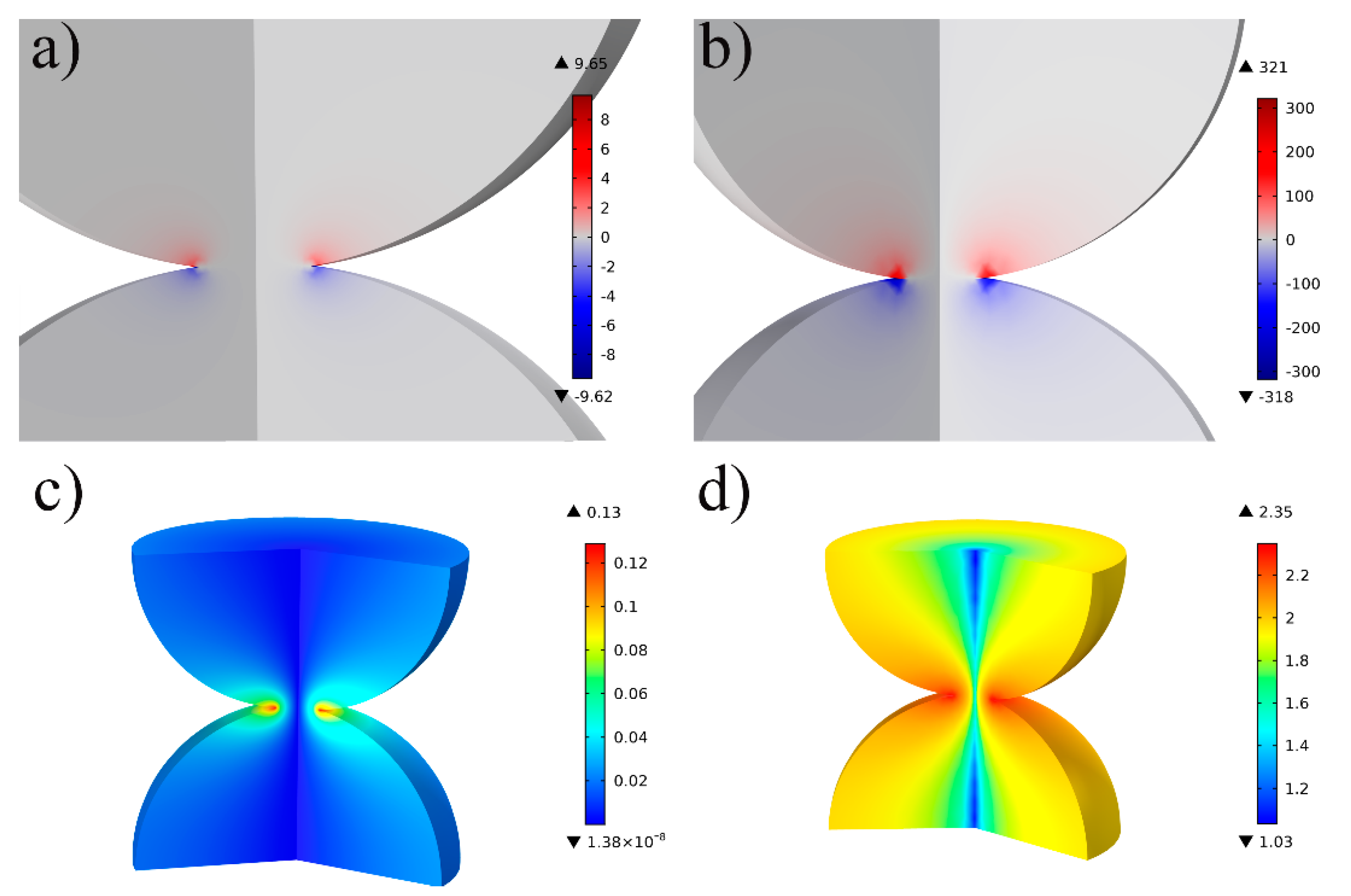
5. Magnetic Field Effects at Interparticle Contacts
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Biesuz, M.; Sauders, T.; Ke, D.; Reece, M.J.; Hu, C.; Grasso, S. A review of electromagnetic processing of materials (EPM): Heating, sintering, joining and forming. J. Mater. Sci. Technol. 2020, 69, 239–272. [Google Scholar] [CrossRef]
- Guo, L.; Li, Y.Y.; Li, X.; Yang, J.Y. Numerical Analysis on Temperature Field of Axial Alternating Magnetic Field-Assisted Electric Field-Activated Sintering. Mater. Sci. Forum 2008, 575, 702–708. [Google Scholar] [CrossRef]
- Resistance Welder Manufacturers’ Association. Resistance Welding Manual, 4th ed.; Resistance Welder Manufacturers’ Association: Miami, FL, USA, 2009. [Google Scholar]
- Deffenbaugh, J.F. Resistance Welding; Resistance Welder Manufacturers Association: Miami, FL, USA, 1940; Volume 146. [Google Scholar] [CrossRef]
- Vikrant, K.; Wang, H.; Jana, A.; Wang, H.; García, R.E. Flash sintering incubation kinetics. NPJ Comput. Mater. 2020, 6, 1–8. [Google Scholar] [CrossRef]
- Semenov, A.S.; Trapp, J.; Nöthe, M.; Eberhardt, O.; Wallmersperger, T.; Kieback, B. Experimental and numerical analysis of the initial stage of field-assisted sintering of metals. J. Mater. Sci. 2017, 52, 1486–1500. [Google Scholar] [CrossRef]
- Ray, N.; Kempf, B.; Wiehl, G.; Mützel, T.; Heringhaus, F.; Froyen, L.; Vanmeensel, K.; Vleugels, J. Novel processing of Ag-WC electrical contact materials using spark plasma sintering. Mater. Des. 2017, 121, 262–271. [Google Scholar] [CrossRef]
- Grasso, S.; Saunders, T.; Porwal, H.; Cedillos-Barraza, O.; Jayaseelan, D.D.; Lee, W.E.; Reece, M.J. Flash Spark Plasma Sintering (FSPS) of Pure ZrB2. J. Am. Ceram. Soc. 2014, 97, 2405–2408. [Google Scholar] [CrossRef]
- White, D.A.; Fasenfest, B.J. Performance of Low-Rank QR Approximation of the Finite Element Biot-Savart Law. In Proceedings of the 2006 12th Biennial IEEE Conference on Electromagnetic Field Computation, Miami, FL, USA, 30 April–3 May 2006. [Google Scholar] [CrossRef]
- Wheeler, H. Formulas for the Skin Effect. Proc. IRE 1942, 30, 412–424. [Google Scholar] [CrossRef]
- Ahmad, M.K.; Ali, M.S.; Majid, A.; Saleem, J.; Kazmi, S.M.R. Design and optimization of high frequency (250 kHz) planar transformer for micro solar converter application. In Proceedings of the 2018 IEEE 12th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG 2018), Hilton Doha Hotel, Doha, Qatar, 10–12 April 2018. [Google Scholar]
- Runte, E. Continuous high-frequency induction tube welding. In The Brown Boveri Review; Brown, Boveri & Company: Baden, Switzerland, 1968; pp. 113–118. [Google Scholar]
- Zhao, D.X.; Zhao, Z.M.; Zhang, Z.K.; Dai, X. Research and Numerical Simulation of Contactor of High-Frequency Welding Device. Adv. Mater. Res. 2011, 189, 3575–3578. [Google Scholar] [CrossRef]
- Trapp, J. Mechanical Forces in the Microscopic Powder Contact during Field Assisted Sintering 2017; Fraunhofer Institute of Manufacturing and Advanced Materials—IFAM Dresden. Available online: http://doi.org/doi:10.13140/RG.2.2.14345.47206 (accessed on 1 July 2020).
- Yurlova, M.S.; Demenyuk, V.D.; Lebedeva, L.Y.; Dudina, D.V.; Grigoryev, E.G.; Olevsky, E.A. Electric pulse consolidation: An alternative to spark plasma sintering. J. Mater. Sci. 2013, 49, 952–985. [Google Scholar] [CrossRef]
- Ueyama, T.; Era, T.; Uezono, T.; Tong, H. Application of digital inverter-controlled AC pulsed MIG welding system to light metal joining. Weld. Int. 2011, 25, 676–682. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Katada, Y.; Itou, T.; Uesugi, Y.; Tanaka, Y.; Ishijima, T. Experimental investigation of magnetic arc blow in plasma arc cutting. Weld. World 2014, 59, 45–51. [Google Scholar] [CrossRef]
- Vural, M. Welding Processes and Technologies; Elsevier: London, UK, 2014; Volume 6, pp. 3–48. [Google Scholar] [CrossRef]
- Lockwood, L.F.; Phillips, A.L.; Walter, S.T. Welding Processes: Gas, Arc and Resistance. In Welding Handbook, 6th ed.; Cambridge University Press: Cambridge, UK, 1969; pp. 76–175. [Google Scholar] [CrossRef]
- Adamian, Y.; Shneerson, G. Mechanism of Wire Explosion Plasma Acceleration in Strong Axial Magnetic Field. Acta Phys. Pol. A 2009, 115, 1069–1071. [Google Scholar] [CrossRef]
- Zhang, H.; Senkara, J. Resistance Welding: Fundamentals and Applications, 1st ed.; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2005. [Google Scholar] [CrossRef]
- Burkhard, D.G. A Heuristic Derivation of Coulomb’s Law and the Biot-Savart Law. Am. J. Phys. 1972, 40, 1858–1859. [Google Scholar] [CrossRef]
- Hovey, A. The Biot-Savart Law—Another Approach. Phys. Teach. 2008, 46, 261. [Google Scholar] [CrossRef]
- Lou, Y.-T.; Li, H.-Y.; Li, B.-M. Research on proximity effect of electromagnetic railgun. Def. Technol. 2016, 12, 223–226. [Google Scholar] [CrossRef]
- Dresden, M. Highest Pulsed Magnetic Fields in Science and Technology, Assisted by Advanced Finite-Element Simulations. In Proceedings of the COMSOL Conference 2008 Hannover, Hannover, Germany, 4–6 November 2008. [Google Scholar]
- Sales, B.C.; Maple, M.B. Low-frequency electrical resistance of iron, cobalt, and nickel in the vicinity of their Curie temperatures. Appl. Phys. A Solids Surf. 1983, 31, 115–117. [Google Scholar] [CrossRef]
- Mani, M.K.; Viola, G.; Hall, J.P.; Grasso, S.; Reece, M.J. Observation of Curie transition during spark plasma sintering of ferromagnetic materials. J. Magn. Magn. Mater. 2015, 382, 202–205. [Google Scholar] [CrossRef]
- Mal’Tsev, I.M. The effect of the electromagnetic field and skin and pinch effects on electrorolling metal powder materials under high-density pulse currents. Russ. J. Non-Ferrous Met. 2009, 50, 142–146. [Google Scholar] [CrossRef]
- Olevsky, E.A.; Dudina, D.V. Field-Assisted Sintering: Science and Applications; Spinger: Cham, Switzerland, 2018; pp. 1–425. [Google Scholar] [CrossRef]
- COMSOL Multiphysics. AC/DC Module User’s Guide. Vers.5.2; COMSOL: Stockholm, Sweden, 2015. [Google Scholar]
- Maizza, G.; Grasso, S.; Sakka, Y. Moving finite-element mesh model for aiding spark plasma sintering in current control mode of pure ultrafine WC powder. J. Mater. Sci. 2009, 44, 1219–1236. [Google Scholar] [CrossRef]
- Savvatimskiy, A. Measurements of the melting point of graphite and the properties of liquid carbon (a review for 1963–2003). Carbon 2005, 43, 1115–1142. [Google Scholar] [CrossRef]
- Guidelines for limiting exposure to time-varying electric and magnetic fields (1 Hz to 100 kHz). Health Phys. 2010, 99, 818–836. [CrossRef]
- Bowler, N. Four-point potential drop measurements for materials characterization. Meas. Sci. Technol. 2010, 22. [Google Scholar] [CrossRef]
- Eikeland, A.Z.; Stingaciu, M.; Granados-Miralles, C.; Saura-Múzquiz, M.; Andersen, H.L.; Christensen, M. Enhancement of magnetic properties by spark plasma sintering of hydrothermally synthesised SrFe12O19. CrystEngComm 2017, 19, 1400–1407. [Google Scholar] [CrossRef]
- Li, X.; Ye, Y.; Tang, Y.; Qu, S. Effect of Pulsed Magnetic Field on Spark Plasma Sintering of Iron-Based Powders. Mater. Trans. 2010, 51, 1308–1312. [Google Scholar] [CrossRef]
- Grasso, S.; Sakka, Y.; Maizza, G. Electric current activated/assisted sintering (ECAS): A review of patents 1906–2008. Sci. Technol. Adv. Mater. 2009, 10, 053001. [Google Scholar] [CrossRef] [PubMed]
- Kvartskhava, I.F.; Bondarenko, V.V.; Meladze, R.D.; Suladze, K.V. Electrical Explosion of Wires in Vacuum. Sov. Phys. JETP 1957, 4, 637–644. [Google Scholar]
- Guyot, P.; Rat, V.; Coudert, J.F.; Jay, F.; Maître, A.; Pradeilles, N. Does the Branly effect occur in spark plasma sintering? J. Phys. D Appl. Phys. 2012, 45. [Google Scholar] [CrossRef]
- Magonov, S.N.; Reneker, D.H. Characterization of Polymer Surfaces with Atomic Force Microscopy. Annu. Rev. Mater. Res. 1997, 27, 175–222. [Google Scholar] [CrossRef]



| Effect Name | Principle and Mathematical Formulation | Typical Use, Implications on Sintering |
|---|---|---|
Biot–Savart Law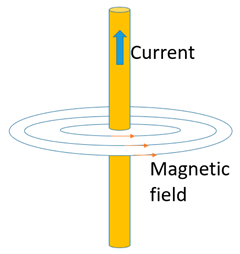 | This formulation resembles well the magnetic-induced effect in using DC currents. The Biot–Savart Law quantifies the magnetic field strength inside and outside the conductor. It refers to an infinitely long wire with radius r [9,22,23]. r0 is the radius of the conductor | It can be used to calculate the magnetic field strength in the vicinity of a conductor. It can accurately identify the health and safety exposure distance [9,22,23]. Health and safety hazard for the operators and magnetization of the electrically conductive sample under an electrical discharge. |
Skin effect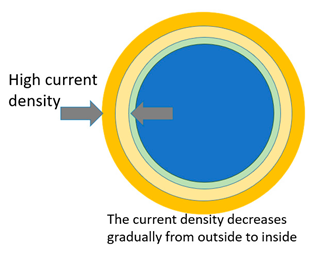 | It commonly occurs in high-frequency alternating current, resulting in preferential current flow within the skin depth. Where , and are angular frenquency, permeability, and conductivity. According to Lenz’s law, the induced current is always in the opposite direction to the imposed current, which eventually leads to the current in the conductor tending to approach the surface of the conductor [10,11,12,24]. Eddy currents are loops of electrical current within a conductor resulting from a changing magnetic field [24,25]. | Heat generation localized on the skin depth. This effect was commonly used in induction heating of a workpiece [10,11,13,24]. Preferential heating by skin effect. Possibility to counterbalance radiative heat losses. |
AC resistance change in the vicinity of the Curie temperature  | An alternating (i.e., time-variable) current flowing across a ferromagnetic conductor sees an increase in resistivity due to the skin effect. These effects disappear above the Curie temperature [26,27]. | For ferromagnetic materials (i.e., Ni, Fe, Co), the Curie temperature should be considered during heating [26,27]. Precise calibration of the temperatures and rapid drop of electrical resistance at a temperature greater than the Curie point. |
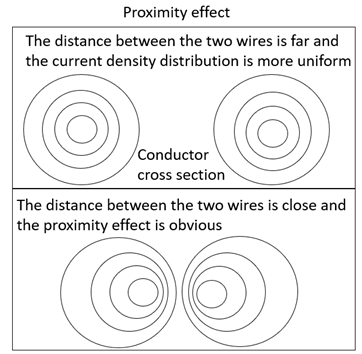 | This effect occurs under high-frequency current (100 kHz) and it was typically used to generate overheating by promoting an interaction between magnetic fields. Eddy currents result in preferential current distribution [11,13,24]. | When using high-frequency alternating current for welding, the proximity effect should be considered [11,13]. Not investigated in sintering. It is expected to provide further overheating at interparticle contact points. |
Pinch effect | Pinch effect refers to the compressive forces acting on the conductive media as a result of the magnetic forces. The conductive media can be in the form of a liquid, a solid, or a plasma. These effects are particularly strong in the presence of large currents as in the case of a capacitor discharge [14,15,28,29]. | The pinch effect induces a shape change of the sample, easing its extraction out of the die [15]. Might not have strong implications in pressure-assisted sintering. Pinch-related pressure is several orders of magnitude lower than the sintering pressure (≈ MPa). |
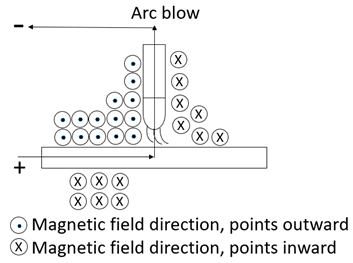 | This phenomenon was often encountered in the welding. The magnetic bias blow is caused by the unbalanced magnetic field around the electrical arc [17,18,19]. | An AC current is less susceptible to arc blowing compared to DC [17,18,19]. Arcing is usually seen as an undesired effect in sintering. |
Reactance dependence on duty cycle | Ferromagnetic materials significantly increase the reactance, reducing the welding or sintering current [19]. | Ferromagnetic materials increase the reactance, and leads to an increase in impedance, ultimately resulting in a decrease in current [19]. Implications on the material selected as tooling. |
| Standard Commercialized SPS Types | Dimension Components [mm] | Max Pressing Force [kN] | Max Current [A] | Safety Distance without Shield (DC) [cm] | Biot–Savart Distance Calculation [cm] * |
|---|---|---|---|---|---|
| HP D 2.5 | Ø 30 | 25 | 3000 | 118.9 | 120 |
| HP D 10 | Ø 50 | 100 | 5500 | 217.7 | 200 |
| HP D 25 | Ø 80 | 250 | 8000 | 314.7 | 320 |
| HP D 60 | Ø 120 | 600 | 16,000 | 629.8 | 640 |
| HP D 125 | Ø 150 | 1250 | 24,000 | 956.3 | 960 |
| HP D 250 | Ø 300 | 2500 | 48,000/24,000 | 1894/1949 | 1920/960 |
| Electrical Conductivity (S m) | Relative Permeability | |
|---|---|---|
| Graphite | 8.3 × 104 | 1 |
| Iron | 1.12 × 107 | 200,000 |
| Alumina | 1 × 10−12 | 1 |
| Copper | 5.714 × 107 | 1 |
| Inventor, Year, Reference | Pressure, Discharge Time, Voltage, Current Density | Sintered Material |
|---|---|---|
| Cremer, US1944 | ≈100 MPa, 10 ms, 5–20 V, ≈60 kAcm−2 | Cu, Al, brass |
| Parker, US1968 | 10 MPa, 1 ms, >150 kAcm−2 2000 Jcm−3 | Ti, Fe |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, H.; Dong, J.; Boi, F.; Saunders, T.; Hu, C.; Grasso, S. Magnetic Field Generated during Electric Current-Assisted Sintering: From Health and Safety Issues to Lorentz Force Effects. Metals 2020, 10, 1653. https://doi.org/10.3390/met10121653
Deng H, Dong J, Boi F, Saunders T, Hu C, Grasso S. Magnetic Field Generated during Electric Current-Assisted Sintering: From Health and Safety Issues to Lorentz Force Effects. Metals. 2020; 10(12):1653. https://doi.org/10.3390/met10121653
Chicago/Turabian StyleDeng, Huaijiu, Jian Dong, Filippo Boi, Theo Saunders, Chunfeng Hu, and Salvatore Grasso. 2020. "Magnetic Field Generated during Electric Current-Assisted Sintering: From Health and Safety Issues to Lorentz Force Effects" Metals 10, no. 12: 1653. https://doi.org/10.3390/met10121653
APA StyleDeng, H., Dong, J., Boi, F., Saunders, T., Hu, C., & Grasso, S. (2020). Magnetic Field Generated during Electric Current-Assisted Sintering: From Health and Safety Issues to Lorentz Force Effects. Metals, 10(12), 1653. https://doi.org/10.3390/met10121653







