Variation of Grain Height Characteristics of Electroplated cBN Grinding-Wheel Active Surfaces Associated with Their Wear
Abstract
1. Introduction
2. Materials and Methods
2.1. Experiment
2.2. Examination of Surface Texture
- 35 parameters of texture joined to the SPIP 6.4.2 software library using own developed procedures (scripts):
- –
- –
- Smc(mr)—the height of surface (elevation value) for a bearing area value mr, for obtaining values from to with step (computed according to the ISO 25178-2:2012 standard [36]);
- –
- Smc(mr1_mr2)—average value of elevation between two bearing area values mr1 and mr2 (expressed with Formula (1)): Smc(0_5), Smc(0_10), Smc(0_15), Smc(0_20), Smc(0_30), Smc(0_40);where: —elevation values from within the range of bearing area (, ), n—the number of points from within the range of bearing area values (mr1,mr2);
- –
- dSmc(mr1_mr2)—relative average value of elevation between two bearing area values mr1 i mr2 (where ), assuming elevation value equal 0 on the level associated with Smc(mr2) (expressed with Formula (2)): dSmc(0_5), dSmc(0_10), dSmc(0_15), dSmc(0_20), dSmc(0_30), dSmc(0_40).where: —elevation values from within the range of bearing area values (mr1,mr2), Smc(mr2)—the height associated with bearing area mr2, n—the number of points from within the range of bearing area values (mr1,mr2);
- the base area of the islands: mean value , standard deviation , the percentage of islands in the entire area of analysis ;
- the volume of the islands V: sum value , mean value , standard deviation ;
- the maximum height of the island : average value for all islands , standard deviation value of all islands ;
- the average altitude of the island : average value for all islands , standard deviation value of all islands ;
- equivalent diameter of the islands (diameter of a circle with the same surface area as the island): average value , standard deviation ;
- the largest Ferret diameter of the islands : mean value , standard deviation ;
- the length of the islands L defined in [45]: mean value , standard deviation ;
- the width of the islands B defined in [45]: mean value , standard deviation ;
- the circumference of the islands P: mean value , standard deviation ;
- the distance to the nearest island : mean value , standard deviation ;
- the number of islands Lw.
3. Results and Discussion
3.1. Forms of Grinding Wheel as Wear
- grain crushing,
- grain grinding,
- breaking grains from the binder.
3.2. The Selection of Parameters Sensitive to Wear of Grinding-Wheel AS
- Fisher testem (F test),
- Greenhouse–Geisser test (G-G test).
3.3. Model Relations Concerning Wear Depending on Adjustable Process Parameters
- 4 main linear effects: , , and ;
- 3 effects, related to squares of variables: , and ;
- 2 interaction effects: and .
- grinding speed decreased,
- grinding depth increased,
- feed increased,
- specific material loss increased.
4. Conclusions
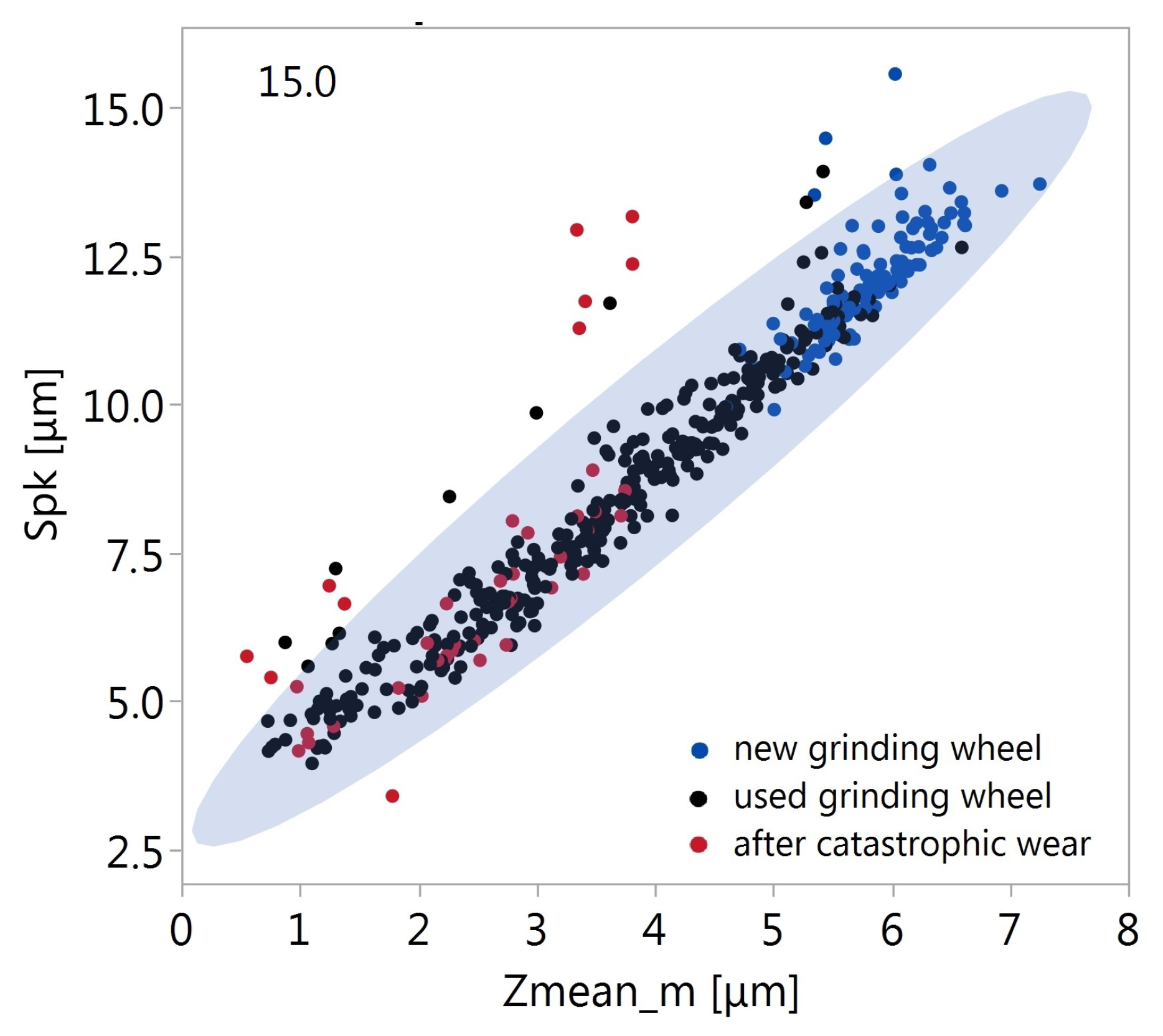
- In the conducted tests, the highest sensitivity to changes in grinding-wheel AS caused by wear was shown by the average value of the mean island heights Zmean_m (Table 3).
- This decrease in Zmean_m and Spk was related to the loss of abrasive resulting from various types of wear processes. In the presented studies, the above-mentioned parameters changed mainly due to grain breaking and, to a lesser extent, due to tearing them out of the binder (Section 3.1).
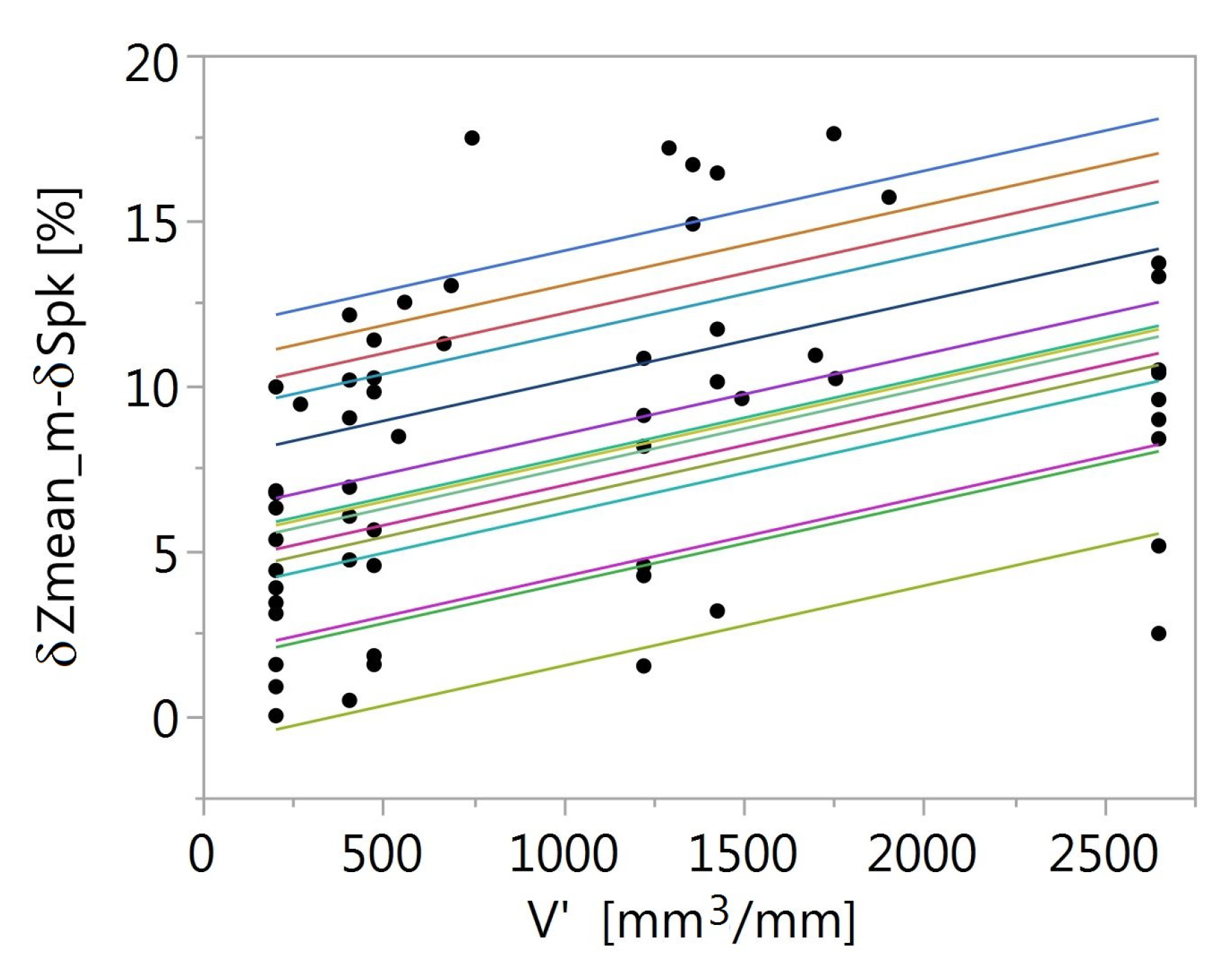
- As wheel wear increased, the Spk parameter, compared to Zmean_m, became less susceptible to grinding-wheel AS changes (Figure 7). The analysis of grinding-wheel AS state based on Spk with high wear is therefore more error-prone than would be the case with the value of the parameter Zmean_m.
- The Zmean_m parameter turned out to be a better measure of wear than Spk (Table 4), especially in the case of large sticking areas (Section 3.2, p. 11).
- Without taking into account the grinding wheel on which very large areas of sticking were observed, the average relative change Zmean_m on a given grinding wheel was almost 11% greater than the change in parameter Spk (Section 3.2, p. 11).
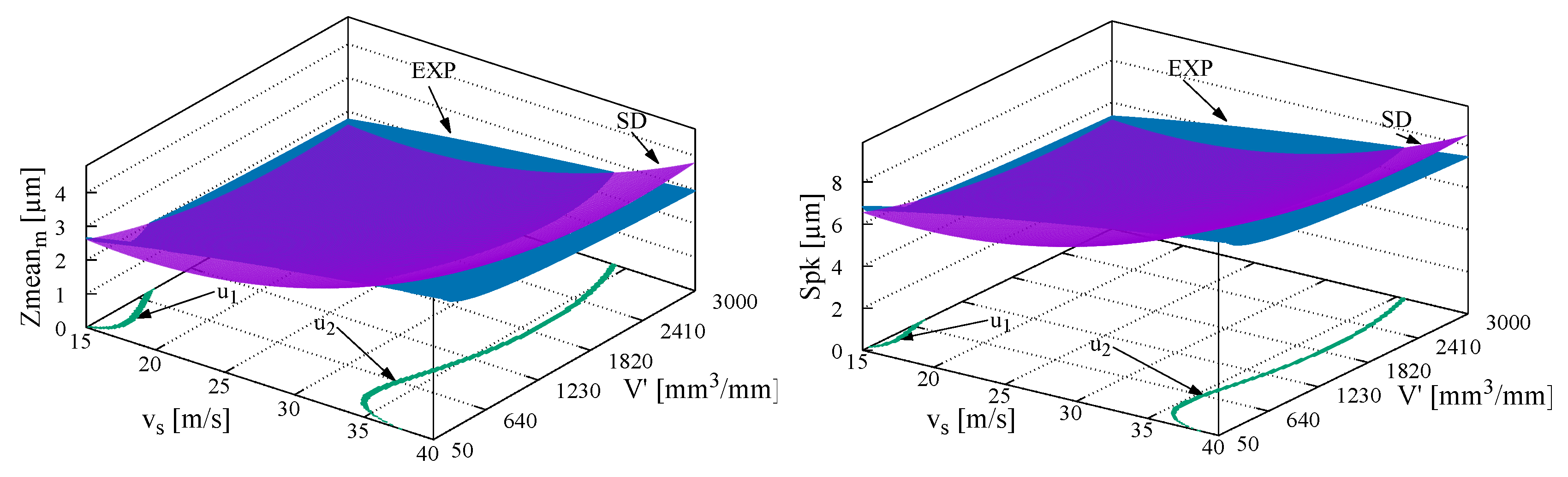
- The developed polynomial models of the response surface linking Zmean_m and Spk with the process parameters and the specific material loss were very well suited to the empirical data ( and 0.94).
- The developed polynomial models linking textitZmean_m and Spk with the process parameters and the specific material loss were well suited to the empirical data ( and 0.70).
- The tendencies of the influence of the adjustable process parameters on the grinding-wheel wear predicted by the models can be explained in the context of physics of the grinding process. They are consistent with the general grinding theory. Reducing and increasing and lead to a greater load operating on the wheel. In turn, the bigger forces acting on the abrasive grains contribute to their faster wear (Section 3.3).
- The effect of the specific material loss on the parameters Zmean_sr and Spk is greater for its small values. This effect results from the greater wear intensity in the initial phase of the grinding wheel’s work (Figure 8).
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AS | Active surface |
| EXP | Exponential |
| SD | Second-degree |
| SLGW | Single-layer grinding wheel |
References
- Bhaduri, D.; Chattopadhyay, A. Study on the role of PVD TiN coating in improving the performance of electroplated monolayer superabrasive wheel. Surf. Coat. Technol. 2010, 205, 658–667. [Google Scholar] [CrossRef]
- Upadhyaya, R.; Fiecoat, J. Factors Affecting Grinding Performance with Electroplated CBN Wheels. CIRP Ann. Manuf. Technol. 2007, 56, 339–342. [Google Scholar] [CrossRef]
- You, H.Y.; Ye, P.Q.; Song, W.J.; Deng, X.Y. Design and application of CBN shape grinding wheel for gears. Int. J. Mach. Tools Manuf. 2003, 43, 1269–1277. [Google Scholar] [CrossRef]
- Jackson, M.J. A review of the design of grinding wheels operating at excessive speeds. Int. J. Adv. Manuf. Technol. 2018, 94, 3979–4010. [Google Scholar] [CrossRef]
- Tawakoli, T.; Rabiey, M.; Wegener, K. The Effect of Special Structured Electroplated CBN Wheel in Dry Grinding of 100Cr6. Adv. Mater. Res. 2009, 76, 119–124. [Google Scholar] [CrossRef]
- Choudhary, A.; Naskar, A.; Paul, S. Effect of minimum quantity lubrication on surface integrity in high-speed grinding of sintered alumina using single layer diamond grinding wheel. Ceram. Int. 2018, 44, 17013–17021. [Google Scholar] [CrossRef]
- Lv, M.; Zhang, M.D.; Zhao, H. The Deformation Analysis on Tooth Profiles with Electroplated CBN Hard Gear-Honing-Tools. Adv. Mater. Res. 2012, 426, 159–162. [Google Scholar] [CrossRef]
- Kohler, J.; Schindler, A.; Woiwode, S. Continuous generating grinding. Tooth root machining and use of CBN-tools. CIRP Ann. Manuf. Technol. 2012, 61, 291–294. [Google Scholar] [CrossRef]
- Guo, C.; Ranganath, S.; McIntosh, D.; Elfizy, A. Virtual high performance grinding with CBN wheels. CIRP Ann. Manuf. Technol. 2008, 57, 325–328. [Google Scholar] [CrossRef]
- Xun, L.; Fanjun, M.; Wei, C.; Shuang, M. The CNC grinding of integrated impeller with electroplated CBN wheel. Int. J. Adv. Manuf. Technol. 2015, 79, 1353–1361. [Google Scholar] [CrossRef]
- Zhao, Z.; Qian, N.; Ding, W.; Wang, Y.; Fu, Y. Profile grinding of DZ125 nickel-based superalloy: Grinding heat, temperature field, and surface quality. J. Manuf. Process. 2020, 57, 10–22. [Google Scholar] [CrossRef]
- Xun, L.; Fanjun, M.; Shuang, M. Surface integrity of {GH4169} affected by cantilever finish grinding and the application in aero-engine blades. Chin. J. Aeronaut. 2015, 28, 1539–1545. [Google Scholar] [CrossRef]
- Guo, C.; Shi, Z.; Attia, H.; McIntosh, D. Power and Wheel Wear for Grinding Nickel Alloy with Plated CBN Wheels. CIRP Ann. Manuf. Technol. 2007, 56, 343–346. [Google Scholar] [CrossRef]
- Aspinwall, D.; Soo, S.; Curtis, D.; Mantle, A. Profiled Superabrasive Grinding Wheels for the Machining of a Nickel Based Superalloy. CIRP Ann. Manuf. Technol. 2007, 56, 335–338. [Google Scholar] [CrossRef]
- Caggiano, A.; Teti, R. CBN Grinding Performance Improvement in Aircraft Engine Components Manufacture. Procedia CIRP 2013, 9, 109–114. [Google Scholar] [CrossRef]
- Gift, F.; Misiolek, W. Fluid Performance Study for Groove Grinding a Nickel-Based Superalloy Using Electroplated Cubic Boron Nitride (CBN) Grinding Wheels. J. Manuf. Sci. Eng. 2004, 126, 451–458. [Google Scholar] [CrossRef]
- Zhao, Z.; Fu, Y.; Xu, J.; Zhang, Z.; Liu, Z.; He, J. An investigation on high-efficiency profile grinding of directional solidified nickel-based superalloys DZ125 with electroplated CBN wheel. Int. J. Adv. Manuf. Technol. 2016, 83, 1–11. [Google Scholar] [CrossRef]
- Tian, Y.B.; Zhong, Z.W.; Rawat, R. Comparative study on grinding of thin-walled and honeycomb-structured components with two CBN wheels. Int. J. Adv. Manuf. Technol. 2015, 81, 1097–1108. [Google Scholar] [CrossRef]
- Ding, W.; Xu, J.; Chen, Z.; Su, H.; Fu, Y. Grain wear of brazed polycrystalline CBN abrasive tools during constant-force grinding Ti–6Al–4V alloy. Int. J. Adv. Manuf. Technol. 2011, 52, 969–976. [Google Scholar] [CrossRef]
- Zhang, F.L.; Zhou, Y.M.; Guo, C.W.; Mao, J.B.; Huang, H.P. Performance of Brazed Diamond Tool for Machining Dental Ceramic. Adv. Mater. Res. 2014, 1027, 84–87. [Google Scholar] [CrossRef]
- Upadhyaya, R.P.; Malkin, S. Thermal Aspects of Grinding With Electroplated CBN Wheels. J. Manuf. Sci. Eng. 2004, 126, 107–114. [Google Scholar] [CrossRef]
- Shi, Z.; Malkin, S. Wear of Electroplated CBN Grinding Wheels. J. Manuf. Sci. Eng. 2005, 128, 110–118. [Google Scholar] [CrossRef]
- Shi, Z.; Malkin, S. An Investigation of Grinding with Electroplated CBN Wheels. CIRP Ann. Manuf. Technol. 2003, 52, 267–270. [Google Scholar] [CrossRef]
- Ghosh, A.; Chattopadhyay, A. Performance enhancement of single-layer miniature cBN wheels using CFUBMS-deposited TiN coating. Int. J. Mach. Tools Manuf. 2007, 47, 1799–1806. [Google Scholar] [CrossRef]
- Bhaduri, D.; Chattopadhyay, A. Effect of Pulsed DC CFUBM Sputtered TiN Coating on Performance of Nickel Electroplated Monolayer cBN Wheel in Grinding Steel. Surf. Coatings Technol. 2010, 204, 3818–3832. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Butler, D.L. Correlation of grinding wheel topography and grinding performance: A study from a viewpoint of three-dimensional surface characterisation. J. Mater. Process. Technol. 2008, 208, 14–23. [Google Scholar] [CrossRef]
- Blunt, L.; Ebdon, S. The application of three-dimensional surface measurement techniques to characterizing grinding wheel topography. Int. J. Mach. Tools Manuf. 1996, 36, 1207–1226. [Google Scholar] [CrossRef]
- Butler, D.; Blunt, L.; See, B.; Webster, J.; Stout, K. The characterisation of grinding wheels using 3D surface measurement techniques. J. Mater. Process. Technol. 2002, 127, 234–237. [Google Scholar] [CrossRef]
- Kapłonek, W.; Nadolny, K. Skaterometryczna ocena ściernic po procesie szlifowania walcowych powierzchni wewnętrznych materiałów trudnoobrabialnych. In XXXIV Naukowa Szkoła Obróbki Ściernej; Pismo PG: Gdansk, Poland, 2011; pp. 39–52. [Google Scholar]
- Jamshidi, H.; Gurtan, M.; Budak, E. Identification of active number of grits and its effects on mechanics and dynamics of abrasive processes. J. Mater. Process. Technol. 2019, 273, 116239. [Google Scholar] [CrossRef]
- Kang, M.; Zhang, L.; Tang, W. Study on three-dimensional topography modeling of the grinding wheel with image processing techniques. Int. J. Mech. Sci. 2020, 167, 105241. [Google Scholar] [CrossRef]
- Li, P.; Jin, T.; Xiao, H.; Chen, Z.; Qu, M.; Dai, H.; Chen, S. Topographical characterization and wear behavior of diamond wheel at different processing stages in grinding of N-BK7 optical glass. Tribol. Int. 2020, 151, 106453. [Google Scholar] [CrossRef]
- Setti, D.; Kirsch, B.; Aurich, J.C. Characterization of micro grinding tools using optical profilometry. Opt. Lasers Eng. 2019, 121, 150–155. [Google Scholar] [CrossRef]
- Kacalak, W.; Tandecka, K. A method and new parameters for assessing the active surface topography of diamond abrasive films. J. Mach. Eng. 2016, 16, 95–108. [Google Scholar]
- Zhao, Q.; Guo, B. Ultra-precision grinding of optical glasses using mono-layer nickel electroplated coarse-grained diamond wheels. Part 1: {ELID} assisted precision conditioning of grinding wheels. Precis. Eng. 2015, 39, 56–66. [Google Scholar] [CrossRef]
- ISO 25178-2:2012 Geometrical Product Specifications (GPS). Surface Texture: Areal–Part 2: Terms, Definitions and Surface Texture Parameters; International Organization for Standardization: Geneva, Switzerland, 2012. [Google Scholar]
- ASME B46:1 Surface Texture. Surface Roughness, Waviness, and Lay; The American Society of Mechanical Engineers: New York City, NY, USA, 2019. [Google Scholar]
- Velazquez-Hernandez, R.; Melnikov, A.; Mandelis, A.; Sivagurunathan, K.; Rodriguez-Garcia, M.E.; Garcia, J. Non-destructive measurements of large case depths in hardened steels using the thermal-wave radar. NDT E Int. 2012, 45, 16–21. [Google Scholar] [CrossRef]
- Dychton, K.; Kocurek, P.; Rokicki, P.; Wierzba, B.; Drajewicz, M.; Sieniawski, J. Microstructure and Residual Stress in AMS 6308 Steel after Vacuum Carburizing and Gas Quenching. Acta Phys. Pol. A 2016, 130, 953–955. [Google Scholar] [CrossRef]
- Rokicki, P.; Dychton, K.; Nownotnik, A.; Goral, M.; Drajewicz, M.; Sieniawski, J.; Zagula-Yavorska, M. Heat treatment process effect on carburized layer of aircraft engine heavily-loaded steel components. Sustain. Ind. Process. Summit SIPS Compos. Ceram.-Quasi-Crystals, Nanomater. Coatings 2014, 5, 543–550. [Google Scholar]
- JMP 12 Design of Experiments Guide; SAS Institute: Cary, NC, USA, 2015.
- Helmli, F. Focus Variation Instruments. In Optical Measurement of Surface Topography; Leach, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 131–166. [Google Scholar] [CrossRef]
- Stout, K.J.; Sullivan, P.J.; Dong, W.P.; Mainsah, E.; Luo, N.; Mathia, T.; Zahouani, H. The Development of Methods for the Characterization of Roughness in Three Dimensions; Butterworth-Heinemann: Oxford, UK, 1994. [Google Scholar]
- Bazan, A.; Kawalec, A. Methods of grain separation from single-layer grinding wheel topography. Mechanik 2018, 91, 926–928. [Google Scholar] [CrossRef]
- Jorgensen, J. Scanning Probe Image Processor SPIP Version 6. User’s and Reference Guide; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2012. [Google Scholar]
- Francuz, P.; Mackiewicz, R. Liczby Nie Wiedzą, Skąd Pochodzą. Przewodnik Po Metodologii i Statystyce Nie Tylko Dla Psychologów; Wydawnictwo KUL: Lublin, Poland, 2007. [Google Scholar]
- Kot, S.M.; Jakubowski, J.; Sokołowski, A. Statystyka; Difin: Warsaw, Poland, 2011. [Google Scholar]
- Sobczyk, M. Statytstyka; Wydawnictwo Naukowe PWN: Warsaw, Poland, 2016. [Google Scholar]
- Nithin, M.T.; Dhanavathu, N.N.; Vijayaraghavan, L. Wear of Electroplated Super Abrasive CBN Wheel during Grinding of Inconel 718 Super Alloy. J. Manuf. Process. 2019, 43, 1–8. [Google Scholar]
- Hood, R.; Medina Aguirre, F.; Soriano Gonzalez, L.; Novovic, D.; Soo, S.L. Evaluation of superabrasive grinding points for the machining of hardened steel. CIRP Ann. 2019, 68, 329–332. [Google Scholar] [CrossRef]
- Myers, R. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Liu, Q.; Chen, X.; Wang, Y.; Gindy, N. Empirical modelling of grinding force based on multivariate analysis. J. Mater. Process. Technol. 2008, 203, 420–430. [Google Scholar] [CrossRef]
- Brinksmeier, E.; Tönshoff, H.K.; Czenkusch, C.; Heinzel, C. Modelling and optimization of grindingprocesses. J. Intell. Manuf. 1998, 9, 303–314. [Google Scholar] [CrossRef]
- Chatterjee, A.H.; Price, B. Regression Analysis by Example, 3rd ed.; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- McDonald, B. A Teaching Note on Cook’s Distance—A Guideline. Res. Lett. Inf. Math. Sci. 2002, 3, 122–128. [Google Scholar]
- Malkin, S.; Guo, C. Grinding Technology: Theory and Application of Machining with Abrasives; Industrial Press: New York, NY, USA, 2008. [Google Scholar]

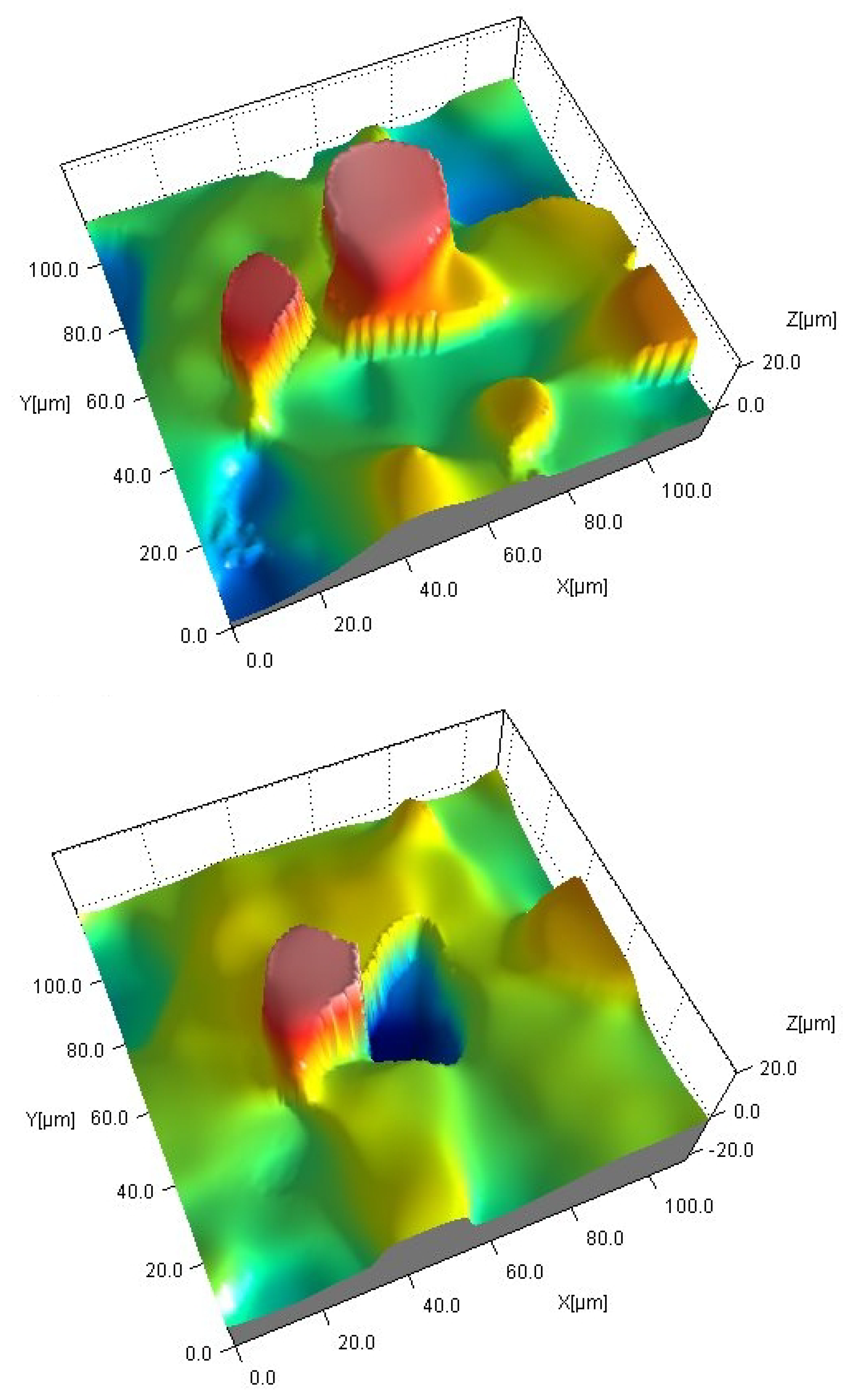

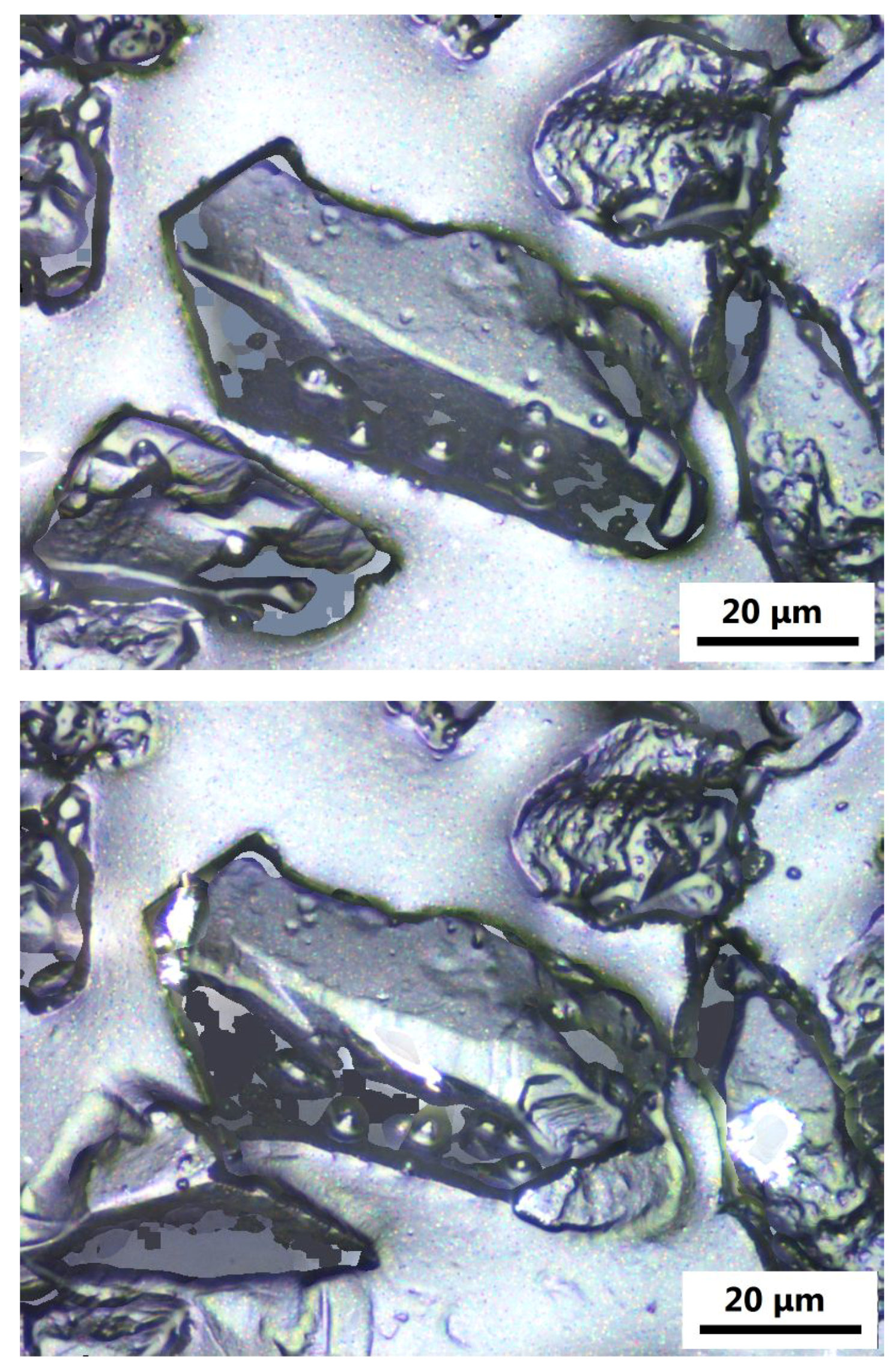
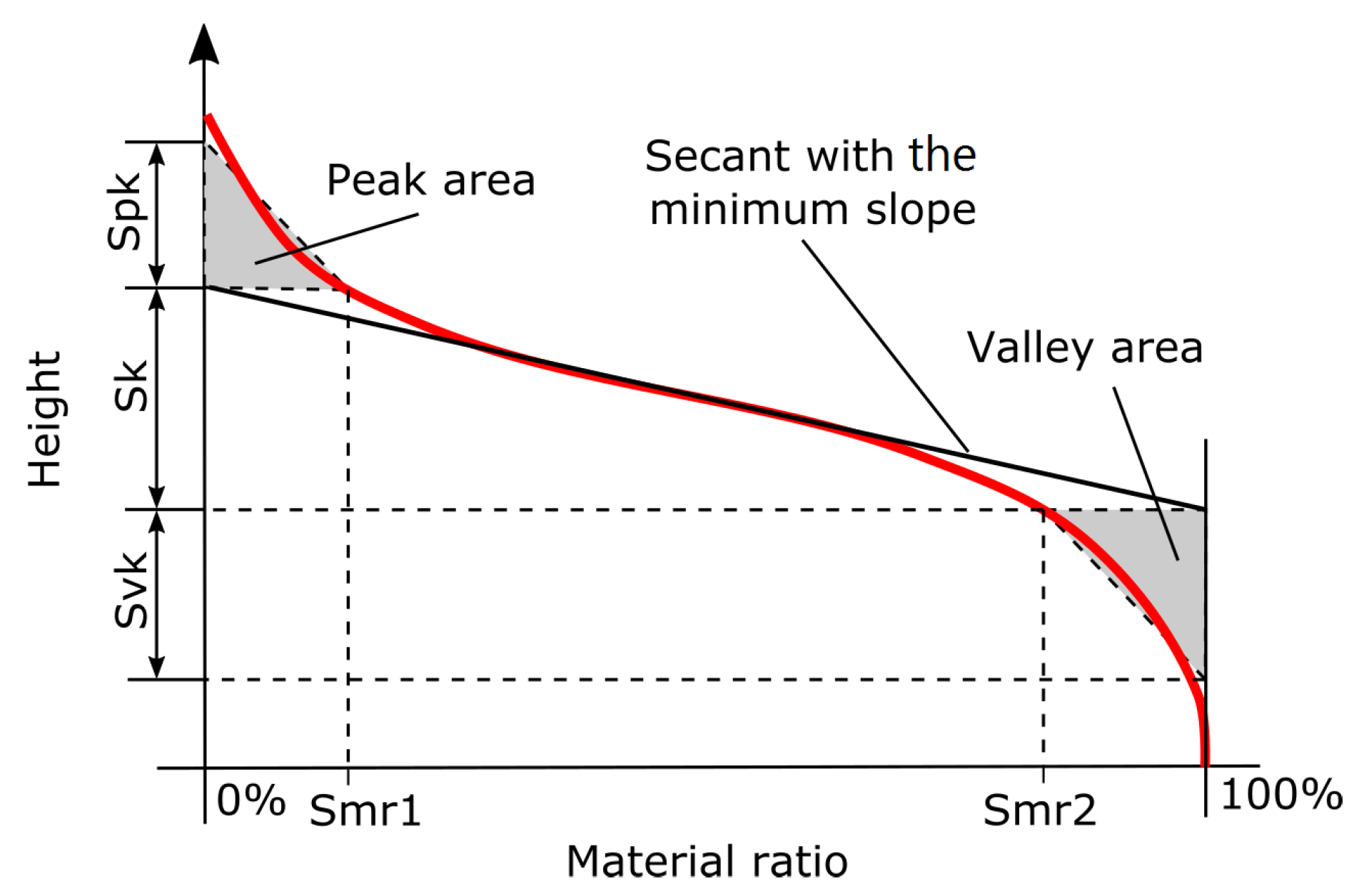
| Grinding conditions | |
|---|---|
| Grinder | Fortis firmy Michael Deckel |
| Type of process | plane grinding |
| Processing liquid | grinding oil |
| Grinding speed () | – |
| Feed speed | – |
| Grinding depth | – |
| Grinding wheel | |
| Shape | conical |
| Cone angle | |
| Max. diameter d | 100 mm |
| Binder | electroplated (Ni) |
| Abrasive | cBN |
| Grain number | B35 |
| Workpiece | |
| Material | Pyrowear 53 |
| Treatment | thermo-chemical treatment |
| Hardness | 81 HRA |
| Material of replicas | RepliSet-F5 by Struers |
| Resolution of replicas | |
| Measurement microscope | InfiniteFocus G4 by Alicona |
| Lens | |
| Measurement area | 2.35 mm × 2.59 mm |
| Vertical resolution | 5 |
| Horizontal resolution | 3.91 |
| Pixel size | 0.44 × 0.44 |
| Parameter AS | Mean of Ranks | Parameter AS | Mean of Ranks | Parameter AS | Mean of Ranks | |||
|---|---|---|---|---|---|---|---|---|
| Zmean_m | (−) | 1.5 | Sa | (−) | 36.5 | (−) | 62 | |
| (−) | 1.5 | Zmean_sd(p) | (+) | 37 | (−) | 62.5 | ||
| (−) | 3 | Svi | (+) | 37.5 | (−) | 63 | ||
| Vsr | (−) | 4 | Sq | (−) | 38 | Ssc | (−) | 65 |
| dSmc(0_30) | (−) | 7.5 | Smc(_40) | (+) | 39 | Sfd | (−) | 67.5 |
| Smc(0_5) | (−) | 7.5 | Smr1 | (−) | 40 | Bsr | (−) | 68.5 |
| Smc(_60) | (+) | 8.5 | Sk | (−) | 40.5 | Vsr(p) | (+) | 69 |
| dSmc(0_20) | (−) | 9 | Vsum | (−) | 41 | Asr(p) | (−) | 69 |
| dSmc(0_15) | (−) | 10 | Smc(_15) | (−) | 41.5 | Smc(_25) | (−) | 72 |
| Smc(_65) | (+) | 10 | Zmax_sd | (−) | 43.5 | NDsr | (+) | 73 |
| Smc(_55) | (+) | 10.5 | Sdc5_10 | (−) | 44 | Bsr(p) | (−) | 73 |
| dSmc(0_40) | (−) | 11.5 | Smc(_85) | (+) | 44.5 | Asd(p) | (−) | 74 |
| Smc(0_10) | (−) | 13 | Zmax_sd(p) | (+) | 45 | dDsr(p) | (−) | 74.5 |
| Smc(_70) | (+) | 15.5 | Zmean_m(p) | (+) | 45 | S10z | (−) | 75 |
| Vsd | (−) | 15.5 | Zmax_m(p) | (+) | 46 | Str37 | (−) | 75.5 |
| Smc(_50) | (+) | 16.5 | Sp | (−) | 46.5 | Sz_tph | (−) | 76 |
| Spk | (−) | 16.5 | Vmc | (−) | 47.5 | St | (−) | 77 |
| Smc(0_15) | (−) | 17 | Sdq6 | (−) | 48 | Vvv | (+) | 77 |
| dSmc(0_10) | (−) | 20 | Sdq | (−) | 49.5 | Zmean_m(s) | (−) | 78 |
| Smc(0_20) | (−) | 20.5 | S3A | (−) | 50.5 | dDsr | (−) | 79 |
| Vmp | (−) | 21 | Sdr | (−) | 51.5 | Vsum(p) | (+) | 81 |
| Smc(_75) | (+) | 22.5 | Smc(_20) | (−) | 52.5 | A%(p) | (−) | 81.5 |
| dSmc(0_5) | (−) | 23 | Sci | (−) | 54 | NDsd | (+) | 82 |
| Sdc10_50 | (−) | 25 | Smr2 | (−) | 54 | Sds | (−) | 84.5 |
| Smc(0_30) | (−) | 25.5 | Sdc0_5 | (−) | 56 | Str20 | (−) | 85 |
| Smc(_45) | (+) | 26.5 | Smc(_90) | (+) | 57 | dFsr | (−) | 87 |
| Vvc | (−) | 27 | Sbi | (+) | 57 | Asr | (−) | 88 |
| Smc(_5) | (−) | 28.5 | Zmax_(s) | (−) | 58 | Lsr | (−) | 88.5 |
| Smc(0_40) | (−) | 29.5 | Svk | (+) | 58.5 | Sv | (+) | 90.5 |
| Ssk | (−) | 31.5 | Psd(p) | (−) | 59 | Smc(_95) | (+) | 92 |
| A% | (−) | 31.5 | Psr(p) | (−) | 59 | Zmax_sd(s) | (−) | 93 |
| Smc(_80) | (+) | 32.5 | dFsd(p) | (−) | 60 | Psr | (−) | 94 |
| Lw | (−) | 32.5 | Lsd(p) | (−) | 60.5 | Shw | (+) | 94.5 |
| Smc(_10) | (−) | 34.5 | Smc(_35) | (+) | 61 | Scl37 | (+) | 96 |
| Relative Change | Mean | Min | Max |
|---|---|---|---|
| Zmean_m [%] | 50.6 | 22.3 | 73.5 |
| Spk [%] | 39.7 | 19.8 | 56.4 |
| Zmean_mSpk [%] | 12.4 | 2.5 | 34.7 |
| Lp. | [m/s] | [m/min] | [m] | [mm/mm] |
|---|---|---|---|---|
| 1 | 20 | 7.50 | 20 | 5 |
| 2 | 20 | 4.25 | 20 | 58 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bazan, A.; Kawalec, A.; Rydzak, T.; Kubik, P. Variation of Grain Height Characteristics of Electroplated cBN Grinding-Wheel Active Surfaces Associated with Their Wear. Metals 2020, 10, 1479. https://doi.org/10.3390/met10111479
Bazan A, Kawalec A, Rydzak T, Kubik P. Variation of Grain Height Characteristics of Electroplated cBN Grinding-Wheel Active Surfaces Associated with Their Wear. Metals. 2020; 10(11):1479. https://doi.org/10.3390/met10111479
Chicago/Turabian StyleBazan, Anna, Andrzej Kawalec, Tomasz Rydzak, and Pawel Kubik. 2020. "Variation of Grain Height Characteristics of Electroplated cBN Grinding-Wheel Active Surfaces Associated with Their Wear" Metals 10, no. 11: 1479. https://doi.org/10.3390/met10111479
APA StyleBazan, A., Kawalec, A., Rydzak, T., & Kubik, P. (2020). Variation of Grain Height Characteristics of Electroplated cBN Grinding-Wheel Active Surfaces Associated with Their Wear. Metals, 10(11), 1479. https://doi.org/10.3390/met10111479





