Abstract
In this paper, the effects of a super-gravity field with multi-rotational speeds on the grain refinement and tensile properties of as-cast H13 steel were investigated systematically. The experimental results showed that compared to the single-rotational speed (conventional) super-gravity field, the as-cast grains of H13 steel can be significantly refined in a multi-rotational speed (speed increased in stages) super-gravity field. In the conventional super-gravity field, with the decrease in rotational radius, the secondary dendrite arm spacing (SDAS) and the prior austenite grain size (PAGS) increase, and the maximum values of SDAS and PAGS are 90 and 55 µm, respectively, while in multi-speed super-gravity fields, at the range of increasing rotational speeds, SDAS and PAGS decrease as the rotational radius decreases. In the three-rotational speed super-gravity field, the maximum values of SDAS and PAGS are 80 µm and 50 µm. In the five-rotational speed super-gravity field, the maximum values of SDAS and PAGS are reduced to 58 µm and 34 µm. Accordingly, both the tensile strength and the plasticity are enhanced when increasing the number of rotational speeds in the super-gravity field, especially for the inner position of the super-gravity sample. The ultimate tensile strengths at outer, middle, and inner positions of H13 steel solidified in the conventional super-gravity field are 1445 MPa, 1378 MPa, and 1023 MPa, corresponding to elongations of 2%, 1.5%, and 0.5%, respectively, while in the five-rotational speed super-gravity field, they are 1408, 1443, and 1453 MPa, corresponding to elongations of 1.8%, 3.9%, and 2.2%, respectively. The mechanism for the grain refinement is that multi-speed super-gravity can reduce the critical nucleation work of austenite and the tangential force produced by increasing the rotational speed break dendrites at the solidification front, refining the solidified structure.
1. Introduction
H13 hot work die steel is widely used in extrusion, die casting, hot forging and other industries due to its high strength, high hardness, high toughness and temper softening [1,2]. Because of the ripening phenomenon during solidification, the solidified structure of H13 steel coarsens with the increase in time [3]. The coarsening solidified structure leads to casting defects such as segregation, shrinkage and microcracking, which severely degrade the performance of the product [4,5]. A lot of studies were performed on the method of refining the solidified structure [6,7,8,9,10,11]. The traditional refinement methods include optimizing melting, changing casting process and adding a nucleating agent [6].
There are also new refinement methods such as applying an electric field [7], a magnetic field [8], an ultrasonic field [9], and a super-gravity field obtained by rotating equipment [10]. In particular, the refinement method of applying a super-gravity field has the advantages of low cost, low pollution and strong operability [10]. For the study of the super-gravity solidified structure, most scholars focus on the influence of casting temperature [10], the effective solidification stage of super-gravity [11], casting material [12,13,14], and super-gravity coefficients [11,12]. The definition of the super-gravity coefficient [11,12] is given in Equation (1).
where G is the gravity coefficient, ω is the angular speed (rad/s), N is the rotational speed (r/min), R is the distance between the centrifugal axis and the observation position (i.e., rotational radius, m), and g is the normal gravitational acceleration (9.8 m/s2).
Many studies have shown that super-gravity can refine the solidification structure [12,13,14]. For example, Zhao et al. [12] have investigated the influence of the super-gravity field on aluminum grain refining, and concluded that the grain size decreased rapidly as the gravity coefficient increases from 1 to 250, and then remained nearly unchanged from 250 to 1000. Unfortunately, for the super-gravity samples, the refinement of the solidified structure at the upper region is worse than that at the lower one. This phenomenon has appeared in the super-gravity samples of many materials, such as Al-Cu alloys [13] and Cu-Sn alloys [14]. In order to further refine the solidified structure at the upper region in the super-gravity sample, many researchers [12,13,14,15,16] have discussed the refinement mechanisms of different alloys in the super-gravity field, such as the ”heavy crystal rain” [12], the increase in the cooling rate of the melt [15], and the smaller critical nucleation work [16]. Based on the above refinement mechanisms, researchers proposed the improvement measures of increasing the super-gravity coefficient at the effective solidification stage of super-gravity [13,14,16]. Compared with the sample before improvement, the solidified structure has a certain degree of refinement, but the solidified structure at the upper region accounts for a quarter of the entire sample, which still cannot be effectively refined [13,14,16].
It is worth noting that due that the fact that the current super-gravity technology was limited by the experimental apparatus, the super-gravity ingots in the current literature are all less than 200 g. If the super-gravity refinement method in the literature is applied to industrial-grade steel ingots above 30 kg, the refining effect at the upper region of the ingot will be even worse. In addition, low-melting temperature metals, such as Al-Cu alloys and Cu-Sn alloys, were studied in early research, and higher-melting temperature metals (e.g., steel) were not payed attention. Therefore, it is necessary to explore a new super-gravity method suitable for refining the solidified structure of the entire industrial steel-grades ingot. In the present article, the effect of super-gravity on the solidified structure and tensile properties of H13 tool steel was investigated by industrial experiments under the conventional super-gravity field and the super-gravity field with multiple rotational speeds (speed is increased in stages), defined as “the multi-rotational speed super-gravity field”.
2. Experimental Procedures
The contents of the main elements of the used H13 steel were measured by a spark-optical emission spectrometer. The metal phases were analyzed by an oxygen and nitrogen hydrogen analyzer (TCH600, LECO, San Jose, CA, USA) for their oxygen and nitrogen contents. The chemical composition of the sample is listed in Table 1. The electrode of H13 was placed in a 50 kg electroslag crucible furnace to obtain molten steel. The slag in the electroslag crucible was a mixture of 60 wt% CaF2, 20 wt% CaO and 20 wt% Al2O3 to prevent oxidation of molten steel as much as possible during the experiment.

Table 1.
Chemical composition of the H13 tool steel (wt. %).
The super-gravity device is shown in Figure 1a. The inner size of the cast iron mold is approximately D × H = 450 mm × 90 mm. The super-gravity experiment was performed at room temperature (25 °C). The molten metal (35 kg) and slag (7 kg) were poured into a rotating mold with a rotational speed of 500 r/min. At this time, the molten steel and molten slag temperature were 1550 ± 20 and 1750 ± 20 °C, respectively. The temperatures were measured by an infrared thermometer (IR-HOH, Beijing Duhelichuang Technology Co. Ltd., Beijing, China). The mixtures of steel and slag was completely poured into the mold within 10 s, and the entry sequence is a small amount of slag, the mixture of slag and molten steel and the remaining slag in the ladle. It is worth noting that due to the density difference between molten slag and molten steel, the small amount of molten slag prior to the molten steel enters into mold, and the molten slag that enters first will quickly form a slag skin to prevent adhesion of the casting and the mold. This is because the density of the molten slag is lower than that of molten steel, and the temperature of the steel slag is higher than that of molten steel. Under the action of centrifugal force, the remaining slag in the ladle is poured into the mold, which makes the center temperature of mold higher than the external temperature. Therefore, it is ensured that the solidification direction of the molten steel is from the outside to the center of the centrifuge.
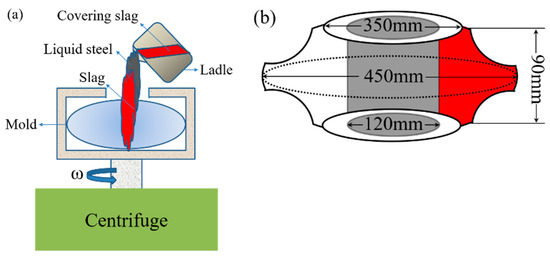
Figure 1.
(a) Schematic diagram of super-gravity apparatus; (b) schematic diagram of super-gravity casting.
The speed parameters and sample numbers of different super-gravity experiments are shown in Table 2. Sample A is solidified in a traditional super-gravity field, and Samples B and C are solidified in multi-rotational speed super-gravity fields.

Table 2.
Rotational speed(r∙min−1) and time (min) of each stage during super-gravity solidification.
For the samples under super-gravity fields, the cooling rate for all the samples was ranged from 3 °C/s to 5 °C/s. The apparatus was kept under operation until the sample was completely solidified, after which the super-gravity apparatus was turned off. Due to the fact that the high carbon and chromium contents in H13 steel increase the tendency of cold cracking [17], the sample was taken out of the mold and immediately covered with asbestos to avoid cracks. The macrostructures of the super-gravity ingots were obtained from the vertical section of samples (as shown by the red cross section in Figure 1b). All surfaces were mechanically flattened and polished, followed by chemical etching with a solution of HCl (150 mL) + H2O (150 mL). The samples were cut from the observed area, as shown in Figure 3a. These samples were mechanically flattened, polished, and chemically etched in a solution of HNO3 (4 mL) + absolute ethanol (96 mL) for 30 s to reveal the dendritic structures and the prior austenite grains. The secondary dendrite arm spacing (SDAS) and the average diameter of the austenite grains were measured based on multiple optical micrographs (OM; Leica-DM4M) using the linear intercept method [18].
In order to study the effects of the super-gravity field on tensile properties of H13 steel, tensile tests were performed using a computerized universal testing machine (CMT4105) with the standard of GB/T228.1-2010 [19] at room temperature. Figure 2a shows the testing specimen with 1.2 mm thickness [13]. The sampling positions of tensile samples in Samples A, B, and C are shown in Figure 3b, which are defined as the outer, middle and inner positions. Three parallel test specimens at the same position were taken from each sample, and the distance between the two adjacent positions in each sample is 45 mm.
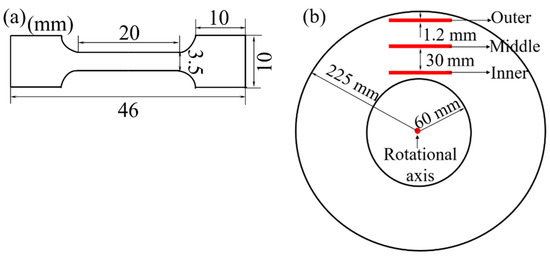
Figure 2.
Schematic diagram of the tested specimen: (a) sample size; (b) sampling positions.

Figure 3.
Macro-structure of the as-cast H13 steel samples obtained in conventional super-gravity and composite super-gravity fields: (a) observed area of (b); (b) macro-structure at different positions in the observation area of Samples A, B and C.
3. Results and Discussion
3.1. Macro- and Micro-Structures of As-Cast H13 Samples in Super-Gravity Fields
The macro-structure of the as-cast H13 steel samples obtained with different super-gravity fields is shown in Figure 3. In order to study the influence of different super-gravity fields on the solidified structure of the castings at different positions, the observation area of the solidified structure is selected as shown in Figure 3a. The macro-structure in the observation area for Samples A, B, and C is shown in Figure 3b. For Sample A, there are orderly arranged columnar crystals at Position 1, an obvious hollow at Position 2, and center porosity between Position 1 and Position 2. Compared with Sample A, there are no obvious hollows and center porosities for Samples B and C. The possible reason is that during the solidification of Samples B and C, the number of rotational speeds in the super-gravity field is increased, which makes the forced feeding effect of the centrifugal force stronger. In addition, the macro-structures at Position 1 for Samples B and C are finer than that for Sample A. At Position 2, there are coarse columnar crystals for Sample B, and small columnar crystals for Sample C, which could result from the change in the rotational speeds in the super-gravity field at the late solidification stage of Sample C.
Figure 4 shows the dendrite structures at different locations in the longitudinal section of the samples. It can be found from Figure 4 that the primary dendrite spacings and the secondary dendrite spacings of Sample A increase with the decrease in R. The crystals are so developed in dendritic morphology that an entire dendrite structure cannot be fully included in the picture at the position of R = 0.149 m. When the super-gravity field contains three rotational speeds (i.e., Sample B), both the primary and the secondary dendrite sizes decrease at the range of 0.149 m < R < 0.199 m compared with those of Sample A. When the number of rotational speeds in the super-gravity field is increased to five, the dendrite structure is further refined, especially for the range of 0.149 m < R < 0.209 m, illustrating that the increase in the number of rotational speeds can greatly refine the solidified structure of the as-cast H13 steel in super-gravity field.


Figure 4.
Dendrite structures at different locations in the longitudinal section of Samples A, B, and C. Notes: the blue arrow points to the primary dendrite; the yellow arrow points to the secondary dendrite.
According to the observation of the prior austenite grains at different positions for Samples A, B, and C, it can be found that in the super-gravity field with a constant rotational speed, the grain size of austenite increases with the decrease in R. When the number of rotational speeds increases during the solidification under the super-gravity field, the prior austenite grains decrease, especially for the range of R < 0.199 m. Figure 5 shows the typical prior austenite grains at R = 0.149 m of the as-cast H13 samples in the three super-gravity fields. As shown in Figure 5, in a picture at the magnification of 500×, there is more prior austenite grains in Sample B and C than in Sample A. On the whole, the prior austenite size decreases with the increasing number of rotational speeds in the super-gravity field.

Figure 5.
Prior austenite grains at R = 0.149 m in the longitudinal section of the samples. Notes: Due that the fact that the prior austenite grain boundaries eroded by enchant are not very clear in the micrograph, yellow curves were drawn on the prior austenite grain boundary by Photoshop software for clear observation; (a) Sample A: a small number of prior austenite grains; (b) Sample B: a large number of prior austenite grains; (c) Sample C: the number of prior austenite grains is the largest here.
In order to further explore the influence of the super-gravity field on the refinement of a solidified structure, Figure 6a,b summarize the average secondary dendrite arm spacing (SDAS) and the average austenite grain sizes of the samples obtained in super-gravity fields, respectively. Figure 6c shows the super-gravity coefficients at different positions in the three super-gravity fields. It can be seen that when in the gravity field with a constant rotational speed (i.e., Sample A), with the decrease in R, the super-gravity coefficient decreases, and SDAS and the average grain sizes increase. The minimum values of the secondary dendrite spacing and average grain size appear at R = 0.225 m, which are 40 and 27 μm, respectively, and the corresponding super-gravity coefficient is 62. When R decreases to 0.152 m, the coefficient of super-gravity decreases to 42, and SDAS and the average grain sizes reach their own maximum values, which are 92 and 55 μm, respectively. This illustrates that as the super-gravity coefficient increases, the SDAS and the average grain size decrease, which is consistent with the finding of Yang et al. When in super-gravity fields of G = 100, 300, and 600, the average grain sizes of the as-cast Cu-11 wt%Sn are 0.35, 0.173, and 0.074 μm, respectively [14].
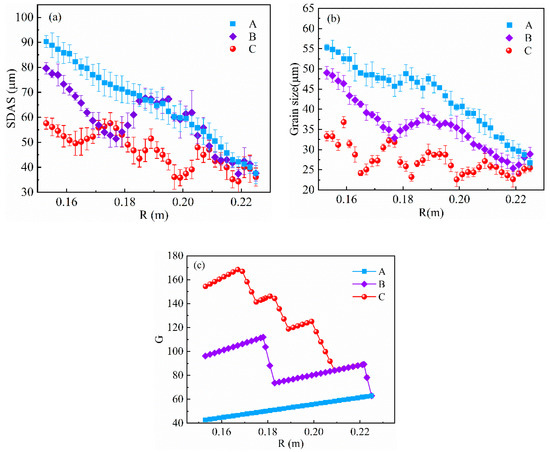
Figure 6.
(a) Secondary dendrite arm spacing (SDAS), (b) grain size, and (c) super-gravity coefficients of different samples solidified in the conventional super-gravity field and multi-speed super-gravity fields.
However, the relationship between the refinement of solidified structure and the super-gravity coefficient in Sample A is not is not fully applicable to Sample B and Sample C. When the rotational speed increases during the solidification in the super-gravity field, with the decrease in R, the secondary dendrite spacings and the austenite grain sizes decrease. For example, in Sample B, the secondary dendrite spacings and the grain sizes decreased from 68 and 39 μm at R = 0.184 m to 51 and 32 μm at R = 0.176 m. It can be found that from Figure 6, the maximum values of the secondary dendrite spacing and the grain sizes in Sample B are 85 and 49 μm at R = 0.152 m, and the minimums are 38 and 26 μm at R = 0.219 m. Similarly, when the number of rotational speeds in the super-gravity field is increased to five, compared with Samples A and B, the secondary dendrite arm spacings and grain sizes in Sample C are significantly decreased. In Sample C, the maximum values of the secondary dendrite spacing and the average grain size are decreased to 58 and 37 μm, respectively, which significantly refines the solidified structure of the entire sample. As a whole, compared with the traditional super-gravity field, the multi-rotational speed super-gravity field is more conducive to refine the solidified structure of as-cast H13 steel.
3.2. The Refinement Mechanism of the H13 Solidified Structure in the Super-Gravity Field
In Section 3.1, it can be found that in Samples B and C, the secondary dendrite spacings and the average grain sizes at multiple locations are the same, but the super-gravity coefficient is different. For example, in Sample C, the average grain size is 27 μm at the positions of R = 0.17, 0.18, 0.184, 0.196, and 0.21 m, and the corresponding super-gravity coefficients are 158, 143, 130, 122, and 80, respectively, which is inconsistent with the view of Yang et al. [13]. Therefore, the possible refining mechanisms for the solidified structure refinement of H13 steel in multi-rotational speed super-gravity fields were explored on the basis of the calculated solidification process via Thermo-Calc software (Thermo-Calc software AB, Pittsburgh, PA, USA) with the TCFE6 database, as shown in Figure 7.
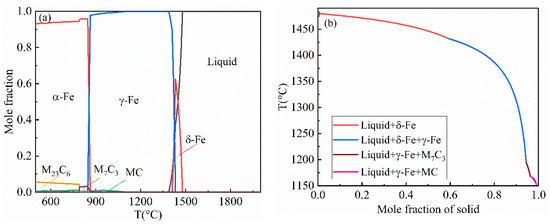
Figure 7.
(a) The phase assemblage diagram for the mole fraction of different equilibrium phases. (b) The phase assemblage diagram for the non-equilibrium phase of H13 steel during solidification Notes: δ-Fe is high-temperature ferrite; γ-Fe is austenite; α-Fe is ferrite; M23C6, M7C3, and MC are carbide types.
Figure 7a is the equilibrium phase diagram of H13 steel during solidification. It can be found that during the solidification of δ-Fe, it is first precipitated from the liquid phase at 1480 °C, and then γ-Fe appears in the liquid at 1425 °C. In fact, the actual solidification process of H13 steel is non-equilibrium. Figure 7b shows the non-equilibrium solidification of H13 steel. The phase of δ-Fe is produced in the temperature range of 1425–1475 °C, and the corresponding solid phase ratio range is 0–0.6. The phases of δ-Fe and γ-Fe coexist in the temperature range of 1200–1425 °C and the stage corresponding to the period that the solid fraction increases from 0.6 to 0.9. When the temperature is less than 1200 °C, δ-Fe disappears and carbides begin to precipitate, such as M7C3 and MC.
During the cooling process of molten steel, δ-Fe is produced prior to austenite. In general, γ-Fe preferentially nucleates at the grain boundaries of δ-Fe. The energy required for nucleation of γ-Fe is called as nucleation work, and its value in the super-gravity field can be estimated via Equation (2) [10].
where ΔG is the nucleation energy; ΔGV is the solid–liquid difference of Gibbs free energy per unit volume; Gg and Gb represent energy per volume exerted on the nucleus provided by normal gravity and super-gravity, respectively; σ is the solid–liquid interfacial tension; V is the volume of the solid; and A is the interfacial area.
To simplify the calculation, the following three assumptions are made in this work.
- The contact angle between the nucleation of austenite and the δ-ferrite grain boundary is 180°; the nucleation energy required for heterogeneous nucleation is equal to that for homogeneous nucleation [20].
- Body shrinkage rate ε, surface tension σ (N/m) and the change of chemical potential ΔFT are independent of super-gravity [10].
- The change in the chemical potential of the test material was replaced by a change in the Gibbs free energy of the pure iron from 1600 °C to 1500 °C (0.002575 J/m3) [21].
- Gg can be ignored under the super-gravity field.
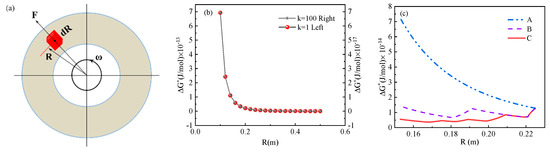
Figure 8.
(a) Schematic diagram of centrifugal force analysis; (b) effect of conversion factor (k = 1 and 100) on the relationship between critical nucleation work and the outer radius (c) ΔG* at different positions of Sample A, B, and C.
During the process of rotation, for the micro-volume element, the centrifugal force and the pressure generated by the radial direction are marked as Equations (4) and (5), respectively.
where m is the mass per unit volume (kg); ρ is the density of the liquid metal (kg/m3). By substituting Equation (4) into Equation (5), Equation (6) can be obtained [10].
The radial integral of p at R,
obtain
Substituting Equation (8) into Equation (3) can results in Equation (9) [10].
With the definition of , the critical nucleation radius under centrifugal pressure can be calculated by Equation (9) [10].
Substituting Equation (10) into Equation (9), critical nucleation work (ΔG*) under centrifugal pressure can result in Equation (11) [10].
The relationship between critical nucleation work (ΔG*) and the super-gravity coefficient can be expressed in Equation (12) [10].
where k, conversion factor; ε, body shrinkage rate: 0.95; ρ, a solid–liquid two-phase total density calculated by JmatPro 7.0 software (Thermotech, Hongkong, China): 7.003 kg/m3; ω, rotational angular speed, rad/s; R, the distance from observation position to centrifugal center (i.e., rotational radius), m; and R0, the inner radius, m.
In Ref. [10], the calculation method of the conversion factor was not mentioned. The effect of the conversion factor on the relationship between critical nucleation work and the outer radius was discussed. In Figure 8b, the abscissa represents the rotational radius, and the ordinates on the left and right sides represent the critical nucleation work at k = 1 and k = 100, respectively. At this time, the rotational speed is assumed to be 300 r/min. It can be found that the size of k value can change the value of ΔG*, but it has no influence on the variation trend of critical nucleation work with the rotational radius. Therefore, the value of k was defined as 1.
At the present rotational speed’s conditions for Samples A, B, and C, the ΔG* of Sample A, B, and C was, respectively, calculated by Equation (12), as shown in Figure 8c. Figure 8c shows that when R decreases from 0.225 m to 0.152 m, the value of ΔG* for Sample A increases from 1.5 × 10−14 J/mol to 7 × 10−14 J/mol, which means that as R decreases in the super-gravity field, the energy required for austenite nucleation increases, and the amount of austenite nucleated decreases. Compared with Sample A, the maximum value of ΔG* for Sample B evidently decreases, which makes austenite easy to nucleate. It also can be found that as the value of R decreases, ΔG* decreases at the range of increasing rotational speed, which can be also proved in the variations trend of ΔG* with R in Sample C. In short, during the process of solidification in the super-gravity field, increasing the number of rotational speeds is beneficial to refine the austenite grains.
In general, γ-Fe easily nucleates on the grain boundaries of δ-Fe during the normal gravity solidification process of steel. The “free” γ dendrites are coarsened and polymerized with the surrounding δ-Fe. Under the same cooling conditions, the degree of polymerization of γ dendrites at the grain boundaries of δ-Fe is significantly higher than that inside the δ-Fe grains. During the cooling process, the dendrites coarsen and compete for growth, thereby forming the dendritic structure. In the super-gravity field, the preferentially precipitated solid phase (dendrite) will undergo centrifugation or centripetal motion, and the dendrite can be broken owing to the difference in density between the solid phase and liquid phase. Because of the fracture of dendrites, known as “fragments”, the crystal nuclei created in the melt cause refinement of the solidified structure during casting. This phenomenon is regarded as the “heavy crystal rain” mechanism [7,8,11].
According to Stokes’ law [23,24], the super-gravity coefficient is positively correlated with the moving speed of the solid phase particles, as shown in Equation (13).
where d is the equivalent diameter of the fragment (m); ρl and ρp are the densities of the liquid and fragment (kg/m3); η is the dynamic viscosity of the liquid (Pa·s); and s is the displacement of the fragment (m).
When the fragment’s movement reaches equilibrium, the right side of Equation (13) equals zero, and the fragment’s moving speed Vr can be expressed as
According to Equation (14), the fragment’s moving speed in equilibrium is proportional to the square of its diameter, gravity coefficient and the difference value of the solid–liquid two-phase density. The moving speed of dendrite fragments represents the ability of super-gravity to break dendrites, that is, the number of dendritic fragments increases as the moving speed of fragments increases. In the calculation, the equivalent diameter of fragment is 2 × 10−10 m [20], and the viscosity of the molten steel is 0.0025 Pa·s [25]. According to the calculation results of Jmat-Pro 7.0 of thermo-physical properties, the difference value of the solid–liquid two-phase density was discussed.
In Figure 9a, the solid line represents the proportion of each phase, and the dotted line represents the density of each phase during solidification. In the initial stage of solidification, the liquid phase ratio is more than 50%, and the solid phase is high-temperature ferrite. The density of high-temperature ferrite and liquid is 6.98 and 7.24 g/cm3, respectively. In the middle of solidification, the liquid phase ratio is less than 50% and greater than 5%, and the solid phase is austenite. The densities of austenite and liquid are 6.98 and 7.28 g/cm3, respectively. At the end of solidification, the liquid phase ratio is less than 5%, and the solid phase is austenite. The density of austenite slightly elevated but not exceeding 7.3 g/cm3. The density of liquid decreased to 6.93 from 6.98 g/cm3. The super-gravity treatment at the nucleation stage had the best refining effect, while the solidified structures were slightly refined with treatment at the beginning and end of crystal growth [26]. The ranges of refinement super-gravity are a solidification fraction of less than 59.18 wt% for Al-4.5 wt% Cu alloys and 23.16% for Al-8 wt% Cu alloys [11]. We assumed that with the liquid phase ratio of more than 50% in H13 steel, the super-gravity can refine the solidified structure. Within this range, the difference value of ρl and ρp almost unchanged, and the value of ρlρp is defined as 0.26 g/cm3. The moving speed of the fragment was calculated by the crystal rain mechanism, as shown in Figure 9b.
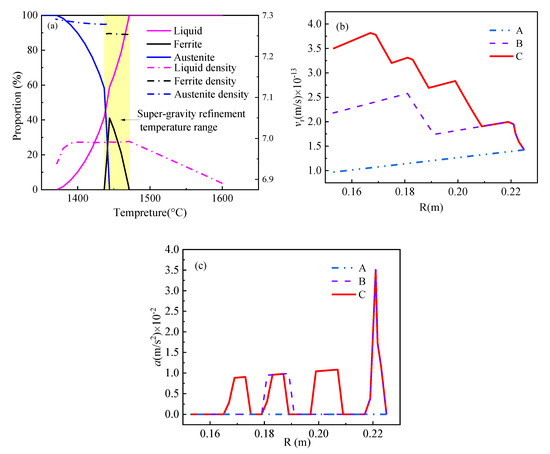
Figure 9.
(a) Density change of solid and remaining liquid in the H13 steel in the solidification process calculated via Jmatpro7.0 software; (b) the fragment’s moving speed at different positions of Samples A, B, and C; (c) the tangential acceleration at different positions of Samples A, B and C.
As R decreases from 0.225 to 0.153 m, the value of vr for Sample A decreases from 1.4 × 10−13 to 1.0 × 10−13 m/s. For Samples B and C, vr increases with the decrease in R in the range of increasing rotational speed, which leads to the reduction of secondary dendrite spacings. For Samples B and C, the variations trends of secondary dendrite spacings with R are opposite to the variation trends of vr with R. If the refinement mechanism of the dendritic structure is only the “heavy crystal rain” mechanism, the difference in SDAS depends on that of vr. Combined with Figure 6a, the differences of SDAS between R = 0.225 m and R = 0.152 m for Samples A and C are 50 and 24 μm, respectively, and the corresponding differences of vr between R = 0.225 m and R = 0.152 m for Samples A and C are 0.5 × 10−13 and 3.2 × 10−13 m/s, respectively. Obviously, the values of SDAS are not completely related to vr, which means that other mechanisms have an effect on SDAS.
In the process of super-gravity casting, the tangential force is generated by the increase or decrease in the rotational speed of the mold, which will change the motion state of the molten metal and break the dendrites, thus refining the solidified structure. This refinement of solidified structure is called the dynamic effect [27,28]. The dynamic effect on the movement state of molten metal can be explained by the Reynolds number (Re) formula of fluid mechanics. For centrifugal casting, the Reynolds number can be expressed by Equation (15) [28].
where v is the average linear speed of the liquid relative to the mold (m/s); b is the thickness of the liquid layer in the mold (m); and ν is the kinematic viscosity coefficient of the liquid (m2/s). In the super-gravity casting process, v quickly becomes smaller, and Re also becomes smaller. At the moment, the flow of the liquid steel to the inner wall of the mold is laminar, and the crystal front is in the laminar layer, which will promote the precipitation of small grains along the solid–liquid interface in one direction, thus forming inclined columnar crystals.
After the implementation of the dynamic effect, both v and Re increase significantly. If Re is greater than a certain value, the flow of liquid steel against the inner wall forms a turbulent layer. The crystallization front is in the turbulent layer, which hinders the normal floating and sinking of the heterogeneous particles. This results in the chaotic motion of particles at different temperatures in the whole turbulent layer, which reduces the temperature difference between the liquid layers and accelerates the melting of the dendrites, thus promoting the transformation of columnar crystals into equiaxed crystals. In the dynamic effect, the tangential force F acting on the dendrite vertex and breaking the dendrite can be expressed as:
where m is the mass of the liquid layer at the dendrite front; a is the tangential acceleration of the dendrite front, which is determined by the angular acceleration of the liquid layer (ωa) and the distance from its center of gravity to the axis of rotation (R)
If the angular speed of the dendritic liquid layer relative to the solidified layer changes by Δω during Δt, then
By combining Equations (17) and (18), the following Equation (19) can be obtained:
when F is greater than a certain value sufficient to break the crystallization front dendrites, the crystallization front will form dendritic fragments that act as the nuclear cores of the grains. Tangential acceleration of the liquid layer at the dendrite front (a) is expressed as Equation (20).
It can be found that the fragment’s tangential acceleration is caused by the change in rotational speed. When the angular acceleration in the super-gravity field is a fixed value, the tangential acceleration of the fragment is positively correlated to the radius.
Figure 9c shows the tangential accelerations of the dendrites front for Samples A, B, and C. As shown by the blue dotted line in Figure 9c, the value of a at each position of Sample A is zero, which demonstrates that there is no dynamic effect mechanism in Sample A. The value of a is not zero at the range of increasing rotational speed. The value of a is proportional to R, and a at R = 0.22 m, it is much more than that at other positions such as R = 0.22, 0.203, 0.185, and 0.17 m. Compared with Sample B, there are many more positions of a > 0 for Sample C, which leads to the value of SDAS being the smallest in this sample at the same position.
In summary, the refinement mechanisms of the solidification microstructure for H13 steel in the super-gravity field include the lower critical nucleation work, the “crystal rain” mechanism, and the dynamic effect mechanism. Among them, the “crystal rain” mechanism does not contribute much more to the refinement effect of H13 solidified structure than binary alloy such as Al-Cu alloys. The reason for this is that during solidification in super-gravity fields, the density difference between the solid and liquid phases is an important factor in the generation of dendritic rain, and compared with the density difference between the solid and liquid phases of the Al-Cu alloy (i.e., 0.9 g/cm3), the density difference between the solid and liquid phases of H13 (0.27 g/cm3) is smaller.
3.3. Tensile Properties of As-Cast H13 Samples in Super-Gravity Fields
The tensile strength and elongation at room temperature for the as-cast H13 samples are shown in Figure 10. It is clear that the tensile strengths and elongations of Samples A, B and C are basically equal at outer positions. However, the tensile strength and elongation of Samples B and C are significantly larger than Sample A at the middle and inner positions, especially for the elongation. It is well-known that the decrease in grain size can increase both the strength and the plasticity [29,30]. In the present study, the grain size at inner position decreases with the increasing rotational speeds, as clearly shown in Figure 6, as a result of which, both the strength and plasticity are enhanced remarkably. Therefore, it is well demonstrated that the multi-rotational speed super-gravity field can effectively enhance both the strength and plasticity of the as-cast H13 steel through decreasing the grain size.
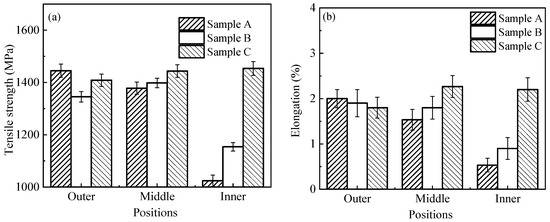
Figure 10.
Tensile strength (a) and elongation (b) at the outer, middle, and inner positions of Samples A, B and C.
4. Conclusions
By applying different super-gravity fields during the solidification of H13 steel, the refining mechanism was revealed experimentally and discussed. The research result provides a theoretical basis for the refining of the solidified structure of H13 steel industrial ingot by super-gravity. The conclusions drawn are as follows:
- (1)
- Compared to a single rotational speed super-gravity field, the solidified structure of H13 steel can be significantly refined in a multi-rotational speed (speed increased in stages) super-gravity field.
- (2)
- The decrease in critical nucleation work for austenite in the multi-rotational speed super-gravity field promotes the grain multiplication, resulting in the refinement of the austenite grain size. The tangential force produced by increasing the rotational speed in the super-gravity field breaks dendrites at the solidification front and finally causes the solidified structure refinement. Due to the smaller density difference between the solid and liquid phases of H13 steel, the “crystal rain” mechanism does not contribute much more to the refinement effect of the H13 solidified structure than binary alloys.
- (3)
- The increasing super-gravity can greatly enhance the tensile properties of as-cast H13 steel through refining austenite grains size and secondary dendrites. Both the tensile strength and plasticity at the inner position of the super-gravity samples are greatly enhanced with the increasing rotational speed.
Author Contributions
S.-Y.L. performed the research, designed the experimental process, analyzed the data, wrote the original manuscript, and reviewed and edited the manuscript. S.-Y.Q. provided the data collection and conducted charts. X.-J.X. participated in research design. G.-Y.S. conducted charts. W.-S.Y. participated in data analysis. J.G. participated in literature search. H.-J.G. provided article supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Program of Sichuan Province, China, grant number 18SYXHZ0069. The authors are thankful for the Beijing Key Laboratory of Special Melting and Preparation of High-End Metal Materials in the School of Metallurgical and Ecological Engineering of University of Science and Technology Beijing, China.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhu, J.; Zhang, Z.H.; Xie, J.X. Improving strength and ductility of H13 die steel by pre-tempering treatment and its mechanism. Mater. Sci. Eng. A 2019, 752, 101–114. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, H.F.; Tong, X.; Cong, D.L.; Wang, C.W.; Ren, L.Q. The comparative study of thermal fatigue behavior of H13 die steel with biomimetic non-smooth surface processed by laser surface melting and laser cladding. Mater. Des. 2013, 51, 886–893. [Google Scholar]
- Kurz, W.; Fisher, D.J.; Li, J.G.; Hu, Q.D. Fundamentals of Solidification, 4th ed.; Higher Education Press: Beijing, China, 1998; pp. 71–73. [Google Scholar]
- Cicutti, C.; Boeri, R.; Cicutti, C.; Boeri, R. On the relationship between primary and secondary dendrite arm spacing in continuous casting products. Scr. Mater. 2001, 45, 1455–1460. [Google Scholar] [CrossRef]
- Ferreira, A.F.; Melo, E.G.; Ferreira, L.O. Prediction of Secondary-Dendrite Arm Spacing for Binary Alloys by Means of a Phase-Field Model. Steel Res. Int. 2015, 86, 58–64. [Google Scholar] [CrossRef]
- Liao, X.; Zhai, Q.; Luo, J.; Chen, W.; Gong, Y. Refining mechanism of the electric current pulse on the solidification structure of pure aluminum. Acta Mater. 2007, 55, 3103–3109. [Google Scholar] [CrossRef]
- Song, W.X. Metal Science, 2nd ed.; Metallurgical Industry Press: Beijing, China, 2008; pp. 125–127. [Google Scholar]
- Gong, Y.Y.; Luo, J.; Jing, J.X.; Xia, Z.Q.; Zhai, Q.J. Structure refinement of pure aluminum by pulse magneto-oscillation. Mater. Sci. Eng. A 2008, 497, 147–152. [Google Scholar] [CrossRef]
- Qi, F.P.; Zhang, H.B.; Gao, S.L.; Zhai, Q.J. Microstructure refinement of Sn-Sb peritectic alloy under high-intensity ultrasound treatment. J. Shanghai Univ. 2005, 9, 74–77. [Google Scholar] [CrossRef]
- Jia, S.J.; Song, B.; Song, G.Y.; Yang, Y.H.; Huang, C.G. Effect of Super-gravity Field on Solidification Structure of Al−6%Cu Alloy. Chin. J. Process Eng. 2014, 14, 881–885. [Google Scholar]
- Yang, Y.H.; Song, B.; Yang, Z.B.; Song, G.Y.; Cai, Z.Y.; Guo, Z.C. The Refining Mechanism of Super Gravity on the Solidification Structure of Al-Cu Alloys. Materials 2016, 9, 1001. [Google Scholar] [CrossRef]
- Zhao, L.X.; Guo, Z.C.; Wang, Z.; Wang, M.Y. Influences of super-gravity field on aluminum grain refining. Metall. Mater. Trans. A 2010, 41, 670–675. [Google Scholar] [CrossRef]
- Yang, Y.H.; Song, B.; Yang, Z.B.; Cheng, J.; Song, G.Y.; Li, L.F. Macrosegregation behavior of solute Cu in the solidifying Al-Cu alloys in super-gravity field. Metall. Res. Technol. 2018, 115, 1–12. [Google Scholar] [CrossRef]
- Yang, Y.H.; Song, B.; Cheng, J.; Song, G.Y.; Yang, Z.B.; Cai, Z.Y. Effect of Super-gravity Field on Grain Refinement and Tensile Properties of Cu–Sn Alloys. ISIJ Int. 2018, 58, 98–106. [Google Scholar] [CrossRef]
- Melgarejo, Z.H.; Suἁrez, O.M.; Sridharan, K. Microstructure and properties of functionally graded Al–Mg–B composites fabricated by centrifugal casting. Compos. Part A 2008, 39, 1150–1158. [Google Scholar] [CrossRef]
- Liu, X.K.; Wang, Q.S.; Wang, Z.D.; Feng, Z.Q.; Zhang, H.; Zhu, J.J.; Fan, M. Effects of Centrifugalization on Behavior of Precipitated Phases in ZCuSn3Zn8Pb6Ni1FeCo Alloy. Foundry 2010, 4, 351–354. [Google Scholar]
- Zhang, X.Z.; Yu, M.; Xia, R.Z. Cause Reaches Casting Crack Formation Guarding Against Method. Coal Mine Mach. 2007, 11, 104–106. [Google Scholar]
- Wei, X.Z. Discussion on area method and cross-section method for determining the number of grains per unit area on the polished metal surface. Phys. Test 1989, 2, 55–60. [Google Scholar]
- Cheng, X.Y. Application analysis of room temperature tensile test standard GB/T 228.1-2010. Phys. Chem. Insp. Phys. Div. 2018, 2, 122–124. [Google Scholar]
- Cui, Z.Q.; Qin, Y.C. Metal Science and Heat Treatment, 2nd ed.; China Machine Press: Beijing, China, 2007; p. 39. [Google Scholar]
- Barin, I.; Knacke, O.; Kubaschewski, O. Thermochemical Data of Pure Substances, 3rd ed.; Springer: Berlin, Germany, 2008; p. 675. [Google Scholar]
- Chen, X.C. New Process Development and Finite Element Simulation of Induction Electroslag Centrifugal Casting. Ph.D. Thesis, University of Science and Technology Beijing, Beijing, China, 2001. [Google Scholar]
- Watanabe, Y.; Inaguma, Y.; Sato, H.; Miura-Fujiwara, E. A novel fabrication method for functionally graded materials under centrifugal force: The centrifugal mixed-powder method. Materials 2009, 2, 2510–2525. [Google Scholar] [CrossRef]
- Watanabe, Y.; Kawamoto, A.; Matsuda, K. Particle size distributions in functionally graded materials fabricated by the centrifugal solid-particle method. Compos. Sci. Technol. 2002, 62, 881–888. [Google Scholar] [CrossRef]
- Chen, J.X. General Steelmaking Chart Data Sheet, 2nd ed.; Higher Education Press: Beijing, China, 2010; p. 534. [Google Scholar]
- Yang, Y.H. Fundamental Study on Solidified Structure Refinement and Elements Segregation of Metals by Super Gravity. Ph.D. Thesis, University of Science and Technology Beijing, Beijing, China, 2017. [Google Scholar]
- Lin, G.W.; Li, Z.B.; Cheng, M.T. Research on Dynamic Effect of Electroslag Centrifugal Casting Pipe. Foundry 1998, 1, 1–7. [Google Scholar]
- Lin, G.W.; Li, Z.B.; Cheng, M.T. Influence of dynamic effects on solidification structure of heat-resistant alloy by electroslag centrifugal casting. Iron Steel 1997, 32, 21–25. [Google Scholar]
- Jiang, H.S.; Zheng, M.Y.; Qiao, X.G.; Wu, K.; Peng, Q.Y.; Yang, S.H.; Yuan, Y.H.; Luo, J.H. Microstructure and mechanical properties of WE43 magnesium alloy fabricated by direct-chill casting. Mater. Sci. Eng. A 2017, 684, 158–164. [Google Scholar] [CrossRef]
- Pourbahari, B.; Mirzadeh, H.; Emamy, M. Toward unraveling the effects of intermetallic compounds on the microstructure and mechanical properties of Mg–Gd–Al–Zn magnesium alloys in the as-cast, homogenized, and extruded conditions. Mater. Sci. Eng. A 2017, 680, 39–46. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).