Through-Thickness Microstructure and Strain Distribution in Steel Sheets Rolled in a Large-Diameter Rolling Process
Abstract
1. Introduction
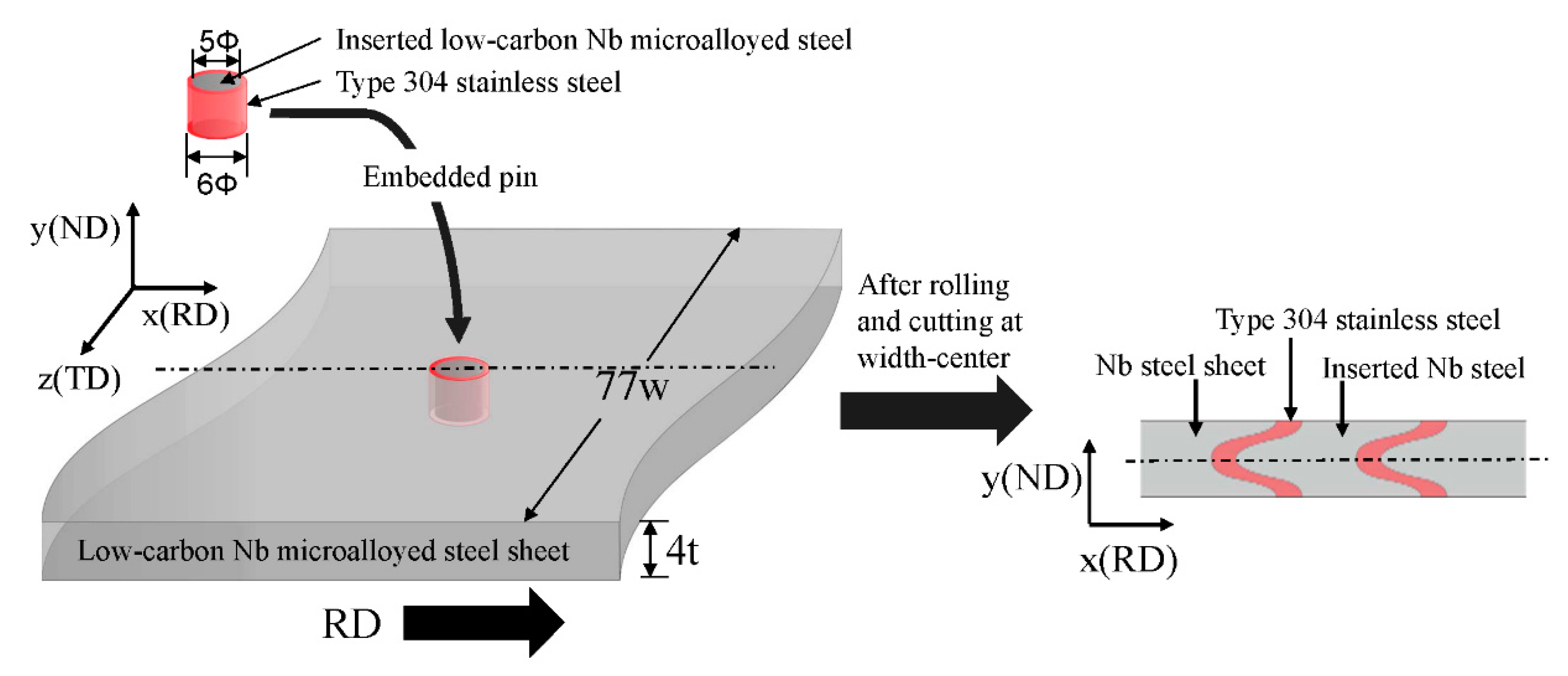
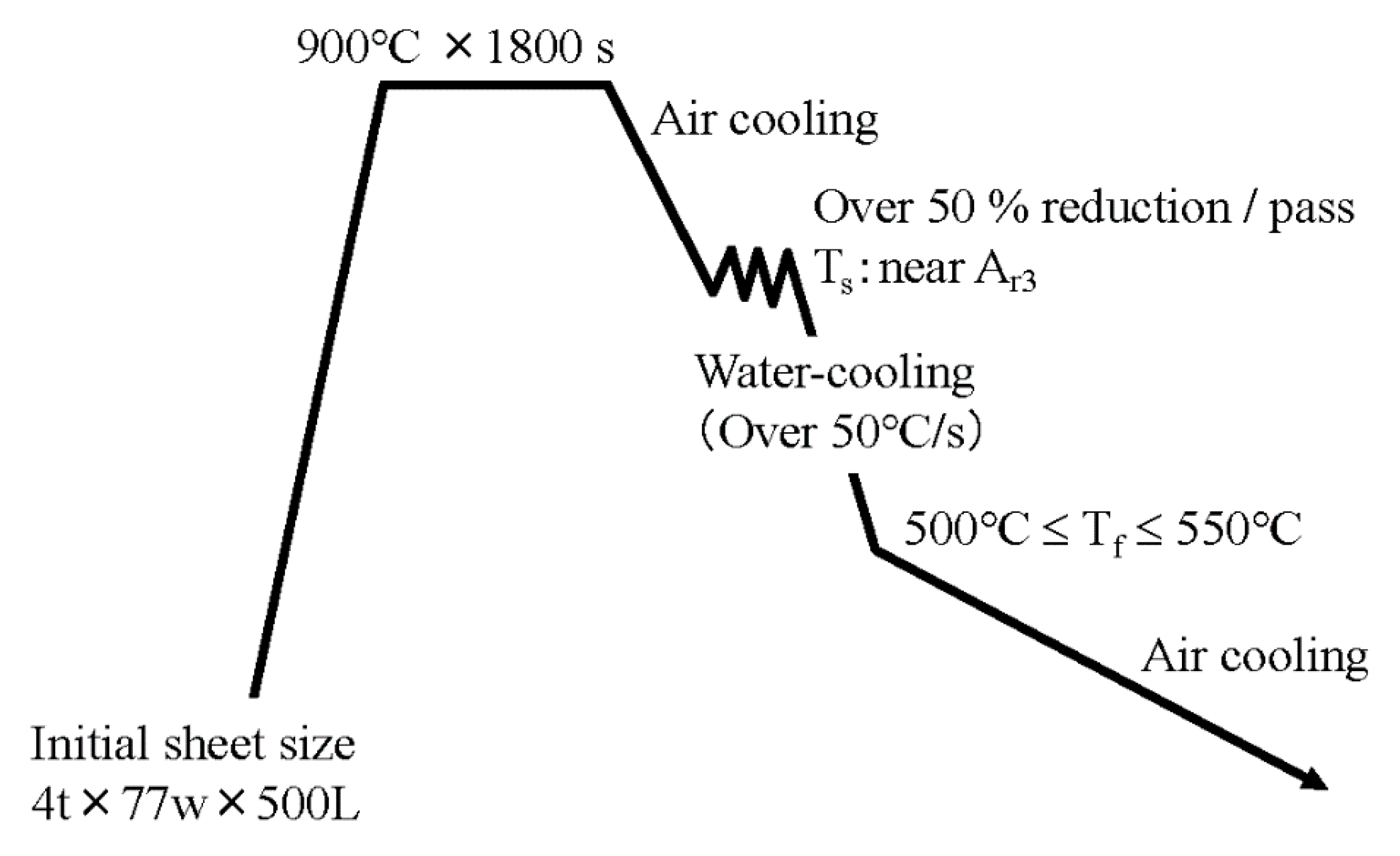
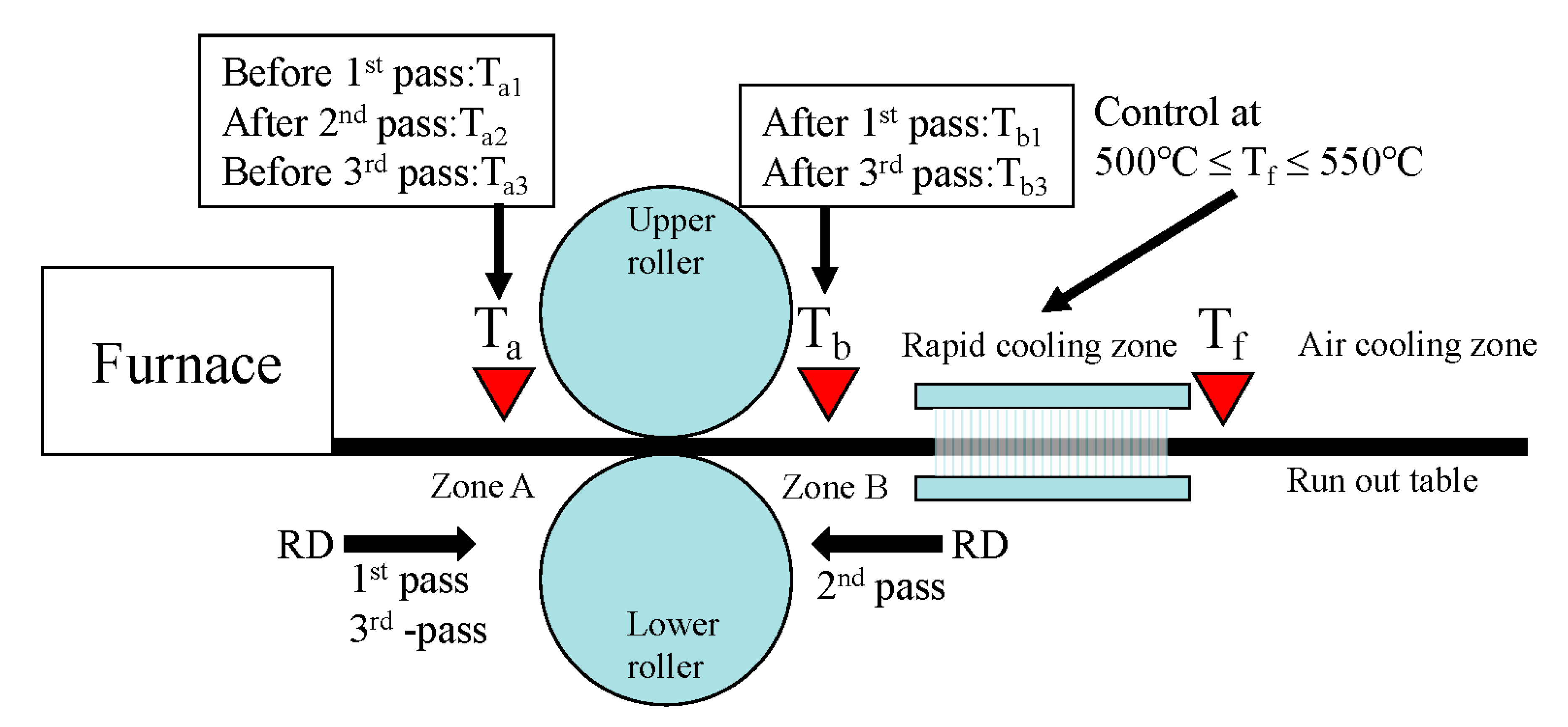
2. Experimental Procedure
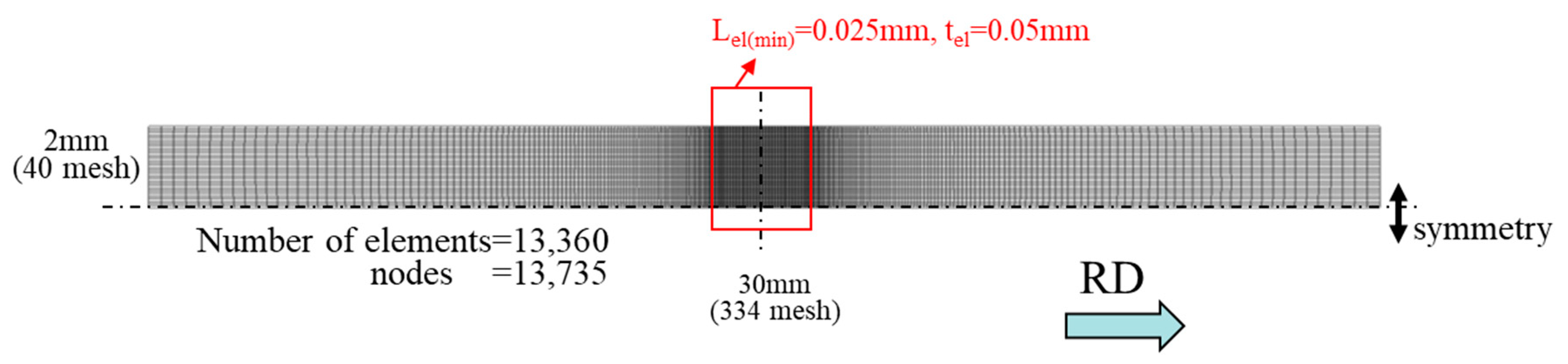
3. Numerical Procedure
4. Results and Discussion
5. Conclusions
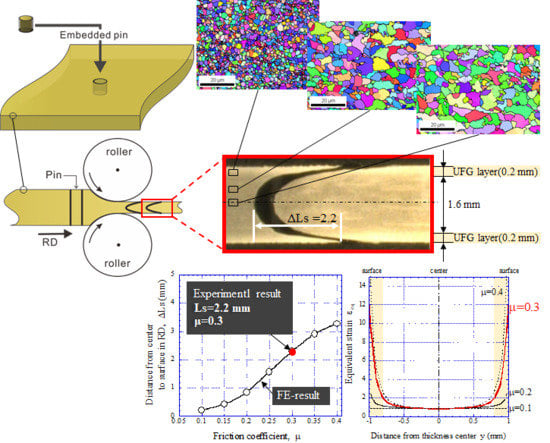
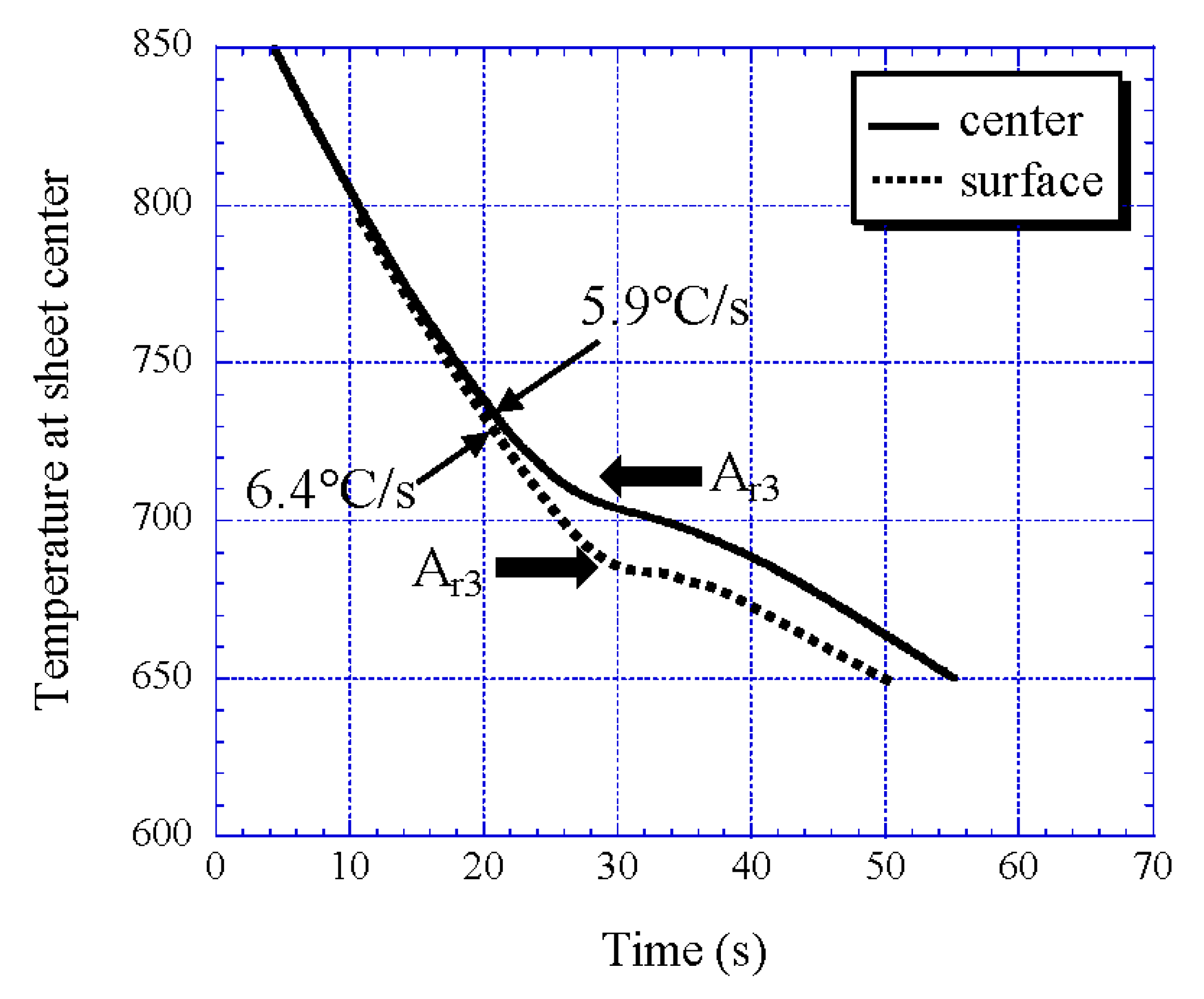
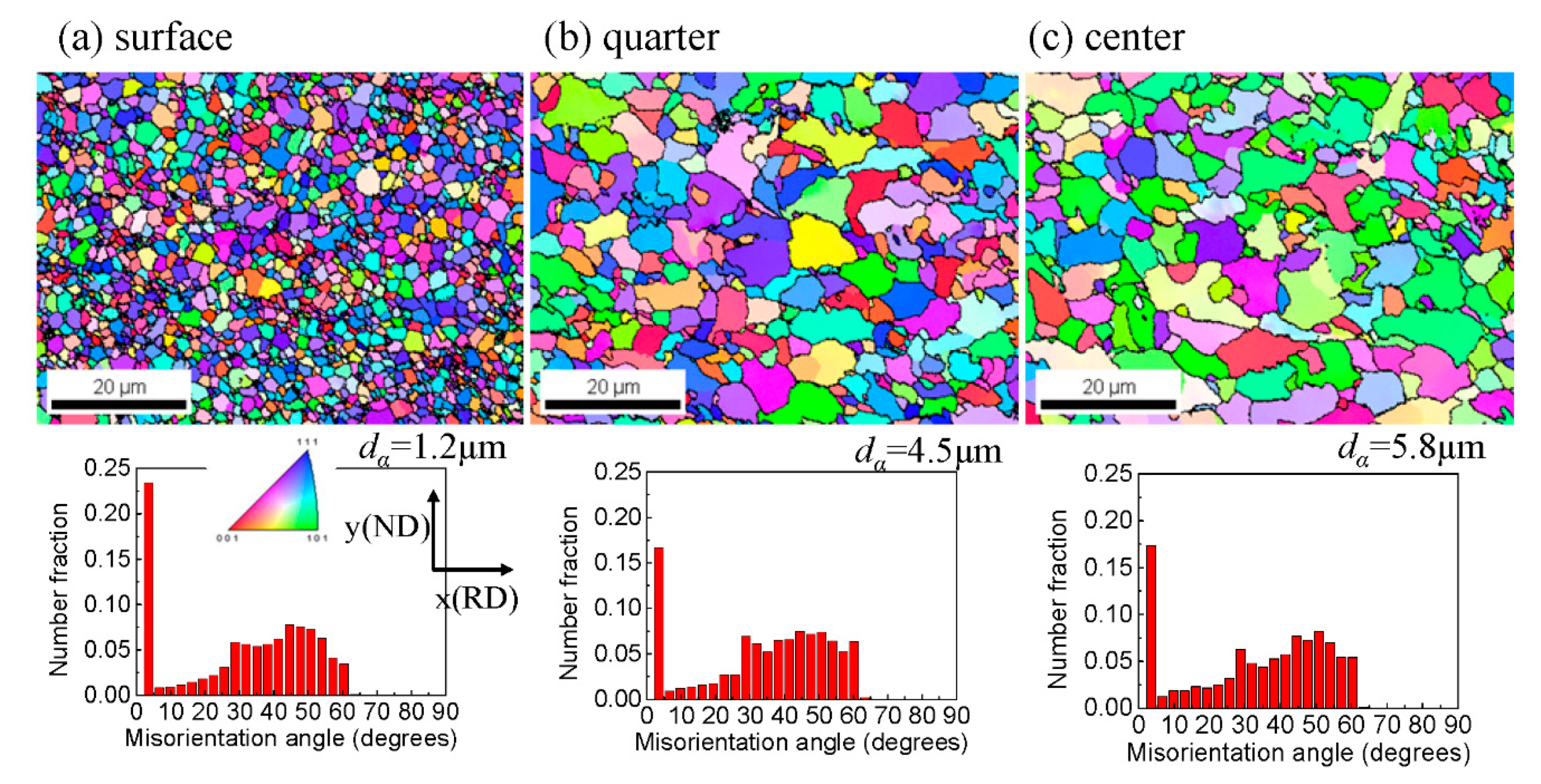
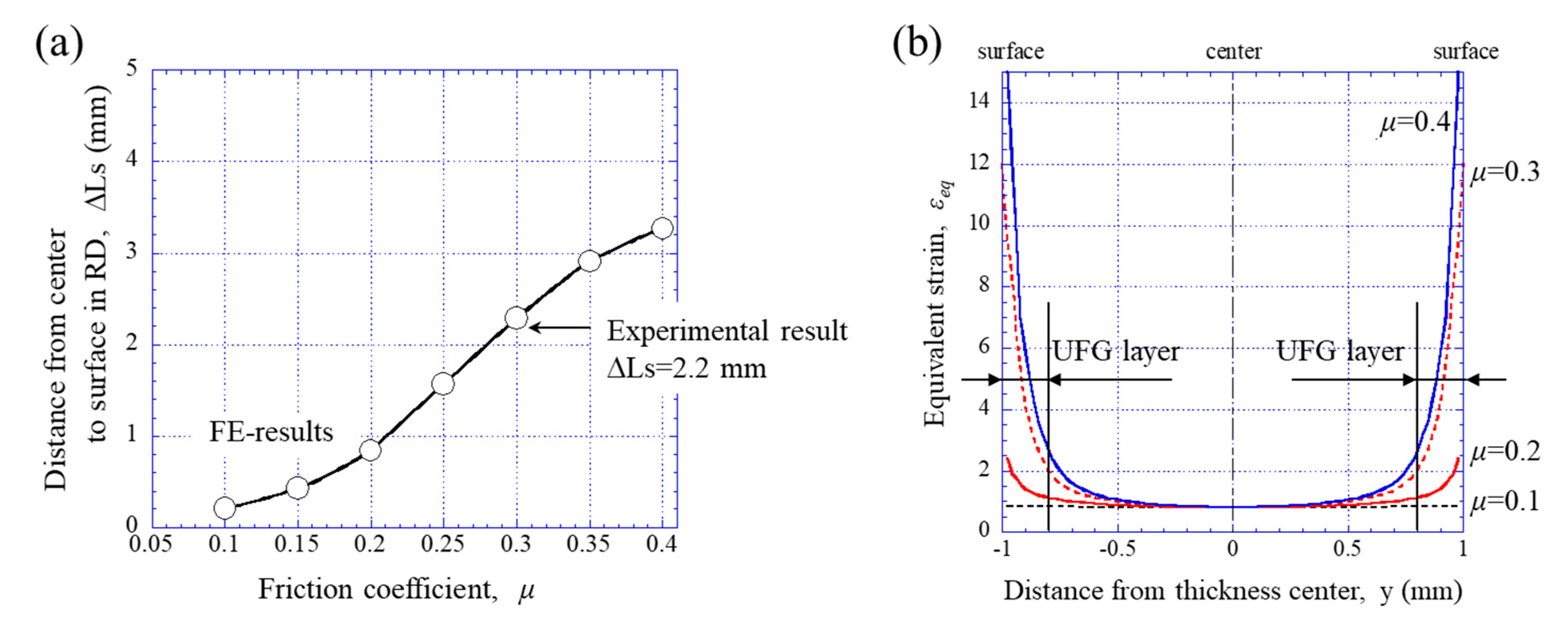
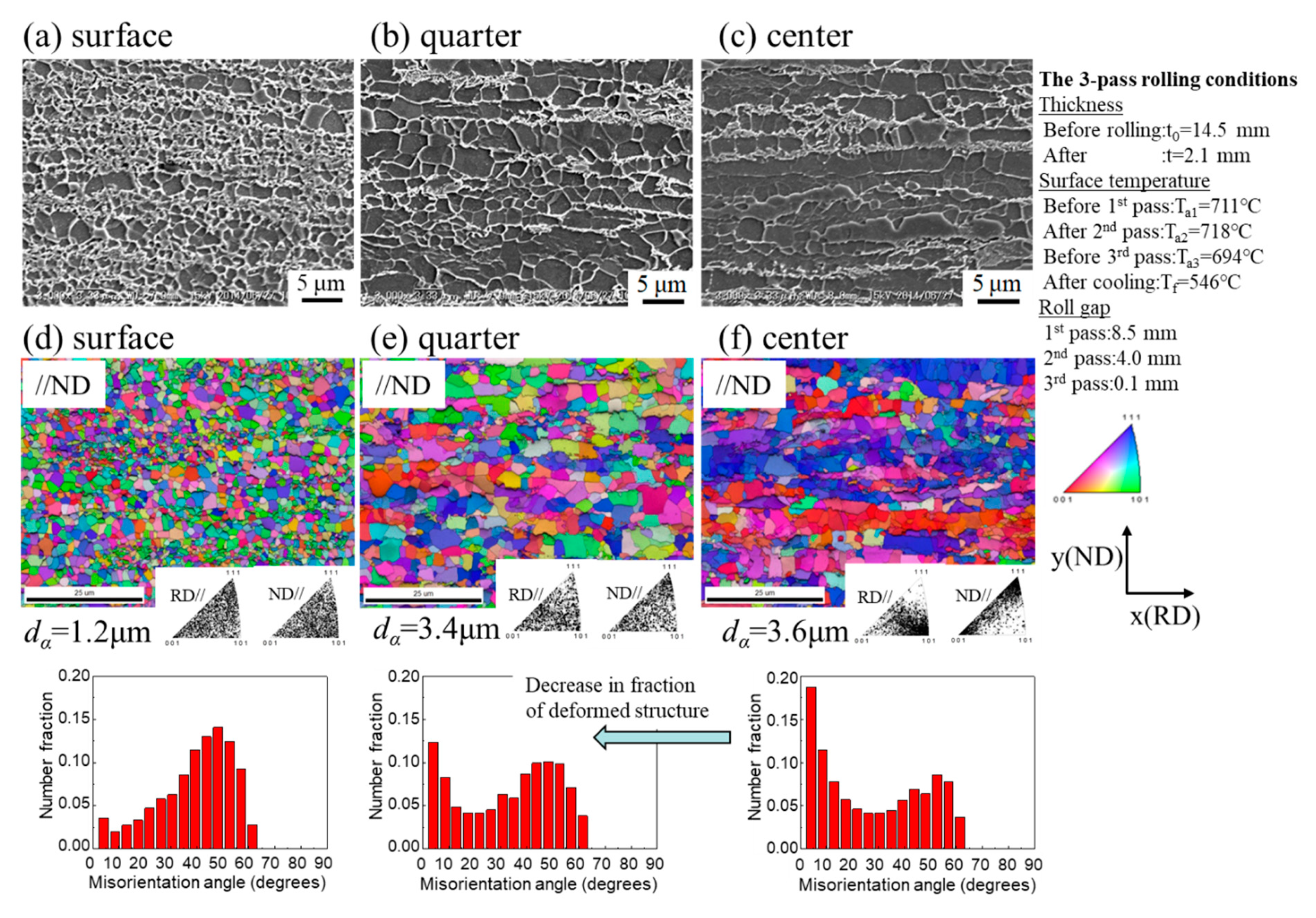
- Ultrafine ferrite grains of 1.2 μm size at the surface layer of 0.2 mm at 2.0 mm sheet thickness were obtained by the large-diameter rolling process of 50% reduction. The rolling was conducted at 690 °C, just above the Ar3, as measured using a surface thermometer.
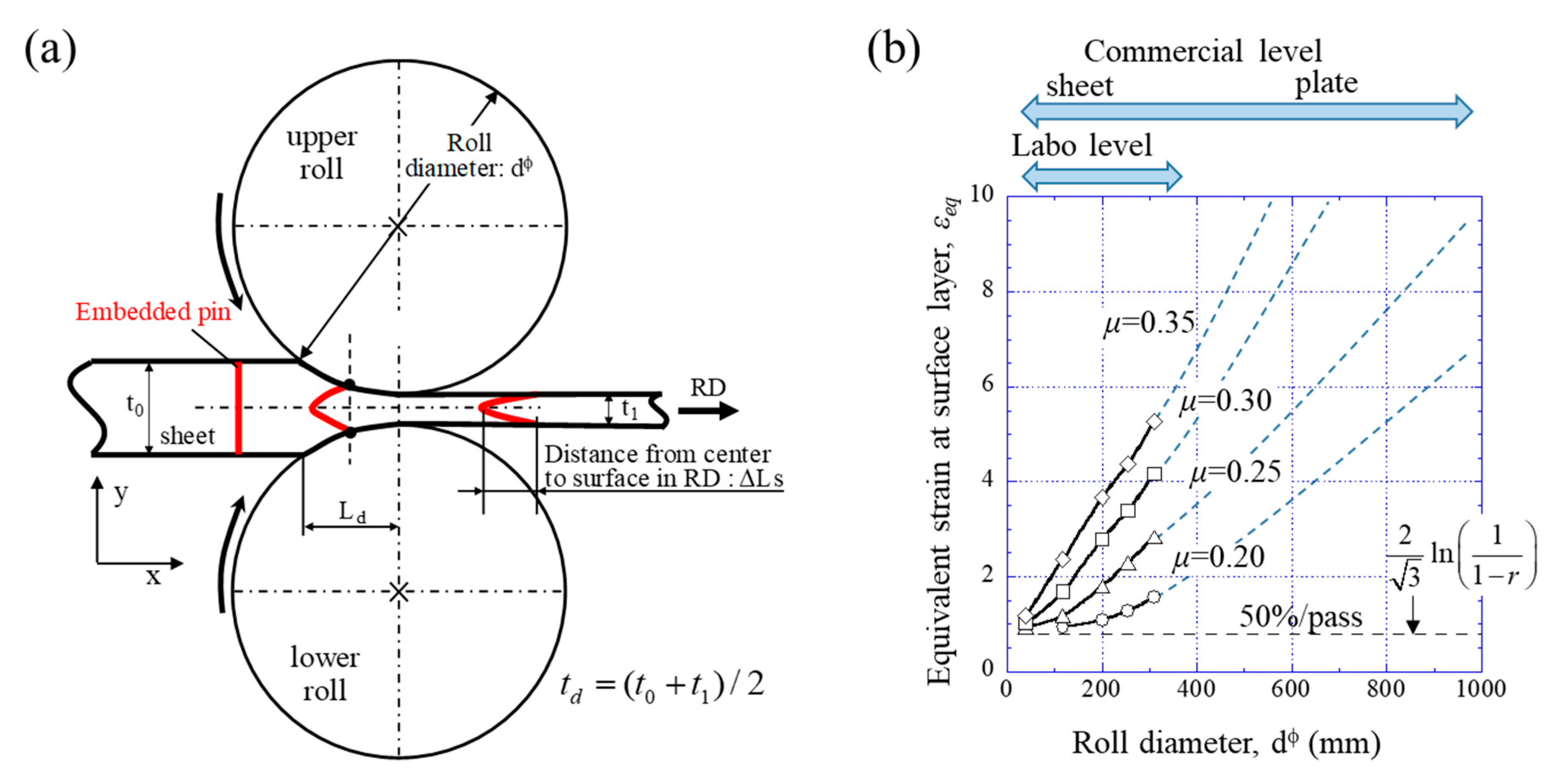
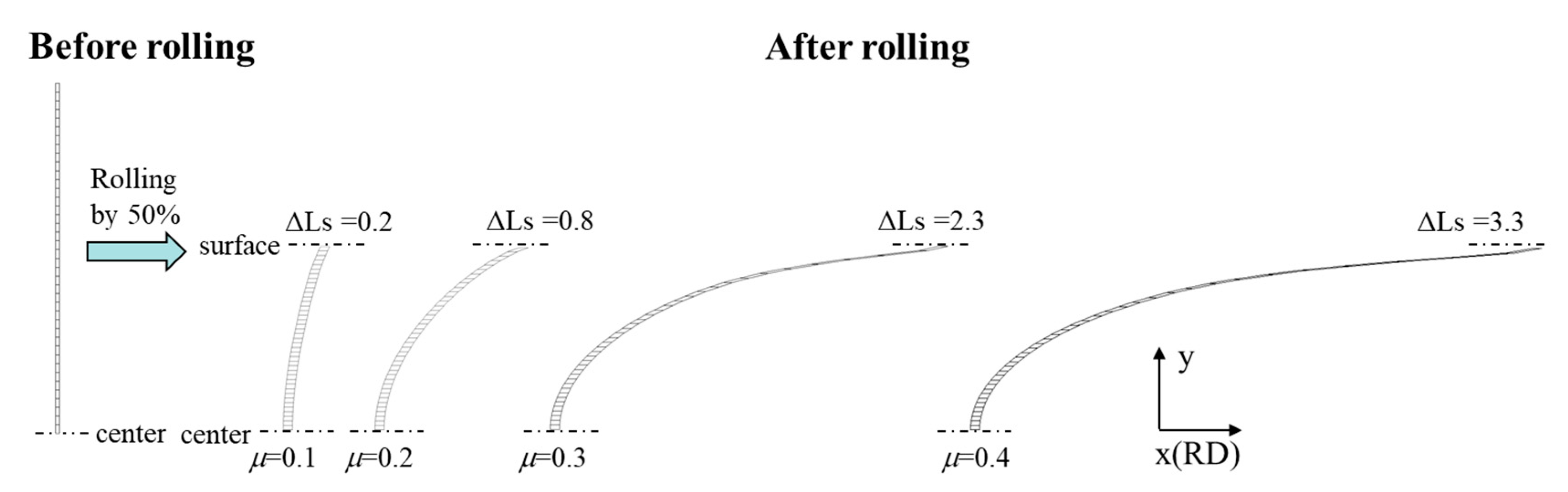
- The friction coefficient is 0.3 under the present hot rolling, and the magnitude of the equivalent strain to obtain a UFG structure was estimated to be 2.0.
- Ultrafine ferrite grains of 1.2 μm size at the surface and fine grains of 3.4 μm size at the quarter in sheets 2.1 mm thick were obtained by 3-pass rolling with a total reduction of 86% over the equivalent strain of 2.0. However, at the center, ferrite grain structures of 3.6 μm size were formed with γ-fiber and α-fiber texture.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nugmanov, D.; Mazilkin, A.; Hahn, H.; Ivanisenko, Y. Structure and tensile strength of pure Cu after high pressure torsion extrusion. Metals 2019, 179, 107864. [Google Scholar] [CrossRef]
- Segal, V.; Reznikov, S.V.; Murching, N.; Hammond, V.H.; Kecskes, L.J. Semi-continuous equal-channel angular extrusion and rolling of AA5083 and AZ31 alloys. Metals 2015, 85, 342–348. [Google Scholar] [CrossRef]
- Inoue, T. Strain variations on rolling condition in accumulative roll-bonding by finite element analysis. In Finite Element Analysis; Moratal, D., Ed.; InTech: Rijeka, Croatia, 2010; pp. 589–610. [Google Scholar] [CrossRef]
- Hohenwarter, A.; Kammerhofer, C.; Pippan, R. The ductile to brittle transition of ultrafine-grained Armco iron: An experimental study. J. Mater. Sci. 2010, 45, 4805–4812. [Google Scholar] [CrossRef]
- Inoue, T.; Yin, F.; Kimura, Y.; Tsuzaki, K.; Ochiai, S. Delamination effect on impact properties of ultrafine-grained low-carbon steel processed by warm caliber rolling. Metall. Mater. Trans. A 2010, 41, 341–355. [Google Scholar] [CrossRef]
- Bourell, D.L. Cleavage delamination in impact tested warm-rolled steel. Metall. Mater. Trans. A 1983, 14, 2487–2496. [Google Scholar] [CrossRef]
- Ohmori, A.; Torizuka, S.; Nagai, K. Properties of warm-rolled steel plates with ultrafine-grained ferrite and cementite structures. Tetsu-to-Hagane 2003, 89, 765–772. [Google Scholar] [CrossRef][Green Version]
- Kimura, Y.; Inoue, T.; Yin, F.; Tsuzaki, K. Inverse temperature dependence of toughness in an ultrafine grain-structure steel. Science 2008, 320, 1057–1060. [Google Scholar] [CrossRef]
- Inoue, T.; Torizuka, S.; Nagai, K.; Tsuzaki, K.; Ohashi, T. Effect of plastic strain on grain size of ferrite transformed from deformed austenite in Si-Mn steel. Mater. Sci Technol. 2001, 17, 1580–1588. [Google Scholar] [CrossRef]
- Patra, S.; Roy, S.; Kumar, V.; Haldar, A.; Chakrabarti, D. Ferrite grain size distributions in ultra-fine-grained high-strength low-alloy steel after controlled thermomechanical deformation. Metall. Mater. Trans. A 2011, 42, 2575–2590. [Google Scholar] [CrossRef]
- Inoue, T.; Yin, F.; Kimura, Y. Strain distribution and microstructural evolution in multi-pass warm caliber rolling. Mater. Sci. Eng. A 2007, 466, 114–122. [Google Scholar] [CrossRef]
- Inoue, T. Chapter 5 Toughening of Low-Alloy Steel by Ultrafine-Grained Structure (Development of Fracture Control from Microstructure Design). In Fracture Mechanics—Properties, Patterns and Behaviours; Alves, L., Ed.; INTECH: Rijeka, Croatia, 2016; pp. 103–120. [Google Scholar] [CrossRef]
- Inoue, T.; Yin, F.; Kimura, Y. Crystallographic texture of warm caliber-rolled low carbon steel. Mater. Trans. 2007, 48, 2028–2035. [Google Scholar] [CrossRef]
- Etou, M.; Fukushima, S.; Sasaki, T.; Haraguchi, Y.; Miyata, K.; Wakita, M.; Tomida, T.; Imai, N.; Yoshida, M.; Okada, Y. Super short interval multi-pass rolling process for ultrafine-grained hot strip. ISIJ Int. 2008, 48, 1142–1147. [Google Scholar] [CrossRef]
- Shen, X.J.; Tang, S.; Chen, J.; Liu, Z.Y.; Misra, R.D.K.; Wang, G.D. Grain refinement in surface layers through deformation-induced ferrite transformation in microalloyed steel plate. Mater. Des. 2017, 113, 137–141. [Google Scholar] [CrossRef]
- Gan, W.; Babu, S.S.; Kapustka, N.; Wagoner, R.H. Microstructural effects on the springback of advanced high-strength steel. Metall. Mater. Trans. 2006, 37, 3221–3231. [Google Scholar] [CrossRef]
- Inoue, T.; Tsuji, N. Quantification of strain in accumulative roll-bonding under unlubricated condition by finite element analysis. Comput. Mater. Sci. 2009, 46, 261–266. [Google Scholar] [CrossRef]
- Utsunomiya, H.; Tanda, K.; Saito, Y.; Sakai, T.; Tsuji, N. Effects of lubrication on accumulative roll-bonding (ARB) of aluminum. J. Jpn. Soc. Technol. Plast. 1999, 40, 1187–1191. [Google Scholar]
- Kozasu, I.; Ouchi, C.; Sampei, T.; Okita, T. Hot rolling as a high-temperature in thermo-mechanical process. In Proceedings of the Microalloying 75; Union Carbide Corp.: New York, NY, USA, 1977; pp. 120–135. [Google Scholar]
- Yanagimoto, J.; Sugiyama, S.; Kawando, S.; Yanagida, A. Interrupt shearing test for evaluating effect of large shear deformation on evolution of microstructure into ultrafine grains. Mater. Trans. 2012, 53, 2–7. [Google Scholar] [CrossRef]
- Ishikawa, T.; Mabuchi, H.; Hasegawa, T.; Nomiyama, Y.; Yoshie, A. High crack arrestability-endowed steel plate with surface-layer of ultra fine grain microstructure. Tetsu-to-Hagane 1999, 85, 544–551. [Google Scholar] [CrossRef][Green Version]
- Matsubara, Y.; Nakata, N.; Hiruta, T. Effect of accumulative bending conditions on grain refinement on hot-rolled sheet. Tetsu-to-Hagane 2012, 98, 19–24. [Google Scholar] [CrossRef]
- Inoue, T.; Torizuka, S.; Nagai, K. Effect of shear deformation on refinement of crystal grains. Mater. Sci. Technol. 2002, 18, 1007–1015. [Google Scholar] [CrossRef]
- Inoue, T.; Torizuka, S.; Nagai, K. Formation of uniformly fine grained ferrite structure through multidirectional deformation. Mater. Sci. Technol. 2001, 17, 1329–1338. [Google Scholar] [CrossRef]
- Cho, J.Y.; Inoue, T.; Yin, F.; Nagai, K. Effect of shear deformation on microstructural evolution of Ni-30Fe alloy during hot deformation. Mater. Trans. 2004, 45, 2966–2973. [Google Scholar] [CrossRef][Green Version]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inoue, T.; Qiu, H.; Ueji, R. Through-Thickness Microstructure and Strain Distribution in Steel Sheets Rolled in a Large-Diameter Rolling Process. Metals 2020, 10, 91. https://doi.org/10.3390/met10010091
Inoue T, Qiu H, Ueji R. Through-Thickness Microstructure and Strain Distribution in Steel Sheets Rolled in a Large-Diameter Rolling Process. Metals. 2020; 10(1):91. https://doi.org/10.3390/met10010091
Chicago/Turabian StyleInoue, Tadanobu, Hai Qiu, and Rintaro Ueji. 2020. "Through-Thickness Microstructure and Strain Distribution in Steel Sheets Rolled in a Large-Diameter Rolling Process" Metals 10, no. 1: 91. https://doi.org/10.3390/met10010091
APA StyleInoue, T., Qiu, H., & Ueji, R. (2020). Through-Thickness Microstructure and Strain Distribution in Steel Sheets Rolled in a Large-Diameter Rolling Process. Metals, 10(1), 91. https://doi.org/10.3390/met10010091