Verification of Fuzzy Inference System for Cutting Speed while WEDM for the Abrasion-Resistant Steel Creusabro by Conventional Statistical Methods
Abstract
1. Introduction
2. Experimental Setup and Material
2.1. Experimental Material
2.2. WEDM Machine Setup
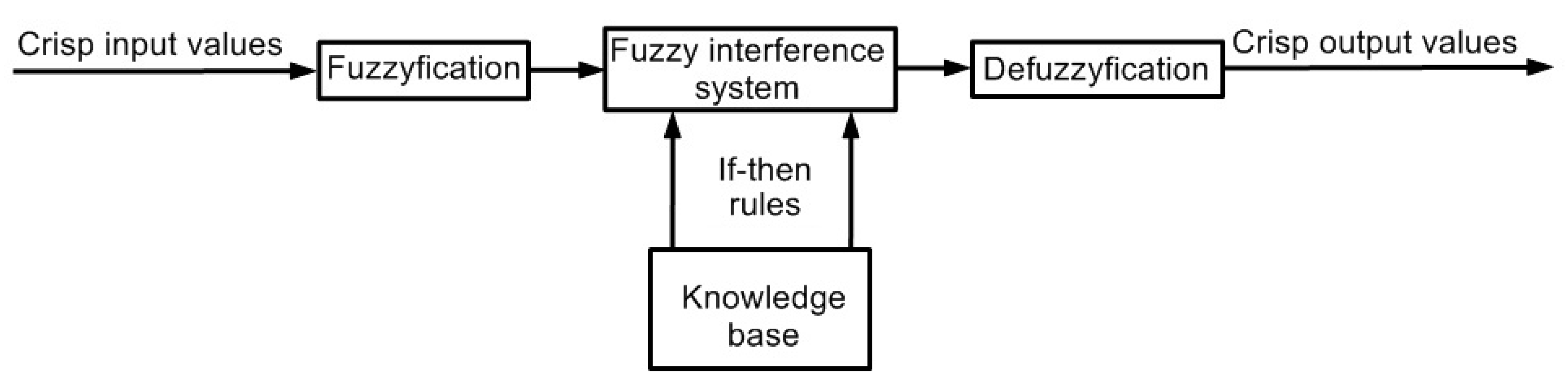
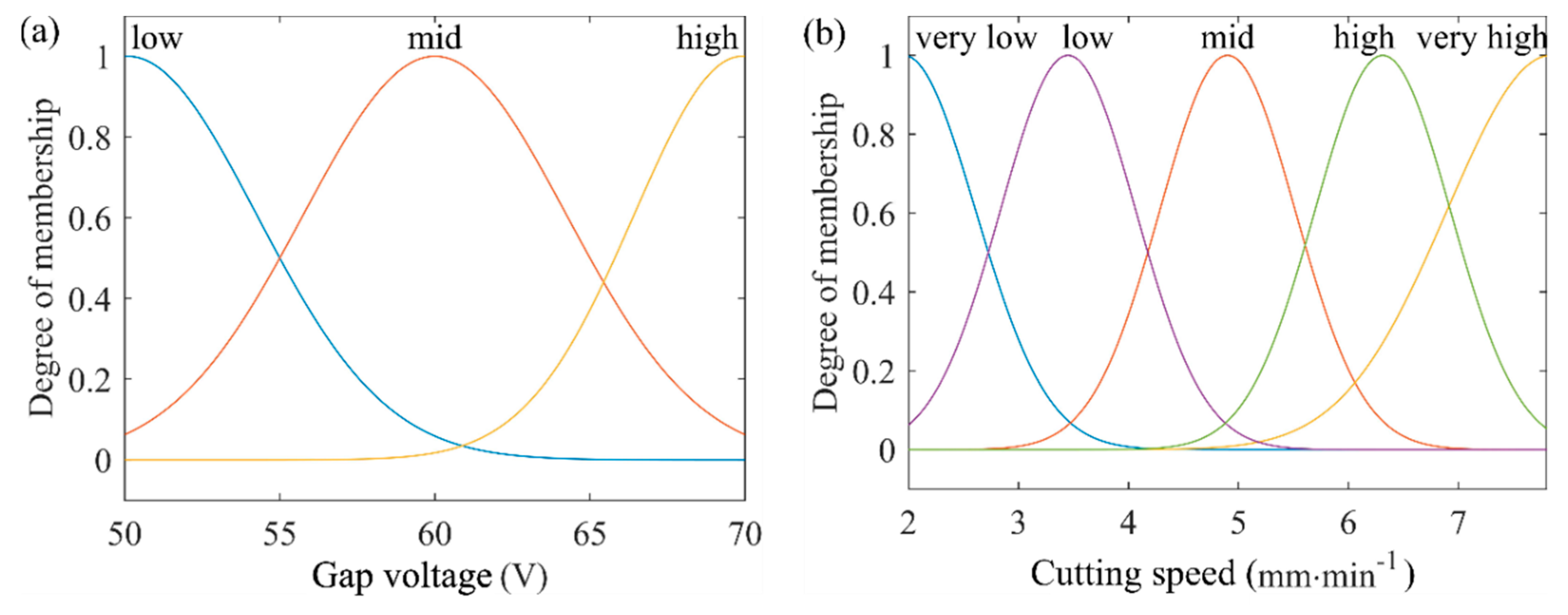
2.3. Mamdani Fuzzy Inference System
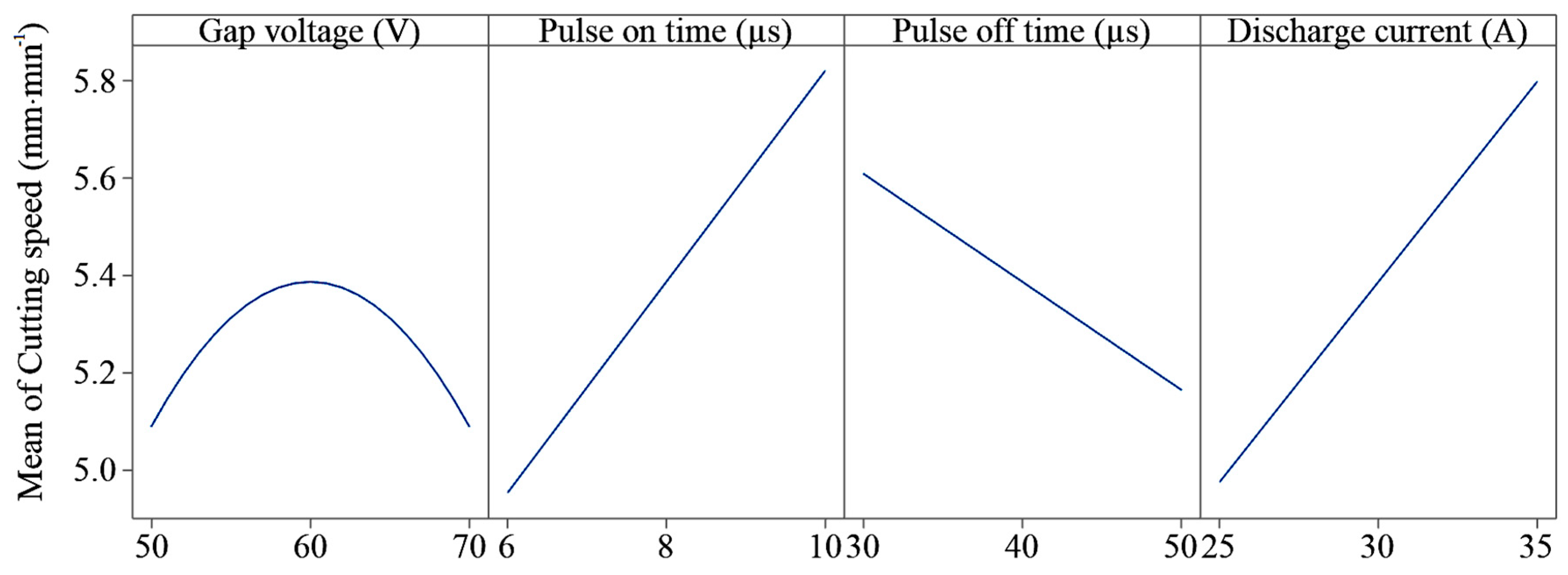
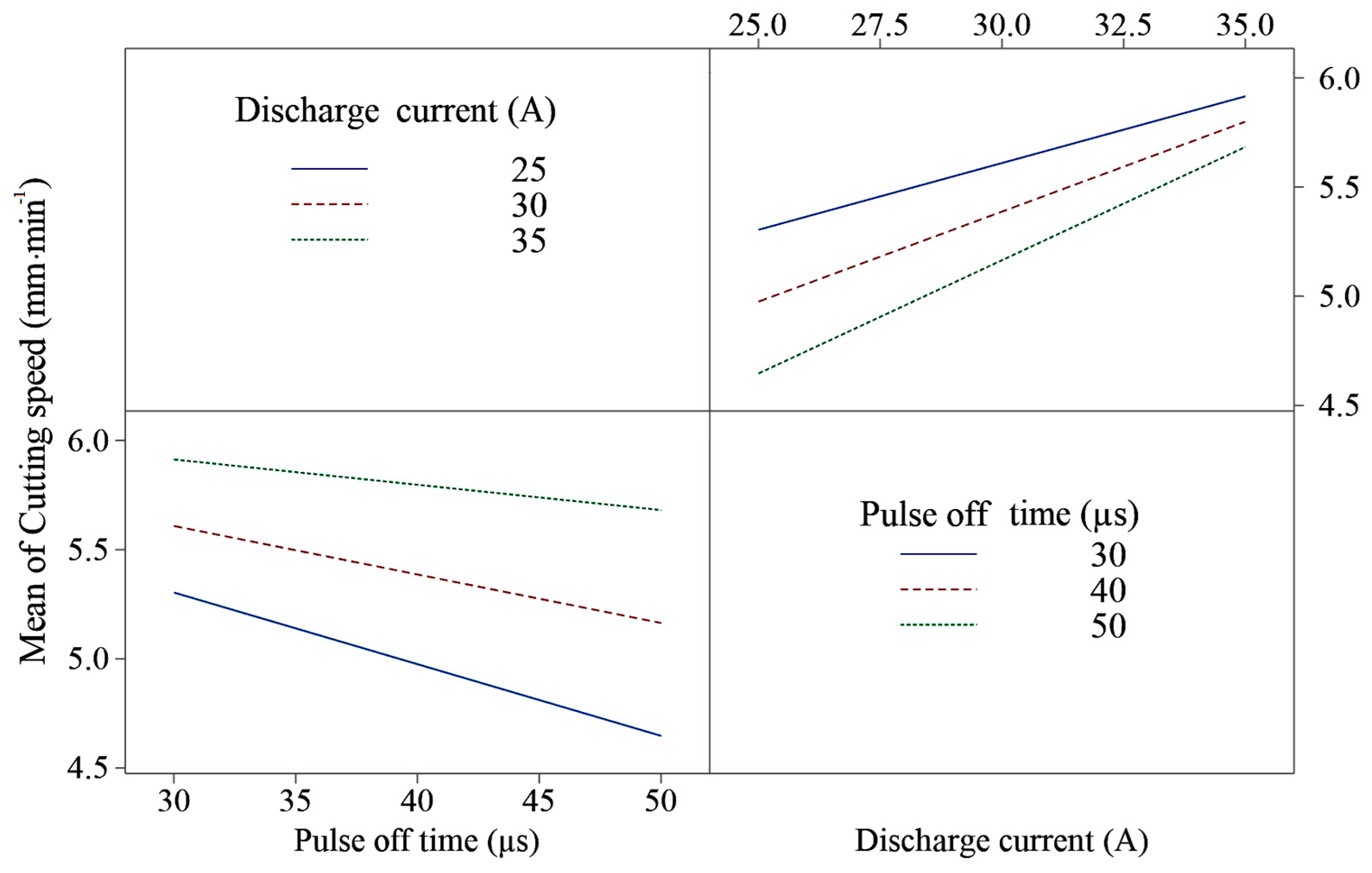
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vates, U.K. Wire-EDM Process Parameters and Optimization; Springer: Berlin/Heidelberg, Germany, 2018; ISBN 978-620-2-30578-5. [Google Scholar]
- Hashmi, S. Comprehensive Materials Finishing; Elsevier: Amsterdam, The Netherlands, 2016; ISBN 978-0-12-803249-7. [Google Scholar]
- Ranjan, R. Optimization of Wire Electrical Discharge Machining; Lap Lambert Academic Publishing: Saarbrucken, Germany, 2016; ISBN 978-3-659-88968-4. [Google Scholar]
- Tonday, H.R.; Tigga, A.M. Wire Electrical Discharge Machining: Empirical Study and Optimization; Lap Lambert Academic Publishing: Saarbrucken, Germany, 2017; ISBN 978-3-330-32464-0. [Google Scholar]
- ArcelorMittal, Creusabro 4800. Available online: https://industeel.arcelormittal.com/products/wear-resistant-steels/creusabro/creusabro-4800/ (accessed on 20 December 2019).
- Klir, G.J.; Yuan, B. Fuzzy Sets and Fuzzy Logic: Theory and Applications; Prentice Hall: Upper Saddle River, NJ, USA, 1995; p. 563. [Google Scholar]
- Zadeh, L.A. Outline of a new approach to the analysis of complex systems and decision processes. IEEE Trans. Syst. Man Cybern. 1973, 1, 28–44. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2016; ISBN 978-1-118-91601-8. [Google Scholar]
- Çaydaş, U.; Hasçalık, A.; Ekici, S. An adaptive neuro-fuzzy inference system (ANFIS) model for wire-EDM. Expert Syst. Appl. 2009, 36, 6135–6139. [Google Scholar] [CrossRef]
- Lin, J.L.; Lin, C.L. The use of grey-fuzzy logic for the optimization of the manufacturing process. J. Mater. Process. Technol. 2005, 160, 9–14. [Google Scholar] [CrossRef]
- Salman, Ö.; Kayacan, M.C. Evolutionary programming method for modeling the EDM parameters for roughness. J. Mater. Process. Technol. 2008, 200, 347–355. [Google Scholar] [CrossRef]
- Tzeng, Y.F.; Chen, F.C. Multi-objective optimisation of high-speed electrical discharge machining process using a Taguchi fuzzy-based approach. Mater. Des. 2007, 28, 1159–1168. [Google Scholar] [CrossRef]
- Yan, M.T.; Fang, C.C. Application of genetic algorithm-based fuzzy logic control in wire transport system of wire-EDM machine. J. Mater. Process. Technol. 2008, 205, 128–137. [Google Scholar] [CrossRef]
- Yan, M.T. An adaptive control system with self-organizing fuzzy sliding mode control strategy for micro wire-EDM machines. Int. J. Adv. Manuf. Technol. 2010, 50, 315–328. [Google Scholar] [CrossRef]
- Rajyalakshmi, G.; Ramaiah, P.V. Application of Taguchi, fuzzy-grey relational analysis for process parameters optimization of WEDM on Inconel-825. Indian J. Sci. Technol. 2015, 8, 1–12. [Google Scholar] [CrossRef]
- Rupajati, P.; Soepangkat, B.O.P.; Pramujati, B.; Agustin, H.C. Optimization of recast layer thickness and surface roughness in the wire EDM process of AISI H13 tool steel using Taguchi and fuzzy logic. Appl. Mech. Mater. 2014, 493, 529–534. [Google Scholar] [CrossRef]
- Soepangkat, B.O.P.; Pramujati, B. Optimization of Surface Roughness and Recast Layer Thickness in the Wire-EDM Process of AISI D2 Tool Steel using Taguchi-Grey-Fuzzy. Appl. Mech. Mater. 2013, 393, 21–28. [Google Scholar] [CrossRef]
- Mouralova, K.; Kovar, J.; Klakurkova, L.; Bednar, J.; Benes, L.; Zahradnicek, R. Analysis of surface morphology and topography of pure aluminium machined using WEDM. Measurement 2018, 114, 169–176. [Google Scholar] [CrossRef]
- Mouralova, K.; Kovar, J.; Klakurkova, L.; Prokes, T.; Horynova, M. Comparison of morphology and topography of surfaces of WEDM machined structural materials. Measurement 2017, 104, 12–20. [Google Scholar] [CrossRef]
- Mouralova, K.; Kovar, J.; Klakurkova, L.; Blazik, P.; Kalivoda, M.; Kousal, P. Analysis of surface and subsurface layers after WEDM for Ti-6Al-4V with heat treatment. Measurement 2018, 116, 556–564. [Google Scholar] [CrossRef]
- Mouralova, K.; Kovar, J.; Klakurkova, L.; Prokes, T. Effect of Width of Kerf on Machining Accuracy and Subsurface Layer After WEDM. J. Mater. Eng. Perform. 2018, 24, 1908–1916. [Google Scholar] [CrossRef]
- Mouralova, K.; Klakurkova, L.; Matousek, R.; Prokes, T.; Hrdy, R.; Kana, V. Influence of the cut direction through the semi-finished product on the occurrence of cracks for X210Cr12 steel using WEDM. Arch. Civ. Mech. Eng. 2018, 18, 1318–1331. [Google Scholar] [CrossRef]
- Abraservice, Creusabro 4800. Available online: https://www.abraservice.com/files/ABRA-gmo_en.pdf (accessed on 20 December 2019).
- Mouralova, K. Moderní technologie drátového elektroerozivního řezání kovových slitin. Ph.D. Thesis, Brno University of Technology, Brno, Czech Republic, 2015. [Google Scholar]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; Wiley: Hoboken, NJ, USA, 2013; ISBN 978-1118146927-X. [Google Scholar]
- Singh, T.; Misra, J.P.; Upadhyay, V.; Rao, P.S. An Adaptive neuro-fuzzy inference system (ANFIS) for wire-EDM of ballistic grade aluminium alloy. Int. J. Automot. Mech. Eng. 2018, 15, 5295–5307. [Google Scholar] [CrossRef]
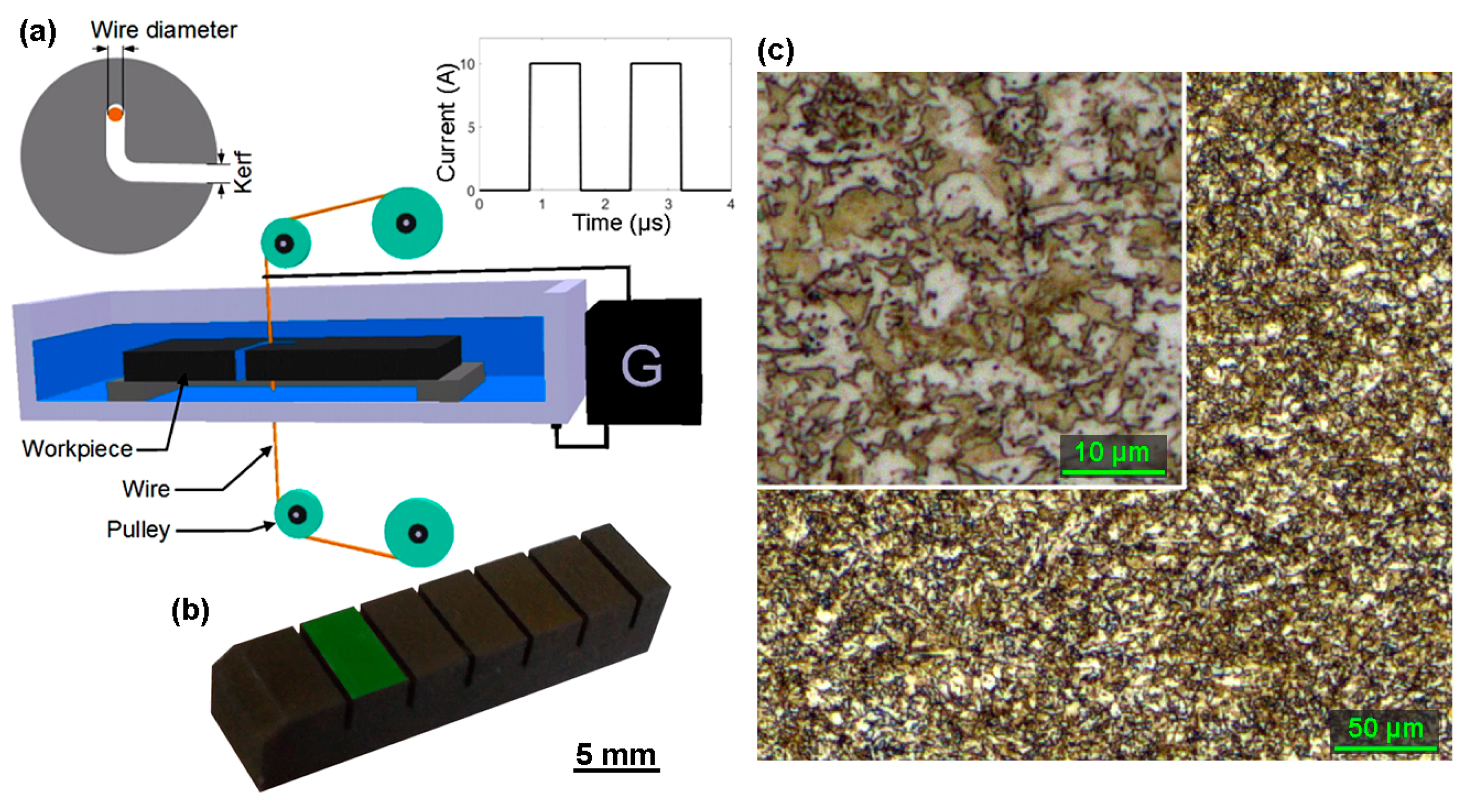


| Parameter | Gap Voltage | Pulse on Time | Pulse off Time | Wire Feed | Discharge Current |
|---|---|---|---|---|---|
| (V) | (µs) | (µs) | (m·min−1) | (A) | |
| Minimum | 50 | 6 | 30 | 10 | 25 |
| Maximum | 70 | 10 | 50 | 14 | 35 |
| Number of Sample | Gap Voltage (V) | Pulse on Time (µs) | Pulse off Time (µs) | Wire Feed (m·min−1) | Discharge Current (A) | Cutting Speed (mm∙min−1) | Number of Sample | Gap Voltage (V) | Pulse on Time (µs) | Pulse off Time (µs) | Wire Feed (m·min−1) | Discharge Current (A) | Cutting Speed (mm∙min−1) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 70 | 8 | 40 | 12 | 30 | 5.4 | 18 | 60 | 8 | 40 | 12 | 30 | 5.4 |
| 2 | 60 | 8 | 30 | 12 | 30 | 5.6 | 19 | 60 | 8 | 40 | 12 | 30 | 5.4 |
| 3 | 60 | 8 | 40 | 12 | 25 | 4.9 | 20 | 70 | 6 | 50 | 14 | 25 | 3.9 |
| 4 | 60 | 10 | 40 | 12 | 30 | 6.1 | 21 | 50 | 6 | 30 | 14 | 25 | 4.9 |
| 5 | 50 | 8 | 40 | 12 | 30 | 5.3 | 22 | 60 | 8 | 40 | 12 | 30 | 5.4 |
| 6 | 60 | 8 | 50 | 12 | 30 | 5.1 | 23 | 70 | 10 | 30 | 14 | 25 | 4.9 |
| 7 | 60 | 6 | 40 | 12 | 30 | 4.8 | 24 | 50 | 6 | 50 | 10 | 25 | 3.9 |
| 8 | 60 | 8 | 40 | 12 | 35 | 5.8 | 25 | 60 | 8 | 40 | 12 | 30 | 5.3 |
| 9 | 60 | 8 | 40 | 10 | 30 | 5.4 | 26 | 50 | 10 | 50 | 14 | 25 | 4.7 |
| 10 | 60 | 8 | 40 | 14 | 30 | 5.4 | 27 | 50 | 10 | 30 | 10 | 25 | 5.5 |
| 11 | 60 | 8 | 40 | 12 | 30 | 5.4 | 28 | 50 | 6 | 50 | 14 | 35 | 4.8 |
| 12 | 50 | 6 | 30 | 10 | 35 | 5.3 | 29 | 50 | 10 | 50 | 10 | 35 | 5.8 |
| 13 | 70 | 10 | 50 | 10 | 25 | 4.8 | 30 | 70 | 6 | 30 | 14 | 35 | 4.9 |
| 14 | 70 | 10 | 30 | 10 | 35 | 6.2 | 31 | 50 | 10 | 30 | 14 | 35 | 5.9 |
| 15 | 60 | 8 | 40 | 12 | 30 | 5.4 | 32 | 60 | 8 | 40 | 12 | 30 | 5.4 |
| 16 | 70 | 6 | 50 | 10 | 35 | 4.9 | 33 | 70 | 6 | 30 | 10 | 25 | 4.6 |
| 17 | 70 | 10 | 50 | 14 | 35 | 5.9 | - | - | - | - | - | - | - |
| Parameter | P-Value |
|---|---|
| Linear | |
| pulse on time | 0.000 |
| pulse off time | 0.000 |
| discharge current | 0.000 |
| 2–Way Interaction | - |
| pulse off time and discharge current | 0.023 |
| Quadratic | - |
| gap voltage | 0.000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mouralova, K.; Hrabec, P.; Benes, L.; Otoupalik, J.; Bednar, J.; Prokes, T.; Matousek, R. Verification of Fuzzy Inference System for Cutting Speed while WEDM for the Abrasion-Resistant Steel Creusabro by Conventional Statistical Methods. Metals 2020, 10, 92. https://doi.org/10.3390/met10010092
Mouralova K, Hrabec P, Benes L, Otoupalik J, Bednar J, Prokes T, Matousek R. Verification of Fuzzy Inference System for Cutting Speed while WEDM for the Abrasion-Resistant Steel Creusabro by Conventional Statistical Methods. Metals. 2020; 10(1):92. https://doi.org/10.3390/met10010092
Chicago/Turabian StyleMouralova, Katerina, Pavel Hrabec, Libor Benes, Jan Otoupalik, Josef Bednar, Tomas Prokes, and Radomil Matousek. 2020. "Verification of Fuzzy Inference System for Cutting Speed while WEDM for the Abrasion-Resistant Steel Creusabro by Conventional Statistical Methods" Metals 10, no. 1: 92. https://doi.org/10.3390/met10010092
APA StyleMouralova, K., Hrabec, P., Benes, L., Otoupalik, J., Bednar, J., Prokes, T., & Matousek, R. (2020). Verification of Fuzzy Inference System for Cutting Speed while WEDM for the Abrasion-Resistant Steel Creusabro by Conventional Statistical Methods. Metals, 10(1), 92. https://doi.org/10.3390/met10010092






