A 3D FEM-Based Numerical Analysis of the Sheet Metal Strip Flowing Through Drawbead Simulator
Abstract
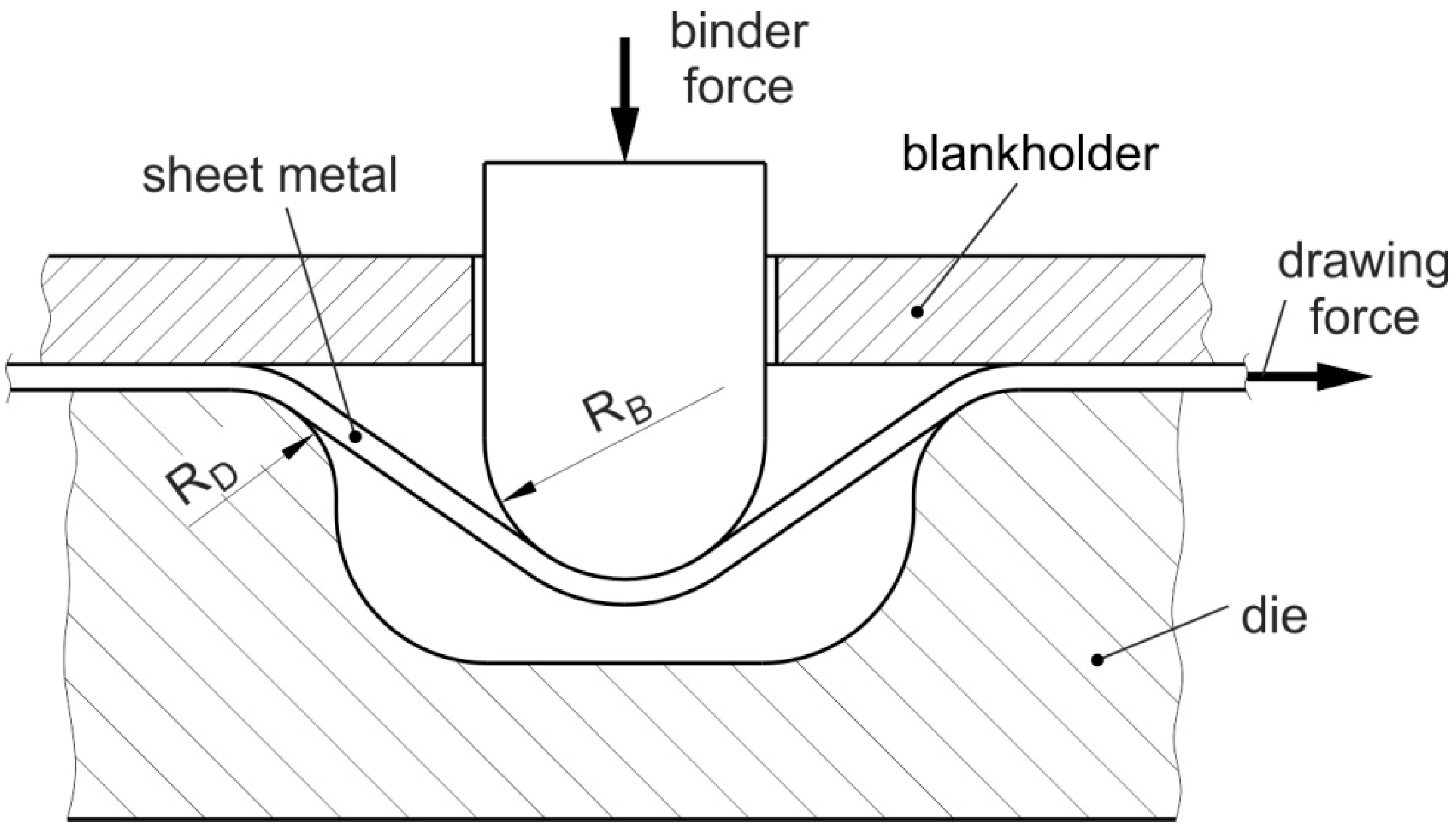
1. Introduction
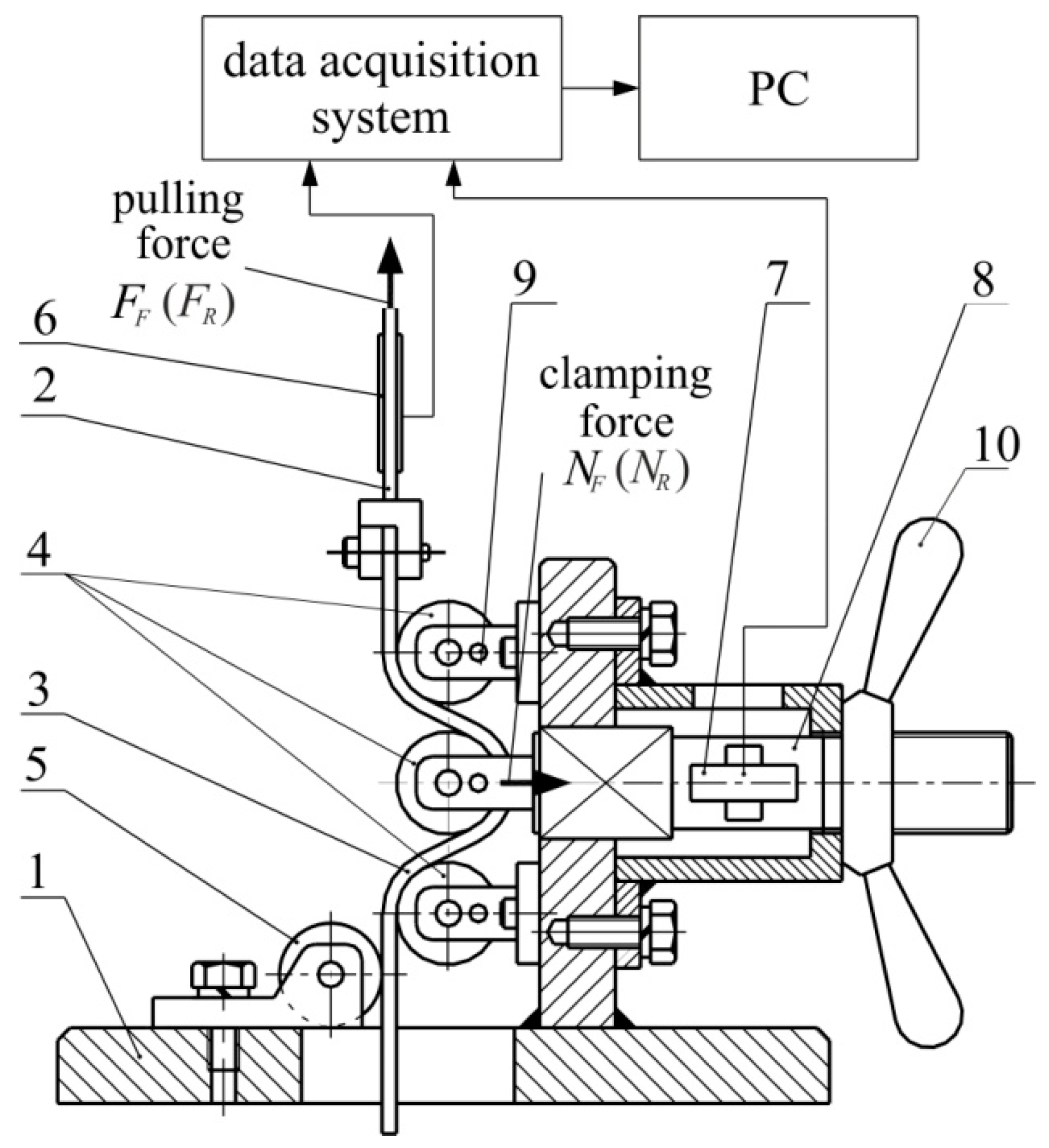
2. Experimental
2.1. Material
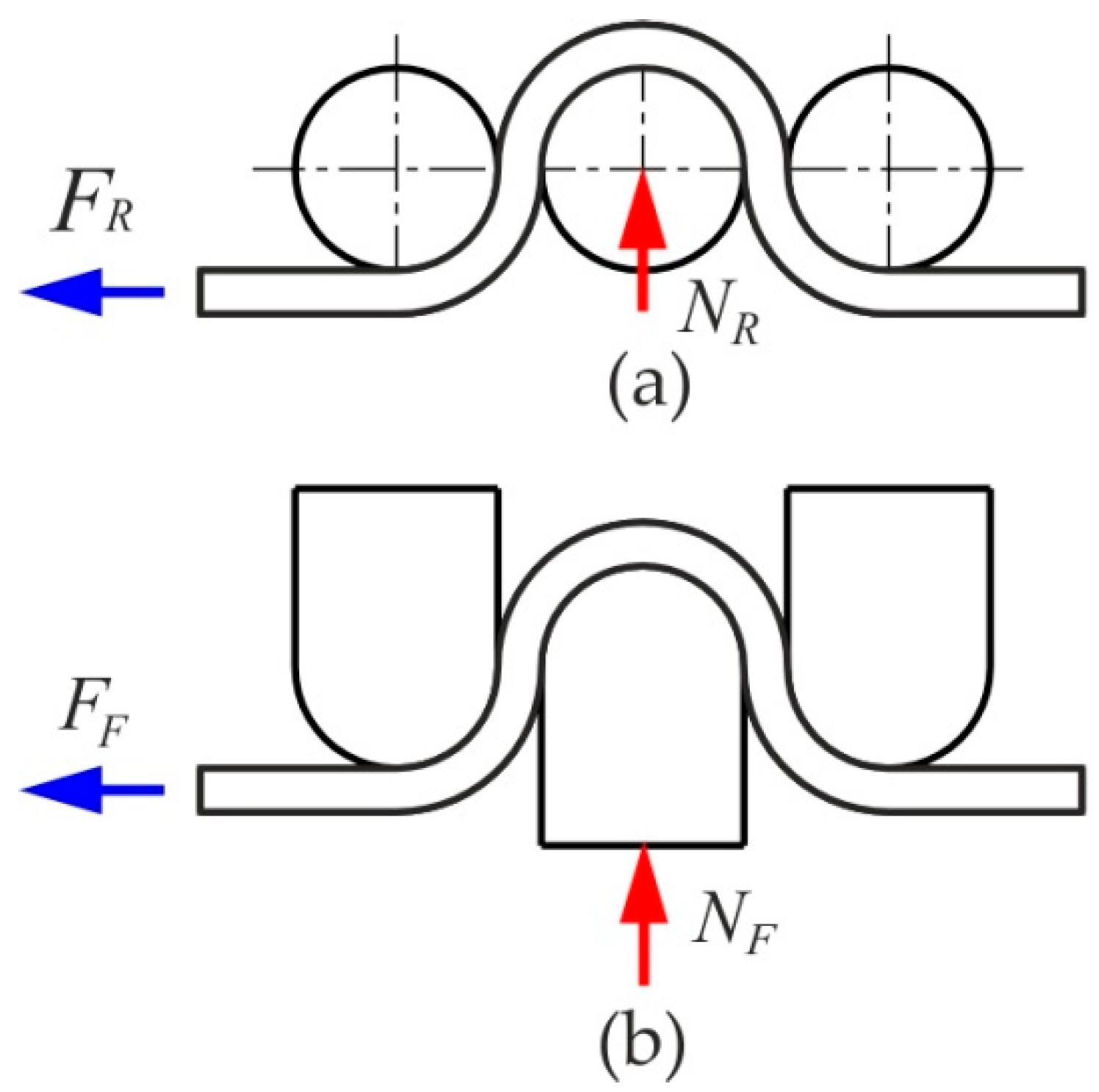
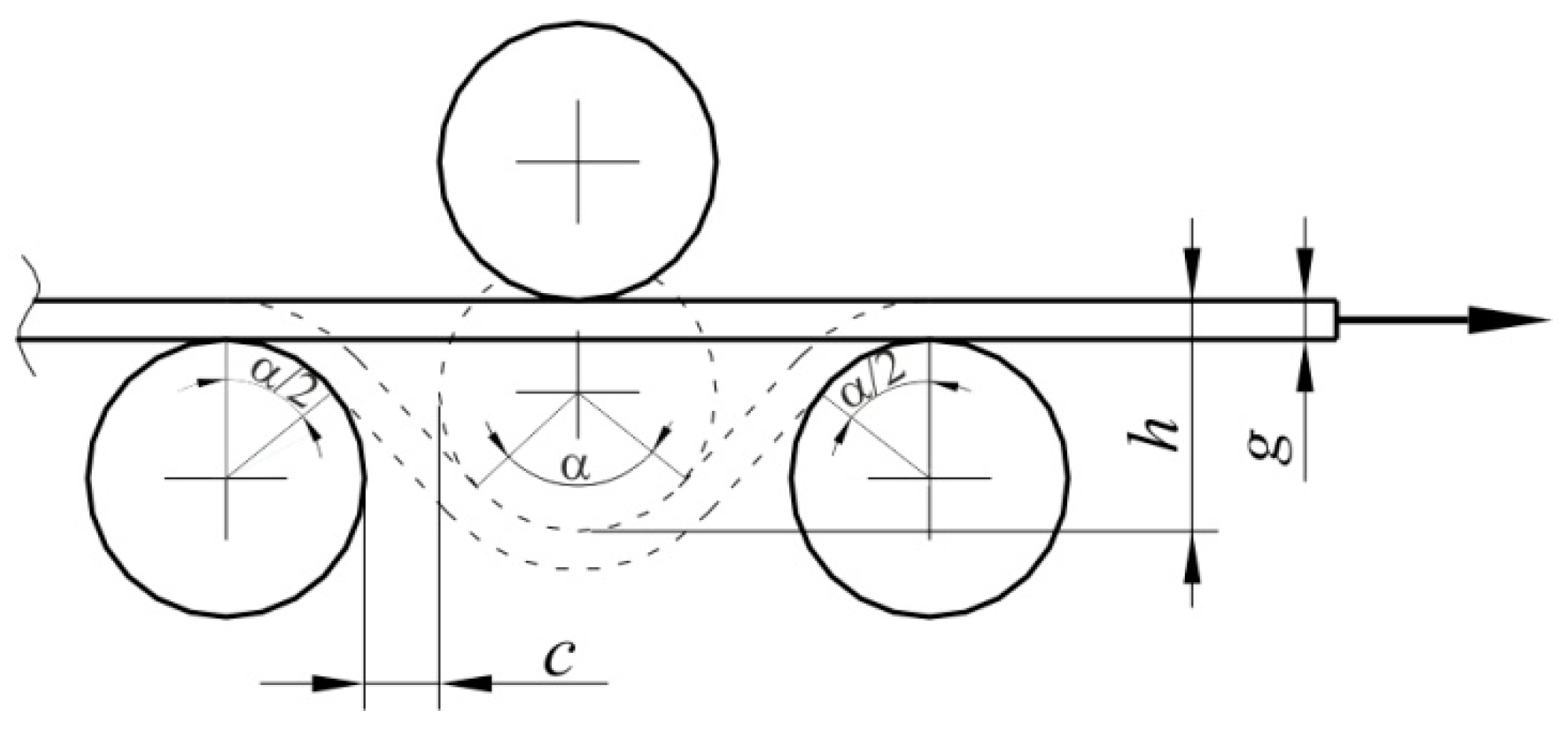
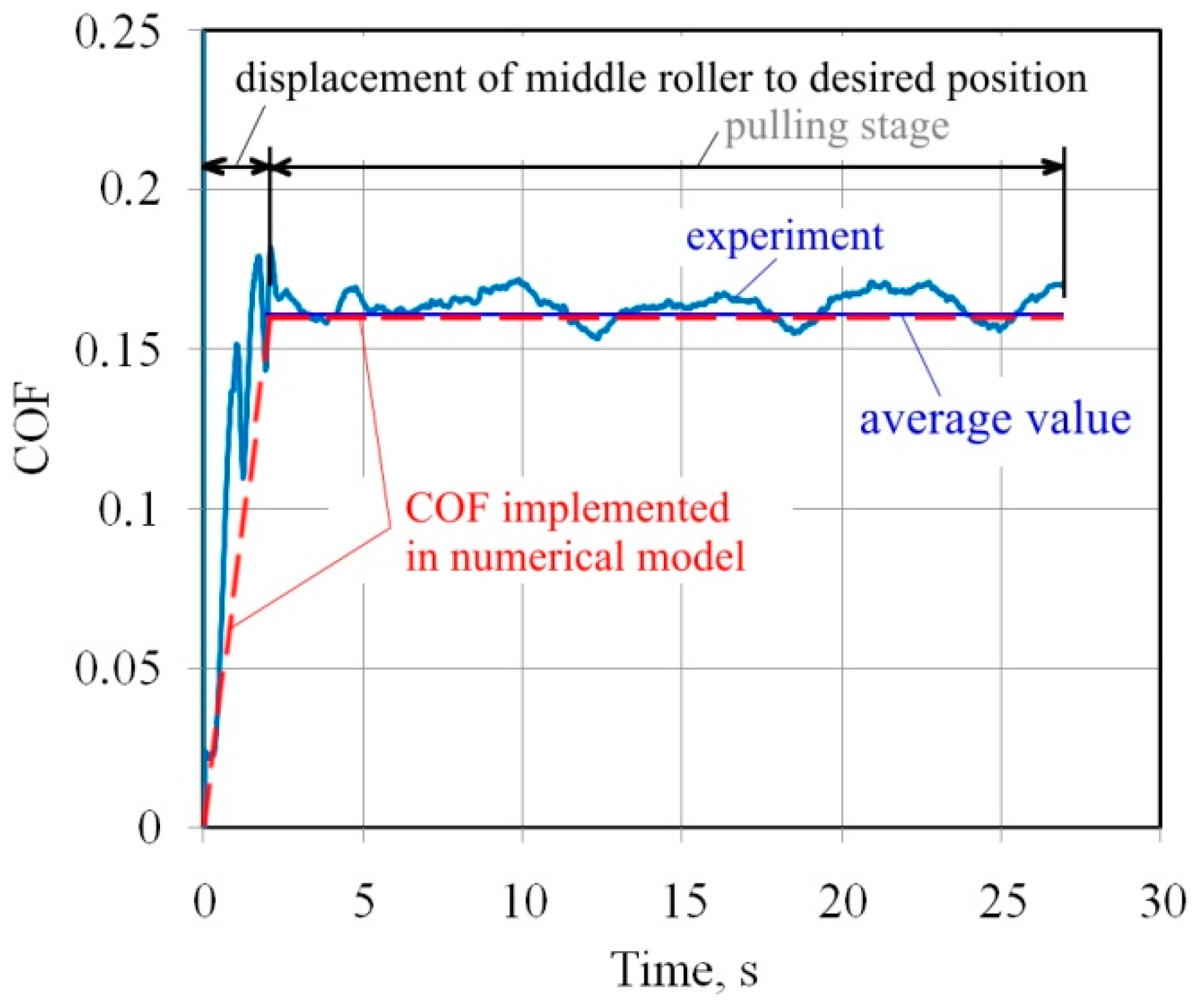
2.2. Method
3. Numerical Modeling
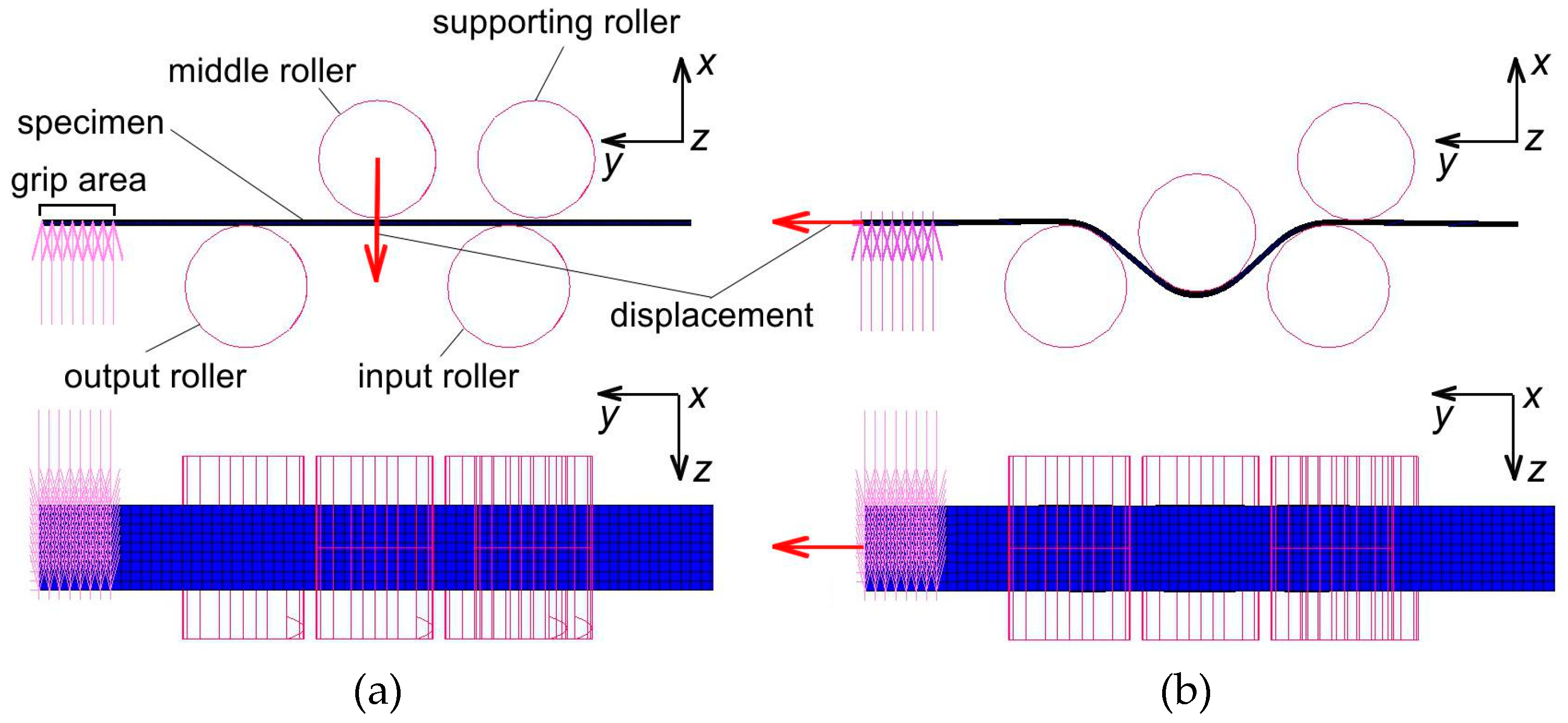
3.1. Description of the FE Model
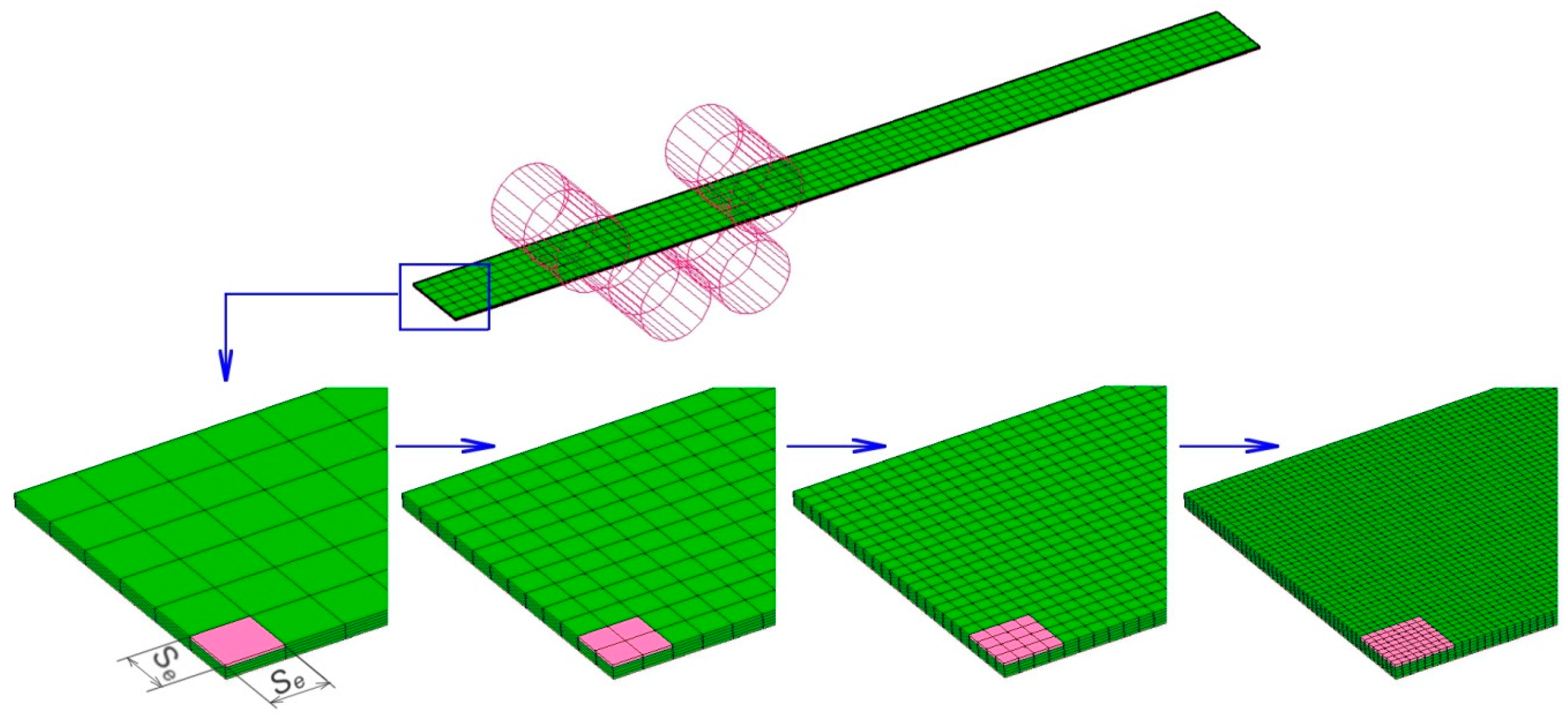
3.2. Mesh Sensitivity Analysis
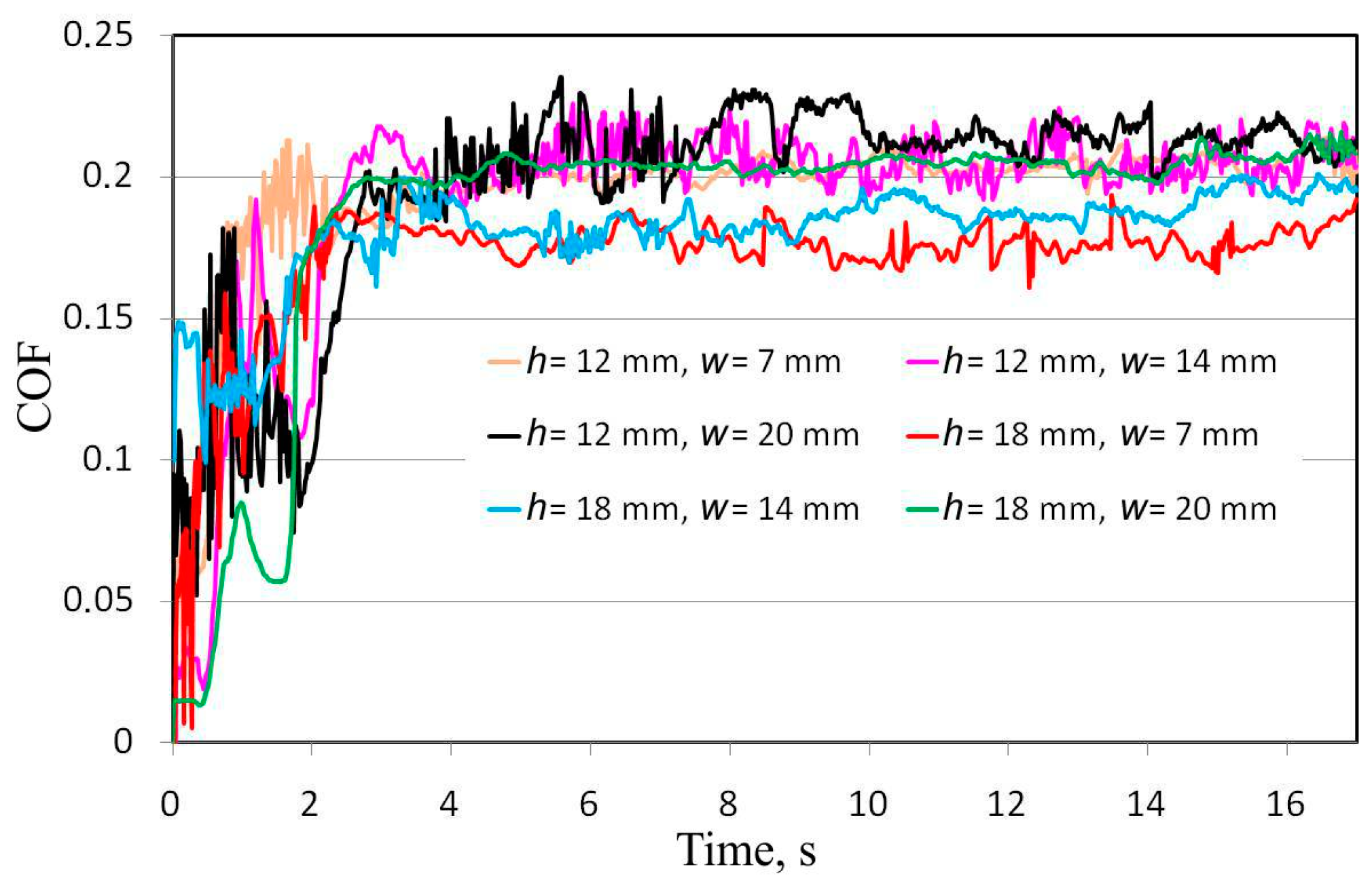
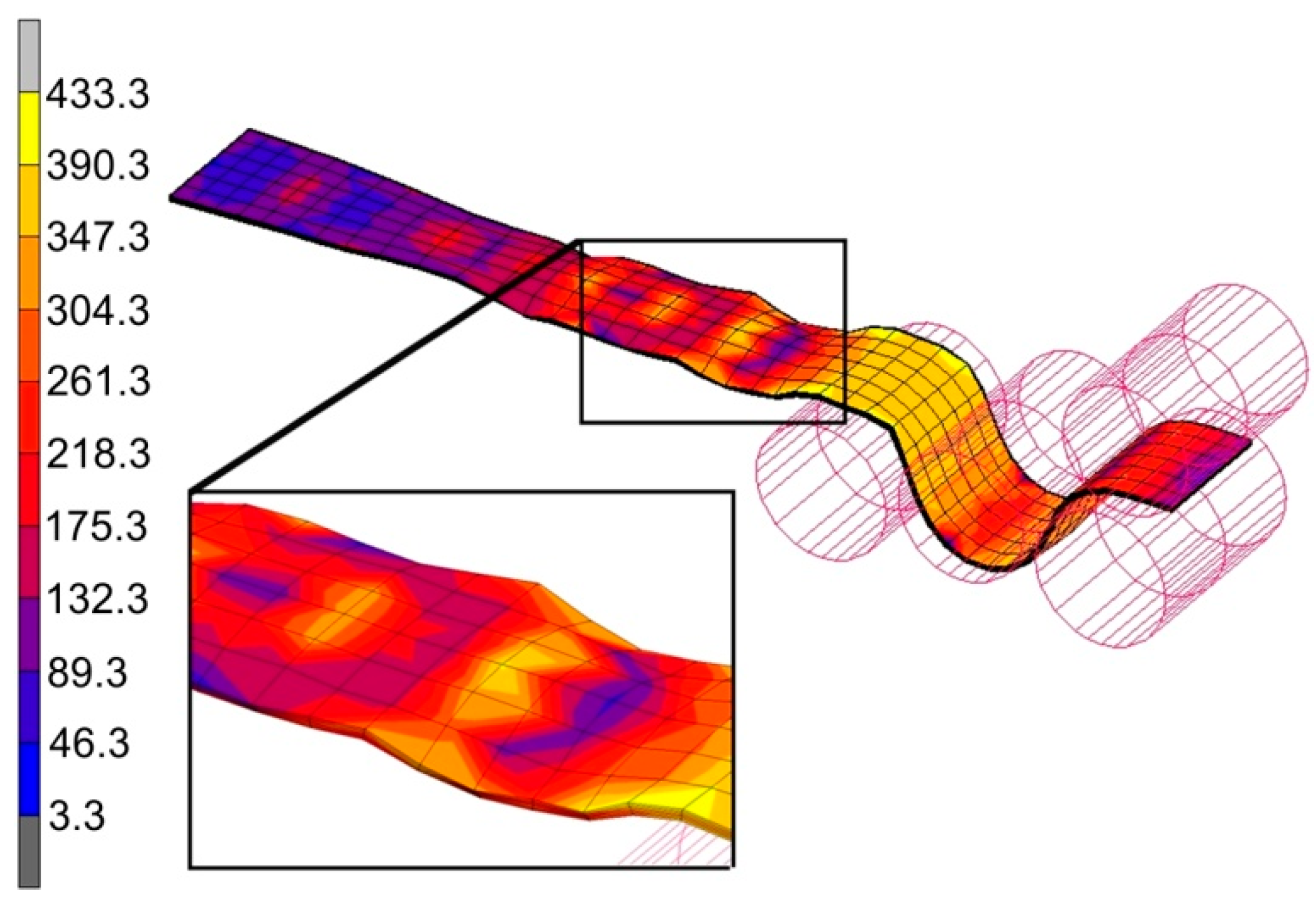
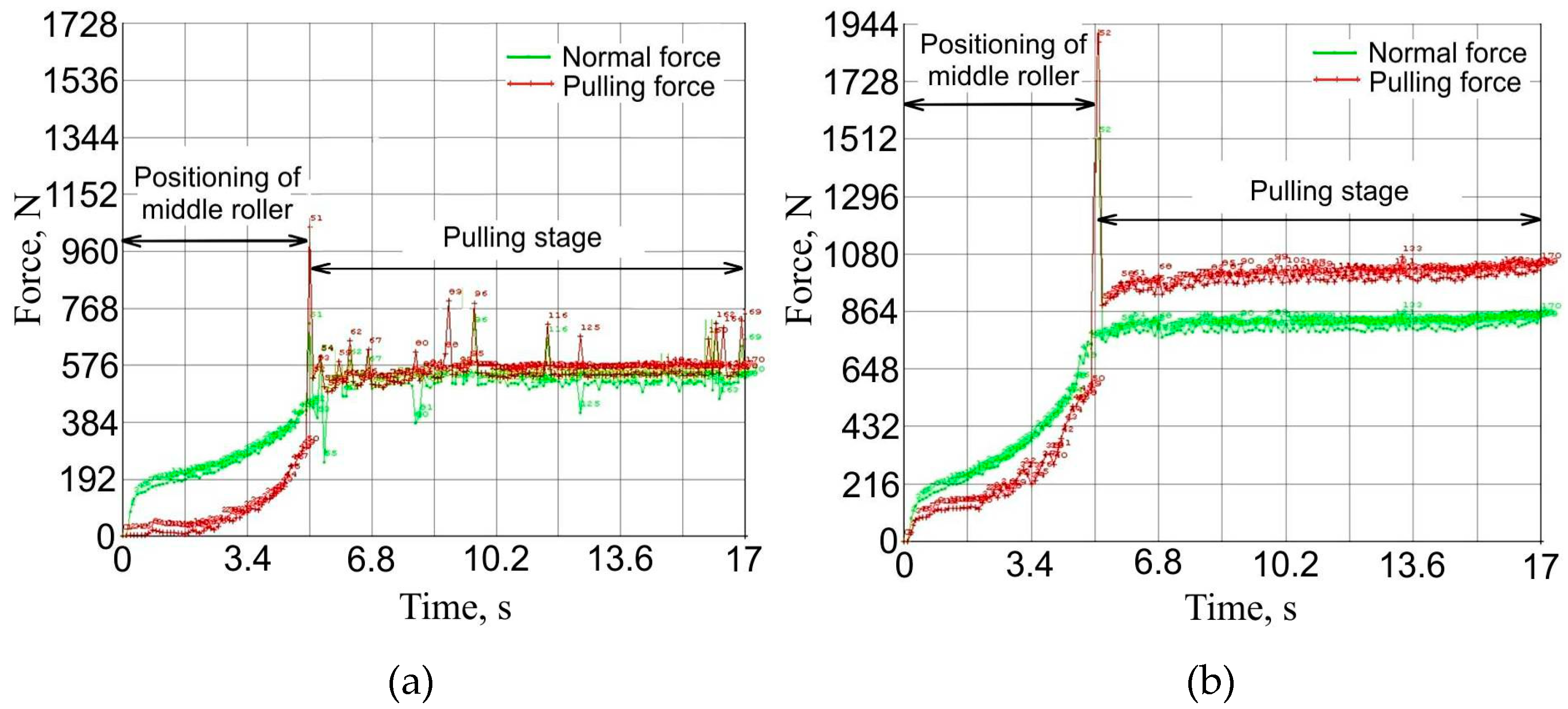
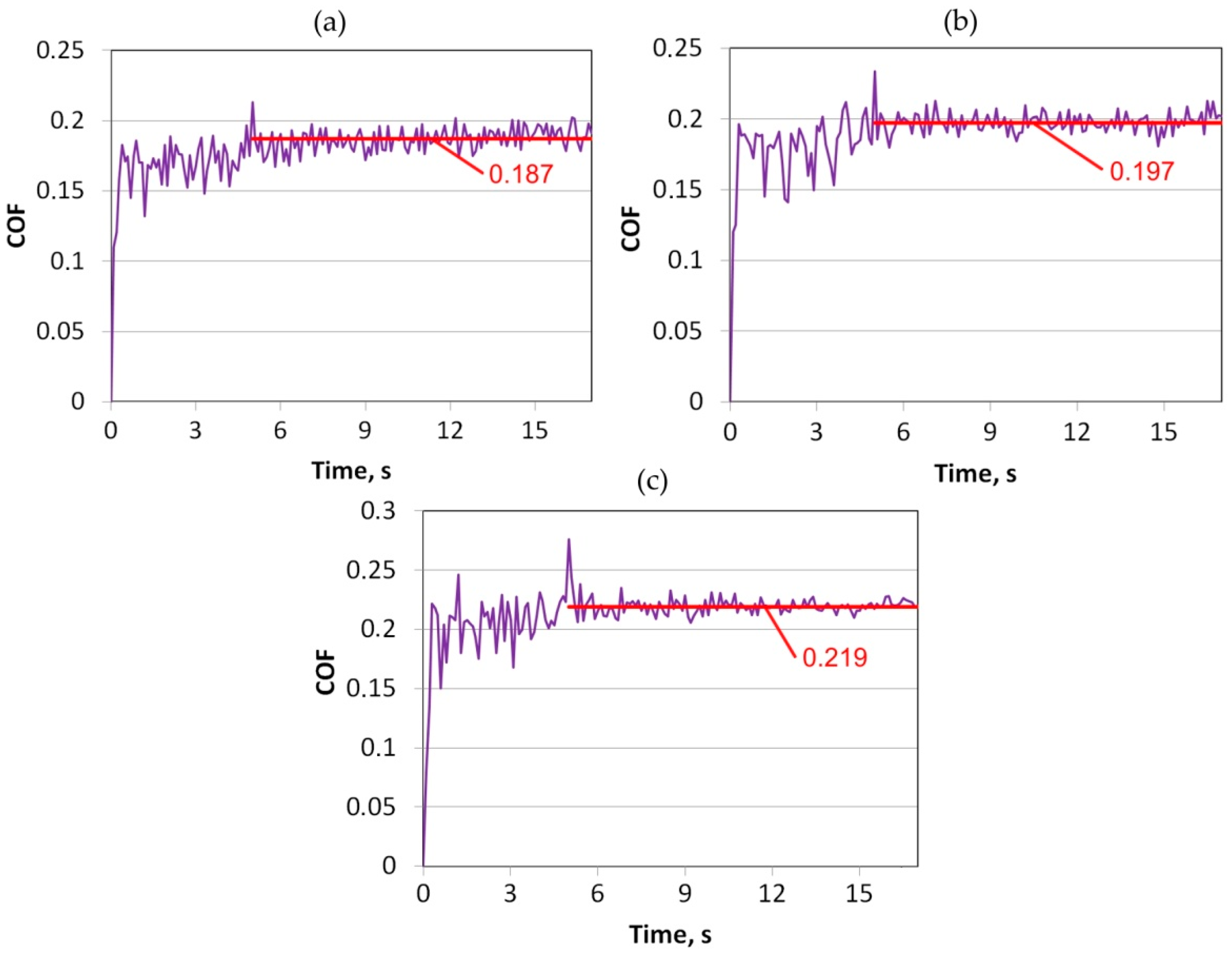
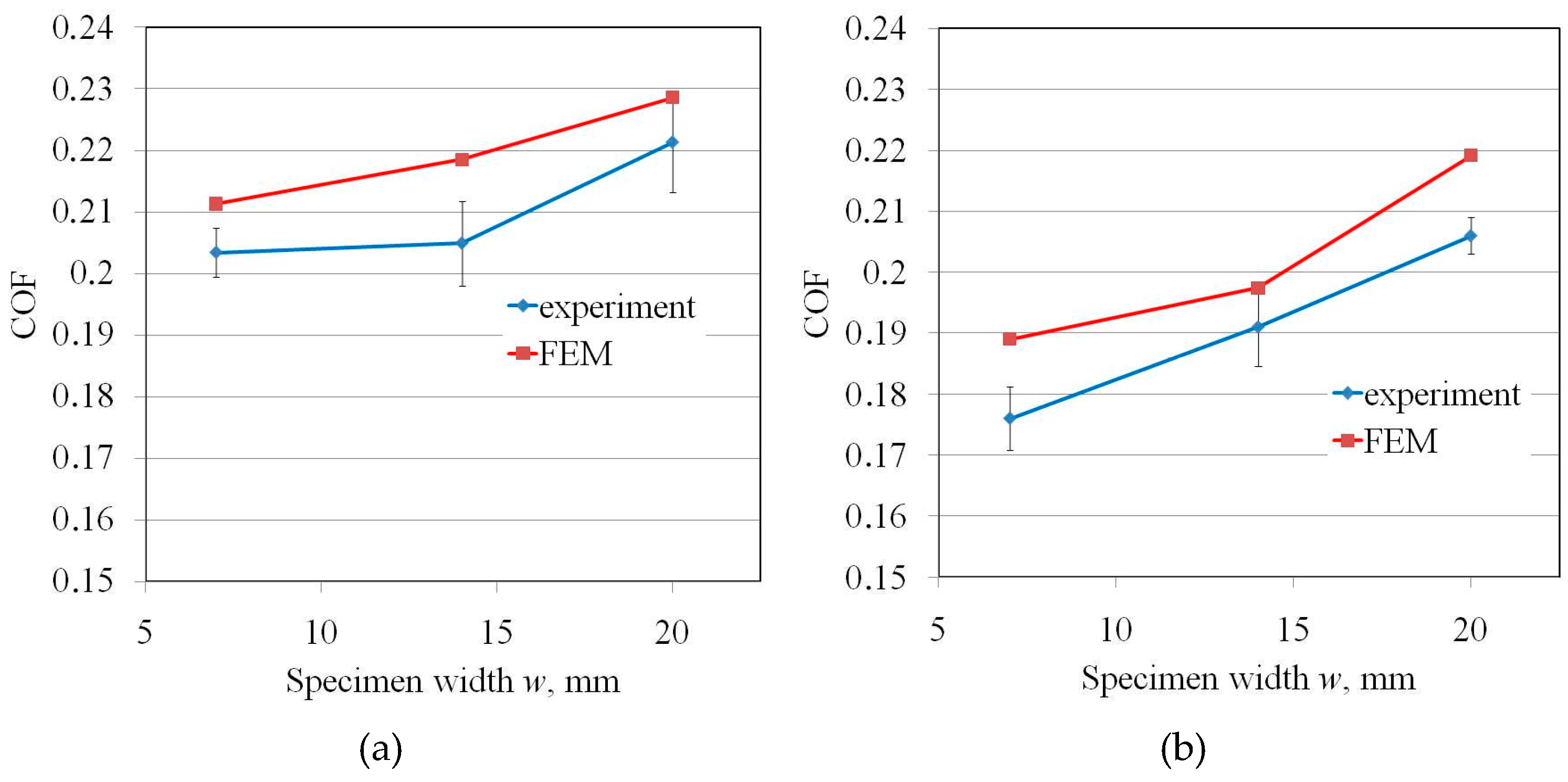
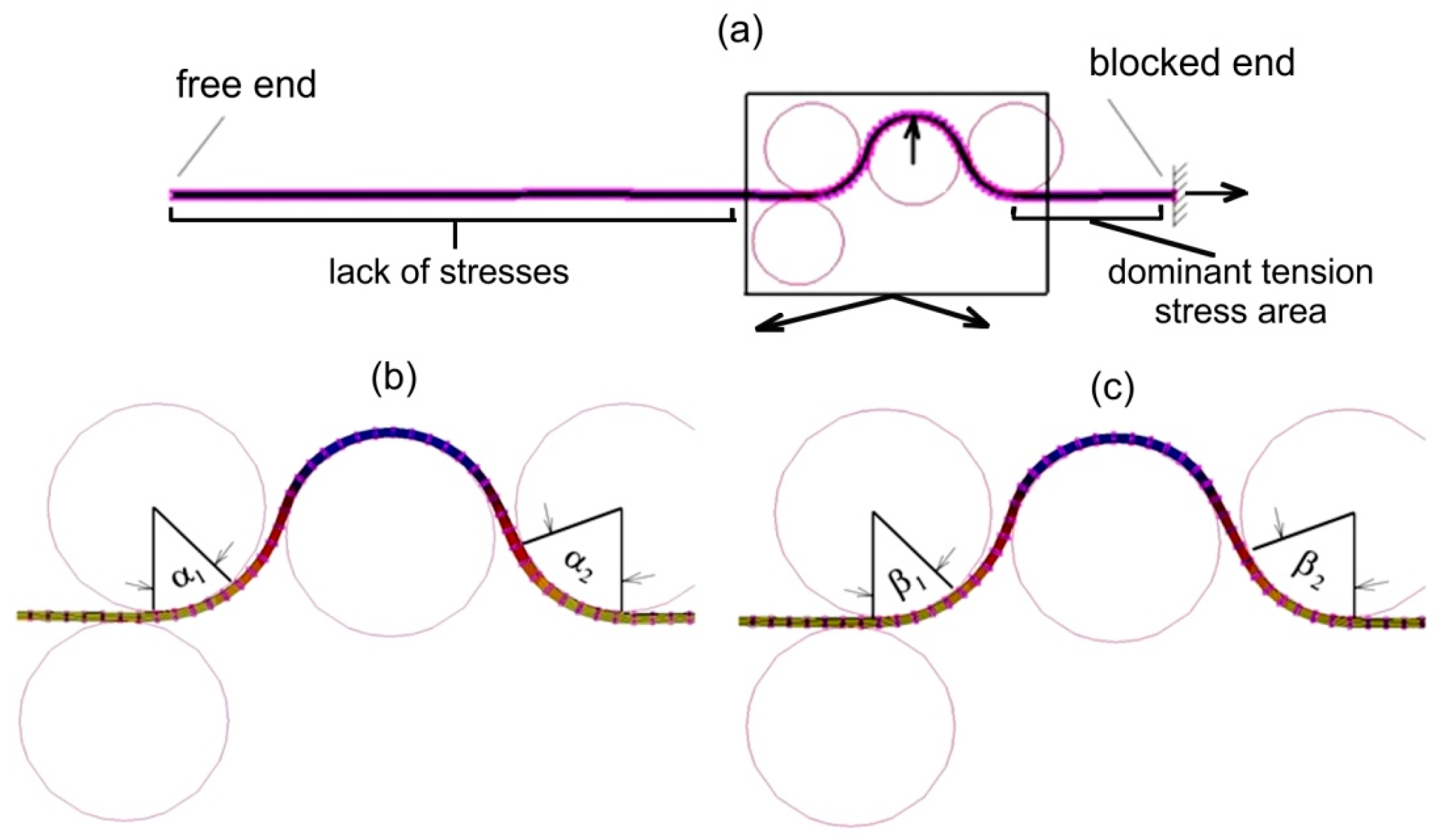
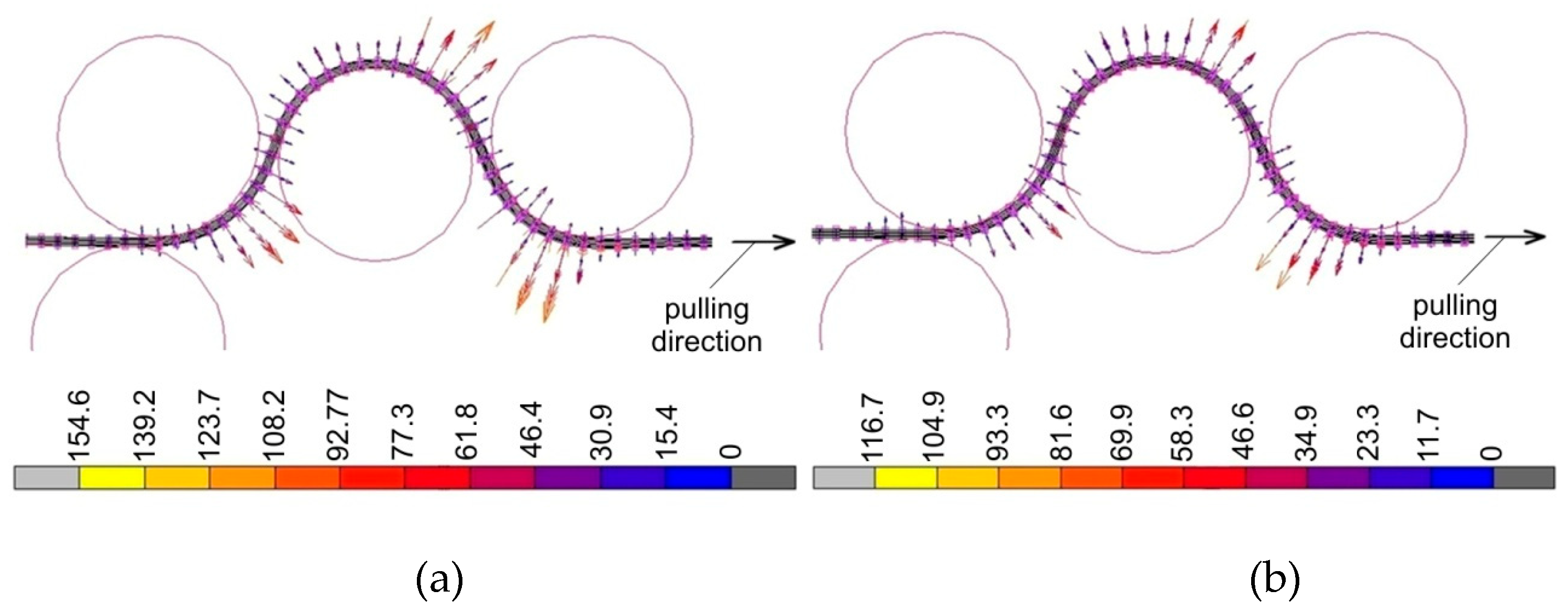
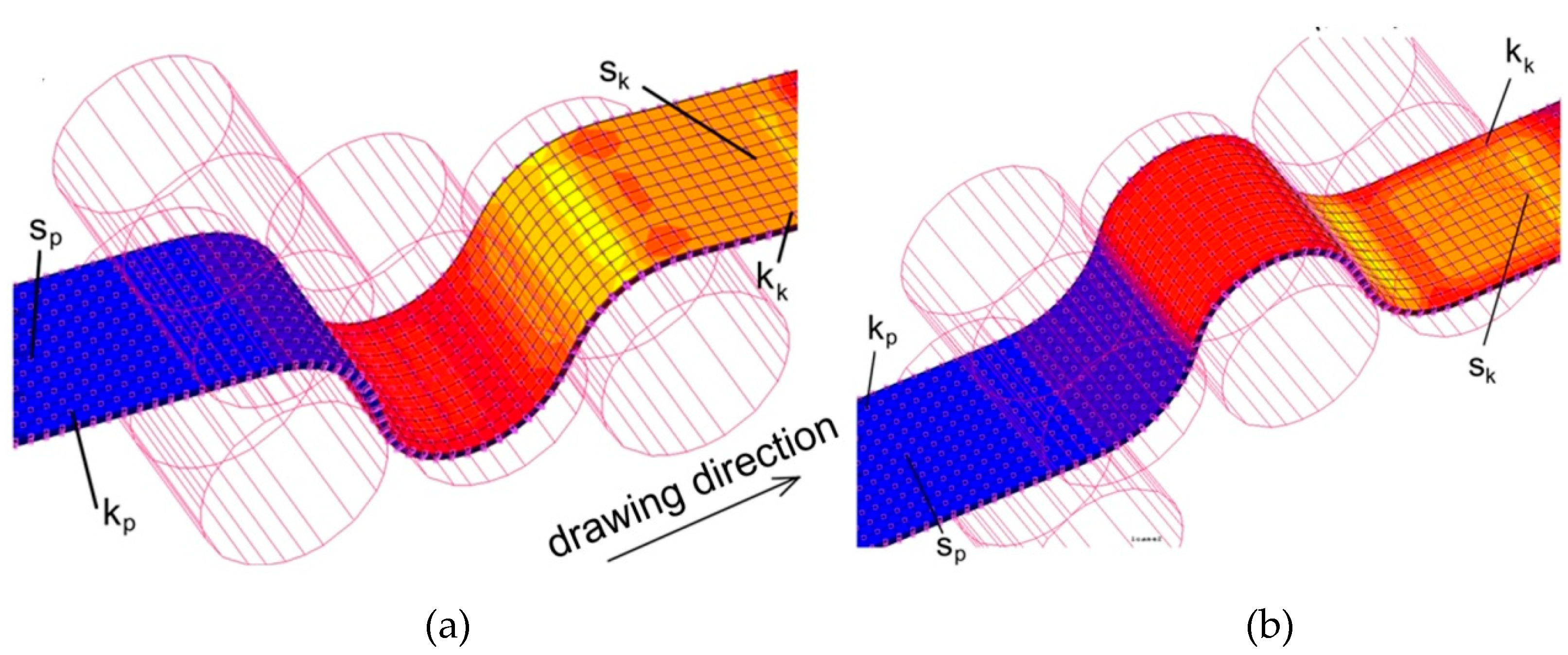
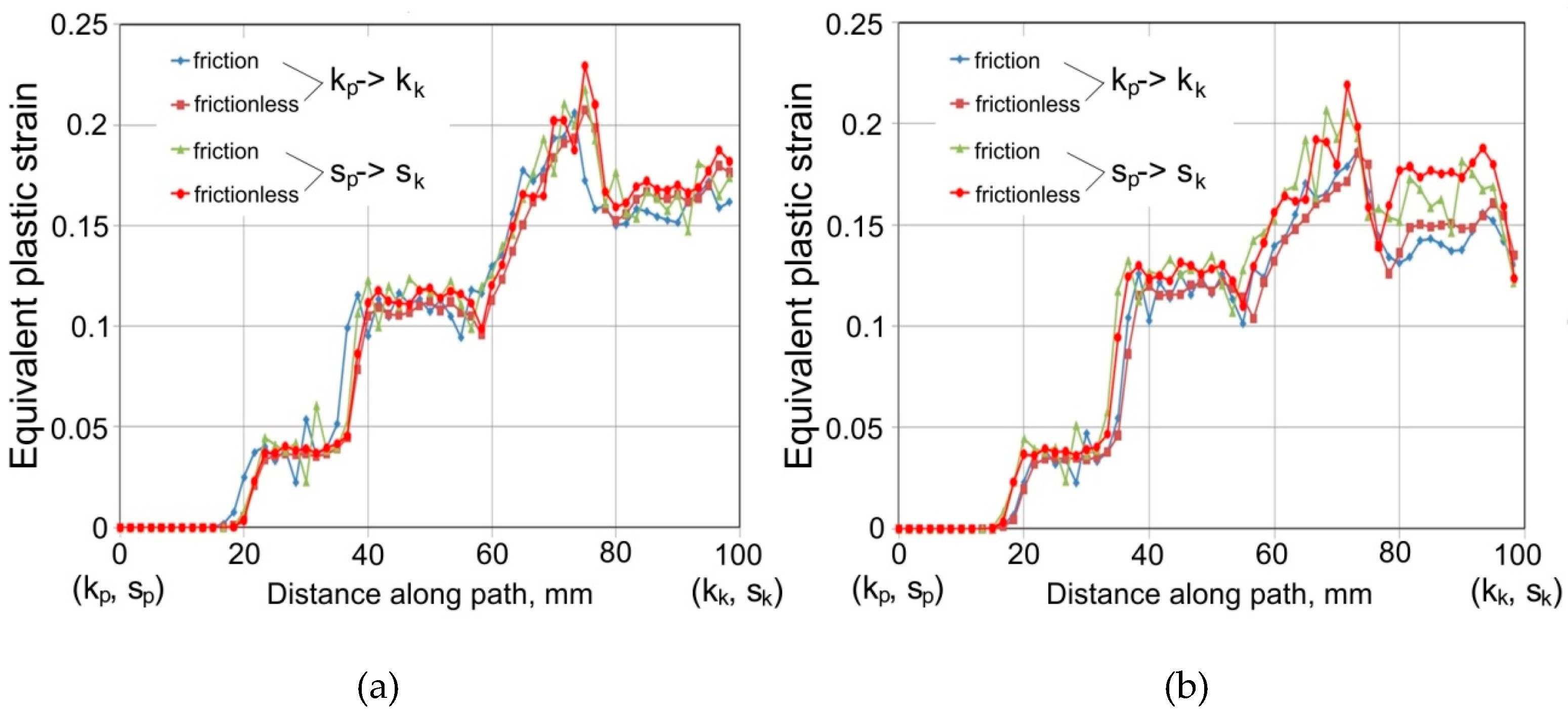
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Trzepieciński, T.; Bazan, A.; Lemu, H.G. Frictional characteristics of steel sheets used in automotive industry. Int. J. Automot. Technol. 2015, 16, 849–863. [Google Scholar] [CrossRef]
- Olsson, D.D.; Bay, N.; Andreasen, J.L. Direct Friction Measurement in Draw Bead Testing. In Proceedings of the 8th International Conference on Technology of Plasticity, Verona, Italy, 9–13 October 2005. [Google Scholar]
- Trzepieciński, T.; Lemu, H.G. Effect of computational parameters on springback prediction by numerical simulation. Metals 2017, 7, 380. [Google Scholar] [CrossRef]
- Zhang, R.; Shao, Z.; Lin, J. A review on modelling techniques for formability prediction of sheet metal forming. Int. J. Lightweight Mater. Manuf. 2018, 1, 115–125. [Google Scholar] [CrossRef]
- Figueiredo, L.; Ramalho, A.; Oliveira, M.C.; Menezes, L.F. Experimental study of friction in sheet metal forming. Wear 2011, 271, 1651–1657. [Google Scholar] [CrossRef]
- Wang, C.; Ma, R.; Zhao, J.; Zhao, J. Calculation method and experimental study of coulomb friction coefficient in sheet metal forming. J. Manuf. Process. 2017, 27, 126–137. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Gelgele, H.L. Investigation of anisotropy problems in sheet metal forming using finite element method. Int. J. Mater. Form. 2011, 4, 357–369. [Google Scholar] [CrossRef]
- Dou, S.; Xia, J. Analysis of sheet metal forming (stamping process): A study of the variable friction coefficient on 5052 aluminium alloy. Metals 2019, 9, 853. [Google Scholar] [CrossRef]
- Nine, H.D. Drawbead forces in sheet metal forming. In Mechanics of Sheet Metal Forming, 1st ed.; Koistinen, D.P., Wang, N.M., Eds.; Springer: Boston, MA, USA, 1978; pp. 179–211. [Google Scholar]
- Jadhav, S.; Schoiswoh, M.; Buchmayr, B. Tribology test methods and simulations of the effect of friction on the formability of automotive steel sheets. Metall. Ital. 2018, 9, 56–63. [Google Scholar]
- Sigvant, M.; Pilthammar, J.; Hol, J.; Wiebenga, J.H.; Chezan, T.; Carleer, B.; van den Boogard, T. Friction in sheet metal forming: Influence of surface roughness and strain rate on sheet metal forming simulation results. Procedia Manuf. 2019, 29, 512–519. [Google Scholar] [CrossRef]
- Recklin, V.; Dietrich, F.; Groche, P. Influence of test stand and contact size sensitivity on the friction coefficient in sheet metal forming. Lubricants 2018, 6, 41. [Google Scholar] [CrossRef]
- Li, G.; Long, X.; Yang, P.; Liang, Z. Advance on friction of stamping forming. Int. J. Adv. Manuf. Technol. 2018, 96, 21–38. [Google Scholar] [CrossRef]
- Murali, A.; Gopal, B.; Rajadurai, C. Analysis of influence od draw bead location and profile in hemispherical cup forming. Int. J. Eng. Technol. 2010, 2, 356–360. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Q.; Liu, Y.; Zhang, Z. A robust and accurate geometric model for automated design of drawbeads in sheet metal forming. Comput. Aided Des. 2017, 92, 42–57. [Google Scholar] [CrossRef]
- Larsson, M. Computational characterization of drawbeads: A basic modeling method for data generation. J. Mater. Process. Technol. 2009, 209, 376–386. [Google Scholar] [CrossRef]
- Lee, M.G.; Chung, K.; Wagoner, R.H.; Keum, Y.T. A numerical method for rapid estimation of drawbead restraining force based on non-linear, anisotropic constitutive equations. Int. J. Solids Struct. 2008, 45, 3375–3391. [Google Scholar] [CrossRef][Green Version]
- Xie, Y. Geometric parameter inverse model for drawbeads based on grey relational analysis and GA-BP. AIP Conf. Proc. 2013, 1567, 1044–1047. [Google Scholar]
- Zhang, Q.; Liu, Y.; Zhang, Z. A new method for automatic optimization of drawbead geometry in the sheet metal forming process based on an iterative learning control mode. Int. J. Adv. Manuf. Technol. 2017, 88, 1845–1861. [Google Scholar] [CrossRef]
- Halkaci, H.S.; Turkoz, M.; Dilmec, M. Enhancing formability in hydromechanical deep drawing process adding a shallow drawbead to the blank holder. J. Mater. Process. Technol. 2014, 214, 1638–1646. [Google Scholar] [CrossRef]
- Bassoli, E.; Sola, A.; Denti, L.; Gatto, A. Experimental approach to measure the restraining force in deep drawing by means of a versatile draw bead simulator. Mater. Manuf. Process. 2019, 34, 1286–1295. [Google Scholar] [CrossRef]
- Nanayakkara, N.K.B.M.P.; Hodgson, P. Determination of drawbead contacts with variable bead penetration. Comput. Methods Mater. Sci. 2006, 6, 188–194. [Google Scholar]
- Alves, J.L.; Oliveira, M.C.; Menezes, L.F. Modeling Drawbeads in Deep Drawing Simulations. In III European Conference on Computational Mechanics; Motasoares, C.A., Ed.; Springer: Dordrecht, The Netherlands, 2006; p. 533. [Google Scholar]
- Duarte, E.N.; Oliveira, S.A.G.; Weyler, R.; Neamtu, L. A hybrid approach for estimating the drawbead restraining force in sheet metal forming. J. Braz. Soc. Mech. Sci. Eng. 2010, 32, 283–291. [Google Scholar] [CrossRef][Green Version]
- Moon, S.J.; Lee, M.G.; Lee, S.H.; Keum, Y.T. Equivalent drawbead models for sheet forming simulation. Met. Mater. Int. 2010, 16, 595–603. [Google Scholar] [CrossRef]
- Joshi, Y.; Christiansen, P.; Masters, I.; Bay, N.O.; Dashwood, R. Numerical modelling of drawbeads for forming of aluminium alloys. J. Phys. Conf. Ser. 2016, 734, 032082. [Google Scholar] [CrossRef]
- Stoughton, T.B. Model of Drawbead Forces in Sheet Mmetal Forming. In Proceedings of the 15th International Deep Drawing Research Group, Dearbon, MI, USA, 16–18 May 1988; p. 205. [Google Scholar]
- Bramhakshatriya, G.M.; Sharma, S.K.; Patel, B.C. Analysis on Effect of Die Fillet Radius and Draw Bead on Hemispherical Cup Forming. In Proceedings of the 2012 Students Conference on Engineering and Systems, Allahabad, Uttar Pradesh, India, 16–18 March 2012; pp. 1–6. [Google Scholar]
- Trzepieciński, T. 3D elasto-plastic FEM analysis of the sheet drawing of anisotropic steel sheet. Arch. Civ. Mech. Eng. 2010, 10, 95–106. [Google Scholar] [CrossRef]
- Tisza, M.; Lukács, Z.; Kovács, P.; Budai, D. Some recent developments in sheet metal forming for production of lighteight automotive parts. J. Phys. Conf. Ser. 2017, 896, 012087. [Google Scholar] [CrossRef]
- EN 10130 2009. Cold Rolled Low Carbon Steel Flat Products for Cold Forming—Technical Delivery Conditions; European Committee for Standardization: Brussels, Belgium, 2009. [Google Scholar]
- ISO 6892-1:2016. Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature; International Organization for Standardization: Geneva, Switzerland, 2016. [Google Scholar]
- Nanayakkara, N.K.; Kelly, G.L.; Hodgson, P.D. Determination of the coefficient of friction in partially penetrated draw beads. Steel Gr. 2004, 2, 677–680. [Google Scholar]
- Meinders, V.T. Developments in Numerical Simulations of the Real-Life Deep Drawing Process. Ph.D. Thesis, University of Twenty, Enschede, Holland, 11 February 2000. [Google Scholar]
- Von-Mises, R. Mechanik der festen Körper im plastisch—Deformablen Zustand. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen. Mathematisch. Physikalische Klasse 1913, 1913, 582–592. [Google Scholar]
- Marc® Volume B: Element Library; MSC Software Corporation: Santa Ana, CA, USA, 2010.
- Fejkiel, R. An Analysis of Frictional Resistance during Sheet Metal Passing Through the Draw Bead in the Sheet Metal Forming Process. Ph.D. Thesis, Rzeszow University of Technology, Rzeszów, Poland, 4 July 2019. [Google Scholar]
| C | Mn | P | S | Fe |
|---|---|---|---|---|
| ≤0.08 | ≤0.4 | ≤0.03 | ≤0.03 | remainder |
| Specimen Orientation | Yield Stress Rp0.2 (MPa) | Ultimate Tensile Stress Rm (MPa) | Elongation A50 (%) | Strengthening Coefficient K (MPa) | Strain Hardening Exponent n |
|---|---|---|---|---|---|
| 0° | 179 | 311 | 22 | 471 | 0.19 |
| 45° | 189 | 305 | 21 | 488 | 0.19 |
| 90° | 183 | 289 | 23 | 479 | 0.17 |
| Drawbead Height h, mm | Specimen Width w, mm | COF |
|---|---|---|
| 12 | 7 | 0.202 |
| 14 | 0.205 | |
| 20 | 0.221 | |
| 18 | 7 | 0.176 |
| 14 | 0.191 | |
| 20 | 0.206 |
| Element Size se × se mm2 | Number of Elements | Number of Nodes | Average Drawing Force, N | Computation Time, s |
|---|---|---|---|---|
| 3.334 × 3.334 | 1620 | 2695 | - | 1240 |
| 1.667 × 1.667 | 6480 | 8502 | 1041.6 | 6115 |
| 0.833 × 0.833 | 35,920 | 32,550 | 1050.1 | 56,829 |
| 0.417 × 0.417 | 103,680 | 127,302 | 1061.0 | 381,197 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trzepiecinski, T.; Fejkiel, R. A 3D FEM-Based Numerical Analysis of the Sheet Metal Strip Flowing Through Drawbead Simulator. Metals 2020, 10, 45. https://doi.org/10.3390/met10010045
Trzepiecinski T, Fejkiel R. A 3D FEM-Based Numerical Analysis of the Sheet Metal Strip Flowing Through Drawbead Simulator. Metals. 2020; 10(1):45. https://doi.org/10.3390/met10010045
Chicago/Turabian StyleTrzepiecinski, Tomasz, and Romuald Fejkiel. 2020. "A 3D FEM-Based Numerical Analysis of the Sheet Metal Strip Flowing Through Drawbead Simulator" Metals 10, no. 1: 45. https://doi.org/10.3390/met10010045
APA StyleTrzepiecinski, T., & Fejkiel, R. (2020). A 3D FEM-Based Numerical Analysis of the Sheet Metal Strip Flowing Through Drawbead Simulator. Metals, 10(1), 45. https://doi.org/10.3390/met10010045






