Scaling in the Local Strain-Rate Field during Jerky Flow in an Al-3%Mg Alloy

Abstract

Jerky flow in alloys, or the Portevin-Le Chatelier effect, presents an outstanding example of self-organization phenomena in plasticity. Recent acoustic emission investigations revealed that its microscopic dynamics is governed by scale invariance manifested as power-law statistics of intermittent events. As the macroscopic stress serrations show both scale invariance and characteristic scales, the micro-macro transition is an intricate question requiring an assessment of intermediate behaviors. The first attempt of such an investigation is undertaken in the present paper by virtue of a one-dimensional (1D) local extensometry technique and statistical analysis of time series. The data obtained complete the missing link and bear evidence to a coexistence of characteristic large events and power laws for smaller events. The scale separation is interpreted in terms of the phenomena of self-organized criticality and synchronization in complex systems. Furthermore, it is found that both the stress serrations and local strain-rate bursts agree with the so-called fluctuation scaling related to general mathematical laws and unifying various specific mechanisms proposed to explain scale invariance in diverse systems. Prospects of further investigations including the duality manifested by a wavy spatial organization of the local bursts of plastic deformation are discussed.

1. Introduction

Plastic flow of alloys is prone to instability caused by the interaction of mobile dislocations with solute atoms diffusing in their elastic fields, or dynamic strain aging (DSA) [1]. In the mathematical sense, the instability stems from the DSA transforming the monotonous dependence of the flow stress on the plastic strain rate, σ($\dot{\epsilon }$), into an N-shaped function with an interval of negative strain-rate sensitivity (SRS). In tensile tests with a constant applied strain rate, ${\dot{\epsilon }}_a$, this nonlinearity must give rise to stress serrations caused by repetitive strain-rate jumps within localized deformation bands [2,3,4,5,6,7,8,9,10,11,12,13]. Such jerky flow is observed in various alloys and is well-known as the Portevin-Le Chatelier, or PLC, effect [14]. It is generally agreed that the PLC effect is governed by the DSA mechanism. Were the motion of all dislocations identical, it would result in periodic relaxation oscillations [2,3]. The intrinsic strain heterogeneity leads to complex behaviors of real materials.

The application of various methods of time-series analysis to serrated deformation curves showed that jerky flow cannot be described as random fluctuations about the ideal case of periodic oscillations [15,16,17,18,19,20,21]. Moreover, distinct kinds of complex dynamics arise when experimental conditions are varied. In particular, whereas power-law distributions of stress drop amplitudes and durations, tantamount to scale-free dynamics, are found close to the high-strain rate boundary of the instability domain, peaked histograms reflecting intrinsic scales of deformation processes are reported for lower strain rates [15,17]. The latter behavior is neither random but is characterized by various scaling properties. For example, dynamic chaos was detected for strain rates in the middle of the instability domain using such model objects as CuAl single crystals and AlMg polycrystals [16,17]. Multifractal features of stress serration series were identified at all strain rates for AlMg alloys [17,21].

In view of the persisting scaling behaviors, the further step to the comprehension of the plastic flow in the instability conditions implies similar analyses with resolutions higher than that of the mechanical tests. At the same time, high-resolution measurements carried out on materials not subject to macroscopic instability, e.g., by measuring strain bursts during the deformation of microsamples or recording acoustic emission (AE) in the case of bulk samples, revealed ubiquitous scale-free statistics testifying to inherently intermittent or, more exactly, avalanche-like deformation processes in a microscopic scale range [22,23,24,25,26,27]. Application of the AE technique to jerky flow showed that AE events occur in the same range of amplitudes both at the instants of stress serrations and during stable flow, either before the critical strain ${\epsilon }_{cr}$ for the onset of the PLC effect or during reloading between stress drops [28,29]. Moreover, in contrast to the diverse statistics of stress serrations, the AE amplitudes obey power-law distributions at all strain rates, in agreement with the avalanche dynamics conjectured to be general for various materials [30,31,32]. This apparent contradiction was solved due to the observation of a correlation between the occurrence of macroscopic stress serrations and the clustering (chaining) of AE events [29]. Accordingly, taking into account a relationship between the relaxation oscillations and the phenomenon of synchronization in lattice models [33,34], the transition from power-law distributions of AE to distinct kinds of statistics of stress serrations was ascribed to the synchronization of dislocation avalanches, depending on the strain rate [35,36].

An important consequence of this complexity, almost unexplored so far, is that the apparent behavior may depend on the scale of observation. This statement is also confirmed by another body of studies, based on optical methods of recording the local displacement field on the specimen surface, e.g., digital image correlation [37] or speckle interferometry [38], and developed independently of the research into intermittence. The spatial and/or temporal resolutions of these methods occupy a somewhat intermediate position with regard to the AE and mechanical tests. It occurs that they reveal another ubiquitous feature of the macroscopically smooth flow, namely, wavy patterns in the time evolution of the spatial repartition of plastic strain [39,40,41,42,43]. Moreover, a few recent works reported on a duality in the sense that the strain-rate bursts obey scaling distributions and, at the same time, are organized in wavy structures in the spatiotemporal maps [44,45,46].

As far as the PLC effect is concerned, although the macroscopic instability is caused by exceptional strain heterogeneities, the intermittence reflected in the evolution of the local strains has not been examined so far. The studies applying optical (and also thermal) methods of surveying local strains were mainly focused on the kinematics and evolution of the average parameters of PLC bands [4,5,6,7,8,9,10,11,12]. In particular, it was established for various alloys that the fast straining is characterized by a quasi-continuous propagation of deformation bands along the tensile axis, and this pattern is progressively replaced by a correlated and finally random occurrence of short-term localized bands when ${\dot{\epsilon }}_a$ is decreased, although a quasi-continuous band propagation may take place at low ${\dot{\epsilon }}_a$ in alloys with complex microstructures. [47,48].

The present work was aimed at a statistical analysis of the intermittence revealed in the local strain-rate maps during jerky flow of a model AlMg alloy. The choice of the object of investigation was not only motivated by the availability of a large amount of literature data on the properties of jerky flow and AE for such materials, but also by the robustness of these properties regarding the Mg content in a range from 2% to 5%. To provide the best basis for the comparison of behaviors on different scales, experiments were done on the same Al-3%Mg alloy as in [28,29]. The interest to such an analysis is twofold. On the one hand, both the stress serrations and AE represent a global temporal response of the sample to deformation processes taking place in its various parts. It is known that in nonlinear systems, the relationship between the global and local responses may not be trivial [49]. Therefore, to assess spatiotemporal behavior is essential for the understanding of the dislocation dynamics during jerky flow. Besides seizing the spatial aspect, the interest of this method is motivated by its intermediate time and amplitude resolution, enabling filling the gap between the scale ranges pertinent to the AE and deformation curves.

The first analysis reported here was realized in the high strain-rate regime. This type of jerky flow attracts particular interest due to the observation of power-law statistics for both these scale ranges. Therewith, the respective exponents do not take on the same values for the AE and stress serrations but are considerably higher in the former case [50]. Thus, it is meaningful to perform the analysis in an intermediate scale range. Besides, the nature of such scale-free statistics is a matter of current debate. Alternative interpretations in terms of either self-organized criticality (SOC)—a paradigm of avalanche dynamics first suggested to explain earthquakes statistics [51,52]—or turbulent flow were suggested to explain this regime of the PLC effect [15,16,17,53,54]. Recently, it has been argued that SOC is related to a general phenomenon known as a fluctuation scaling and stating on a power-law relationship between the average and variance of fluctuations in complex systems [55,56]. The present study allowed for a verification of such scaling in the conditions of jerky flow.

2. Materials and Methods

2.1. Experiment

Polycrystalline tensile samples with a dog-bone shape and a 25 × 6.8 × 2.5 mm³ gage part were cut from a cold-rolled sheet of Al-3% Mg in the rolling direction, solution treated by annealing at 400 °C for two hours and quenched in water. Polycrystalline grains had an approximately equiaxed shape and size between 30 and 100 μm [57]. Mechanical tests were implemented using a Zwick 1476 testing machine (Zwick, Ulm, Germany) with a software package testExper. The specimens were deformed at room temperature at a constant crosshead velocity corresponding to the nominal (i.e., referred to the initial specimen length) applied strain rate ${\dot{\epsilon }}_a$ = 6 × 10⁻³ s⁻¹.

The local extensometry technique was described in detail earlier (e.g., [58]) and is briefly presented below. Using a mask, a sequence of 20 1-mm wide black and white stripes was painted normal to the tensile axis on one side of the specimen. A charge-coupled device (CCD) Line Scan Sensor ZS16D (H.D. Rudolph GMBH, Reinheim, Germany) with a sampling frequency of 10³ Hz and pixel size of 1.3 μm was set to record the longitudinal displacements of the intersections of black-and-white transitions with the centerline of the specimen, $x_i(t)$, where index i designates such successive survey points, starting from the upper edge of the field of vision. Thus, the so obtained spatiotemporal kinematic field corresponds to the Lagrangian representation [59]. With a 20 mm field of vision of the CCD camera, this setup implements a series of 20 local extensometers. As the total strain before necking was about 25% for all samples, usually about 15 upper extensometers remained in the field of vision during the test.

To avoid any bias caused by a possibly unequal sensitivity of the CCD camera to black-white and white-black transitions, local strains ${\epsilon }_{i,i+2}(t)$ were calculated using next-nearest-neighbor transitions corresponding to the same kind of light contrast:

$${\epsilon }_i(t)=\ln \frac{x_{i+2}(t)-x_i(t)}{x_{i+2}(0)-x_i(0)}$$

(1)

where the second index in the strain notation is omitted for simplification. The local strain rate field ${\dot{\epsilon }}_i(t)$ was calculated by the numerical derivation of the local strains.

As described previously [58], digital noise in $x_i(t)$ records was reduced using the running-average technique. It was found that the optimum window size for denoising at the strain rate explored in the present work corresponds to the average duration of stress drops, about 80 ms. This value allowed for revealing strain heterogeneities without smoothing out the steep fronts of such intense strain localizations as the PLC bands (see the spatiotemporal maps presented below). To avoid arbitrariness, the same running-average window was used for all the tested samples. It was checked that a variation of the window size by one-third does not reduce the scaling interval nor lead to a noticeable biasing of the estimate of the power-law exponent, which would exceed the experimental uncertainty. The reduction of the window down to 20 ms did not bias this estimate either. However, it was impractical because of a considerable increase in the scatter of the calculated distributions.

It is noteworthy that although such measurements are limited to one dimension, their advantage is due to a favorable combination of the time and space resolution. Even more importantly for the present study, the method based on the direct measurement of the markers positions is free from the approximations that are inevitable in the techniques using the local strain field calculation from the displacements of a randomly deposited speckle pattern.

2.2. Statistical and Fluctuation Scaling Analysis

The processing of stress serrations was presented in detail in previous works (e.g., [17,29,50]). The main precaution consists of taking into account a slow average increase in the size Δσ of stress drops, which may accompany the material work hardening. Various approaches have been tested earlier, e.g., the normalization of Δσ values by a polynomial fit of their time dependence, Δσ(t), or, alternatively, normalization of the deformation curve itself by either a running average or a polynomial fit. In the present work, the latter approach with polynomial fitting was applied so that serrations were determined using the curves $\varsigma (t)=\sigma (t)/\overline{\sigma (t)}$.

As will be seen in the next section, the local strain-rate fluctuations did not noticeably evolve in the strain interval of interest (before the onset of necking). Due to this stationarity, the analysis was applied directly to the as-measured ${\dot{\epsilon }}_i(t)$ signal. The procedure was the same as in the case of ς(t) signals, i.e., drops on a ${\dot{\epsilon }}_i(t)$ curve were taken as a characteristic of its intermittence. It was also checked that the distributions are virtually the same for downward and upward serrations (drops and rises in the signal).

To simplify the notations, the amplitudes of ${\dot{\epsilon }}_i(t)$ serrations are further designated as A; τ is used for durations; Δς and Δt respectively denote such characteristics of stress serrations. Hereinafter, histograms of a variable u, where u refers to any of these four quantities, will be traced for the data rescaled by their average value, i.e., u/<u>. This reduction makes it possible to compare statistical distributions of different quantities by bringing together their probability density functions (PDF). Besides, it allows avoiding arbitrariness in the choice of the bin size by using a unique dimensionless bin in all cases.

Since power-law statistics mean that large values are rare, various approaches were suggested to correctly handle the high-scale limit [60,61,62]. To provide a basis for comparison with the earlier statistical studies of stress and AE signals accompanying the PLC effect [29,50], the direct method of calculation of PDF by counting the fraction n(u)/N of events within intervals u ± δu/2 was applied. Here, n is the number of events within the corresponding bin, and N is the total number of events in the dataset. The bin size δu was taken as a constant in the intervals rich of events, but it was increased in the deprived regions until gathering a meaningful number of events (five in this work). Accordingly, the probability density was calculated to take into account the bin variation,

$$PDF(u)=\frac{n}{N\delta u}.$$

(2)

More exact methods of detecting power-law distributions in empirical data have been developed during the last decade [61,62]. As verified for stress serrations and acoustic emission (e.g., [50]), the direct calculation with the varied-bin correction renders satisfactory estimates of the power-law exponents for the signals characterizing the PLC effect, in the sense that the deviation from the values obtained by the exact methods does not exceed the experimental uncertainty. Accordingly, this method was adapted in the present work.

The fluctuation scaling was tested following the procedure described in [56]. The measured signals, ς(t) or ${\dot{\epsilon }}_i(t)$, are represented by times series with equidistant data points. Let us designate the studied series as $Y_i$, where i = 1…K, K is the number of data points in the analyzed time interval T = Kδt, and δt is the sampling time for the corresponding signal. Fluctuations $y_i$ of the signal about its mean value $\overline{Y}$ are calculated as $y_i=\left|Y_i-\overline{Y}\right|$. The scaling analysis is started by covering the interval T with a grid of k non-overlapping bins with an equal size r. The members of the new time series $z_k(r)$ are defined as the sum of $y_i$-values within the kth bin. The fluctuation scaling is verified if a power-law relationship between the variance $\mathrm{var}[z_k(r)]$ and the mean $E[z_k(r)]$,

$$\mathrm{var}[z_k(r)]\propto E{[z_k(r)]}^p$$

(3)

is satisfied when the bin size r is varied. In the present work, linear and logarithmic bin expanding rules were tested and rendered close results.

3. Results

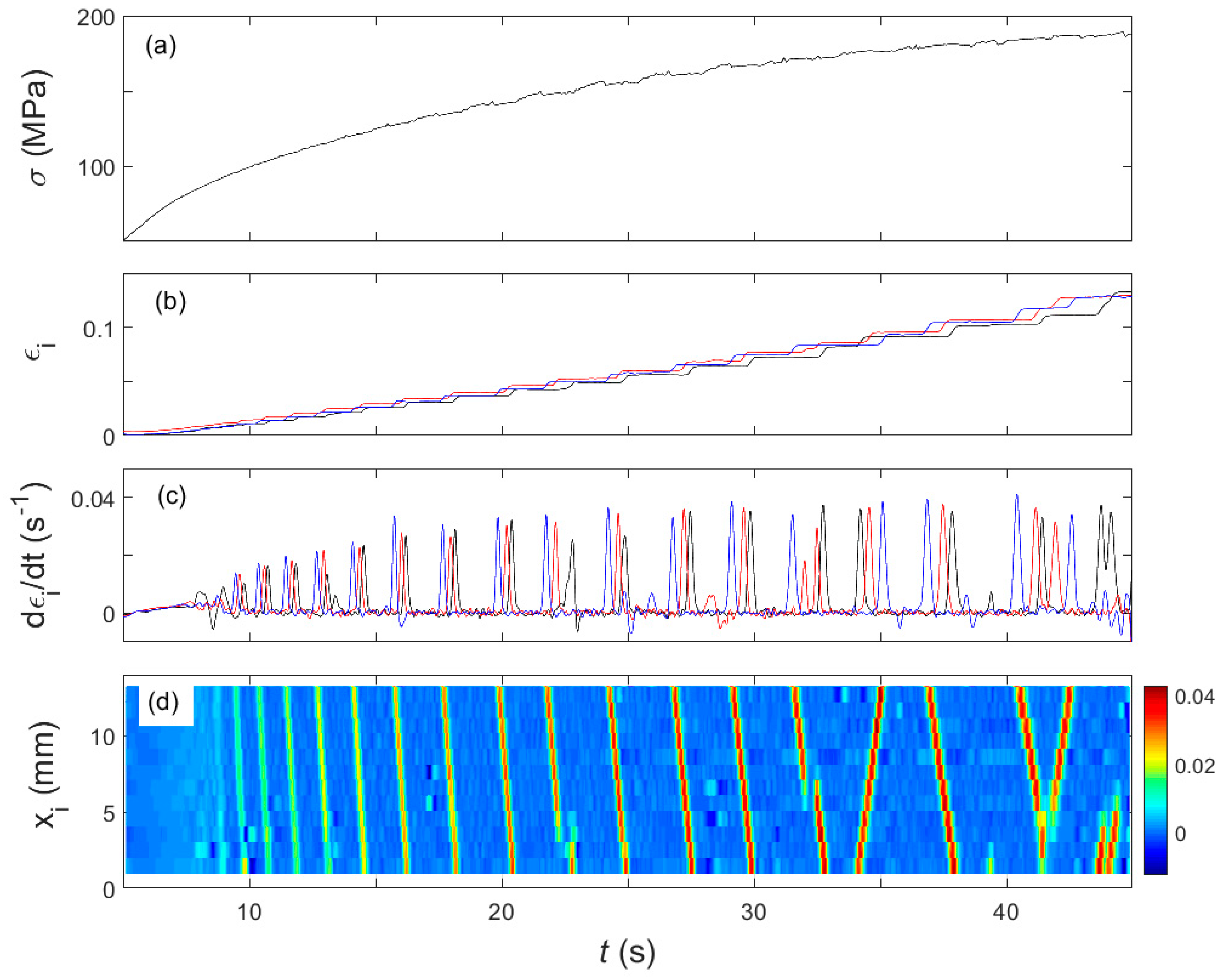
3.1. Spatiotemporal Maps

An example of mapping of the evolution of local strains and strain rates onto a serrated σ(t) curve is presented in Figure 1. Figure 1a displays stress fluctuations that are typical of the high-${\dot{\epsilon }}_a$ behavior of the PLC effect and are often considered as a signature of the propagative nature of deformation bands. Indeed, the propagation is explicitly demonstrated in plots (c), (b), and (d): Figure 1b shows a step-wise character of ${\epsilon }_i(t)$ dependences for three local extensometers (data for other extensometers, as well as raw $x_i(t)$ records, are not shown); Figure 1c presents the corresponding ${\dot{\epsilon }}_i(t)$ curves. Then, the ensemble of data for all the local extensometers is used to build up a spatiotemporal map $(t,x_i(t),{\dot{\epsilon }}_i(t))$ in Figure 1d. The propagative character of deformation bands may already be assumed from the observation that each step in ${\epsilon }_i(t)$ and the respective intense peak in ${\dot{\epsilon }}_i(t)$, which reflect the passage of a deformation band through the ith extensometer, are systematically shifted in time for successive extensometers. Indeed, the map of Figure 1d visualizes the onward passage of PLC bands through the entire sequence of extensometers. Their progression is seen as inclined bright lines imaging the (quasi)continuous shift of the local region with the highest ${\dot{\epsilon }}_i$ value —a PLC band—along the tensile axis. The nucleation of each band is known to require a rise in the stress, followed by a drop back to the general stress level when the band has been formed [2,3,4,5,6,7,8,9,10,11,12,13], as can be traced, e.g., at t ≈ 32.5 s, when a band is nucleated within the field of vision of the CCD camera. In other cases, when the band occurs outside the visible part (the nucleation often takes place near the specimen head), the corresponding stress peak slightly precedes the band entering the field of vision. The lower-amplitude stress fluctuations between two subsequent stress rise/drop events accompany the deformation band propagation along the gage length (see [4,5,6,7,8,9,10,11,12,47,48]).

The description of high-${\dot{\epsilon }}_a$ behavior in the literature was often reduced to such sequences of stress rises and drops, the so-called type A serrations, whereas the intervals of band propagation were considered as smooth plastic flow (e.g., [63]). In other words, smaller and rather irregular stress fluctuations accompanying the band propagation were believed to be caused by the experimental noise and disregarded as a part of the collective dislocation dynamics. However, the statistical analysis proved that the entire set of stress fluctuations obeys power-law distributions and therefore cannot be ascribed to random noise [15,17,29]. In the cited works, these small irregularities were interpreted as being due to fluctuations in the width and velocity of the propagating PLC bands. Figure 1c,d testify that there may be another source of small stress variations. Indeed, besides the PLC bands, these plots reveal heterogeneity at finer scales. Even if the bright lines dominate the overall contrast in Figure 1d, the presence of weaker heterogeneities, which must also contribute to the irregular stress fluctuations, can be discerned outside them. Although the analysis of stress serrations presented in the next section does not allow for separating different contributions because of the global character of the stress response, such discrimination becomes possible by virtue of the local extensometry. The small strain heterogeneities will be analyzed in Section 3.3.

3.2. Statistics of Stress Serrations

A comprehensive statistical analysis of both the amplitude and time characteristics of stress serrations for similar alloys was reported elsewhere (e.g., [15,17,29]). The data succinctly presented below are aimed to verify the conclusions on the scale-free distributions of stress drop size at high ${\dot{\epsilon }}_a$ and, notably, provide a basis for comparison with the local strain-rate statistics. Figure 2a shows a typical statistical sample of Δς values for one of the deformed specimens in a time interval corresponding to a stabilized jerky flow. For each specimen, the processed dataset comprised more than 100 data points (up to 200 values). It can be recognized in the figure that the data scatter is denser in the range of small Δς and becomes rarer far from the ordinate origin. This qualitative observation agrees with the results of the statistical analysis illustrated in Figure 2b. Indeed, the examples of PDF bear witness to a power law, PDF(Δς)~Δς^−β, over more than two orders of magnitude of Δς, with β values close to 1, in consistence with the β-range between 1 and 1.5 reported in the papers cited above.

Similar to [17,29,54], the power-law nature of the probability law was also verified for the durations, PDF(Δt)~Δt^−α, although in a narrower scale range, this lack is common with the previous investigations, perhaps because of a typically worse time resolution provided in mechanical tests in comparison with the force resolution. According to the constraints imposed by such probability laws, it was also verified that the conditional averages of Δς for a given Δt (here designated as [Δς]) and the corresponding duration values are also related by a power law, [Δς]~Δt^h, with the exponents satisfying the scaling relation [64]:

α = h(β − 1) + 1.

(4)

A quantitative example of such a relation will be illustrated below for the case of the local strain-rate serrations.

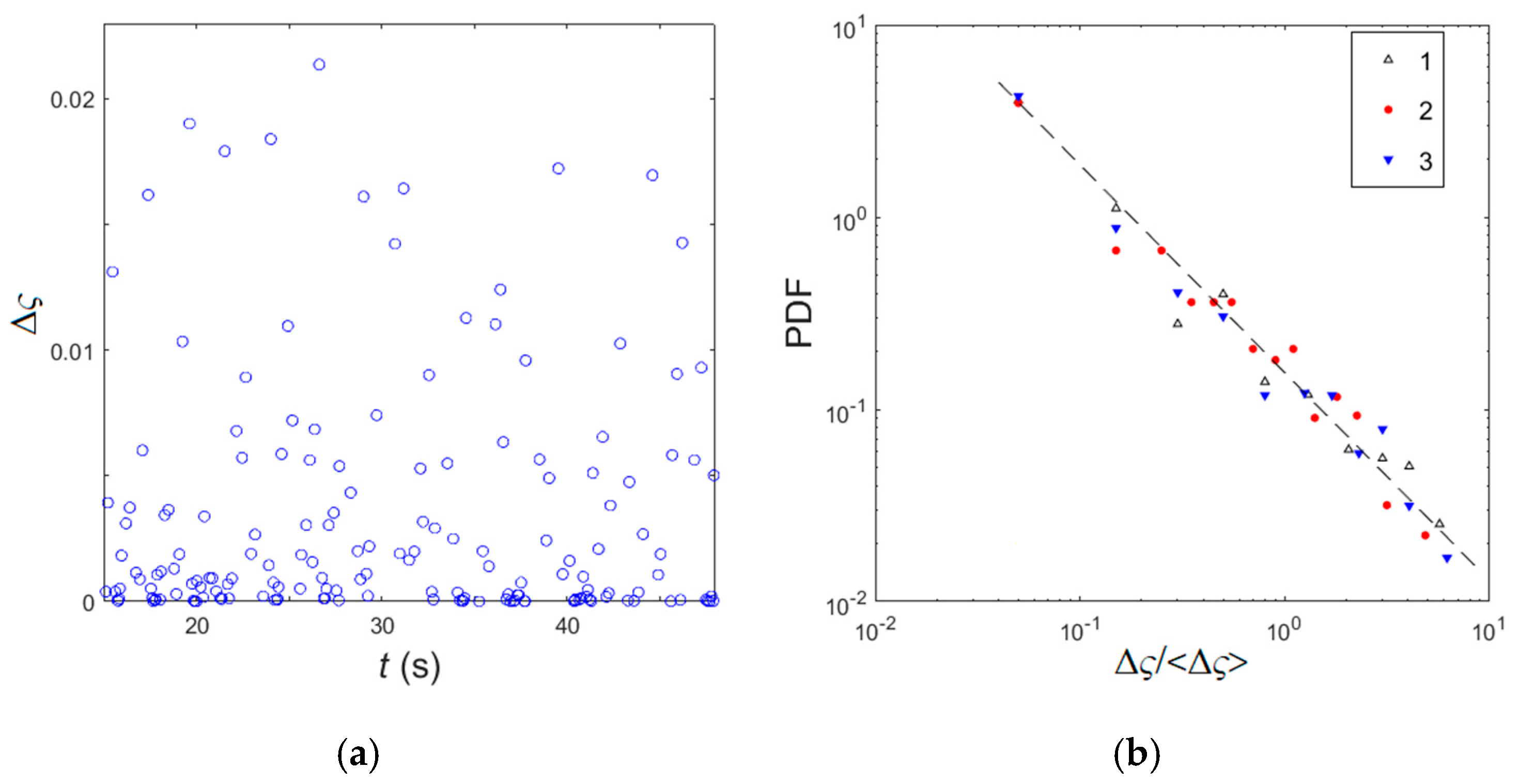
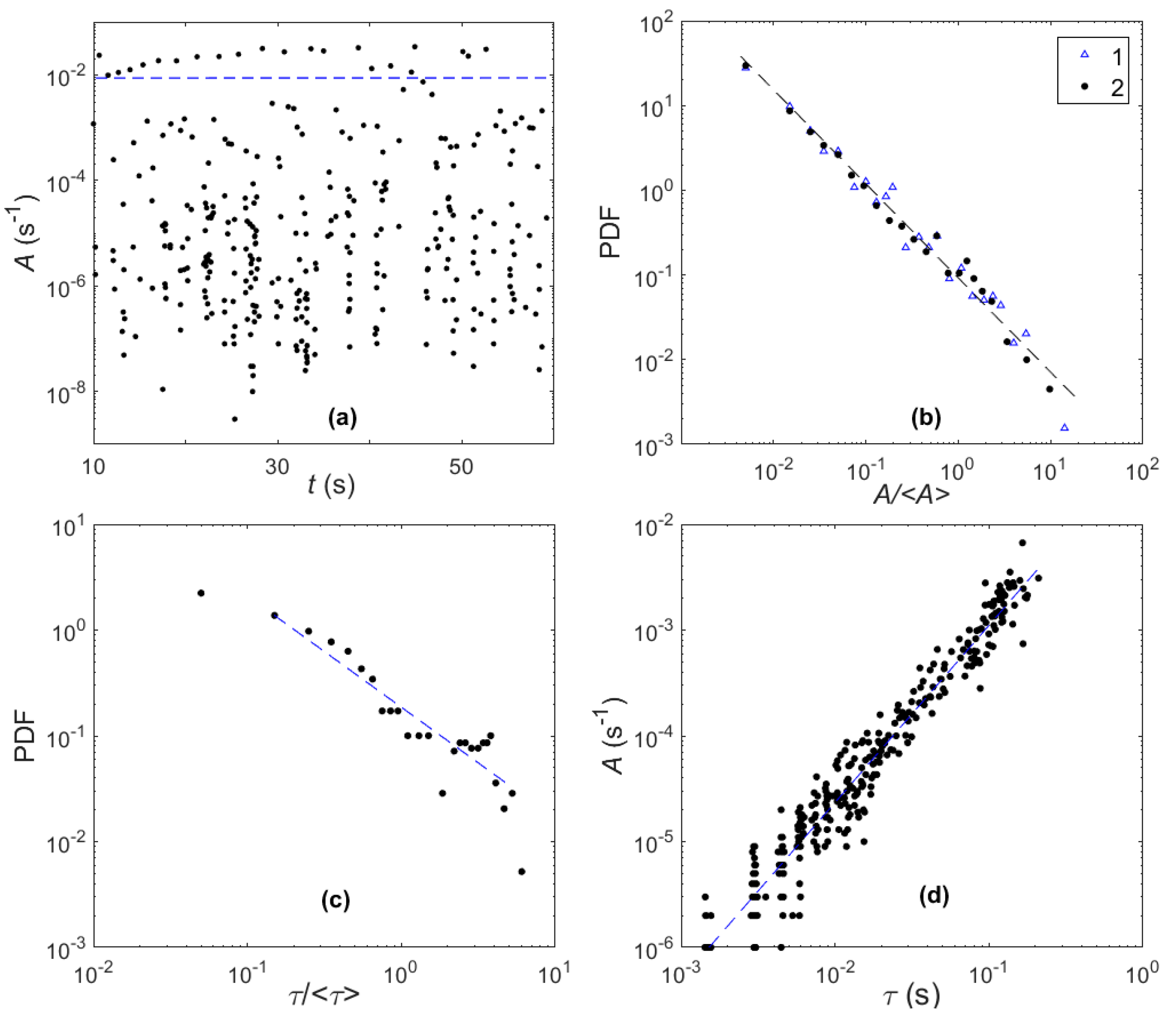
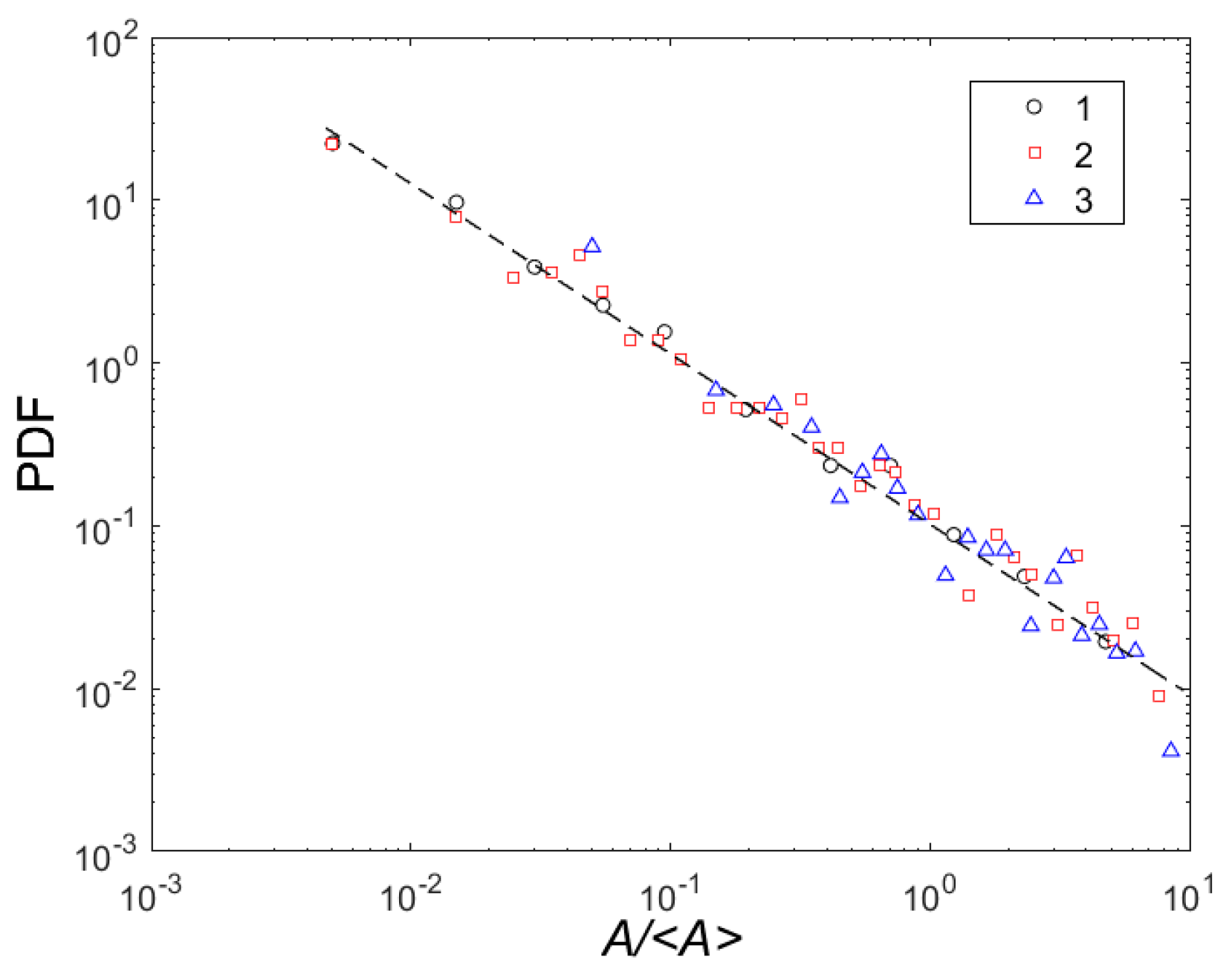
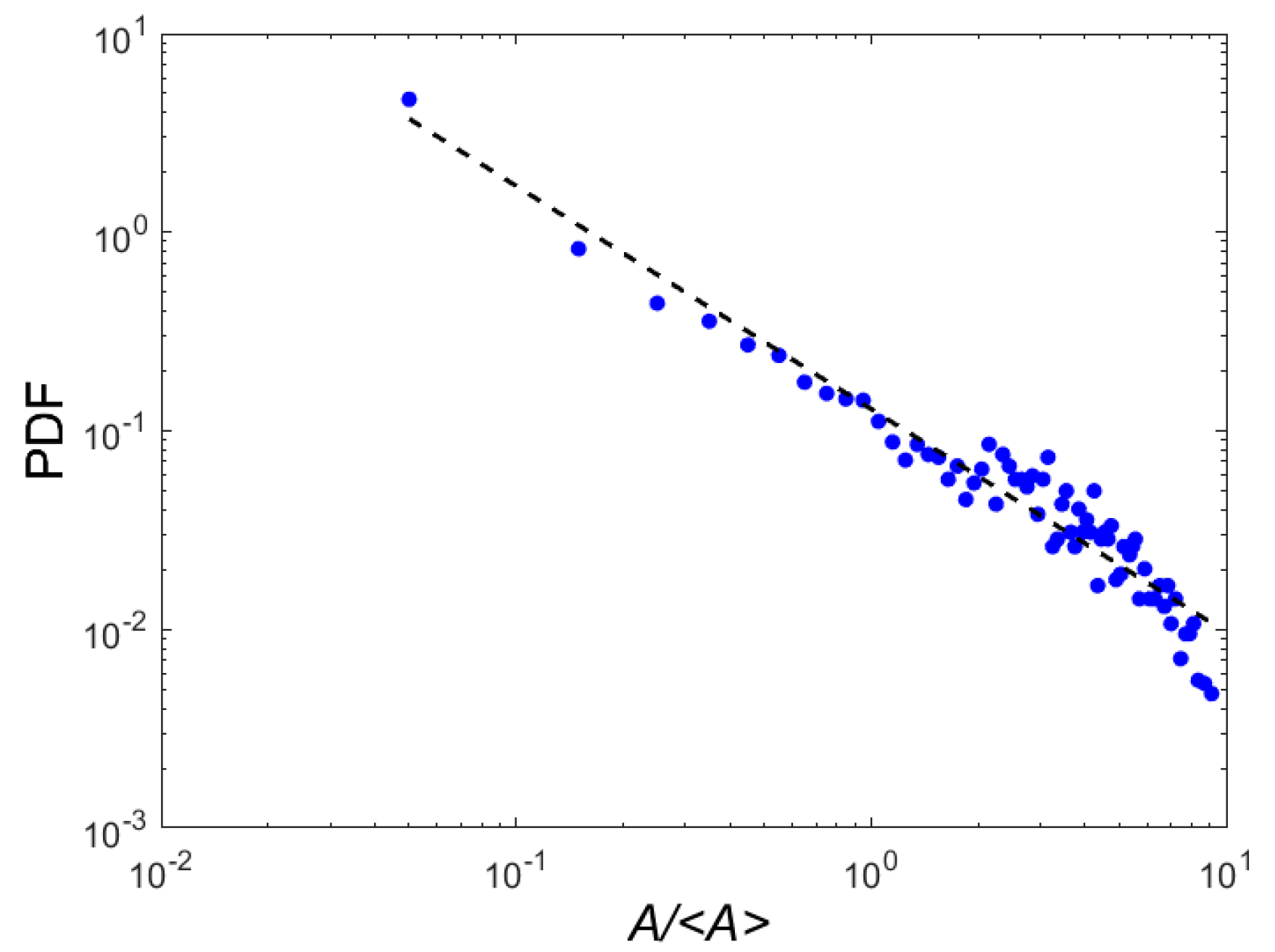
3.3. Statistics of Local Strain-Rate Serrations

Similar to the representation of stress serrations, Figure 3a gives an example of the scatter of amplitudes A of $\dot{\epsilon }$ oscillations (index i is omitted when its omission is not misleading) gathered by one local extensometer in a strain range corresponding to jerky flow, i.e., beyond ${\epsilon }_{cr}$. Figure 3b displays examples of PDF functions for two extensometers in different cross-sections of the same specimen. Although the extensometers gather information from short sections of the deforming material, as contrasted with the global stress response, the $\dot{\epsilon }$ signals are significantly richer due to the high sensitivity of the CCD camera to the markers’ displacements. The analyzed datasets typically comprised 350 to 550 events. The other two charts present examples of verification of the power-law behavior for the probability of durations and the scaling relation between the amplitudes and durations of the events (see Section 3.2). As in the case of stress serrations, the power-law is much less convincing for the durations than for amplitudes. The direct reason for this, namely the worse accuracy of time measurements, was mentioned above in relation with the analysis of stress serrations. However, this problem was also reported for the AE that provides a much higher time resolution [29]. It was suggested that the deviations may also be caused by a possible overlapping of dislocation avalanches, whereas amplitude distributions were shown to be rather robust with regard to this effect [65]. Despite these difficulties, the estimates of various exponents satisfy Equation (4) quite well (see the legend of Figure 3).

The local extensometry also provides an additional view on the relationship between local and global aspects of the plastic flow heterogeneity and intermittence. When strain is calculated using distant markers, i.e., on a larger base covered by more than one local extensometer, the number of the recorded $\dot{\epsilon }$ bursts gradually decreases with increasing the width of such a “composed” extensometer. The decrease may be caused by two factors. First, the time intervals during which the PLC bands propagate through the extensometer and overshadow the weak heterogeneities become more important. Their fraction with regard to the total examined period is more significant the larger the extensometer. Second, the local $\dot{\epsilon }$ bursts occurring quasi-simultaneously in its different sites would give rise to a sole event in the resultant signal. As a matter of example, the number of bursts recorded over a 16-mm wide base is typically less than 200. It should be underlined that although it is similar to the number of stress serrations, the information provided even by the largest extensometer is not equivalent to that stemming from the stress signal. In particular, most of the PLC band nucleation events occur outside the field of vision of the CCD camera.

Figure 4 brings together examples of PDF for three kinds of signals, namely, stress (cf. Figure 2b), strain rate from the shortest extensometer (cf. Figure 3b), and from the largest 16-mm wide extensometer. The latter was calculated using a similar procedure as in the case of the local extensometers. Namely, the highest amplitudes of $\dot{\epsilon }$ bursts occurring during the PLC band propagation and characterized by an intrinsic scale were disregarded. It can be seen that although the three kinds of signals highlight different aspects of the intermittence, the corresponding PDF dependences are quite close. Similar to the case of stress serrations, some tendency to a shallower slope for $\dot{\epsilon }$ fluctuations measured by large extensometers, as compared with the individual ones, could be conjectured. However, the accuracy of the estimates does not allow for a certain conclusion.

Since the examined $\dot{\epsilon }$ fluctuations occur all over the surveyed gage length and also at any time, it would be enlightening to perform a similar analysis before the onset of the PLC instability. Indeed, similar fluctuations already occurred in the seemingly elastic region, thus corroborating an important role of microplastic flow on the early stages of deformation [66]. However, the number of events recorded by each local extensometer in relatively short intervals before ${\epsilon }_{cr}$ was statistically insufficient. To provide a significant dataset for a given specimen, the data were collected from all its extensometers. Figure 5 presents the calculation results in two ways. Curves 1 and 2 display examples of PDF obtained for one of the specimens at the macroscopically elastic stage and at the stage of the elastoplastic transition, respectively. Curve 3 shows the PDF obtained using the entirety of these data for both stages together. The data bear evidence that the dependences obtained for $\epsilon <{\epsilon }_{cr}$ also obey a power law with the exponent close to 1.

To verify that this result is not biased by the blending of data from various local extensometers, the same procedure was applied to the interval $\epsilon \ge {\epsilon }_{cr}$, and the statistical analysis was repeated for the blended dataset. The results of such processing are presented in Figure 6, which are to be compared with the dependences for individual extensometers in Figure 3b. The PDF shows clear power-law behavior with β = 1.04 (±0.05), which agrees with the results illustrated in Figure 3b, thus corroborating the validity of the analysis of blended datasets in the interval $\epsilon <{\epsilon }_{cr}$.

Figure 6 highlights two additional nuances that are vaguely discernible in the dependences obtained for individual extensometers. First, it shows a clear cutoff at large scales, which is typical of empirical power-law statistics and is considered as evidence for the existence of natural limits of scale-invariant behavior in real systems [30,31]. Second, the cutoff is preceded by a bump leading to a distinction between small events obeying scale invariance and large events deviating from the extrapolation of the power-law dependence. Hints to this deviation can also be recognized in Figure 3, Figure 4 and Figure 5, but it has become clear due to blending of many signals. Such a deviation from SOC-like behavior at large scales was reported for earthquake models and attributed to the triggering of a sequence of avalanches, providing that the triggering avalanche is powerful enough to store sufficient elastic energy [67].

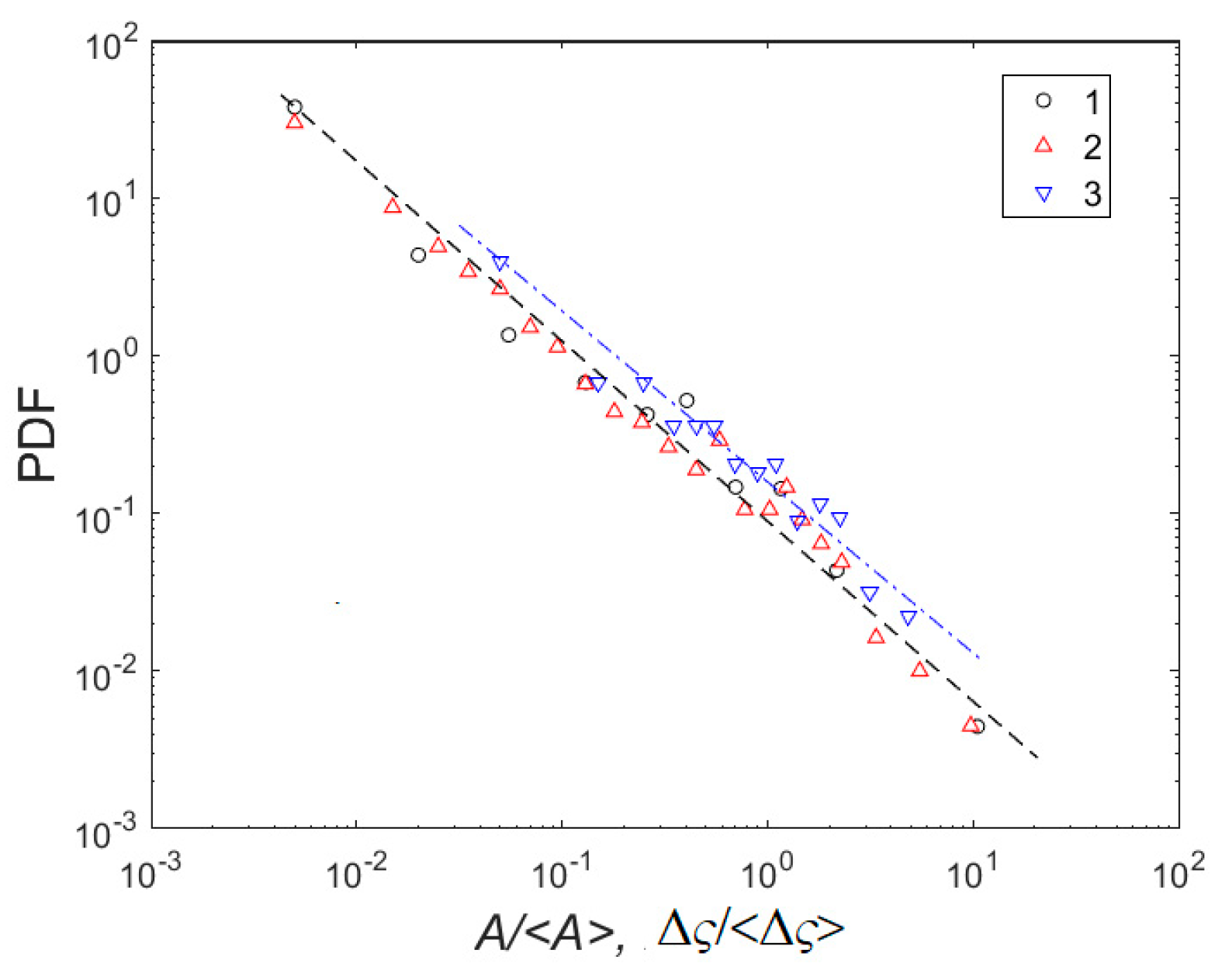
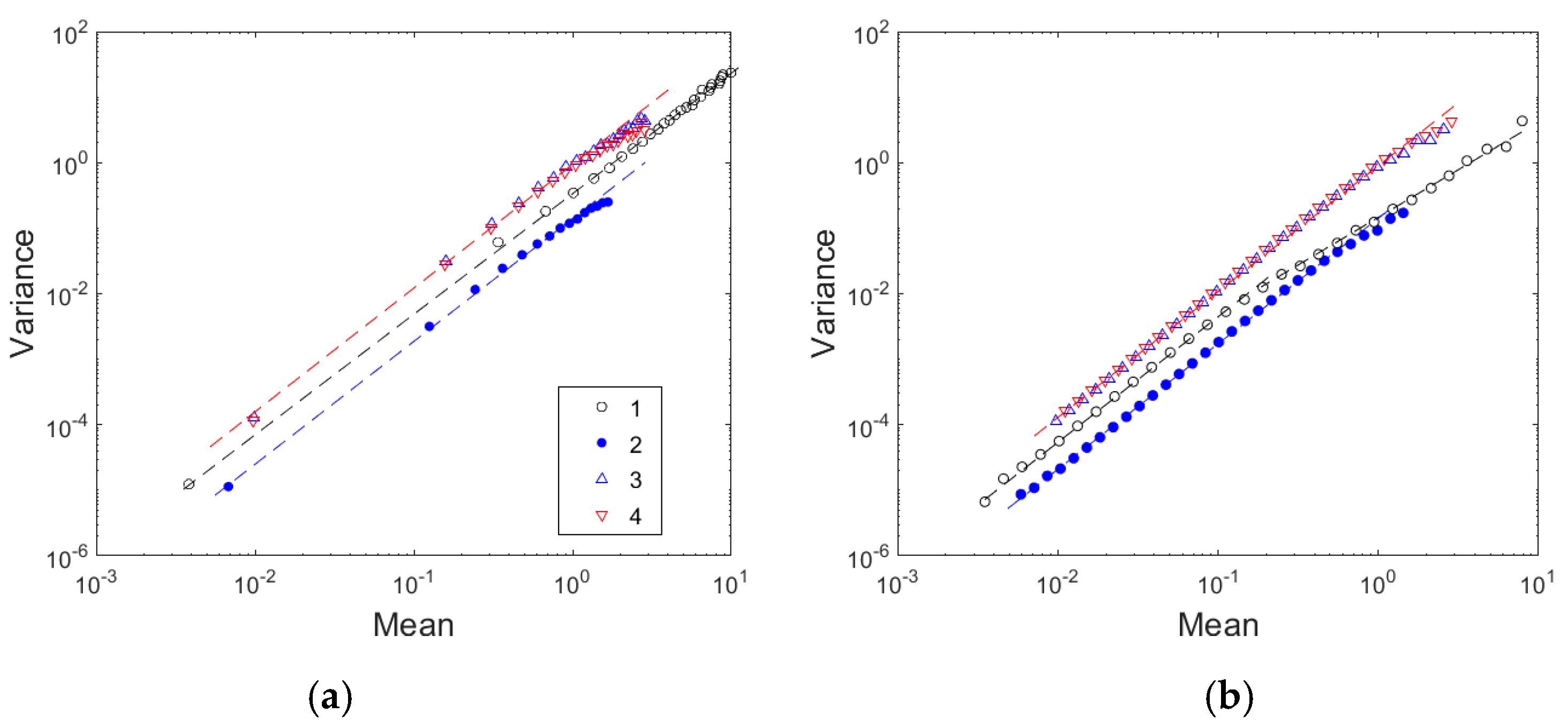
3.4. Fluctuation Scaling

Figure 7 presents examples of verification of the fluctuation scaling for two samples and different kinds of signals. To provide a general view, both linear (Figure 7a) and logarithmic (Figure 7b) bin expanding rules are illustrated. The major result of this section is that the entirety of examples allows for a conclusion that all dependences exhibit fluctuation scaling in a significant scale range.

Some specific observations are noteworthy. The analysis of deformation curves leads to a distinction of two qualitatively different cases, one corresponding to a single power-law dependence and another revealing a crossover between two power laws. Curve 1 in Figure 7a illustrates the first case. Indeed, it verifies the power-law behavior for the normalized deformation curve ς(t) over the entire scale range covering three orders of magnitude of the mean value. The index p (see Equation (3)) is approximately 1.86 ± 0.02. A similar slope is also observed at small scales for another sample presented by the example of Figure 7b, while the right-hand part is characterized by a lower p value, p = 1.34 ± 0.05. The $\dot{\epsilon }$ signals from both narrow and large extensometers show one power-law in each case, with a gradual deviation at large scales. Moreover, the respective slopes agree well with each other and also with the former of the above values obtained for ς(t)-curves. More exactly, the totality of estimates varies between approximately 1.73 and 1.9.

4. Discussion and Conclusions

As recalled in the Introduction, the high-${\dot{\epsilon }}_a$ plastic flow of alloys prone to the PLC effect is characterized by power-law statistical distributions on multiple scales. Whereas for materials non-subject to plastic instability, avalanche-like intermittent behavior is only visible on fine scales revealed by the AE [25,26,27] or the local extensometry technique [44,45,46]; it engrosses deformation curves in the DSA conditions, giving rise to a macroscopically unstable deformation. At the same time, there is no consensus in the literature on the PLC effect as to which of the observed serrations should be taken into consideration in the analysis of jerky flow. In the early research, only stress rises followed by sharp drops were believed to pertain to plastic instability at high ${\dot{\epsilon }}_a$ (type A serrations). Such serrations are caused by the nucleation of new PLC bands which then propagate along the specimen. Taken alone, they would be described by some characteristic scale [63]. However, the deformation curves display a much larger spectrum of stress fluctuations that, taken together, manifest power-law distributions of both amplitudes and durations [15,17,29,50]. Recent studies showed that the AE accompanying the plastic deformation of alloys obeys such critical-type statistics at all strain rates, even though the decrease in ${\dot{\epsilon }}_a$ results in a transition to peaked distributions of stress drops [29,36]. Therewith, the AE does not only occur at the instants of stress drops but also during reloading periods corresponding to macroscopically stable deformation. It was conjectured that at high ${\dot{\epsilon }}_a$ values, the avalanche mechanism of plastic flow may extend to a wide scale range, including serrated deformation curves. However, the AE and stress fluctuations pertain to two outermost scales, while a large intermediate interval remained unexplored so far. One of the major aims of the present work was to fill this gap by virtue of the local extensometry technique. Moreover, this approach opens a way to assess the spatiotemporal dynamics of dislocations, as compared with the only temporal aspect revealed by the AE or deformation curves. The first results obtained for an AlMg alloy confirm the scale-free statistics of plastic deformation and therefore corroborate the hypothesis of a critical-type dislocation dynamics controlling the plastic flow of dynamically strain-aging alloys in the high-${\dot{\epsilon }}_a$ regime.

At the same time, two aspects of experimental observations need clarification. First, Figure 3 bears evidence that not all events obey scale invariance, but there exists a distinction between small and large $\dot{\epsilon }$-bursts. Whereas scale-free distributions characterize small events, strong bursts corresponding to the passage of the PLC bands reveal a characteristic scale. Second, whereas the power-law exponents are close to 1 for the bursts of σ and $\dot{\epsilon }$, the literature data report on β values varying from about 1.5 to almost 3 for the AE energy in the same experimental conditions [29].

Let us first consider the former question. To explain the transition from scale-free to peaked distributions of stress drops with a decrease in ${\dot{\epsilon }}_a$, a hypothesis of the coexistence of SOC and synchronization phenomena was advanced in [29]. It can be highlighted as follows. A PLC band generates a strong strain heterogeneity giving rise to incompatibility stresses that may relax via small deformation events. At low ${\dot{\epsilon }}_a$, small events effectively smooth out the heterogeneities. As a result, many sections of the specimen reach the instability threshold (the top of the N-shaped SRS-function) quasi-simultaneously, and a new intense PLC band is formed. Its development is stopped by the elastic unloading of the machine-specimen system, this process being the main factor determining the characteristic scale of stress serrations. This reasoning was confirmed by the observation of bimodal distributions of stress drops at low ${\dot{\epsilon }}_a$, i.e., a power law with β about 1 at small scales and a peak for deep stress drops. Very similar behavior was found in seismicity models revealing SOC for small earthquakes but also characteristic catastrophic earthquakes [67]. The data of Figure 6 in the present paper testify to a general character of the trend to scale separation. Indeed, the $\dot{\epsilon }$ signal does not only display a characteristic scale corresponding to the PLC bands, but the smaller events also show a tendency to a deviation from the scale-invariant distribution and the formation of a bump on its right-hand side, which is clearly revealed by summing signals from many local sources.

The application of the AE method to the PLC effect provided an explicit explanation of the scale separation [29,36]. It occurred that despite the coexistence of two scale ranges for stress fluctuations at low ${\dot{\epsilon }}_a$, there is virtually no distinction between the amplitudes of AE events occurring at the instants of stress drops and during smooth reloading. Instead, a distinction occurs between their durations because stress serrations are accompanied by clustering of the AE, giving rise to events in a millisecond range for deep stress drops, while individual AE events accompanying the reloading have durations in the microsecond range. Based on these observations, abrupt serrations with a characteristic size were attributed to a brief synchronization of many dislocation avalanches, proceeding through their successive triggering [29,36,50].

It is clear which changes to this picture may occur when ${\dot{\epsilon }}_a$ is increased. The faster loading must be accommodated by a more intense plastic deformation and, therefore, lead to a globally stronger clustering and also the superposition of dislocation avalanches, as was confirmed by virtue of the AE technique [29,36]. At the same time, the smoothing of the recurrent heterogeneities becomes less efficient because of shorter reloading periods, so that there constantly exist some parts of the material close to the instability threshold. This has two consequences. On the one hand, the strain gradient sustained at the front of the deformation band leads to its propagation along the specimen. On the other hand, avalanches of any size may occur, and the critical behavior of both amplitudes and the durations of events is virtually observed in the entire scale range spreading from the AE to stress serrations. This conjecture is consistent with the observation of scale-free distributions of $\dot{\epsilon }$ fluctuations in the present work. However, it should be noted that there is an essential difference between the global σ and AE responses and the local $\dot{\epsilon }$ response. Namely, while the scale separation disappears from the former ones due to a strong overall plastic activity, it persists in the local response because of the recurrent propagation of the PLC bands.

The supposed effect of ${\dot{\epsilon }}_a$ conforms to the observation made in [29] that the exponent β of AE distributions is lesser at higher ${\dot{\epsilon }}_a$, which is in agreement with the higher probability of larger (composed) events. Moreover, as pointed out in [50], the same factor may be responsible for lower β values in the case of σ and $\dot{\epsilon }$ in comparison with the AE, because the time resolution of these signals does not allow resolving microsecond events. Thus, it may be suggested that the β values correctly characterizing dislocation avalanches in the DSA conditions are provided by the AE technique, while the apparent value of 1 rendered by σ and $\dot{\epsilon }$ signals should be considered with precaution. Thus, it would be challenging to verify this suggestion by drastically increasing the time resolution of the local extensometry.

Another challenge concerns the choice between the specific mechanisms that can be responsible for critical-type statistics. The entirety of the results discussed above, including the literature data, may be explained within the framework combining the SOC and synchronization phenomena. In particular, it explains the paradox noticed in the first studies of statistical distributions of stress serrations. Namely, SOC models require vanishing driving rates [51,52]. Even if the high ${\dot{\epsilon }}_a$ values necessary for type A behavior still correspond to quasi-static tests, the fact that peaked distributions were found at slow loading and scale-invariant behavior at a relatively fast loading remained puzzling. The above results bear evidence to SOC manifestations in the entire strain-rate range corresponding to the PLC domain, although the synchronization of dislocations avalanches gives rise to scale separations depending on ${\dot{\epsilon }}_a$.

An alternative interpretation of scale-free statistics was proposed in [53,54] on the basis of the analysis of Lyapunov exponents [68] for type A serrations in a physically-based model of the PLC effect, considering the reactions and dynamics of distinct dislocation ensembles. It was found that the Lyapunov spectrum, which quantifies the rate of divergence of close trajectories of dynamical systems, is similar to that characterizing turbulent flow [69,70]. However, while this model successfully predicts the transitions from the states with a characteristic scale of stress serrations to scale-invariant behavior when ${\dot{\epsilon }}_a$ is varied, it does not account for the scale separation at the same strain rate.

In view of these alternative hypotheses, the question of the specific mechanism of the critical-type behavior of the PLC effect needs further investigation. A special interest deserves a conceptually different approach to the power-law statistics proposed recently [55,56]. Among various issues, it conjectures that the SOC-type behavior may be related to a general feature of complex systems of various nature, which are known as fluctuation scaling or Taylor’s law (after investigations in ecology [71]) and are expressed by Equation (3). Moreover, it states that although numerous system-specific dynamical models were proposed with more or less success in each discipline, the statistical power laws emerging in such systems may be explained on a general basis as stemming from the mathematical convergence toward the so-called Tweedie distributions [72]. In the spirit of this concept, fluctuation scaling was verified in Section 3.4 for the experimental data obtained in the present paper. It was found that both σ and $\dot{\epsilon }$ signals obey approximately the same power law with the slope p about 1.8, which is similar to p-values obtained for some sandpile models [55,56]. From the general point of view, this result attests to the behavior of the PLC effect at high ${\dot{\epsilon }}_a$ as belonging to a certain class of complex dynamical systems. Namely, the exponent 1 < p < 2 corresponds to compound Poisson–gamma distributions, which are particularly used to mimic the process of capturing clusters in ecological data such as biomasses [73]. Therewith, the observation of a crossover in the scaling for some deformation curves (Figure 7b) may be indicative of multifractality [74], which is in consistence with multifractal behaviors detected for the PLC effect [17,21,28]. More specifically, since the sandpile models serve as a paradigm of SOC, the above-mentioned similarity between p-values corroborates the conclusion that the statistical distributions presented here are compatible with the conjecture of SOC-like behavior. On the whole, the first results of such an analysis attest to the PLC effect as a candidate for the investigation of the applicability of these general concepts to collective behaviors in plastic deformation.

In summary, it may be concluded that the local extensometry brings information that is complementary to the AE or mechanical tests. This new angle of view of the problem of plastic heterogeneity requires extending such investigations to a wide strain-rate range, in particular, to verify alternative interpretations of a strikingly rich pattern of various dynamical regimes of plastic flow in model binary alloys. Furthermore, this approach is also promising for investigations of plastic deformation in such novel materials as metallic glasses and high-entropy alloys that are also prone to jerky flow [75,76,77].

Finally, although the present paper was devoted to a statistical analysis of the intermittence of plastic flow in the conditions of plastic instability, a qualitatively different phenomenon arising from these experiments is worth noting. Similar to several other materials for which similar data have been reported [44,45,46], the scale of observation provided by the local extensometry reveals both intermittent and wavy patterns of local strain heterogeneities beyond the PLC bands (see Figure 1). Therewith, the intermittence manifests itself as localized bright spots corresponding to ${\dot{\epsilon }}_i$ bursts, and the arrangement of such bursts along inclined straight lines reveals the propagation of strain localizations. Such a duality, unstudied so far, presents a great interest for the understanding of correlations between temporal instabilities and spatial heterogeneities in the system of crystal defects.