The Relationship between Running Power and Running Economy in Well-Trained Distance Runners
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Instruments
2.3. Procedures
2.4. Statistical Analysis
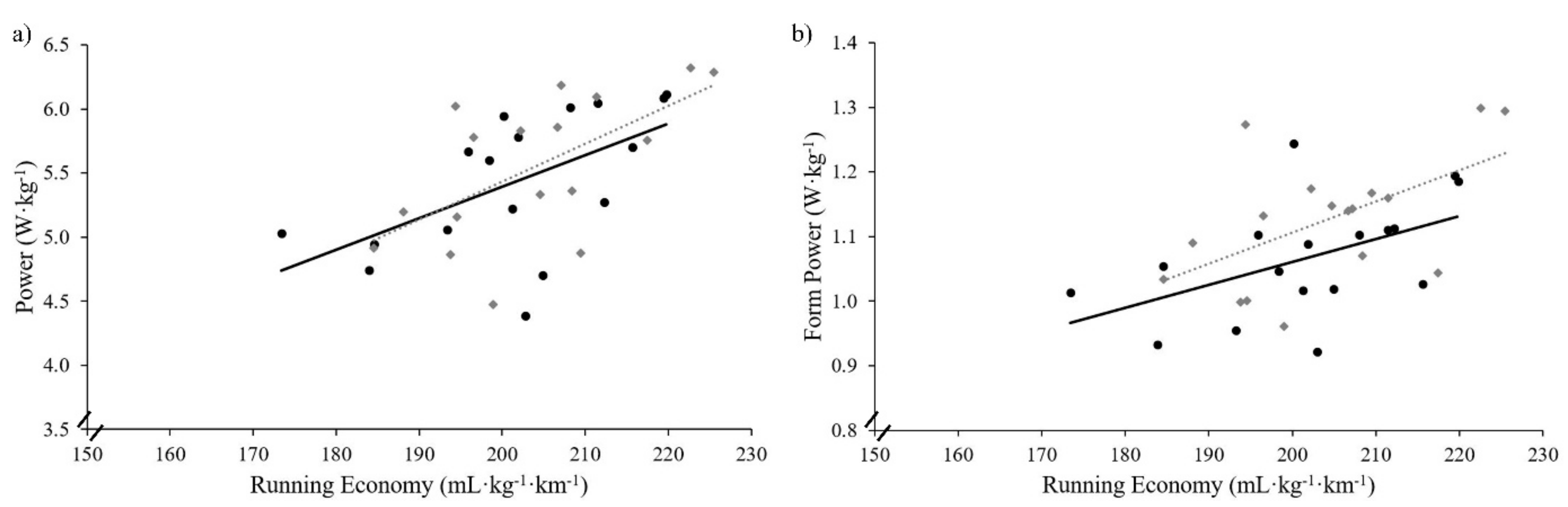
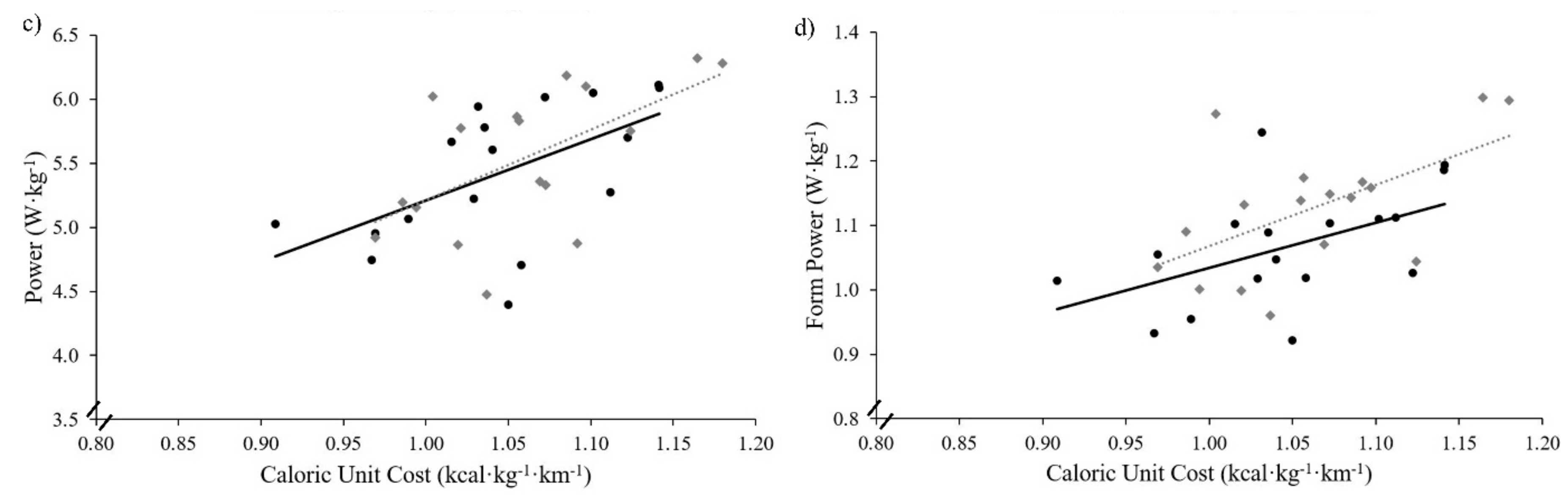
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Woodman, J.A.; Crouter, S.E.; Bassett, D.R.; Fitzhugh, E.C.; Boyer, W.R. Accuracy of consumer monitors for estimating energy expenditure and activity type. Med. Sci. Sports Exerc. 2017, 49, 371–377. [Google Scholar] [CrossRef] [PubMed]
- Meyer, J.; Hein, A. Live long and prosper: Potentials of low-cost consumer devices for the prevention of cardiovascular diseases. J. Med. Internet Res. 2013, 15, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Li, R.T.; Kling, S.R.; Salata, M.J.; Cupp, S.A.; Sheehan, J.; Voos, J.E. Wearable performance devices in sports medicine. Sports Health 2015, 8, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Coyle, E.F.; Feltner, M.E.; Kautz, S.A.; Hamilton, M.T.; Montain, S.J.; Baylor, A.M.; Abraham, L.D.; Petrek, G.W. Physiological and biomechanical factors associated with elite endurance cycling performance. Med. Sci. Sports Exerc. 1991, 23. [Google Scholar] [CrossRef]
- Sunde, A.; Støren, Ø.; Bjerkaas, M.; Larsen, M.; Hoff, J.; Helgerud, J. Maximal strength training improves cycling economy in competitive cyclists. J. Strength Cond. Res. 2010, 24, 2157–2165. [Google Scholar] [CrossRef] [PubMed]
- Moseley, L.; Jeukendrup, A.E. The reliability of cycling efficiency. Med. Sci. Sports Exerc. 2001, 33, 621–627. [Google Scholar] [CrossRef] [PubMed]
- Ettema, G.; Lorås, H.W. Efficiency in cycling: A review. Eur. J. Appl. Physiol. 2009, 106, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Cavagna, G.; Komarek, L.; Mazzoleni, S. The mechanics of sprint running. J. Physiol. 1971, 217, 709–721. [Google Scholar] [CrossRef] [PubMed]
- Fukunaga, T.; Matsuo, A.; Yuasa, K.; Fujimatsu, H.; Asahina, K. Effect of running velocity on external mechanical power output. Ergonomics 1980, 23, 123–136. [Google Scholar] [CrossRef] [PubMed]
- Inbar, O.; Kaiser, P.; Tesch, P. Relationships between leg muscle fiber type distribution and leg exercise performance. Int. J. Sports Med. 1981, 2, 154–159. [Google Scholar] [CrossRef] [PubMed]
- Williams, K.R.; Cavanagh, P.R. A model for the calculation of mechanical power during distance running. J. Biomech. 1983, 16, 115–128. [Google Scholar] [CrossRef]
- Schepens, B.; Willems, P.A.; Cavagna, G.A.; Heglund, N.C. Mechanical power and efficiency in running children. Eur. J. Physiol. 2001, 442, 107–116. [Google Scholar] [CrossRef] [PubMed]
- Daniels, J. A physiologist’s view of running economy. Med. Sci. Sports Exerc. 1985, 17, 332–338. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, J.R.; Esau, S.P.; MacIntosh, B.R. Economy of running: Beyond the measurement of oxygen uptake. J. Appl. Physiol. 2009, 107, 1918–1922. [Google Scholar] [CrossRef] [PubMed]
- Skovgaard, C.; Christiansen, D.; Christensen, P.M.; Almquist, N.W.; Thomassen, M.; Bangsbo, J. Effect of speed endurance training and reduced training volume on running economy and single muscle fiber adaptations in trained runners. Physiol. Rep. 2018, 6, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Shaw, A.J.; Ingham, S.A.; Atkinson, G.; Folland, J.P. The correlation between running economy and maximal oxygen uptake: Cross-sectional and longitudinal relationships in highly trained distance runners. PLoS ONE 2015, 10, e0123101. [Google Scholar] [CrossRef] [PubMed]
- Saunders, P.U.; Pyne, D.B.; Telford, R.D.; Hawley, J.A. Factors affecting running economy in trained distance runners. Sports Med. 2004, 34, 465–485. [Google Scholar] [CrossRef] [PubMed]
- Hunter, G.R.; McCarthy, J.P.; Carter, S.J.; Bamman, M.M.; Gaddy, E.S.; Fisher, G.; Katsoulis, K.; Plaisance, E.P.; Newcomer, B.R. Muscle fiber type, Achilles tendon length, potentiation, and running economy. J. Strength Cond. Res. 2015, 29, 1302–1309. [Google Scholar] [CrossRef] [PubMed]
- Williams, K.R.; Cavanagh, P.R. Relationship between distance running mechanics, running economy, and performance. J. Appl. Physiol. 1987, 63, 1236–1245. [Google Scholar] [CrossRef] [PubMed]
- Hoogkamer, W.; Kipp, S.; Spiering, B.; Kram, R. Altered running economy directly translates to altered distance-running performance. Med. Sci. Sports Exerc. 2016, 48, 2175–2180. [Google Scholar] [CrossRef] [PubMed]
- Hoogkamer, W.; Kipp, S.; Frank, J.H.; Farina, E.M.; Luo, G.; Kram, R. A comparison of the energetic cost of running in marathon racing shoes. Sports Med. 2017, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Cavanagh, P.R.; Pollock, M.L.; Landa, J. A biomechanical comparison of elite and good distance runners. Ann. N. Y. Acad. Sci. 1977, 301, 328–345. [Google Scholar] [CrossRef] [PubMed]
- Tartaruga, M.P.; Brisswalter, J.; Peyré-Tartaruga, L.A.; Ávila, A.O.; Alberton, C.L.; Coertjens, M.; Cadore, E.L.; Tiggemann, C.L.; Silva, E.M.; Kruel, L.F. The relationship between running economy and biomechanical variables in distance runners. Res. Q. Exerc. Sport 2012, 83, 367–375. [Google Scholar] [CrossRef] [PubMed]
- Halvorsen, K.; Eriksson, M.; Gullstrand, L. Acute effects of reducing vertical displacement and step frequency on running economy. J. Strength Cond. Res. 2012, 26, 2065–2070. [Google Scholar] [CrossRef] [PubMed]
- De Ruiter, C.J.; Verdijk, P.W.L.; Werker, W.; Zuidema, M.J.; de Haan, A. Stride frequency in relation to oxygen consumption in experienced and novice runners. Eur. J. Sport Sci. 2014, 14, 251–258. [Google Scholar] [CrossRef] [PubMed]
- Lieberman, D.E.; Warrener, A.G.; Wang, J.; Castillo, E.R. Effects of stride frequency and foot position at landing on braking force, hip torque, impact peak force and the metabolic cost of running in humans. J. Exp. Biol. 2015, 218, 3406–3414. [Google Scholar] [CrossRef] [PubMed]
- Aubry, R.; Power, G.A.; Burr, J.F. An assessment of running power as a training metric for elite and recreational runners. J. Strength Cond. Res. 2018, 32, 2258–2264. [Google Scholar] [CrossRef] [PubMed]
- Daniels, J. Daniels Running Formula, 3rd ed.; Human Kinetics: Leeds, UK, 2014; ISBN 1450431836. [Google Scholar]
- Daniels, J.; Gilbert, J. Oxygen Power: Performance Tables for Distance Runners; J. Daniels, J. Gilbert: Tempe, AZ, USA, 1979. [Google Scholar]
- Daniels, J.; Daniels, N. Running economy of elite male and elite female runners. Med. Sci. Sports Exerc. 1992, 24, 483–489. [Google Scholar] [CrossRef] [PubMed]
- Morgan, D.W.; Bransford, D.R.; Costill, D.L.; Daniels, J.T.; Howley, E.T.; Krahenbuhl, G.S. Variation in the aerobic demand of running among trained and untrained subjects. Med. Sci. Sports Exerc. 1995, 27, 404–409. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawerence Erlbaum: Hillsdale, NJ, USA, 1988. [Google Scholar]
- Fisher, R.A. On the probable error of a coefficient of correlation deduced from a small sample. Metron 1921, 1, 3–32. [Google Scholar]
- Batterham, A.M.; Hopkins, W.G. Making meaningful inferences about magnitudes. Int. J. Sports Physiol. Perform. 2006, 1, 50–57. [Google Scholar] [CrossRef] [PubMed]
- Denadai, B.S.; Aguiar, R.A.; Lima, L.C.; Greco, C.C.; Caputo, F. Explosive training and heavy weight training are effective for improving running economy in endurance athletes: A systematic review and meta-analysis. Sports Med. 2016, 47, 545–554. [Google Scholar] [CrossRef] [PubMed]
- Storen, O.; Helgerud, J.; Stoa, E.M.; Hoff, J. Maximal strength training improves running economy in distance runners. Med. Sci. Sports Exerc. 2008, 40, 1087–1092. [Google Scholar] [CrossRef] [PubMed]
- Paavolainen, L.; Häkkinen, K.; Hämäläinen, I.; Nummela, A.R.I.; Rusko, H. Explosive-strength training improves 5-km running time by improving running economy and muscle power. J. Appl. Physiol. 1999, 86, 1527–1533. [Google Scholar] [CrossRef] [PubMed]
- Berryman, N.; Maurel, D.; Bosquet, L. Effect of plyometric vs. dynamic weight training on the energy cost of running. J. Strength Cond. Res. 2010, 24, 1818–1825. [Google Scholar] [CrossRef] [PubMed]
| Total Sample (n = 17) | Males (n = 9) | Females (n = 8) | |
|---|---|---|---|
| Age (years) | 20.6 ± 2.3 | 19.8 ± 1.9 | 21.5 ± 2.5 |
| Mass (kg) | 62.4 ± 6.9 | 66.4 ± 6.9 | 57.9 ± 3.3 |
| Height (cm) | 175.0 ± 8.2 | 180.6 ± 6.4 | 168.6 ± 4.5 |
| Experience level (years) | 7.9 ± 3.2 | 6.1 ± 2.7 | 10.0 ± 2.4 |
| Estimated VO2max (ml·kg−1·min−1) | 56.6 ± 8.2 | 63.1 ± 4.6 | 49.3 ± 3.7 |
| Estimated 5 km time (mm:ss) | 18:12 ± 2:19 | 16:23 ± 1:05 | 20:17 ± 1:19 |
| Condition | Cadence (Strides·min−1) | VO2 (mL·kg−1·min−1) | Respiratory Exchange Ratio | RPE | Ventilation (L·min−1) |
|---|---|---|---|---|---|
| Self-selected cadence | 179.6 ± 8.4 | 52.8 ± 8.7 | 1.0 ± 0.1 | 11.7 ± 1.7 | 93.8 ± 19.3 |
| Lowered cadence | 172.5 ± 9.5 * | 53.4 ± 8.5 * | 1.0 ± 0.1 * | 12.1 ± 1.7 | 96.0 ± 18.4 |
| Percent change | 3.9 | 1.2 | 2.0 | 3.9 | 2.3 |
| Condition | Running Economy (ml·kg−1·km−1) | Caloric Unit Cost (kcal·kg−1·km−1) | Stryd Power (W·kg−1) | Form Power (W·kg−1) |
|---|---|---|---|---|
| Self-selected cadence | 201.6 ± 12.8 | 1.0 ± 0.1 | 4.4 ± 0.5 | 1.1 ± 0.1 |
| Lowered cadence | 204.5 ± 10.7 * | 1.1 ± 0.1 * | 4.4 ± 0.5 * | 1.1 ± 0.1 * |
| Percent change | 1.4 | 1.0 | 1.1 | 5.3 |
| Cadence | Running Economy | Caloric Unit Cost | Stryd Power | Form Power | |
|---|---|---|---|---|---|
| Cadence | - | ||||
| Running economy | −0.4 (−0.7 to 0.0) | - | |||
| Caloric unit cost | −0.4 * (−0.7 to 0.0) | 1.0 ** (0.98 to 1.0) | - | ||
| Stryd power | −0.4 (−0.7 to 0.0) | 0.6 ** (0.2 to 0.8) | 0.6 ** (0.2 to 0.8) | - | |
| Form power | −0.8 ** (−0.9 to −0.6) | 0.5 * (0.1 to 0.8) | 0.5 * (0.1 to 0.8) | 0.8 ** (0.5 to 0.9) | - |
| Cadence | Running Economy | Caloric Unit Cost | Stryd Power | Form Power | |
|---|---|---|---|---|---|
| Cadence | - | ||||
| Running economy | −0.5 * (−0.8 to −0.1) | - | |||
| Caloric unit cost | −0.5 * (−0.8 to −0.2) | 1.0 ** (0.9 to 1.0) | - | ||
| Stryd power | −0.4 (−0.7 to 0.0) | 0.6 * (0.2 to 0.8) | 0.5 * (0.2 to 0.8) | - | |
| Form power | −0.9 ** (−1.0 to −0.7) | 0.5 * (0.2 to 0.8) | 0.6 ** (0.2 to 0.8) | 0.7 ** (0.4 to 0.9) | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Austin, C.L.; Hokanson, J.F.; McGinnis, P.M.; Patrick, S. The Relationship between Running Power and Running Economy in Well-Trained Distance Runners. Sports 2018, 6, 142. https://doi.org/10.3390/sports6040142
Austin CL, Hokanson JF, McGinnis PM, Patrick S. The Relationship between Running Power and Running Economy in Well-Trained Distance Runners. Sports. 2018; 6(4):142. https://doi.org/10.3390/sports6040142
Chicago/Turabian StyleAustin, Casey L., James F. Hokanson, Peter M. McGinnis, and Steve Patrick. 2018. "The Relationship between Running Power and Running Economy in Well-Trained Distance Runners" Sports 6, no. 4: 142. https://doi.org/10.3390/sports6040142
APA StyleAustin, C. L., Hokanson, J. F., McGinnis, P. M., & Patrick, S. (2018). The Relationship between Running Power and Running Economy in Well-Trained Distance Runners. Sports, 6(4), 142. https://doi.org/10.3390/sports6040142




