Spatial Distribution Characteristics and Driving Factors of Formicidae in Small Watersheds of Loess Hilly Regions
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
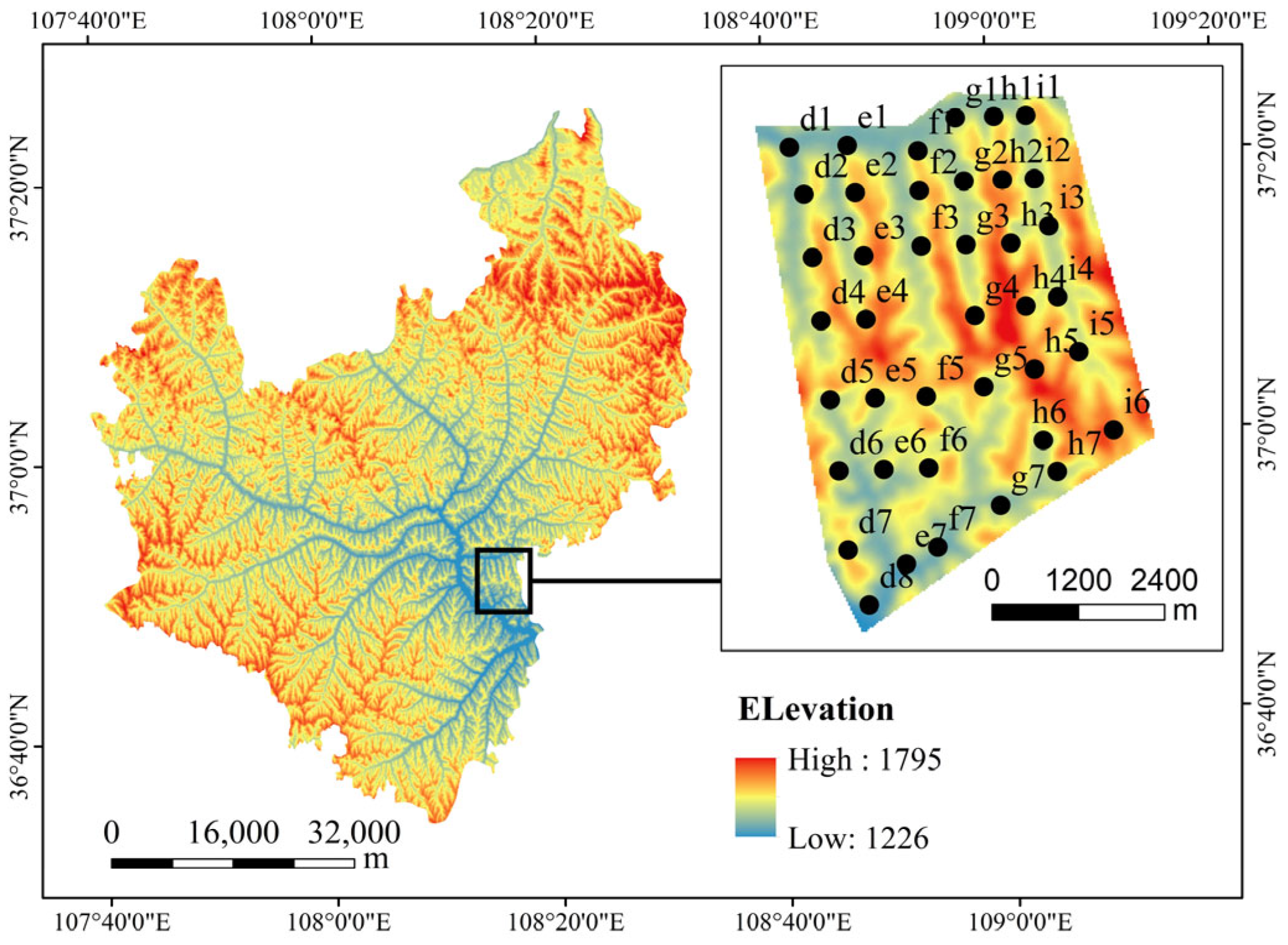
2.1. Overview of the Research Area
2.2. Study Plot Establishment
2.3. Collection and Identification of Soil Fauna
2.4. Soil Parameter Analysis
2.5. Terrain Factor Data Sources
2.6. Research Method
2.6.1. Global Spatial Autocorrelation
2.6.2. OLS and GWR Models
2.6.3. Variance Inflation Factor (VIF)
2.6.4. Radial Basis Function (RBF) Interpolation Method
3. Results and Analysis
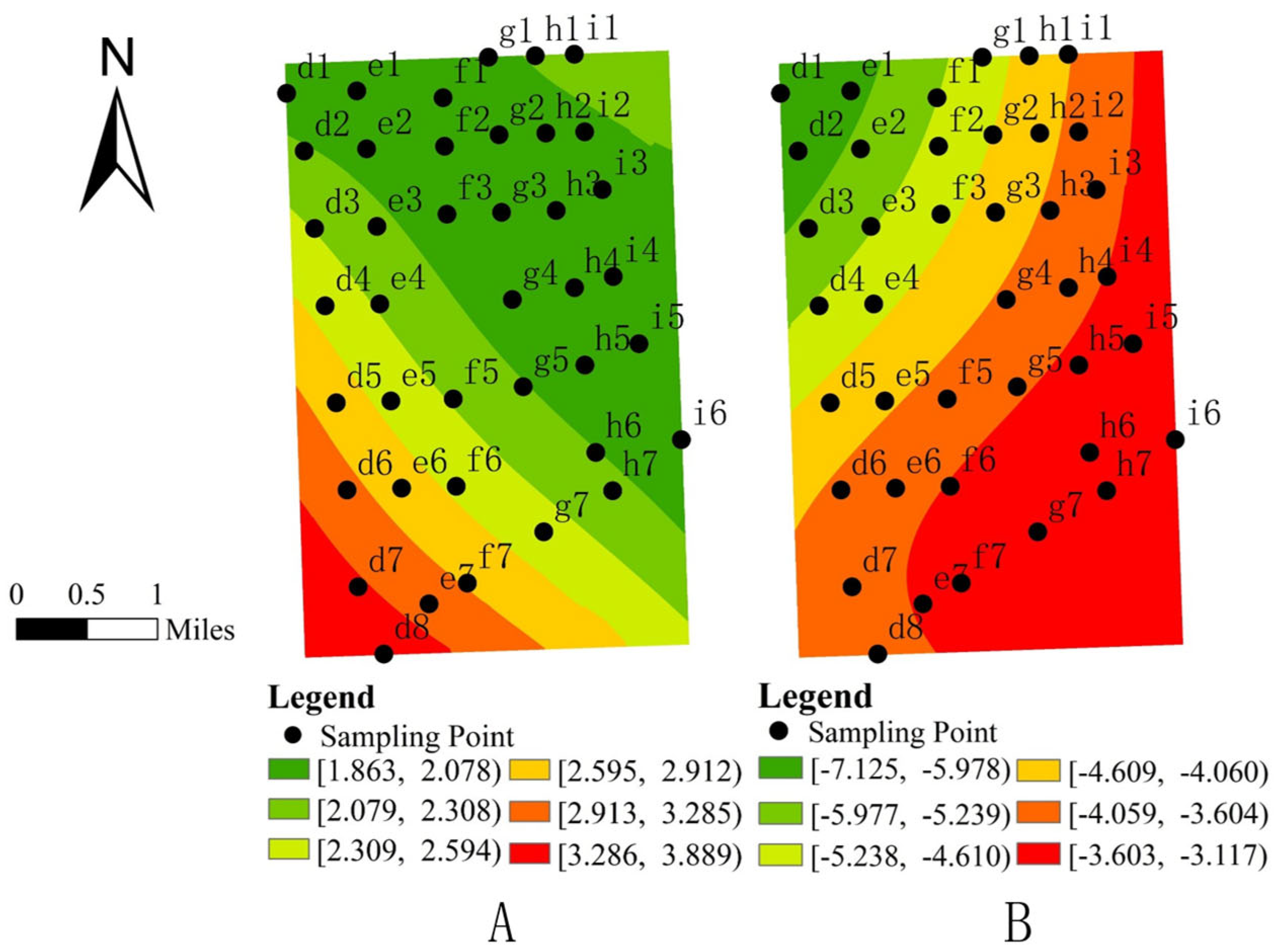
3.1. Spatial Distribution and Spatial Autocorrelation Analysis of Formicidae
3.2. Model Selection of Spatial Distribution Influence Mechanism
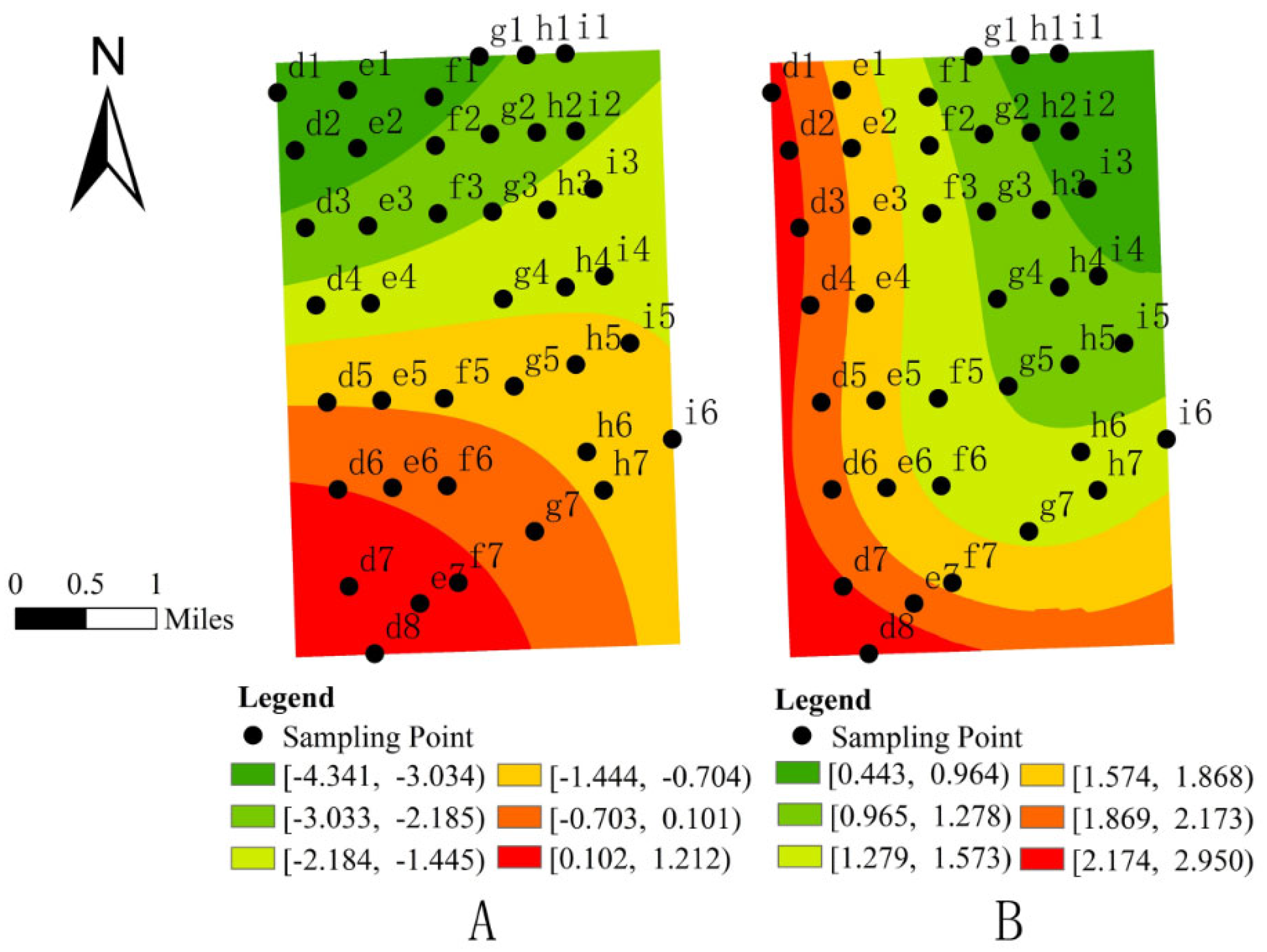
3.3. Analysis of Influencing Factors on the Spatial Distribution of Formicidae
4. Discussion
Analysis of the Spatial Distribution and Influencing Factors of Formicidae
5. Conclusions
- (1)
- The spatial distribution of Formicidae displayed significant clustering patterns, with higher densities predominantly observed in the northwestern and northeastern corners, as well as the southeastern region of the watershed.
- (2)
- Spatial dependence exerted a strong influence on the distribution patterns. Notably, the geographically weighted regression (GWR) model demonstrated a substantially better fit than the ordinary least squares (OLS) model, indicating pronounced spatial heterogeneity in Formicidae distribution.
- (3)
- Spatial visualization analysis further revealed localized effects of soil physicochemical properties and topographic factors. Formicidae abundance exhibited a significant positive correlation with available phosphorus (AP) and slope (SLP), while hydrogen peroxidase (HP) and topographic relief (TR) showed a significant negative correlation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Q.; Shi, X.Y.; Zhao, Z.Q.; Wu, Q.Q. Reference ecosystem construction and adaptive restoration effect evaluation: A case study of a small watershed in the loess hilly region. Land Degrad. Dev. 2024, 35, 3802–3816. [Google Scholar] [CrossRef]
- Zhang, J.; Qu, M.; Wang, C.; Zhao, J.; Cao, Y. Quantifying landscape pattern and ecosystem service value changes: A case study at the county level in the Chinese Loess Plateau. Glob. Ecol. Conserv. 2020, 23, e01110. [Google Scholar] [CrossRef]
- Ren, Q.W.; Qiang, F.F.; Liu, G.Q.; Liu, C.H.; Ai, N. Response of soil quality to ecosystems after revegetation in a coal mine reclamation area. Catena 2025, 257, 109038. [Google Scholar] [CrossRef]
- Brussaard, L. Soil fauna, guilds, functional groups and ecosystem processes. Appl. Soil Ecol. 1998, 9, 123–135. [Google Scholar] [CrossRef]
- Jouquet, P.; Dauber, J.; Lagerlöf, J.; Lavelle, P.; Lepage, M. Soil invertebrates as ecosystem engineers: Intended and accidental effects on soil and feedback loops. Appl. Soil Ecol. 2005, 32, 153–164. [Google Scholar] [CrossRef]
- Podesta, J. Interactions Between the Wood Ant Formica Lugubris and Plantation Forests: How Ants Affect Soil Properties and How Forest Management Affects the Dispersal of an Ecosystem Engineer. Ph.D. Thesis, University of York, York, UK, 2023. [Google Scholar]
- Frouz, J.; Jilková, V. The effect of ants on soil properties and processes (Hymenoptera: Formicidae). Myrmecol. News 2008, 11, 191–199. [Google Scholar]
- Crist, T.O. Biodiversity, species interactions, and functional roles of ants (Hymenoptera: Formicidae) in fragmented landscapes: A review. Myrmecol. News 2009, 12, 3–13. [Google Scholar]
- Collingwood, C.; Heatwole, H. Ants from Northwestern China (Hymenoptera, Formicidae). Psyche A J. Entomol. 2000, 103, 1–24. [Google Scholar] [CrossRef]
- Qin, J.; Liu, C.; Ai, N.; Zhou, Y.; Tuo, X.; Nan, Z.; Shi, J.; Yuan, C. Community Characteristics and Niche Analysis of Soil Animals in Returning Farmland to Forest Areas on the Loess Plateau. Land 2022, 11, 1958. [Google Scholar] [CrossRef]
- Li, T.; Shao, M.; Jia, Y. Effects of activities of ants (Camponotus japonicus) on soil moisture cannot be neglected in the northern Loess Plateau. Agric. Ecosyst. Environ. 2017, 239, 182–187. [Google Scholar] [CrossRef]
- Yang, X.; Shao, M.A.; Li, T.C.; Jia, Y.H.; Jia, X.X.; Huang, L.M. Structural Characteristics of Nests of Camponotus japonicus in Northern Loess Plateau and Their Influencing Factors. Acta Pedol. Sin. 2018, 55, 868–878. [Google Scholar]
- Silva, P.S.; De Azevedo Koch, E.B.; Arnhold, A.; Delabie, J.H.C. A review of distribution modeling in ant (Hymenoptera: Formicidae) biogeographic studies. Sociobiology 2022, 69, e7775. [Google Scholar] [CrossRef]
- Gotelli, N.J.; Ellison, A.M.; Dunn, R.R.; Sanders, N.J. Counting ants (Hymenoptera: Formicidae): Biodiversity sampling and statistical analysis for myrmecologists. Myrmecol. News 2011, 15, 13–19. [Google Scholar]
- Oliveira, A.A.S.; Araújo, T.A.; Showler, A.T.; Araújo, A.C.A.; Almeida, I.S.; Aguiar, R.S.A.; Miranda, J.E.; Fernandes, F.L.; Bastos, C.S. Spatio-temporal distribution of Anthonomus grandis grandis Boh. in tropical cotton fields. Pest Manag. Sci. 2022, 78, 2492–2501. [Google Scholar] [CrossRef]
- Lin, Y.; Hu, X.; Zheng, X.; Hou, X.; Zhang, Z.; Zhou, X.; Qiu, R.; Lin, J. Spatial variations in the relationships between road network and landscape ecological risks in the highest forest coverage region of China. Ecol. Indic. 2019, 96, 392–403. [Google Scholar] [CrossRef]
- Yin, W.Y. Illustrated Keys to Soil Animals of China; Science Press: Beijing, China, 1998. [Google Scholar]
- Yin, W.Y. Soil Animals of Subtropical China; Science Press: Beijing, China, 1992. [Google Scholar]
- Nanjing Institute of Soil Science; Chinese Academy of Sciences. Methods for Physical and Chemical Analysis of Soils; Shanghai Scientific and Technical Publishers: Shanghai, China, 1978. [Google Scholar]
- Bao, S.D. (Ed.) Soil and Agricultural Chemistry Analysis, 3rd ed.; China Agriculture Press: Beijing, China, 2000. [Google Scholar]
- Moran, P.A.P. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Caldas-de-Castro, M.; Singer, B.H. Controlling the false discovery rate: A new application to account for multiple and dependent tests in local statistics of spatial association. Geogr. Anal. 2006, 38, 180–208. [Google Scholar] [CrossRef]
- Ma, M.Y.; Xu, G.C.; Lv, Z.P.; Chen, S.J.; Li, H.Y.; Zhang, G.Z. Urban ecological quality and statistical correlation analysis based on satellite remote sensing. IOP Conf. Ser. Earth Environ. Sci. 2023, 1171, 012042. [Google Scholar] [CrossRef]
- Boori, M.S.; Choudhary, K.; Paringer, R.; Kupriyanov, A.B. Spatiotemporal ecological vulnerability analysis with statistical correlation based on satellite remote sensing in Samara, Russia. Environ. Manag. 2021, 285, 112138. [Google Scholar] [CrossRef]
- Kala, A.K.; Tiwari, C.; Mikler, A.R.; Atkinson, S.F. A comparison of least squares regression and geographically weighted regression modeling of West Nile virus risk based on environmental parameters. PeerJ 2017, 5, e3070. [Google Scholar] [CrossRef]
- Meloun, M.; Militký, J. Detection of single influential points in OLS regression model building. Anal. Chim. Acta 2001, 439, 169–191. [Google Scholar] [CrossRef]
- Fang, Z.; Zhang, L.; Zheng, M. Transferability analysis of built environment variables for public transit ridership estimation in Wuhan, China. Trans. Urban Data Sci. Technol. 2022, 1, 56–85. [Google Scholar] [CrossRef]
- Fang, Z.X.; Wu, Y.C.; Zhong, H.Y.; Liang, J.F.; Song, X. Revealing the impact of storm surge on taxi operations: Evidence from taxi and typhoon trajectory data. Environ. Plan. B Urban Anal. City Sci. 2021, 48, 1463–1477. [Google Scholar] [CrossRef]
- Astari, N.M.M.; Suciptawati, N.L.P.; Sukarsa, I.K.G. Penerapan metode bootstrap residual dalam mengatasi bias pada penduga parameter analisis regresi. E-J. Mat. 2014, 3, 130–137. [Google Scholar] [CrossRef]
- Yu, D. Spatially varying development mechanisms in the Greater Beijing Area: A geographically weighted regression investigation. Ann. Reg. Sci. 2006, 40, 173–190. [Google Scholar] [CrossRef]
- Lu, B.; Charlton, M.; Harris, P.; Fotheringham, A.S. Geographically weighted regression with a non-Euclidean distance metric: A case study using hedonic house price data. Int. J. Geogr. Inf. Sci. 2014, 28, 660–681. [Google Scholar] [CrossRef]
- Ahmad, I.; Ahmad, D.M.; Assefa, F.; Afera, H.; Habtamu, N.; Gebre, A.T.; Aserat, T. Spatial configuration of groundwater potential zones using OLS regression method. J. Afr. Earth Sci. 2021, 177, 104147. [Google Scholar] [CrossRef]
- Ahmad, I.; Shaaikh, J.A.; Fenta, A.; Halefom, A.; Andualem, T.G.; Teshome, A. Influence of determinant factors towards soil erosion using ordinary least squared regression in GIS domain. Appl. Geomat. 2021, 14, 57–63. [Google Scholar] [CrossRef]
- Salleh, A.H.; Rahman, A.K.E.; Ratnayake, U. Assessing the applicability of rainfall index spatial interpolation in predicting landslide susceptibility: A study in Brunei Darussalam. IOP Conf. Ser. Earth Environ. Sci. 2024, 1369, 012006. [Google Scholar] [CrossRef]
- Kinnell, A.I.P. Sediment Transport by Medium to Large Drops Impacting Flows at Subterminal Velocity. J. Soil Sci. Soc. Am. J. 2005, 69, 902–905. [Google Scholar] [CrossRef]
- Orr, M.J.L. Introduction to Radial Basis Function Networks; EB/OL; Physica-Verlag HD: Heidelberg, Germany, 1996. [Google Scholar]
- Huang, Q.H.; Cai, Y.L. Assessment of karst rocky desertification using the radial basis function network model and GIS technique: A case study of Guizhou Province, China. Environ. Geol. 2006, 49, 1173–1179. [Google Scholar]
- Huang, J.P.; Ling, S.X.; Wu, X.Y.; Deng, R. GIS-based comparative study of the bayesian network, decision table, radial basis function network and stochastic gradient descent for the spatial prediction of landslide susceptibility. Land 2022, 11, 436. [Google Scholar] [CrossRef]
- Catarineu, C.; Reyes-López, J.; Herraiz, A.J.; Barberá, G.G. Effect of pine reforestation associated with soil disturbance on ant assemblages (Hymenoptera: Formicidae) in a semiarid steppe. Eur. J. Entomol. 2018, 115, 562–574. [Google Scholar] [CrossRef]
- Bastos, S.D.H.A.; Harada, Y.A. Leaf-litter amount as a factor in the structure of a ponerine ants community (Hymenoptera, Formicidae, Ponerinae) in an eastern Amazonian rainforest, Brazil. Rev. Bras. Entomol. 2011, 55, 589–596. [Google Scholar] [CrossRef]
- Fernandes, T.T.; Silva, R.R.; Souza, D.R.; Araújo, N.; Castro-Morini, M.S. Undecomposed Twigs in the Leaf Litter as Nest-Building Resources for Ants (Hymenoptera: Formicidae) in Areas of the Atlantic Forest in the Southeastern Region of Brazil. Psyche A J. Entomol. 2012, 2012, 896473. [Google Scholar] [CrossRef]
- Ren, J.L.; Liu, J.L.; Wang, Y.Z.; Fang, J.; Feng, Y.L.; Gao, A.L.; Song, Y.X.; Xin, W.D. Response of ground arthropod assemblages to precipitation and temperature changes in the gobi desert. J. Desert Res. 2024, 44, 207–219. [Google Scholar]
- Crist, T.O.; Wiens, J.A. The distribution of ant colonies in a semiarid landscape: Implications for community and ecosystem processes. Oikos 1996, 76, 301–311. [Google Scholar] [CrossRef]
- Wu, D. Spatially and temporally varying relationships between ecological footprint and influencing factors in China’s provinces Using Geographically Weighted Regression (GWR). J. Clean. Prod. 2020, 261, 121089. [Google Scholar] [CrossRef]
- Wang, Y.C.; Zhang, X.N.; Yang, J.F.; Tian, J.Y.; Song, D.H.; Li, X.H.; Zhou, S.F. Spatial heterogeneity of soil factors enhances intraspecific variation in plant functional traits in a desert ecosystem. Front. Plant Sci. 2024, 15, 1504238. [Google Scholar] [CrossRef]
- Pan, F.J.; Wan, Q.; Zeng, J.X.; Wang, H.Z.; Huang, Q. Evolution characteristics and influence factors of spatial conflicts between production-living-ecological space in the rapid urbanization process of Hubei Province, China. Econ. Geogr. 2023, 43, 80–92. [Google Scholar]
- Frouz, J.; Holec, M.; Kalčík, J. The effect of Lasius niger (Hymenoptera, Formicidae) ant nest on selected soil chemical properties. Pedobiol. Int. J. Soil Biol. 2003, 47, 205–212. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, G.; Chen, S. Seasonal variations of soil functions affected by straw incorporation in croplands with different degradation degrees. Soil Tillage Res. 2025, 248, 106426. [Google Scholar] [CrossRef]
- Liu, Y.W.; Yang, F.; Yang, W.Q.; Wu, F.Z.; Xu, Z.F.; Liu, Y.; Zhang, L.; Yue, K.; Ni, X.Y.; Lan, L.Y.; et al. Effects of naphthalene on soil fauna abundance and enzyme activity in the subalpine forest of western Sichuan, China. Sci. Rep. 2019, 9, 2849. [Google Scholar] [CrossRef] [PubMed]
- He, X.J.; Wu, P.F.; Cui, L.W.; Zhang, H.Z. Effects of slope gradient on the community structures and diversities of soil fauna. Acta Ecol. Sin. 2012, 32, 3701–3713. [Google Scholar]
- Oliveira, P.Y.; Souza, J.L.P.; Baccaro, F.B.; Franklin, E. Ant species distribution along a topographic gradient in a “terra-firme” forest reserve in Central Amazonia. Pesqui. Agropecuária Bras. 2009, 44, 852–860. [Google Scholar] [CrossRef]
- Vasconcelos, H.L.; Macedo, A.C.C.; Vilhena, J.M.S. Influence of topography on the distribution of ground-dwelling ants in an Amazonian forest. Stud. Neotrop. Fauna Environ. 2003, 38, 115–124. [Google Scholar] [CrossRef]
- Johnson, R.A.; Ward, P.S. Biogeography and endemism of ants (Hymenoptera: Formicidae) in Baja California, Mexico: Afirst overview. J. Biogeogr. 2002, 29, 1009–1026. [Google Scholar] [CrossRef]

| Type | Index | Determination Method | Numerical Value |
|---|---|---|---|
| Soil physicochemical index | Natural water content (NWC) | Oven-drying method | 6.44 ± 2.71 |
| Bulk density (BD) | Core sampling method | 1.17 ± 0.06 | |
| Saturated water content (SWC) | 34.68 ± 5.88 | ||
| Non-capillary porosity (NCP) | 9.79 ± 2.09 | ||
| Total capillary porosity (TCP) | 40.2 ± 6.38 | ||
| Capillary porosity (CP) | 32.1 ± 5.49 | ||
| Capillary water holding capacity (CWHC) | 27.63 ± 4.71 | ||
| Soil organic carbon (SOC) | Dichromate oxidation method | 5.65 ± 1.89 | |
| Available potassium (AK) | Flame photometry | 73.35 ± 28.56 | |
| Available nitrogen (AN) | Alkaline hydrolysis diffusion method | 21.85 ± 13.24 | |
| Available phosphorus (AP) | Molybdenum–antimony spectrophotometric method | 6.89 ± 3.91 | |
| Total nitrogen (TN) | Sulfuric acid digestion–sodium salicylate method | 0.4 ± 0.15 | |
| Total phosphorus (TP) | Sulfuric acid digestion–molybdenum antimony spectrophotometric method | 0.29 ± 0.18 | |
| Potential of hydrogen (pH) | Soil-to-water ratio of 2.5:1 | 7.93 ± 0.15 | |
| Electrical conductivity (EC) | Determined using a DDS-608 multi-parameter conductivity meter | 97.35 ± 12.04 | |
| Hydrogen peroxidase (HP) | Potassium permanganate titration method | 2.35 ± 0.78 | |
| Alkaline phosphatase (ALP) | Disodium phenyl phosphate colorimetric method | 3.18 ± 0.64 | |
| Urea enzyme (UE) | Starch–phenol blue colorimetric method | 3.85 ± 7.1 |
| Type | Index | Source | Numerical Value |
|---|---|---|---|
| Topographic factor | Evaluation (EVA) | NASA Earth Science data website (https://nasadaacs.eos.nasa.gov/) (accessed on 13 December 2024) | 18.74 ± 8.04 |
| Slope (SLP) | 179.57 ± 93.57 | ||
| Slope variance (SV) | 37 ± 19.07 | ||
| Slope factor (SF) | 82.26 ± 22.7 | ||
| Topographic relief (TR) | 1377.59 ± 65.51 | ||
| Surface roughness (SR) | 1.07 ± 0.06 | ||
| Aspect (ASP) | 12.42 ± 6.25 |
| z-Score (Standard Deviations) | p-Value (Probability) | Confidence Level |
|---|---|---|
| <−1.65 or >+1.65 | <0.10 | 90% |
| <−1.96 or >+1.96 | <0.05 | 95% |
| <−2.58 or >+2.58 | <0.01 | 99% |
| Explanatory Variable | Coefficient | Standard Deviation | T-Value | p-Value | VIF |
|---|---|---|---|---|---|
| AP | 2.832 | 1.307 | 2.166 | 0.037 * | 1.062 |
| HP | −4.328 | 1.344 | −3.221 | 0.003 * | 1.122 |
| TR | −1.884 | 1.338 | −1.408 | 0.168 | 1.113 |
| SLP | 1.553 | 1.422 | 1.093 | 0.282 | 1.256 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Qiang, F.; Liu, G.; Liu, C.; Ai, N. Spatial Distribution Characteristics and Driving Factors of Formicidae in Small Watersheds of Loess Hilly Regions. Insects 2025, 16, 630. https://doi.org/10.3390/insects16060630
Tian Y, Qiang F, Liu G, Liu C, Ai N. Spatial Distribution Characteristics and Driving Factors of Formicidae in Small Watersheds of Loess Hilly Regions. Insects. 2025; 16(6):630. https://doi.org/10.3390/insects16060630
Chicago/Turabian StyleTian, Yu, Fangfang Qiang, Guangquan Liu, Changhai Liu, and Ning Ai. 2025. "Spatial Distribution Characteristics and Driving Factors of Formicidae in Small Watersheds of Loess Hilly Regions" Insects 16, no. 6: 630. https://doi.org/10.3390/insects16060630
APA StyleTian, Y., Qiang, F., Liu, G., Liu, C., & Ai, N. (2025). Spatial Distribution Characteristics and Driving Factors of Formicidae in Small Watersheds of Loess Hilly Regions. Insects, 16(6), 630. https://doi.org/10.3390/insects16060630







