Multi-Scale Contact Localization and Dynamic Instability Related to Brake Squeal
Abstract
1. Introduction
2. Complex Modal Analysis of a Simplified Pin on Disc System
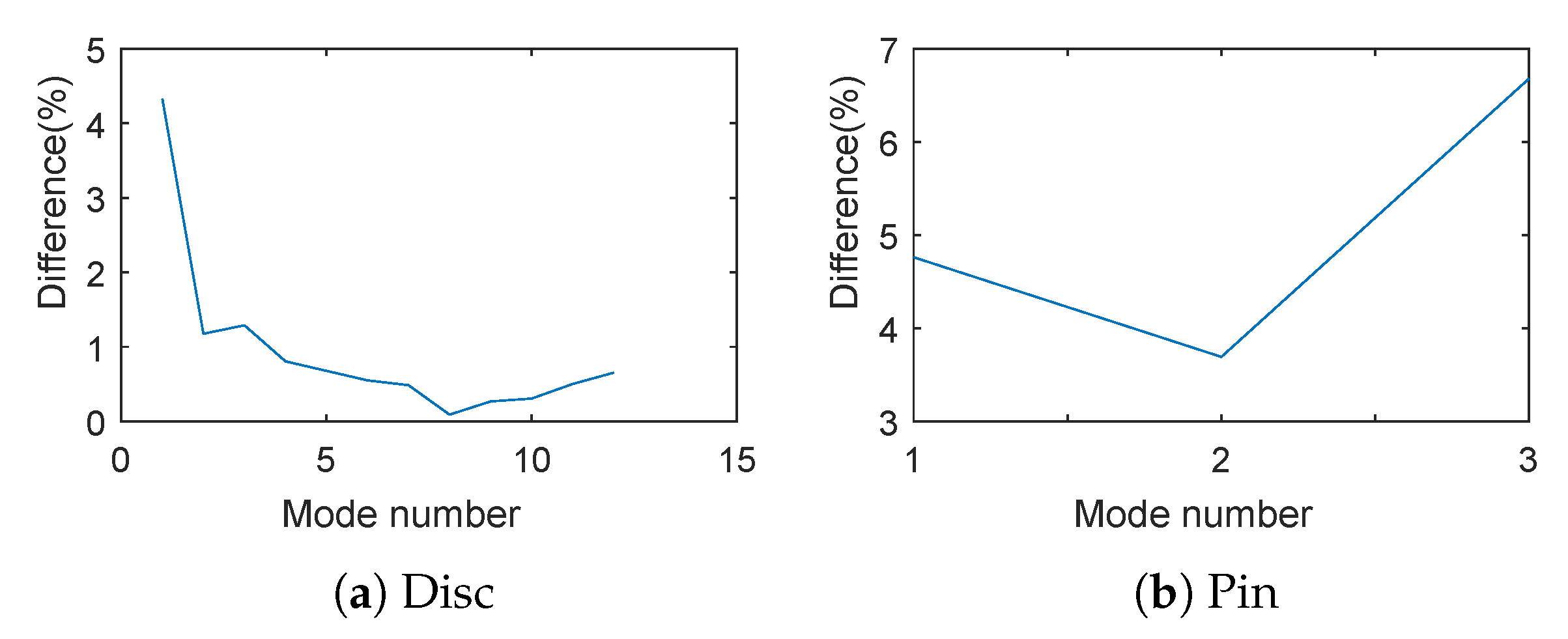
2.1. Finite Element Model
2.2. Stability Study by Complex Eigenvalue Analysis
2.3. Numerical Application: Uniform Zone Contact
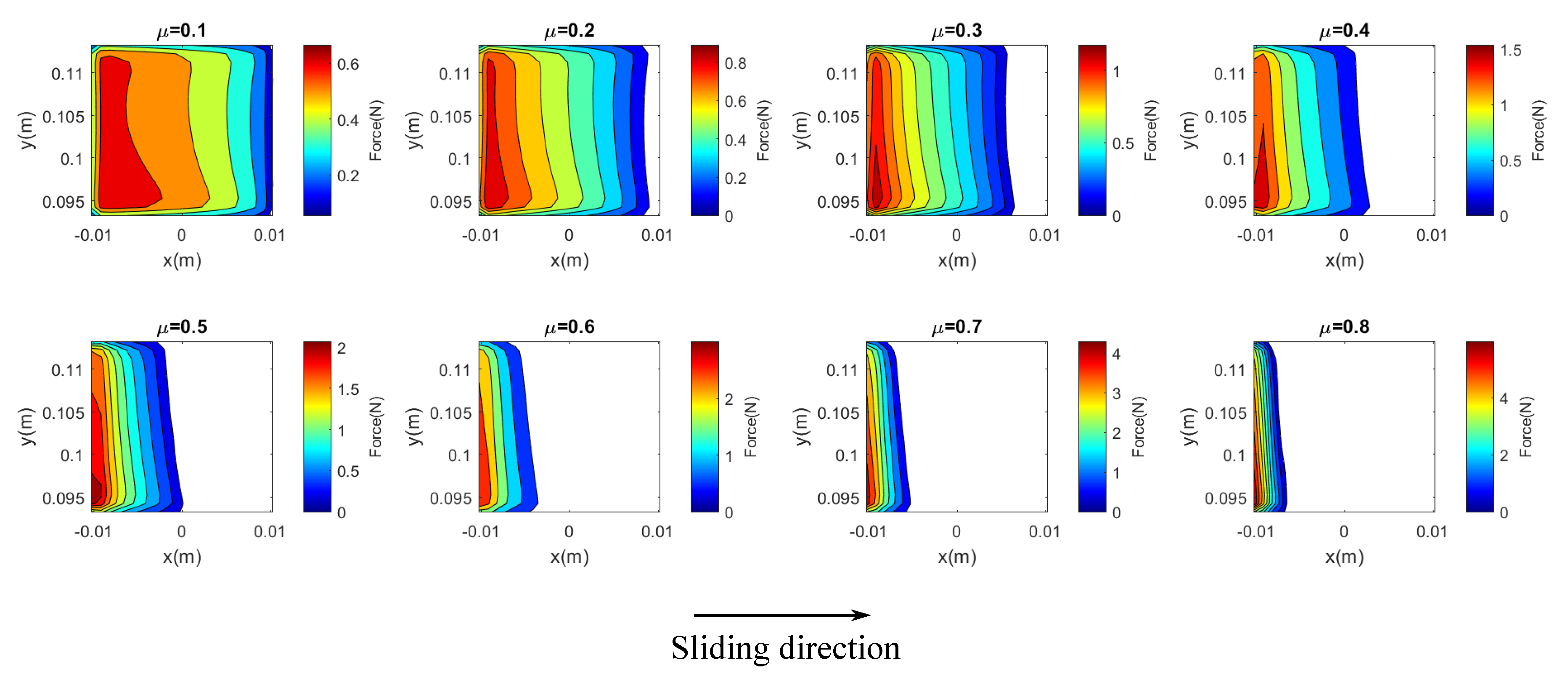
2.3.1. Quasi-Static Equilibrium
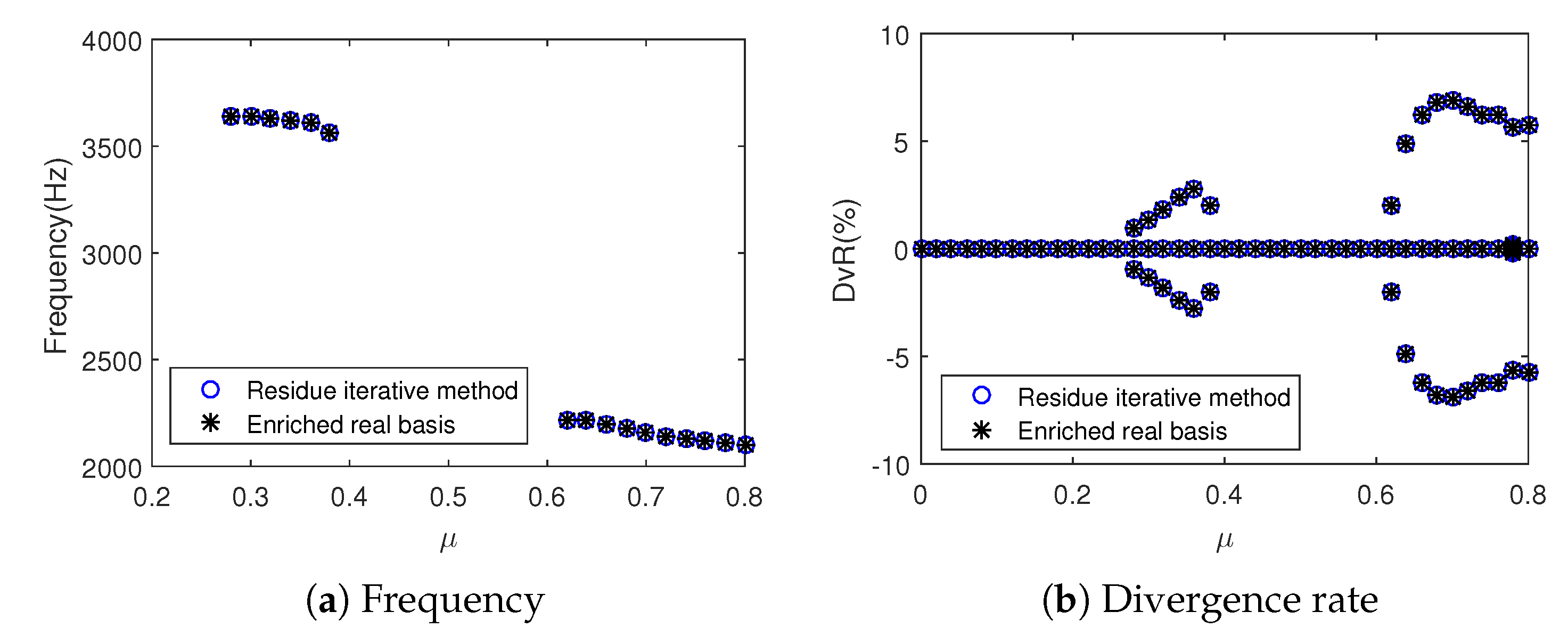
2.3.2. Stability Analysis Results
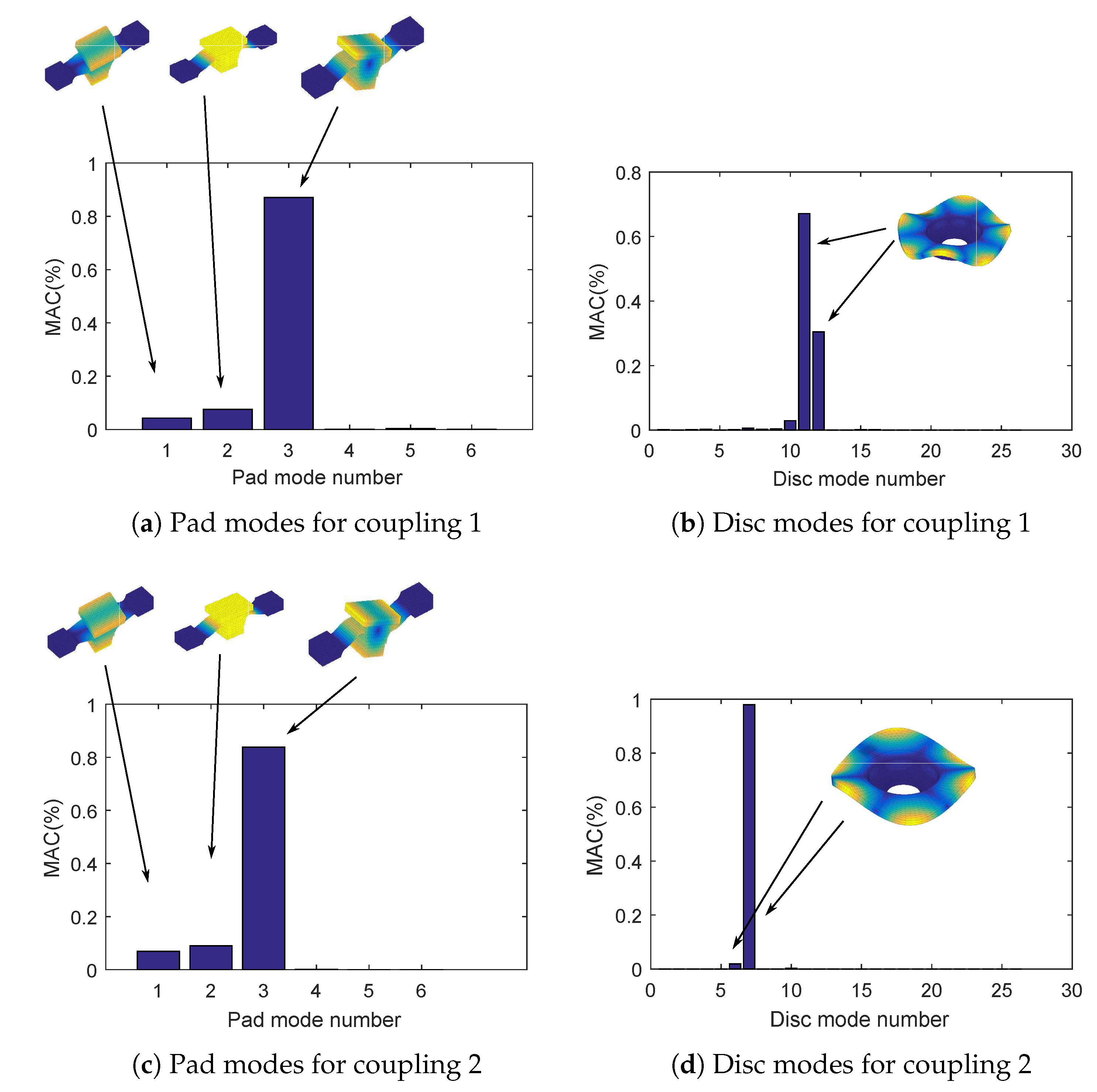
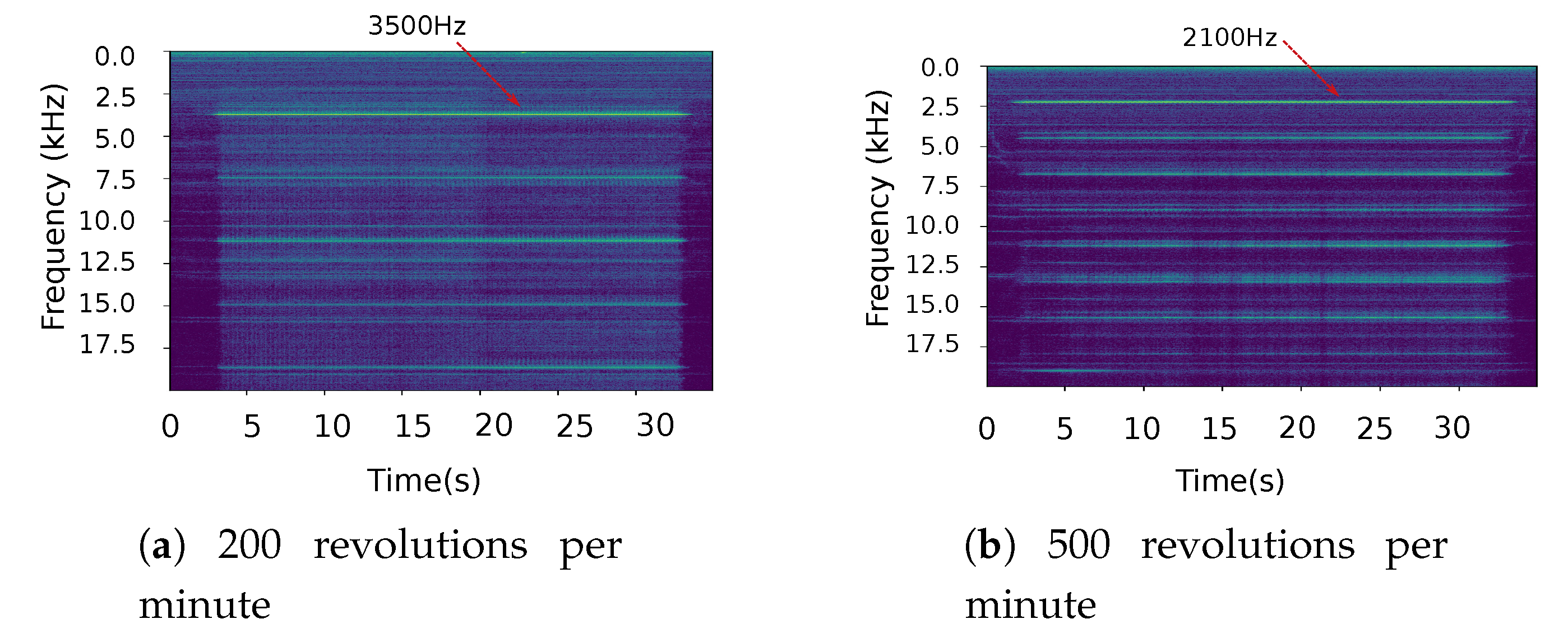
2.4. Experimental Observations
3. Influence of the Contact Distribution at Different Scales
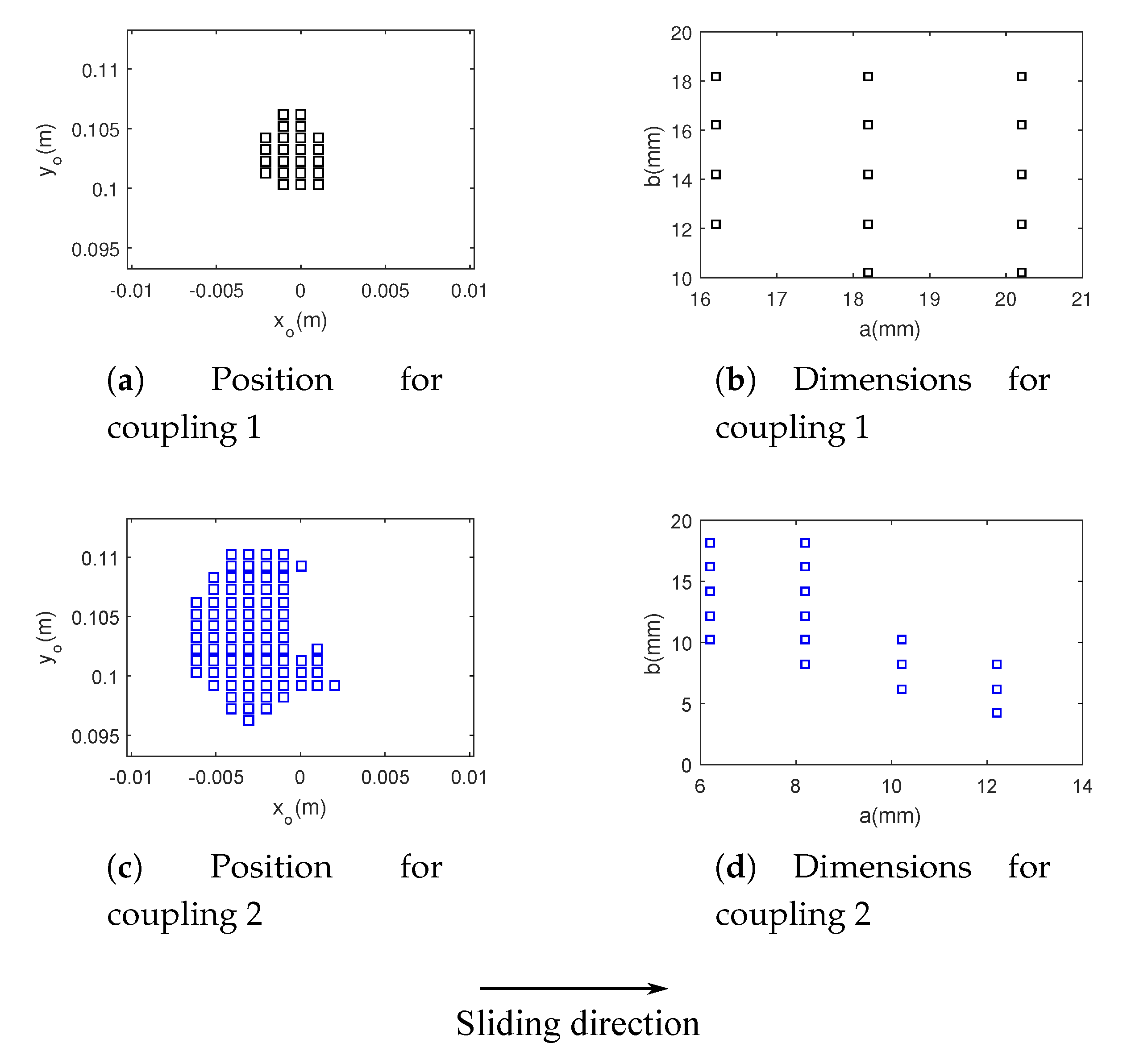
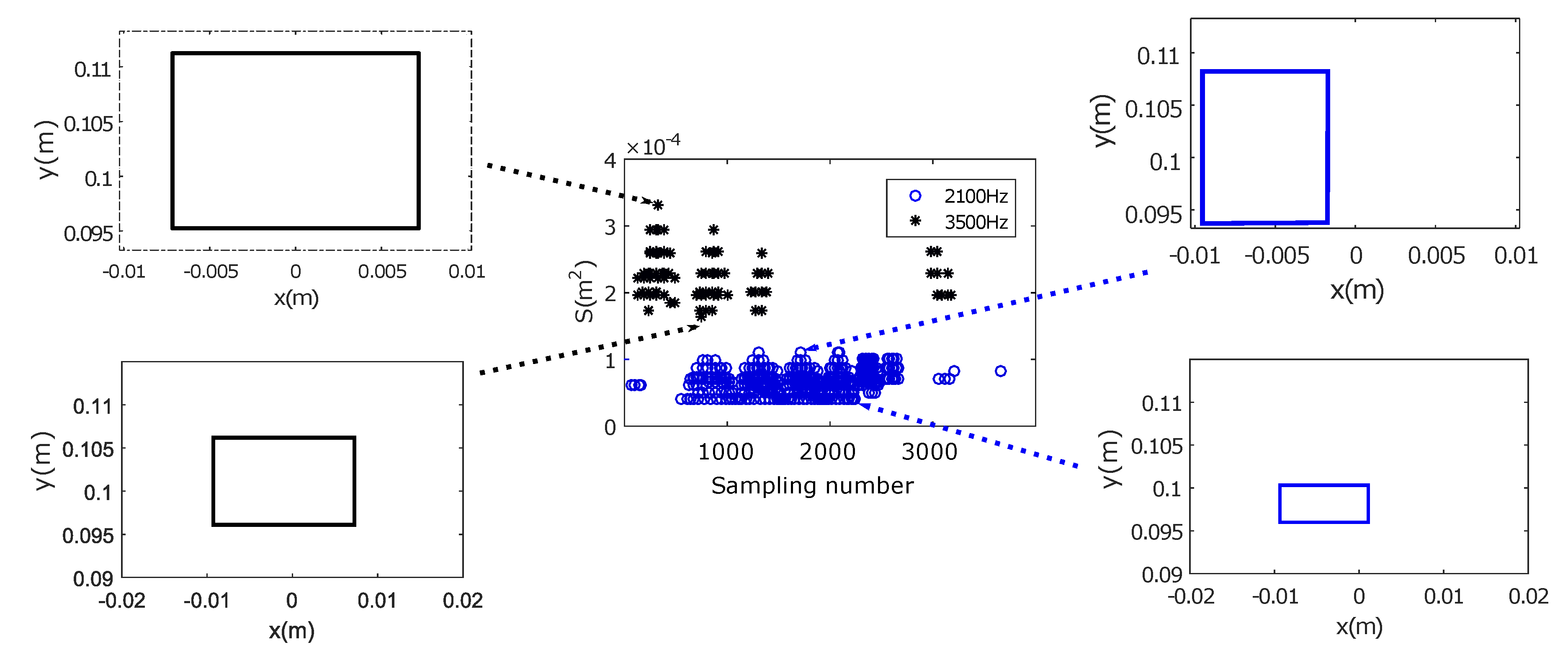
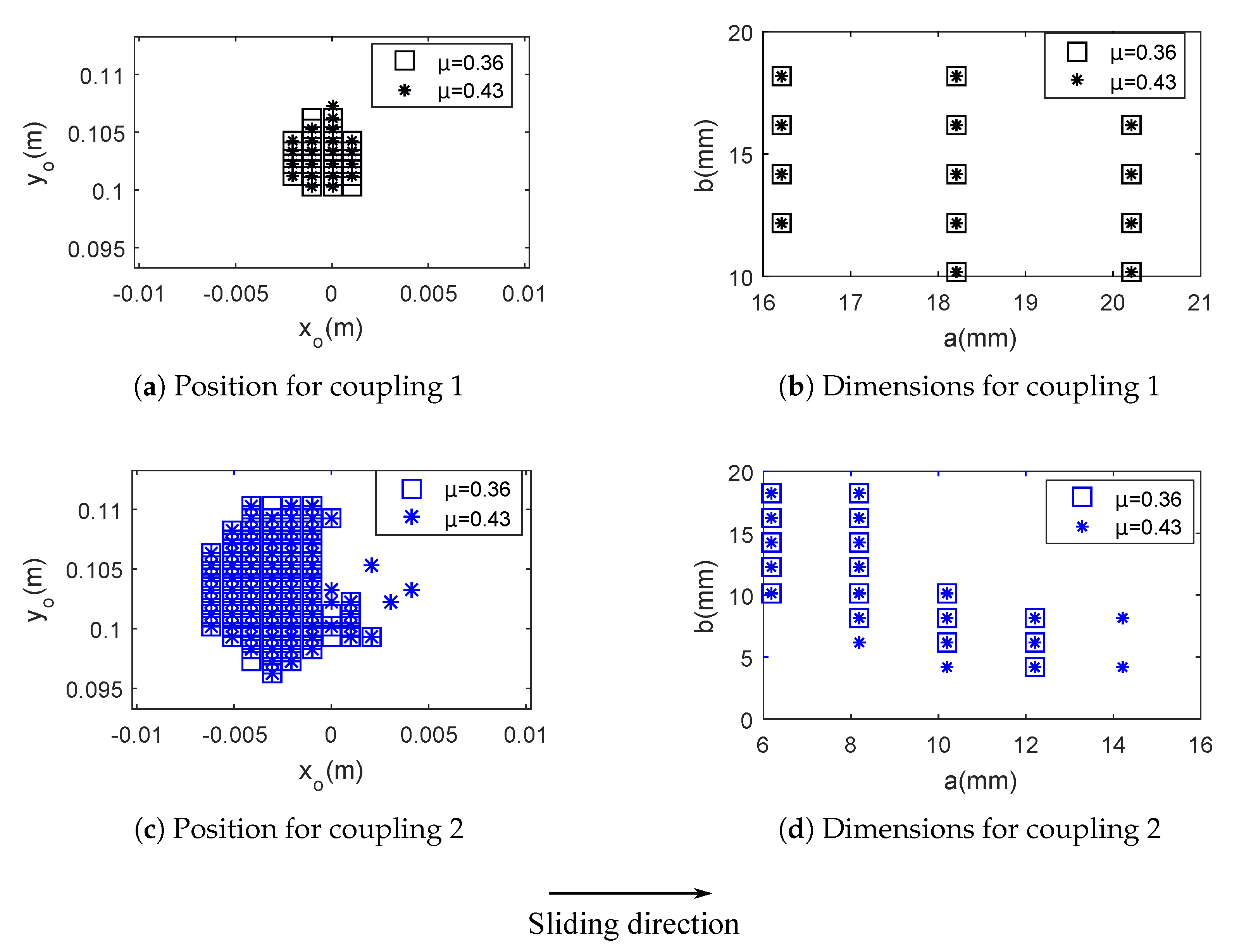
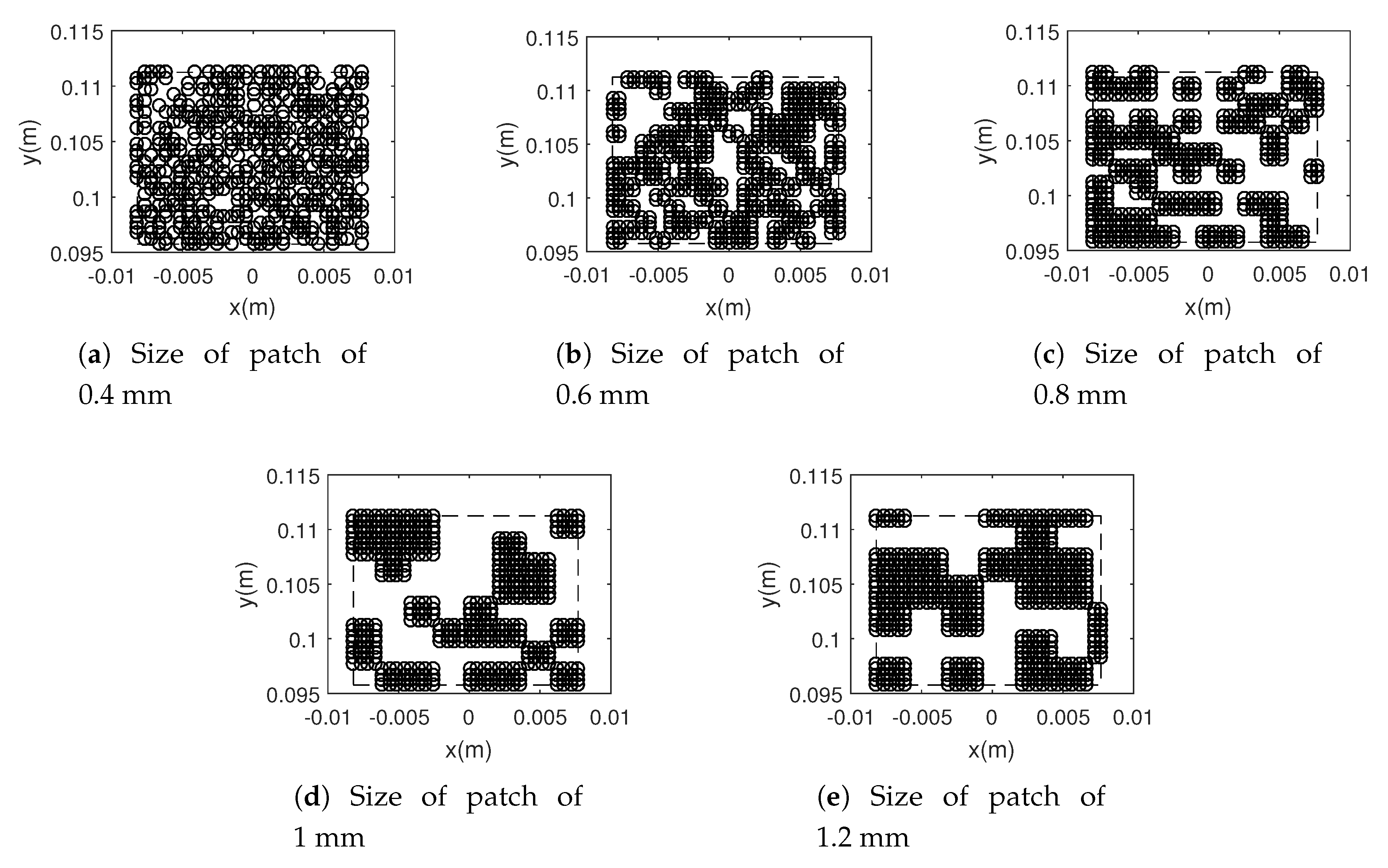
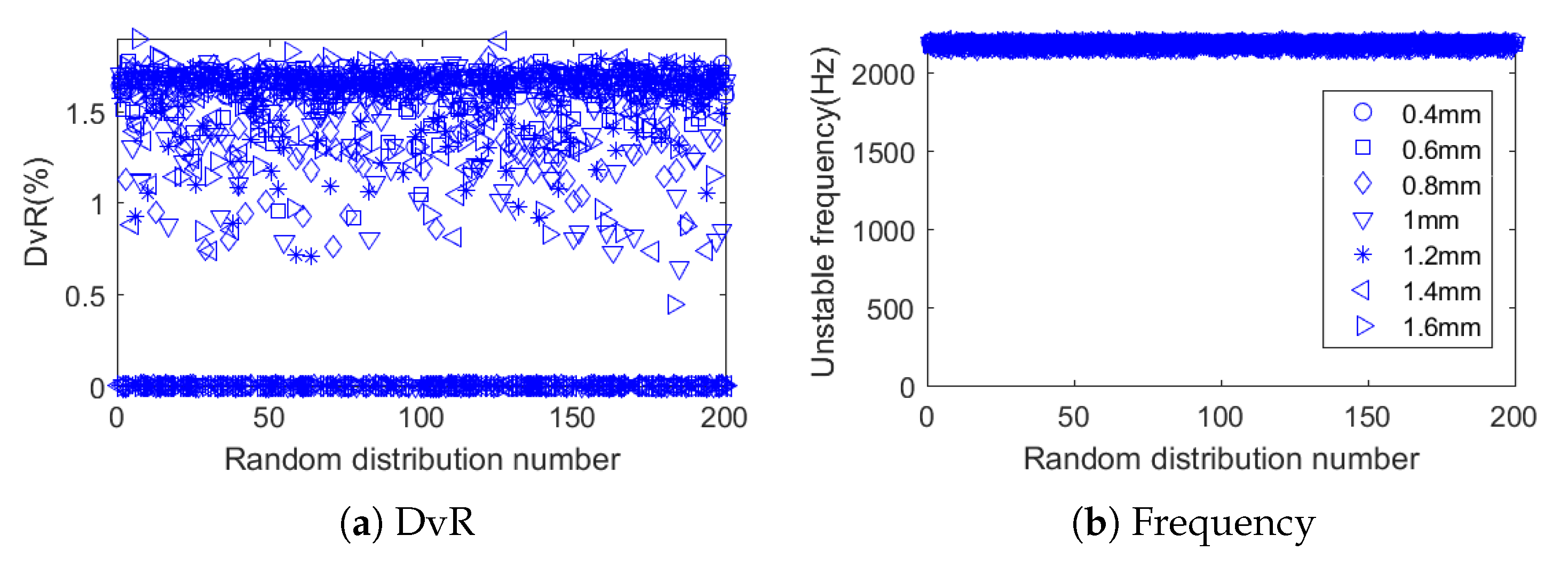
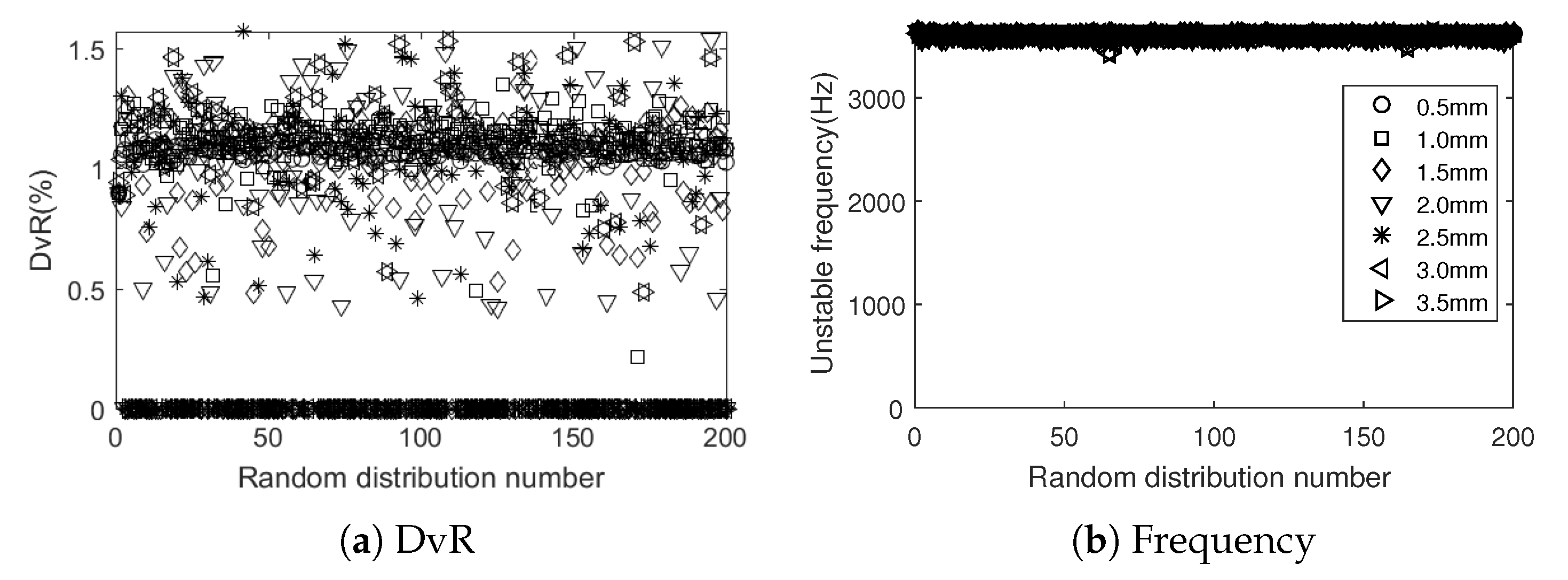
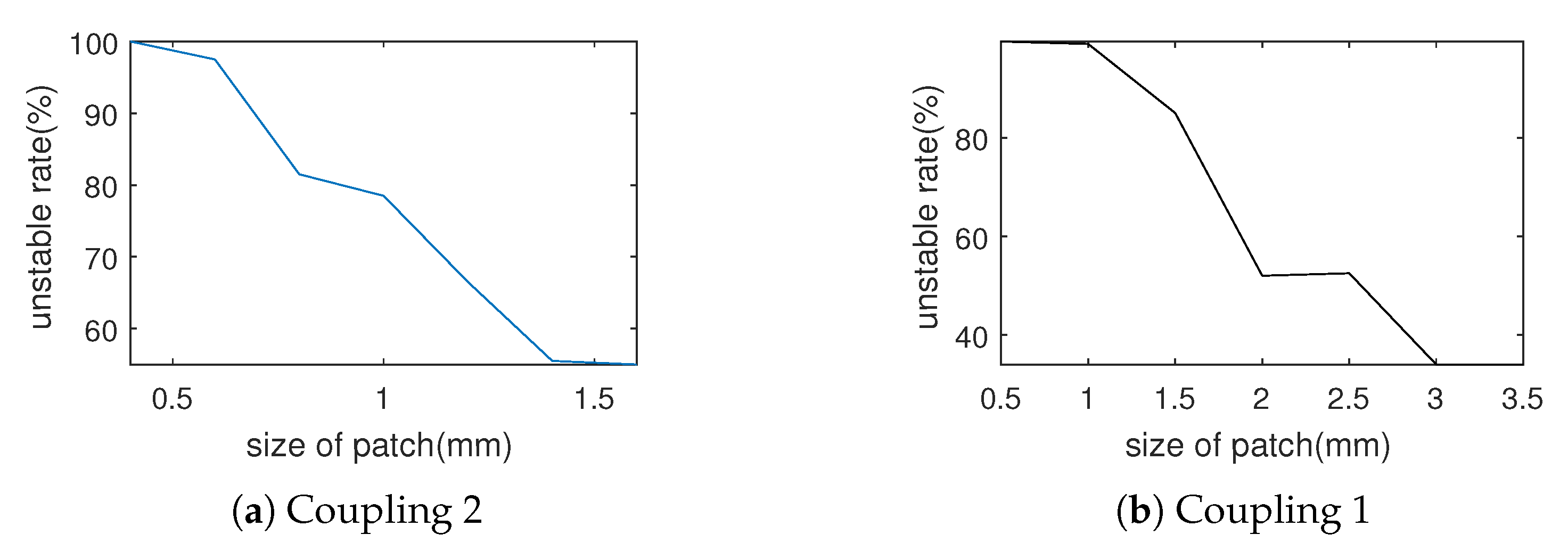
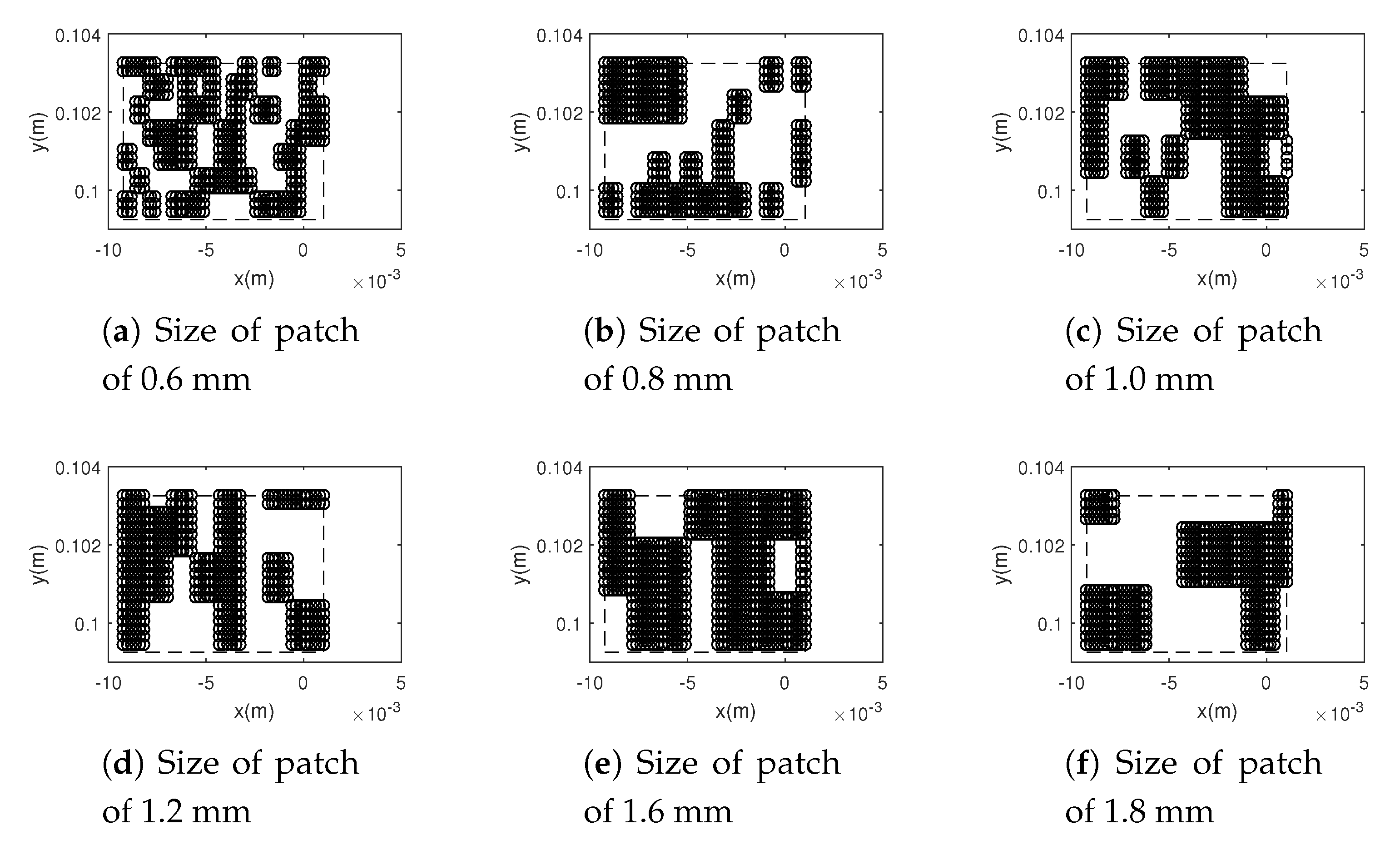
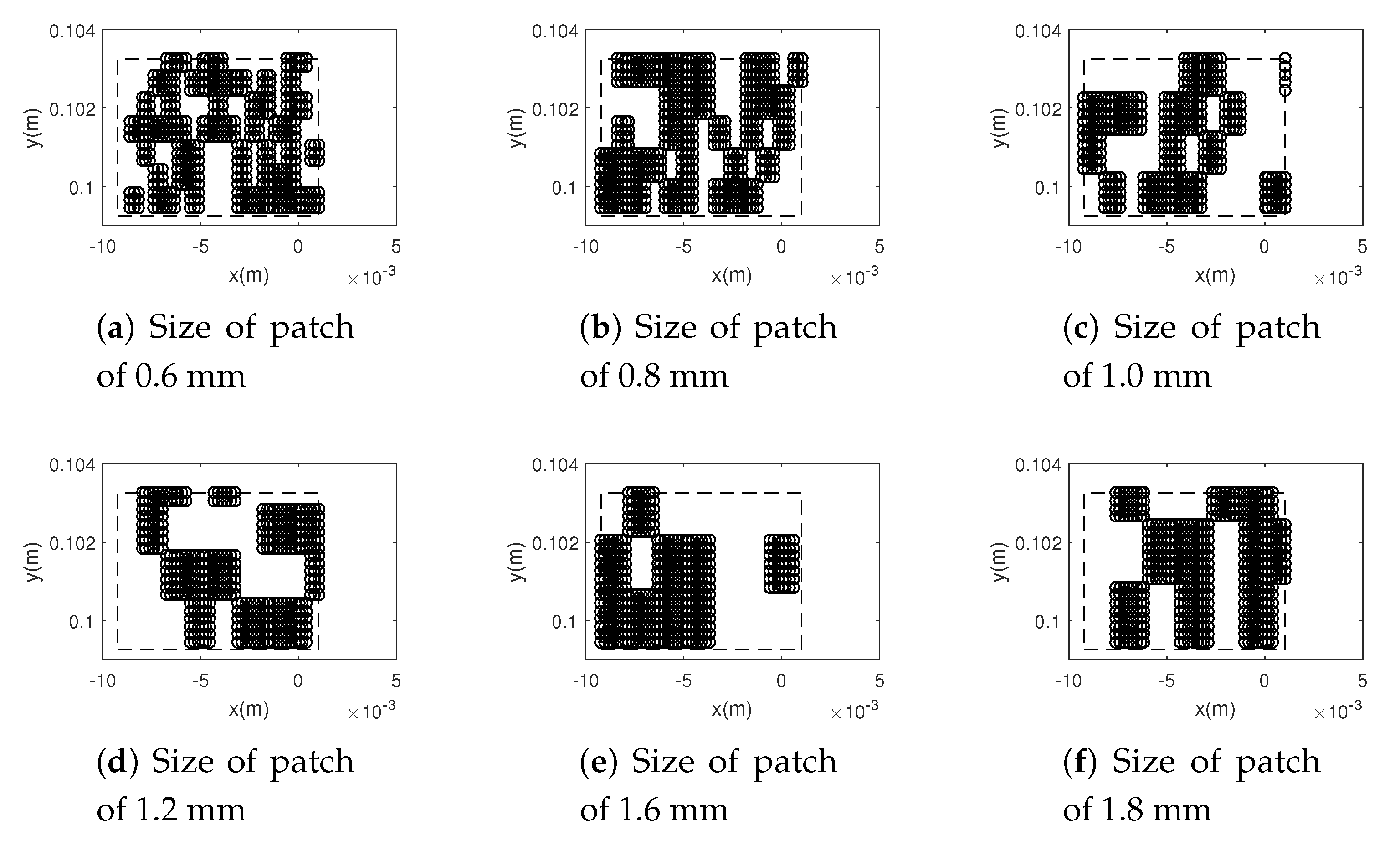
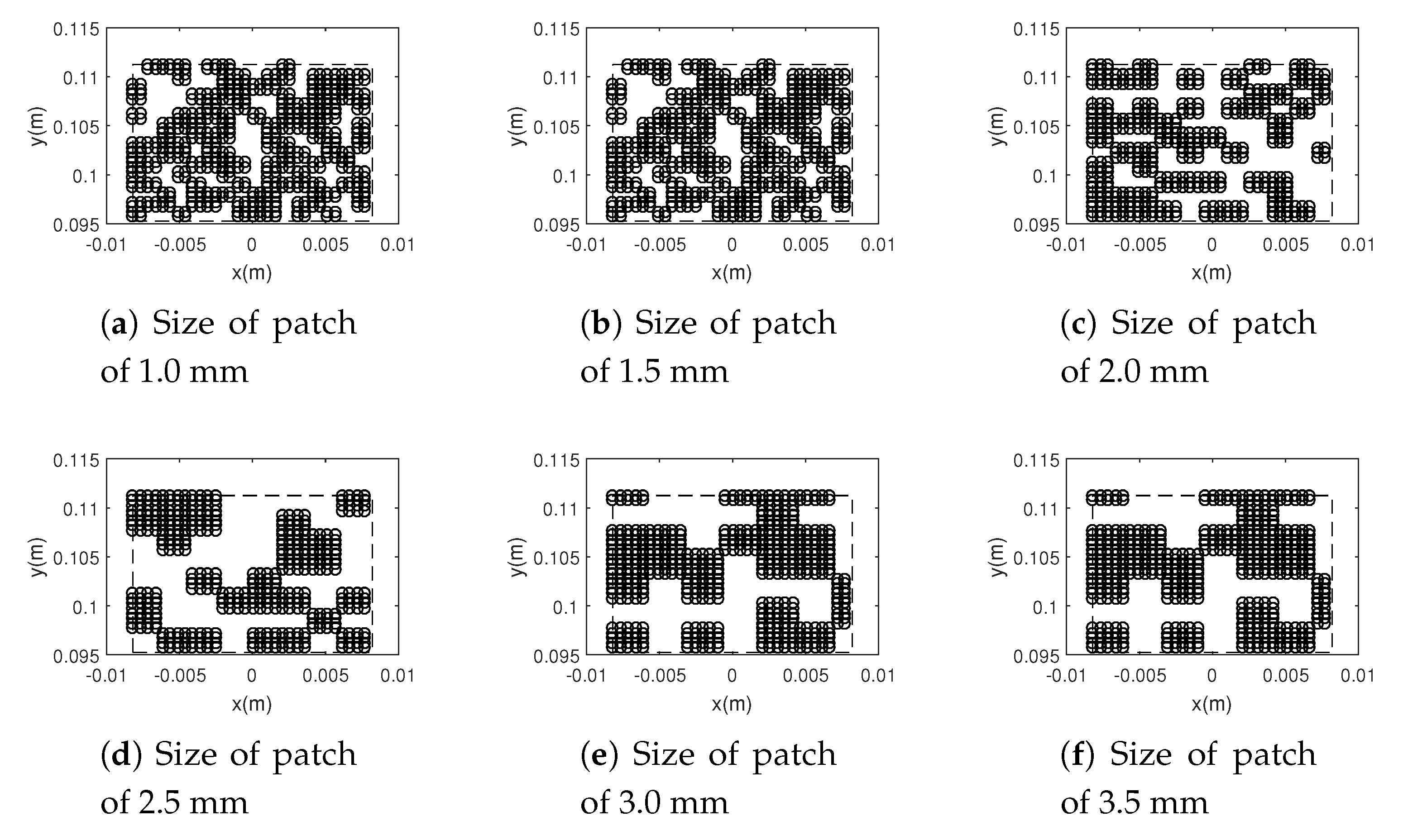
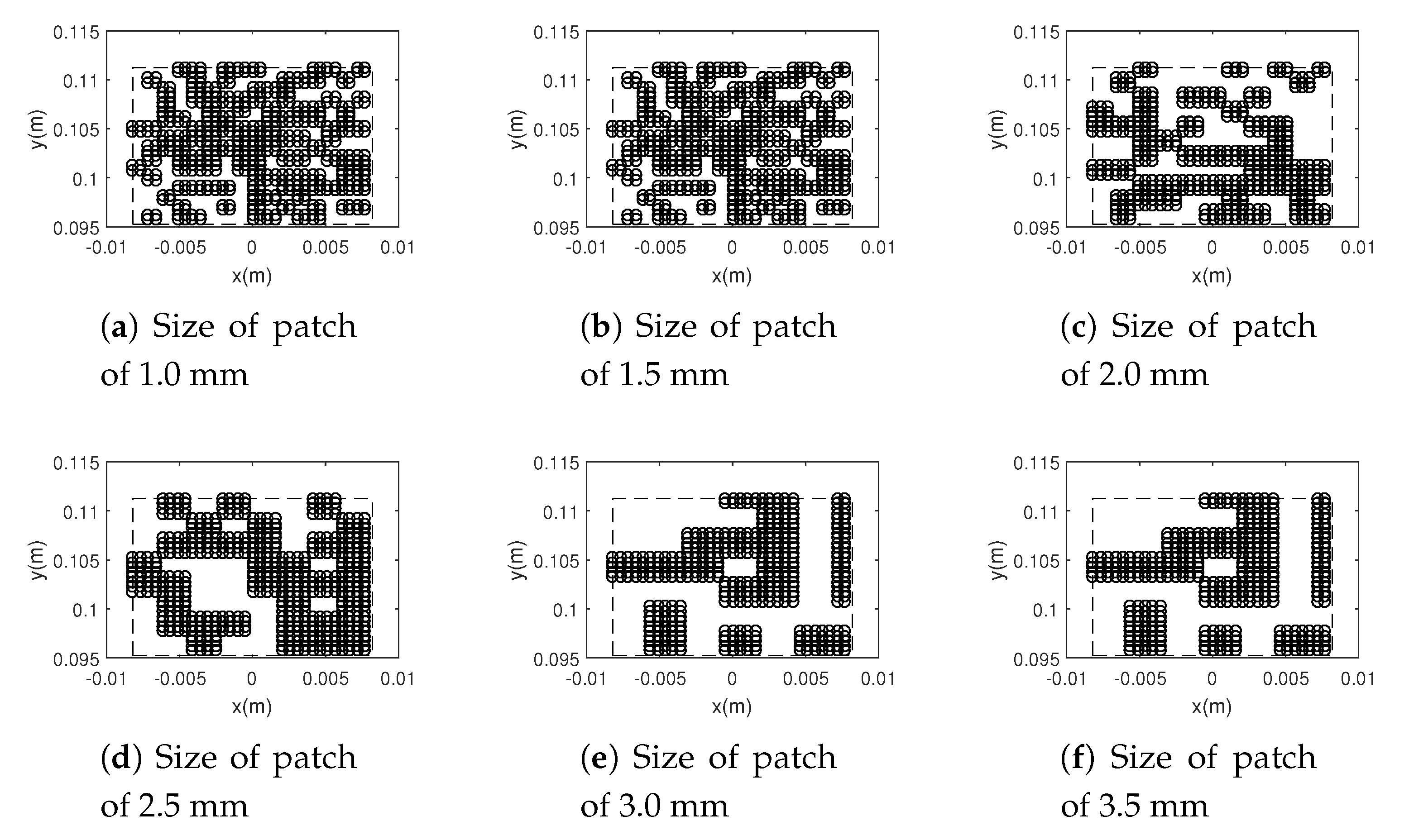
3.1. Macroscopic Scale
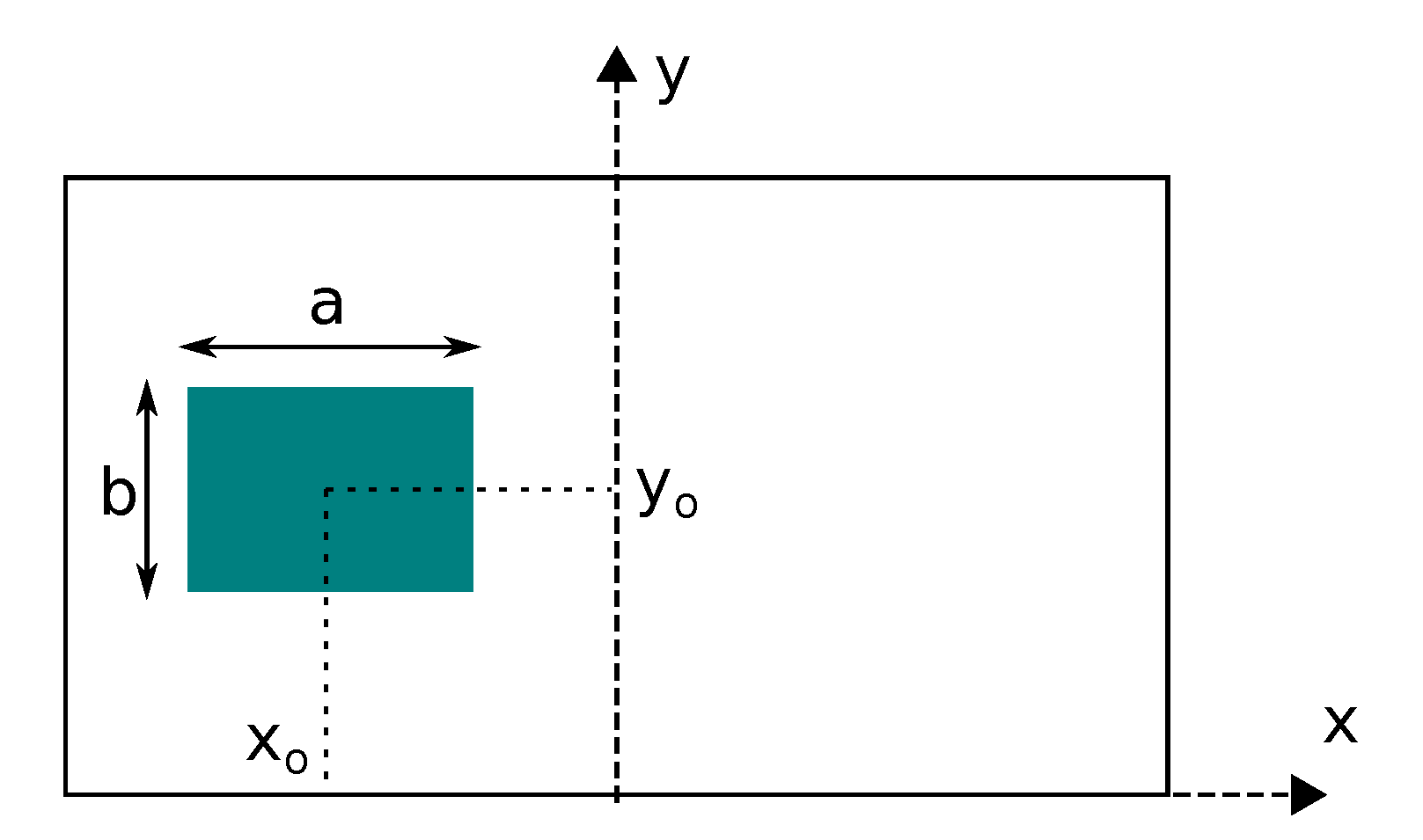
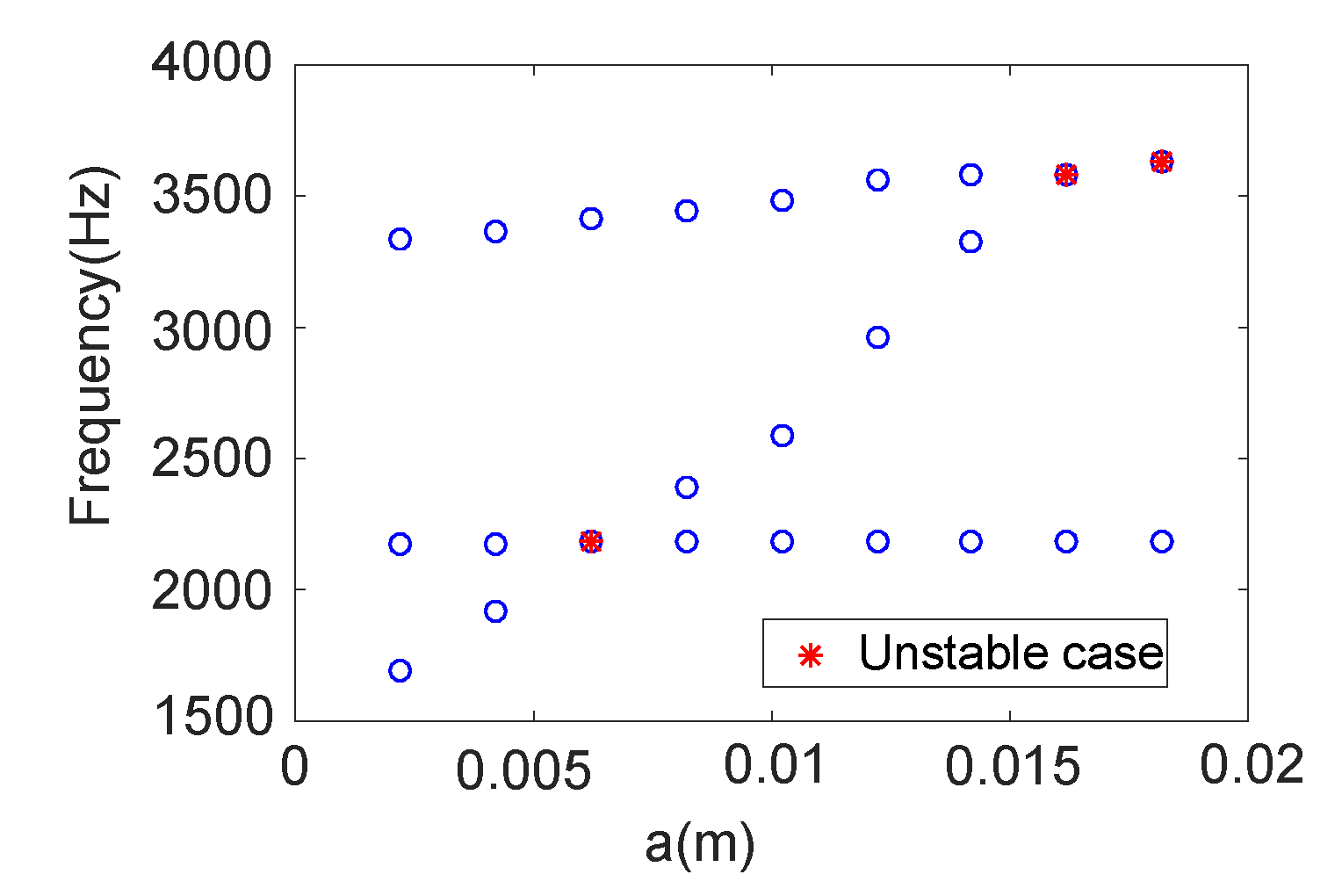
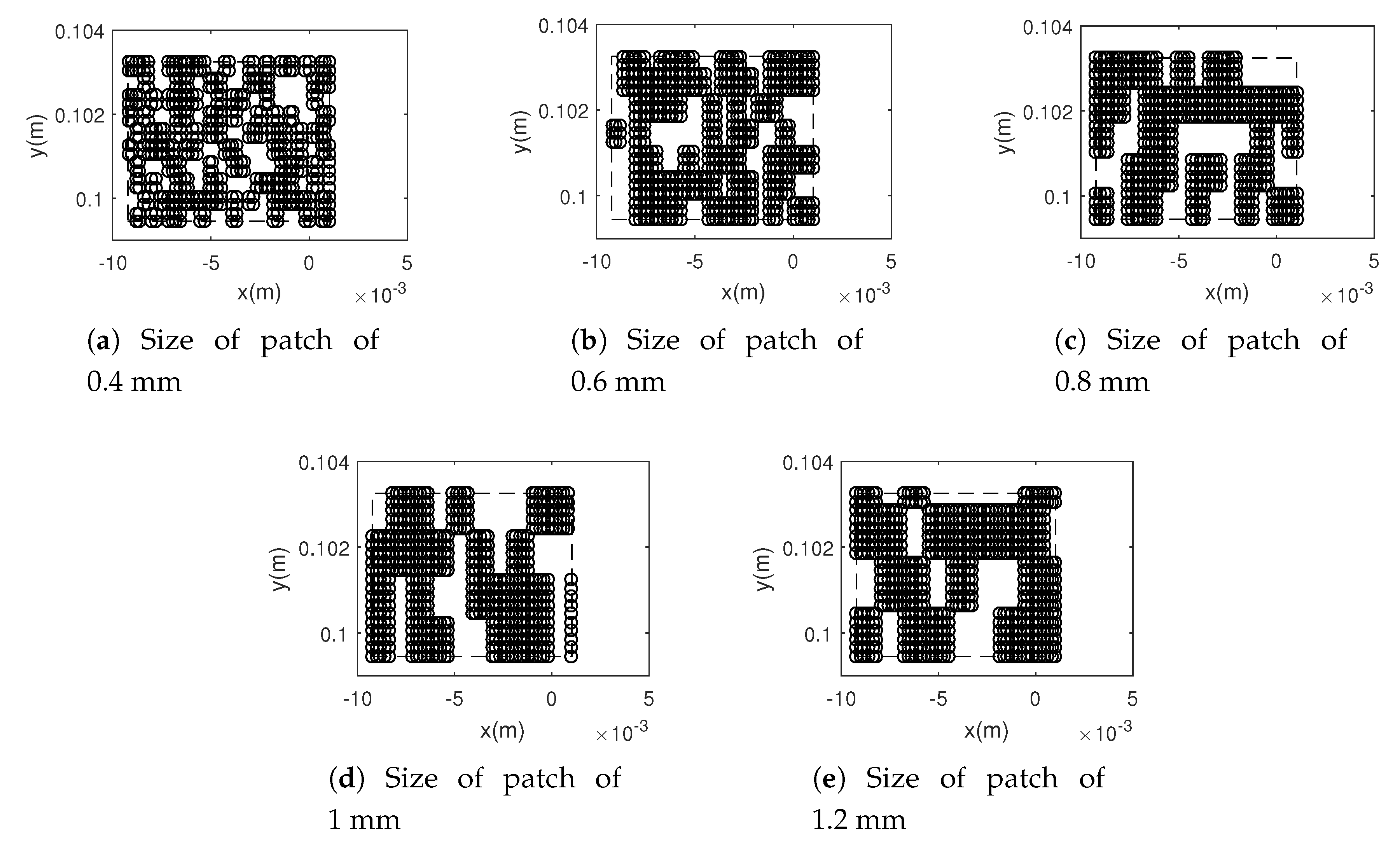
3.2. Mesoscopic Scale
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Akay, A. Acoustics of friction. J. Acoust. Soc. Am. 2002, 111, 1525–1548. [Google Scholar] [CrossRef]
- Junior, M.T.; Gerges, S.N.; Jordan, R. Analysis of brake squeal noise using the finite element method: A parametric study. Appl. Acoust. 2008, 69, 147–162. [Google Scholar] [CrossRef]
- Eriksson, M.; Lundqvist, A.; Jacobson, S. A study of the influence of humidity on the friction and squeal generation of automotive brake pads. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2001, 215, 329–342. [Google Scholar] [CrossRef]
- Ibrahim, R. Friction-Induced Noise and Related Problems in Automotive Brakes. In Research Developments in Sound and Vibration; Transworld Research Network: Kerala, India, 2002. [Google Scholar]
- Desplanques, Y.; Degallaix, G. Interactions between third-body flows and localisation phenomena during railway high-energy stop braking. Sae Int. J. Passeng. Cars-Mech. Syst. 2008, 1, 1267–1275. [Google Scholar] [CrossRef]
- Singla, N.; Brunel, J.-F.; Mège-Revil, A.; Kasem, H.; Desplanques, Y. Experiment to investigate the relationship between the third-body layer and the occurrence of squeals in dry sliding contact. Tribol. Lett. 2020, 68, 4. [Google Scholar] [CrossRef]
- Österle, W.; Dörfel, I.; Prietzel, C.; Rooch, H.; Cristol-Bulthé, A.-L.; Degallaix, G.; Desplanques, Y. A comprehensive microscopic study of third body formation at the interface between a brake pad and brake disc during the final stage of a pin-on-disc test. Wear 2009, 267, 781–788. [Google Scholar] [CrossRef]
- Kasem, H.; Bonnamy, S.; Rousseau, B.; Estrade-Szwarckopf, H.; Berthier, Y.; Jacquemard, P. Interdependence between wear process, size of detached particles and co2 production during carbon/carbon composite friction. Wear 2007, 263, 1220–1229. [Google Scholar] [CrossRef]
- Eriksson, M.; Jacobson, S. Friction behaviour and squeal generation of disc brakes at low speeds. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2001, 215, 1245–1256. [Google Scholar] [CrossRef]
- Sherif, H.A. Effect of contact stiffness on the establishment of self-excited vibrations. Wear 1991, 141, 227–234. [Google Scholar] [CrossRef]
- Sherif, H.A.; Kossa, S. Relationship between normal and tangential contact stiffness of nominally flat surfaces. Wear 1991, 151, 49–62. [Google Scholar] [CrossRef]
- Sherif, H. Investigation on effect of surface topography of pad/disc assembly on squeal generation. Wear 2004, 257, 687–695. [Google Scholar] [CrossRef]
- Lee, S.; Shin, M.; Jang, H. Friction-induced intermittent motion affected by surface roughness of brake friction materials. Wear 2013, 308, 29–34. [Google Scholar] [CrossRef]
- Magnier, V.; Brunel, J.-F.; Dufrénoy, P. Impact of contact stiffness heterogeneities on friction-induced vibration. Int. J. Solids Struct. 2014, 51, 1662–1669. [Google Scholar] [CrossRef]
- Eriksson, M.; Bergman, F.; Jacobson, S. Surface characterisation of brake pads after running under silent and squealing conditions. Wear 1999, 232, 163–167. [Google Scholar] [CrossRef]
- Eriksson, M.; Bergman, F.; Jacobson, S. On the nature of tribological contact in automotive brakes. Wear 2002, 252, 26–36. [Google Scholar] [CrossRef]
- Yoon, S.; Shin, M.; Lee, W.; Jang, H. Effect of surface contact conditions on the stick-slip behavior of brake friction material. Wear 2012, 294, 305–312. [Google Scholar] [CrossRef]
- Lee, S.; Jang, H. Effect of plateau distribution on friction instability of brake friction materials. Wear 2018, 400, 1–9. [Google Scholar] [CrossRef]
- Kim, J.W.; Joo, B.S.; Jang, H. The effect of contact area on velocity weakening of the friction coefficient and friction instability: A case study on brake friction materials. Tribol. Int. 2019, 135, 38–45. [Google Scholar] [CrossRef]
- Bergman, F.; Eriksson, M.; Jacobson, S. The effect of reduced contact area on the occurrence of disc brake squeals for an automotive brake pad. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2000, 214, 561–568. [Google Scholar] [CrossRef]
- Duboc, M.; Magnier, V.; Brunel, J.-F.; Dufrénoy, P. Experimental set-up and the associated model for squeal analysis. Mech. Ind. 2020, 21, 204. [Google Scholar] [CrossRef]
- AbuBakar, A.R.; Ouyang, H. Wear prediction of friction material and brake squeal using the finite element method. Wear 2008, 264, 1069–1076. [Google Scholar] [CrossRef]
- Ramasami, D.N. Influence of Friction Material & Test Sequence on Disc Brake Squeal. Ph.D. Thesis, Lille 1, Villeneuve-d’Ascq, France, 2014. [Google Scholar]
- Gao, C.; Kuhlmann-Wilsdorf, D.; Makel, D.D. Fundamentals of stick-slip. Wear 1993, 162, 1139–1149. [Google Scholar] [CrossRef]
- Gao, C.; Kuhlmann-Wilsdorf, D.; Makel, D.D. The dynamic analysis of stick-slip motion. Wear 1994, 173, 1–12. [Google Scholar] [CrossRef]
- Ibrahim, R. Friction-induced vibration, chatter, squeal, and chaos—Part i: Mechanics of contact and friction. Appl. Mech. Rev. 1994, 47, 209–226. [Google Scholar] [CrossRef]
- Ibrahim, R. Friction-induced vibration, chatter, squeal, and chaos—Part ii: Dynamics and modeling. Appl. Mech. Rev. 1994, 47, 227–253. [Google Scholar] [CrossRef]
- Jarvis, R.; Mills, B. Vibrations induced by dry friction. Proc. Inst. Mech. Eng. 1963, 178, 847–857. [Google Scholar] [CrossRef]
- Spurr, R.T. A theory of brake squeal. Proc. Inst. Mech. Eng. Automob. Div. 1961, 15, 33–52. [Google Scholar] [CrossRef]
- Chambrette, P.; Jezequel, L. Stability of a beam rubbed against a rotating disc. Eur. J. Mech. A Solids 1992, 11, 107–138. [Google Scholar]
- Hoffmann, N.; Fischer, M.; Allgaier, R.; Gaul, L. A minimal model for studying properties of the mode-coupling type instability in friction induced oscillations. Mech. Res. Commun. 2002, 29, 197–205. [Google Scholar] [CrossRef]
- Sinou, J.-J. Transient non-linear dynamic analysis of automotive disc brake squeal-on the need to consider both stability and non-linear analysis. Mech. Res. Commun. 2010, 37, 96–105. [Google Scholar] [CrossRef]
- Lorang, X.; Foy-Margiocchi, F.; Nguyen, Q.; Gautier, P. {TGV} disc brake squeal. J. Sound Vib. 2006, 293, 735–746. [Google Scholar] [CrossRef]
- Massi, F.; Baillet, L.; Giannini, O.; Sestieri, A. Brake squeal: Linear and nonlinear numerical approaches. Mech. Syst. Signal Process. 2007, 21, 2374–2393. [Google Scholar] [CrossRef]
- Tison, T.; Heussaff, A.; Massa, F.; Turpin, I.; Nunes, R. Improvement in the predictivity of squeal simulations: Uncertainty and robustness. J. Sound Vib. 2014, 333, 3394–3412. [Google Scholar] [CrossRef]
- Sinou, J.-J.; Jézéquel, L. Mode coupling instability in friction-induced vibrations and its dependency on system parameters including damping. Eur. J. Mech. A Solids 2007, 26, 106–122. [Google Scholar] [CrossRef]
- Denimal, E.; Sinou, J.-J.; Nacivet, S. Influence of structural modifications of automotive brake systems for squeal events with kriging meta-modelling method. J. Sound Vib. 2019, 463, 114938. [Google Scholar] [CrossRef]
- Denimal, E.; Sinou, J.-J.; Nacivet, S.; Nechak, L. Squeal analysis based on the effect and determination of the most influential contacts between the different components of an automotive brake system. Int. J. Mech. Sci. 2019, 151, 192–213. [Google Scholar] [CrossRef]
- Loyer, A.; Sinou, J.-J.; Chiello, O.; Lorang, X. Study of nonlinear behaviors and modal reductions for friction destabilized systems. Application to an elastic layer. J. Sound Vib. 2012, 331, 1011–1041. [Google Scholar] [CrossRef][Green Version]
- Brizard, D.; Chiello, O.; Sinou, J.-J.; Lorang, X. Performances of some reduced bases for the stability analysis of a disc/pads system in sliding contact. J. Sound Vib. 2011, 330, 703–720. [Google Scholar] [CrossRef]
- Sorensen, D.C. Implicit application of polynomial filters in ak-step arnoldi method. Siam J. Matrix Anal. Appl. 1992, 13, 357–385. [Google Scholar] [CrossRef]
- Bobillot, A. Méthodes de Réduction Pour le Recalage Application au cas D’ariane 5. Ph.D. Thesis, Ecole Centrale Paris, Châtenay-Malabry, France, 2002. [Google Scholar]
- Quéméner, O.; Battaglia, J.-L.; Neveu, A. Résolution d’un problème inverse par utilisation d’un modèle réduit modal. application au frottement d’un pion sur un disque en rotation. Int. J. Therm. Sci. 2003, 42, 361–378. [Google Scholar] [CrossRef]
- Waddad, Y.; Magnier, V.; Dufrénoy, P.; Saxcé, G.D. Multiscale thermomechanical modeling of frictional contact problems considering wear–application to a pin-on-disc system. Wear 2019, 426, 1399–1409. [Google Scholar] [CrossRef]


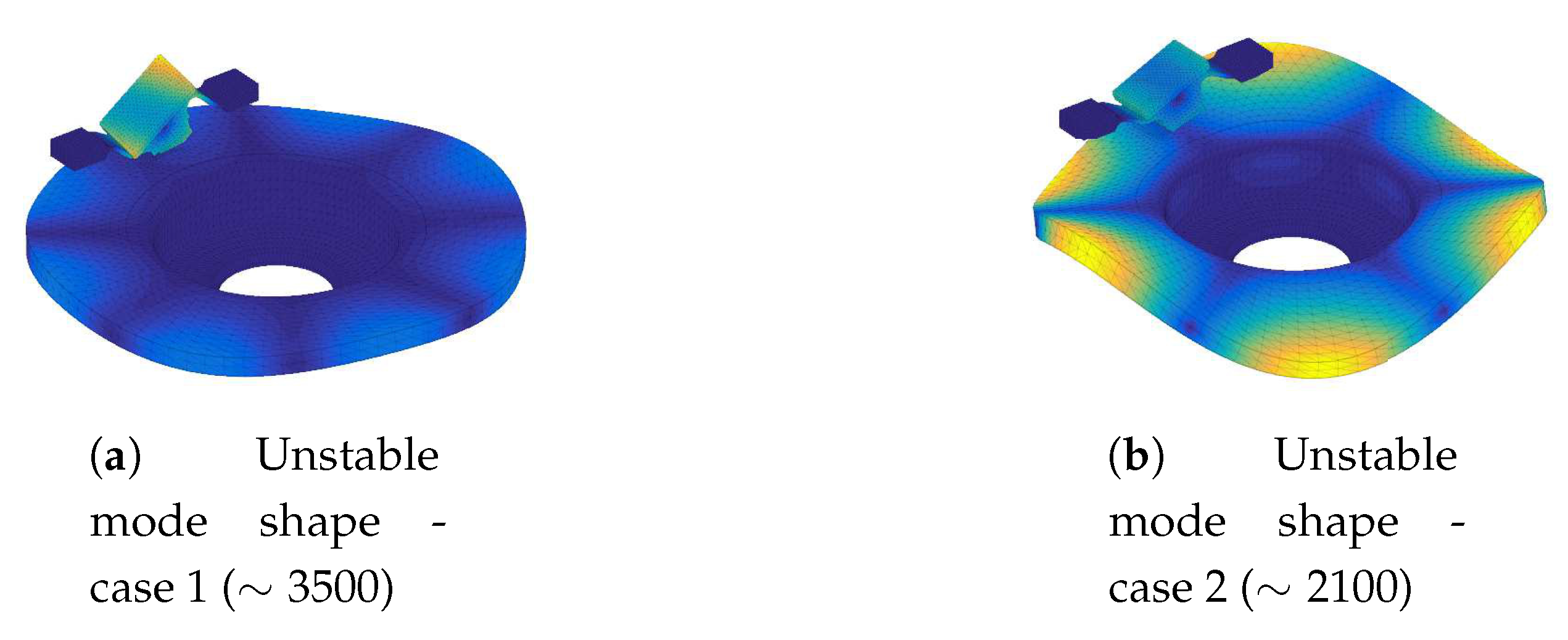




| Data | Disc | Pad | Thin Plate | Thick Plate |
|---|---|---|---|---|
| Young’s modulus (GPa) | 210 | , | 60 | 210 |
| Poisson’s ratio | 0.3 | 0.3 | 0.3 | |
| Density (kg/m3) | 7850 | 4000 | 2500 | 7850 |
| Mode Number | Type | Frequencies (Hz) | Mode Number | Type | Frequencies (Hz) | ||
|---|---|---|---|---|---|---|---|
| 1 | a,0,0 | 892.3 | 15,16 | a,0,5 | double | 5571 | |
| 2,3 | a,0,1 | double | 912.2 | 17,18 | a,0,6 | double | 7776 |
| 4,5 | a,0,2 | double | 1261 | 19 | a,1,0 | 7873 | |
| 6,7 | a,0,3 | double | 2220 | 20 | a,1,1 | double | 8596 |
| 8 | c,0 | 3108 | 21,22 | r,3 | double | 8634 | |
| 9,10 | c,1 | double | 3324 | 23 | r,0 | 9122 | |
| 11,12 | a,0,4 | double | 3694 | 24,25 | a,1,2 | double | 9648 |
| 13,14 | r,2 | double | 4735 | 26,27 | a,0,7 | double | 10,250 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, V.-V.; Paszkiewicz, I.; Brunel, J.-F.; Dufrénoy, P. Multi-Scale Contact Localization and Dynamic Instability Related to Brake Squeal. Lubricants 2020, 8, 43. https://doi.org/10.3390/lubricants8040043
Lai V-V, Paszkiewicz I, Brunel J-F, Dufrénoy P. Multi-Scale Contact Localization and Dynamic Instability Related to Brake Squeal. Lubricants. 2020; 8(4):43. https://doi.org/10.3390/lubricants8040043
Chicago/Turabian StyleLai, Van-Vuong, Igor Paszkiewicz, Jean-François Brunel, and Philippe Dufrénoy. 2020. "Multi-Scale Contact Localization and Dynamic Instability Related to Brake Squeal" Lubricants 8, no. 4: 43. https://doi.org/10.3390/lubricants8040043
APA StyleLai, V.-V., Paszkiewicz, I., Brunel, J.-F., & Dufrénoy, P. (2020). Multi-Scale Contact Localization and Dynamic Instability Related to Brake Squeal. Lubricants, 8(4), 43. https://doi.org/10.3390/lubricants8040043




