Abstract
Hydraulic dynamic seals for reciprocating or alternating motion are machine elements with widespread applications in the automotive, aerospace, marine, pharmaceutical and several other industrial sectors. They have been under commercial development for many decades, and are often met in critical positions, consuming a considerable amount of energy during operation. An objective function of mass leakage rate, friction force and an abrasive-wear representative term is proposed in the present study to evaluate the performance of hydraulic, polymeric sliding seals under suitable constraints. Using Variational Calculus, analytical and numerical techniques, the objective function is minimized, resulting in an optimal seal profile that maximizes sealing performance for given, steady-state operating conditions, in additional consideration of the structural integrity and manufacturability of the modified seal. The obtained seal shape and related pressure distribution are reminiscent of those for U-cup and step seals, designs that dominate the industry. In the course of the mathematical analysis, some major obstacles are documented that show how sensitive and complicated sealing performance really is.
1. Introduction
Several theoretical studies in the past 20 years have focused on the performance of hydraulic dynamic seals in an effort to produce experimentally verifiable results. The importance of this task lies on the applicability of such seals in a variety of industrial applications, including aerospace, automotive, marine and others. Examples involve hydraulic actuators, shock absorbers, excavators, steel and rolling mills, presses, hydraulic/machine tools such as jacks, lift platforms, fork lifts, agricultural machines, injection molding machines, truck cranes, valves and valve stems, down-hole tools, servo hydraulics and many others [1]. There are also dozens of designs of hydraulic seals for linear, sliding motion, including rod and piston seals, which have been developed over a period of several decades. Those vary in morphologic complexity from the solid O-ring to composite seals comprising various elements [1,2,3,4,5]. A multitude of flexible materials (e.g., polymers, thermoplastics, composites) and shapes (e.g., rectangular-rounded, toroidal, U-cup, L-cup, X, step) have been developed to satisfy various demands in regards to sealed pressure, sliding velocity, operating temperature and chemical compatibility with sealed fluids. Examples of typical polymeric rod seals are shown in Figure 1.
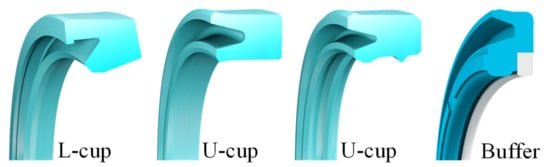
Figure 1.
Examples of rod seals (courtesy of Trelleborg [1]).
It has been theoretically established since at least the 1960s [3,6] that the operating efficiency of sliding hydraulic seals is strongly dependent upon the geometry of a narrow zone known as the elastohydrodynamic (EHD) inlet zone where fluid is entrained during the sliding motion (Figure 2). For given hydraulic fluid, the gradient of the local pressure in that zone is a strongly influential factor that controls the dynamic formation of a thin lubricating film, which then partially or fully separates the seal from its counter-surface. Based on the average thickness of that lubricating film, which is usually less than 1 μm, the performance of the seal for given operating conditions is established in terms of mass leakage rate, frictional force and abrasive wear rate of the tribopair. It is thus imperative for any theoretical analysis to focus on the inlet zone where the secret of sealing success or even failure normally lies. For many types of sliding seals such as the one shown in Figure 2, the working edge (encircled edge C in Figure 2) is relatively sharp, with average radius of curvature in the order of 0.1–0.4 mm [7,8]. Consequently, the length of the inlet zone (L in Figure 2), which is normally smaller than the average curvature radius of the related seal edge, is often very small—sometimes even just a few microns [7]. To optimize sealing performance, it is then desirable to optimize the shape of a seal’s “working” edge such as edge C in Figure 2.
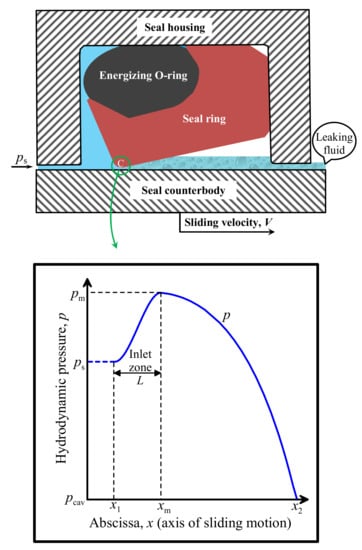
Figure 2.
Example of a pressurized polymeric seal and its hydrodynamic pressure curve for steady sliding.
Ideally, optimizing sealing performance means concurrently minimizing the mass leakage rate (eliminating leaking), the frictional force on the seal (reducing power consumption and frictional heating) and the abrasive wear rate of the tribopair (e.g., seal-rod) to extend the life of the sealing contact and avoid damage or failure. However, the aforementioned objectives are in conflict if the seal geometry is to remain unmodified [9]. For example, minimizing leakage for given seal geometry is achieved by reducing the average film thickness in the sealing contact (e.g., by reducing the sliding velocity), but at the expense of increasing friction and abrasive wear as theoretically demonstrated in previous studies [8,10,11]. A compromise is then inevitable.
In most published theoretical studies dealing with the performance of polymeric sliding seals [3], the problem solved involves calculating the film thickness distribution in a sealing contact and from that point on, calculating the leakage rate and the frictional force or the coefficient of friction; some of the most representative numerical studies in this respect are references [7,8,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. Abrasive wear modeling of seals is not included, except in a handful of studies, given the uncertainty surrounding a wear coefficient such as that included in the well-known Archard wear equation [24,25,26]. Therefore, the literature is focused on calculating leakage and friction, largely ignoring wear. Moreover, optimization of sealing performance, which is obviously also done on the basis of leakage and friction alone, is only tackled indirectly by parametric studies as for example on elastomeric seals for reciprocating linear or alternating rotary motion [8,10,11]. This involves executing bespoke numerical codes such as the author’s software ROSEAL [7] dozens to hundreds of times to explore the effect of a multitude of operating, geometrical and material parameters on leakage and friction.
The literature lacks a theoretical analysis on the mathematical optimization of sealing performance in terms of leakage, friction and wear. This is covered in the present study for general macroscopic shape of hydraulic, polymeric, sliding seals. An objective function of mass leakage rate, frictional force and abrasive wear is defined, and its minimization explored by means of Variational Calculus, analytical and numerical techniques, leading to an optimized seal profile in the sealing zone. Upper limits are imposed to both leakage and friction to rationalize the results. It is found that the optimal seal edge profile resembles that of a U-cup or step seal and that a narrow contact zone often suffices to achieve the targeted performance. Naturally, long-term sealing performance with consideration of material loss from abrasive wear and subsequent alteration of the optimal seal profile is not accounted for in this study but could be a future step. However, the latter requires reliable and precise modeling of wear, which is complicated as evidenced by previous attempts to validate numerical models [26].
2. Mathematical Analysis
2.1. Elastohydrodynamics
The analysis presented herein holds for steady-state and axisymmetric conditions about the axis of sliding motion (x-axis) and is not restricted by seal geometry. For the sake of visualization and reference, the discussion is based on the configuration of the stationary seal shown in Figure 2. The counterbody of a rod slides against the seal from left to right with steady velocity V > 0. Sealed fluid is maintained under sealed pressure ps on the left of the seal (). A thin film of sealed fluid is elastohydrodynamically developed in the sealing contact zone under the seal and leaks to the low-pressure side on the right of the seal. Hydrodynamic pressure p rises from ps at the entrance of the inlet zone to pm at the exit of the inlet zone. Maximum pressure pm is normally dictated by the amount of initial principal interferences of the seal, which are given to establish sealing even at very low sealed pressure and avoid a leak even when the temperature drops well below room temperature and the seal inevitably shrinks. Thus, for nearly incompressible seal materials such as elastomers, pm is approximately the sum of the preloading contact pressure and the sealed pressure ps.
The film thickness h at the sealing contact satisfies the Reynolds equation, the integrated form of which is [7]
where a prime henceforth denotes the first-order x-derivative, ρ and η are the pressure-dependent and temperature-dependent mass density and dynamic viscosity of the sealed fluid, respectively, and c is an integration constant calculated by the boundary condition and Equation (1), resulting in
where and . As in Nikas et al. [7,10,11,23], differentiating Equation (1) with respect to x and setting
transforms Equation (1) into a first-order, ordinary differential equation for H:
where a double prime henceforth denotes the second-orderx-derivative. It is obvious by Equation (3) that q is a function of p and that the extremum point x = xm of p coincides with that of q because . Equation (4) is thus numerically solved by using the value of H at the extremum point x = xm of q, that is, Hm, which is analytically calculated as follows [23]:
where xinf ∈ (x1, xm) is the abscissa of the inflexion point of q in the inlet zone, and ρinf and ηinf are the mass density and dynamic viscosity of the sealed fluid at x = xinf, respectively. ρ and η are calculated by the Dowson-Higginson [27] and Barus [28] formulae in SI units, respectively,
ρ0 and η0 are ρ and η, respectively, valued at atmospheric pressure, θ stands for local temperature, and α is the pressure-viscosity coefficient of the sealed fluid in SI units [29],
where S02 is the ASTM slope of the sealed fluid between 40 and 100 °C [30], divided by 0.2,
with ν40 and ν100 standing for the kinematic viscosities of the sealed fluid in mm2/s at 40 °C (313.15 K) and 100 °C (373.15 K). For the sake of simplicity in the present analysis, frictional heating in the sealing contact is ignored. It could be added by copying the analysis presented in Section 2.2 of Nikas [7] but that would introduce a factor of implicitness into the computational algorithm requiring numerical iterations to resolve, which would detract from the scope of the present study.
To solve the EHD problem, Hm must first be computed by Equation (5), which requires locating the inflexion point of q, xinf. At that point, and for ε → 0. Using Equations (3) and (7), and enforcing the nullification of results in
The derivative of ρ with respect to p in Equation (10) is easily calculated by Equation (6). Equation (10) is then numerically solved for xinf after approximating the EHD pressure in the inlet zone by a cubic polynomial as in Nikas [7]:
where the boundary conditions and (Figure 2) have been applied. Derivatives and , which are required in Equation (10), are easily calculated analytically by Equation (11). It is noted that the location of the inflexion point x = xinf depends on the length of the inlet zone, L (Equation (11)). However, L is not known a priori and could actually vary within some limits. This is resolved by initializing L to 1 μm and advancing in 1 μm steps, testing for the existence of a root of Equation (10), that is, computing the corresponding root xinf after each step, until the limits of L are found.
Proceeding with the analysis, the average asperity contact pressure pa, assumed to be nonnegative, is calculated as in Section 2.3 of Nikas [7], based on the Greenwood-Tripp asperity contact model [31] and incorporating a van der Waals intermolecular stress. Specifically,
where Wa, Aa and svdW are the contact load supported by asperities, the area of asperity contact and the van der Waals stress, respectively:
In Equations (13)–(15), Λ is the lambda ratio,
have being the average film thickness in the sealing contact and σ the composite RMS (root mean square) roughness of the sealing surfaces,
where σr and σs stand for the RMS roughness of the rod and the seal, respectively. In Equations (13) and (14), A is the apparent area of the sealing contact,
where R is the outer radius of the rod. In Equation (13), νr, νs and Er, Es stand for Poisson’s ratios and elastic moduli at the operating temperature of the rod and seal, respectively. Da is the boundary film thickness at asperity junctions, ra is the average radius of curvature of roughness asperity tips, and , sa being the surface density of asperities. In Equation (15), the square brackets denote the integer part of the enclosed quantity, which is the expected number of asperity contacts, and cr, cs and cf are the nonretarded Hamaker constants of the rod, seal and sealed fluid, respectively; moreover, the far right approximation is valid for , which is normally true. A negative value of the van der Waals stress declares attraction. Function f in Equations (13)–(15) is defined and approximated as follows:
where n = 1, 2, 5/2 and coefficients (a1, b1, c1) = (0.9208843519, 1.228593189, 0.3391174115), (a2, b2, c2) = (0.6943811167, 1.577822055, 0.3161591307) and (a5/2, b5/2, c5/2) = (0.484485988, 1.727908809, 0.3085072417) are in accord to Nikas [7].
It is noted that, in the numerical solution, EHD pressure p is not allowed to drop below the cavitation pressure pcav, which is taken equal to the atmospheric pressure (1 atm or about 101 kPa). Moreover, numerical testing by this author [7,8] has shown that the film thickness distribution in the main part of the sealing contact is nearly uniform. This allows to initially estimate have in Equation (16) for the all-important lambda ratio by the film thickness hm at the point of maximum pressure, which is calculated with the aid of Equation (5) ().
2.2. Sealing Performance Evaluators
Three evaluators of sealing performance are of importance in this optimization study, namely the mass leakage rate, the friction force and the abrasive wear. The mass leakage rate Q is easily calculated by the Reynolds Equation (1) with the aid of Equation (2), resulting in a simple expression [7]:
Next, the friction force F is calculated as the sum of the hydrodynamic and the asperity component:
A deformation friction force component arising from ploughing of the hard asperities of the rod against those of the softer seal is not considered because it was shown in Nikas [7] to be negligible for a wide range of operating conditions in applications of hydraulic, elastomeric, sliding seals.
Integrating the viscous shear stress over the pressurized area of the sealing contact gives the hydrodynamic friction force component:
In Equation (22), as in Nikas [7], the EHD local shear stress is restricted by the limiting shear stress . The latter is the minimum of the shear strength of the EHD film, approximated by with τ0 being the limiting shear stress of the sealed fluid at atmospheric pressure, and the temperature-dependent shear strength of the sealing ring, (θ in °C; τs in Pa). Thus,
The limiting shear stress constraint is also important in the case of the asperity force component [7]:
In essence, Equation (24) expresses the friction force between engaged roughness asperities separated by an omnipresent fluid film of nanometric thickness, restricted by the minimum value of the shear strengths of the sealed fluid and the seal.
Although the hydrodynamic friction force in Equation (22) is an obvious candidate for performance evaluation, the present author found that it perplexes the minimization process by leading to a solution that cannot be mathematically proved to be optimal. Specifically, the minimization tests by Legendre and Weierstrass are inconclusive, but this is explained later. For now, let us define a performance evaluator that involves the square of the shear stress instead of the net shear stress in Equation (22) as follows:
We will shortly return to this term in the definition of the objective function.
Finally, an abrasive-wear representative term is proposed. There are extremely few publications dealing with the abrasive wear modeling of elastomers or polymers [24,25,26] because the topic is not amenable to simple analytical equations such as the Archard wear equation, which is popular in hard contacts. To the best of the author’s knowledge, there is no universal or reliable equation to use in polymeric contacts. Nevertheless, it is well known that abrasive wear depends on the contact load, the sliding velocity and the sliding distance [32]. In the process of optimization, the sliding distance is kept constant and so excluded. This clearly leaves the abrasive wear as being entirely dependent upon the film thickness distribution h(x) in the sealing contact given that both pressure and velocity are strongly linked with h. Moreover, it is also well known by the Stribeck curve that abrasive wear is largely avoided by maintaining the lambda ratio (Equation (16)) greater than 3 to avoid partial lubrication and asperity collisions [33]. This is in total agreement with Equation (19), which shows that for Λ > 3 and therefore the asperity contact load Wa (Equation (13)) and the asperity contact area Aa (Equation (14)) are both zero for all practical purposes. Furthermore, instead of using the average film thickness have in the definition of Λ and attempting to maximize Λ in order to minimize wear, it would be better to use the local film thickness h and pursue the “Λ > 3” objective everywhere in the contact. Therefore, a dimensionless term that is representative of abrasive wear and incorporating a local “lambda ratio” h/σ and its critical value of 3 is proposed:
where W is the width of the seal along its axis of symmetry (x) prior to installation. Clearly, a thicker film or a narrower contact zone result in lower wt. Naturally, the expression for wt in Equation (26) is not unique; other suitable expressions could be used. What is essentially implied here is that the actual abrasive wear in the sense of amount of material loss for given sliding distance could be considered proportional to wear term wt of Equation (26), that is, equal to , where k is a constant wear coefficient. Extending this to include abrasive wear in the algorithm in the sense of dynamic modification of seal dimensions by worn material loss entangles several difficulties.
- (a)
- Proposed models of polymer-metal abrasive wear in the literature are empirical/semi-empirical and rely on experimentally determined coefficients. They are thus tight to specific materials and sealed fluids. For example, the trend of the results may be different if water is used as sealed fluid instead of, say, hydraulic oil. There are secondary parameters to consider here such as fluid uptake by the seals, chemical compatibility of polymers and hydraulic fluids, generation of wear debris and others that hinder a precise, quantitative formulation of polymeric abrasive wear [3,4,9,32].
- (b)
- A dynamic modification of seal dimensions by abrasive wear would inevitably have to be linked to a sliding distance (say S) of the contact. But in that case, the so-derived “optimum” seal would be linked to the given S for which the optimization was done in the first place. This means that sealing performance for distances smaller or greater than S would not be optimal. Essentially, we would end up with a seal that not only is designed on the basis of a potentially restrictive abrasive-wear model but also a seal that is designed to operate “optimally” on average for a specific sliding distance S, no more and no less than S. This does not seem plausible or even beneficial for flexible and interactive elements such as polymeric seals that are dynamically affected by many factors during their operation and throughout their service life [9], even off their normal duty cycle.
2.3. Objective Function of Sealing Performance and Optimization
Of the three performance evaluators defined so far, only the wear term is dimensionless. The other two are now non-dimensionalized by defining the following variables: , and , where Qu and Fu are the maximum acceptable mass leakage rate and the maximum acceptable friction force, respectively, in a given application. The constraint on the mass leakage rate is enforced:
The friction force constraint is desirable but not binding or in any way enforced in the analysis.
Applying the leakage constraint (27) to Equation (20) and using the definition of H from Equation (3) gives
where ρm is readily computed by Equation (6) for pm is known. Therefore, an upper limit of hm is immediately established. This is crucial because as earlier stated, hm is used as an approximant for the average film thickness have, which in turn is used to compute the Λ ratio (Equation (16)) appearing in function and needed for the computation of the average asperity pressure pa (Equations (12)–(14)).
Using the previous definitions, the performance evaluators defined thus far are summed up to form an objective function of sealing performance:
Equation (29), upon substitution of all previously defined variables, gives
where
By selecting a value of hm satisfying the leakage constraint (28) and permitting the existence of a root of Equation (10) (i.e., L > 0), the first couple of terms on the right-hand side of Equation (30), namely the dimensionless leakage term and the dimensionless asperity friction term, are set. This leaves the integral in Equation (30), which contains the dimensionless hydrodynamic friction term and the wear term. Given that the hydrodynamic pressure in the inlet zone is already prescribed by Equation (11) to satisfy the boundary conditions , we seek to find a relative minimum of the functional
in the main contact zone (xm, x2), subject to the equality derivative constraint expressed by the Reynolds equation (Equation (1)) for given velocity V. In other words, we seek to find a hydrodynamic pressure distribution p(x) that locally minimizes functional I subject to the constraint imposed by Equation (1). Note that the ratio in Equation (30) equals according to Equation (14), which is straightforward to compute for known Λ. Moreover, the shear stress limitation in Equation (30) has been dropped in Equation (32) to simplify the equations of the optimization algorithm but it is included in the algorithm as an after-treatment to check and restrict the computed shear stress if necessary.
Using Variational Calculus [34,35,36], the previously posed constrained optimization problem is transformed into an unconstrained optimization problem by incorporating the equality derivative constraint to a new functional
where
and λ is a Lagrange multiplier, which is a function of x given that the equality constraint is in the form of a differential equation on one of the derivatives (). Functional J contains three functions of x: h(x), p(x) and the newly introduced λ(x). Let us now define vector to compact Equation (33) as
where . The stationary vectors and potential extremals of J are obtained by setting its first variation equal to zero (δJ = 0), which results in the following Euler-Lagrange equation:
Equation (36) is decomposable into three equations, for Y is a three-dimensional vector. The third of those equations, , returns the Reynolds equation (Equation (1)):
After lengthy algebra, the remaining two equations from the decomposition of Equation (36) give
where
The Lagrange multiplier is found to be
and its derivative .
Equations (37) and (38) comprise a system of two nonlinear, first-order, ordinary differential equations of the form , where (T representing the transpose operator) and N is a nonlinear vector operator. This is an initial value problem. The initial values are set at x = xm: . Setting xm = 0 henceforth, we effectively seek a solution on the interval 0 ≤ x ≤ x2. In the present study, this system is solved by Hamming’s method, a high-precision, variable-step numerical method previously utilized by the author in sealing research [7,8,10,11,23] and available by the HAMNG subroutine of the FORTRAN Fujitsu Scientific Subroutine library [37].
2.4. Necessary and Sufficient Conditions for a Minimum
Recall that we have set xm = 0. For the solution vector to the system of Equations (37) and (38), say Y0, to be a relative (local) minimum, the second variation of J, must be nonnegative:
where , and are 3 × 3 symmetric matrices containing the indicated second-order and mixed derivative elements, and υ(x) = δG is any allowable variation of G (allowable in the sense that it satisfies the homogeneous Dirichlet boundary conditions ). The minimization of functional J at a critical vector Y0 is guaranteed on the interval 0 < x < x2 if the quadratic functional in Equation (46) is positive definite for all variations that are not identically zero (υ(x) ≢ 0), where C1 stands for “class 1” (differentiable function with continuous first-order derivatives). To put the minimization problem into a rigorous mathematical context, a sufficient condition for an extremal Y0 to be a relative minimum is that the second variation be strongly positive definite, which requires that , where is the Sobolev space of functions with distributional derivatives in functional space and D is independent of Y0. Directly testing this condition or evaluating the second variation for that matter is extremely laborious or rather futile in view of Equations (37)–(45) and beats the point of a relatively compact analytical solution. There are some necessary conditions that could be checked to this effect first. These refer to either weak or strong extrema (for explanations, interested readers are referred to Section 2.3 in Kot [35]). These terms actually refer to weak norms, , and strong norms, for x ∈ [a, b]. If both and are small, the extremum is weak; if is small but is large, the extremum is strong [34].
Let us begin with the necessary condition for a weak minimum. The classic Legendre’s condition [35] is applied in this respect. Legendre’s necessary condition for the functional J[Y] to have a relative minimum at Y = Y0 is
For the given problem,
Matrix is positive definite because given that B > 0 (Equation (31)) and both the film thickness h and the hydrodynamic pressure p are nonzero for nontrivial solutions. Therefore, Legendre’s necessary condition for a relative minimum is satisfied. In fact, as just shown, for any Y in the sealing-contact zone and not just for the solution Y0 of the Euler-Lagrange equation. This constitutes the so-called strengthened Legendre condition.
Let us now check the possibility of a strong relative minimum, for which Weierstrass’ necessary condition is commonly used [35,36,38]. For the functional J[Y] to have a strong relative extremum at Y = Y0, the Weierstrass excess function
where , must be nonnegative: . The functional expressions in Equation (49) are calculated with the aid of Equation (34) as follows:
With the aid of Equations (50)–(52), Equation (49) gives . Therefore, Weierstrass’ necessary condition for a strong relative minimum is satisfied.
We may now briefly return to an earlier comment in Section 2.2 about the choice of the hydrodynamic friction force for performance evaluation. Had Fh (Equation (22)) been used instead of (Equation (25)) in the objective function, then and , meaning that both the Legendre and Weierstrass tests would have been inconclusive. Additionally, higher-order derivatives, which are normally resorted to in such extreme cases, would equally lead to a dead end because they would have all been zero: ). Therefore, it would be impossible to build an irrefutable case for a relative minimum, although, using the second variation test (Equation (46)), it appears that we would have had an extremum because, generally, , resulting in . These complications were avoided by the change of the evaluator for the hydrodynamic friction force.
Finally, having shown that the necessary conditions for a strong relative minimum are satisfied, we must now explore sufficient conditions for a relative minimum. For this purpose and according to sections 6.3, 7.3 and 12.4 in Kot [35], a solution vector Y0 must satisfy the following three conditions:
- (a)
- the Euler-Lagrange equation (Equation (36))
- (b)
- the strengthened Legendre condition or the Weierstrass condition (see Equation (49));
- (c)
- Jacobi’s condition, which requires that Jacobi’s Equation (53) has a solution u that is nonzero for all .
Conditions (a) and (b) are satisfied as earlier proved. Condition (c) (Jacobi’s condition), after laborious algebraic work leads to a system of three equations with unknowns u1, u2 and u3:
where
Substituting u1 from Equation (56) and u3 from Equation (54) into Equation (55) yields
where
Equation (65) is a second-order, linear, homogeneous, ordinary differential equation with variable coefficients ( are functions of x for the given solution vector Y0). Its coefficients and are continuous functions of x because, for all , (a) B ≠ 0 ≠ h and (b) function t (Equation (66)) is continuous because all terms in Equation (57) to (64) are continuous and , the denominator in Equation (66), is nonzero. The latter is easy to verify by Equation (59) because and (this is graphically demonstrated in the examples later), thus .
Having just proved that Equation (65) has continuous coefficients, we may now choose boundary conditions and , where d1 and d2 are arbitrary constants. The boundary value problem consisting of Equation (65) and the boundary conditions just prescribed has a unique analytical solution for all (refer to Theorem 2.1 in O’Neil [39]). The plan here is to show that it is possible to find , for it would mean that vector u has at least one nonzero element (u2) for all and Jacobi’s condition would be satisfied. In fact, if at some point x0, Equation (56) gives, generally, and, subsequently, by Equation (54), otherwise the determinant of the linear homogeneous system of Equations (54) and (56) for would have to be zero, which can be shown to be generally untrue. Thus, having nonzero u2 at a point x0 generally means having nonzero u1 and u3 at that point, too, and of course .
Unfortunately, finding the general solution of Equation (65) analytically requires knowing or guessing a particular solution, which is impossible by the complexity of its coefficients. Therefore, we will resort to an approximate solution. For that purpose, the Variational Iteration Method is employed as specifically formulated for second-order ordinary differential equations by Wazwaz [40]. Applying that method to Equation (65) results in the following iteration formula:
The initial approximation is taken as . Finally, the solution is . It is later shown in the examples that the so obtained approximant for sufficiently large index i is a strictly positive function of x. Generally, satisfaction of Jacobi’s condition, sufficiency and thus optimality of the obtained (h, p)-solution should be verified on a case-by-case basis.
2.5. Solid and Contact Mechanics
The total contact pressure p in the apparent area of the sealing contact comprises the average asperity pressure pa applicable to the asperity contact area Aa and the hydrodynamic pressure p ≥ pcav applicable to the remaining area A − Aa. Load balancing in the related areas yields
where and are the average values of the related pressures. Substituting and into Equation (68) yields
where K is constant,
All quantities on the right side of Equation (70) are already calculated. In particular, p(x) has been calculated by the numerical solution of the system of Equations (37) and (38) and the leakage Constraint (27) is satisfied. Therefore, constant K is readily calculated. Equation (69) is a Fredholm integral equation of the first kind. This is an ill-posed problem and could have an infinite number of solutions. However, given that the total contact pressure pc(x) is the resultant of a uniform pressure pa and a variable pressure p(x), it is logical to assume that the variation of pc resembles that of p. Therefore, let us accept a linear solution
where k1 and k2 are constants. In compliance with the algebraic expression of Equation (68) and the constraint p ≥ pcav, suppose now that, at the end of the contact zone
Given that , Equation (71) yields
Next, substituting K, p(x) and k2 from Equations (70), (71) and (73) into Equation (69) yields
Thus, pc(x) is completely defined by Equation (71). Note that in the process of computing the hydrodynamic pressure distribution p(x), the boundaries x1 and x2 of the sealing contact zone (Figure 2) are numerically located as follows (recall that xm = 0):
Granted that with the formulation just accepted, pressure pc is not restricted at the entry point x1 and may thus slightly deviate from the sealed pressure ps. Nevertheless, this is deemed an acceptable approximation in the course of dealing with an ill-posed problem (Equation (69)) having an infinite number of possible solutions.
For given macro-geometry of the seal and with the total contact pressure distribution pc(x) calculated as above, a finite-element-analysis (FEA) software could be used to compute the local geometry of the seal in the sealing contact area. For example, consider the seal shown in Figure 2, its main dimensions preset and the local pressure of the working tip (area C) optimized with the proposed method. Using the main dimensions of the seal, the material properties and the operating conditions as inputs in an FEA software, and the local pressure distribution pc(x) for boundary loading in the tip area C, allows to reverse-engineer the shape of the tip. For complex seal macro-geometry or composite seals, the use of FEA towards this goal is rather difficult to avoid. However, for simple seal shapes such as rectangular-rounded, an approximate analysis may be feasible.
Application to a Rectangular-Rounded Seal
Consider a rectangular-rounded seal, that is, a rectangular seal ring with its four corners having a small radius of curvature in the order of 0.1 to 0.4 mm, as in Nikas [7]. Suppose that the seal has been installed without circumferential interference, meaning that the hoop strain is zero (εy = 0), and ignore thermal effects for simplicity in this example. As in Nikas [7], using the classic equations of Hookean elasticity, the radial stress on the seal is
where λs and Gs stand for the Lamé constant and the shear modulus of the seal, respectively,
and is the average axial strain,
where stands for the average radial strain, which is calculated by integration of the local radial strain along the sealing contact width,
Solving Equation (76) for εz(x) with the aid of Equations (79) and (80), and setting results in
Equation (81) is of the form with m being constant, which is a Fredholm integral equation of the second kind with constant limits of integration. This type of equation has the following unique solution [41]: where and . Upon application of this solution to Equation (81), the result is
where
Thus, the radial strain of the seal in the sealing contact is analytically calculated by Equation (82). This allows checking whether such that the use of linear elasticity for the polymeric seal as opposed to finite elasticity or hyperelasticity (e.g., via a neo-Hookean, a Mooney-Rivlin or another suitable model) is satisfactory according to Nikas and Sayles [42]. However, the ultimate goal is to find the geometry of the seal in the sealing contact for the established optimal pressure distribution and design an optimal seal for the given criteria and operating conditions.
The optimal geometry can be approximately found by considering that the sealing contact is small in comparison with the width of the seal and so the main body of the seal can be treated as a half-space. It is then straightforward to calculate the normal (radial) surface displacement of the seal by Equation (2.24b) of Johnson [43], ignoring tangential tractions:
where b3 is an integration constant. Upon selecting the datum for normal displacements at point x = x2, that is, , Equation (85) gives
Thus, the optimal seal profile in the sealing contact in reference to a datum set at pointx = x2 is given by the function in Equation (85) with the aid of Equation (86).
3. Application Example
3.1. Input Data
The preceding analysis is here applied to an elastomeric rod seal, which, prior to its profile optimization, has rectangular shape so that analytical calculations are feasible by Equations (76)–(86). The initial shape of the seal is actually unimportant because the outlined analysis is applicable to any seal shape. The operating conditions and material properties are detailed in Table 1 and are mostly the same or close to those used in the experimentally validated studies of Nikas [7,8].

Table 1.
Input data for the numerical example, mostly as in Nikas [7,8].
In unstressed form, the inner diameter of the seal coincides with the outer diameter of the rod at 30 mm and its width is 3 mm. The rod has typical material properties of steel. The operating temperature is 23 °C. Using the stress–strain curve of a typical elastomer for reciprocating seals [48], the average elastic modulus at the given operating temperature is equal to 7 MPa for engineering strain in the interval [–0.1, 0.0], a range that is representative of the average strain values calculated later for the optimized seal. Moreover, the seal is nearly incompressible, with Poisson’s ratio equal to 0.499. The sealed pressure is 10 MPa (100 bar) and the maximum EHD pressure is set at 15 MPa. The cavitation pressure is set at 101 kPa (1 atm). The sliding velocity (stroking velocity of the rod) is 0.5 m/s, a common value for reciprocating seals. The hydraulic fluid is of MIL-H-5606 specification normally used in aviation and its mass density and dynamic viscosity at operating temperature are accordingly specified [44]. An average value of 4 MPa for its limiting shear stress is used according to the experimental work of Jacobson [45], as was also done in Nikas [7,8]. The RMS roughness of the rod is 0.07 μm, while that of the seal is 1.70 μm, both typical values for applications of reciprocating seals [7,8]. The average radius of asperity tips and the boundary film thickness at asperity junctions are set in accordance with experimental measurements [46,47] and as detailed in Nikas [7,8]. Similarly, the nonretarded Hamaker constants are as previously used by this author [7,8] and taken from the authoritative work of Israelachvili [47]. Product Π of roughness asperity parameters is taken equal to 0.12, a value shown in Nikas [7] to give the closest agreement with experimental results over a wide range of operating conditions. Finally, for the sake of this example, the maximum acceptable mass leakage rate and friction force are set equal to 30 mg/s and 80 N, respectively, both values in the order of magnitude of those expected for similar sealing applications [7,8]. For simplicity in the results that follow, the position of the maximum hydrodynamic pressure is set at xm = 0 as before.
3.2. Results
For Qu = 30 mg/s, inequality (28) gives hm ≤ 1.50 μm. On the other side, for hm < 0.05 μm, Equation (10) has no root and the inlet zone disappears (L = 0 in Figure 2), which means that the EHD problem has no solution. Therefore, the film thickness at maximum hydrodynamic pressure, hm, must be selected between 0.05 and 1.50 μm. In that range of hm, the length of the inlet zone, L, is plotted in Figure 3. It is clearly seen that thicker films (increasing hm) can only be sustained by a longer inlet zone (increasing L). Indeed, a longer converging-inlet zone better promotes the development of hydrodynamic conditions. It is also seen in Figure 3 that, for given hm, L can vary between two limits. For example, for hm= 1 μm, L can vary between approximately 0.5 mm and 0.8 mm. Naturally, the length of the inlet zone cannot exceed the width of the seal: L < W. In Figure 3, this is true even for the global maximum of L of about 1.8 mm because W = 3 mm.
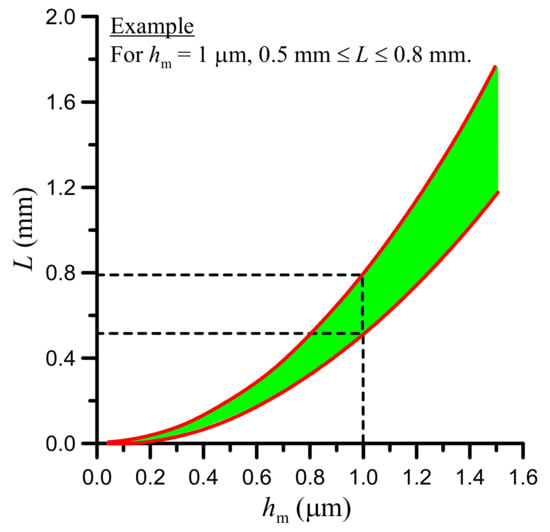
Figure 3.
Limits of the length of the inlet zone, L, as function of the film thickness at maximum hydrodynamic pressure, hm (input data in Table 1).
We first return to the issue of sufficiency for optimality of the calculated (h, p)-solution on the interval 0 ≤ x ≤ x2. As was earlier asserted, this is to be checked numerically by showing that there exists a solution to Jacobi’s Equation (53), , that is nonzero for all x ∈ [0, x2]. Approximants are computed by Equation (67) with boundary conditions and for arbitrary constants d1 ≠ 0 and d2. The initial approximation is . For the sake of this example, let us set d1 = d2 = 1. The integration in Equation (67) is carried out numerically for unequally spaced grid points by the trapezium rule and the necessary derivatives of u2 are computed by cubic spline interpolation. Up to quadruple-precision floating-point arithmetic (approximately 33 decimal digits) has been used in the computational algorithm for some critical variables such as u2 and its derivatives. It is noted that what is of importance here is not the absolute value of u2 but whether u2 changes sign on the interval 0 ≤ x ≤ x2. Figure 4 shows the variation of the 10,000th u2-approximant with x for hm = 0.3 μm, where it is seen that u2 ≥ 1 for x ≥ 0. Similar results of positive (and thus, nonzero) values of u2 are obtained for other values of hm, except for some quite low values of less than 0.14 μm. Even in those thin-film cases though, there is strong evidence towards the optimality of the (h, p)-solution provided by the Euler-Lagrange equation and Legendre’s and Weierstrass’ necessary conditions, which are all satisfied as proved.
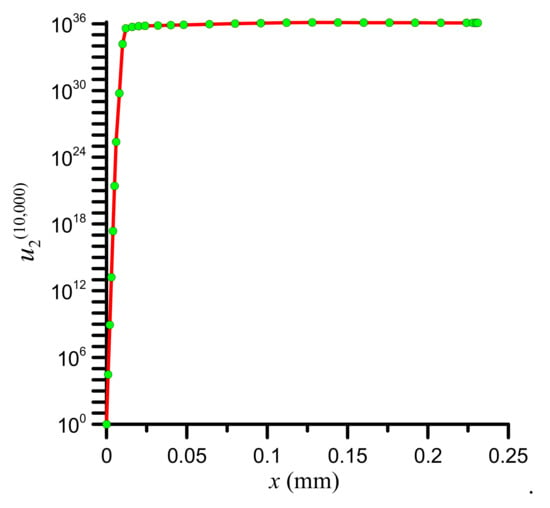
Figure 4.
The 10,000th approximant of u2(x) by Equation (68) (hm = 0.3 μm, d1 = d2 = 1; input data in Table 1).
Let us now proceed with the results and vary hm in the range previously established, that is, 0.05 μm ≤ hm ≤ 1.50 μm. The hydrodynamic pressure distribution and the corresponding film thickness distribution calculated by the system of Equations (37) and (38), are plotted for selected values of hm in Figure 5a,b, respectively. For visualization purposes, the length of the inlet zone is set at its maximum value for given hm. The width of the sealing contact in Figure 5 obviously increases for increasing hm. The morphology of the curves in the main contact zone (x > 0) resembles that found by FEA and fluid-structure-interaction coupling for rubber O-rings [49,50].
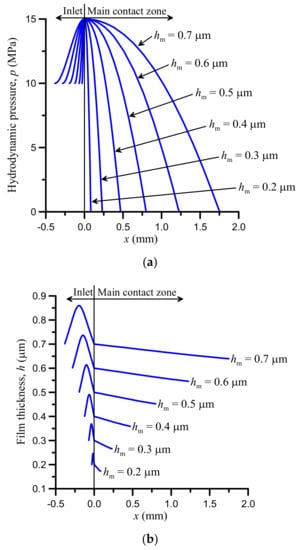
Figure 5.
(a) Optimal hydrodynamic pressure distributions for various values of hm, with L set at its maximum value for given hm; (b) corresponding film thickness distributions (input data in Table 1).
The value of the objective function (Equations (29) and (30)) alongside the sealing performance dimensionless evaluators of mass leakage rate, friction force and abrasive wear are plotted in Figure 6 for variable average film thickness. Although the actual friction evaluator used in the objective function g is (Equation (25)) instead of (Equation (22)) as earlier explained, the latter has direct physical meaning and is chosen to appear in Figure 6. The lambda ratio is also plotted for an alternative assessment of the risk of abrasive wear. Λ being proportional to have, it is linearly increasing with have. The mass leakage rate is proportional to hm for constant peak density ρm (Equation (20)) and have is close to hm, hence the approximately linear increase of leakage with have in the figure. The wear term, wt (Equation (26)), is a nonlinear function involving two competing actions: increasing have reduces the integrand in Equation (26) but expands the interval (x2 − x1) of the integration, thereby counteracting the integrand reduction. The outcome seen in Figure 6 is that the wear term is low for low have but rapidly increases and peaks before starting to drop for increasing have. Seen in isolation, wt is better off at low as well as high values of have. Moreover, the strong magnitude of wt masks the other two performance evaluators. However, this is caused by the choice of weighting factors, namely Qu for Q, Fu for F and W for wt.
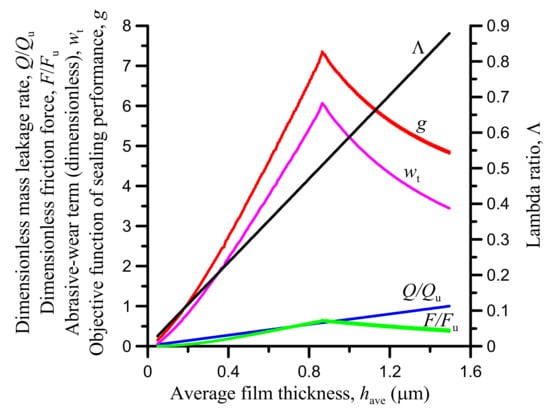
Figure 6.
Sealing performance evaluators and objective function for variable average film thickness (input data in Table 1).
The friction force variation in Figure 6 comes from the changing shear stress in conjunction with the increasing contact width (x2 − x1) for increasing have (Equations (22)–(24)). Moreover, increasing have and thus Λ alters the asperity contact area Aa (Equation (14) and, cumulatively, the remaining, lubricated contact area (A − Aa), including the respective pressures pa (Equation (12)) and p. For the imposed leakage and friction-force limits, Qu and Fu, respectively, which function as weighting factors, the dimensionless friction force is on parity with the dimensionless leakage and both are dominated by the wear term for middle values of have. Obviously, selecting different weighting factors Qu and/or Fu—or a different function for the wear term wt—can alter the balance of those terms in the objective function. For the particular example and on the studied interval of have, it is found that the objective function is minimized for the lowest value of have (have ≅ 0.05 μm), which corresponds to a lambda ratio of about 0.03 and asperity area of contact Aa equal to 6.8% of the apparent area of contact A. However, there are other issues to consider such as the strength of the modified seal lip and its manufacturability, which are discussed later. In any case, the final decision of the working point on the g-curve is a matter of priorities and can be facilitated by the graph in Figure 6. Unavoidably, the optimal values established are strictly valid for the given operating conditions such as the sliding velocity and sealed pressure. Establishing the sensitivity of the optimal values to the operating conditions—or the material properties of the seal and the sealed fluid—requires a parametric study.
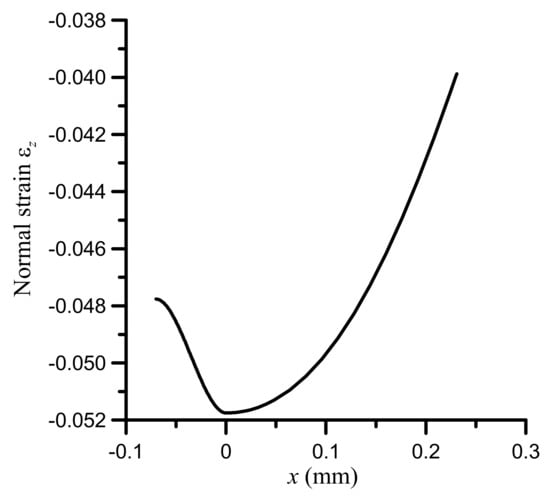
Suppose now that we select for locally optimal solution the one corresponding to have = 0.3 μm, for which the lambda ratio is slightly higher (Λ ≅ 0.16). For have = 0.3 μm then, the length of the inlet zone, L, can be between 48 and 70 μm. For the sake of this example, let us select L = 70 μm. For the selected values, the hydrodynamic pressure and the total contact pressure are plotted in Figure 7. In this case, the width of the sealing contact is x2—x1 ≅ 0.30 mm. The pressure distributions in Figure 7 are partly reminiscent of those found in the case of U-cup and step seals near their working tip [20,21]. Accordingly, the normal strain of the seal, εz, is shown in Figure 8 and it is obvious that it appears as the total pressure distribution vertically flipped. Its negative value indicates that it is compressive. Moreover, the maximum normal strain is much less than 0.1. Therefore, the classic Hookean elasticity analysis used in the present study is satisfactory and a model of finite elasticity is not necessary according to Nikas and Sayles [42].
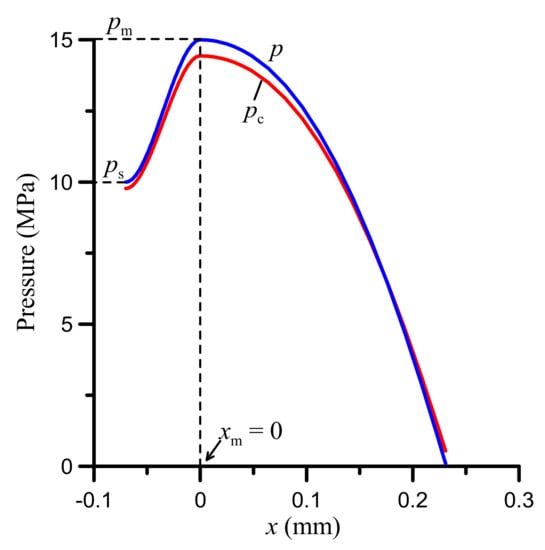
Figure 7.
Optimal hydrodynamic pressure p and the corresponding total contact pressure pc (hm = 0.3 μm; L = 70 μm; other input data as in Table 1).
Finally, the distribution of the normal displacement on the sliding surface of the seal, uz, is plotted in Figure 9. It is noted that, as earlier stated in the present analysis, the datum for normal displacements is taken at the right edge of the sealing contact (x = x2). The normal surface displacement may be viewed as the local profile of the seal (e.g., area C in Figure 2) when not suppressed by the contact pressure. Extrapolating the results upstream of the inlet zone (x < x1) to complete the seal profile is possible by using the same average radius of curvature of the seal flank for x1 ≤ x < 0. The radius of curvature is calculated and discussed later.
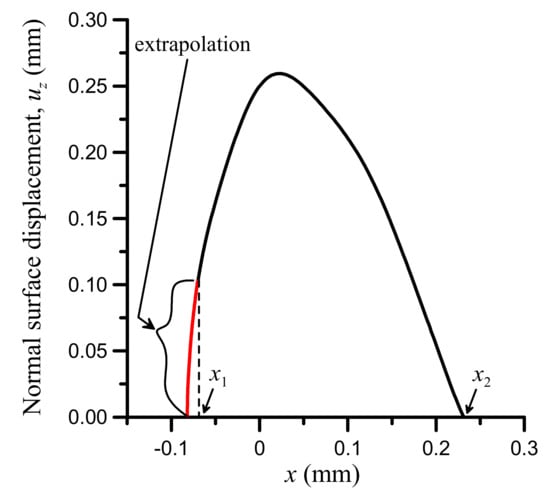
According to Figure 9, a hill of about 0.26-mm height (for the selected displacement datum) and 0.30 mm bottom width is the geometrical shape for locally minimizing the objective function and thus maximizing sealing performance for the input-data case of Table 1, pertaining to hm = 0.3 μm and L = 70 μm. It is realized that the width of the actual sealing contact (0.30 mm) is just one tenth of the width of the seal. In other words, a narrow lip on the working surface of the seal as the one implied by Figure 9 suffices to satisfy the leakage constraint and optimize sealing performance in terms of mass leakage rate, friction force and abrasive wear. Subsequently, the seal may be further modified by changing its width to a value no greater than that required for structural integrity under the given operating conditions. Although the present analysis does not directly account for structural strength or fatigue of the seal, it could be crucial in the case of reciprocating motion of either the seal or its counter-surface. In fact, the alternating loading of the modified seal lip could cause a type of wear known as frictional wear, which is specific to rubber seals and is simply the formation of rolls from detached or delaminated seal material [32]. To eliminate this possibility, optimal results corresponding to a thicker film (greater hm) could be selected from Figure 6 and thus have a modified seal lip of greater volume. For example, Figure 10 shows the normal surface displacement of the seal, uz, for selected values of film thickness hm, where the length of the inlet zone in each case is set at the maximum value for given hm. Naturally, increasing hm to gain in bending and shear strength by designing a bulkier seal tip comes at the expense of sealing performance according to the objective function in Figure 6. Alternatively, a seal material of higher elastic modulus could be used but that should also be contemplated against the higher abrasive wear of the seal’s sliding counterbody, which is the rod in this case (Figure 2).
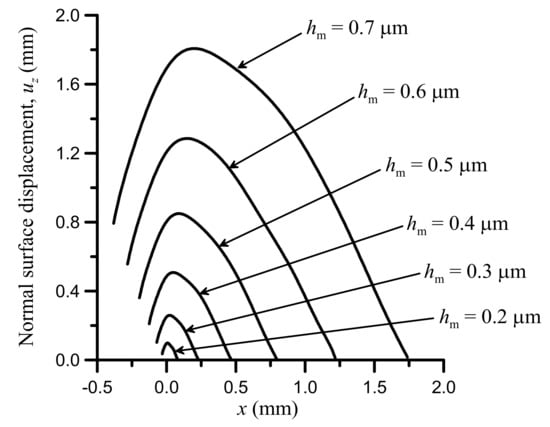
Figure 10.
Normal surface displacement of the seal, uz, for selected values of the film thickness at maximum hydrodynamic pressure, hm. L set at its maximum value for given hm; other input data as in Table 1. The displacement datum is at the exit of the inlet zone, x = x2.
A further issue to consider with the optimal modification is the average radius of curvature of the seal lip in the inlet zone. This can be related to the radius of curvature of the radial surface displacement uz(x). For a plane curve and using Equation (85), the radius of curvature of uz(x) is
The derivatives in Equation (87) are computed using second-order finite differences. For the example presented earlier in this section, the average value of r is approximately 0.03 mm. This is difficult to precisely manufacture given the softness of the polymeric surface of the seal. For comparison, commercial rectangular-rounded seals have corner radii of 0.1 to 0.4 mm [7,44,48]. A corner radius of less than 0.1 mm is considered sharp for polymers. It is then unavoidable to accept a solution with a higher value of the objective function by increasing the thickness at maximum pressure, hm, which in turn would produce a bulkier lip with greater average radius of curvature in the inlet zone. For example, instead of having hm = 0.3 μm and L = 70 μm as previously, accept the solution corresponding to hm = 0.6 μm and L = 280 μm (189 μm ≤ L ≤ 281 μm in this case). The particular choice gives a much wider sealing zone of 1.5 mm (instead of 0.3 mm) and the average radius of curvature of uz(x) is a much more feasible 0.13 mm.
4. Discussion and Conclusions
The performance evaluation of hydraulic seals in sliding motion against a hard counterbody such as a rod should include the three most influential factors, namely, the mass leakage rate, the friction force and the abrasive wear of the tribopair. An objective function of the aforementioned sealing performance evaluators for steady-state conditions is a means pursued in the present study to design optimally profiled dynamic seals such as rod seals. By means of the objective function and by applying Variational Calculus and other analytical and numerical techniques for its minimization, optimal seal profile modifications are calculated, simultaneously considering constraints in terms of leakage, friction force and abrasive wear. There is in fact great flexibility regarding the choice and control of performance parameters through the proposed method that allows even the structural integrity of the modified seal profile to be considered in view of consistent, long-term performance. Moreover, the manufacturability of the proposed seal profile is checked against the norms for soft polymeric surfaces in terms of the average radius of curvature of the profile (Equation (87)). It is shown that it is straightforward to choose a solution through the proposed method which gives a profile with sufficiently large average radius of curvature (e.g., greater than 0.1 mm), again at the controlled expense of some sealing performance.
Furthermore, although the presented analysis deals with unidirectional sliding motion, it can readily be used in case of reciprocating motion by applying it to both corners of a dynamic seal along the axis of motion. In the latter case, the dissimilar conditions at each corner, as for example, high sealed pressure at one corner and low (ambient) pressure at the opposite corner, will give slightly different modifications at each side.
Inevitably, the results are strictly valid for the given operating conditions (sealed pressure, sliding velocity, operating temperature). The sensitivity of the results on the variability of the operating conditions may be examined in a parametric study. Furthermore, as in any frictional process, material loss by abrasion will eventually spoil the optimal geometry of the designed seal lip. However, this is inevitable in any operation involving abrasive wear. What is particularly worrisome though with hydraulic, polymeric, sliding seals is how sensitive their performance is to minute changes of their working conditions in the EHD inlet zone, a zone that is often just a small fraction of 1 mm in length. This is easy to realize by Equation (5), which reveals that the film thickness at the point of maximum pressure is a function of the hydrodynamic pressure derivate at a point where the slope of p is normally very steep and thus the magnitude of is very high and rapidly changing with location x. The slightest perturbation in that sensitive zone caused by, for example, geometrical modification by abrasive wear, deflection by dynamic stress or obstruction by debris particles could destabilize sealing performance causing increased leakage and wear. Therefore, it should be realized that, regardless of how sophisticated the design of a seal is, its initially optimal performance cannot be sustained for long. Nevertheless, even a worn seal can often still function within acceptable performance limits in many, non-critical applications. The method proposed in the present study may thus be viewed as a means to deliver a seal that will perform optimally within a narrow range of operating conditions and for as long as the optimized geometry can be sustained without significant wear, disturbance by fluid contaminants or other cause for deterioration.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
Nomenclature
| A | apparent area of the sealing contact (Equation (18)) |
| Aa | area of asperity contact (Equation (14)) |
| A1 … A5 | functions (Equations (39)–(43)) |
| b1, b2, b3 | constants (Equations (83), (84) and (86), respectively) |
| B | dummy variable (Equation (31)) |
| c | integration constant (Equation (2)) |
| cr, cs, cf | nonretarded Hamaker constants of the rod, seal and sealed fluid, respectively |
| cτ1, cτ2 | coefficients of the shear strength function |
| c4 | dummy variable (Equation (44)) |
| d1, d2 | arbitrary constants (d1 ≠ 0) |
| D | constant |
| Da | boundary film thickness at asperity junctions |
| E | Weierstrass excess function (Equation (49)) |
| Er, Es | elastic modulus of the rod and the seal, respectively |
| f | function (Equation (19)) |
| F | friction force (Equation (21)) |
| Fa, Fh | asperity (Equation (24) and hydrodynamic (Equation (22) friction force, respectively |
| friction-force representative performance-evaluator (Equation (25)) | |
| Fu | maximum acceptable friction force |
| g | objective function of sealing performance (Equations (29) and (30)) |
| G | function (Equation (34)) |
| Gij, | functions; refer to Equation (57)–(64) |
| Gs | shear modulus of the seal (Equation (78)) |
| h, have | film thickness and its average value, respectively |
| hm | h at x = xm |
| H | product ρh (Equation (3)) |
| Hm | H at x = xm (Equation (5)) |
| I, J | functionals (Equations (32) and (33), respectively) |
| k1, k2 | coefficients (Equations (74) and (73), respectively) |
| K | constant (Equation (70)) |
| L | length of the inlet zone (Figure 2) |
| n | parameter equal to either 1, 2 or 5/2 |
| p, | hydrodynamic pressure and its average value, respectively |
| pa | average asperity contact pressure (Equation (12)) |
| pc, | total contact pressure (Equation (71)) and its average value, respectively |
| pcav | cavitation pressure |
| pm | maximum hydrodynamic pressure at the exit of the inlet zone (Figure 2) |
| ps | sealed pressure (Figure 2) |
| q | variable defined through its derivative in Equation (3) |
| Q, Qu | mass leakage rate (Equation (20)) and its maximum acceptable value, respectively |
| r | radius of curvature (Equation (87)) |
| ra | average radius of curvature of roughness asperity tips |
| R | outer radius of the rod |
| sa | surface density of roughness asperities |
| svdW | van der Waals stress (Equation (15)) |
| S02 | ASTM slope of the sealed fluid between 40 and 100 °C, divided by 0.2 (Equation (9)) |
| u | vector |
| uz | normal (radial) surface displacement of the seal (Equation (85)) |
| u1, u2, u3 | elements of vector u |
| V | sliding velocity (Figure 2) |
| wt | wear term (Equation (26)) |
| W | width of the seal along its axis of symmetry |
| Wa | contact load supported by roughness asperities (Equation (13)) |
| x | axial coordinate (Figure 2) |
| xinf | abscissa of the inflexion point of q in the inlet zone |
| xm | abscissa of the point of maximum hydrodynamic pressure (Figure 2) |
| x1, x2 | abscissa of the entry and exit point of the sealing contact, respectively (Figure 2; Equation (75)) |
| Y | vector |
| Y0 | stationary (critical) vector of functional J |
| Greek Symbols | |
| α | pressure-viscosity coefficient of the sealed fluid (Equation (8)) |
| ε | infinitesimal number |
| average axial strain of the seal (Equation (79)) | |
| εz, | radial strain of the seal (Equation (82)) and its average value (Equation (80)), respectively |
| η, ηinf | dynamic viscosity of the sealed fluid (Equation (7)) and its value at x = xinf, respectively |
| η0 | η at atmospheric pressure and local temperature |
| θ | operating temperature |
| λ | Lagrange multiplier, a function of x (Equation (45)) |
| λs | Lamé constant (Equation (77)) |
| Λ | lambda ratio (Equation (16)) |
| νr, νs | Poisson’s ratios of the rod and the seal |
| ν40, ν100 | kinematic viscosities of the sealed fluid at 40 and 100 °C in mm2/s |
| Π | product saraσ |
| ρ | mass density of the sealed fluid (Equation (6)) |
| ρinf, ρm | ρ at x = xinf and at x = xm, respectively |
| ρ0 | ρ at atmospheric pressure and local temperature |
| σ | composite RMS roughness of the sealing surfaces (Equation (17)) |
| σr, σs | RMS roughness (rod, seal) |
| σz | radial stress of the seal in the sealing contact (Equation (76)) |
| τL | limiting shear stress (Equation (23)) |
| τs | shear strength of the sealing ring, (θ in °C; τs in Pa) |
| τ0 | limiting shear stress of the sealed fluid at atmospheric pressure and operating temperature |
| υ | variation of G |
| Abbreviations | |
| ASTM | American Society for Testing and Materials |
| EHD | elastohydrodynamic |
| inf | inflexion (referring to the inflexion point of q) |
| RMS | root mean square |
| sup | supremum (standard mathematical definition) |
References
- Hydraulic Seals–Linear; Trelleborg Sealing Solutions: Trelleborg, Sweden, 2017.
- Flitney, R. Seals and Sealing Handbook, 6th ed.; Chapter 4; Butterworth-Heinemann: Oxford, UK, 2014; ISBN 9780080994161. [Google Scholar]
- Nikas, G.K. Eighty years of research on hydraulic reciprocating seals: Review of tribological studies and related topics since the 1930s. Proc. IMechE Part J. J. Eng. Tribol. 2010, 224, 1–23. [Google Scholar] [CrossRef]
- Nikas, G.K. Research on the tribology of hydraulic reciprocating seals. In Tribology Research Trends; Chapter 1; Hasegawa, T., Ed.; Nova Science Publishers: New York, NY, USA, 2008; ISBN 9781604569124. [Google Scholar]
- Nikas, G.K. Fundamentals of Sealing and Tribology of Hydraulic Reciprocating Seals. In Proceedings of the IMechE 1-Day Seminar “Focus on Reciprocating Seals”, London, UK, 25 June 2008; Available online: http://www.tribology.me.uk/Nikas_IMechE_25-06-2008.pdf (accessed on 2 April 2020).
- Müller, H.K.; Nau, B.S. Fluid Sealing Technology: Principles and Applications; Marcel Dekker Inc.: New York, NY, USA, 1998; ISBN 0824799690. [Google Scholar]
- Nikas, G.K. Fast performance-analysis of rectangular-rounded hydraulic reciprocating seals: Mathematical model and experimental validation at temperatures between –54 and +135 °C. Tribol. Int. 2018, 128, 34–51. [Google Scholar] [CrossRef]
- Nikas, G.K. Parametric and optimization study of rectangular-rounded, hydraulic, elastomeric, reciprocating seals at temperatures between –54 and +135 °C. Lubricants 2018, 6, 77. [Google Scholar] [CrossRef]
- Nikas, G.K. Friction and Wear of Seals. In ASM Handbook, Volume 18: Friction, Lubrication, and Wear Technology; Totten, G., Ed.; ASM International: Ohio, OH, USA, 2017; pp. 957–968. ISBN 9781627081412. [Google Scholar] [CrossRef]
- Nikas, G.K.; Sayles, R.S. Modelling and optimization of composite rectangular reciprocating seals. Proc. IMechE—Part J. J. Eng. Tribol. 2006, 220, 395–412. [Google Scholar] [CrossRef]
- Nikas, G.K.; Burridge, G.; Sayles, R.S. Modelling and optimization of rotary vane seals. Proc. IMechE—Part J. J. Eng. Tribol. 2007, 221, 699–715. [Google Scholar] [CrossRef]
- Field, G.J.; Nau, B.S. A theoretical study of the elastohydrodynamic lubrication of reciprocating rubber seals. Trans. ASLE 1975, 18, 48–54. [Google Scholar] [CrossRef]
- Johannesson, H.L. Oil leakage and friction forces of reciprocating O-ring seals considering cavitation. ASME J. Lubr. Technol. 1983, 105, 288–296. [Google Scholar] [CrossRef]
- Karaszkiewicz, A. Hydrodynamics of rubber seals for reciprocating motion. Ind. Eng. Chem. Prod. Res. Dev. 1985, 24, 283–289. [Google Scholar] [CrossRef]
- Karaszkiewicz, A. Hydrodynamics of rubber seals for reciprocating motion, lubricating film thickness, and out-leakage of O-seals. Ind. Eng. Chem. Prod. Res. Dev. 1987, 26, 2180–2185. [Google Scholar] [CrossRef]
- Kanters, A.F.C. On the Calculation of Leakage and Friction of Reciprocating Elastomeric Seals. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 1990. [Google Scholar] [CrossRef]
- Kanters, A.F.C.; Verest, J.F.M.; Visscher, M. On reciprocating elastomeric seals: Calculation of film thicknesses using the inverse hydrodynamic lubrication theory. STLE Tribol. Trans. 1990, 33, 301–306. [Google Scholar] [CrossRef]
- Salant, R.F.; Maser, N.; Yang, B. Numerical model of a reciprocating hydraulic rod seal. ASME J. Tribol. 2007, 129, 91–97. [Google Scholar] [CrossRef]
- Grimble, D.; Theodossiades, S.; Rahnejat, H.; Wilby, M. Tribology of rough ultra-film contacts in drug delivery devices. Proc. IMechE—Part C J. Mech. Eng. Sci. 2008, 222, 2209–2216. [Google Scholar] [CrossRef]
- Yang, B.; Salant, R.F. Soft EHL simulations of U-cup and step hydraulic rod seals. ASME J. Tribol. 2009, 131, 021501. [Google Scholar] [CrossRef]
- Yang, B.; Salant, R.F. Elastohydrodynamic lubrication simulation of O-ring and U-cup hydraulic seals. Proc. IMechE—Part J. J. Eng. Tribol. 2011, 225, 603–610. [Google Scholar] [CrossRef]
- Fatu, A.; Hajjam, M. Numerical modelling of hydraulic seals by inverse lubrication theory. Proc. IMechE—Part J. J. Eng. Tribol. 2011, 225, 1159–1173. [Google Scholar] [CrossRef]
- Nikas, G.K.; Sayles, R.S. Study of leakage and friction of flexible seals for steady motion via a numerical approximation method. Tribol. Int. 2006, 39, 921–936. [Google Scholar] [CrossRef]
- Békési, N. Friction and Wear of Elastomers and Sliding Seals. Ph.D. Thesis, Department of Machine and Product Design, Faculty of Mechanical Engineering, Budapest University of Technology and Economics, Budapest, Hungary, 2011. [Google Scholar]
- Alkadhimi, F. Wear Testing and Finite Element Analysis of Nitrile Rubber (NBR) Hand Pump Seals. M.Eng. Thesis, School of Mechanical and Manufacturing Engineering, Dublin City University, Dublin, Ireland, 2015. [Google Scholar]
- Bhaumik, S.; Kumaraswamy, A.; Guruprasad, S.; Bhandari, P. Study of effect of seal profile on tribological characteristics of reciprocating hydraulic seals. Tribol. Ind. 2015, 37, 264–274. [Google Scholar]
- Dowson, D.; Higginson, G.R. Elasto-Hydrodynamic Lubrication: The Fundamentals of Roller and Gear Lubrication; Pergamon Press: Oxford, UK, 1966. [Google Scholar]
- Barus, C. Isothermals, isopiestics, and isometrics relative to viscosity. Am. J. Sci. 1893, 45, 87–96. [Google Scholar] [CrossRef]
- Wu, C.S.; Klaus, E.E.; Duda, J.L. Development of a method for the prediction of pressure-viscosity coefficients of lubricating oils based on free-volume theory. ASME J. Tribol. 1989, 111, 121–128. [Google Scholar] [CrossRef]
- Denis, J.; Briant, J.; Hipeaux, J.C. Lubricant Properties, Analysis and Testing; Section 2.5.5.1; Editions Technip: Paris, France, 2000; ISBN 2710807467. [Google Scholar]
- Greenwood, J.A.; Tripp, J.H. The contact of two nominally flat rough surfaces. Proc. IMechE 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Zhang, S.-W. Tribology of Elastomers; Elsevier: London, UK, 2004; ISBN 0444513183. [Google Scholar]
- Hamrock, B.J.; Schmid, S.R.; Jacobson, B.O. Fundamentals of Fluid Film Lubrication, 2nd ed.; Section 3.9; Marcel Dekker, Inc.: New York, NY, USA, 2004; ISBN 0824753712. [Google Scholar]
- Komzsik, L. Applied Calculus of Variations for Engineers, 2nd ed.; CRC Press: New York, NY, USA, 2014; ISBN 9781482253597. [Google Scholar]
- Kot, M. A First Course in the Calculus of Variations; Series: Student Mathematical Library; American Mathematical Society: Providence, RI, USA, 2014; Volume 72, ISBN 9781470414955. [Google Scholar]
- Gregory, J.; Lin, C. Constrained Optimization in the Calculus of Variations and Optimal Control Theory; Chapman & Hall: London, UK, 1992; ISBN 9789401052955. [Google Scholar]
- SSL II User’s Guide (Scientific Subroutine Library); Fujitsu Ltd.: Tokyo, Japan, 1998.
- Gelfand, I.M.; Fomin, S.V. Calculus of Variations; Prentice Hall, Inc.: Englewood Cliffs, NJ, USA, 1963. [Google Scholar]
- O’Neil, P.V. Advanced Engineering Mathematics, 7th ed.; Cengage: Stamford, CT, USA, 2012; ISBN 9781111427412. [Google Scholar]
- Wazwaz, A.-M. The variational iteration method for analytic treatment for linear and nonlinear ODEs. Appl. Math. Comput. 2009, 212, 120–134. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Manzhirov, A.V. Handbook of Integral Equations, 2nd ed.; Section 13.2.1; Chapman & Hall/CRC: New York, NY, USA, 2008; ISBN 9781584885078. [Google Scholar]
- Nikas, G.K.; Sayles, R.S. Nonlinear elasticity of rectangular elastomeric seals and its effect on elastohydrodynamic numerical analysis. Tribol. Int. 2004, 37, 651–660. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985; ISBN 0521347963. [Google Scholar]
- Nikas, G.K.; Almond, R.V.; Burridge, G. Experimental study of leakage and friction of rectangular, elastomeric hydraulic seals for reciprocating motion from –54 to +135 °C and pressures from 3.4 to 34.5 MPa. Tribol. Trans. 2014, 57, 846–865. [Google Scholar] [CrossRef]
- Jacobson, B. A high pressure-short time shear strength analyzer for lubricants. ASME J. Tribol. 1985, 107, 220–223. [Google Scholar] [CrossRef]
- Prokopovich, P.; Theodossiades, S.; Rahnejat, H.; Hodson, D. Friction in ultra-thin conjunction of valve seals of pressurised metered dose inhalers. Wear 2010, 268, 845–852. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press (Elsevier): Oxford, UK, 2011; ISBN 9780123919274. [Google Scholar]
- Nikas, G.K. Determination of Polymeric Sealing Principles for End User High Reliability; Technical Report DOW-08/01; Department of Mechanical Engineering, Tribology Group, Imperial College: London, UK, 2001; Available online: www.tribology.me.uk/project5.htm (accessed on 2 April 2020).
- Stupkiewicz, S.; Marciniszyn, A. Elastohydrodynamic lubrication and finite configuration changes in reciprocating seals. Tribol. Int. 2009, 42, 615–627. [Google Scholar] [CrossRef]
- Öngün, Y.; André, M.; Bartel, D.; Deters, L. An axisymmetric hydrodynamic interface element for finite-element computations of mixed lubrication in rubber seals. Proc. IMechE—Part J. J. Eng. Tribol. 2008, 222, 471–481. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).