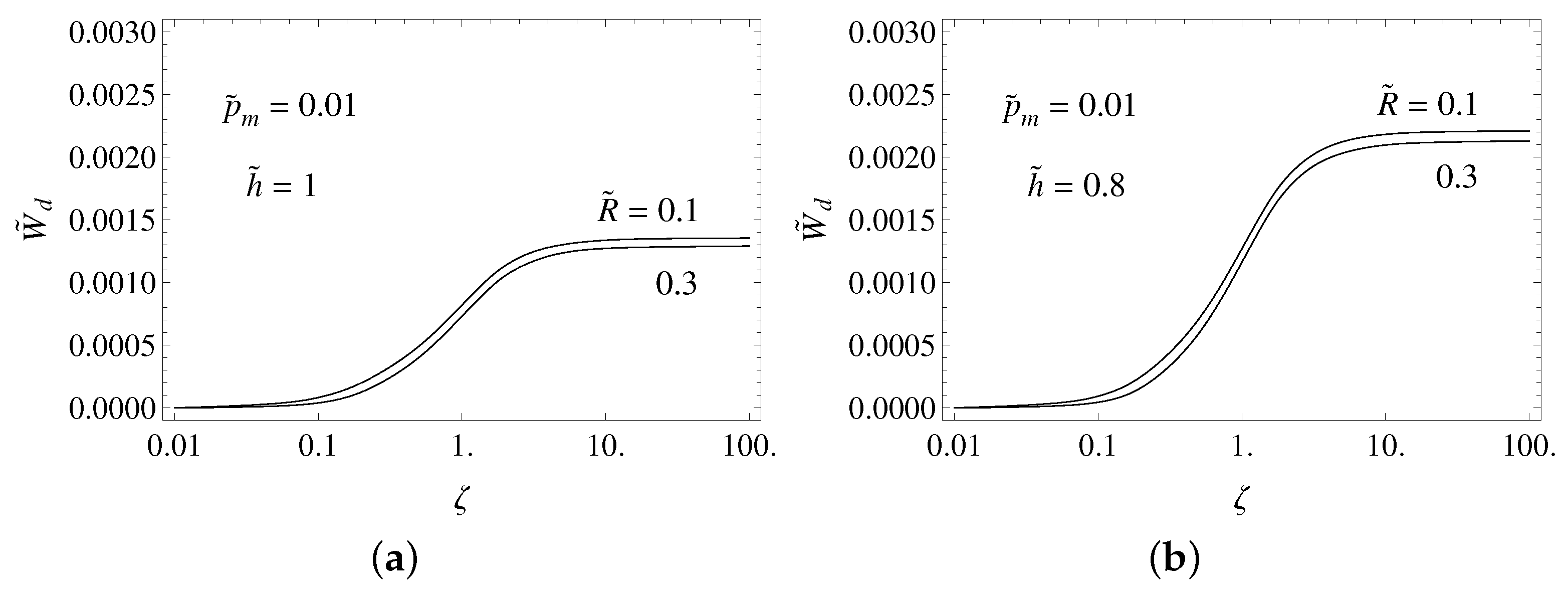1. Introduction
Polymers and rubber-like materials have found increasing utilization in mechanical devices and machines, because of some of their very relevant physical properties. Tires, seals, conveyor belts, power transmission belts, and seismic isolation devices are only a few examples of how important they are in commonly used mechanical systems. Rubber-like materials are characterized by a relatively high compliance (with respect to the metal materials they are usually coupled with), a large static and dynamic friction coefficient (specifically in the case of polymeric materials [
1]), vibration absorption [
2,
3], resistance to some aggressive chemicals and environments [
4], and much more. Since they are very often employed in contact pairs, there is a huge interest in deep understanding the details of the contact behavior of this kind of materials in static and dynamic conditions.
Their valuable characteristics, however, sometimes leads to some competing properties, thus the system design is critical. In belt conveyors, for example, rubber materials are used to protect the core of the belt (usually made of synthetic or metal fibers to bear the tensile load), preventing damages coming from aggressive environments and mechanical interactions, such as the rolling contact with the load-carrying idle rollers, as well as the abrasion induced by the conveyed material. As a side effect, while the belt is running, the rubber part of the belt undergoes time dependent cyclic deformation, which in turn leads to energy dissipation. A viscoelastic friction arises, which is often known as indentation rolling resistance [
5]. Such power loss can be responsible for up to 60% of the total energy consumption in long horizontal conveying systems [
6], thus making it critical to develop both accurate experimental techniques for the characterization of the belt cover material properties [
7] and numerical approaches for accurately estimating the power loss in relation with the geometrical and operative characteristics of the conveyors systems. Indeed, a combination of a deep knowledge of the employed rubber compounds and an accurate modeling of the contact behavior is the basis of a smart design of such devices.
As far as contact modeling is concerned, the topic has been faced in the literature by analytical approaches [
8,
9,
10,
11,
12,
13,
14,
15], numerical simulations [
16,
17,
18,
19,
20,
21] and experiments [
22,
23,
24,
25,
26]. Most of the literature about analytical or semi-analytical approaches to the study of the contacts involving rubber-like materials relies on the assumption that the contact bodies can be well represented by semi-infinite solids [
12,
27,
28,
29]. This hypothesis holds true for a large class of contact mechanics problems. As a rule of thumb, it can be considered that contact quantities are correctly calculated by modeling the bodies as half-spaces when the size of the contact area is sufficiently small compared to the thickness of the bodies (as in the Hertzian assumption [
30]). However, the correctness of such approach breaks when dealing with contacts involving thin layers of deformable materials, either in the case they are backed to a stiffer body on the opposite side of the contact [
14,
31,
32], or in the case they are unconstrained [
33,
34]. Under such circumstances, proper methodologies must be developed. Because of the relative complexity in deriving rigorous analytical results, researchers have proposed some oversimplified approaches based on the viscoelastic Winkler foundation approximation of the deformable body [
35,
36]. Similarly, a very sophisticated theoretical formulation exists able to deal with such a demanding problem [
37,
38], however, due to the fundamental mean-field nature of such a theory, its applicability to studies tailored to engineering applications is weak. As an alternative, semi-analytical models have been carried out [
39,
40]. In particular, in [
40], the authors studied the sliding contact of viscoelastic layers of finite thickness on rigid sinusoidal substrates within the framework of Green’s functions approach. They considered two different boundary conditions of the viscoelastic layer: confined and free layer. In [
41], the authors exploited the results of the confined viscoelastic layer achieved in [
40] to investigate the viscoelastic contact between rigid, equally spaced cylinders and a thin layer of rubber material constrained to a rigid substrate. They have characterized the viscoelastic friction arising in a moving contact, with the purpose of determining the damping behavior of a roller bearing viscoelastic isolator for seismic applications. Further, the effectiveness of such a semi-analytical approach has also been proved in a fundamental investigation on the rough contact behavior of viscoelastic layers [
42], showing significant agreement with one of the most advanced closed-form theories on the topic [
11,
43].
Moving from the formalism presented in [
40], in this work, we investigate the viscoelastic rolling contact between a rubber belt and a row of rigid cylinders, spaced by equal intervals of length
. An external uniformly distributed pressure is assumed to act on the opposite side of the belt, forcing the contact with the cylinders. Specifically, the rubber belt is assimilated to a free layer of linear viscoelastic material. The study allows determining the tangential viscoelastic frictional force (indentation rolling resistance) arising at the contact interface, as well as the energy dissipation per unit time, as functions of the system geometry, the mechanical properties of the viscoelastic layer and the operative conditions such as the layer velocity and the remote applied pressure.
2. Physical Model
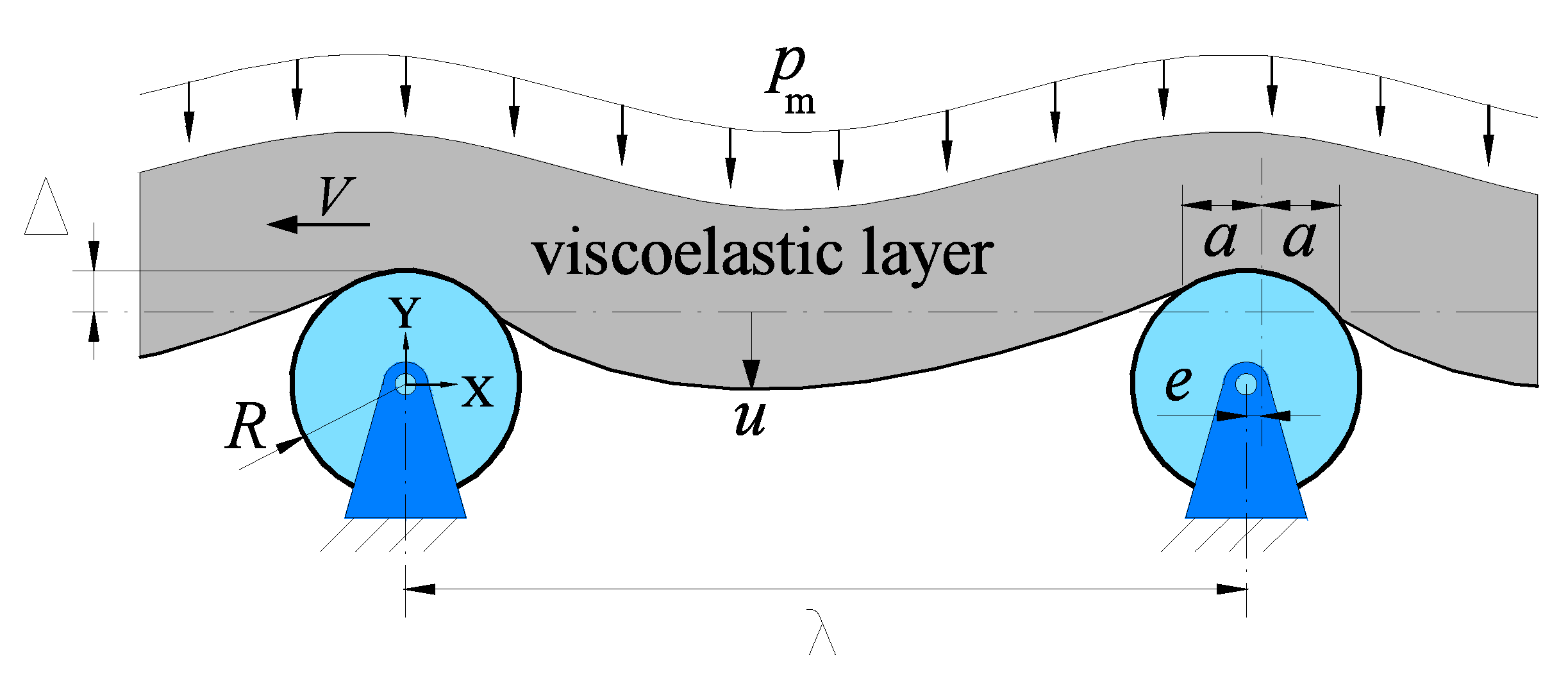
A schematic picture of the physical system under investigation is shown in
Figure 1. A thin layer of viscoelastic material is pushed against a row of equally spaced rigid cylinders by a uniform pressure distribution. The layer is kept in motion at constant velocity
V and we assume no friction at the interface between the layer and the cylinders. The viscoelastic “friction” is thus only the resultant of the horizontal components of the infinitesimal forces given by the contact pressure distribution between the cylinders and the layer. Indeed, a neat horizontal force on the belt arises as a consequence of the asymmetrical contact areas and pressure distribution. Under the contact mechanics perspective, it is equivalent to consider idle rollers with absent bearing resistance, or resistance to rotation of any other kind. This model can be applied as it is only in the practical cases in which the tangential stress distribution is weak enough not to alter considerably the stress and strain of the material in comparison with the frictionless case. Such a physical configuration resembles the case of a horizontal belt conveyor for granular materials, in which the belt, running at velocity
V, is pressed against idle rollers by an almost uniform pressure due to the load of the granular material. The schematic picture in
Figure 1 shows the contact penetration
, defined as the distance between the mean line of the deformed lower surface of the viscoelastic layer and the upper point of the cylinder cross-section, whereas
is the layer interfacial displacement field. In our paper, we deal with linear viscoelasticity, thus we neglect any large deformation effect, as well as material response nonlinearity. This assumption may be quite restrictive in particular conditions, e.g., when the penetration
takes values close to the layer thickness
h; nonetheless, it should not affect the main physical scenario and conclusions.
The steady-state periodic viscoelastic contact problem depicted resembles the aperiodic rolling contact problem already treated semi-analytically by Hunter [
5], and the periodic one studied by some of the authors of the present paper in [
12] for the case of viscoelastic half-plane (i.e.,
). However, in the case of contacts with viscoelastic free layers of finite thickness, closed form solutions are not available, and a numerical procedure has to be adopted to treat the problem at hand. Here, we exploit the formalism firstly proposed in [
20] and then extended to finite thickness free layers [
40], which relies on a Green’s functions approach. Therefore, under the assumption of steady moving at velocity
V, the contact problem can be formalized in terms of an integral equation with a translational invariant kernel
, which parametrically depends on the velocity
V
where
is the contact domain (see
Figure 1). In Equation (
1), the kernel
represents the viscoelastic Green’s function for steady moving contacts. Examples of
can be found for single asperity contacts in [
5], and periodic contact in [
12]. In the case of periodic contacts with free layers of finite thickness, according to the authors of [
40], it takes the form
where
is the viscoelastic creep function, whose general form is
with
the Heaviside step function,
the zero-frequency elastic modulus of the viscoelastic material, and
the spectrum of elastic compliances. Further, the term
in Equation (
2) is the so-called
purely elastic Green’s function. Such a shape function is strictly related to the specific geometry of the problem under investigation (see [
44])
where
being
h the viscoelastic layer thickness, and
. As a first example of application, the case of a linear viscoelastic material with a unique relaxation time
is considered herein. In this case,
with
.
Substituting Equation (
6) into Equation (
2) and recalling that
and
, where
is the high frequency elastic modulus, the long time response viscoelastic Green’s function writes as
Moreover, it has been shown that the layer surface mean-plane displacement with respect to the underformed configuration is (see [
40]):
where
is the mean contact pressure.
In
Figure 1, it is shown that the contact area is not centered with respect to the mean line of the rollers cross-section. In fact, depending on the translational speed
V, the contact area may exhibit a certain degree of eccentricity
e (see [
12]), due to the delay in the viscoelastic response of the material. In this regard, we observe that, within the contact strip
, the layer displacement must copy the profile of the rigid cylinder
. Therefore, for
, Equation (
1) can be rewritten as a Fredholm equation of the first kind
where
.
Interestingly, given
and
V, Equation (
9) can be inverted, allowing the calculation of the contact pressure distribution
as a function of the contact size
a and eccentricity
e. Solving Equation (
9) has been accomplished numerically, by exploiting the numerical procedure proposed in [
44], which has been specifically developed for periodic contact mechanics, relying on a self-adaptive non-uniform discretization of the contact area. Indeed, to properly calculate the stress intensity factors, it is mandatory to solve the contact pressure field close to the contact leading and trailing edges at high resolution, thus a finer mesh is required. On the contrary, far from the contact edges, a coarser mesh allow to reduce the computational effort.
Dealing with adhesiveless contact conditions, the pressure distribution must remain positive (i.e., repulsive) everywhere, vanishing at the edge of the contact. Thus, for any given
and
V, there is only one single choice of the couple
fulfilling these conditions. Therefore, to calculate
a and
e, following the authors of [
40,
45,
46,
47], we also require that the “mode I” stress intensity factors vanish at the contact edges.
3. Results and Discussion
Results are obtained assuming
and are shown in terms of dimensionless quantities. The following ones are therefore defined:
,
,
,
,
, and
. It is well known that in cases such as the one under investigation, in which the contact area is not negligibly small in comparison with the thickness of the deformable (e.g., viscoelastic) layer, the thickness
h strongly affects the results. For this reason, some results are shown for a couple of values of
to discuss the influence of the layer thickness on the contact quantities, whereas the limiting case of contact with rigid indenters and a viscoelastic half-plane (i.e.,
) can be found elsewhere in the literature [
41].
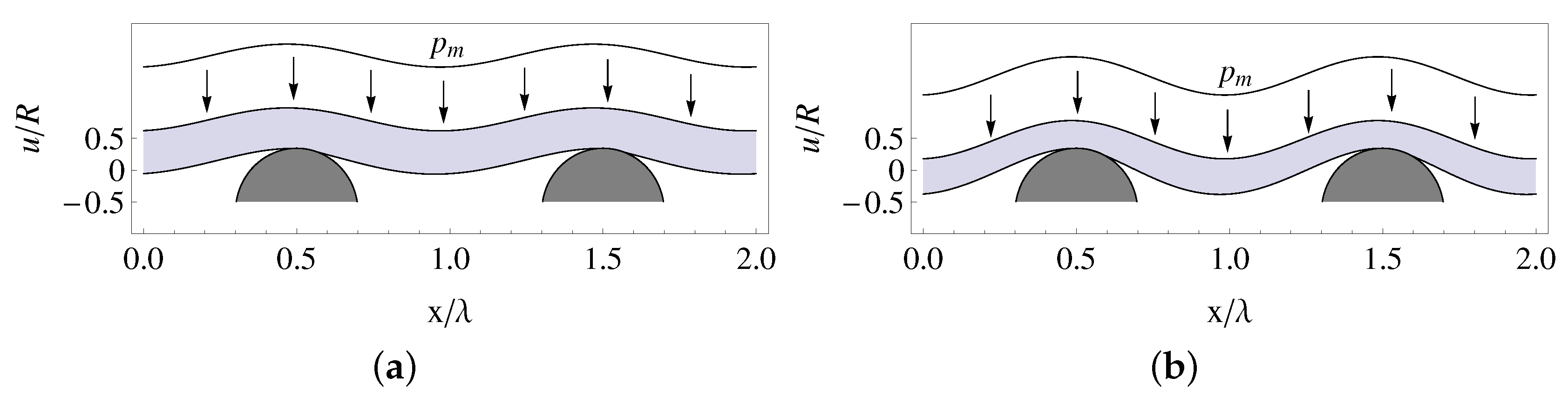
Figure 2 shows the contact between a rigid indenter made with equally spaced cylinders of dimensionless radius
and a viscoelastic layer with dimensionless thickness
, for two different values of the layer thickness, namely
(
Figure 2a) and
(
Figure 2b). The layer is pressed against the indenter by a uniform pressure. The schematic picture backs in mind the belt of a conveyor pressed against idle rollers by, for example, the distributed weight of some granular material. The layer has a leftward relative velocity with respect to the indenter and there is no friction at the interface between the cylinder and the belt. Because of the viscoelastic behavior of the layer, the area of contact with each cylinder is not symmetrically distributed with respect to the vertical symmetry line of each cylinder, but it is slightly displaced on the right side of the indenter.
Figure 2 shows that the thinner layer is more compliant, thus the contact area is larger and, more evidently, the bending deflection of the layer is much more evident. This apparently trivial consideration is very important to understand the results discussed below.
It is worth noting that typical belt conveyors present a certain belt pre-tension, which is usually sustained by the stiffer metallic or fiber belt core. Due to the belt curvature between two successive rollers, such membrane pre-stresses give rise to a large deformation effect, increasing the bending stiffness of the belt, and in turn reducing the overall bending at fixed load. This effect is not considered in our model, which moves in the framework of small-deformations linear viscoelasticity. However, the results presented herein in terms of viscoelastic friction are not qualitatively affected by this assumption, because the pre-stress is not cyclically varying (i.e., it is constant), thus does not give rise to any viscoelastic dissipation. On the other hand, its effect in the real-world is to increase the apparent bending stiffness of the belt, thus a quantitive mismatch is expected: at given value of mean load , our model overestimates both the bending deflection of the belt and the contact area with the rollers (which is strictly related to the bending deflection in the free layer case, such as the one under investigation).
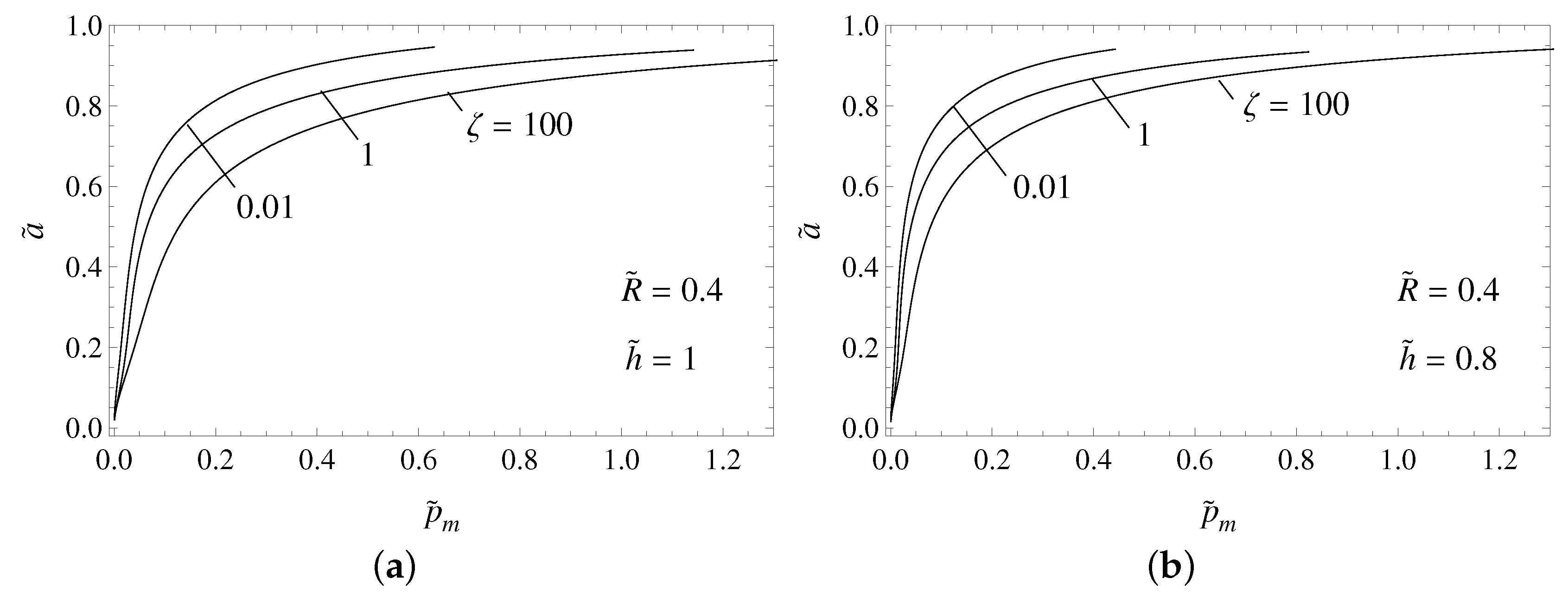
Figure 3 shows, for different values of dimensionless velocity
and given
, the dimensionless contact semi-width
as a function of the dimensionless load
.
Figure 3a is for
and
Figure 3b is for
. In
Figure 3a,b, it emerges that the increase of the contact patch size with load is very steep when the value of
is below
-
(within the investigated range of tangential velocity), whereas it slows down suddenly when such values are overcome, as
is an unrealistic asymptotic contact limit, in agreement with the authors of [
40]. The effect of increasing the tangential velocity is to reduce the contact area, due to the viscoelastic stiffening of the material, and also to reduce the threshold value of
which determines the transition from compliant to stiff behavior. Finally, reducing the thickness of the layer (
Figure 3b), the contact compliance noticeably increases throughout the whole load range. Such a result is well expected under load controlled conditions, since a reduction of the thickness of the viscoelastic layer increases the bending compliance, which enhances the attitude of the free layer to copy the indenter shape.
Regardless of the specific shape of the viscoelastic body, under rolling contact conditions, a kind of mechanical keying occurs as a consequence of the viscoelastic dissipation within the bulk material, which makes contact spots asymmetrical even on symmetrically shaped asperities, as observed in
Figure 2. Thus, even in the ideal case of vanishing Coulomb friction, a tangential load opposing the relative motion occurs. This is the resultant of the projection of the local contact forces in the direction of the relative movement between the two bodies. Because of the dissipative origin of such force (viscoelastic dissipation in the bulk), it is usually referred to as viscoelastic friction force. Thus, a friction coefficient (rolling friction coefficient or indentation rolling resistance coefficient) can be defined as the ratio between the friction force and the normal load:
where
is the average “tangential” stress,
and
, and
b is the tranverse width of the system.
The frictional behavior of the viscoelastic systems strongly depends on the excitation frequency
, through the viscoelastic complex modulus
Indeed, at very small tangential velocity (i.e., at very small
), although the viscoelastic material is softer (
) and, in turn, the contact area is relatively large, the time-dependent layer deformation occurs sufficiently slow to allow the material to elastically deform and recover the original shape, thus leading to almost symmetrical distributions of contact pressure and to almost symmetrical contact area. Since the viscoelastic dissipation depends on the the cyclic deformation of the material, under this condition, we expect a small friction force and friction coefficient. On the other extreme, when the tangential velocity is very large (i.e., at very large
), the elastic modulus of the layer increases (
) and, under load controlled conditions, the contact area reduces compared to the low speed results. Since the amount of viscoelastic material involved in the cyclic deformation is roughly proportional to the contact area size, we have that at high velocity, small friction is expected as well. At intermediate values of tangential velocity, instead, the friction coefficient follows a characteristic bell-like curve with a pronounced local maximum. The maximum dissipation occurs when the excitation frequency
maximizes the ratio
. From Equation (
10), we have that such a condition implies that
.
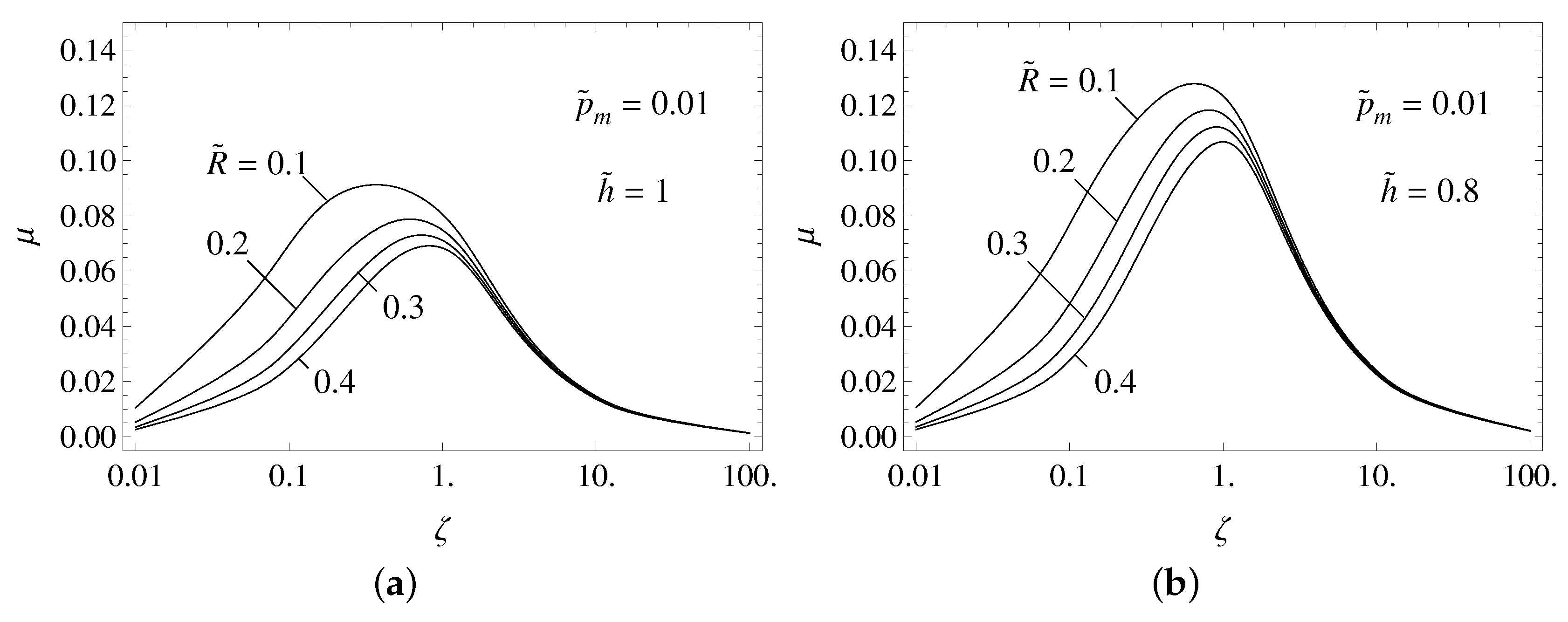
The friction coefficient
is shown in
Figure 4 as a function of the dimensionless tangential velocity for different values of the dimensionless radius
of the rollers. In
Figure 4a, the dimensionless thickness of the layer is
and in
Figure 4b
. A close look at
Figure 4a,b suggests that maximum friction occurs for
, even though the cylinder dimensionless radii
may significantly affect the overall result, depending on the layer thickness. A possible explanation of such a difference can be found by relying on dimensional arguments. Indeed, in the case of a relatively thick viscoelastic layer (
Figure 4a), the main deformation involves the contact area zone, as the bending deformation is negligible (notably the bending stiffness is proportional to
). Thus, the main excitation frequency of the viscoelastic material is related to the size of the contact
a, and can be estimated as
, assuming
. Considering that
, one obtains that for a relatively thick layer the estimated dimensionless velocity which maximizes the friction coefficient is
, thus it reduces by reducing
(it is worth noting that in our physical problem
). On the other hand, for relatively thin layers (
Figure 4b) most of the dissipation occurs in the bulk of the layer as a consequence of the cyclic bending deformation. In this case, the main excitation frequency can be estimated as
, thus similar arguments as those discussed before lead to estimate that the tangential velocity which maximizes the friction coefficient as
, disregarding the value of
. Finally, in
Figure 4a,b, we also observe that the friction coefficient increases with decreasing
. This result is even clearer in
Figure 5, where average “tangential” stress
is shown as a function of the dimensionless layer thickness
under given normal load
, tangential velocity
and indenter radius
.
Figure 5 also shows a comparison with the case of moving indentation of a half-plane, which, of course, is approached asymptotically when
is very large. The increase of average friction stress with decreasing
is the consequence of the combined effect of increasing both the bending deformation and the contact area. Such a result is opposite to the one described in [
41] where the case of confined viscoelastic layer is investigated. Indeed, in that case, the smaller is the thickness, the stiffer is the contact, leading to a reduction of the amount of material deformed under load and thus reducing the energy dissipation (down to zero for a layer with infinitesimal thickness).
For practical applications, it could be interesting to quantify the amount of energy dissipated (per unit time and in steady-state condition) by the viscoelastic loss. If the energy dissipated per unit time is calculated as
, the related dimensionless quantity is
.
Figure 6 shows
as a function of the dimensionless relative velocity
for two values of the dimensionless radius of the indenter, namely
and
.
Figure 6a shows
and
Figure 6b shows
At small velocity values the dissipation vanishes since the layer deforms almost elastically. In the range
, there is a sudden increase of the dissipated energy before it reaches plateaux for
. Thus, in applications where the energy dissipation must be minimized, it is very important to design the device keeping
. Remembering that
and considering that
V in general can not be set arbitrarily since it depends on the specific application, engineering design guidelines can be inferred aiming at tuning the relaxation time of the viscoelastic material
and the spacing
of the cylinders to keep
within the desired range.
Figure 6 also shows that the effect of reducing the cylinder radius is to increase dissipated energy per unit time and that the reduction of adimensionalized thickness has a similar effect. In both cases, such a behavior can be ascribed to the increase of layer bending deformation.
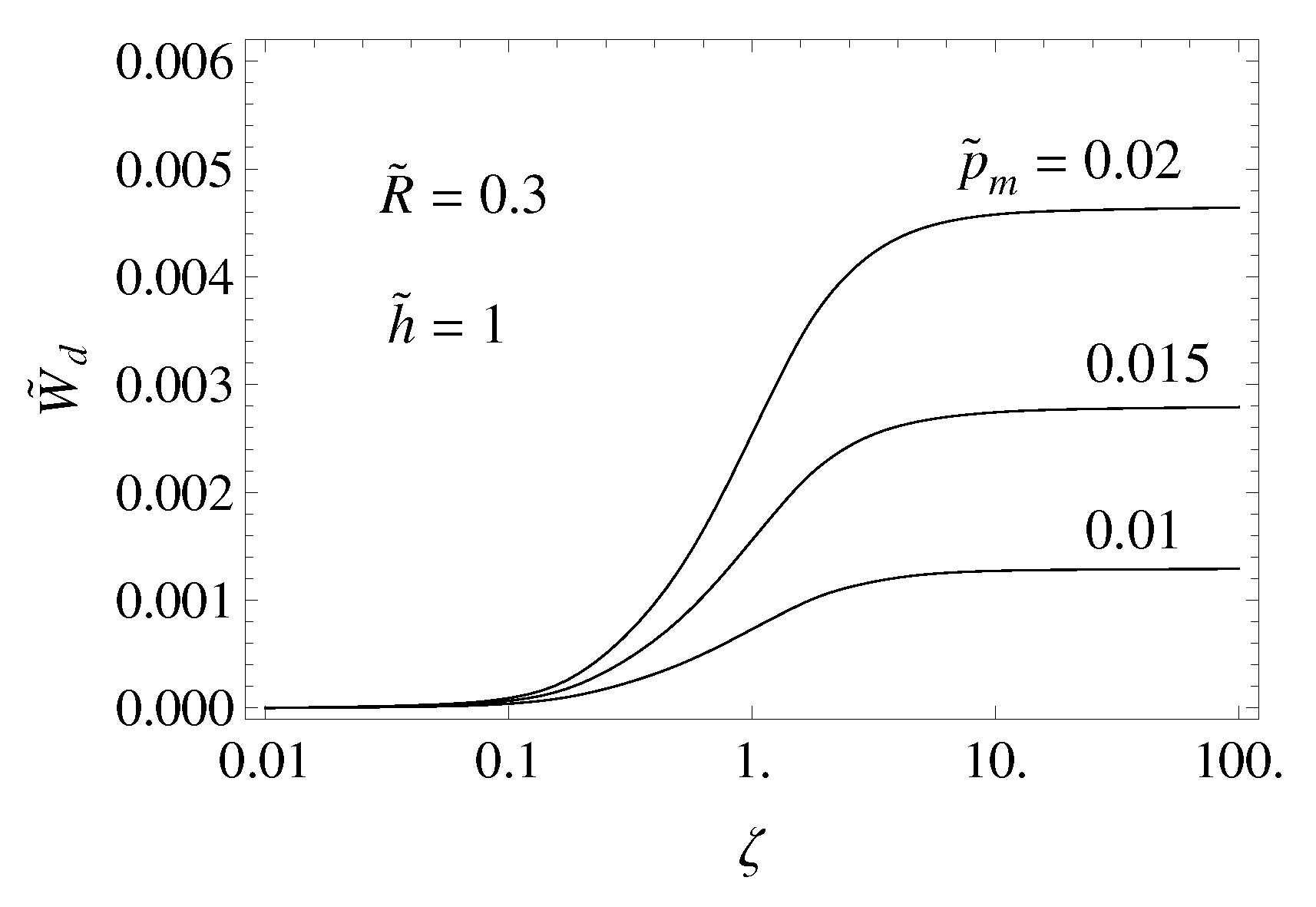
The adimensionalized energy dissipated per unit time is also shown in
Figure 7 as a function of the relative velocity
at several pressure
values. We observe that increasing the load has two effects: (i) increasing the system deformations; and (ii) increasing the amount of material involved in the cyclic deformation. Indeed,
Figure 7 shows that, increasing the load always leads to an increase of the energy dissipation, regardless of the tangential velocity. Further, in the plateaux region, it can be seen that the effect of increasing the load is more than linear since, when the load is doubled, the energy dissipated per unit time is almost multiplied by four. The asymptotic behavior of the energy dissipated per unit time at increasing velocity is rigorously studied in [
41]. The energy dissipation does not fall to zero even though the material approaches an elastic behavior when the speed is increased, because the viscoelastic friction force only asymptotically goes to zero, but its product with the velocity has a finite asymptotic value.
4. Conclusions
In this paper, the steady-state rolling contact between a periodic array of rigid cylinders and a free, finite-thickness layer of single-relaxation time viscoelastic material is investigated. The influences of the layer thickness, the material properties, the cylinders radii and spacing are analyzed. Besides, the effects of working parameters such as the load and the tangential velocity are also studied. As typical of viscoelasticity, the system behavior is dominated by the velocity. At very low and very high velocities, the system behaves elastically, even though, in the very low limit, the material is more compliant, thus the deformations are larger, whereas, in the very high limit, the system is stiffer. At intermediate range of velocity values, viscous effects dominate and typical characteristics of the viscoelastic contacts are emphasized. In particular, the contact area is evidently non-symmetrical and the contact pressures have a resultant force with a quite large component opposing the relative motion between the cylinders and the layer: a viscoelastic friction arises. The curve of viscoelastic friction vs. velocity has a typical bell-like shape, with a local maximum in the intermediate velocity range. The location of the local maximum depends on the material relaxation time. This force, also known as indentation rolling resistance, is important in many applications, for example in belt conveyors. In such devices, it is one of the largest contributes to energy consumption. The energy dissipated per unit time is thus also studied as a function of the tangential velocity. It is small until the value of the adimensionalized velocity is below a threshold (about equal to 0.1), which is only mildly dependent on the applied load. It is also shown how the dissipation is nonlinearly affected by the applied load, and that increasing the load very rapidly increases the dissipated energy per unit time. In addition, the effect of the system geometrical and material parameters can be opportunely tuned to enhance the component functionality. For example, increasing the thickness of the layer or the cylinder radii at given load, reduces the viscoelastic friction and the related energy dissipation. On the other hand, at large thickness values, modifying the cylinder radii changes also the velocity profile of the viscoelastic friction force, since the local maximum is shifted upwards and towards smaller velocities as the cylinder radius is decreased. Instead, at small values of thickness, the shift happens only upwards, thus it is here shown how the influence of geometrical parameters is somehow interrelated in a complicated fashion with the material properties.