A Discussion on Present Theories of Rubber Friction, with Particular Reference to Different Possible Choices of Arbitrary Roughness Cutoff Parameters
Abstract
1. Introduction
2. Experimental Data
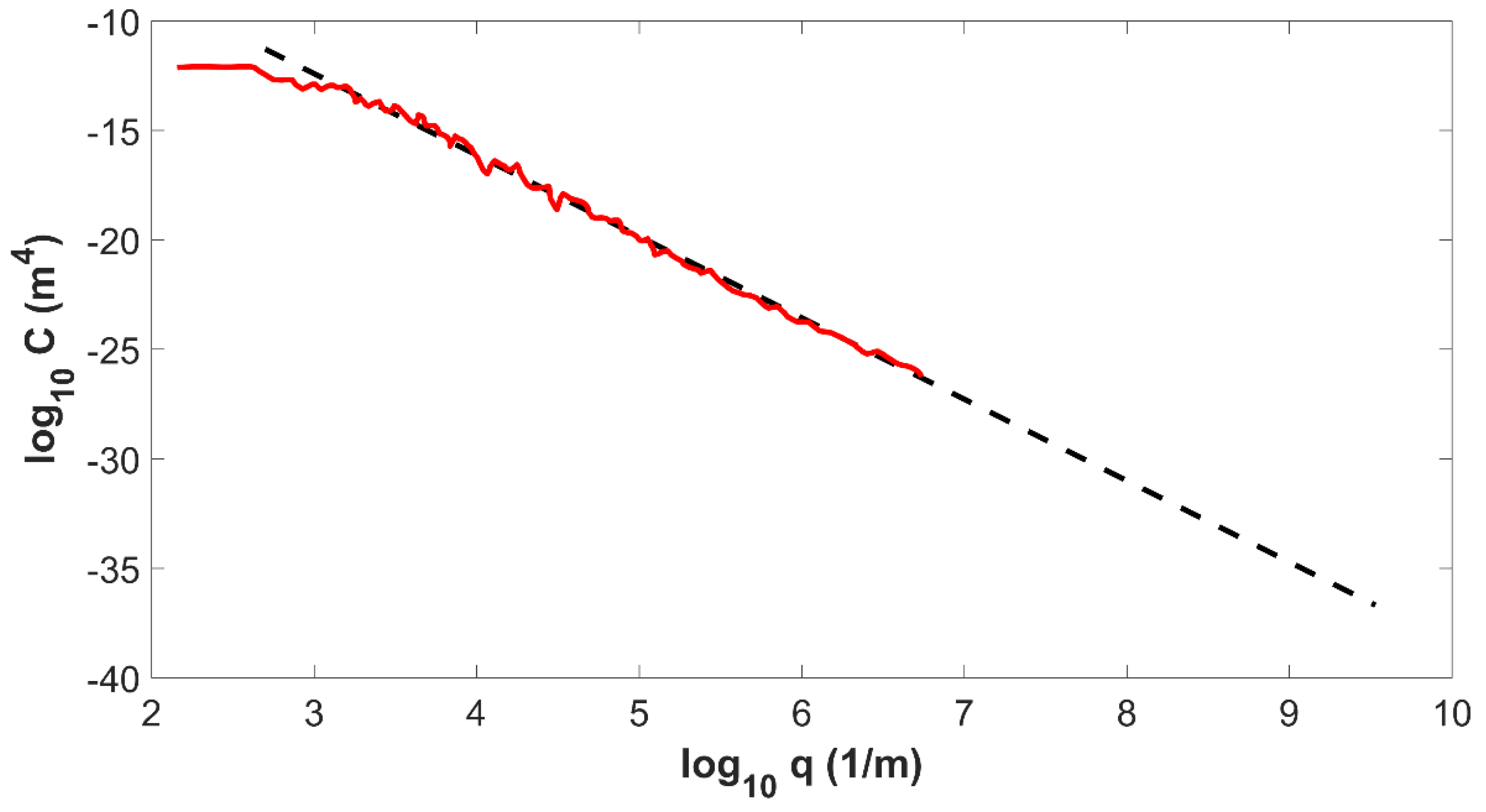
2.1. Surface PSD
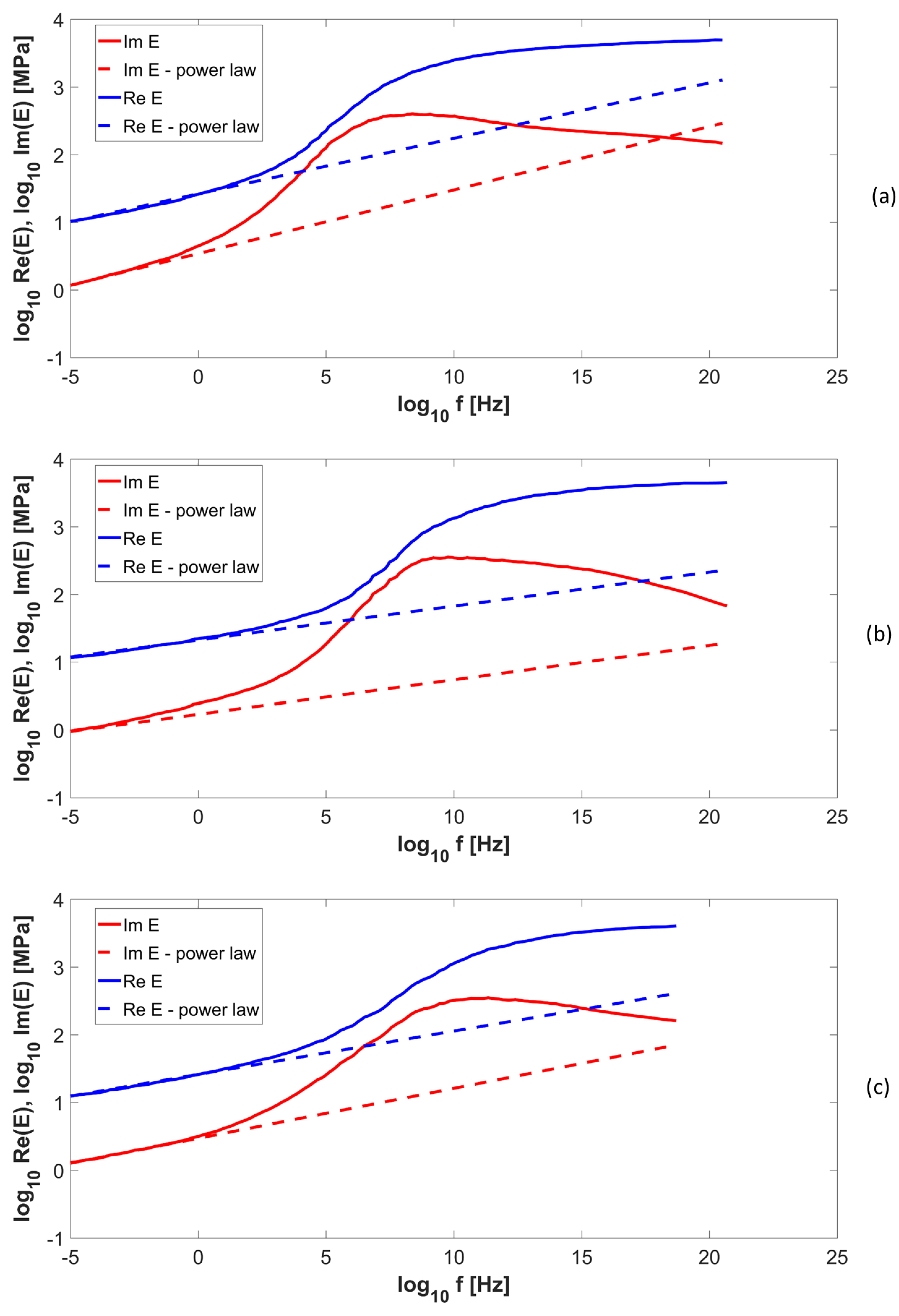
2.2. Material Viscoelastic Properties
2.3. Friction
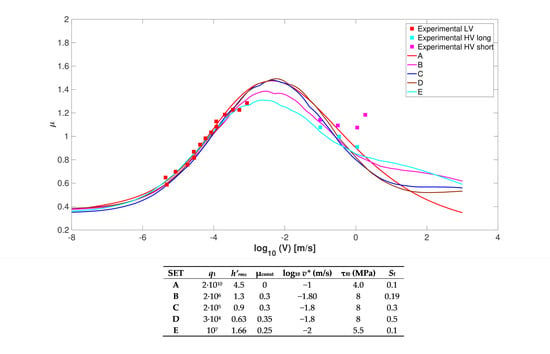
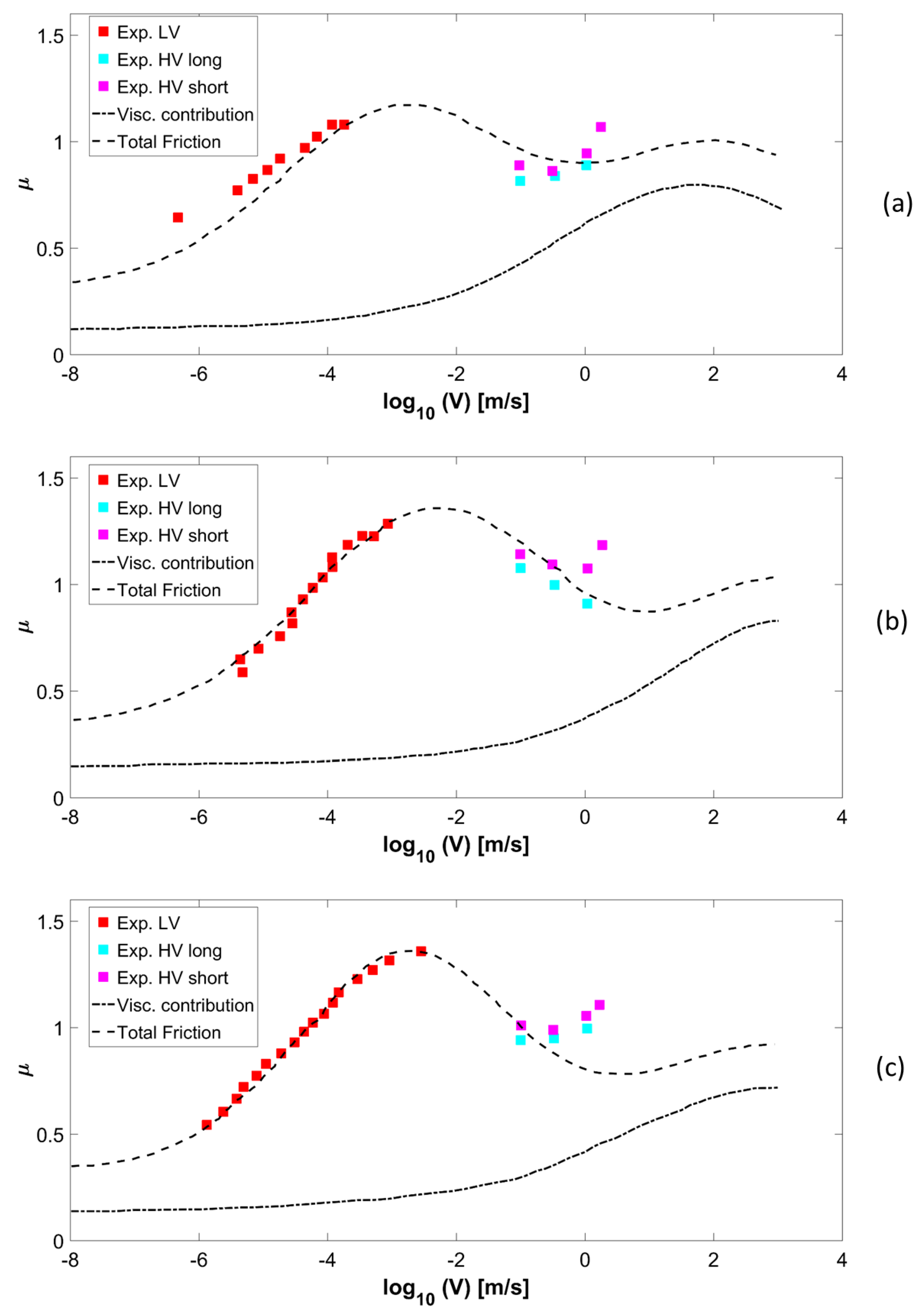
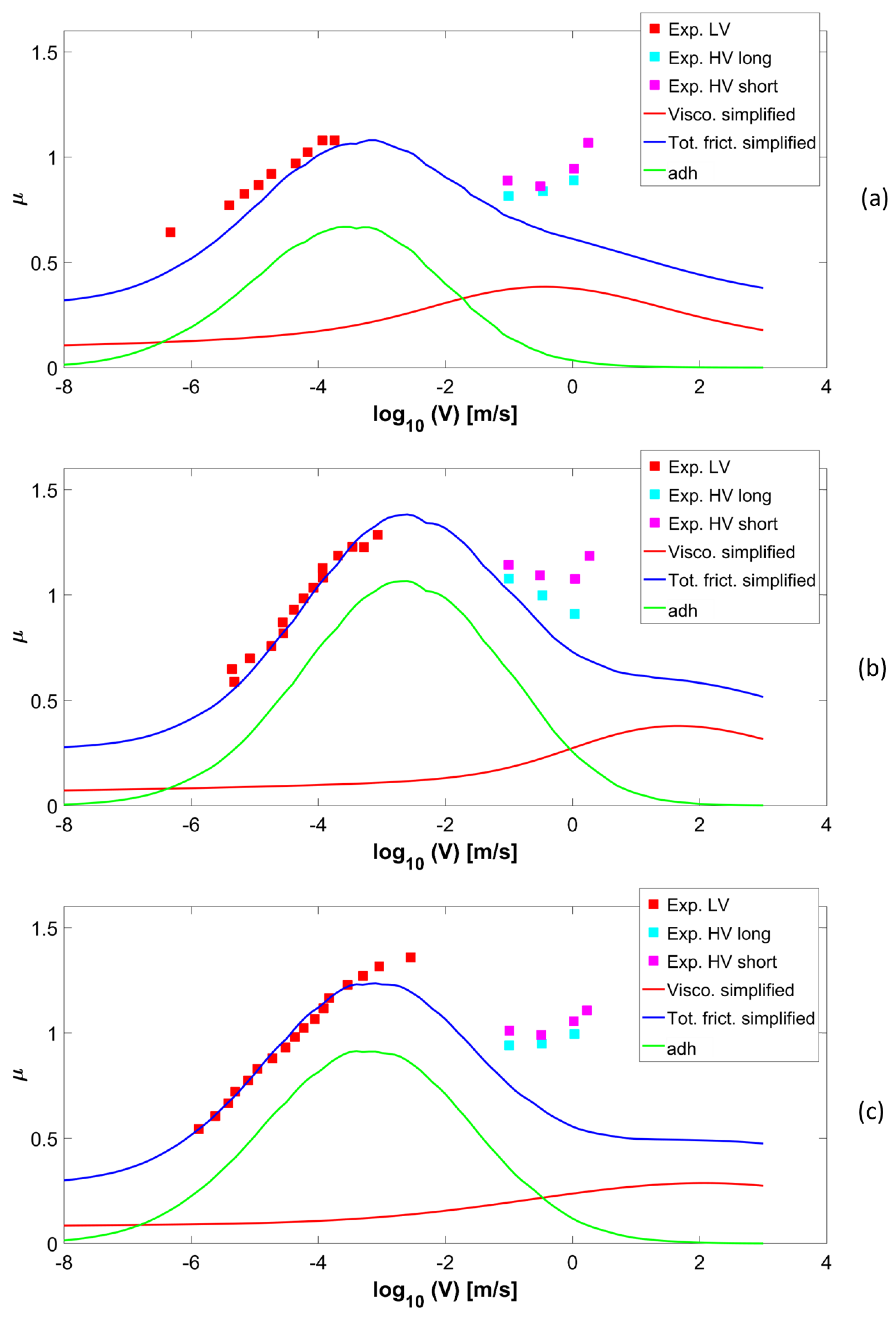
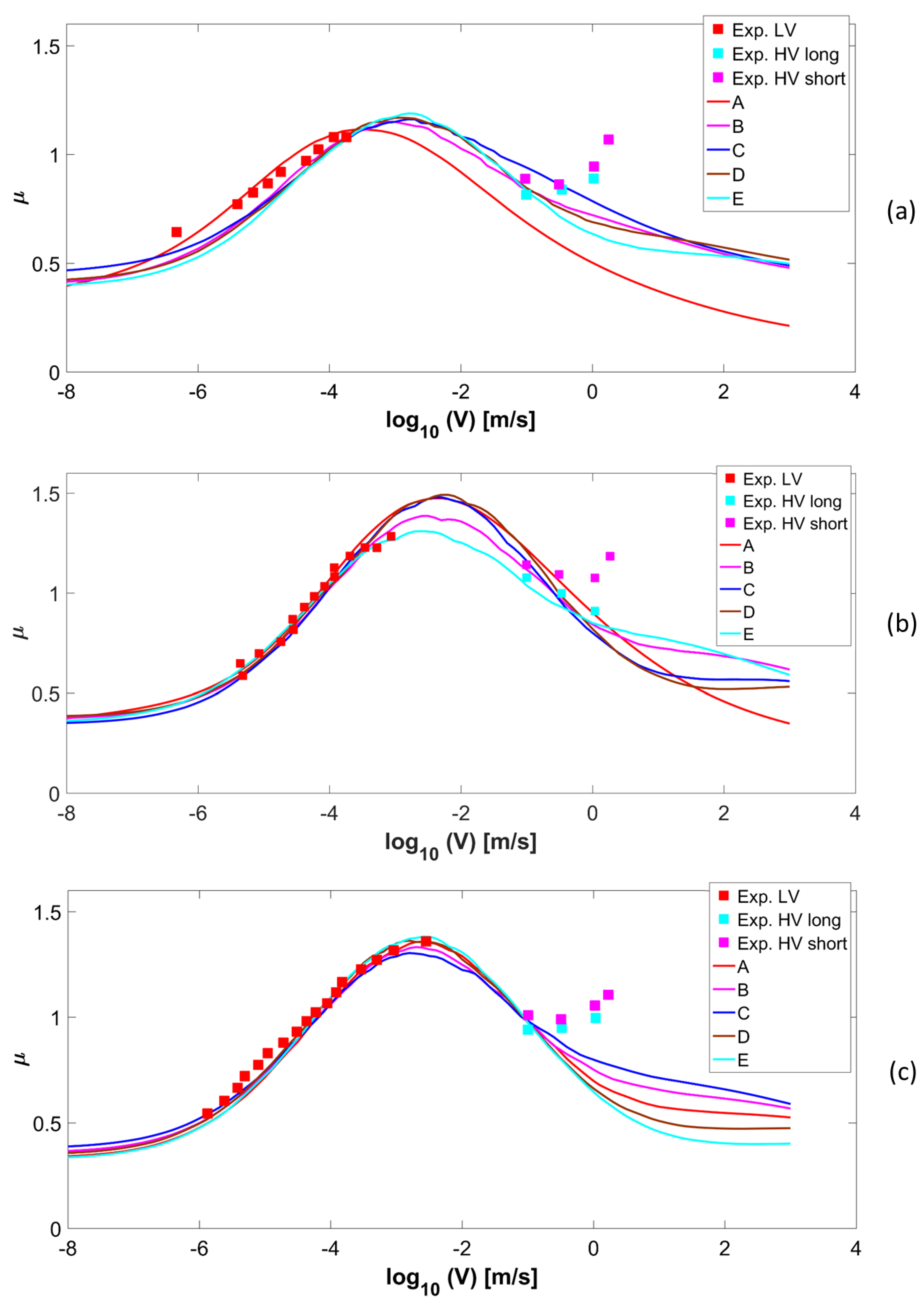
3. Discussion on the Viscoelastic and Adhesive Contributions
- -
- the choice of the cutoff wavenumber q1 influences strongly both viscoelastic and adhesive contributions;
- -
- the term μconst = 0.2 which is attributed to scratching of the concrete surface by the hard filler particles is quite arbitrary;
- -
- The reference velocity v* and the τf0 significantly influence the adhesive curve;
- -
- The assumption that for sliding friction on the rough surfaces the deformation is ε ≅ 1 implies a reduction of the strain modulus E(ω) of a strain factor Sf ≅ 0.1. Due to the non-linear effects related to the viscoelastic modulus of the rubber, lower strain values would cause sensible variation of the Sf and therefore of the adhesive friction.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Grosch, K.A. Visco-elastic properties and the friction of solids: Relation between the friction and visco-elastic properties of rubber. Nature 1963, 197, 858–859. [Google Scholar] [CrossRef]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-forming Liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Klüppel, M.; Heinrich, G. Rubber Friction on Self-Affine Road Tracks. Rubber Chem. Technol. 2000, 73, 578–606. [Google Scholar] [CrossRef]
- Persson, B.N.J. Theory of rubber friction and contact mechanics. J. Chem. Phys. 2001, 115, 3840–3861. [Google Scholar] [CrossRef]
- Ciavarella, M.; Papangelo, A. Discussion of “Measuring and Understanding Contact Area at the Nanoscale: A Review” (Jacobs, T.D.B., and Ashlie Martini, A., 2017, ASME Appl. Mech. Rev., 69 (6), p. 060802). Appl. Mech. Rev. 2017, 69, 065502. [Google Scholar] [CrossRef]
- Persson, B.N.J. Relation between Interfacial Separation and Load: A General Theory of Contact Mechanics. Phys. Rev. Lett. 2007, 99, 125502. [Google Scholar] [CrossRef] [PubMed]
- Papangelo, A.; Hoffmann, N.; Ciavarella, M. Load-separation curves for the contact of self-affine rough surfaces. Sci. Rep. 2017, 7, 6900. [Google Scholar] [CrossRef]
- Lorenz, B.; Oh, Y.R.; Nam, S.K.; Jeon, S.H.; Persson, B.N.J. Rubber friction on road surfaces: Experiment and theory for low sliding speeds. J. Chem. Phys. 2015, 142, 194701. [Google Scholar] [CrossRef]
- Carbone, G.; Putignano, C. Rough viscoelastic sliding contact: Theory and experiments. Phys. Rev. E 2014, 89, 032408. [Google Scholar] [CrossRef]
- Le Gal, A.; Yang, X.; Klüppel, M. Evaluation of sliding friction and contact mechanics of elastomers based on dynamic-mechanical analysis. J. Chem. Phys. 2005, 123, 014704. [Google Scholar] [CrossRef] [PubMed]
- Le Gal, A.; Klüppel, M. Investigation and modelling of rubber stationary friction on rough surfaces. J. Phys. Condens. Matter 2008, 20, 015007. [Google Scholar] [CrossRef]
- Lang, A.; Klüppel, M. Influences of temperature and load on the dry friction behaviour of tire tread compounds in contact with rough granite. Wear 2017, 380, 15–25. [Google Scholar] [CrossRef]
- Persson, B.N.J.; Volokitin, A.I. Rubber friction on smooth surfaces. Eur. Phys. J. E 2006, 21, 69–80. [Google Scholar] [CrossRef] [PubMed]
- Tolpekina, T.V.; Persson, B.N.J. Adhesion and Friction for Three Tire Tread Compounds. Lubricants 2019, 7, 20. [Google Scholar] [CrossRef]
- Tolpekina, T.; Pyckhout-Hintzen, W.; Persson, B.N.J. Linear and Nonlinear Viscoelastic Modulus of Rubber. Lubricants 2019, 7, 22. [Google Scholar] [CrossRef]
- Jacobs, T.D.B.; Junge, T.; Pastewka, L. Quantitative characterization of surface topography using spectral analysis. Surf. Topogr. Metrol. Prop. 2017, 5, 013001. [Google Scholar] [CrossRef]
| Compound | αr | βr | αi | βi |
|---|---|---|---|---|
| Compound A | 1.4193 | 0.0820 | 0.5375 | 0.0939 |
| Compound B | 1.3262 | 0.0501 | 0.2312 | 0.0507 |
| Compound C | 1.4140 | 0.0639 | 0.4713 | 0.0737 |
| Compound | q1 | h′rms | μconst | log10 v* (m/s) | τf0 (MPa) | Sf |
|---|---|---|---|---|---|---|
| Compound A | 2·106 | 1.3 | 0.2 | −2.47 | 3.6 | 0.1 |
| Compound B | 2·106 | 1.3 | 0.2 | −1.97 | 4.0 | 0.1 |
| Compound C | 2·106 | 1.3 | 0.2 | −2.53 | 4.1 | 0.1 |
| SET | q1 | h′rms | μconst | log10 v* (m/s) | τf0 (MPa) | Sf |
|---|---|---|---|---|---|---|
| A | 2·109 | 3.6 | 0 | −1.5 | 8 | 0.1 |
| B | 2·106 | 1.3 | 0.3 | −2.2 | 4.1 | 0.1 |
| C | 2·107 | 1.85 | 0.3 | −1.9 | 7 | 0.1 |
| D | 2·105 | 0.9 | 0.35 | −2.1 | 7 | 0.3 |
| E | 3·104 | 0.63 | 0.35 | −2.1 | 7 | 0.5 |
| SET | q1 | h′rms | μconst | log10 v* (m/s) | τf0 (MPa) | Sf |
|---|---|---|---|---|---|---|
| A | 2·1010 | 4.5 | 0 | −1 | 4.0 | 0.1 |
| B | 2·106 | 1.3 | 0.3 | −1.80 | 8 | 0.19 |
| C | 2·105 | 0.9 | 0.3 | −1.8 | 8 | 0.3 |
| D | 3·104 | 0.63 | 0.35 | −1.8 | 8 | 0.5 |
| E | 107 | 1.66 | 0.25 | −2 | 5.5 | 0.1 |
| SET | q1 | h′rms | μconst | log10 v* (m/s) | τf0 (MPa) | Sf |
|---|---|---|---|---|---|---|
| A | 2·106 | 1.3 | 0.25 | −2.0 | 5.25 | 0.1 |
| B | 107 | 1.66 | 0.25 | −2 | 6.9 | 0.1 |
| C | 3·107 | 1.96 | 0.25 | −2 | 8 | 0.1 |
| D | 105 | 0.8 | 0.3 | −2.1 | 7.1 | 0.3 |
| E | 104 | 0.5 | 0.3 | −2.1 | 6.4 | 0.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Genovese, A.; Farroni, F.; Papangelo, A.; Ciavarella, M. A Discussion on Present Theories of Rubber Friction, with Particular Reference to Different Possible Choices of Arbitrary Roughness Cutoff Parameters. Lubricants 2019, 7, 85. https://doi.org/10.3390/lubricants7100085
Genovese A, Farroni F, Papangelo A, Ciavarella M. A Discussion on Present Theories of Rubber Friction, with Particular Reference to Different Possible Choices of Arbitrary Roughness Cutoff Parameters. Lubricants. 2019; 7(10):85. https://doi.org/10.3390/lubricants7100085
Chicago/Turabian StyleGenovese, Andrea, Flavio Farroni, Antonio Papangelo, and Michele Ciavarella. 2019. "A Discussion on Present Theories of Rubber Friction, with Particular Reference to Different Possible Choices of Arbitrary Roughness Cutoff Parameters" Lubricants 7, no. 10: 85. https://doi.org/10.3390/lubricants7100085
APA StyleGenovese, A., Farroni, F., Papangelo, A., & Ciavarella, M. (2019). A Discussion on Present Theories of Rubber Friction, with Particular Reference to Different Possible Choices of Arbitrary Roughness Cutoff Parameters. Lubricants, 7(10), 85. https://doi.org/10.3390/lubricants7100085