Polymer Brush Friction in Cylindrical Geometries
Abstract
1. Introduction
2. Models and Methods
3. Results and Discussion
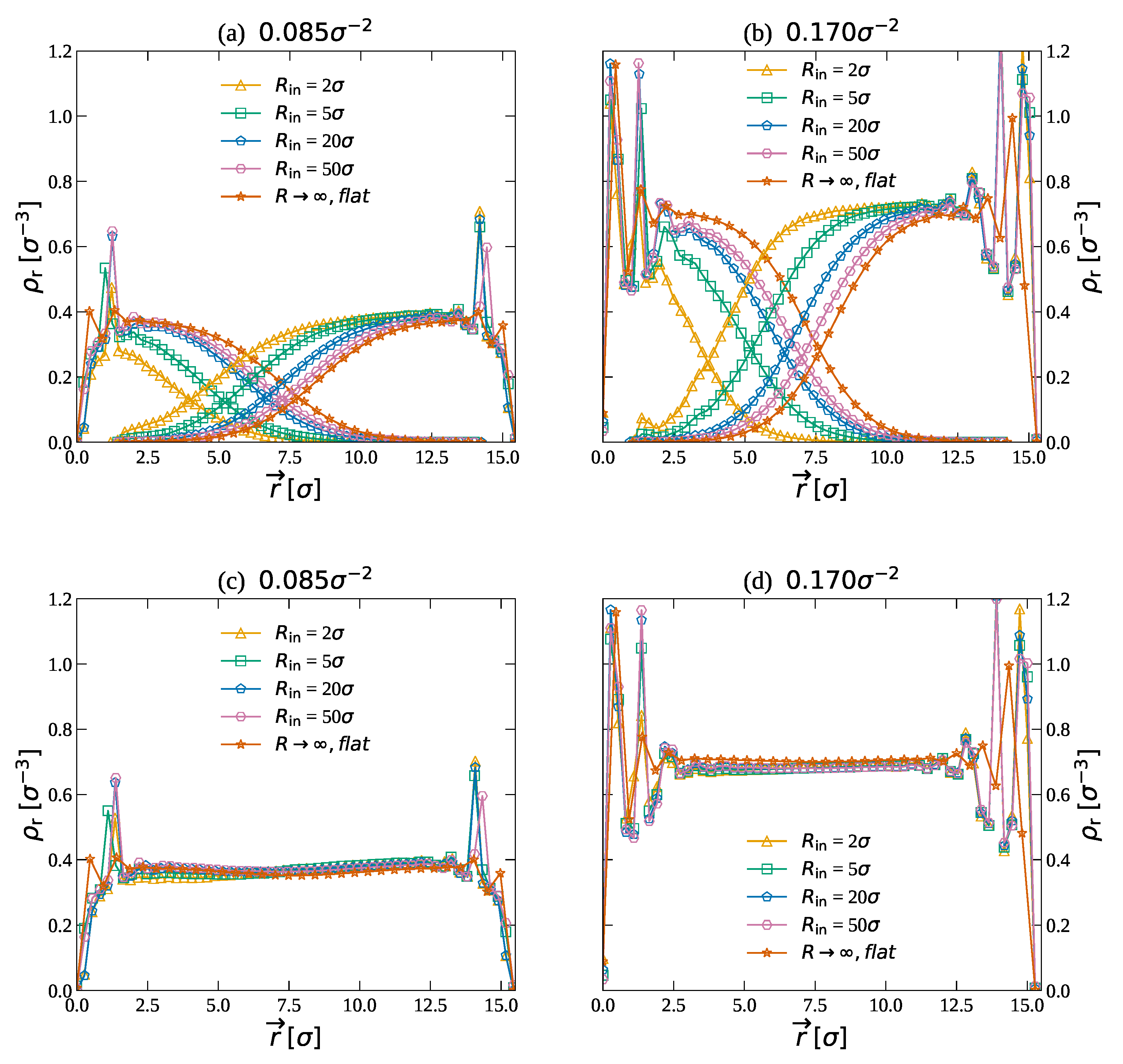
3.1. Density Profiles
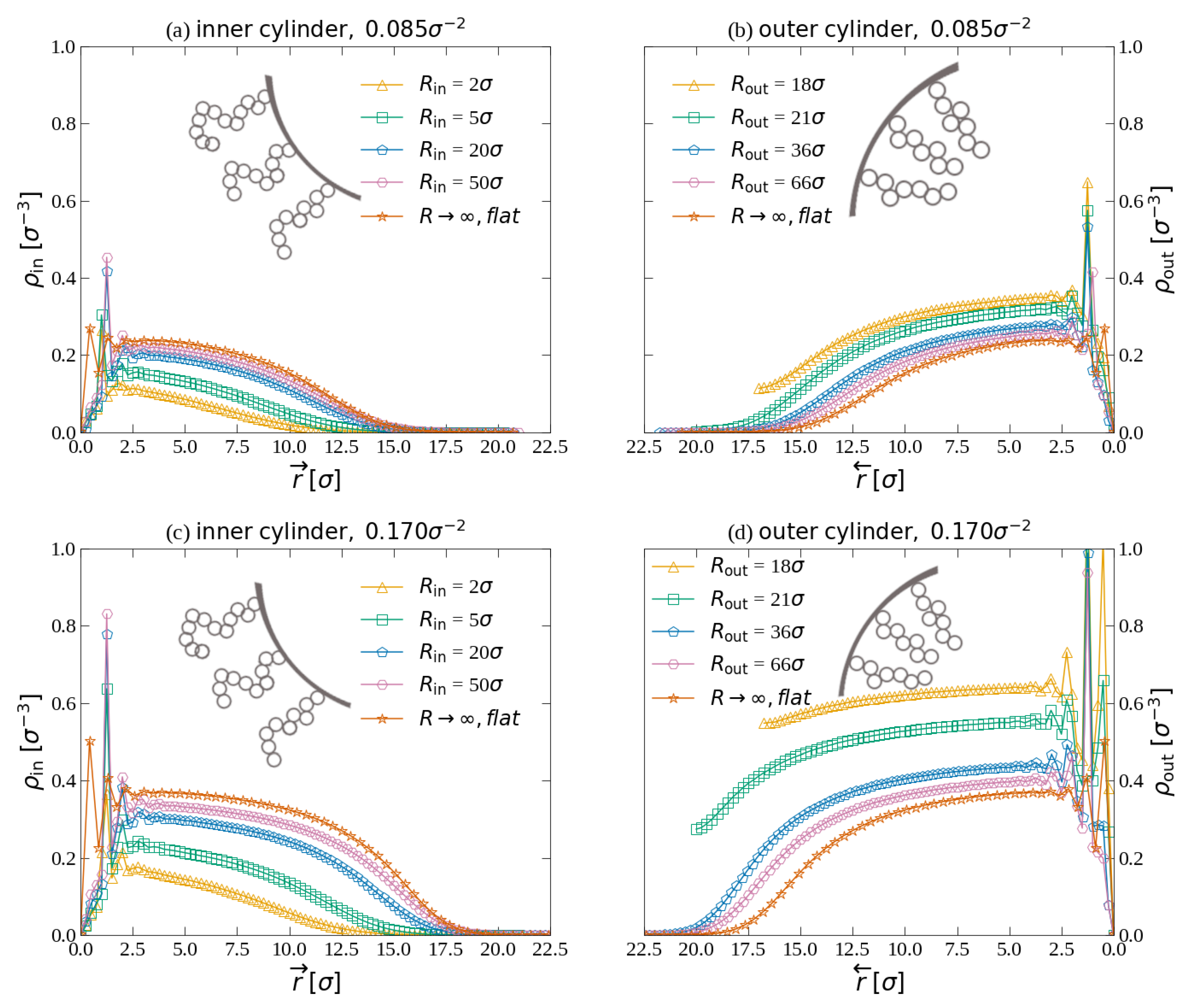
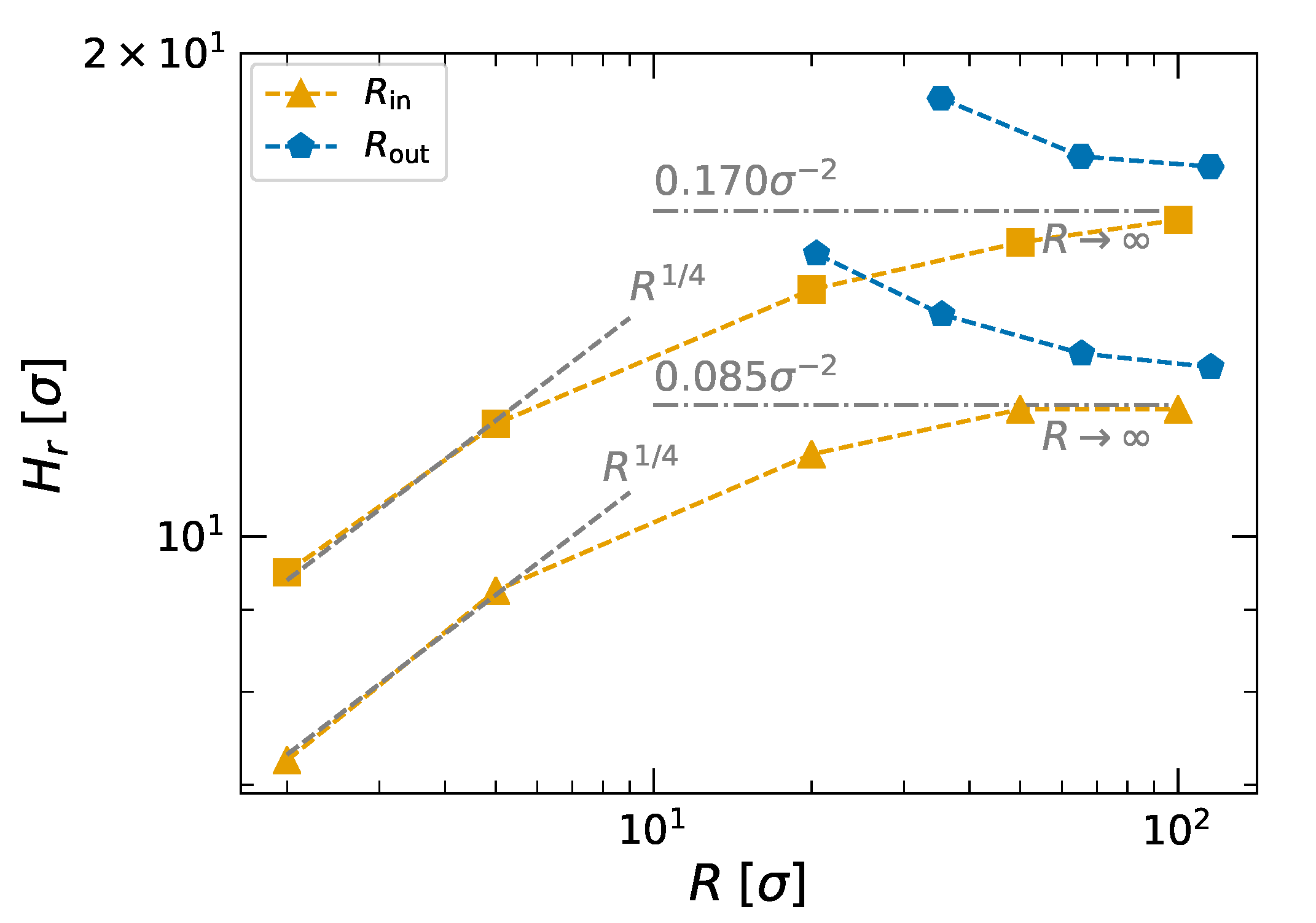
3.1.1. Brushes on Individual Cylinders
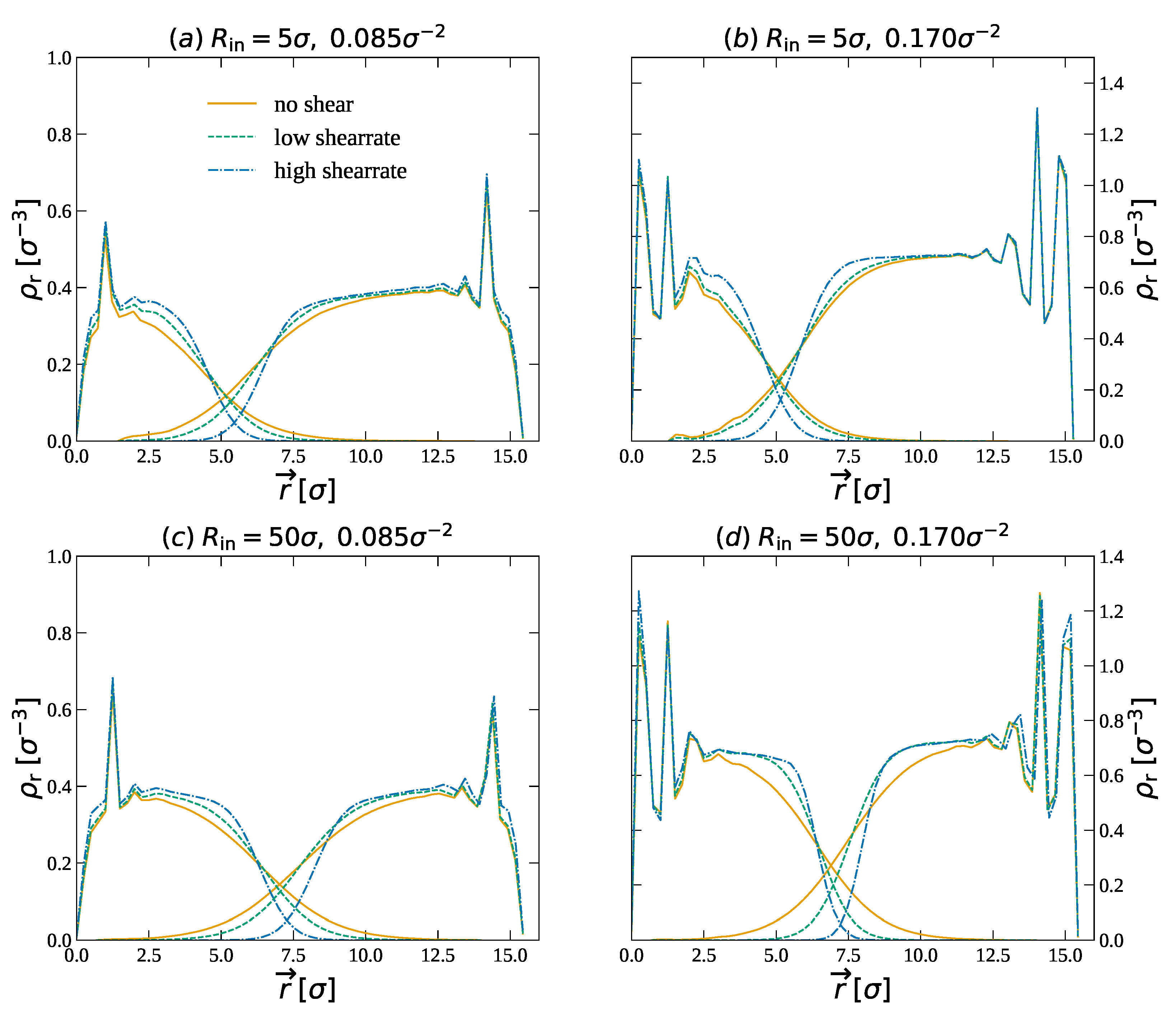
3.1.2. Bilayer Brushes between Two Cylinders
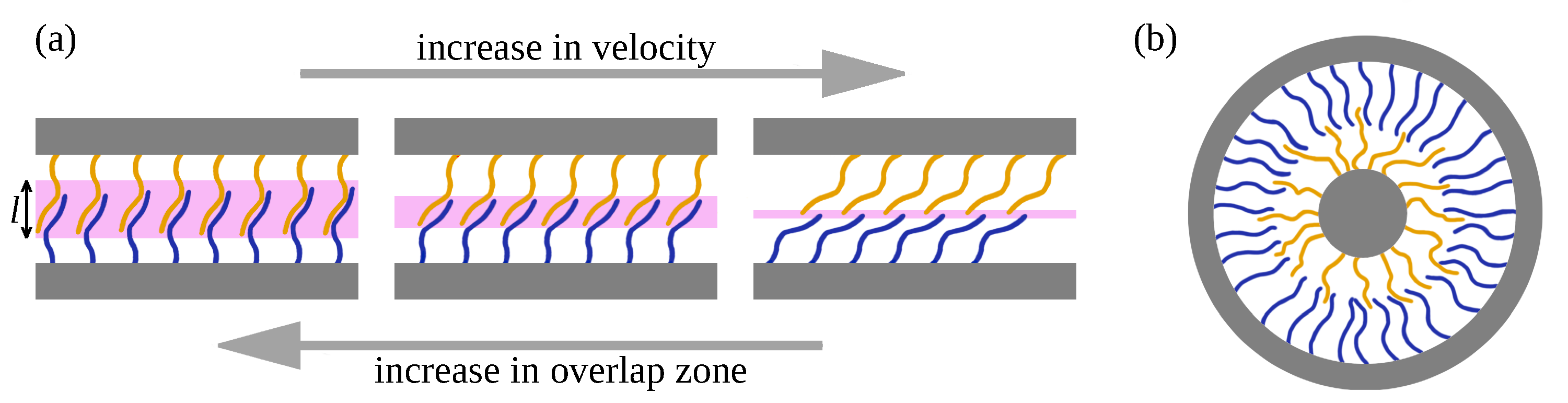
3.1.3. Bilayer Brushes between Two Cylinders in Relative Motion
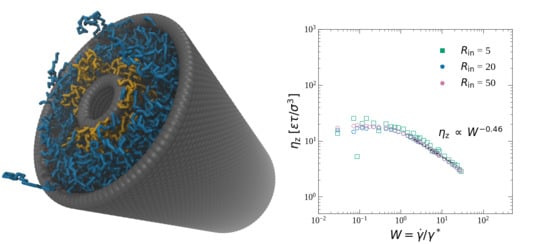
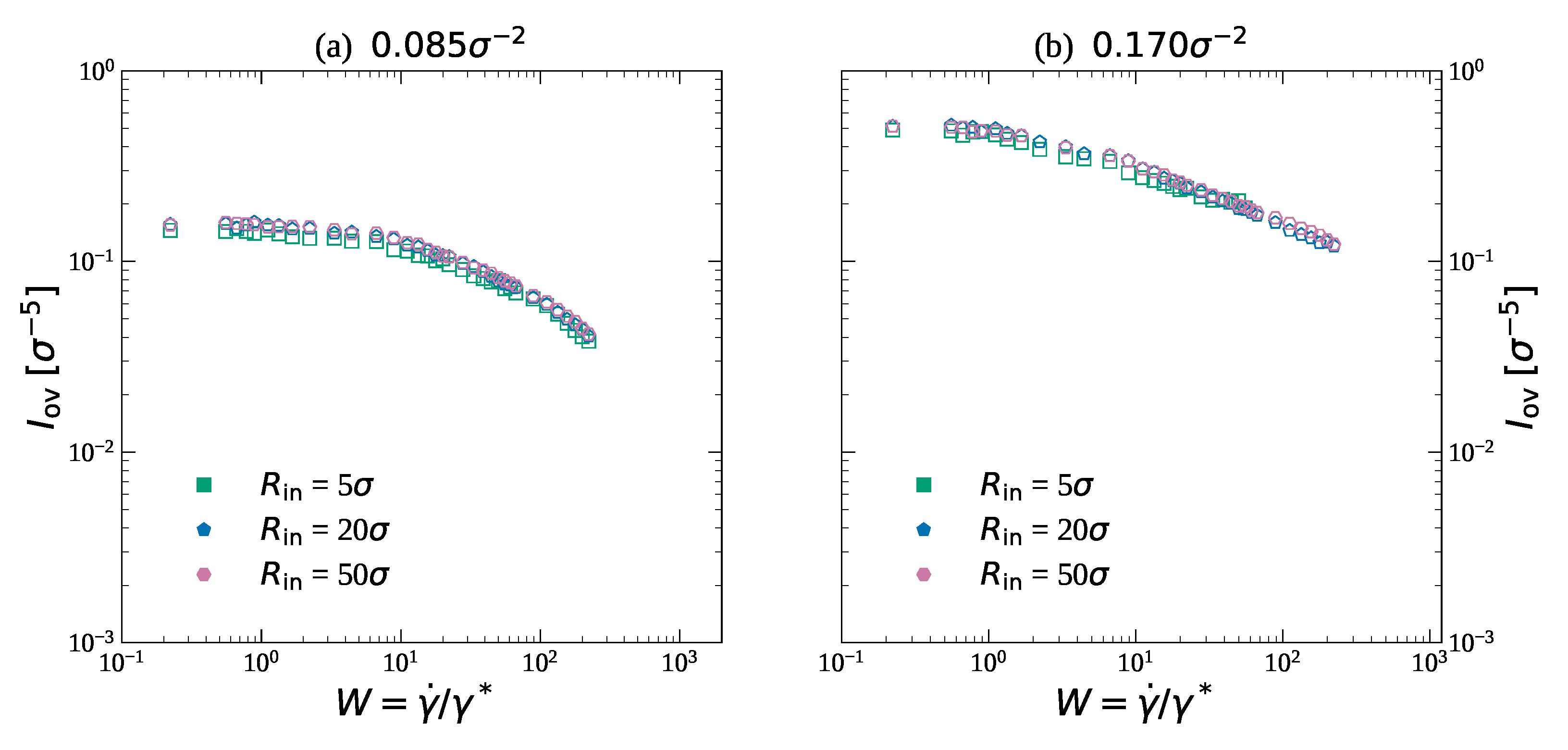
3.2. Friction and Effective Viscosity
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lee, S.; Spencer, N.D. Sweet, hairy, soft, and slippery. Science 2008, 319, 575. [Google Scholar] [PubMed]
- Jahn, S.; Seror, J.; Klein, J. Lubrication of Articular Cartilage. Annu. Rev. Biomed. Eng. 2016, 18, 235–258. [Google Scholar] [PubMed]
- Klein, J. Repair or Replacement—A Joint Perspective. Science 2009, 323, 47. [Google Scholar] [CrossRef] [PubMed]
- Klein, J.; Kumacheva, E.; Mahalu, D.; Perahia, D.; Fetters, L.J. Reduction of frictional forces between solid surfaces bearing polymer brushes. Nature 1994, 370, 634. [Google Scholar]
- Zhang, Z.; Moxey, M.; Alswieleh, A.; Morse, A.J.; Lewis, A.L.; Geoghegan, M.; Leggett, G.J. Effect of salt on phosphorylcholine-based zwitterionic polymer brushes. Langmuir 2016, 32, 5048–5057. [Google Scholar] [PubMed]
- Yu, Y.; Yao, Y.; van Lin, S.; de Beer, S. Specific anion effects on the hydration and tribological properties of zwitterionic phosphorylcholine-based brushes. Eur. Polym. J. 2019, 112, 222–227. [Google Scholar]
- Bielecki, R.M.; Crobu, M.; Spencer, N.D. Polymer-Brush Lubrication in Oil: Sliding Beyond the Stribeck Curve. Tribol. Lett. 2013, 49, 263–272. [Google Scholar]
- Milner, S.T. Polymer brushes. Science 1991, 251, 905. [Google Scholar]
- Benetti, E.M.; Divandari, M.; Ramakrishna, S.N.; Morgese, G.; Yan, W.; Trachsel, L. Loops and Cycles at Surfaces: The Unique Properties of Topological Polymer Brushes. Chem. Eur. J. 2017, 23, 12433. [Google Scholar]
- Espinosa-Marzal, R.M.; Bielecki, R.M.; Spencer, N.D. Understanding the role of viscous solvent confinement in the tribological behaviour of polymer brushes: A bioinspired approach. Soft Matter 2013, 9, 10572. [Google Scholar]
- Chen, M.; Briscoe, W.H.; Armes, S.P.; Klein, J. Lubrication at Physiological Pressures by Polyzwitterionic Brushes. Science 2009, 323, 1698–1701. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Loureiro, I.; Scoppola, E.; Bertinetti, L.; Barbetta, A.; Fragneto, G.; Schneck, E. Neutron reflectometry yields distance-dependent structures of nanometric polymer brushes interacting across water. Soft Matter 2017, 13, 5767–5777. [Google Scholar] [CrossRef] [PubMed]
- Micciulla, S.; Gerelli, Y.; Campbell, R.A.; Schneck, E. A Versatile Method for the Distance-Dependent Structural Characterization of Interacting Soft Interfaces by Neutron Reflectometry. Langmuir 2018, 34, 789–800. [Google Scholar] [CrossRef] [PubMed]
- De Beer, S.; Kutnyanszky, E.; Schön, P.M.; Vancso, G.J.; Müser, M.H. Solvent induced immiscibility of polymer brushes eliminates dissipation channels. Nat. Commun. 2014, 5, 3781. [Google Scholar] [PubMed]
- Abbott, S.B.; de Vos, W.M.; Mears, L.L.E.; Skoda, M.; Dalgliesh, R.; Edmondson, S.; Richardson, R.M.; Prescott, S.W. Switching the Interpenetration of Confined Asymmetric Polymer Brushes. Macromolecules 2016, 49, 4349–4357. [Google Scholar] [CrossRef]
- De Beer, S. Switchable Friction Using Contacts of Stimulus-Responsive and Nonresponding Swollen Polymer Brushes. Langmuir 2014, 30, 8085–8090. [Google Scholar] [PubMed]
- Grest, G.S. Interfacial sliding of polymer brushes: A molecular dynamics simulation. Phys. Rev. Lett. 1996, 76, 4979. [Google Scholar]
- Kreer, T.; Müser, M.H.; Binder, K.; Klein, J. Frictional drag mechanisms between polymer-bearing surfaces. Langmuir 2001, 17, 7804. [Google Scholar]
- Kreer, T.; Binder, K.; Müser, M.H. Friction between polymer brushes in good solvent conditions: steady-state sliding versus transient behavior. Langmuir 2003, 19, 7551. [Google Scholar] [CrossRef]
- Carrillo, J.M.Y.; Brown, W.M.; Dobrynin, A.V. Explicit Solvent Simulations of Friction between Brush Layers of Charged and Neutral Bottle-Brush Macromolecules. Macromolecules 2012, 45, 8880–8891. [Google Scholar] [CrossRef]
- Ou, Y.; Sokoloff, J.B.; Stevens, M.J. Comparison of the kinetic friction of planar neutral and polyelectrolyte polymer brushes using molecular dynamics simulations. Phys. Rev. E 2012, 85, 011801. [Google Scholar]
- Goujon, F.; Ghoufi, A.; Malfreyt, P.; Tildesley, D.J. The kinetc friction coefficient of neutral and charged polymer brushes. Soft Matter 2013, 9, 2966. [Google Scholar]
- Singh, M.K.; Ilg, P.; Espinosa-Marzal, R.M.; Kröger, M.; Spencer, N.D. Polymer Brushes under Shear: Molecular Dynamics Simulations Compared to Experiments. Langmuir 2015, 31, 4798–4805. [Google Scholar] [CrossRef]
- Goicochea, A.G.; López-Esparza, R.; Altamirano, M.B.; Rivera-Paz, E.; Waldo-Mendoza, M.; Pérez, E. Friction coefficient and viscosity of polymer brushes with and without free polymers as slip agents. J. Mol. Liquids 2016, 219, 368–376. [Google Scholar] [CrossRef]
- Singh, M.K.; Ilg, P.; Espinosa-Marzal, R.M.; Spencer, N.D.; Kröger, M. Influence of Chain Stiffness, Grafting Density and Normal Load on the Tribological and Structural Behavior of Polymer Brushes: A Nonequilibrium-Molecular-Dynamics Study. Polymers 2016, 8, 254. [Google Scholar] [CrossRef]
- Desai, P.R.; Sinha, S.; Das, S. Polyelectrolyte brush bilayers in weak interpenetration regime: Scaling theory and molecular dynamics simulations. Phys. Rev. E 2018, 97, 032503. [Google Scholar] [CrossRef]
- Galuschko, A.; Spirin, L.; Kreer, T.; Johner, A.; Pastorino, C.; Wittmer, J.; Baschnagel, J. Frictional forces between strongly compressed, nonentangled polymer brushes: molecular dynamics simulations and scaling theory. Langmuir 2010, 26, 6418. [Google Scholar]
- Spirin, L.; Galuschko, A.; Kreer, T.; Johner, A.; Baschnagel, J.; Binder, K. Polymer brush lubrication in the limit of strong compression. Eur. Phys. J. E 2010, 33, 307. [Google Scholar]
- Binder, K.; Kreer, T.; Milchev, A. Polymer brushes under flow and in other out-of-equilibrium conditions. Soft Matter 2011, 7, 7159. [Google Scholar]
- De Beer, S.; Müser, M.H. Friction in (Im-) Miscible Polymer Brush Systems and the Role of Transverse Polymer Tilting. Macromolecules 2014, 47, 7666. [Google Scholar] [CrossRef]
- Kreer, T. Polymer-brush lubrication: A review of recent theoretical advances. Soft Matter 2016, 12, 3479. [Google Scholar]
- Desai, P.R.; Das, S. Lubrication in polymer-brush bilayers in the weak interpenetration regime: Molecular dynamics simulations and scaling theories. Phys. Rev. E 2018, 98, 022503. [Google Scholar] [CrossRef]
- Neratova, I.V.; Kreer, T.; Sommer, J.U. Translocation of Molecules with Different Architectures through a Brush-Covered Microchannel. Macromolecules 2015, 48, 3756–3766. [Google Scholar] [CrossRef]
- Binder, K.; Milchev, A. Polymer brushes on flat and curved surfaces: How computer simulations can help to test theories and interpret experiments. J. Polym. Sci. Part B Polym. Phys. 2012, 50, 1515. [Google Scholar]
- Milner, S.T.; Witten, T.A.; Cates, M.E. Theory of the grafted polymer brush. Macromolecules 1988, 21, 2610. [Google Scholar] [CrossRef]
- Skvortsov, A.M.; Gorbunov, A.A.; Pawlushkov, I.V.; Zhulina, Y.B.; Borisov, O.V.; Pryamitsyn, V.A. Structure of densely grafted polymeric monolayers. Polym. Sci. USSR 1988, 30, 1706–1715. [Google Scholar] [CrossRef]
- Murat, M.; Grest, G.S. Polymers end-grafted onto a cylindrical surface. Macromolecules 1991, 24, 704. [Google Scholar]
- Wijmans, C.M.; Zhulina, E.B. Polymer brushes at curved surfaces. Macromolecules 1993, 26, 7214–7224. [Google Scholar] [CrossRef]
- Dimitrov, D.I.; Milchev, A.; Binder, K.; Heermann, D.W. Structure of Polymer Brushes in Cylindrical Tubes: A Molecular Dynamics Simulation. Macromol. Theory Simul. 2006, 15, 573–583. [Google Scholar] [CrossRef]
- Dimitrov, D.I.; Milchev, A.; Binder, K. Polymer brushes in cylindrical pores: Simulation versus scaling theory. J. Chem. Phys. 2006, 125, 034905. [Google Scholar] [CrossRef]
- Li, C.W.; Merlitz, H.; Wu, C.X.; Sommer, J.U. Nanopores as Switchable Gates for Nanoparticles: A Molecular Dynamics Study. Macromolecules 2018, 51, 6238–6247. [Google Scholar] [CrossRef]
- Grest, G.S.; Kremer, K. Molecular dynamics simulation for polymers in the presence of a heat bath. Phys. Rev. A 1986, 33, 3628. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD - Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: a molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057. [Google Scholar]
- Brittain, W.J.; Minko, S. A Structural Definition of Polymer Brushes. Polym. Sci. Part A Polym. Chem. 2007, 45, 3505. [Google Scholar] [CrossRef]
- Descas, R.; Sommer, J.U.; Blumen, A. Grafted polymer chains interacting with substrates: Computer simulations and scaling. Macromol. Theory Simul. 2008, 17, 429. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1. [Google Scholar] [CrossRef]
- Pastorino, C.; Kreer, T.; Müller, M.; Binder, K. Comparison of dissipative particle dynamics and Langevin thermostats for out-of-equilibrium simulations of polymeric systems. Phys. Rev. E 2007, 76, 026706. [Google Scholar]
- The LAMMPS Datafiles and Inputfiles Are Available Free of Charge at. Available online: https://doi.org/10.4121/uuid:7d4fb6a6-14e7-4573-b08e-ae75183a1f9b (accessed on 5 September 2019).
- Grest, G.S.; Murat, M. Structure of grafted polymeric brushes in solvents of varying quality: a molecular dynamics study. Macromolecules 1993, 26, 3108–3117. [Google Scholar] [CrossRef]
- Dimitrov, D.I.; Milchev, A.; Binder, K. Polymer brushes in solvents of variable quality: Molecular dynamics simulations using explicit solvent. J. Chem. Phys. 2007, 127, 084905. [Google Scholar] [CrossRef]
- De Beer, S.; Mensink, L.I.S.; Kieviet, B.D. Geometry-Dependent Insertion Forces on Particles in Swollen Polymer Brushes. Macromolecules 2016, 49, 1070–1078. [Google Scholar] [CrossRef]
- Ball, R.C.; Marko, J.F.; Milner, S.T.; Witten, T.A. Polymers grafted to a convex surface. Macromolecules 1991, 24, 693–703. [Google Scholar] [CrossRef]
- Semenov, A.N. Contribution to the theory of microphase layering in block-copolymer melts. Sov. Phys. JETP 1985, 61, 733–742. [Google Scholar]
- Wittmer, J.; Johner, A.; Joanny, J.F.; Binder, K. Chain desorption from a semidilute polymer brush: A Monte Carlo simulation. J. Chem. Phys. 1994, 101, 4379–4390. [Google Scholar] [CrossRef]
- Kim, J.U.; Matsen, M.W. Finite-stretching corrections to the Milner-Witten-Cates theory for polymer brushes. Eur. Phys. J. E 2007, 23, 135–144. [Google Scholar] [CrossRef] [PubMed]
- Birshtein, T.; Borisov, O.; Zhulina, Y.; Khokhlov, A.; Yurasova, T. Conformations of comb-like macromolecules. Polym. Sci. USSR 1987, 29, 1293–1300. [Google Scholar] [CrossRef]
- Coluzza, I.; Hansen, J.P. Transition from Highly to Fully Stretched Polymer Brushes in Good Solvent. Phys. Rev. Lett. 2008, 100, 016104. [Google Scholar] [CrossRef]
- Elliott, I.G.; Kuhl, T.L.; Faller, R. Molecular Simulation Study of the Structure of High Density Polymer Brushes in Good Solvent. Macromolecules 2010, 43, 9131–9138. [Google Scholar] [CrossRef]
- Quintana, R.; Gosa, M.; Janczewski, D.; Kutnyanszky, E.; Vancso, G.J. Enhanced Stability of Low Fouling Zwitterionic Polymer Brushes in Seawater with Diblock Architecture. Langmuir 2013, 29, 10859. [Google Scholar]
- Yu, Y.; Vancso, G.J.; de Beer, S. Substantially enhanced stability against degrafting of zwitterionic PMPC brushes by utilizing PGMA-linked initiators. Eur. Polym. J. 2017, 89, 221–229. [Google Scholar]
- Klein, J. Shear, friction and lubrication forces between polymer-bearing surfaces. Annu. Rev. Mater. Sci. 1996, 26, 581. [Google Scholar]
- Witten, T.A.; Leibner, L.; Pincus, P.A. Stress relaxation in the lamellar copolymer mesophase. Macromolecules 1990, 23, 824. [Google Scholar]

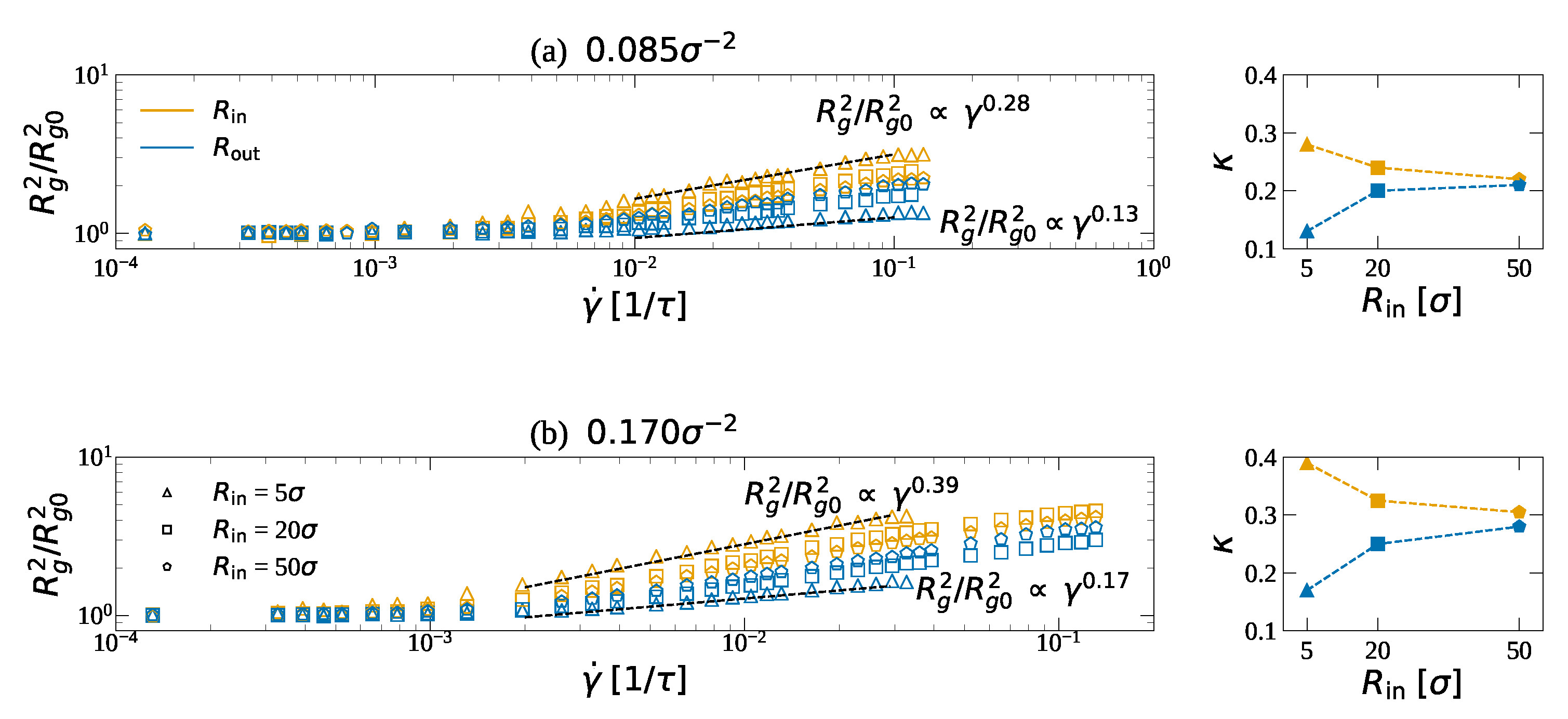
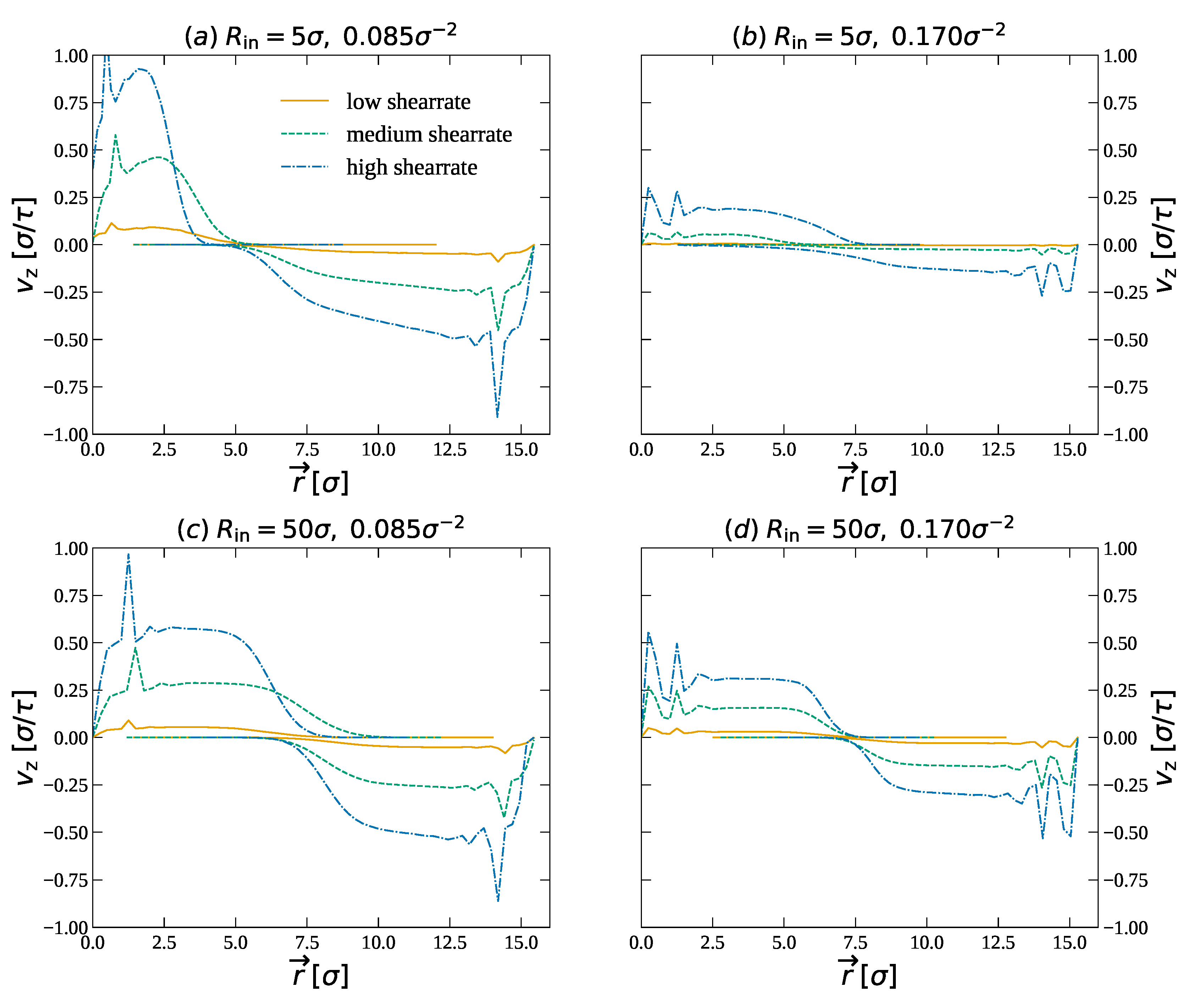

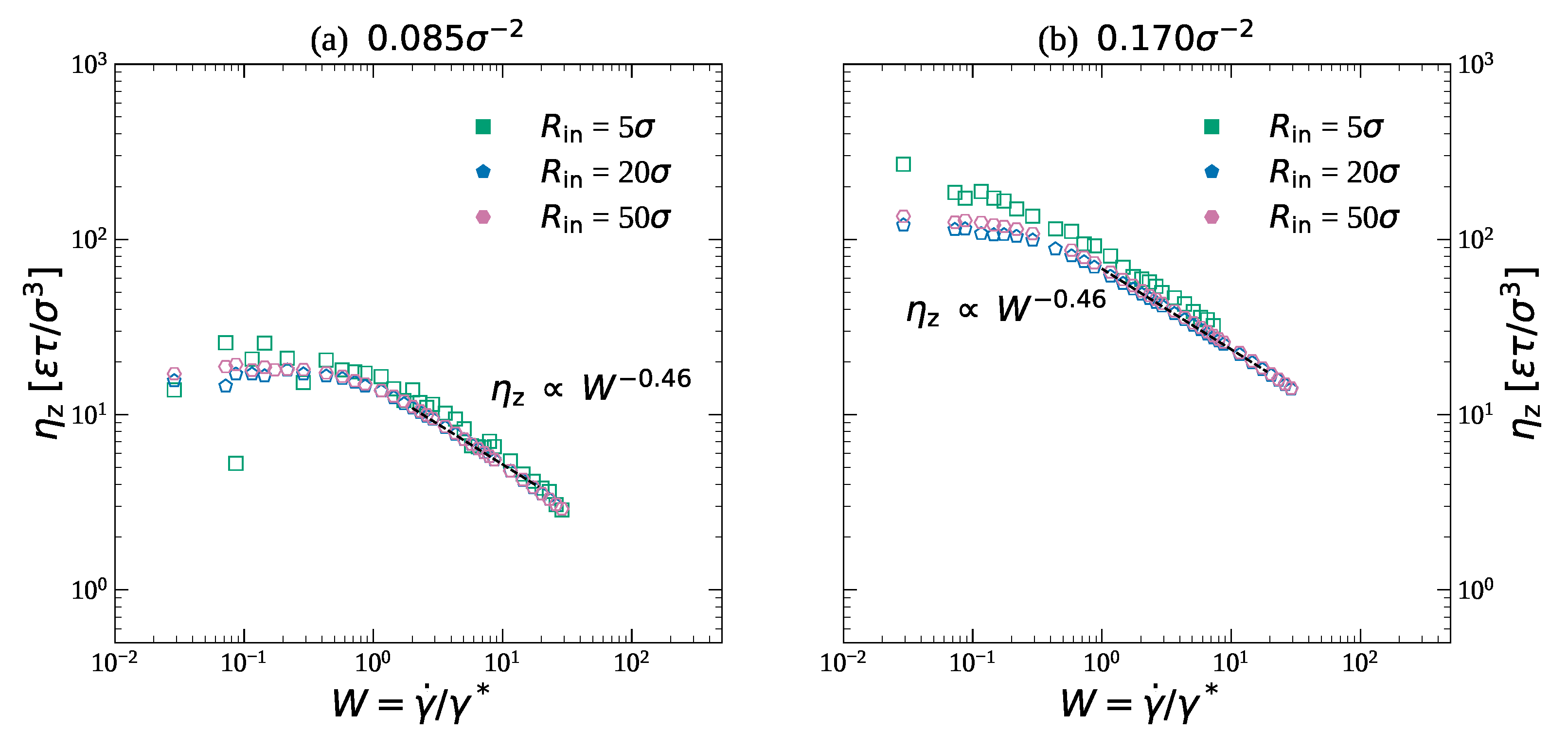
| System | D | |||
|---|---|---|---|---|
| 1 | 2.3 2 | 17.76 | 15.44 | 0.085 |
| 2 | 5.40 | 20.84 | 15.44 | 0.085 |
| 3 | 20.07 | 35.51 | 15.44 | 0.085 |
| 4 | 50.18 | 65.62 | 15.44 | 0.085 |
| 5 | 2.18 | 17.47 | 15.29 | 0.170 |
| 6 | 5.46 | 20.75 | 15.29 | 0.170 |
| 7 | 20.20 | 35.49 | 15.29 | 0.170 |
| 8 | 50.22 | 65.51 | 15.29 | 0.170 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
van der Weg, K.J.; Ritsema van Eck, G.C.; de Beer, S. Polymer Brush Friction in Cylindrical Geometries. Lubricants 2019, 7, 84. https://doi.org/10.3390/lubricants7100084
van der Weg KJ, Ritsema van Eck GC, de Beer S. Polymer Brush Friction in Cylindrical Geometries. Lubricants. 2019; 7(10):84. https://doi.org/10.3390/lubricants7100084
Chicago/Turabian Stylevan der Weg, Karel J., Guido C. Ritsema van Eck, and Sissi de Beer. 2019. "Polymer Brush Friction in Cylindrical Geometries" Lubricants 7, no. 10: 84. https://doi.org/10.3390/lubricants7100084
APA Stylevan der Weg, K. J., Ritsema van Eck, G. C., & de Beer, S. (2019). Polymer Brush Friction in Cylindrical Geometries. Lubricants, 7(10), 84. https://doi.org/10.3390/lubricants7100084