The Influence of Surface Texturing on the Film Thickness in Starved Lubricated Parallel Sliding Contacts
Abstract
:1. Introduction
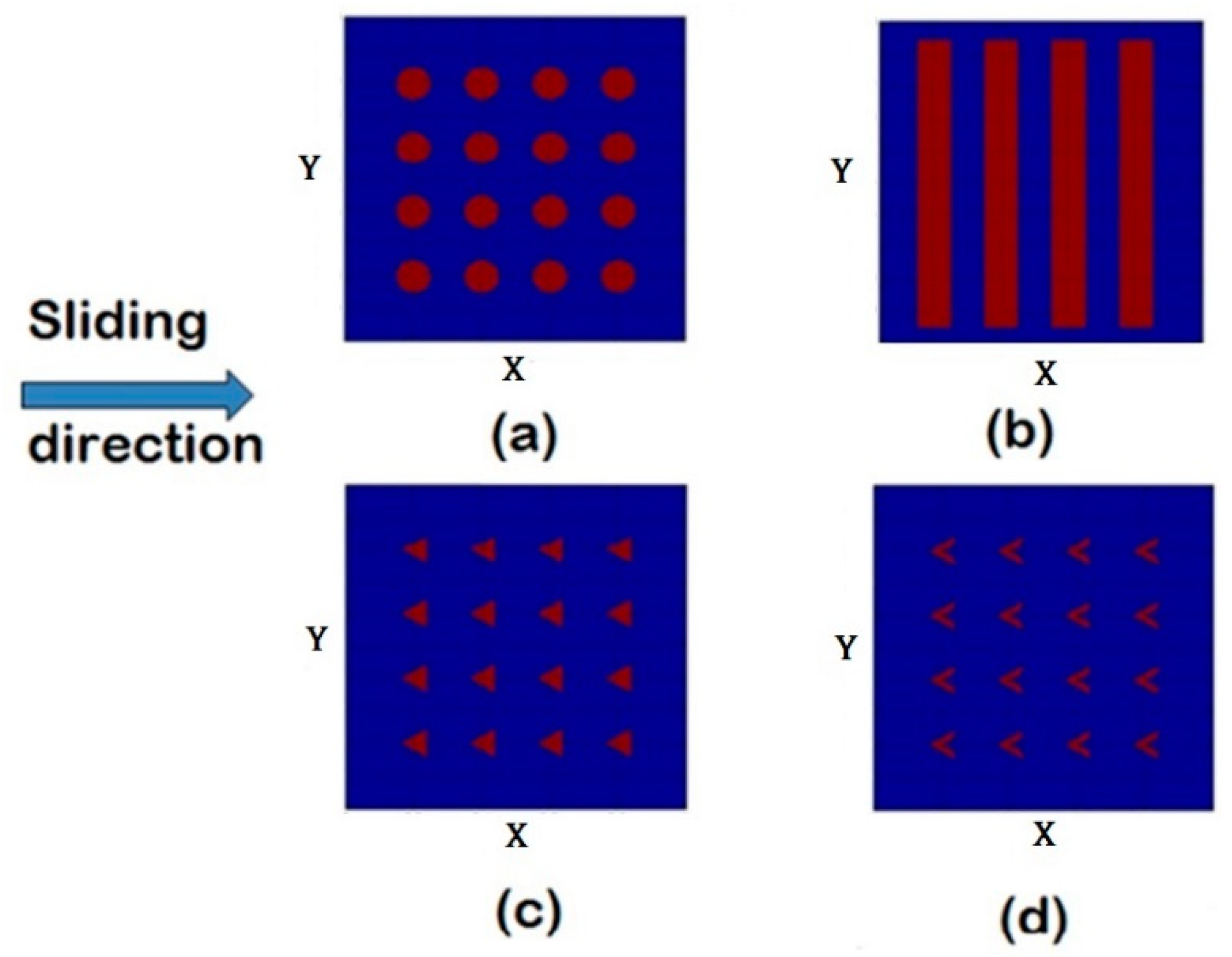
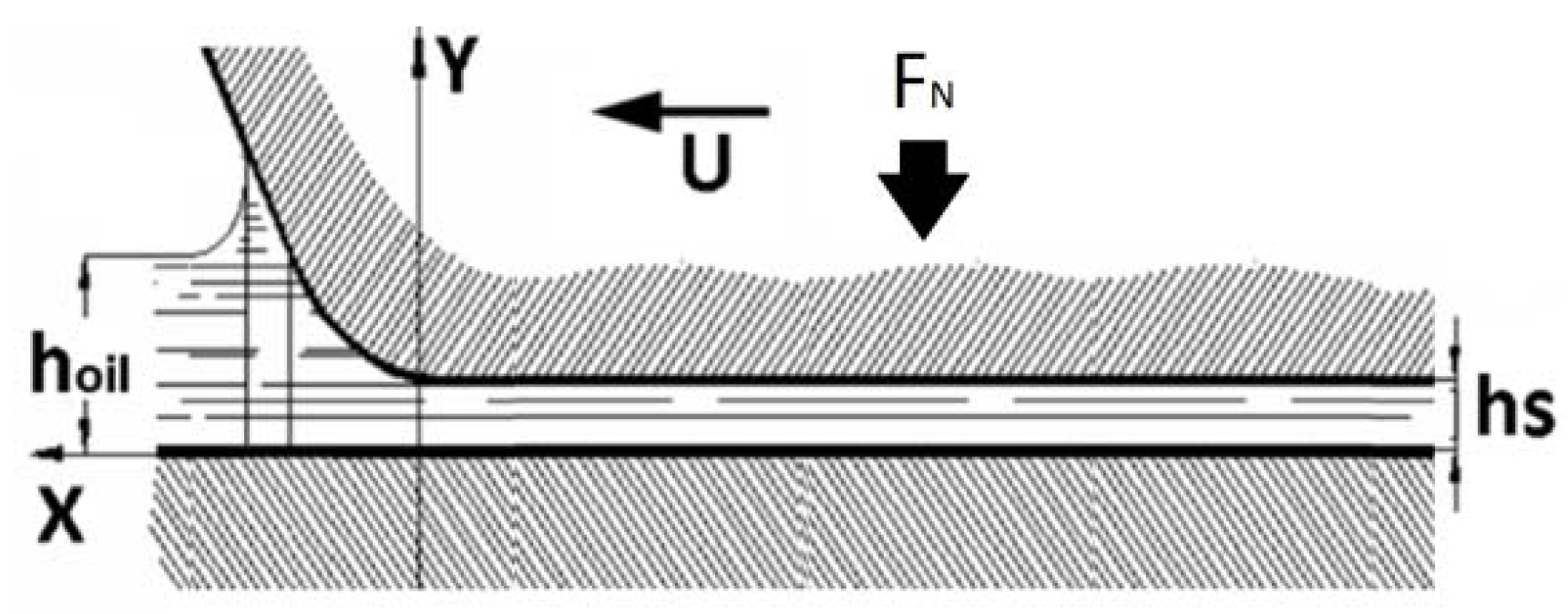
2. Materials and Methods
Mathematical Solution
3. Results
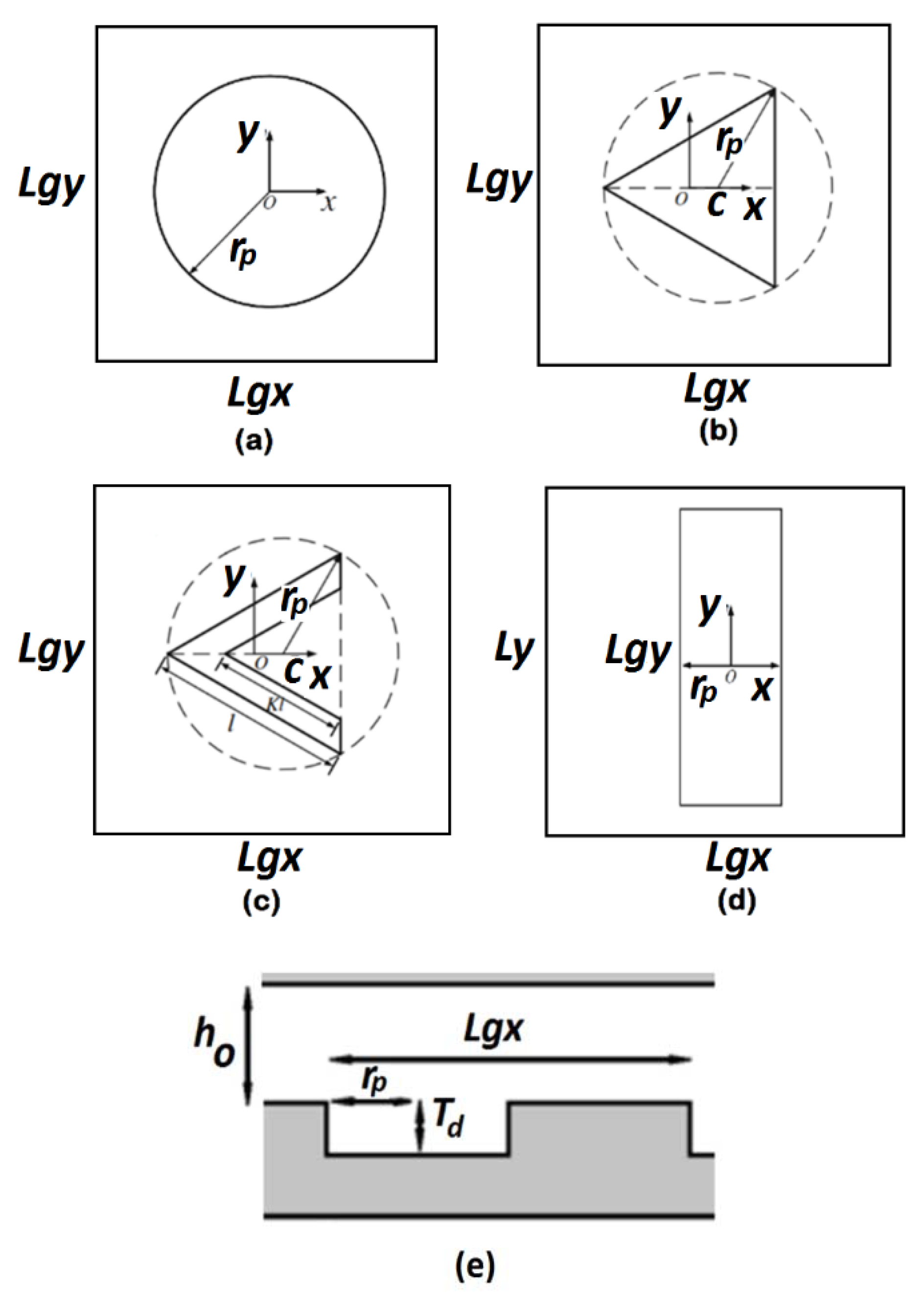
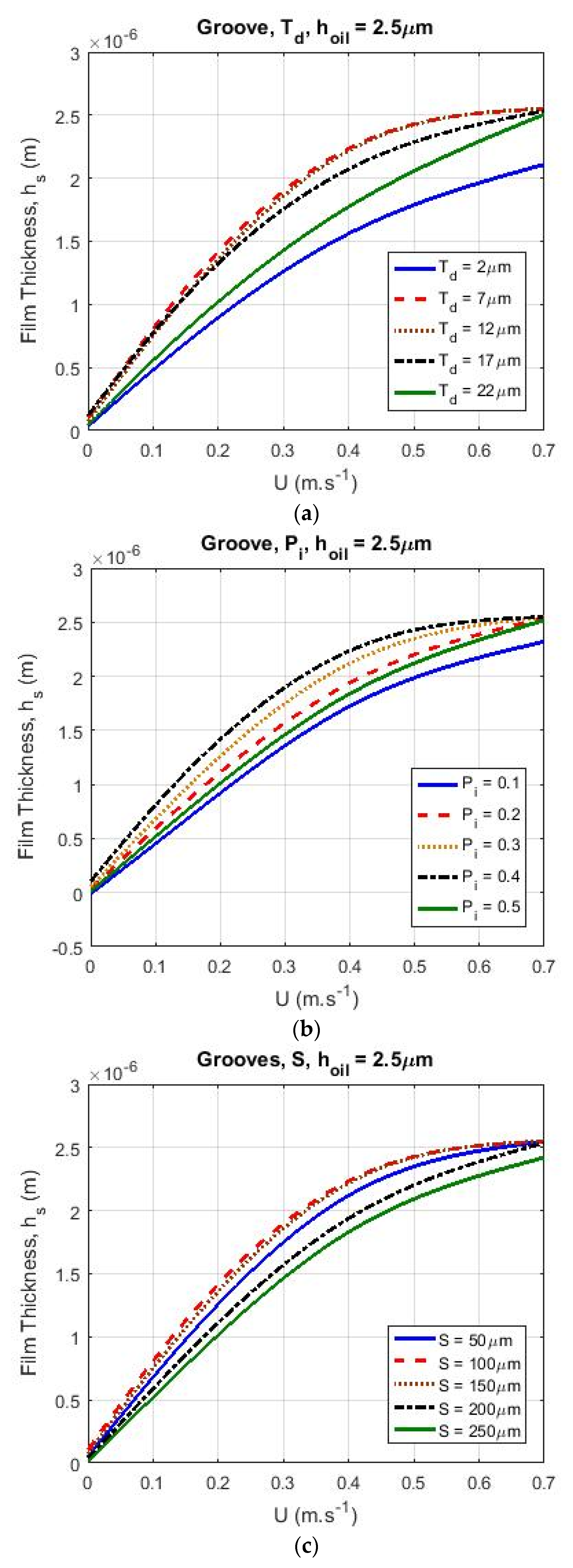
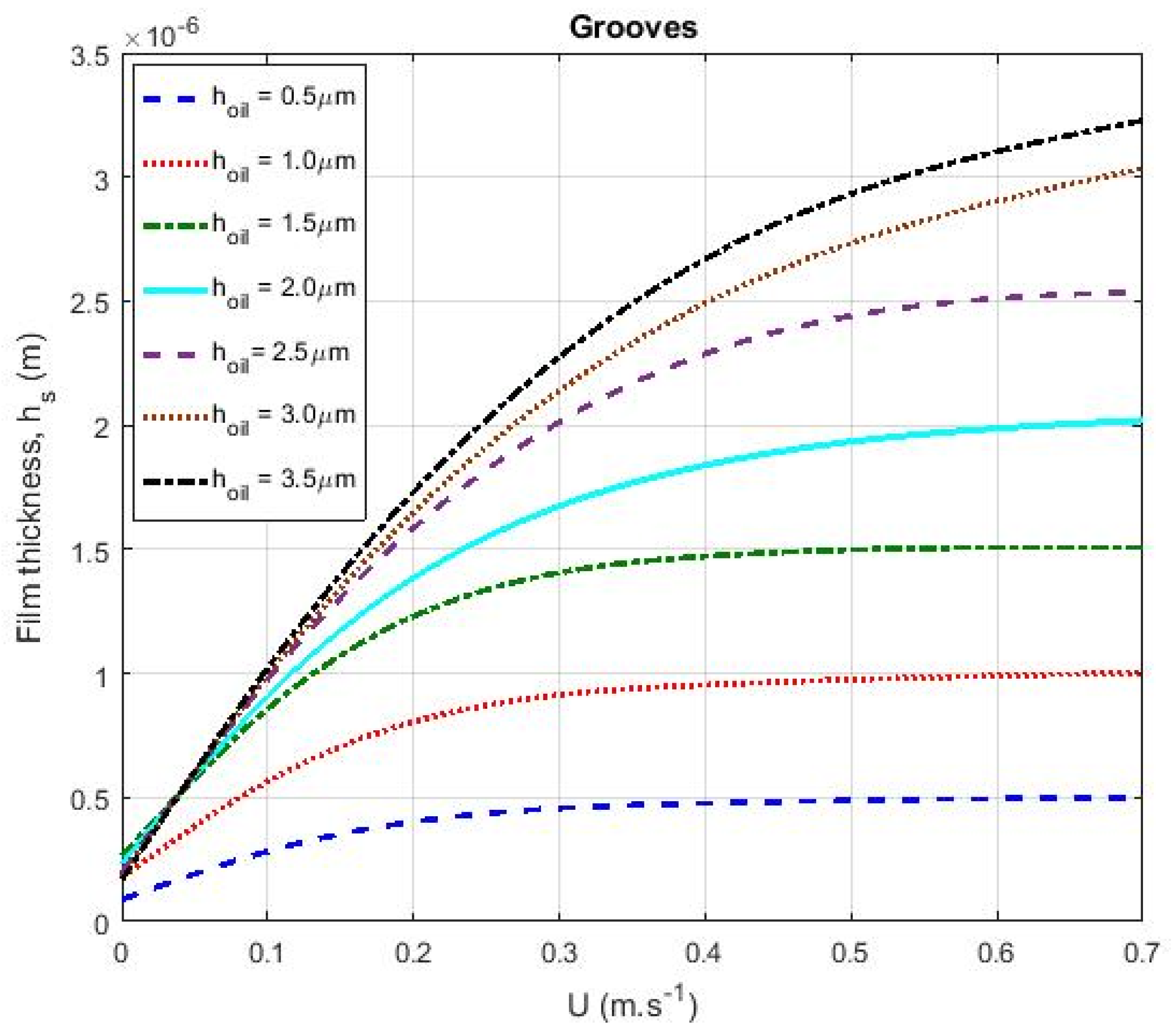
3.1. Grooves
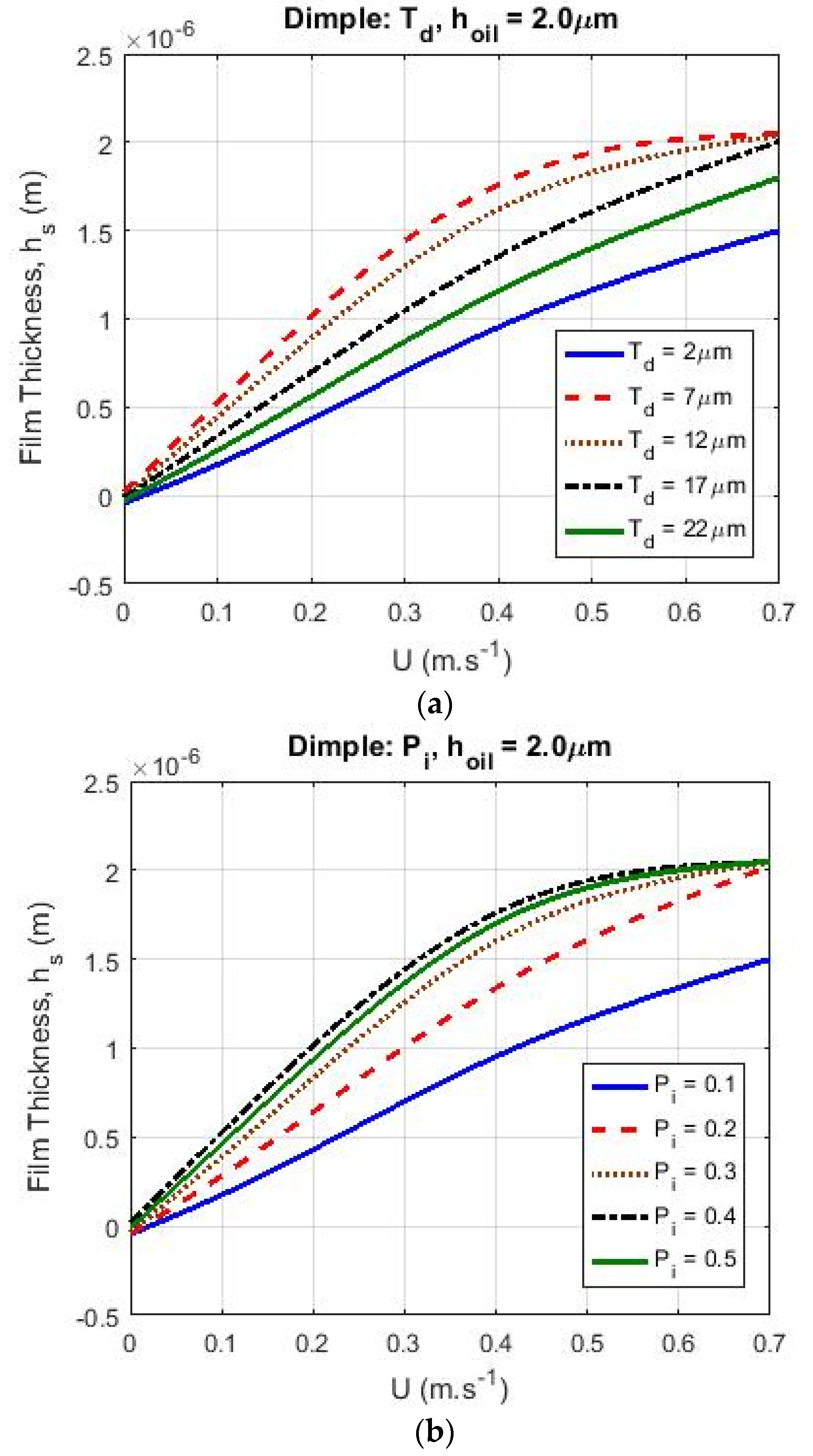
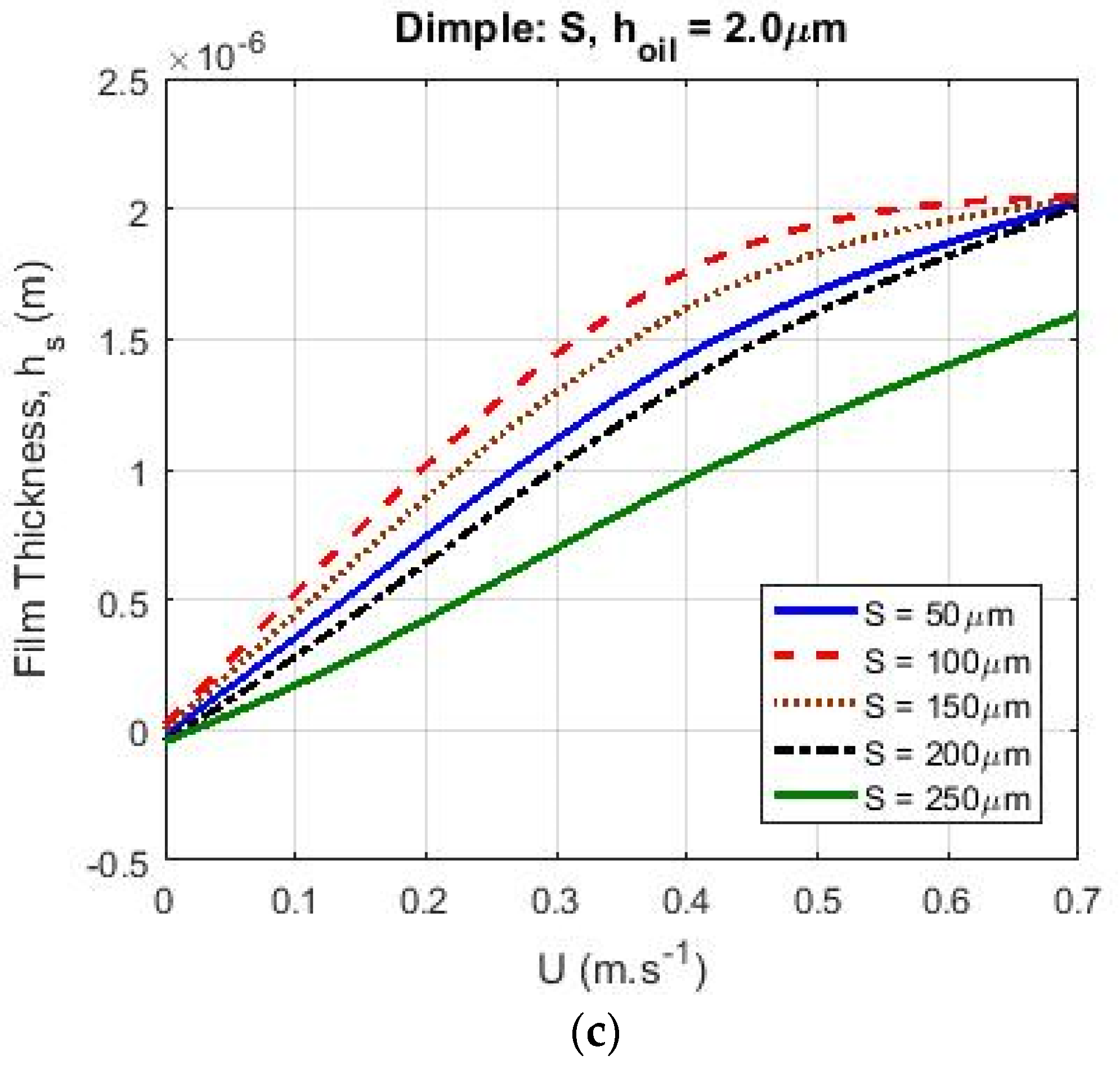
3.2. Dimples
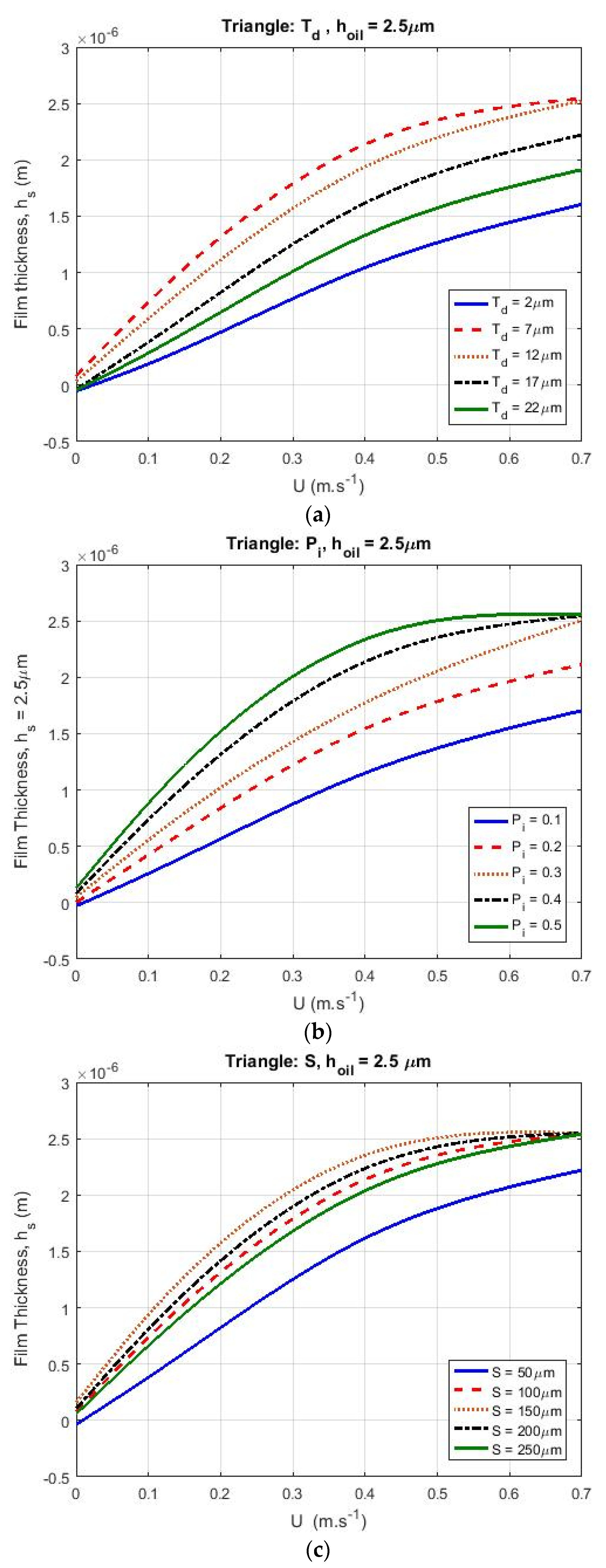
3.3. Triangular Pockets
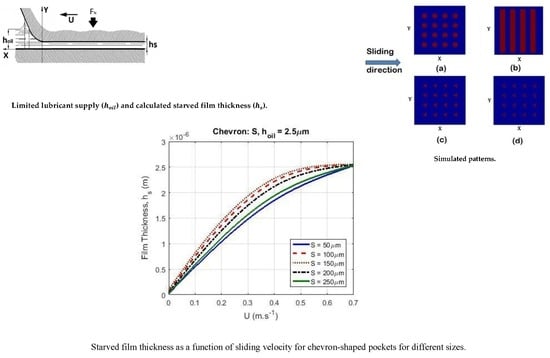
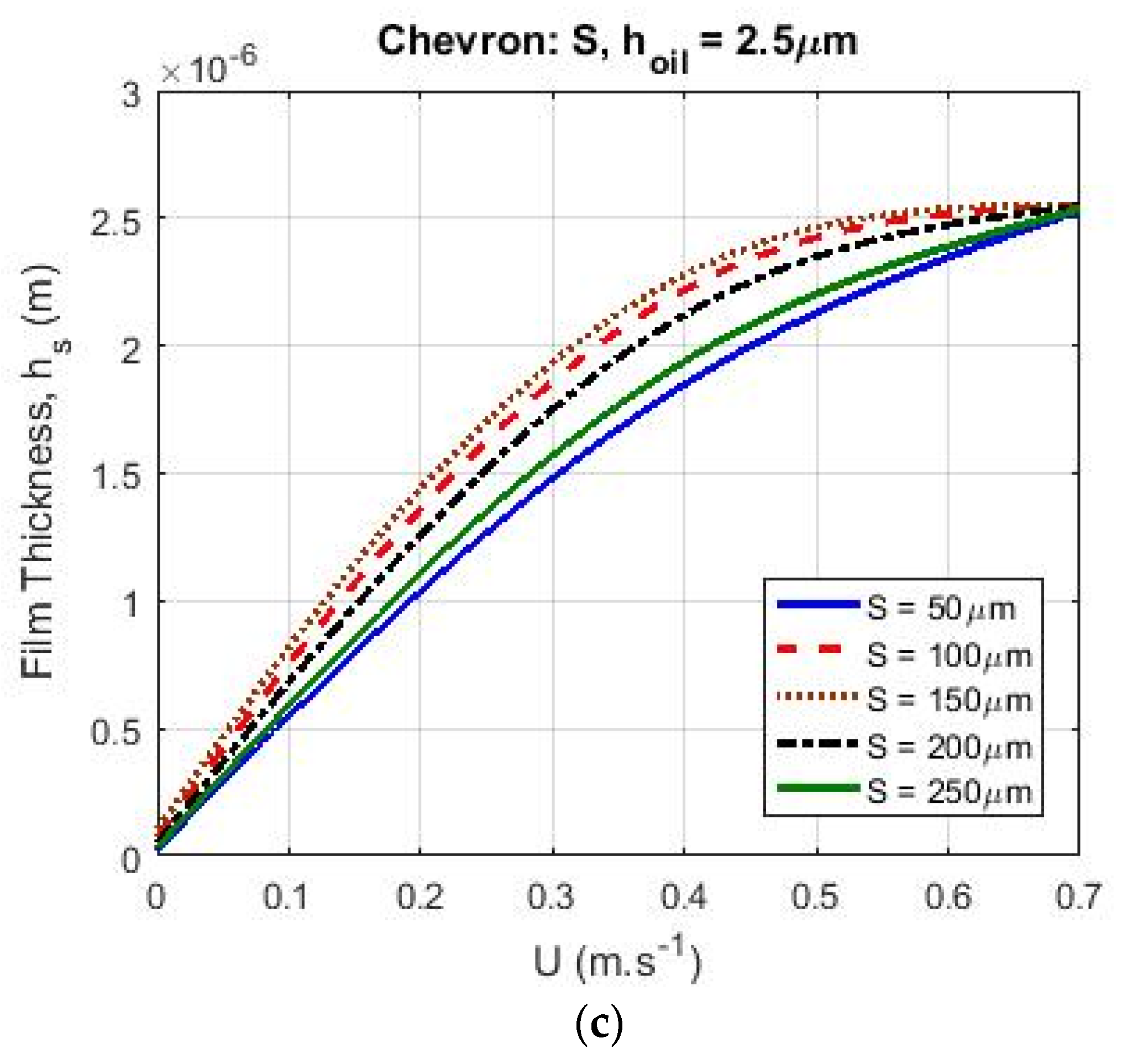
3.4. Chevrons
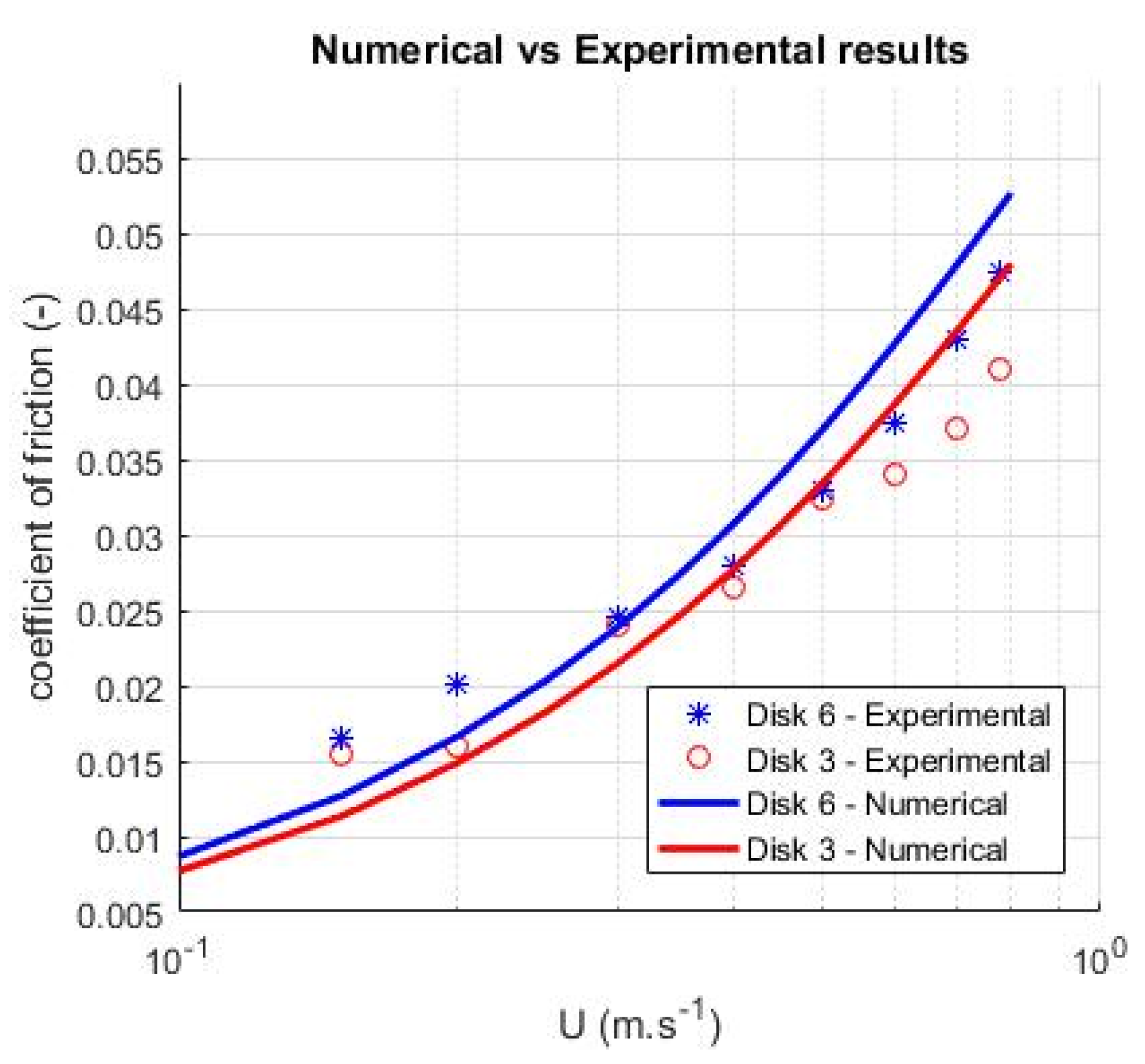
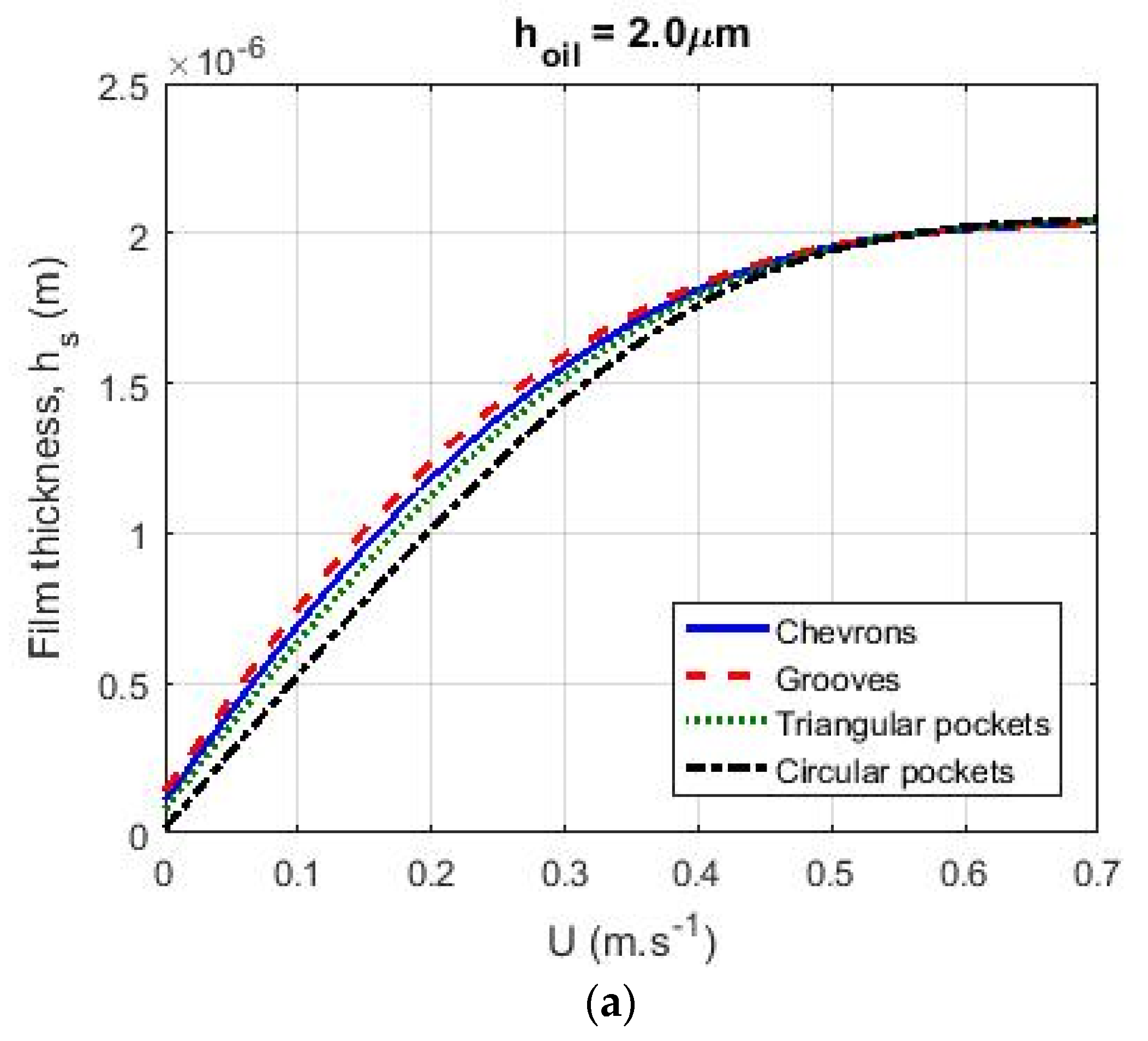
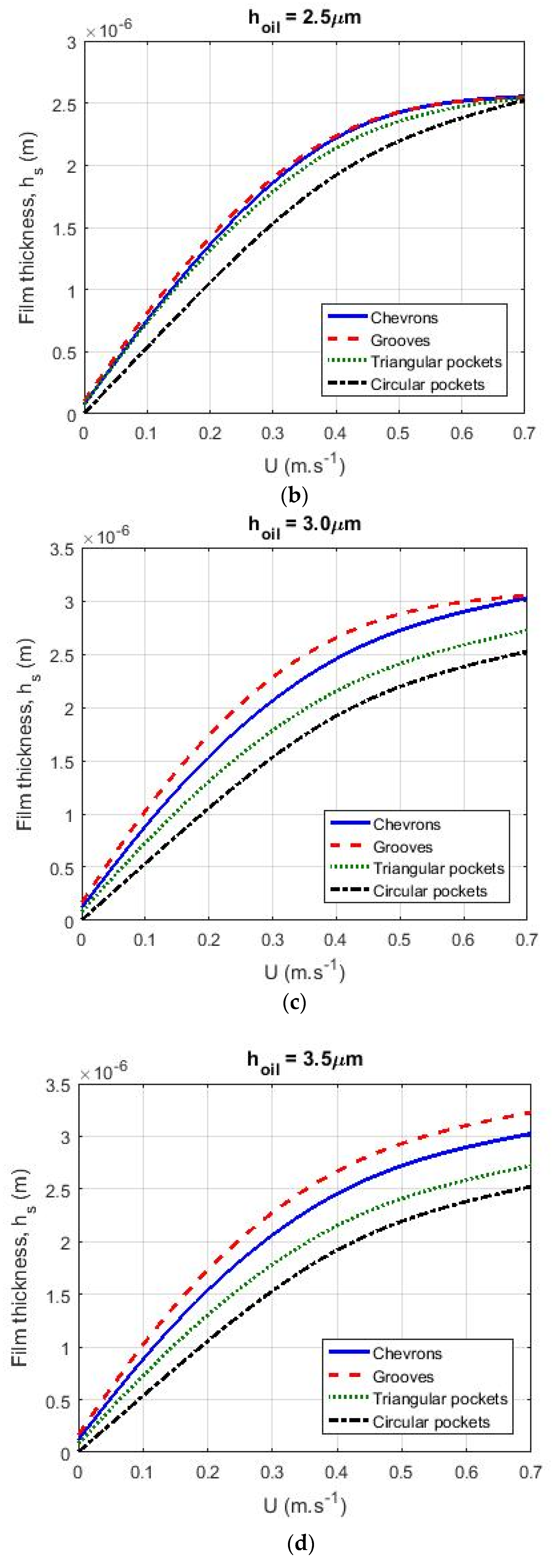
3.5. Comparison of Surface Patterns
4. Conclusions
- Of the patterns analyzed, the groove pattern showed the highest lubricant film formation due to the higher textured area fraction of the surface.
- In the case of starved lubrication, increasing the dimensions of the texture parameters (, and ) resulted in increased film thickness at low velocities. After passing the optimum value of the texture parameters for different patterns, there was a decrease in film thickness. The aforementioned effect on film thickness was visible when the surface sliding velocity was low. At high velocities when the influence of geometry and the optimization of texturing parameters are more sensible, the starvation effect exerted a greater influence on the film thickness. It is worth mentioning that this sensitivity to the texturing parameters depended on the pattern type and operational conditions for different cases. Further, at velocities higher than , the film thickness was less sensitive to texture properties.
- For different lubricant supply values , the groove pattern showed the highest film thickness at low velocities. The chevron pattern generated a larger film thickness than the triangular and circular pockets and the lowest film thickness was found for the circular pocket pattern.
- For small values of , the effect of starvation on calculated film thickness was higher. For high velocities, the generated film thickness in this case for the different patterns was the same.
- By increasing the lubricant supply (), the texturing pattern geometry had a larger influence on the generated film thickness, while starvation reduced the effect of the texture on the film thickness.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Parameters | Description | Unit |
| film thickness | ||
| contact separation | ||
| sum velocity | ||
| dimensionless pressure | - | |
| pressure | ||
| ambient pressure | ||
| geometric parameter | - | |
| dynamic viscosity | ||
| density | ||
| lubricant density in full film region | ||
| Elrod cavitation algorithm switch function | - | |
| cavitation dimensionless variable | - | |
| texture depth | ||
| cavity characteristic width | ||
| texture cell length in x & y-direction, in the case of dimples | ||
| texture cell length in the x-direction | ||
| texture cell length in the y-direction | ||
| textured area in the x-direction | ||
| textured area in the y-direction | ||
| dimensionless Cartesian coordination = | - | |
| dimensionless Cartesian coordination = | - | |
| dimensionless local depth of textured surface | - | |
| textured cavity size = | - |
References
- Glavatskih, S.B.; McCarthy, D.M.C.; Sherrington, I. Hydrodynamic performance of a thrust bearing with micropatterned pads. Tribol. Trans. 2005, 48, 492–498. [Google Scholar] [CrossRef]
- Brizmer, V.; Kligerman, Y.; Etsion, I. A laser surface textured parallel thrust bearing. Tribol. Trans. 2003, 46, 397–403. [Google Scholar] [CrossRef]
- Etsion, I. State of the Art in Laser Surface Texturing, in Advanced Tribology; Luo, J., Meng, Y., Shao, T., Zhao, Q., Eds.; Springer: Berlin, Germany, 2010; pp. 761–762. [Google Scholar]
- Etsion, I.; Burstein, L. A model for mechanical seals with regular microsurface structure. Tribol. Trans. 1996, 39, 677–683. [Google Scholar] [CrossRef]
- Etsion, I.; Halperin, G.; Brizmer, V.; Kligerman, Y. Experimental investigation of laser surface textured parallel thrust bearings. Tribol. Lett. 2004, 17, 295–300. [Google Scholar] [CrossRef]
- Etsion, I.; Kligerman, Y.; Halperin, G. Analytical and experimental investigation of laser-textured mechanical seal faces. Tribol. Trans. 1999, 42, 511–516. [Google Scholar] [CrossRef]
- Kovalchenko, A.; Ajayi, O.; Erdemir, A.; Fenske, G.; Etsion, I. The effect of laser surface texturing on transitions in lubrication regimes during unidirectional sliding contact. Tribol. Int. 2005, 38, 219–225. [Google Scholar] [CrossRef]
- Ronen, A.; Etsion, I.; Kligerman, Y. Friction-reducing surface-texturing in reciprocating automotive components. Tribol. Trans. 2001, 44, 359–366. [Google Scholar] [CrossRef]
- Ryk, G.; Kligerman, Y.; Etsion, I. Experimental investigation of laser surface texturing for reciprocating automotive components. Tribol. Trans. 2002, 45, 444–449. [Google Scholar] [CrossRef]
- Wedeven, L.D.; Evans, D.; Cameron, A. Optical analysis of ball bearing starvation. J. Lubr. Technol. 1971, 93, 349–361. [Google Scholar] [CrossRef]
- Pemberton, J.; Cameron, A. A mechanism of fluid replenishment in elastohydrodynamic contacts. Wear 1976, 37, 185–190. [Google Scholar] [CrossRef]
- Kingsbury, E. Cross flow in a starved EHD contact. ASLE Trans. 1973, 16, 276–280. [Google Scholar] [CrossRef]
- Chiu, Y.P. An analysis and prediction of lubricant film starvation in rolling contact systems. ASLE Trans. 1974, 17, 22–35. [Google Scholar] [CrossRef]
- Chevalier, F.; Lubrecht, A.A.; Cann, P.M.E.; Colin, F.; Dalmaz, G. Film thickness in starved EHL point contacts. J. Tribol. 1998, 120, 126–132. [Google Scholar] [CrossRef]
- Damiens, B.; Venner, C.H.; Cann, P.M.E.; Lubrecht, A.A. Starved lubrication of elliptical EHD contacts. J. Tribol. 2004, 126, 105–111. [Google Scholar] [CrossRef]
- Jakobsson, B.; Floberg, L. The Finite Journal Bearing, Considering Vaporization: (Das Gleitlager Von Endlicher Breite Mit Verdampfung); Gumperts Förlag: Göteborg, Sweden, 1957. [Google Scholar]
- Olsson, K.O. Cavitation in Dynamically Loaded Bearings; Scandinavian University Press: Oslo, Norway, 1965. [Google Scholar]
- Floberg, L. Boundary conditions of cavitation regions in journal bearings. ASLE Trans. 1961, 4, 282–286. [Google Scholar] [CrossRef]
- Dalmaz, G.; Godet, M. Traction, load and film thickness in lightly-loaded lubruicated point contacts. J. Mech. Eng. Sci. 1973, 15, 400–409. [Google Scholar] [CrossRef]
- Brewe, D.; Hamrock, B. Analysis of starvation effects on hydrodynamic lubrication in nonconforming contacts. Trans. ASME J. Lubr. Technol. 1982, 104, 410–417. [Google Scholar] [CrossRef]
- Boness, R.J. Effect of oil supply on cage and roller motion in a lubricated roller bearing. J. Lubr. Technol. Trans. ASME 1970, 92, 39–51. [Google Scholar] [CrossRef]
- Chevalier, F.; Lubrecht, A.A.; Cann, P.M.E.; Colin, F.; Dalmaz, G. Starved film thickness: A qualitative explanation. Tribol. Ser. 1995, 30, 249–257. [Google Scholar]
- Elrod, H.G. A Cavitation algorithm. J. Lubr. Technol. 1981, 103, 350–354. [Google Scholar] [CrossRef]
- Elrod, H.G.; Adams, M.L. A Computer Program for Cavitation and Starvation Problems; University of Leeds: Leeds, UK, 1974. [Google Scholar]
- Cann, P.M.E.; Lubrecht, A.A. Bearing performance limits with grease lubrication: The interaction of bearing design, operating conditions and grease properties. J. Phys. D Appl. Phys. 2007, 40, 5446–5451. [Google Scholar] [CrossRef]
- Coyne, J.C.; Elrod, J.H.G. Conditions for the rupture of a lubricating film. Part I: Theoretical model. J. Lubr. Technol. 1970, 92, 451–456. [Google Scholar] [CrossRef]
- Payvar, P.; Salant, R.F. Computational method for cavitation in a wavy mechanical seal. J. Tribol. 1992, 114, 199–204. [Google Scholar] [CrossRef]
- Braun, M.J.; Hannon, W.M. Cavitation formation and modelling for fluid film bearings: A review. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 839–863. [Google Scholar] [CrossRef]
- Xiong, S.; Wang, Q.J. Steady-state hydrodynamic lubrication modeled with the payvar-salant mass conservation model. J. Tribol. 2012, 134, 031703. [Google Scholar] [CrossRef]
- Dobrica, M.B.; Fillon, M.; Pascovici, M.D.; Cicone, T. Optimizing surface texture for hydrodynamic lubricated contacts using a mass-conserving numerical approach. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 737–750. [Google Scholar] [CrossRef]
- Qiu, M.; Minson, B.R.; Raeymaekers, B. The effect of texture shape on the friction coefficient and stiffness of gas-lubricated parallel slider bearings. Tribol. Int. 2013, 67, 278–288. [Google Scholar] [CrossRef]
- Qiu, M.; Delic, A.; Raeymaekers, B. The effect of texture shape on the load-carrying capacity of gas-lubricated parallel slider bearings. Tribol. Lett. 2012, 48, 315–327. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow/Suhas V. Patankar; Series in Computational Methods in Mechanics and Thermal Sciences; Taylor & Francis Group: Thames, UK, 1980. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics; Longman Group Ltd.: Harlow, UK, 1995. [Google Scholar]
- Kovalchenko, A.; Ajayi, O.; Erdemir, A.; Fenske, G.; Etsion, I. The effect of laser texturing of steel surfaces and speed-load parameters on the transition of lubrication regime from boundary to hydrodynamic. Tribol. Trans. 2004, 47, 299–307. [Google Scholar] [CrossRef]
- Bijani, D.; Deladi, L.E.; Schipper, D.J. The Influence of Surface Texturing on the Film Thickness in Parallel Sliding Surfaces. In Proceedings of the 20th International Colloquium Tribology Industrial and Automotive Lubrication, Stuttgart/Ostfildern, Germany, 12–14 January 2016. [Google Scholar]

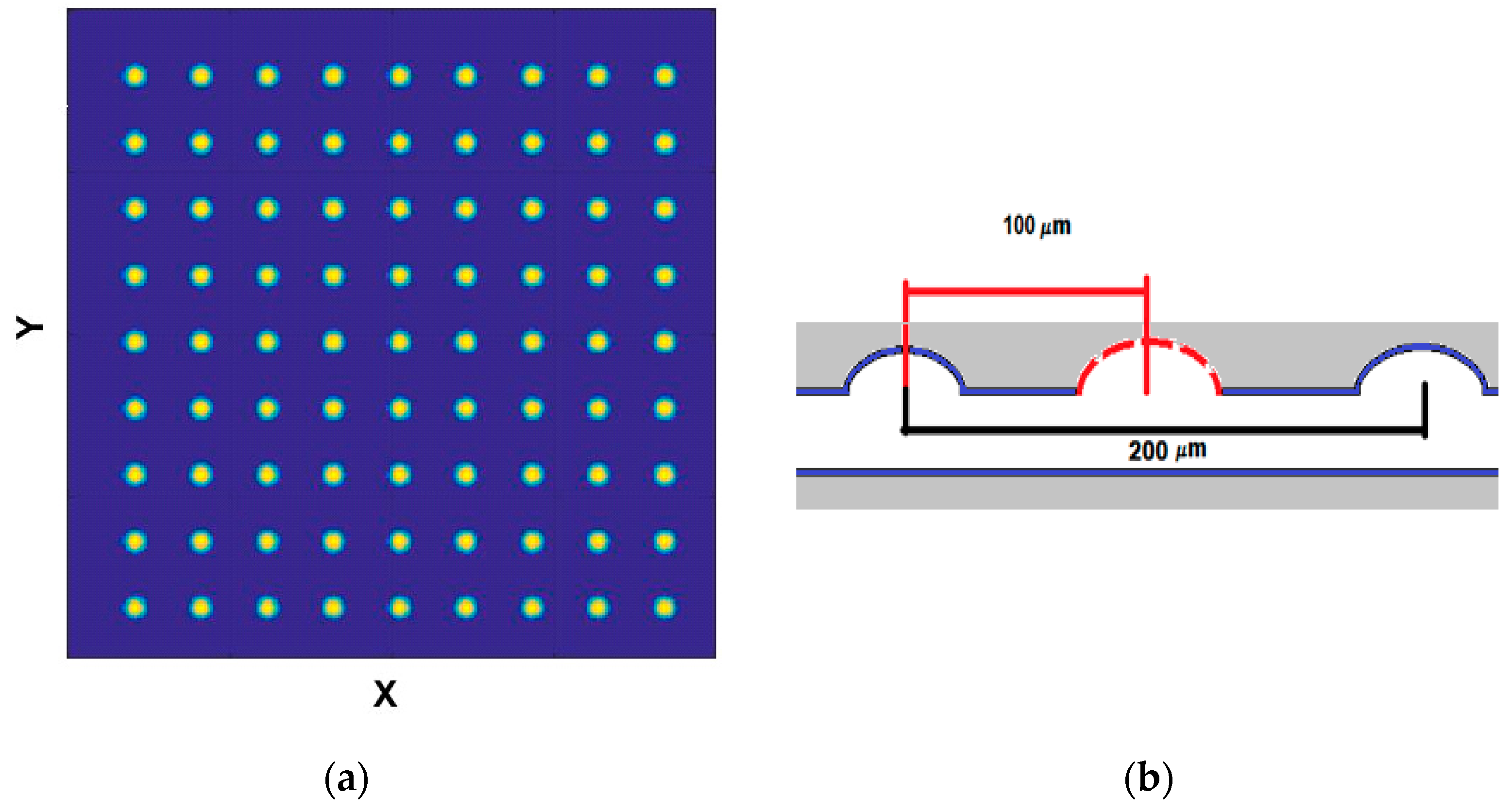

| Parameter | Standard | High Density of Dimples |
|---|---|---|
| Disk 3 | Disk 6 | |
| Depth of dimples | 5.5 | 5 |
| Diameter of dimples | 78 | 58 |
| Distance between dimples | 200 | 100 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bijani, D.; Deladi, E.L.; De Rooij, M.B.; Schipper, D.J. The Influence of Surface Texturing on the Film Thickness in Starved Lubricated Parallel Sliding Contacts. Lubricants 2018, 6, 61. https://doi.org/10.3390/lubricants6030061
Bijani D, Deladi EL, De Rooij MB, Schipper DJ. The Influence of Surface Texturing on the Film Thickness in Starved Lubricated Parallel Sliding Contacts. Lubricants. 2018; 6(3):61. https://doi.org/10.3390/lubricants6030061
Chicago/Turabian StyleBijani, Dariush, Elena L. Deladi, Matthijn B. De Rooij, and Dirk J. Schipper. 2018. "The Influence of Surface Texturing on the Film Thickness in Starved Lubricated Parallel Sliding Contacts" Lubricants 6, no. 3: 61. https://doi.org/10.3390/lubricants6030061
APA StyleBijani, D., Deladi, E. L., De Rooij, M. B., & Schipper, D. J. (2018). The Influence of Surface Texturing on the Film Thickness in Starved Lubricated Parallel Sliding Contacts. Lubricants, 6(3), 61. https://doi.org/10.3390/lubricants6030061