Nonlinear Dynamic Response of an Unbalanced Flexible Rotor Supported by Elastic Bearings Lubricated with Piezo-Viscous Polar Fluids
Abstract
:1. Introduction
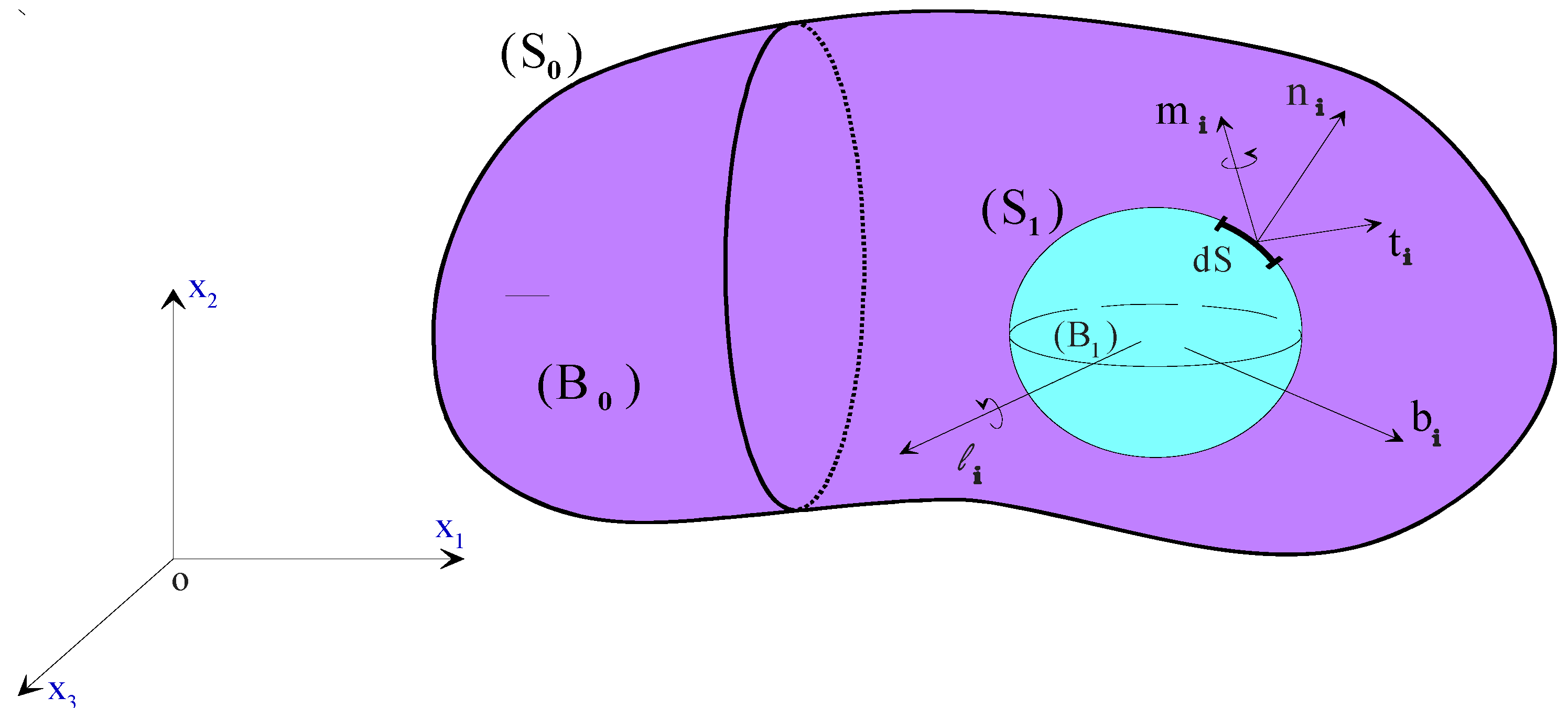
2. Governing Equations
2.1. Momentum Equations of the Polar or Couple Stress Fluid
2.2. Modified Transient Nonlinear Piezo-Viscous Reynolds’ Equation and Boundary Conditions
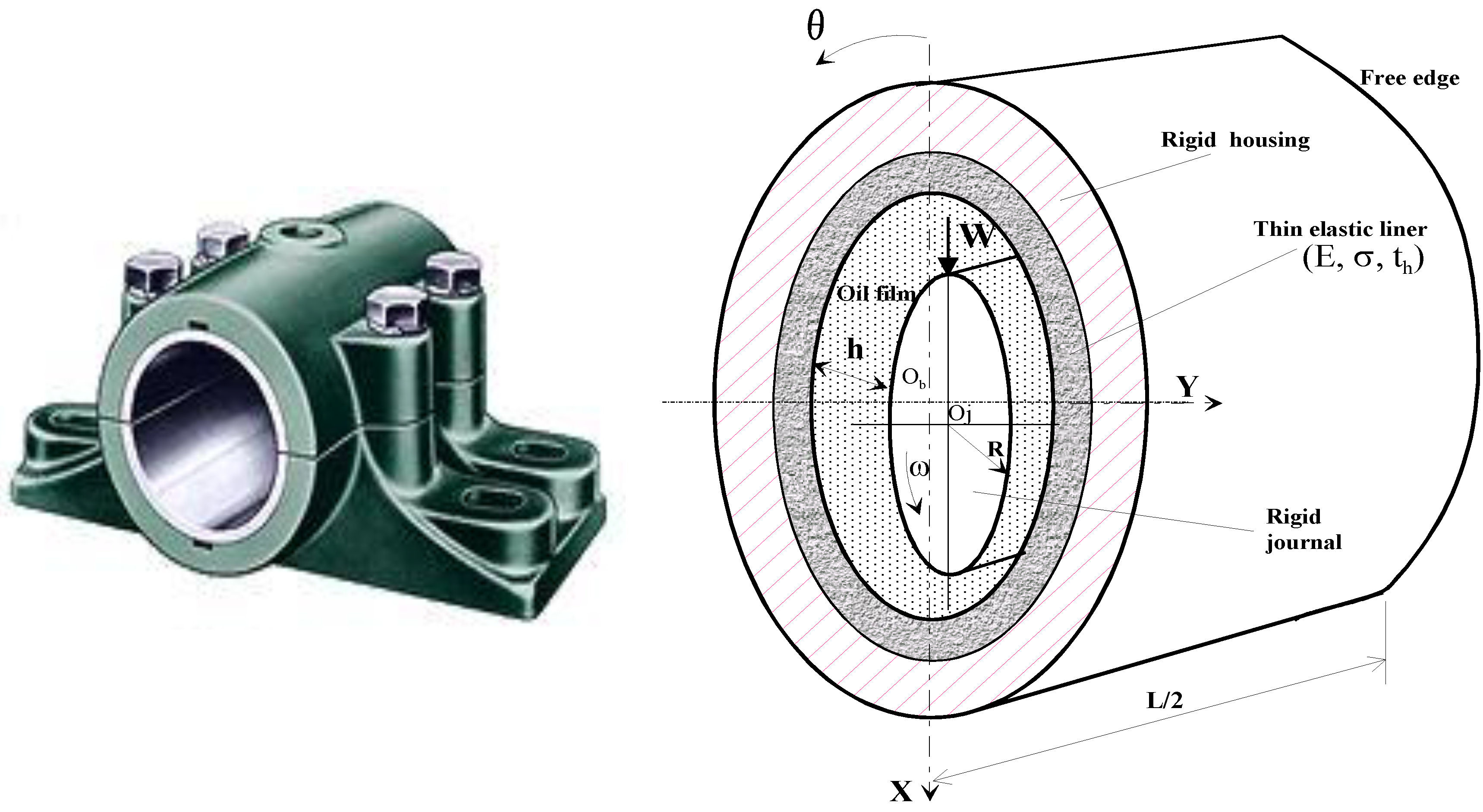
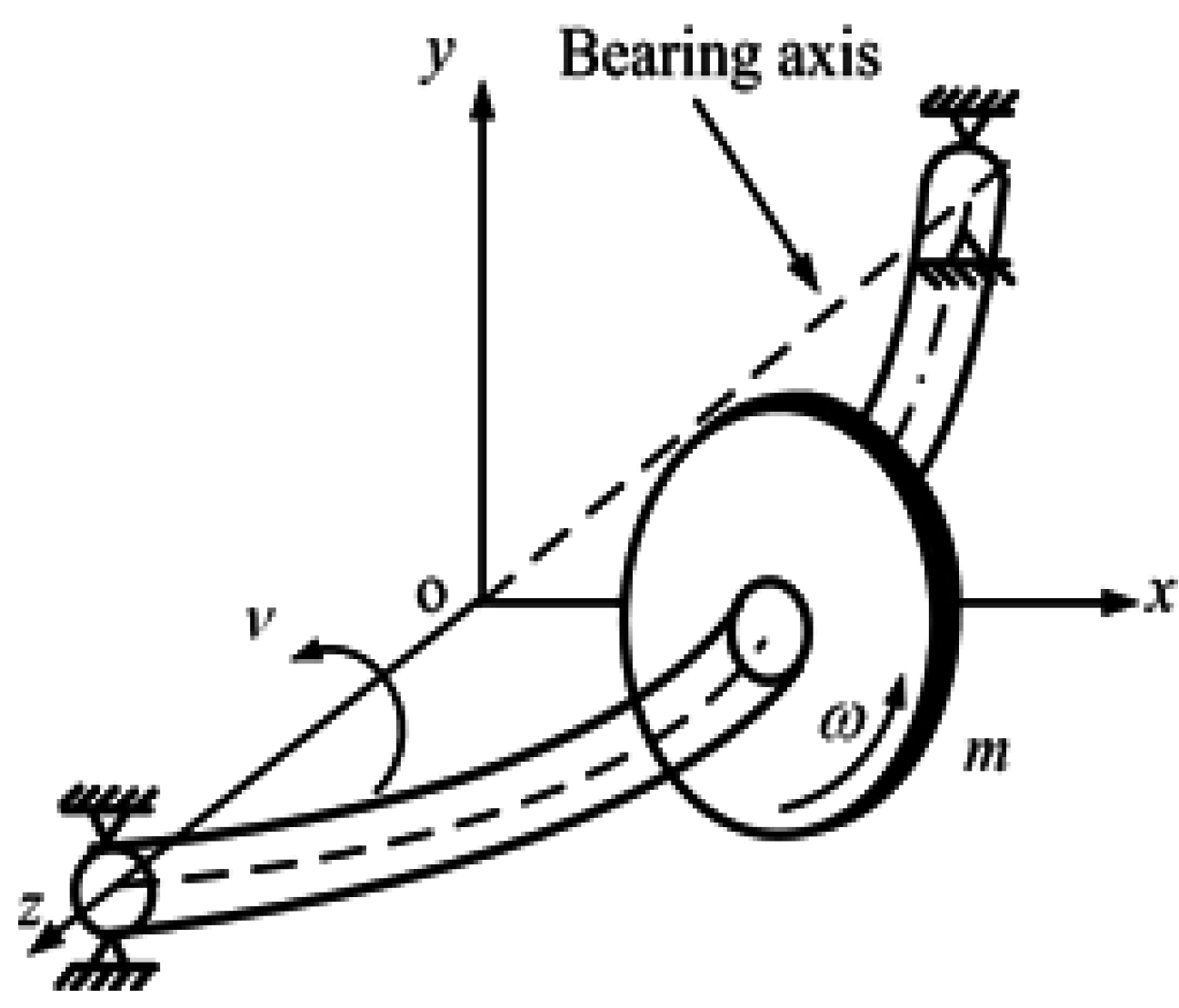
2.3. Rotor-Dynamic Equations
- -
- the weight of the rotor 2W0 = 2 mg;
- -
- the dynamic load components and due an unbalance mass characterized by its eccentricity e;
- -
- the hydrodynamic forces FX and FY due to the presence of the lubricating oil film.
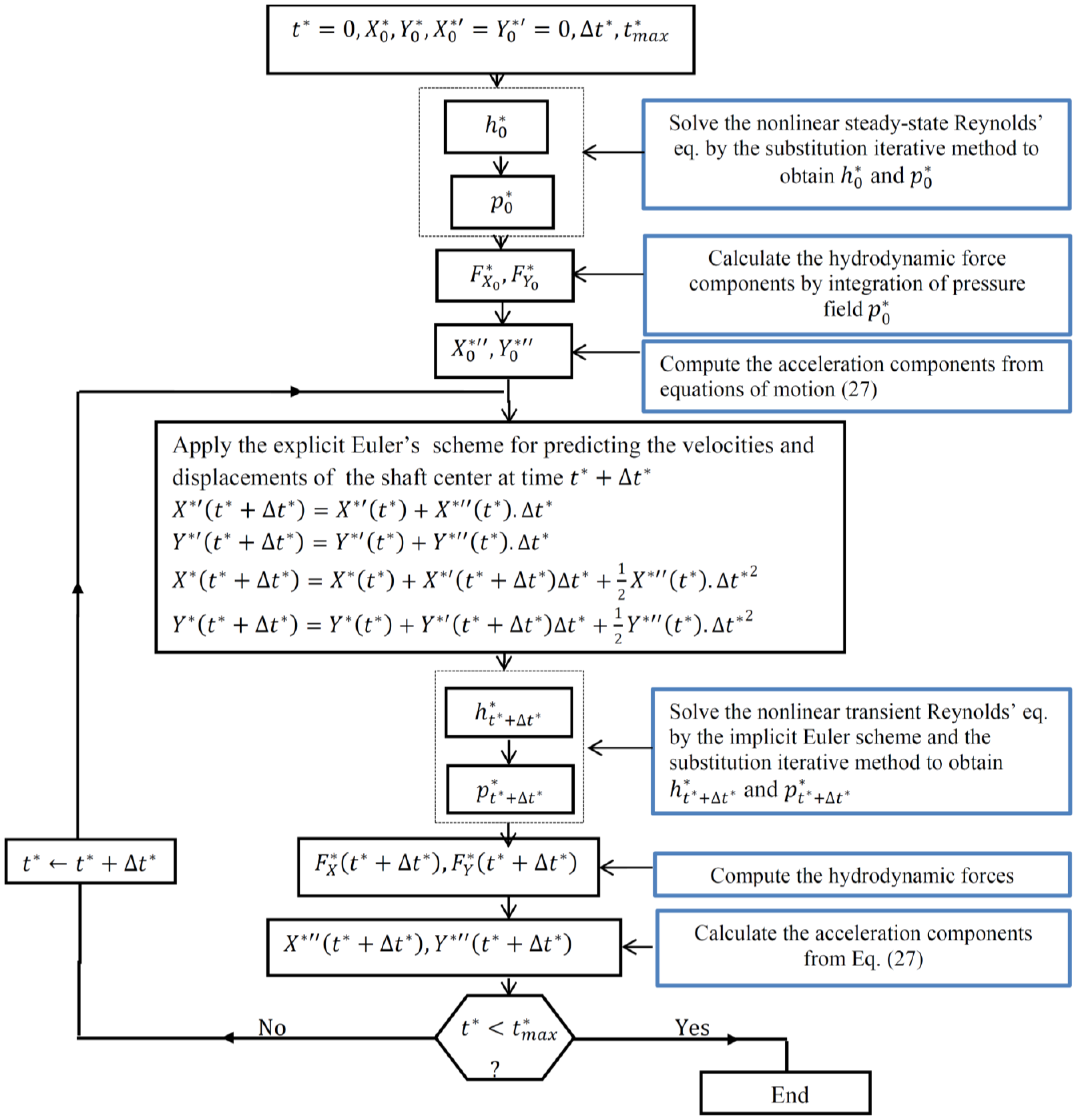
3. Computation Procedure of the Journal Bearing Nonlinear Dynamic Response
4. Finite Element Treatment of the Steady-State Modified Reynolds’ Equation
4.1. Weak Integral Formulation and Finite Element Discretization
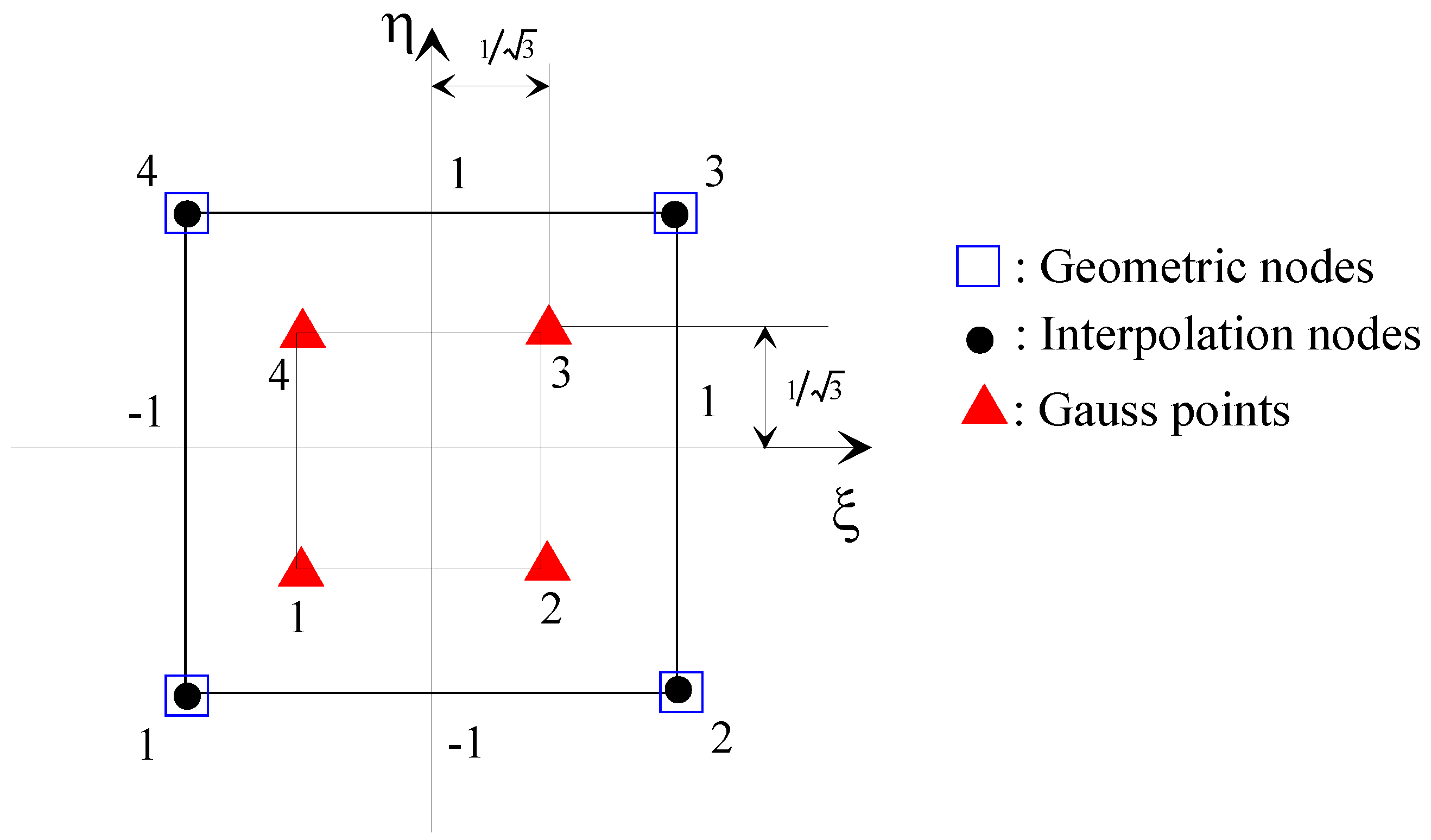
4.2. Method of Solution of Steady-State Nonlinear Modified REYNOLDS’ Equation
4.3. Iterative Research of the Steady-State Equilibrium Position
5. Finite Element Treatment of the Transient Modified Reynolds’ Equation
5.1. Weak Integral Formulation and Finite Element Discretization
5.2. Method of Solution of Transient Nonlinear Modified Reynolds’ Equation
6. Results and Discussions
6.1. Transient Solution vs. Steady-State Solution
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Bearing length | L | m | 0.320 |
| Journal diameter | D = 2R | m | 0.500 |
| Radial clearance | C | m | 3.5 × 10−4 |
| Bearing-liner thickness | m | 10−2 | |
| Young’s modulus of the bearing-liner (polyethylene high density at 20 °C) [41] | E | Pa | 0.9 × 109 |
| Poisson’s ratio of the bearing-liner at 20 °C [41] | σ | - | 0.35 |
| Dynamic viscosity of lubricant at atmospheric pressure | Pa·s | 15 × 10−3 | |
| Density of lubricant | ρ | kg·m−3 | 870 |
| Pressure-viscosity coefficients | α | Pa−1 | 0 |
| 17 × 10−9 | |||
| 42.5 × 10−9 | |||
| 212.5 × 10−9 | |||
| Rotor speed | rpm | 3 × 103 | |
| Rotor mass (disc) | 2m | kg | 68 × 103 |
| Rotor length | Lr | m | 10 |
| Young’s modulus of the rotor (steel) at 20 °C | Er | Pa | 210 × 109 |
| Rotor stiffness | kr | N/m | 5 × 106 |
| Rotor damping | br | N·s/m | 0 |
| Mass unbalance eccentricities | e | m | 0 |
| 70 × 10−6 | |||
| 280 × 10−6 | |||
| Unbalance dynamic loads | meω2 | kN | 0 235 940 |
| Static load applied per bearing | W0 = mg | kN | 340 |
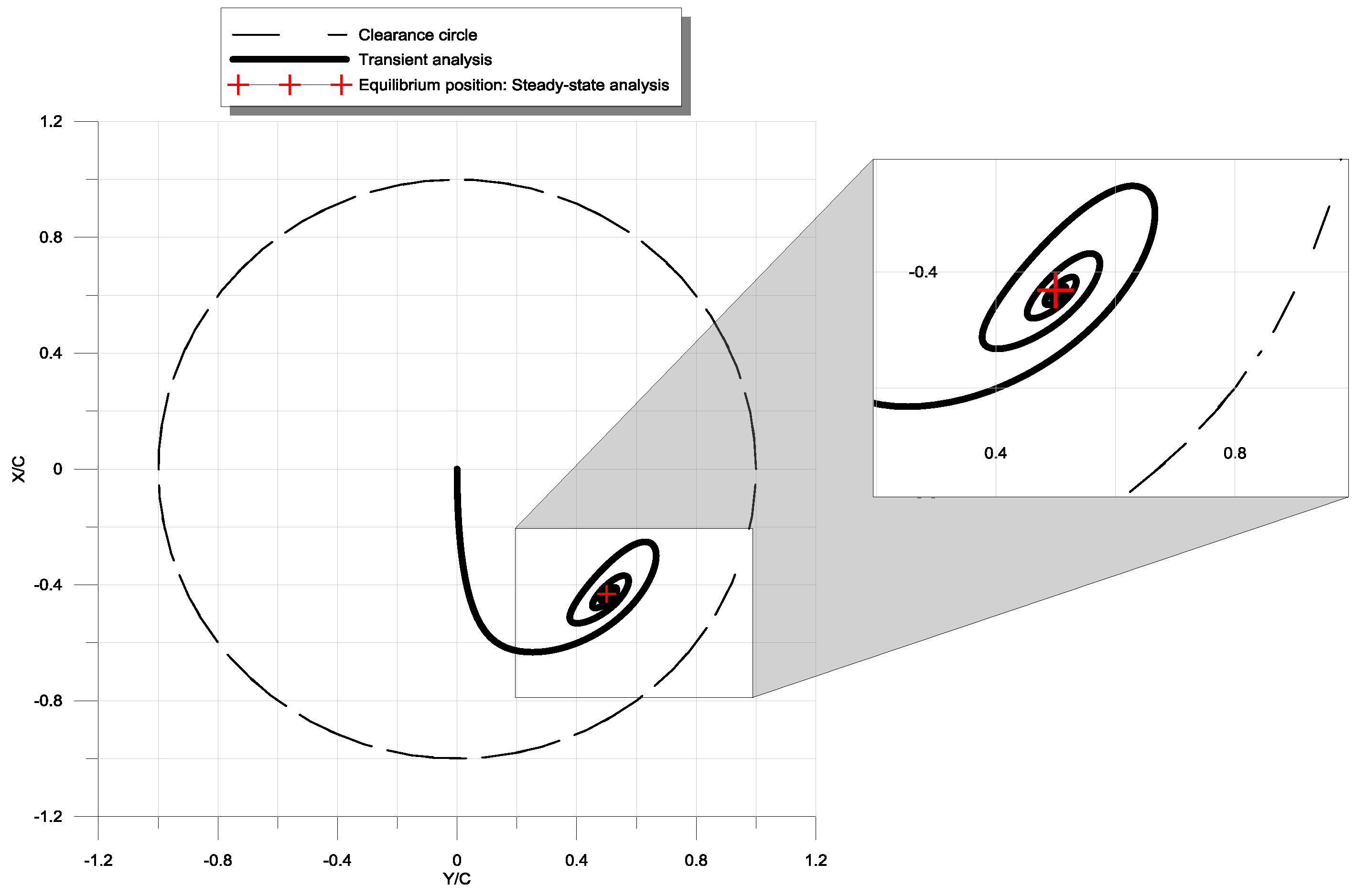
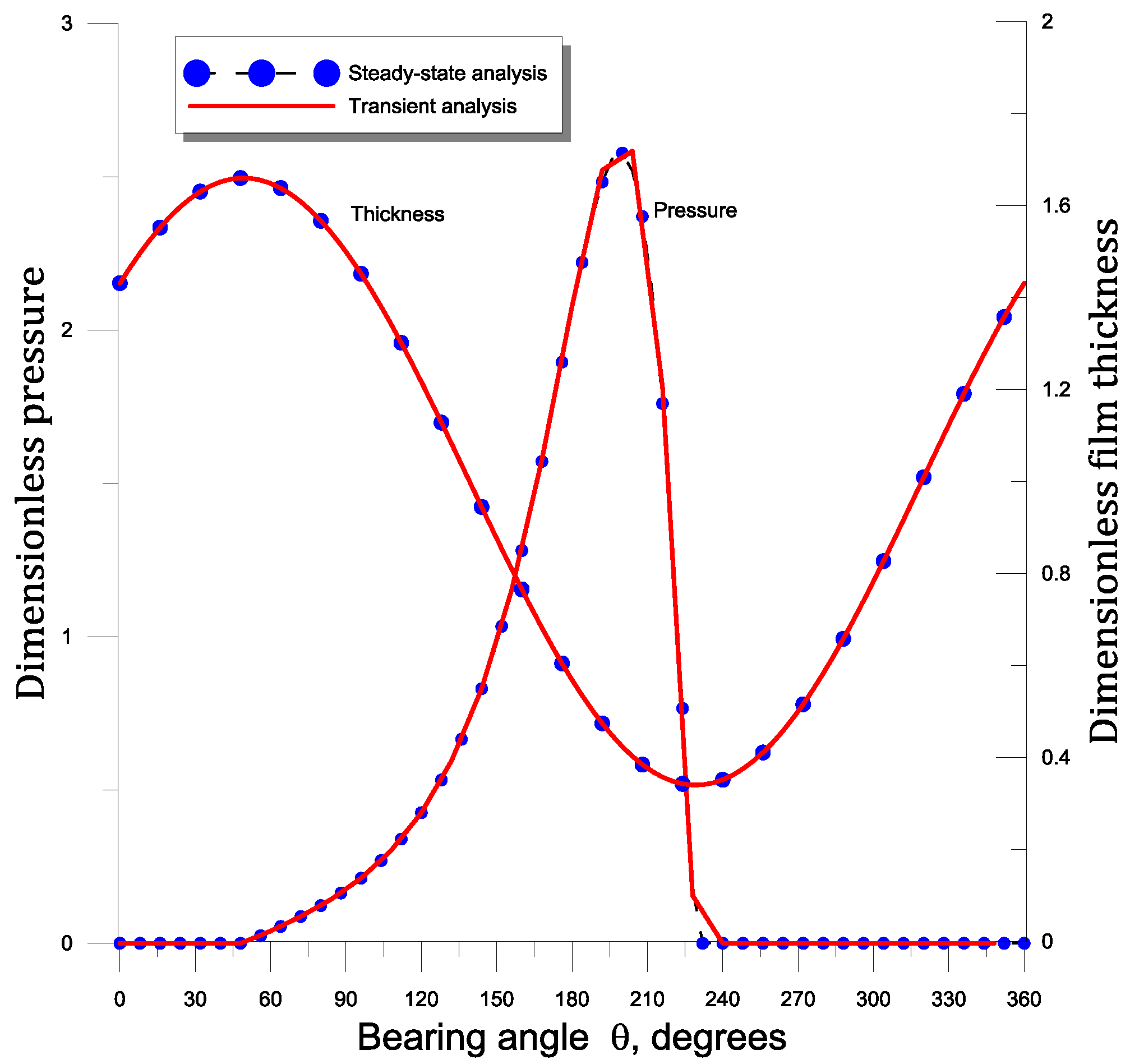
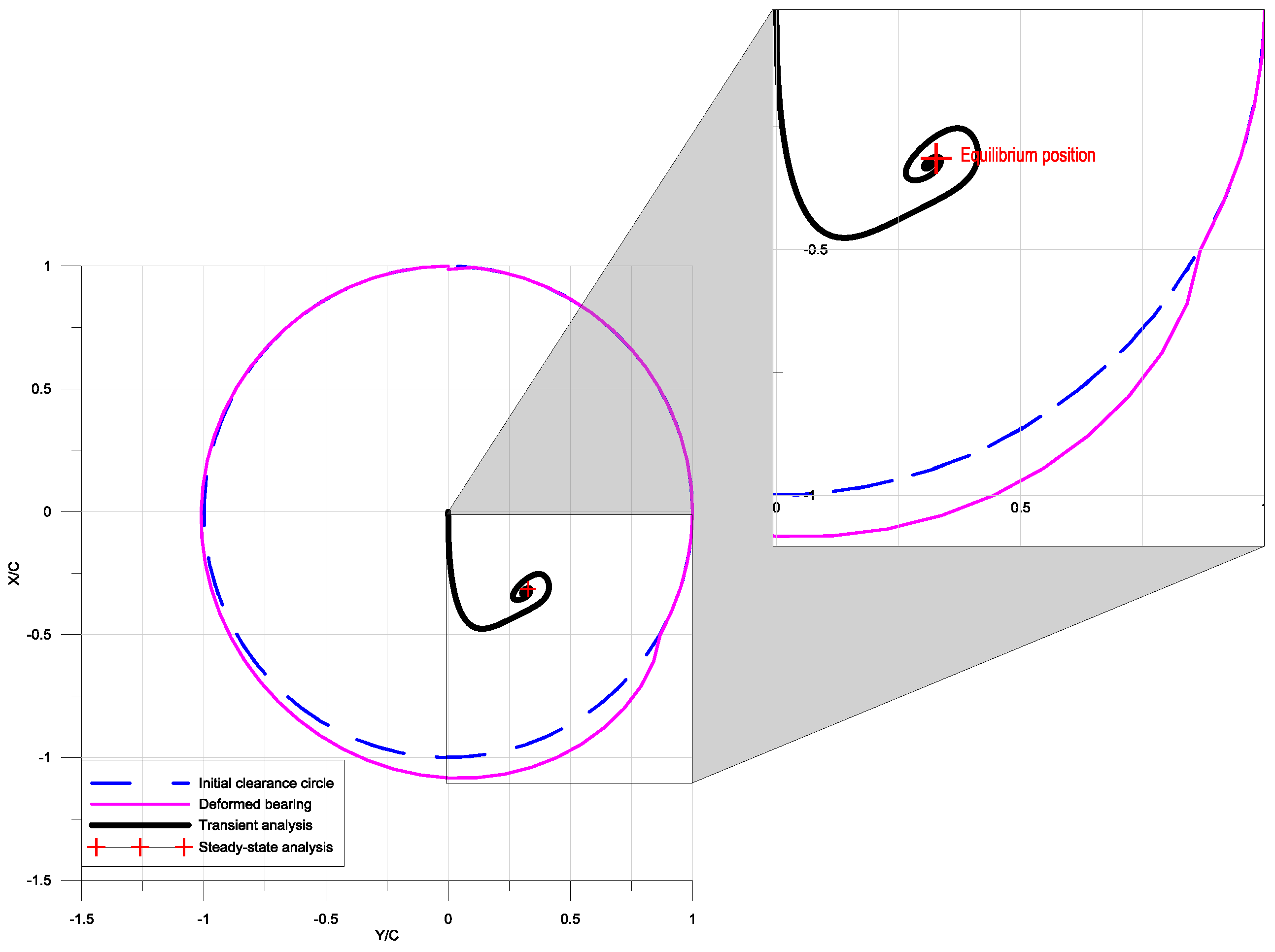
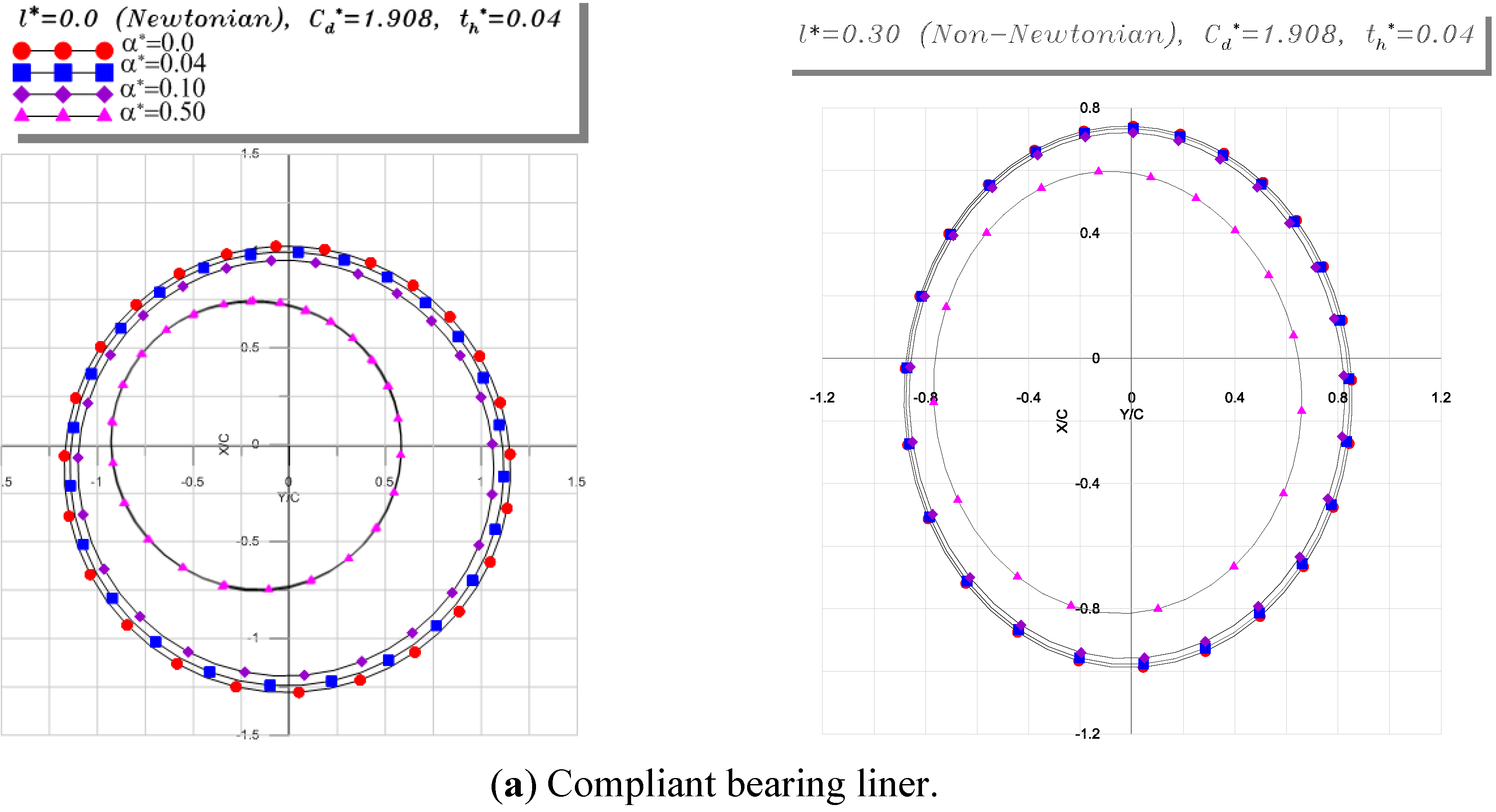
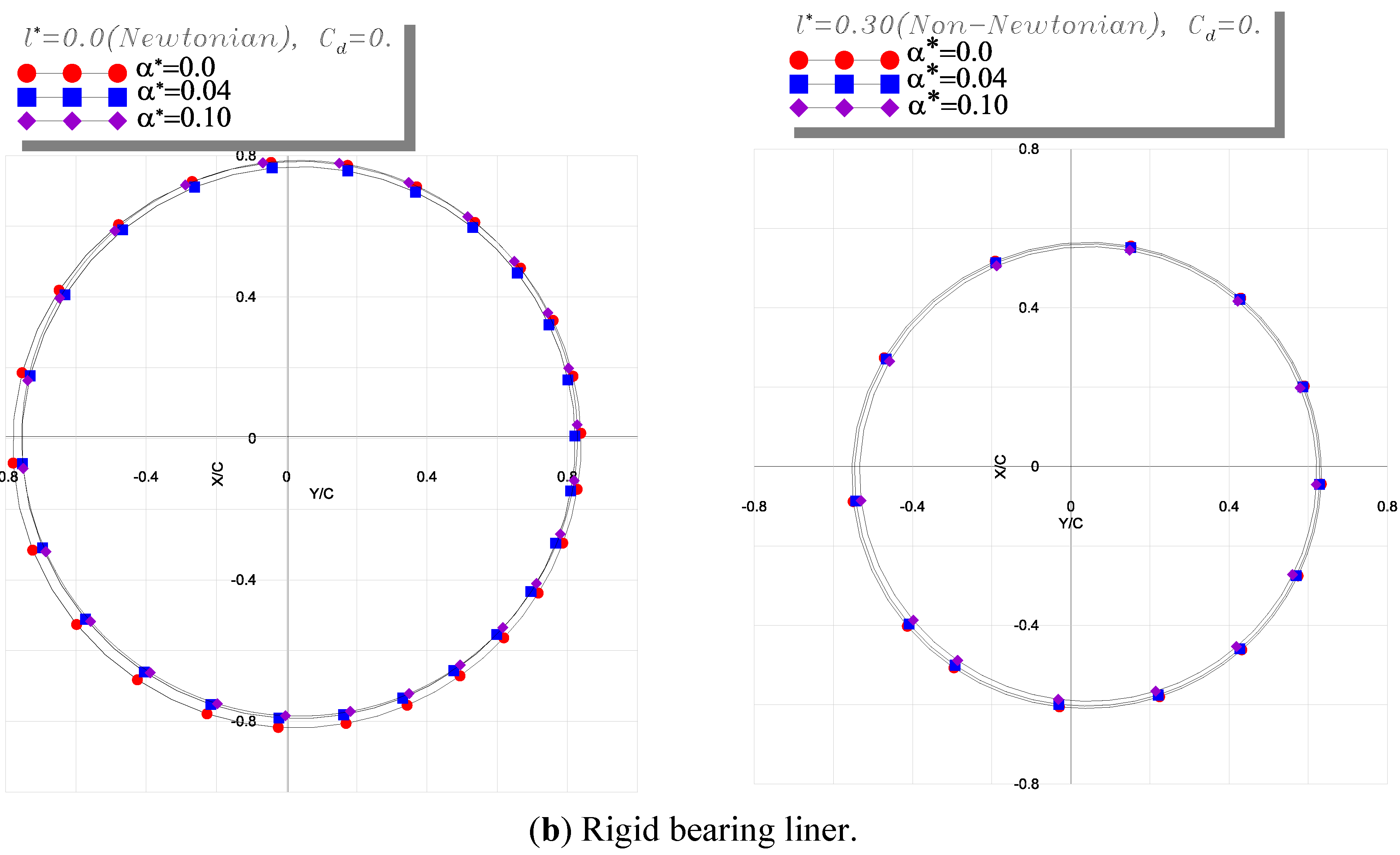
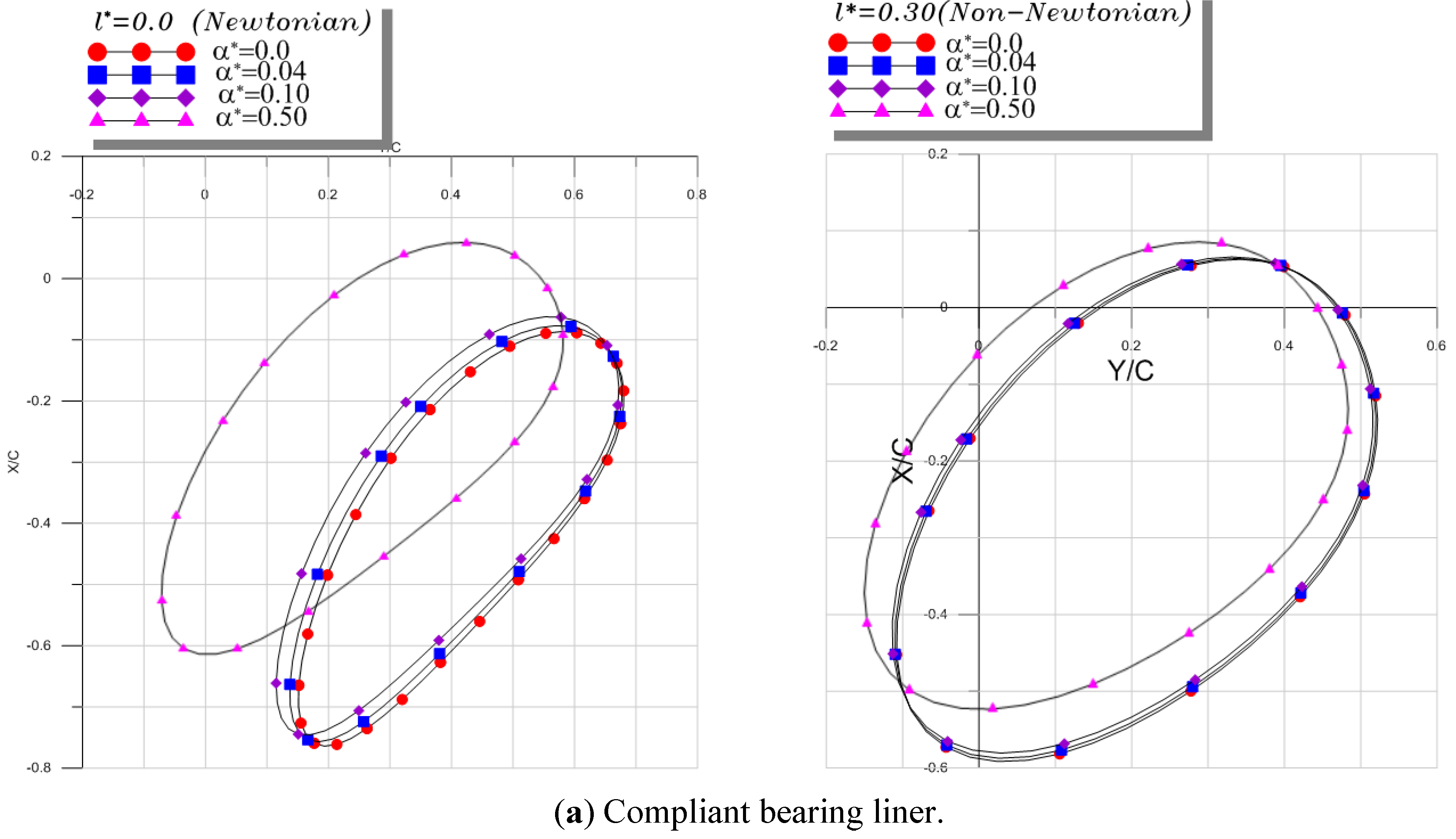
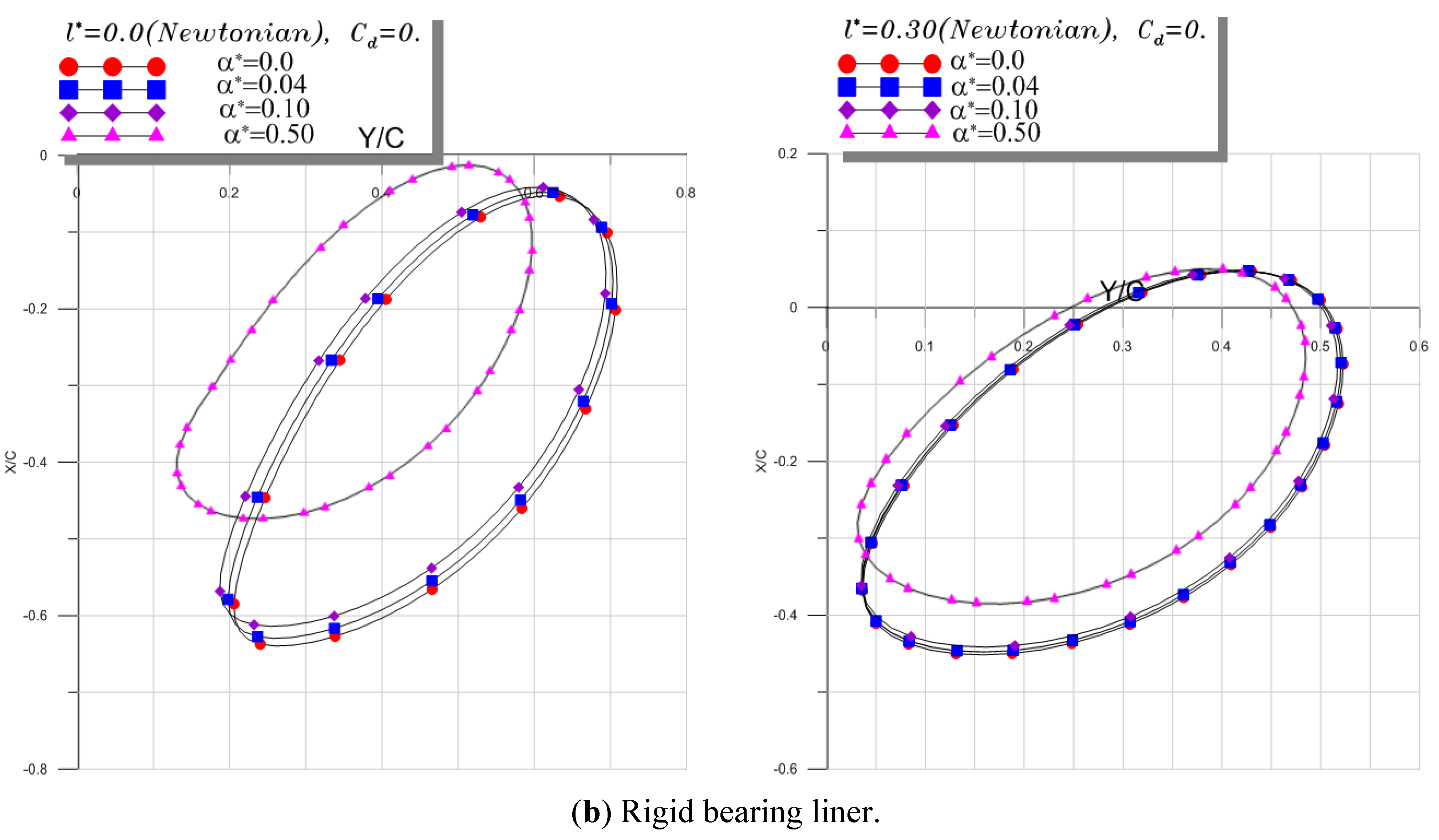
6.2. Parametric Study
6.2.1. Flexible Rotor with Large Unbalance Mass
6.2.2. Flexible Rotor with Small Unbalance Mass
| Parameter | Symbol | Value |
|---|---|---|
| Number of elements in the circumferential direction of bearing | Nθ | 30 |
| Number of elements in the axial direction of half-bearing | Nz | 10 |
| Number of Gauss integration points in ξ-direction | - | 2 |
| Number of Gauss integration points in η-direction | 2 | |
| Under-relaxation factor for the substitution iterative method | Ω0 | 0.10 |
| Convergence criterion of the substitution iterative method | εp | 10−5 |
| Dimensionless time increment | Δ | |
| Time limit | 40π † |
7. Conclusions
Acknowledgments
Author Contributions
Nomenclature
bearing radial clearance, m | |
Young’s modulus of the bearing-liner, Pa | |
| e | unbalance eccentricity, m |
lift force components, N | |
fluid-film thickness, m | |
dimensionless fluid-film thickness , | |
static fluid-film thickness, m | |
dimensionless static fluid-film thickness , | |
rotor stiffness, | |
rotor damping, | |
length of bearing, m | |
couple-stress parameter=, m | |
dimensionless couple-stress parameter=, | |
scalar compliance operator, | |
mass of rotor per bearing, kg | |
| N | rotation velocity of the rotor, rpm |
fluid-film pressure, Pa | |
normalized film pressure , | |
steady-state pressure, Pa | |
journal radius, m | |
| S | Sommerfeld number, |
time, s | |
dimensionless time, | |
thickness of bearing-liner, m | |
static load applied on the journal bearing | |
| X,Y | displacement components of the journal centre, m |
dimensionless displacements, | |
axial co-ordinate measured from middle section plane of the bearing, m | |
non-dimensional axial co-ordinate, | |
pressure-viscosity coefficient, Pa−1 | |
non-dimensionless pressure-viscosity coefficient, | |
unbalance eccentricity ratio, | |
material constant responsible for couple-stresses, kg·m·s−1 | |
absolute viscosity of lubricant, Pa·s | |
absolute viscosity at atmospheric pressure, Pa·s | |
Poisson’s ratio of the bearing-liner | |
bearing angle, rad | |
angular velocity of the rotor (shaft)=, rad/s | |
square matrix | |
line vector, = | |
column vector | |
dimensionless quantity | |
divergence operator |
Appendix A
Computation Procedure of the Journal Bearing Nonlinear Dynamic Response
Appendix B
Method of Solution for Steady-State Nonlinear Modified Reynolds’ Equation
Appendix C
Iterative Research of the Steady-State Equilibrium Position
Conflicts of Interest
References
- Newkirk, B.L. Shaft whipping. Gen. Electr. Rev. 1924, 27, 169–178. [Google Scholar]
- Newkirk, B.L.; Taylor, H.D. Shaft whipping due to oil action in journal bearings. Gen. Electr. Rev. 1925, 28, 985–988. [Google Scholar]
- Stodola, A. Kritische Wellenstörung Infolge der Nachgiebigkeit des Oelpolsters im Lager. Schweizerische Bauzeitung 1925, 85/86. [Google Scholar] [CrossRef]
- Hummel, B.L. Kritische Drehzahlen als folge der Nachgiebigkeit des Schmiermittels im Lager. A.W. Zickfeldt: Berlin, Germany, 1926. [Google Scholar]
- Newkirk, B.L. Whirling balance shafts. In Proceedings of the Third ICAM, Stockholm, Sweden; 1931. [Google Scholar]
- Hori, Y. A theory of oil whip. ASME J. Appl. Mech. 1959, 81, 189–198. [Google Scholar]
- Sternlicht, B. Elastic and damping properties of cylindrical journal bearings. J. Basic Eng. 1959, 81, 101–108. [Google Scholar]
- Holmes, R. The vibration of a rigid shaft on short sleeve bearings. J. Mech. Eng. Sci. 1960, 2, 337–341. [Google Scholar] [CrossRef]
- Lund, J.W. The stability of an elastic rotor in journal bearings with flexible damped supports. ASME J. Appl. Mech. 1965, 32, 911–920. [Google Scholar] [CrossRef]
- Lund, J.W.; Saibel, E. Oil whip orbits of a rotor in sleeve bearings. ASME J. Eng. Ind. 1967, 89, 813–823. [Google Scholar] [CrossRef]
- Badgley, H.; Booker, J.F. Turbo-rotor instability: Effect of initial transients on plain motion. ASME J. Lubr. Technol. 1969, 91, 625–633. [Google Scholar] [CrossRef]
- Akers, A.; Michaelson, S.; Cameron, A. Stability contours for a whirling finite journal bearing. ASME J. Lubr. Technol. 1971, 93, 177–190. [Google Scholar] [CrossRef]
- Kirk, R.G.; Gunter, E.J. Short bearing analysis applied to rotor dynamics. Part 1: Theory. ASME J. Lubr. Technol. 1976, 98, 47–56. [Google Scholar] [CrossRef]
- Kirk, R.G.; Gunter, E.J. Short bearing analysis applied to rotor dynamics. Part 2: Results of journal bearing response. ASME J. Lubr. Technol. 1976, 98, 319–329. [Google Scholar] [CrossRef]
- Hahn, E.J. Stability and unbalance response of centrally preloaded rotors mounted in journal and squeeze film bearings. ASME J. Lubr. Tech. 1979, 101, 120–128. [Google Scholar] [CrossRef]
- Grosby, W.A. The stability of a rigid rotor in ruptured finite journal bearings. Wear 1982, 80, 333–346. [Google Scholar] [CrossRef]
- Akkok, M.; Ettles, C.M. Journal bearing response to excitation and behavior in the unstable region. ASLE Trans. 1984, 27, 341–351. [Google Scholar] [CrossRef]
- Lahmar, M.; Haddad, A.; Nicolas, D. An optimized short bearing theory for nonlinear dynamic analysis of turbulent journal bearings. Eur. J. Mech. A/Solids 2000, 19, 151–177. [Google Scholar] [CrossRef]
- Agnieszka (Agnes) Muszyǹska, Rotodynamics; Taylor & Francis: New York, USA, 2005.
- Laha, S.K.; Kakoty, S.K. Non-linear dynamic analysis of a flexible rotor supported on porous oil journal bearings. Commun. Nonlinear Sci. Numer. Simulat. 2011, 16, 1617–1631. [Google Scholar] [CrossRef]
- Kushare, P.B.; Sharma, S.C. Nonlinear transient stability study of two lobe symmetric hole entry worn hybrid journal bearing operating with non-Newtonian lubricant. Tribol. Int. 2014, 69, 84–101. [Google Scholar] [CrossRef]
- Oliver, D.R. Load enhancement effects due to polymer thickening in a short model journal bearings. J. Non-Newton. Fluid Mech. 1988, 30, 185–196. [Google Scholar] [CrossRef]
- Spikes, H.A. The behaviour of lubricants in contacts: Current understanding and future possibilities. J. Eng Tribol. Proc. IMechE 1994, 28, 3–15. [Google Scholar] [CrossRef]
- Ariman, T.T.; Sylvester, N.D. Microcontinuum fluid mechanics: A review. Int. J. Eng. Sci. 1973, 11, 905–930. [Google Scholar] [CrossRef]
- Ariman, T.T.; Sylvester, N.D. Application of microcontinuum fluid mechanics. J. Eng. Sci. 1974, 12, 273–293. [Google Scholar] [CrossRef]
- Stokes, V.K. Couple-stresses in fluids. Phys. Fluids 1966, 9, 1709–1715. [Google Scholar] [CrossRef]
- Lin, J.R. Static and dynamic characteristics of externally pressurized circular step thrust bearings lubricated with couple-stress fluids. Tribol. Int. 1999, 32, 207–216. [Google Scholar] [CrossRef]
- Mokhiamer, U.M.; Crosby, W.A.; el-Gamal, H.A. A study of a journal bearing lubricated by fluids with couple-stress considering the elasticity of the liner. Wear 1999, 224, 194–201. [Google Scholar] [CrossRef]
- Lin, J.R.; Yang, C.B.; Lu, R.F. Effects of couple-stresses in the cyclic squeeze films of finite partial journal bearings. Tribol. Int. 2001, 34, 119–125. [Google Scholar] [CrossRef]
- Naduvinamani, N.B.; Hiremath, P.S.; Gurubasavaraj, G. Squeeze film lubrication of a short porous journal bearing with couple-stress fluids. Tribol. Int. 2001, 34, 739–747. [Google Scholar] [CrossRef]
- Lahmar, M. Elasto-hydrodynamic analysis of double-layered journal bearings lubricated with couple-stress fluids. J. Eng. Tribol. 2005, 219, 145–171. [Google Scholar]
- Sarangi, M.; Majumdar, B.C.; Sekhar, A.S. Elastohydrodynamically Lubricated Ball Bearings with Couple-Stress Fluids, Part I: Steady-State Analysis. Tribol. Trans. 2005, 48, 404–414. [Google Scholar] [CrossRef]
- Lahmar, M.; Bou-Saïd, B. Couple stress effects on the dynamic behavior of connecting rod bearings in both gasoline and Diesel engines. Tribol. Trans. 2008, 51, 44–56. [Google Scholar] [CrossRef]
- Lin, J.R.; Chu, L.M.; Li, W.L.; Lu, R.F. Combined effects of piezo-viscous dependency and non-Newtonian couple-stresses in wide parallel-plate squeeze-film characteristics. Tribol. Int. 2011, 44, 1598–1602. [Google Scholar] [CrossRef]
- Barus, C. Isothermal, isopiestics, and isometrics relative to viscosity. Am. J. Sci. 1893, 45, 87–96. [Google Scholar] [CrossRef]
- Klamann, D. Lubricants and Related Products; Publ. Verlag Chemie: Weinheim, Germany, 1984; pp. 51–83. [Google Scholar]
- Cameron, A. Basic Lubrication Theory; Ellis Horwood Limited: Chichester, UK, 1981. [Google Scholar]
- Sargent, L.B., Jr. Pressure-Viscosity Coefficients of Liquid Lubricants. ASLE Trans. 1983, 26, 1–10. [Google Scholar] [CrossRef]
- Gümbel, L. Vergleich der ergebnisse der rechnerischen Behaudlung des Lagerschmierungs problem mit neuen Versuchergebnisse; Bezirk, V.D.I., Ed.; Monatsblätter: Berlin, Germany, 1921; pp. 125–128. [Google Scholar]
- Dowson, D.; Taylor, C.M. Cavitation in bearings. Ann. Rev. Fluid Mech. 1979, 11, 35–66. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Schmid, S.R.; Jacobson, B.O. Fundamentals of fluid film lubrication, 2nd ed.; CRC Press: Boca Raton, FL, USA.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lahmar, M.; Bou-Saïd, B. Nonlinear Dynamic Response of an Unbalanced Flexible Rotor Supported by Elastic Bearings Lubricated with Piezo-Viscous Polar Fluids. Lubricants 2015, 3, 281-310. https://doi.org/10.3390/lubricants3020281
Lahmar M, Bou-Saïd B. Nonlinear Dynamic Response of an Unbalanced Flexible Rotor Supported by Elastic Bearings Lubricated with Piezo-Viscous Polar Fluids. Lubricants. 2015; 3(2):281-310. https://doi.org/10.3390/lubricants3020281
Chicago/Turabian StyleLahmar, Mustapha, and Benyebka Bou-Saïd. 2015. "Nonlinear Dynamic Response of an Unbalanced Flexible Rotor Supported by Elastic Bearings Lubricated with Piezo-Viscous Polar Fluids" Lubricants 3, no. 2: 281-310. https://doi.org/10.3390/lubricants3020281
APA StyleLahmar, M., & Bou-Saïd, B. (2015). Nonlinear Dynamic Response of an Unbalanced Flexible Rotor Supported by Elastic Bearings Lubricated with Piezo-Viscous Polar Fluids. Lubricants, 3(2), 281-310. https://doi.org/10.3390/lubricants3020281





