Rolling Friction Torque in Ball-Race Contacts Operating in Mixed Lubrication Conditions
Abstract
:1. Introduction
2. Theoretical Model for Friction Torque
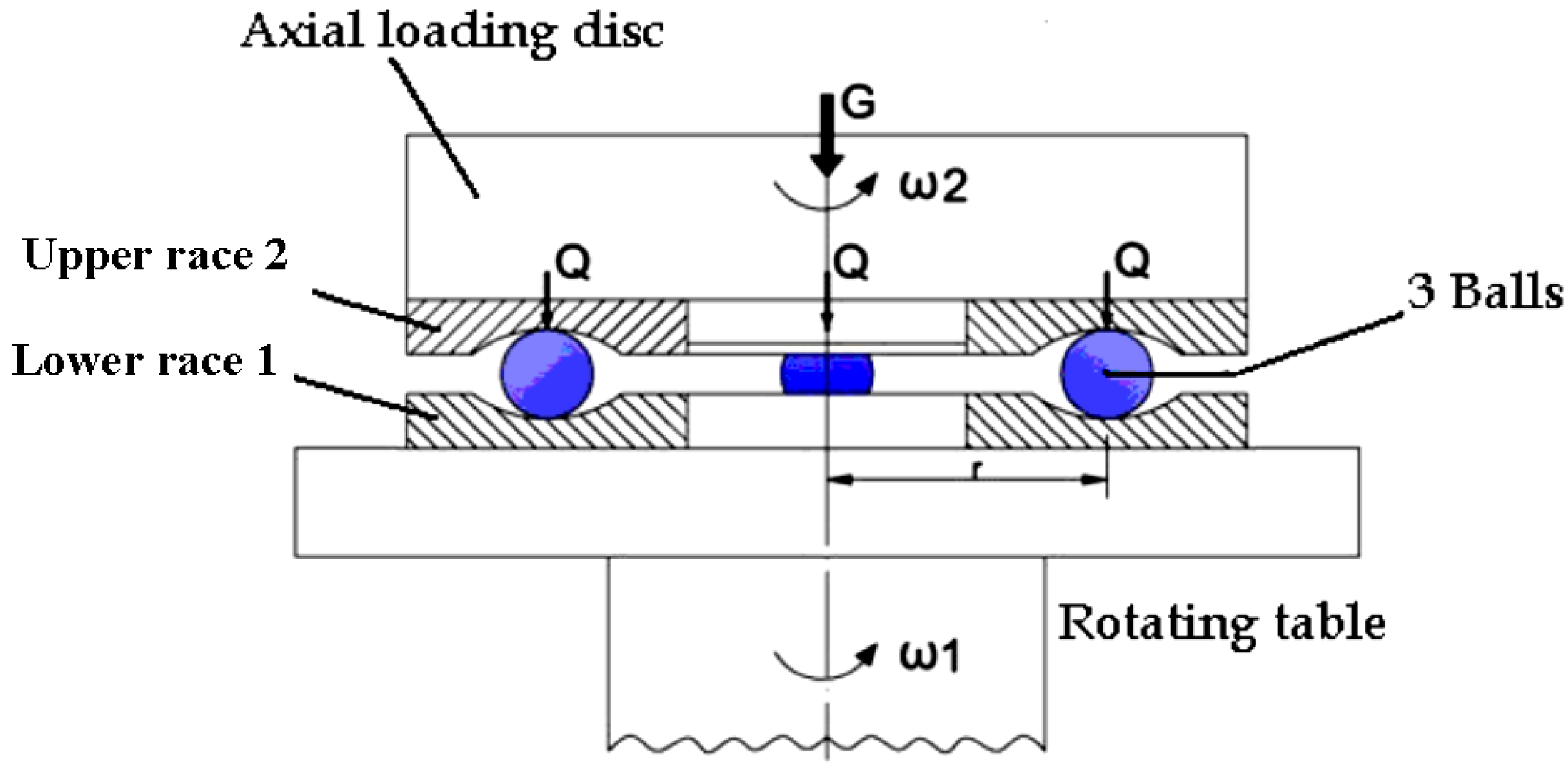

3. Experimental Procedure
3.1. Experimental Equipment

3.2. Experimental Methodology to Determine Friction Torque
3.2.1. Friction Torque in Dry Conditions
3.2.2. Friction Torque in Lubricated Conditions
4. Experimental Results
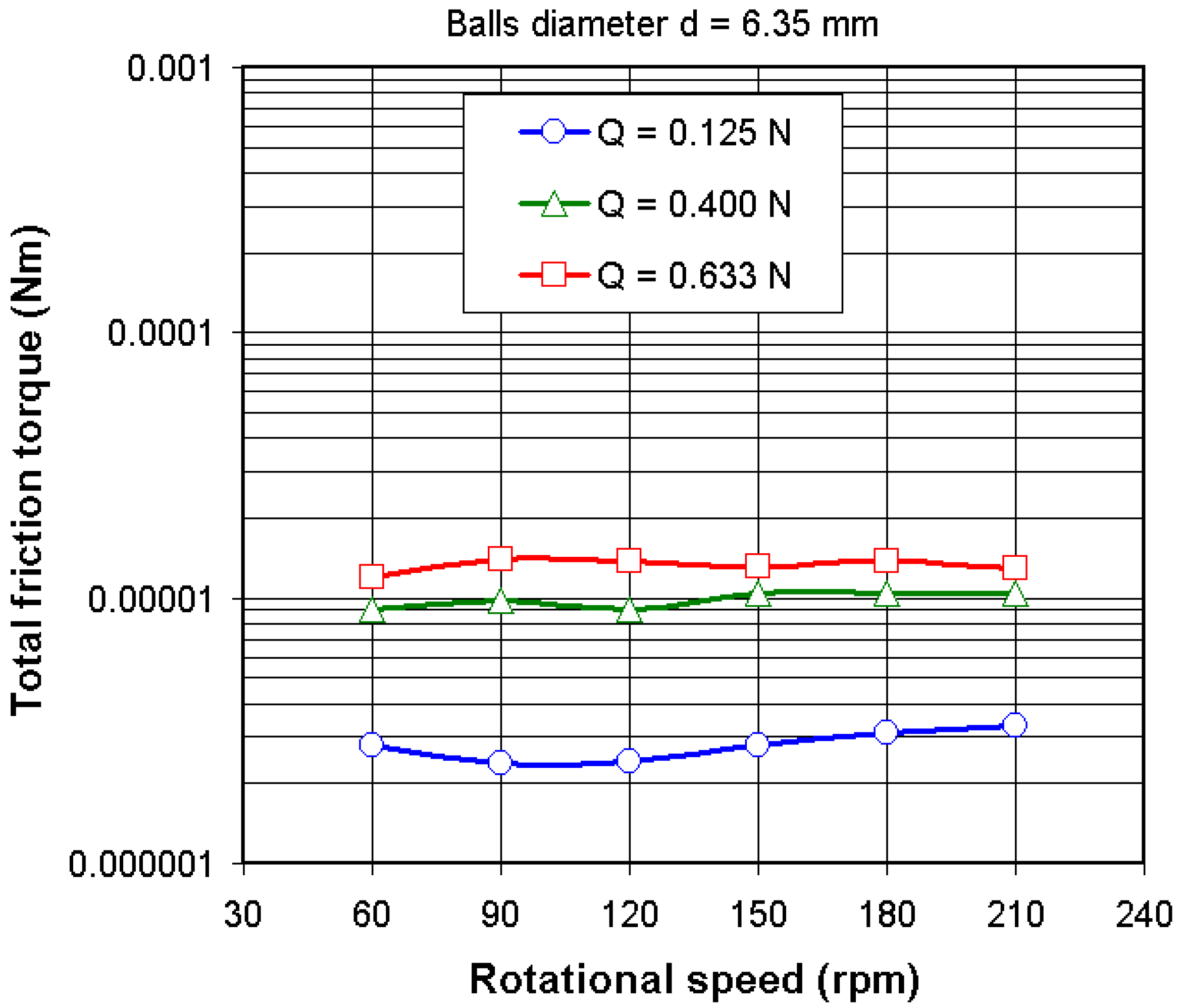
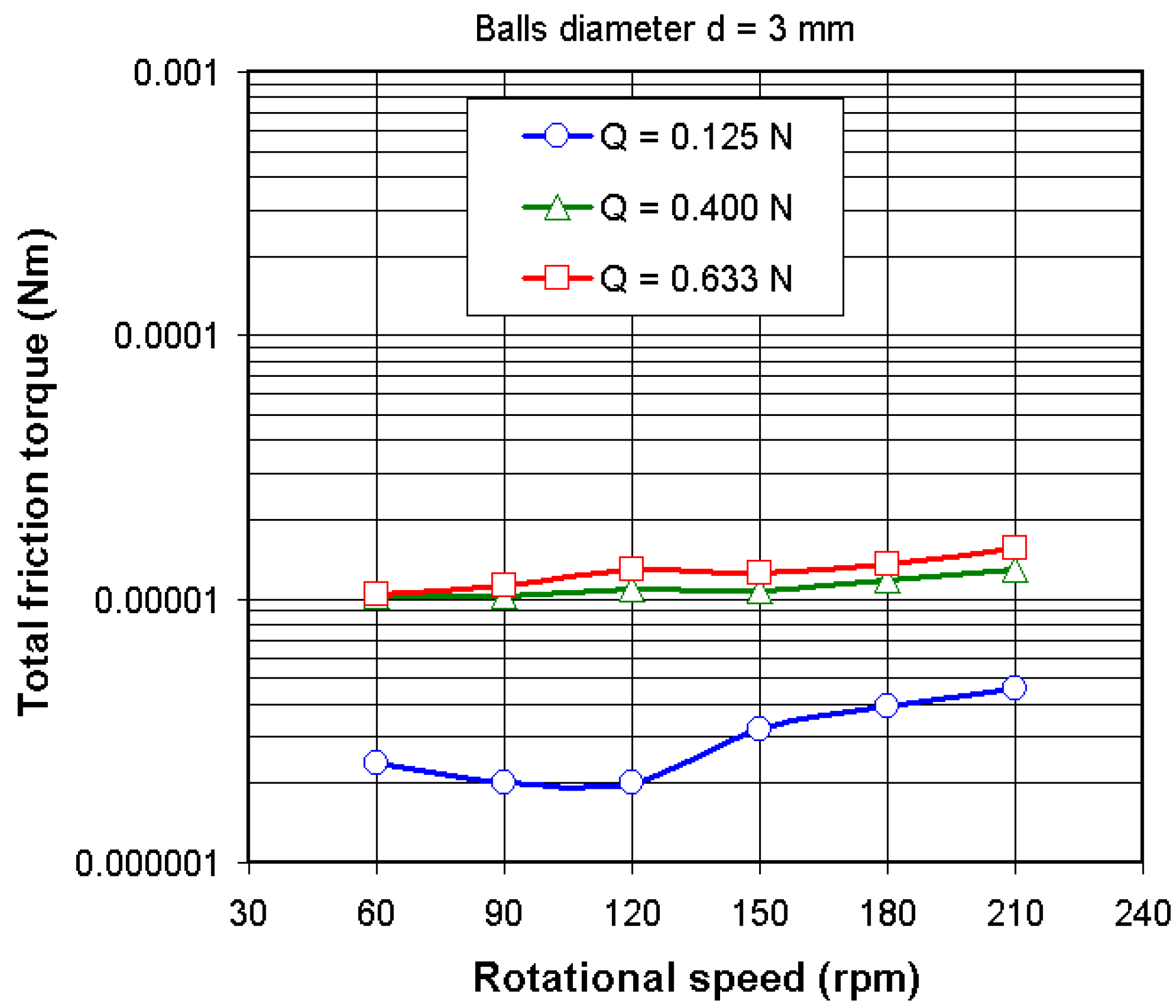
4.1. Total Friction Torque in Dry Conditions

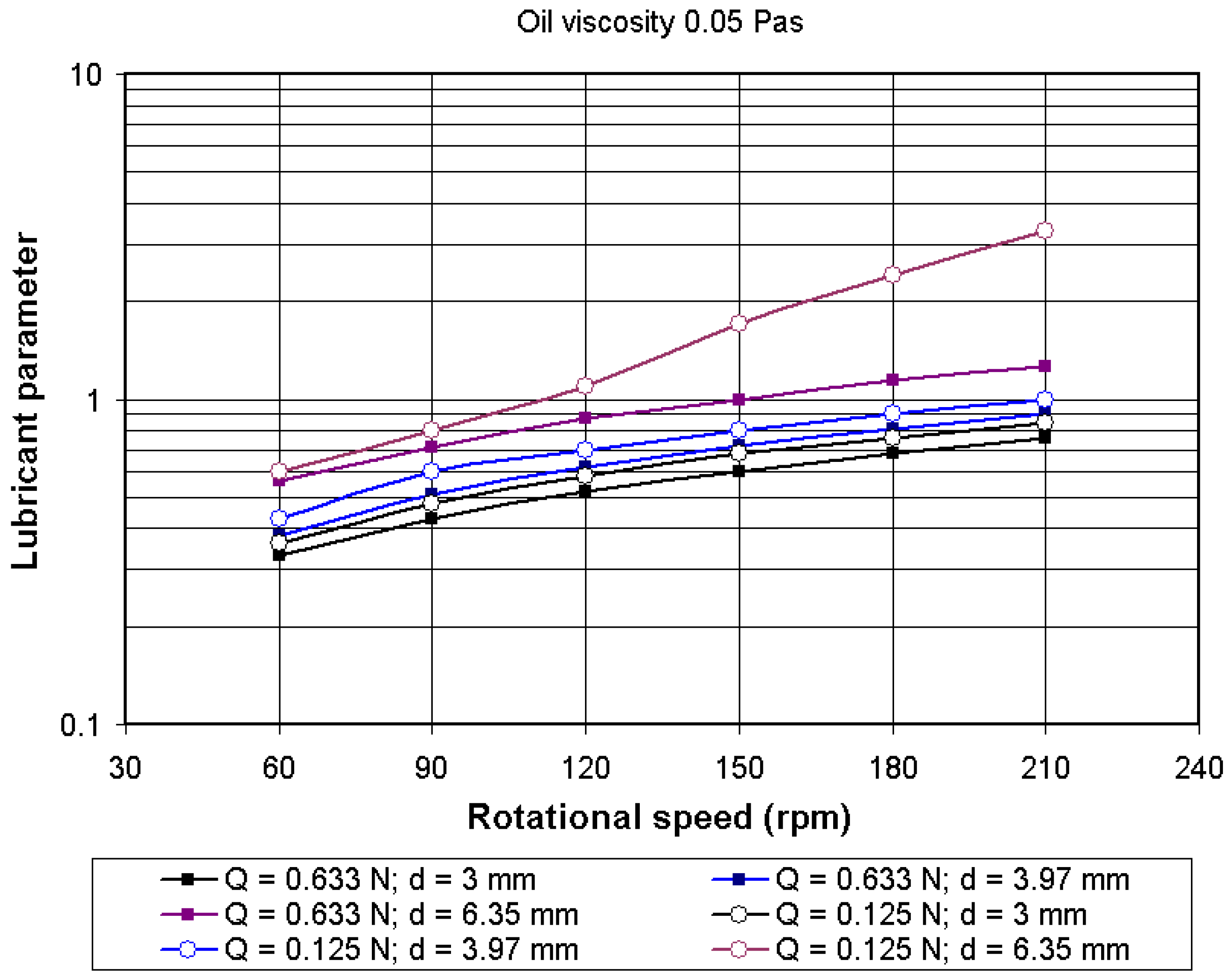
4.2. Variation of the Lubricant Parameter Λ
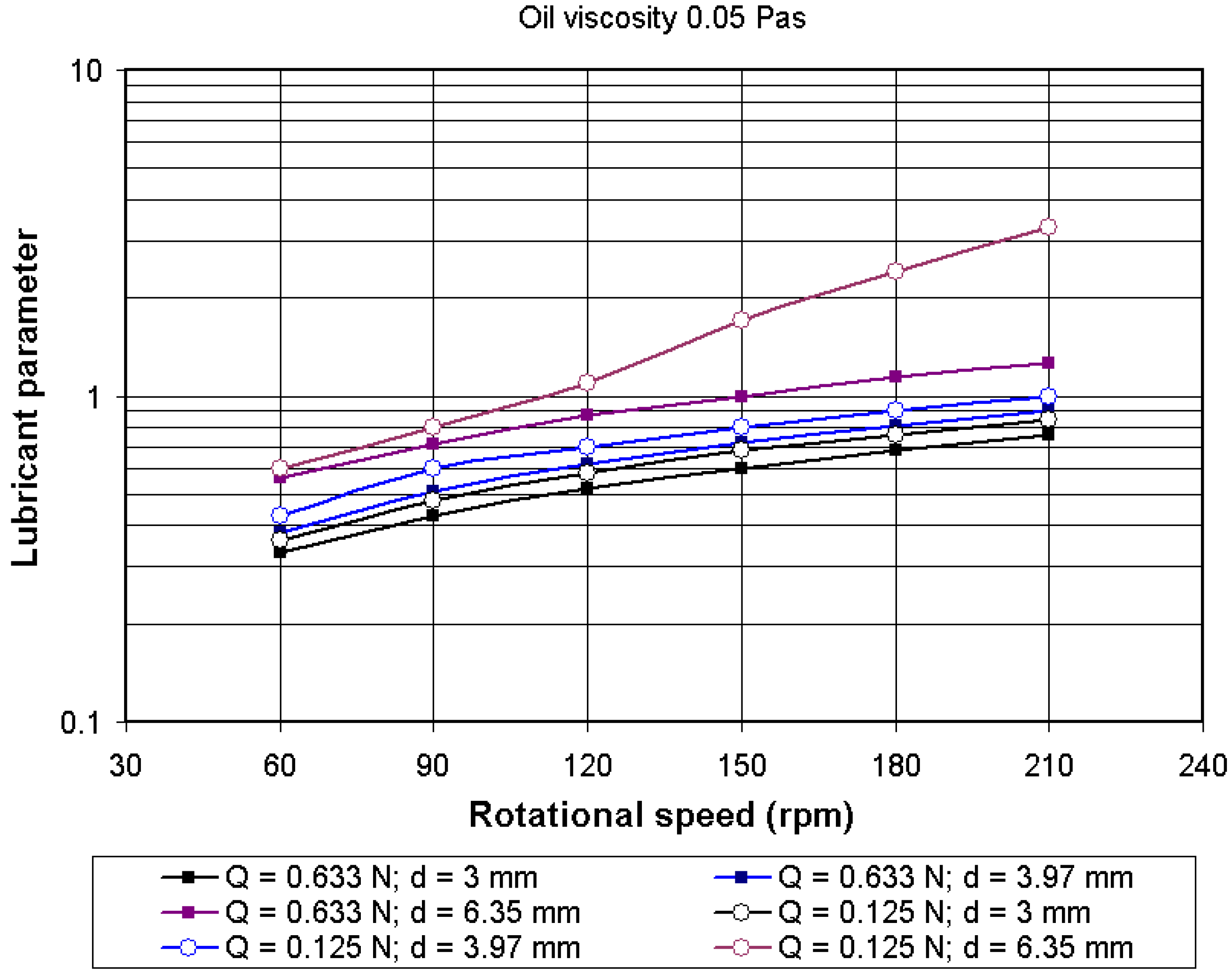
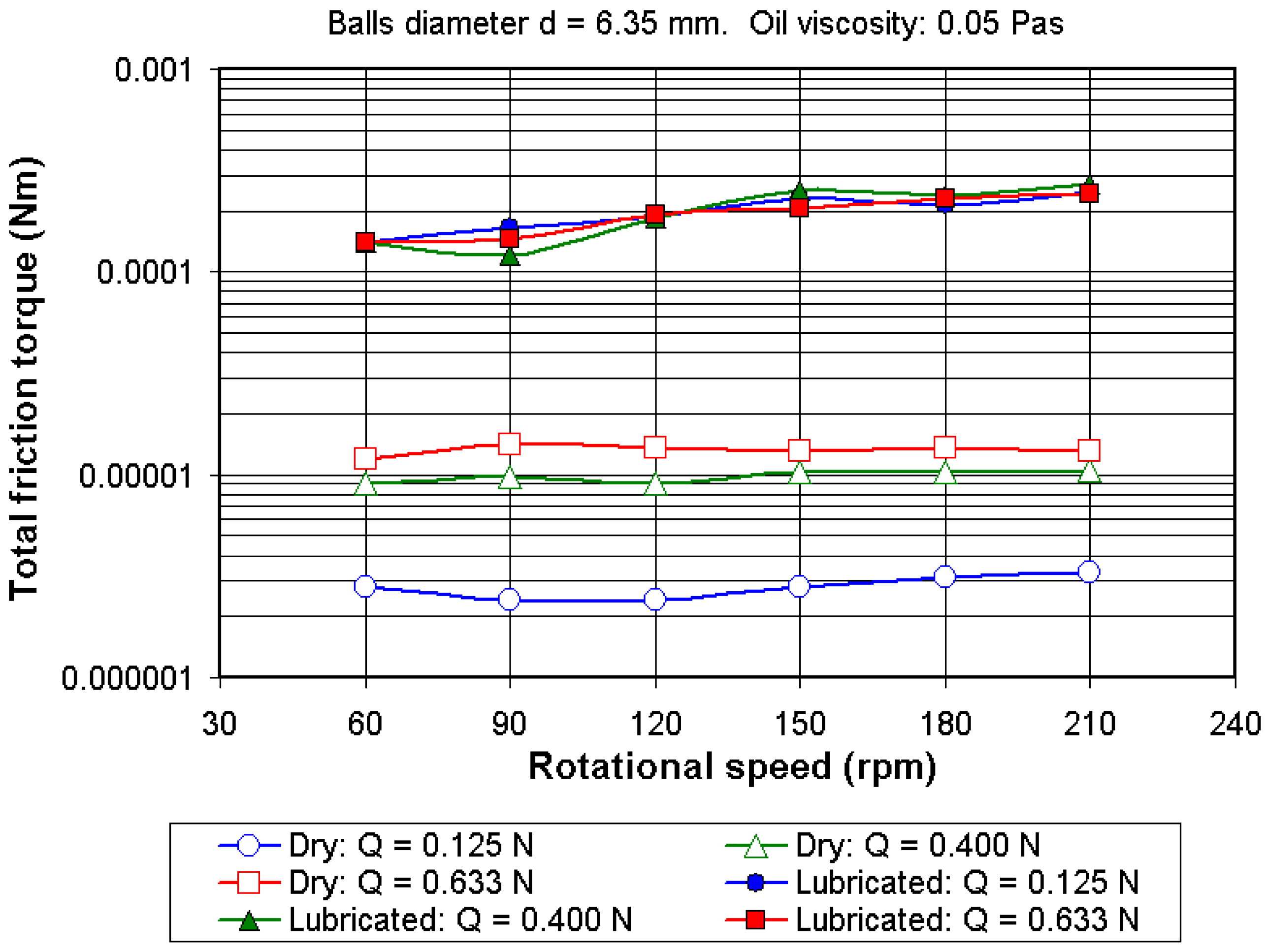
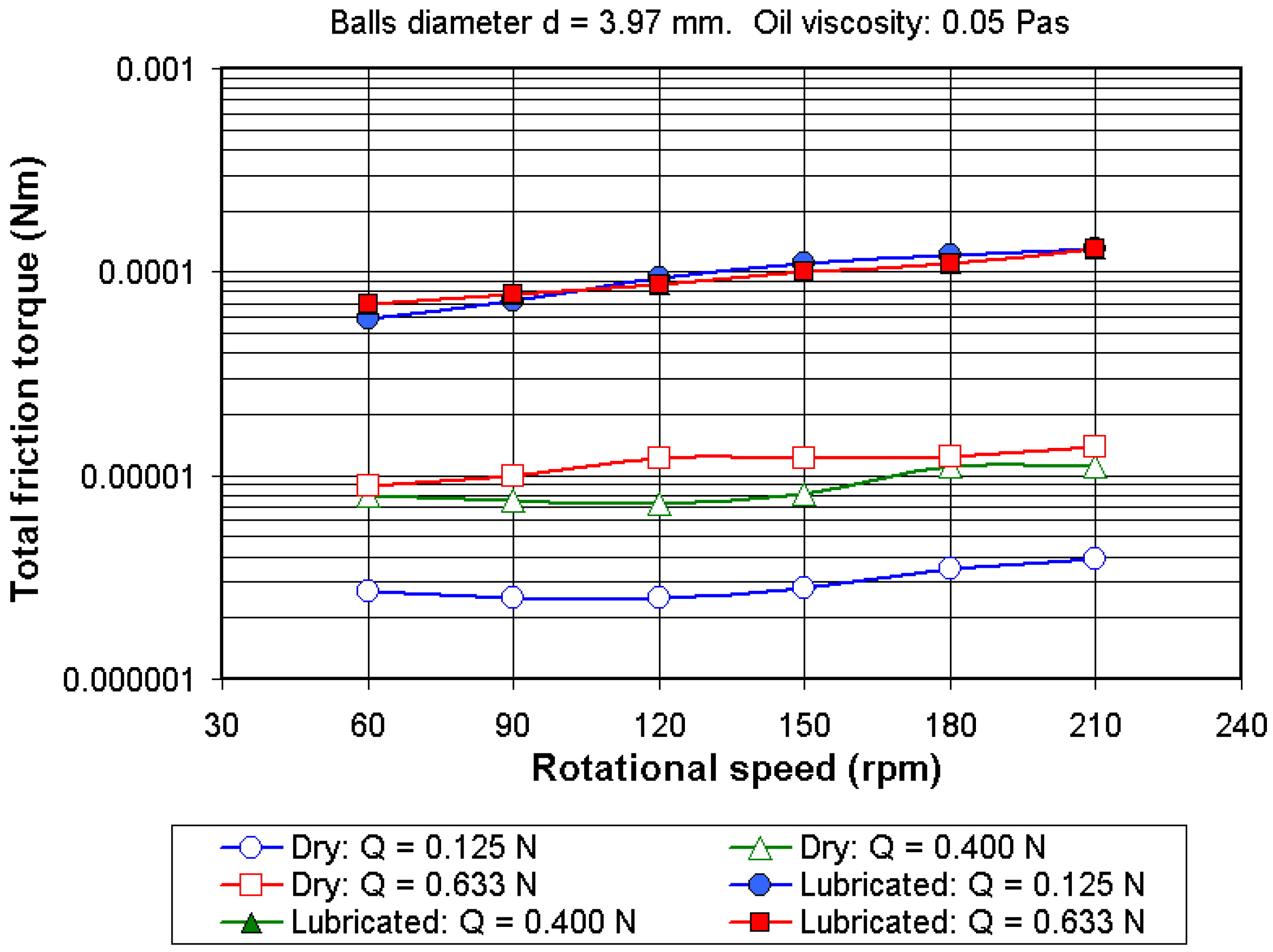
4.3. Total Friction Torque in Lubricated Conditions
- (i)
- By including a very small quantity of oil (two drops), the total friction torque increases substantially as result of the hydrodynamic force FR. It can be observed that total friction torque in dry conditions represents about 2% to 12% of the total friction torque measured in lubricated conditions.
- (ii)
- The total friction torque increases when the rotational speed is increased, and the exponent n used in Equations (19)–(21) has a value varying between 0.11 and 0.65 depending on the lubricant parameter Λ. Table 1 shows the values for K* and n corresponding to small values of the parameter Λ (Λ = 0.3 to 0.8) obtained with 3 mm diameter balls and loaded at Q = 0.633 N. It can be observed that the exponent n varies between 0.11 and 0.36. By increasing the lubricant parameter Λ, the value of the exponent n increases. Table 2 shows the values for K* and n corresponding to large values of the parameter Λ (Λ = 0.6 to 3.2) obtained with 6.35 mm diameter balls and loaded at Q = 0.125 N.
| Initial Rotational Speed, rpm | |
|---|---|
| 60 | |
| 90 | |
| 120 | |
| 150 | |
| 180 | |
| 210 |
| Initial Rotational Speed, rpm | |
|---|---|
| 60 | |
| 90 | |
| 120 | |
| 150 | |
| 180 | |
| 210 |
4.4. Validation of the Analytical Friction Torque in Lubricated Conditions

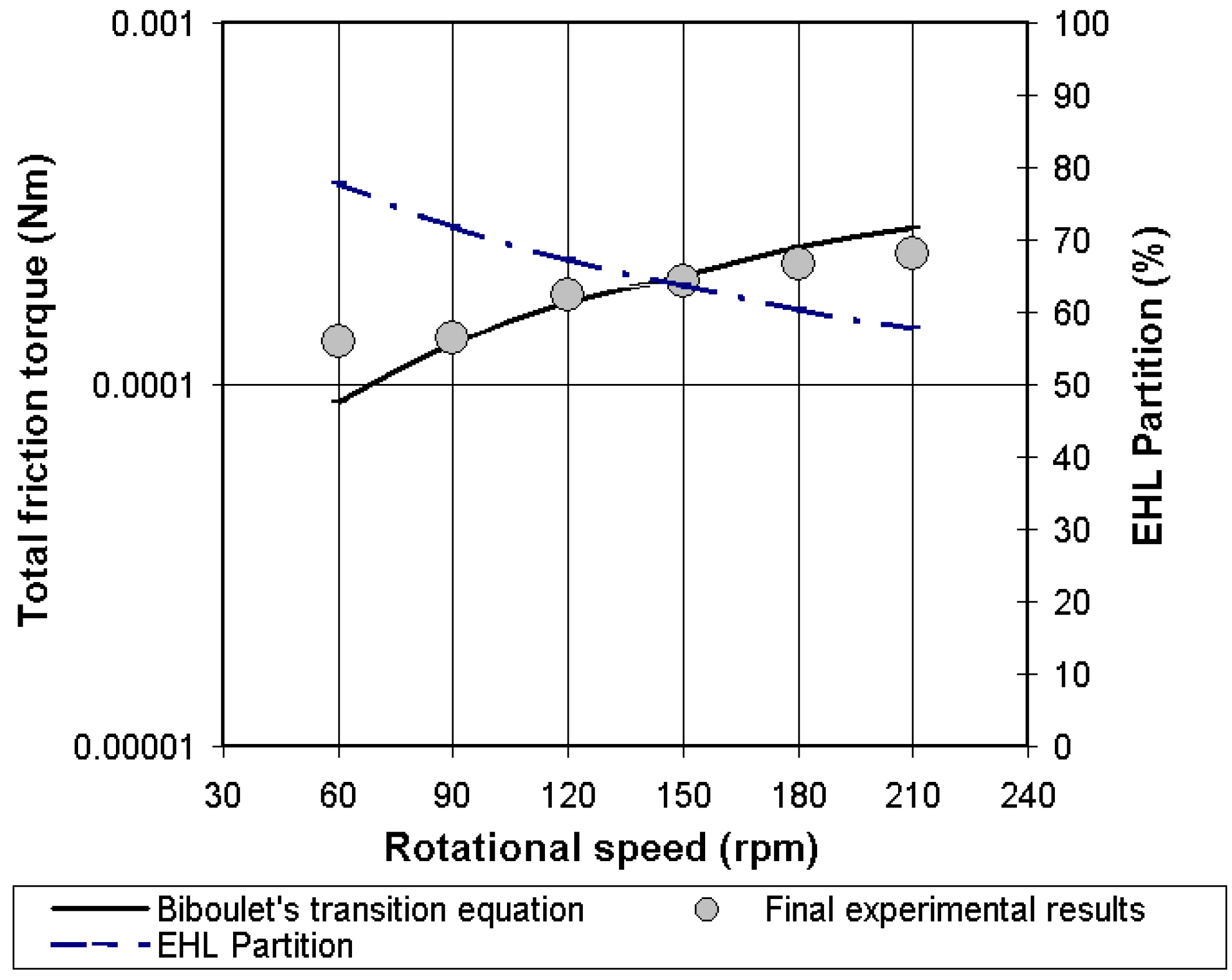
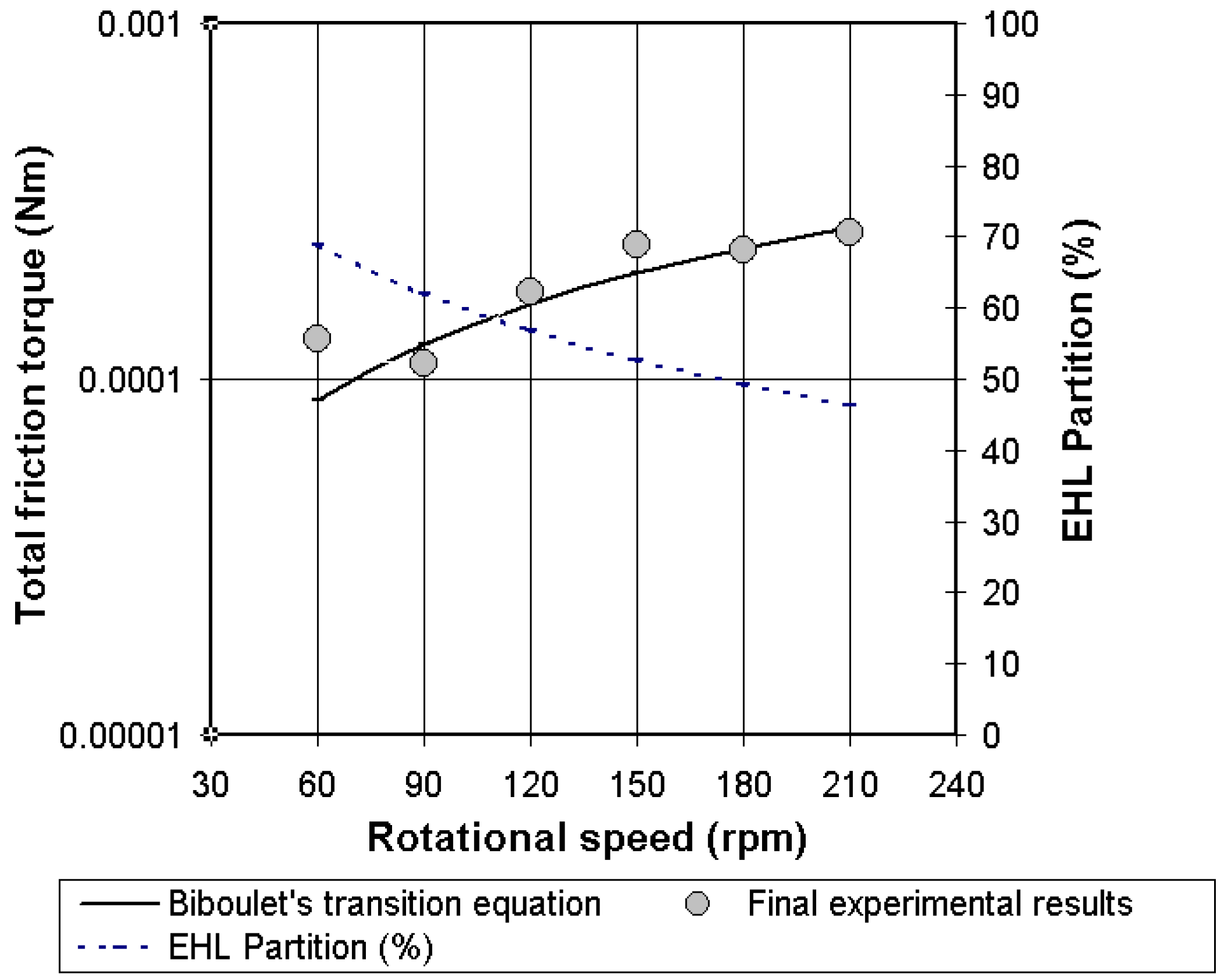
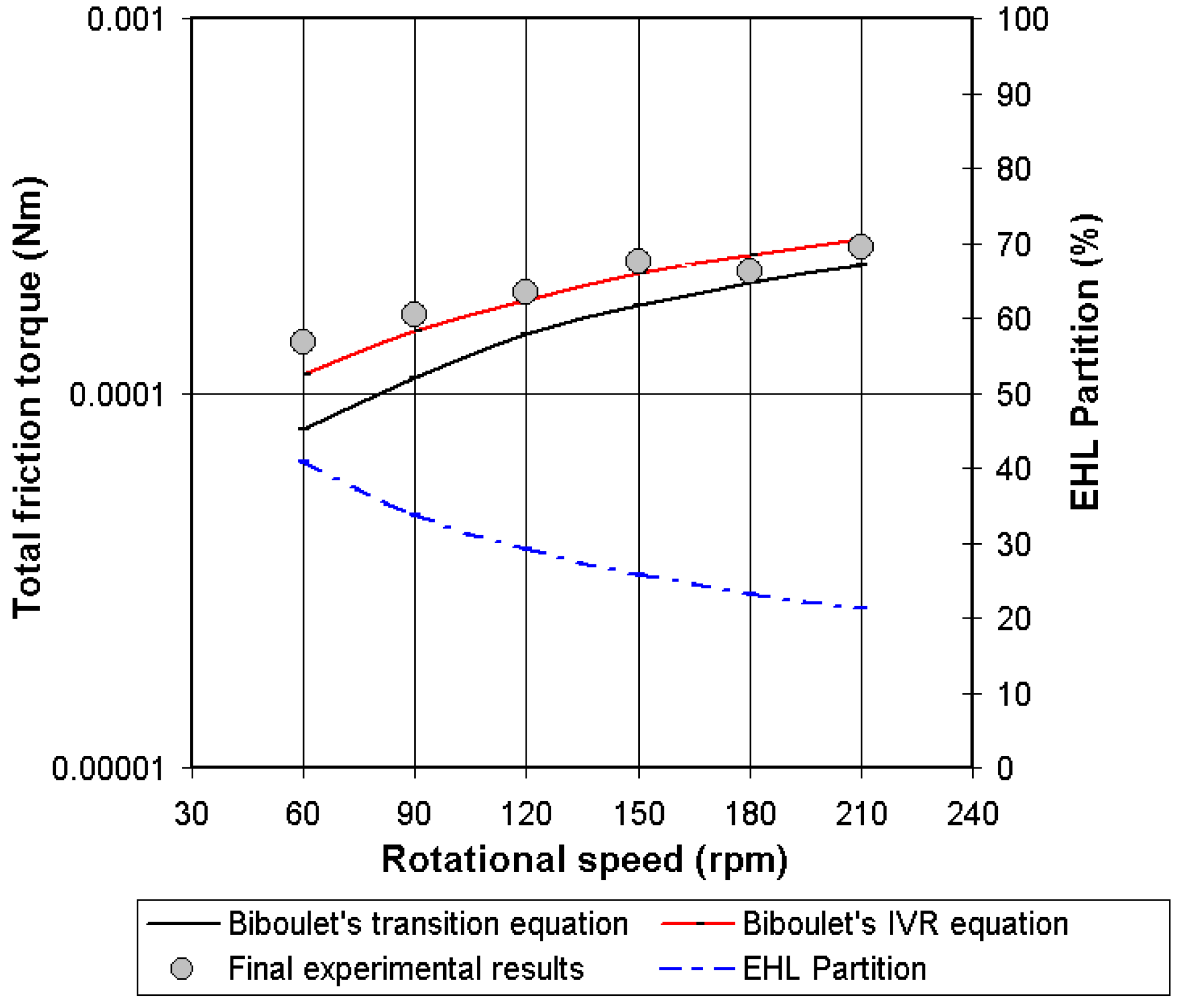
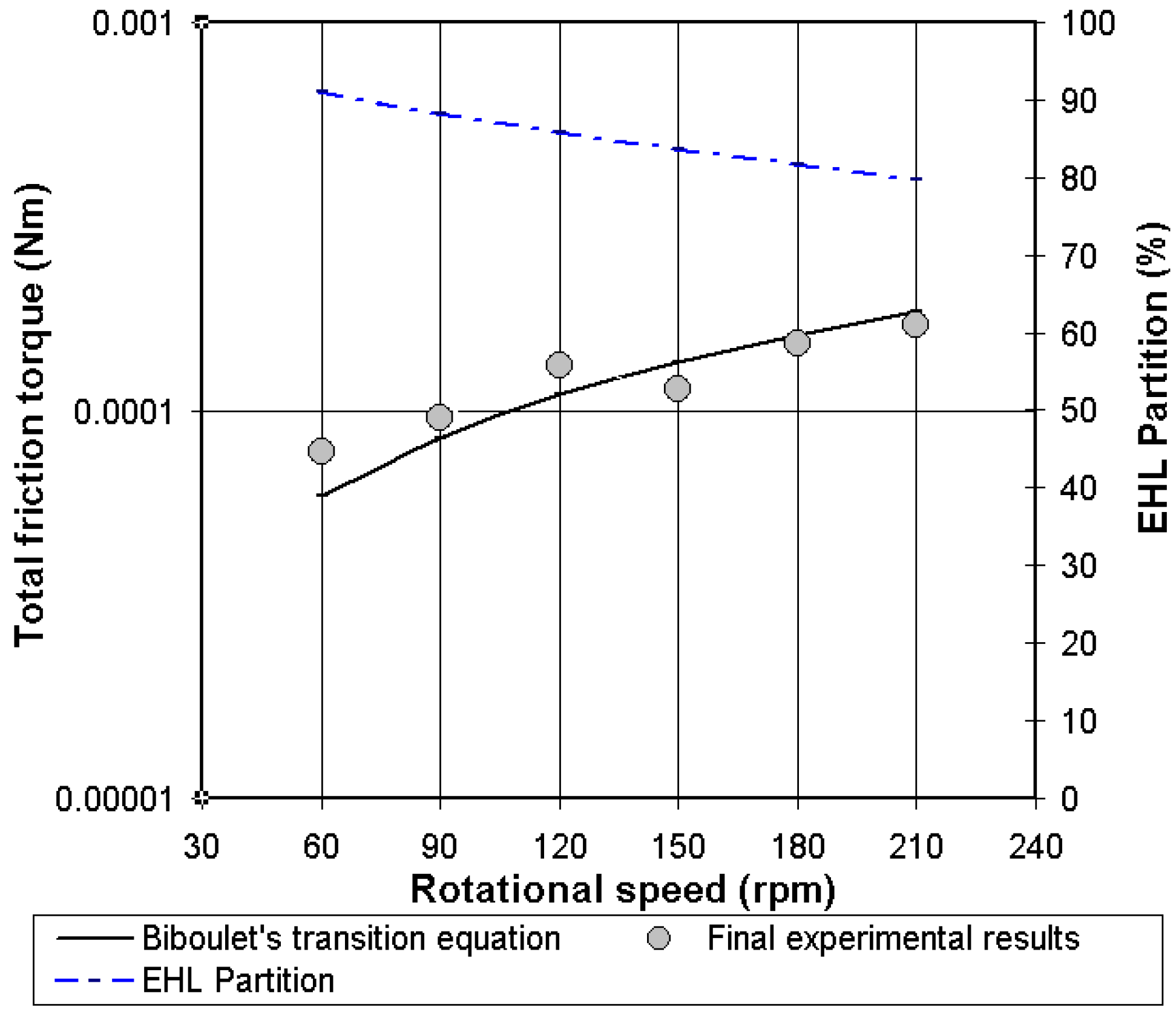
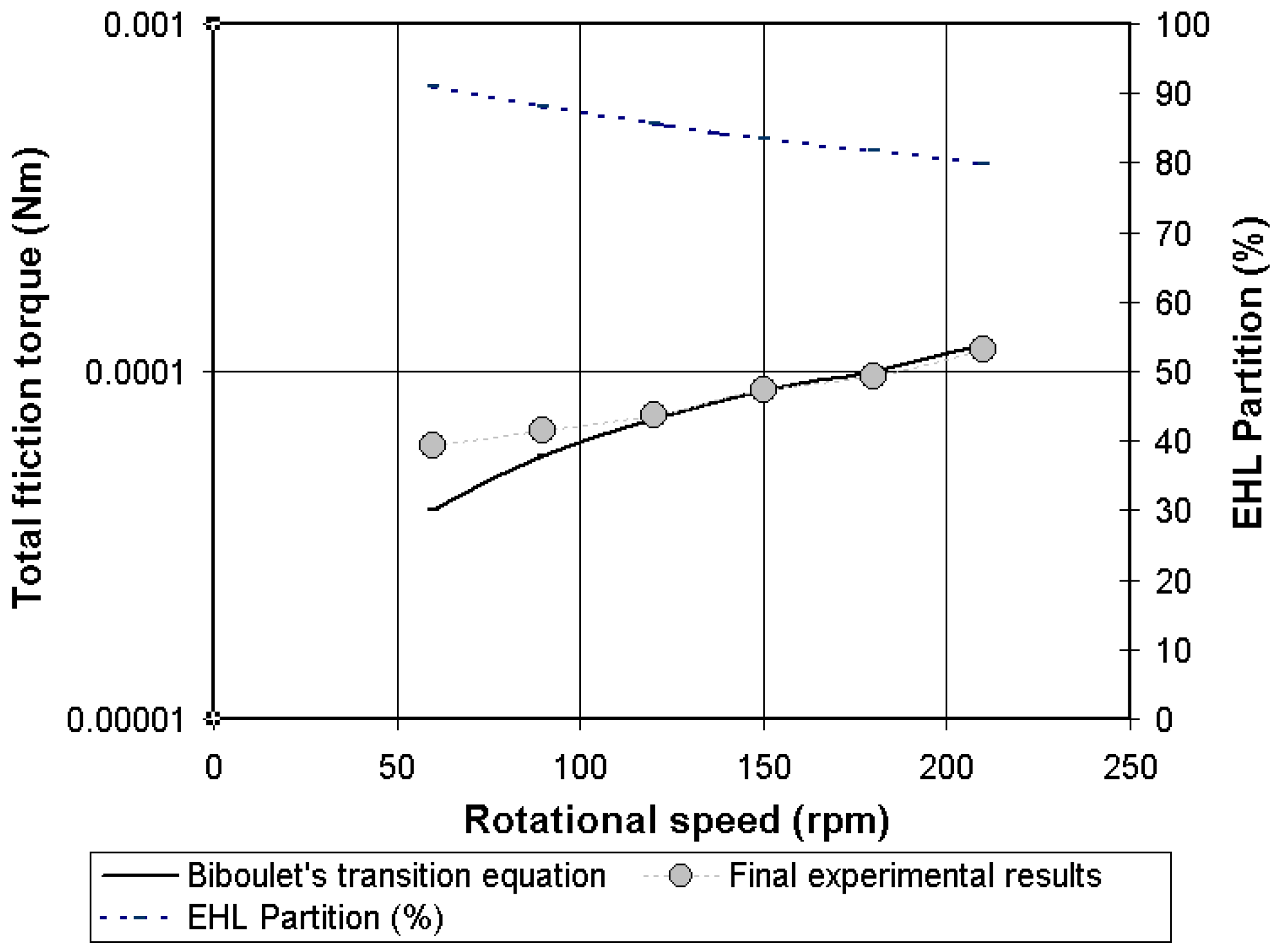
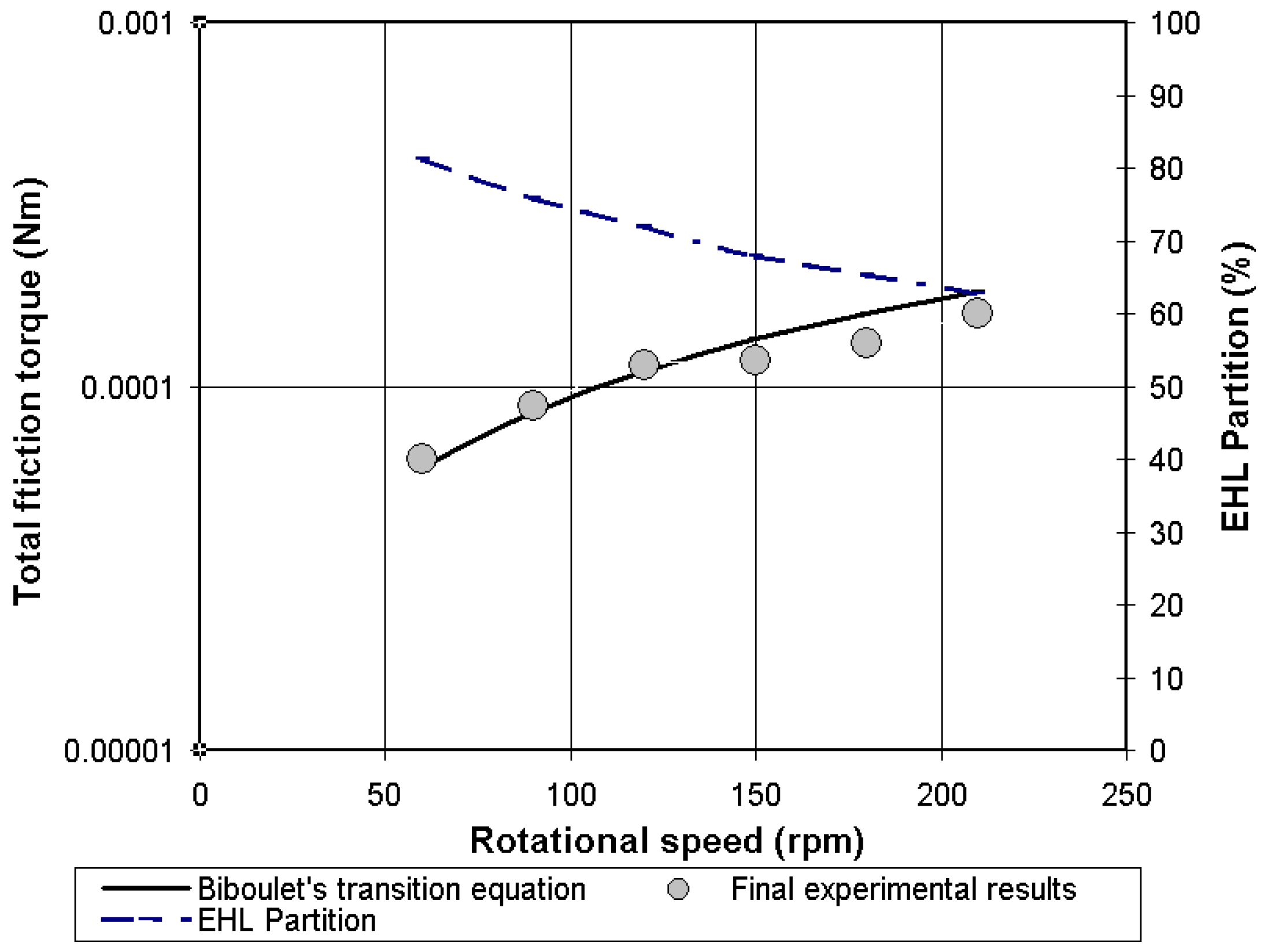
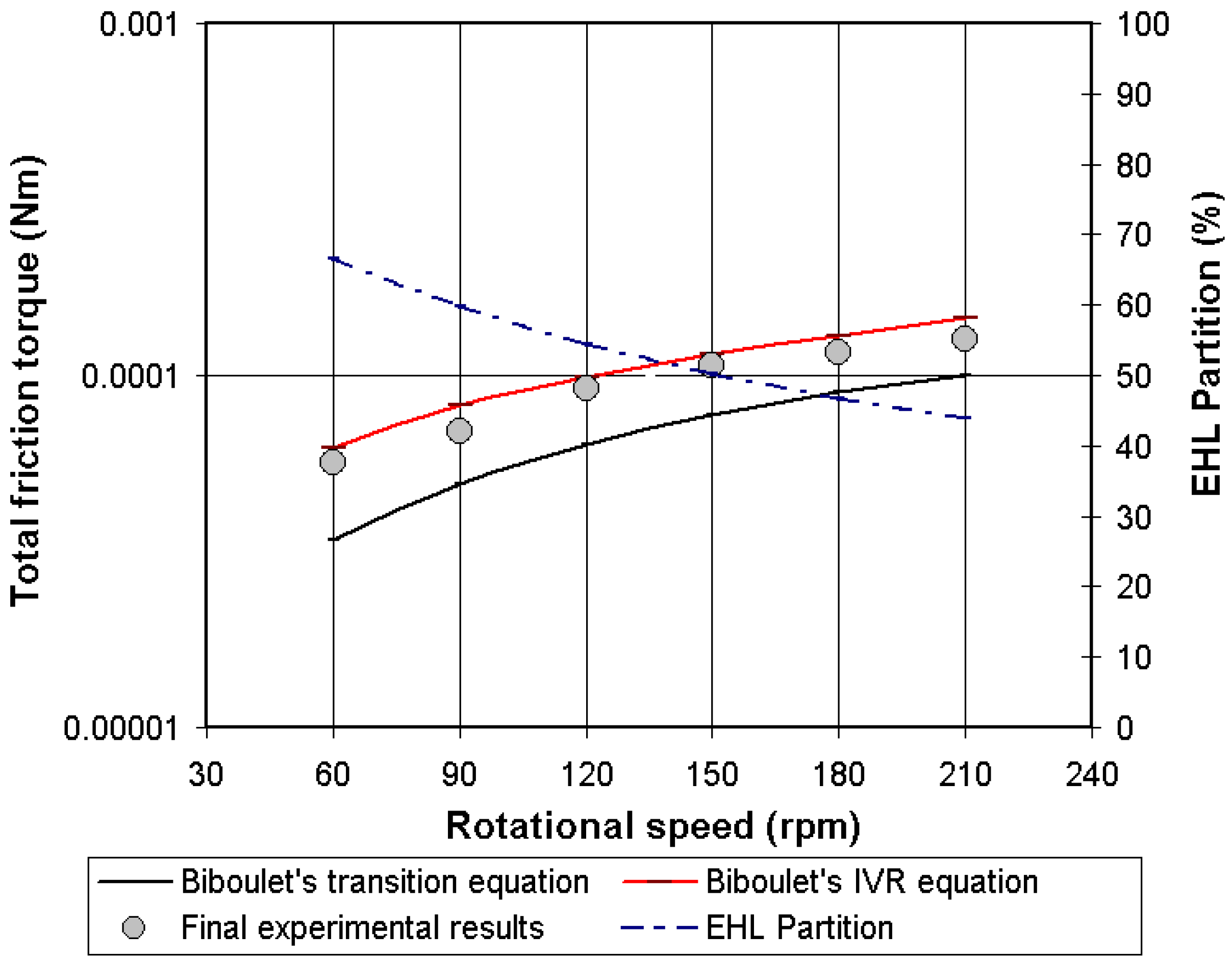
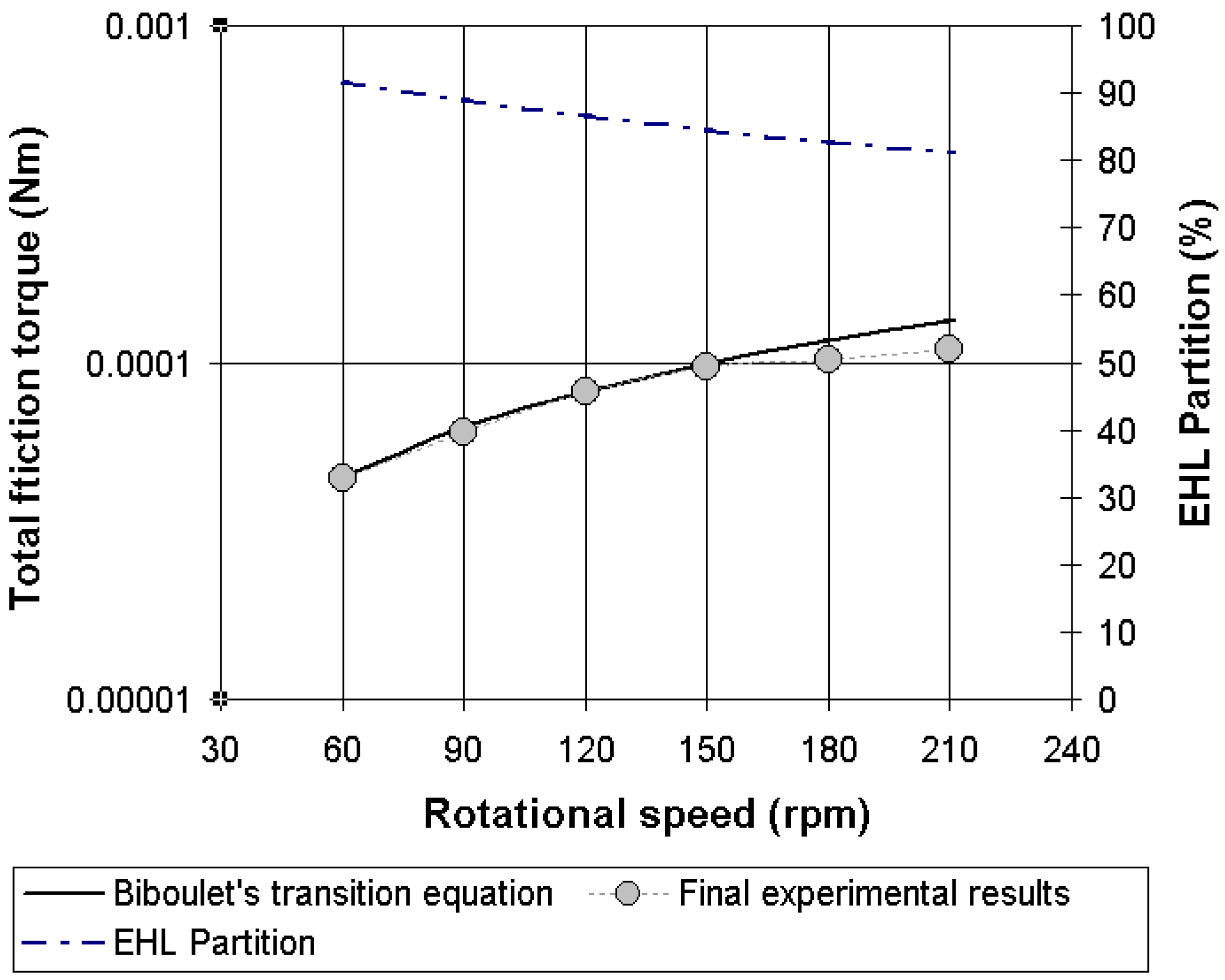
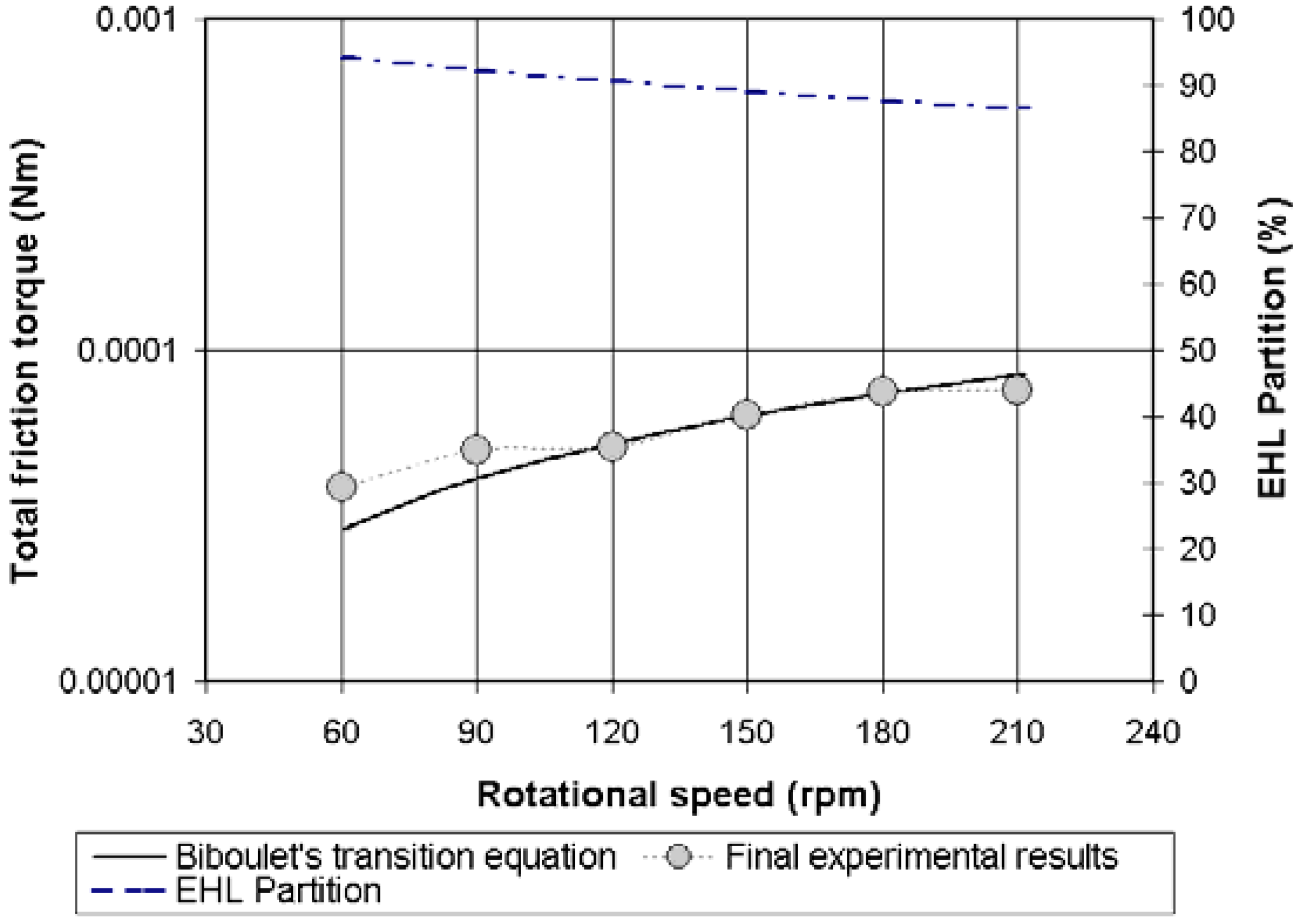
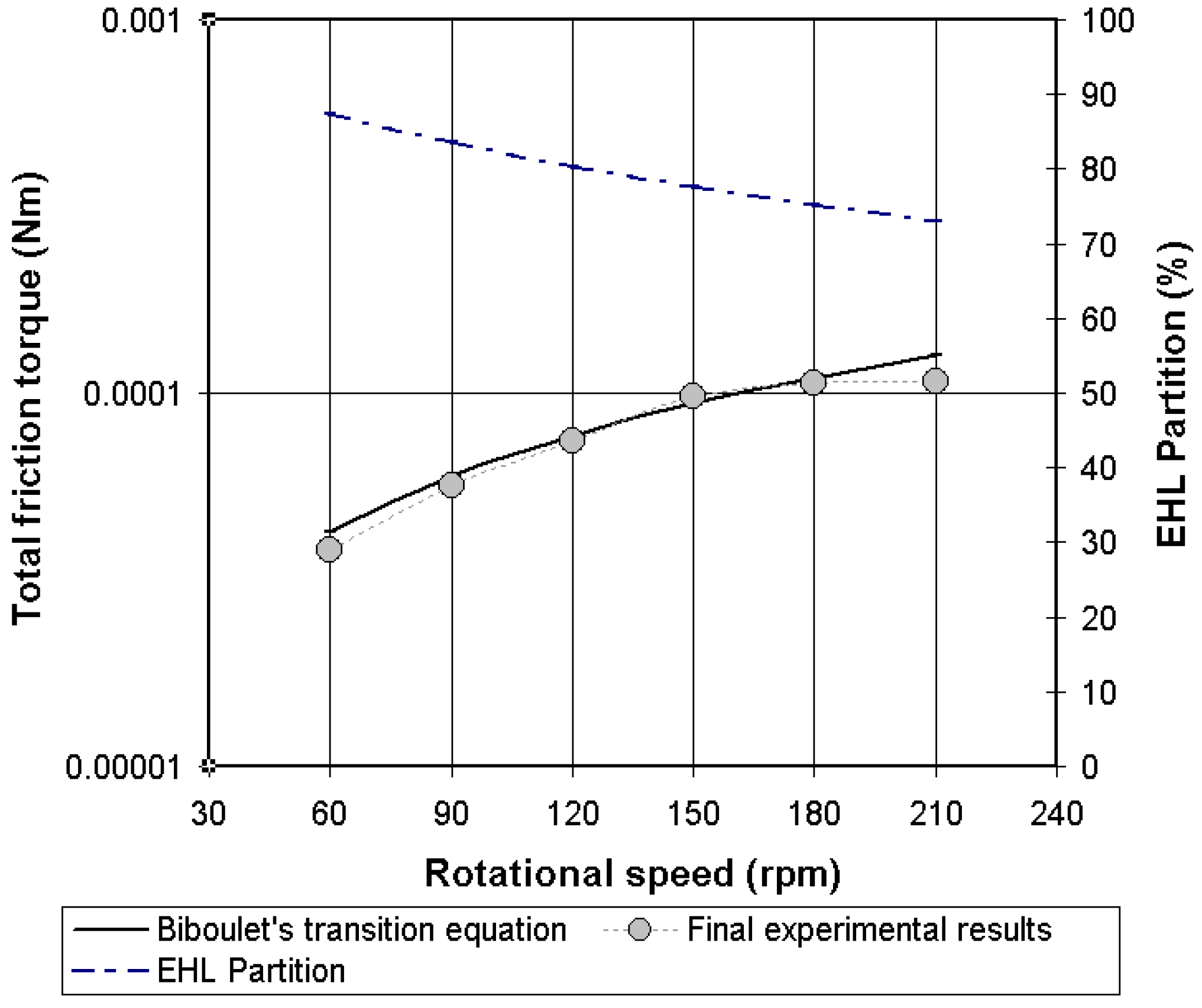
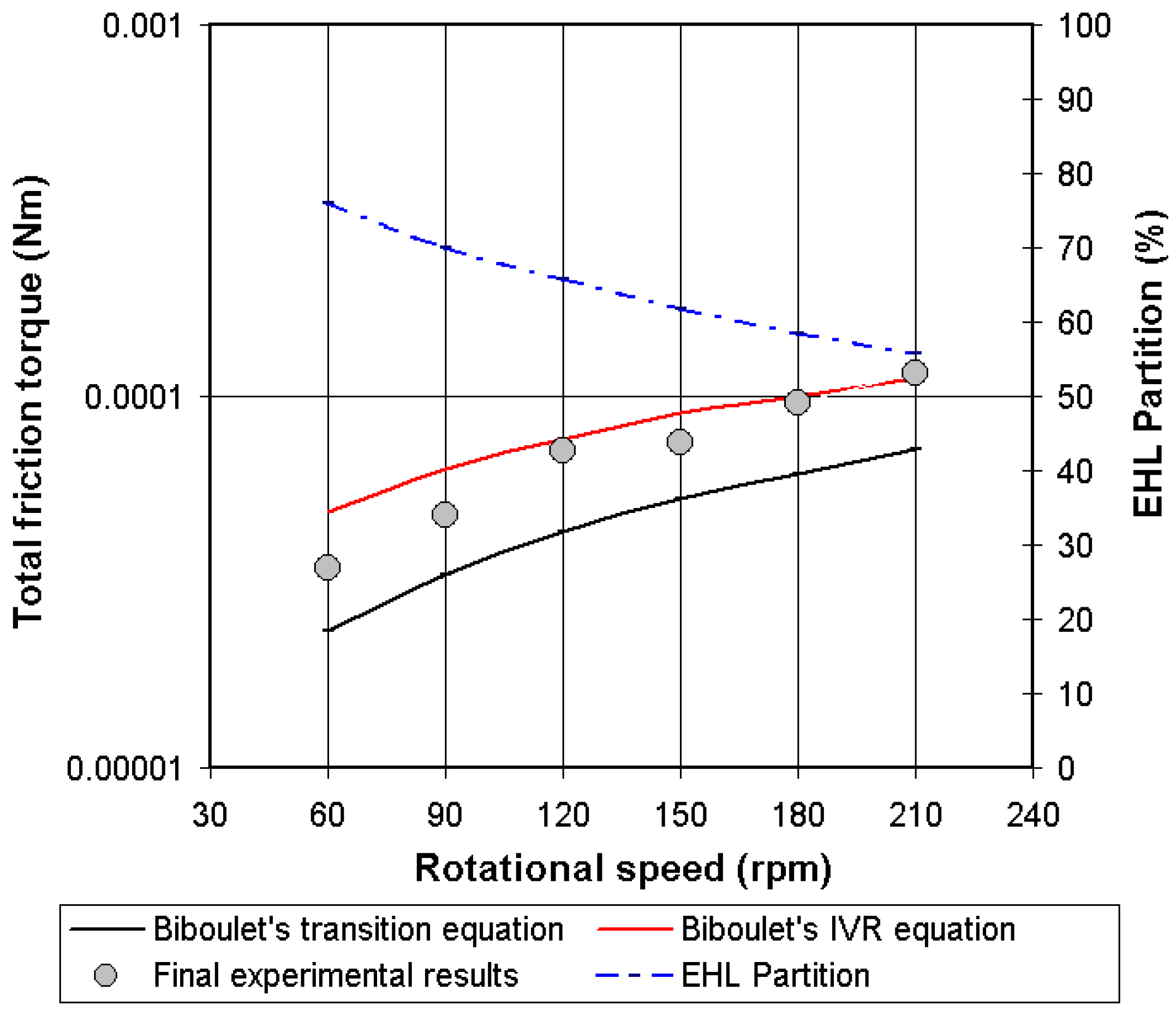
4.5. Comments
5. Conclusions
Author Contributions
Appendix A
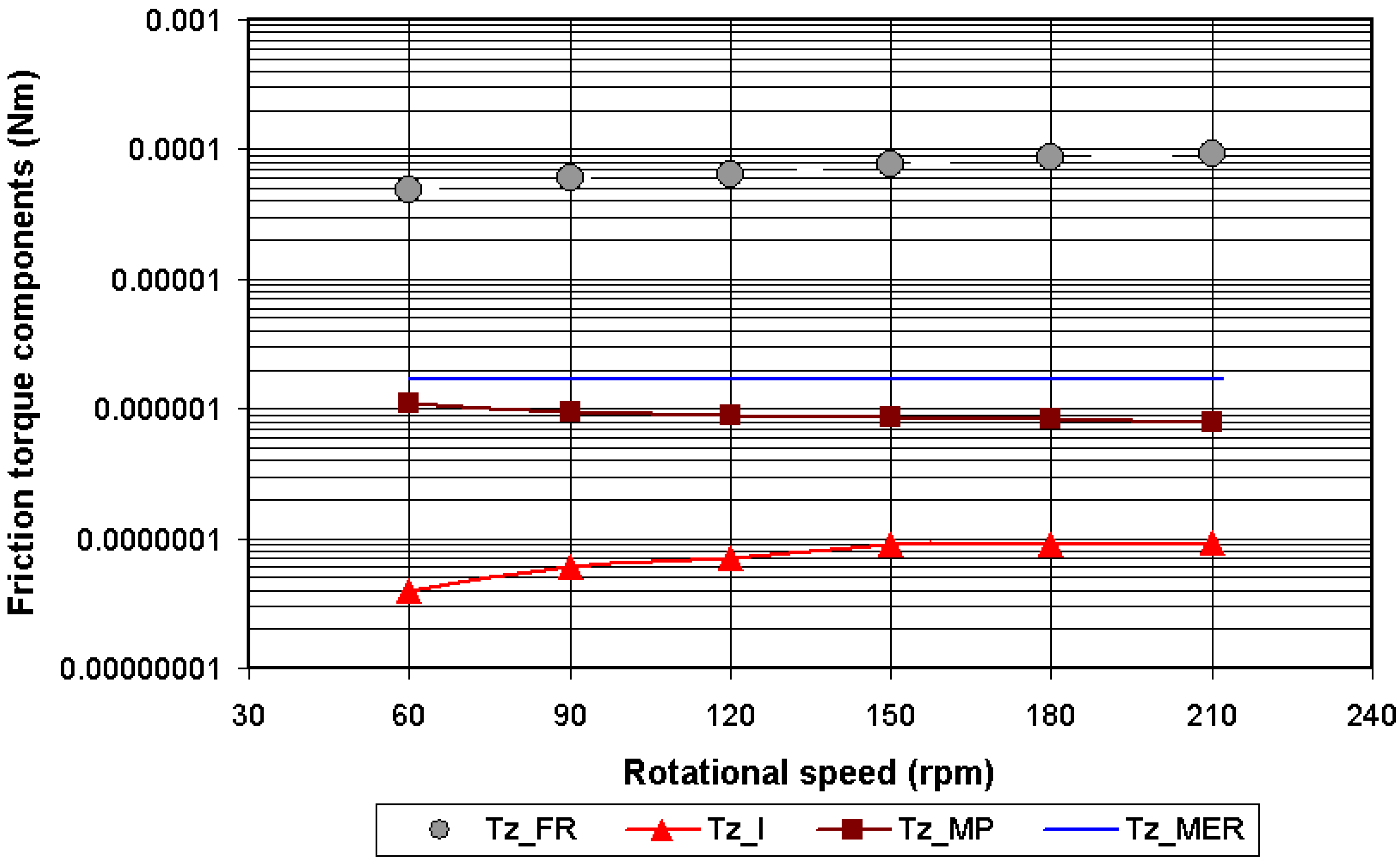
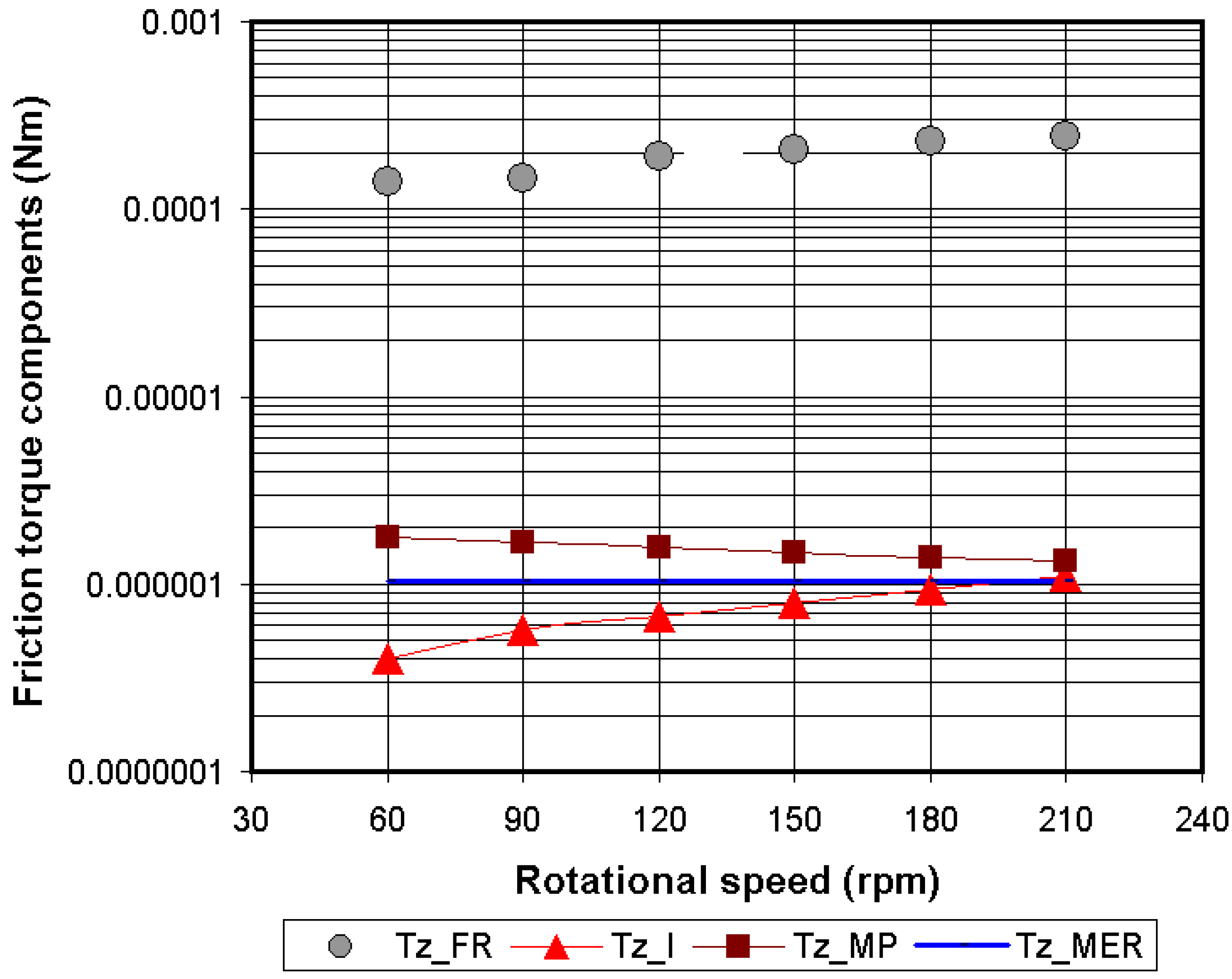
Appendix B
Conflicts of Interest
References
- Houpert, L. Numerical and Analytical Calculations in Ball Bearings. In Proceeding of 8th European Space Mechanism and Tribology Symp, Toulouse, France, 29 September–1 October 1999.
- Houpert, L. Ball Bearing and Tapered Roller Bearing Torque: Analytical, Numerical and Experimental Results. STLE Tribol. Trans. 2002, 45, 345–353. [Google Scholar] [CrossRef]
- Olaru, D.; Stamate, C.; Dumitrascu, A. Prisacaru Gh. New micro tribometer for rolling friction. Wear 2011, 271, 842–852. [Google Scholar] [CrossRef]
- Houpert, L. Piezoviscous-rigid rolling and sliding traction forces. Application: the rolling element-cage pocket contact. Proceedings of the 1986 ASLE/ASME Conference, Pittsburgh. ASME J. Tribol. 1987, 109, 363–371. [Google Scholar] [CrossRef]
- Biboulet, N.; Houpert, L. Hydrodynamic force and moment in pure rolling lubricated contacts: Part 2, Point contacts. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 777–787. [Google Scholar] [CrossRef]
- Bălan, M.R.; Stamate, V.C.; Houpert, L.; Olaru, D. The influence of the lubricant viscosity on the rolling friction torque. Tribol. Int. 2014, 72, 1–12. [Google Scholar] [CrossRef]
- Bălan, M.R.; Stamate, V.C.; Houpert, L.; Tufescu, A.; Olaru, D.N. Influence of the Geometry on the Rolling Friction Torque in Lubricated Ball-Race Contacts. Appl. Mech. Mater. Adv. Concepts Mech. Eng. I 2014, 658, 271–276. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bălan, M.R.D.; Houpert, L.; Tufescu, A.; Olaru, D.N. Rolling Friction Torque in Ball-Race Contacts Operating in Mixed Lubrication Conditions. Lubricants 2015, 3, 222-243. https://doi.org/10.3390/lubricants3020222
Bălan MRD, Houpert L, Tufescu A, Olaru DN. Rolling Friction Torque in Ball-Race Contacts Operating in Mixed Lubrication Conditions. Lubricants. 2015; 3(2):222-243. https://doi.org/10.3390/lubricants3020222
Chicago/Turabian StyleBălan, Mihaela Rodica D., Luc Houpert, Ana Tufescu, and Dumitru N. Olaru. 2015. "Rolling Friction Torque in Ball-Race Contacts Operating in Mixed Lubrication Conditions" Lubricants 3, no. 2: 222-243. https://doi.org/10.3390/lubricants3020222
APA StyleBălan, M. R. D., Houpert, L., Tufescu, A., & Olaru, D. N. (2015). Rolling Friction Torque in Ball-Race Contacts Operating in Mixed Lubrication Conditions. Lubricants, 3(2), 222-243. https://doi.org/10.3390/lubricants3020222





