Discharge Coefficient and Pressure Loss Characteristics of Multi-Branch Oil Jet Nozzles
Abstract
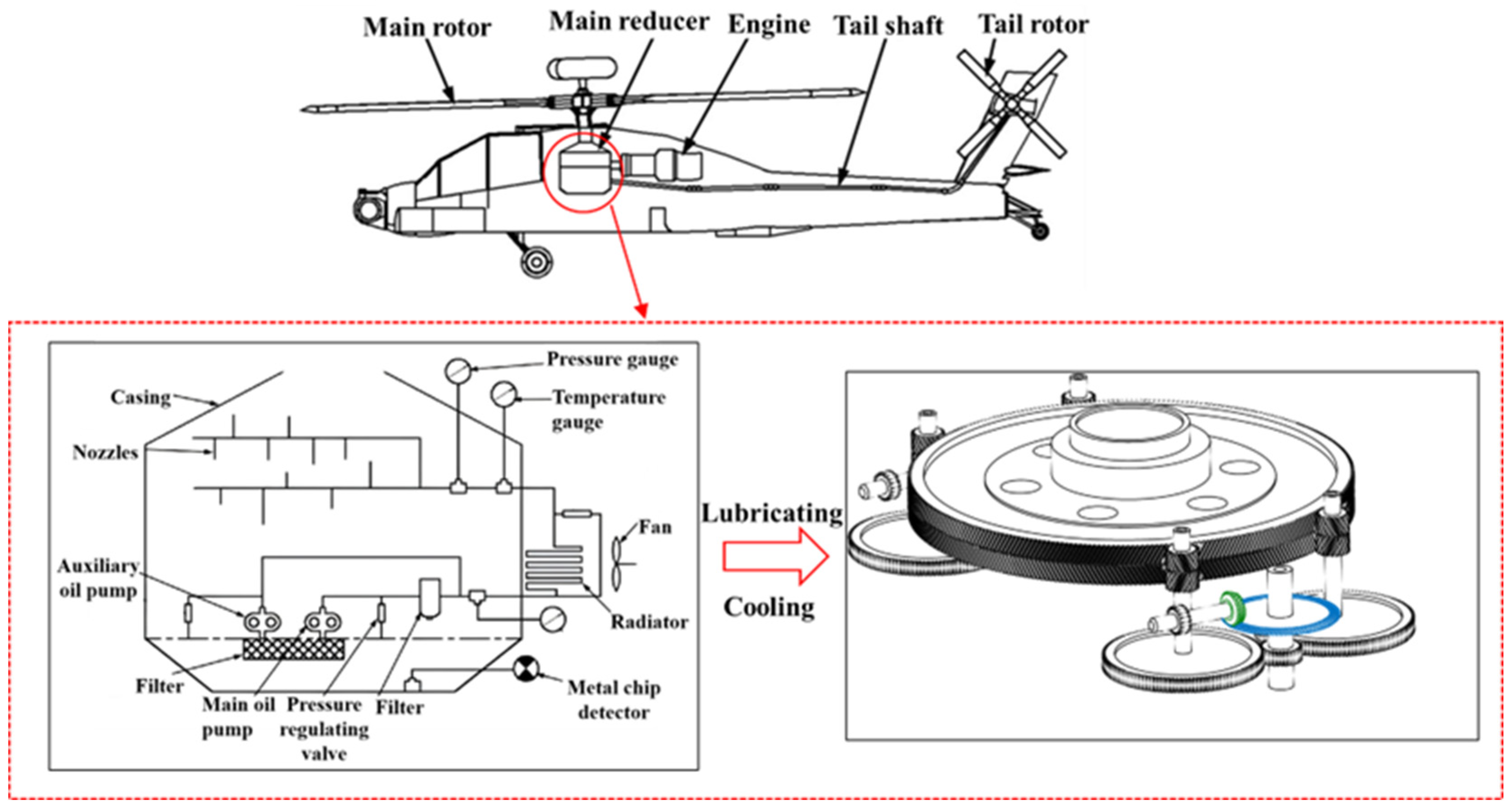
1. Introduction
2. Numerical Methods
2.1. Governing Equations
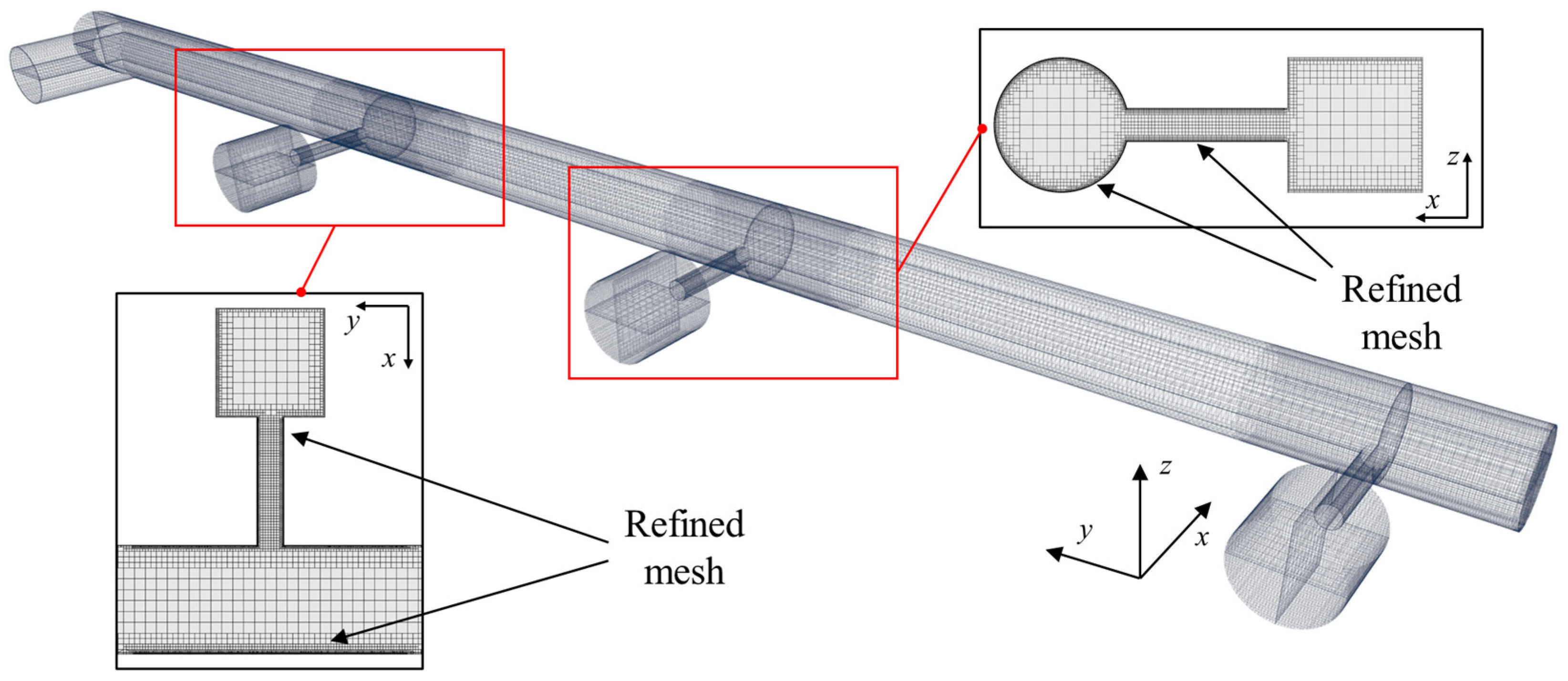
2.2. Numerical Setup
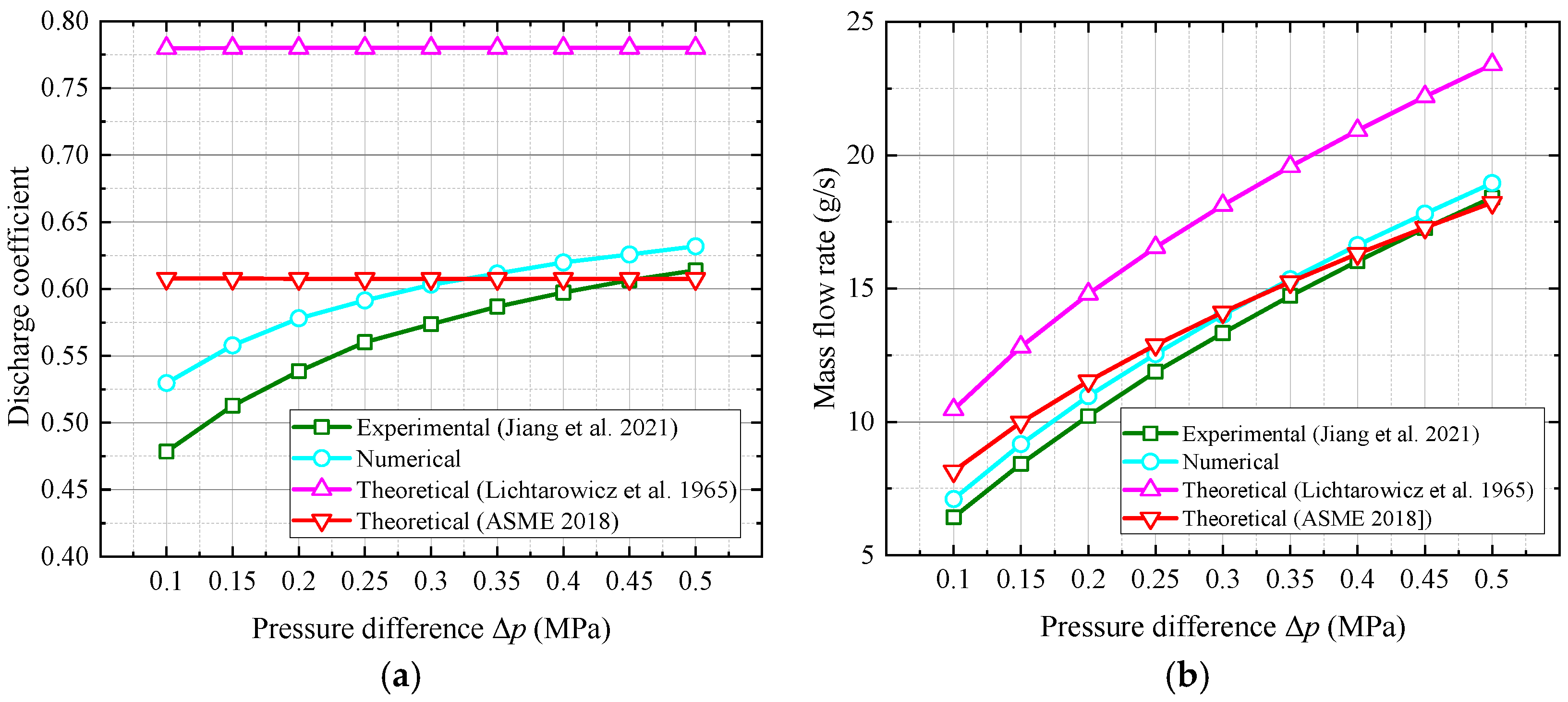
2.3. Validation of Numerical Method
3. Experiments and Analysis
Verification of Numerical Method
4. Results and Discussions
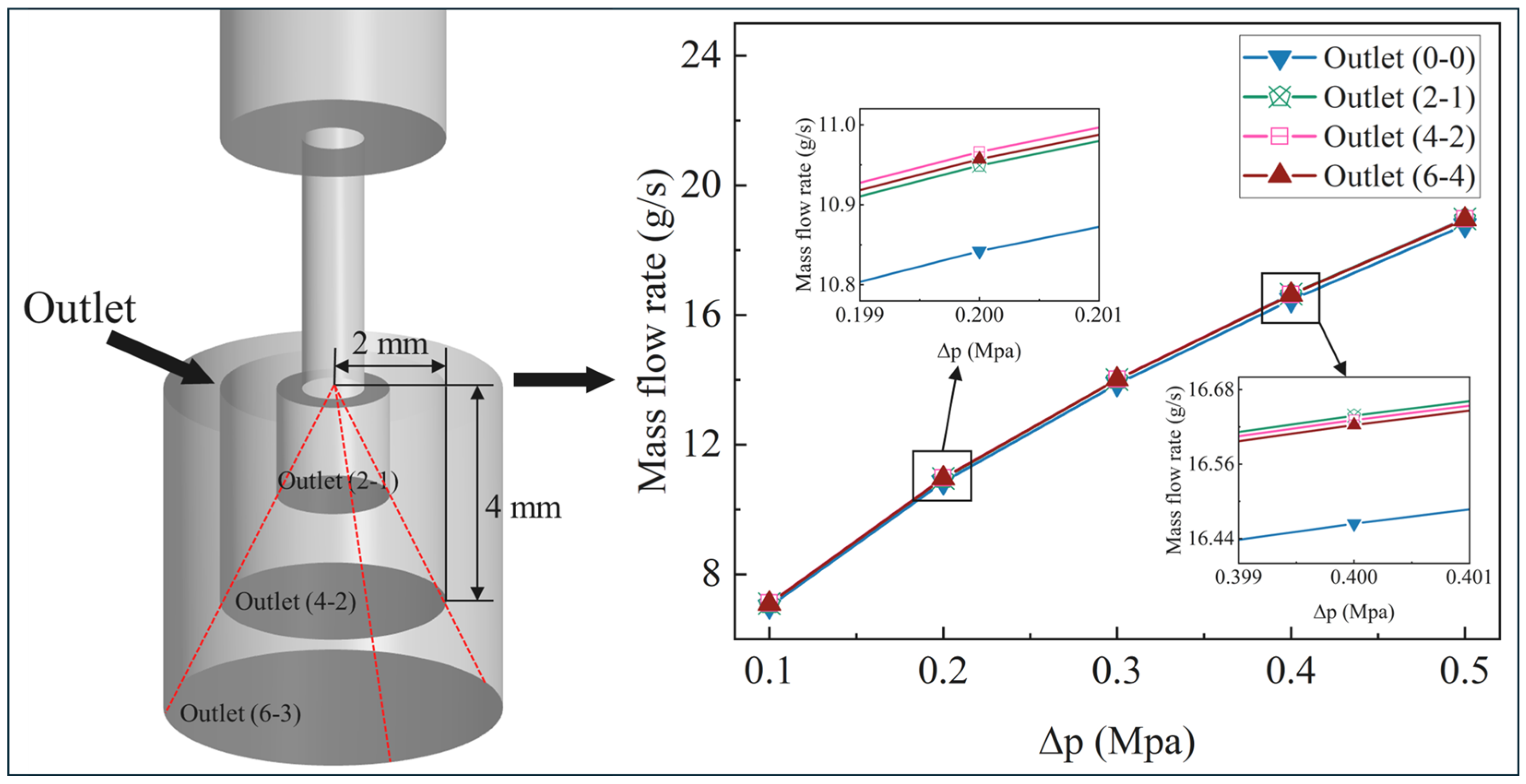
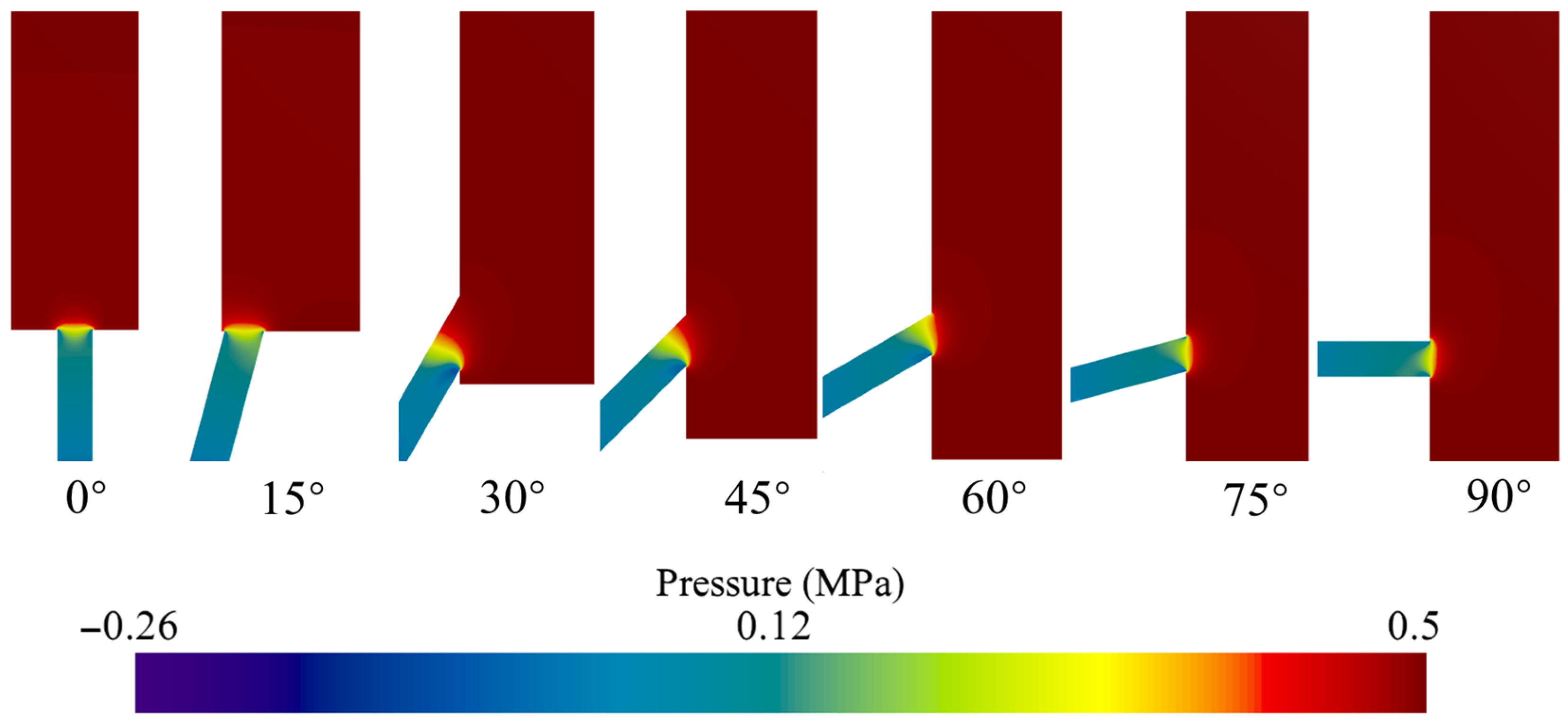
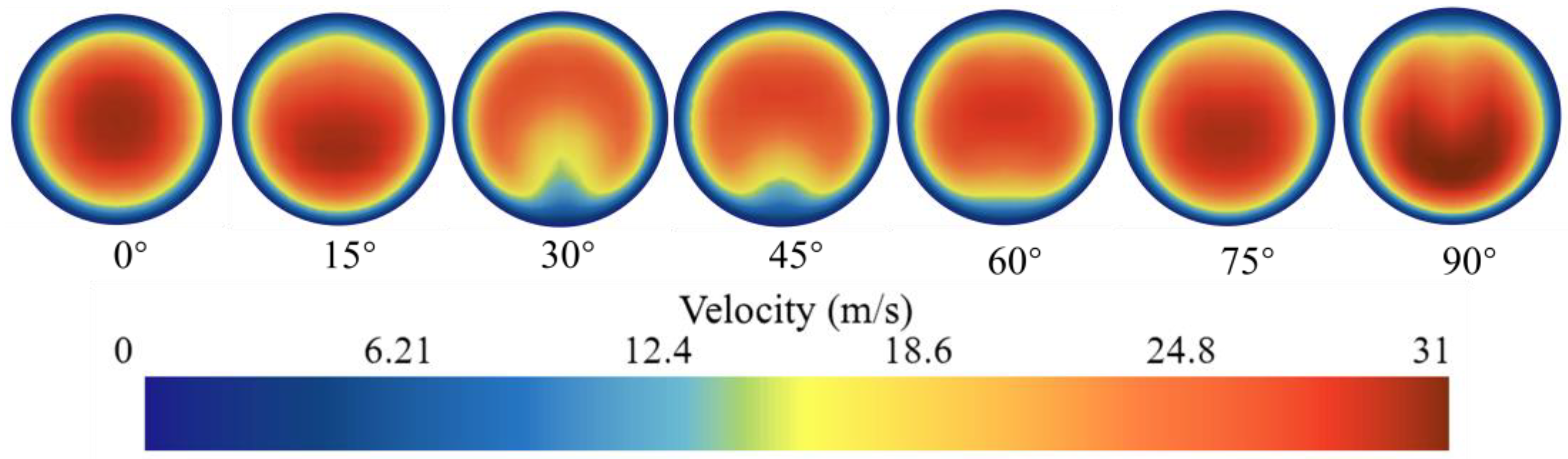
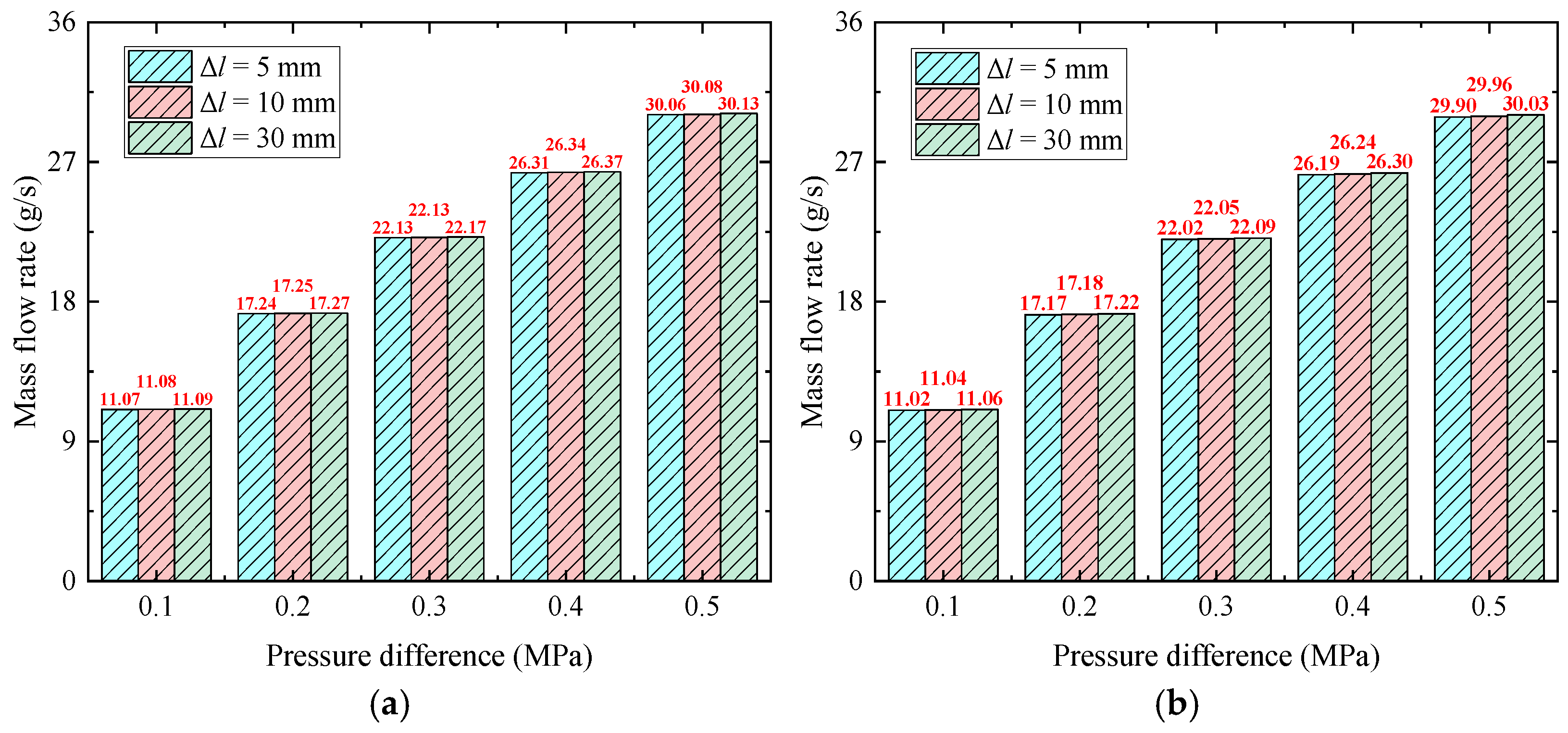
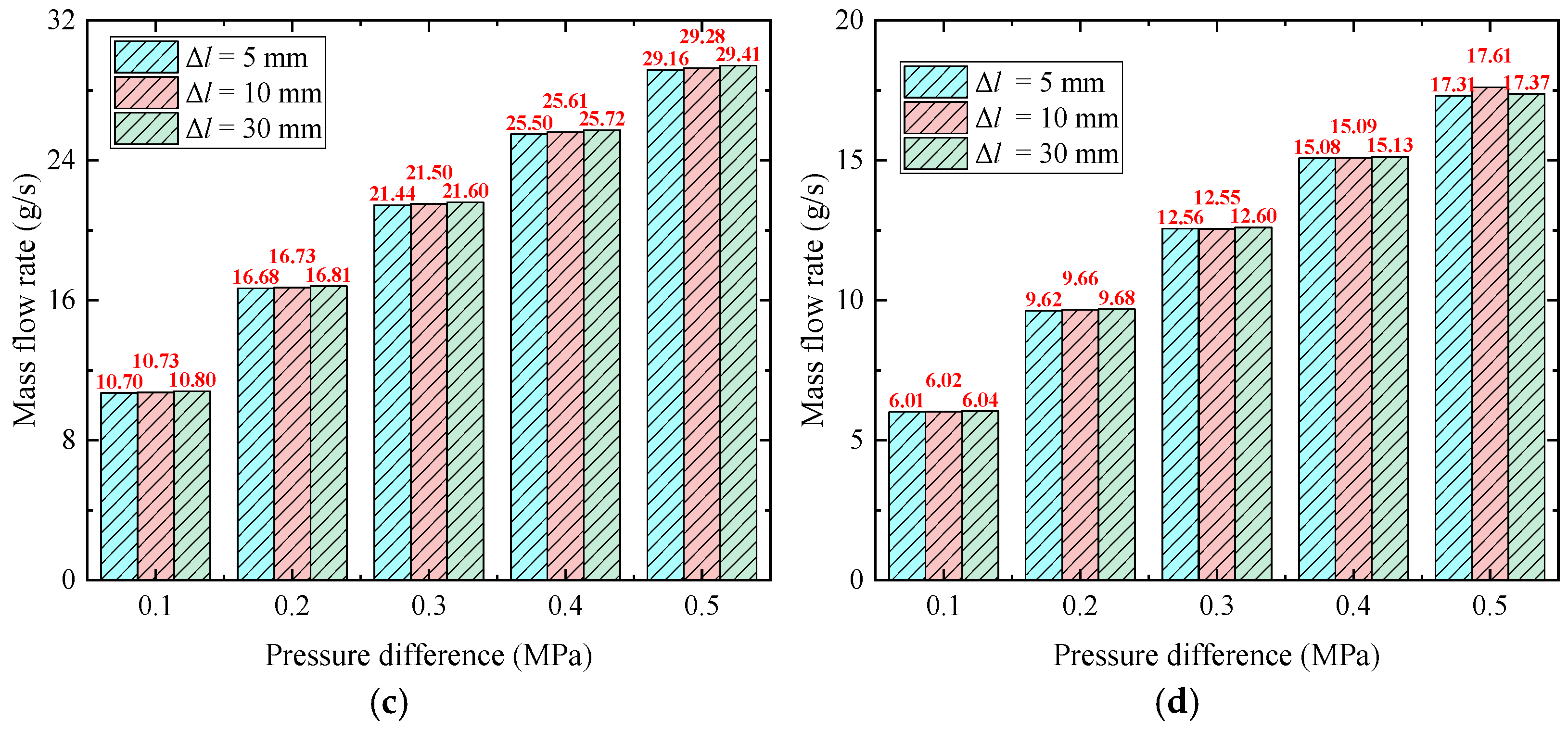
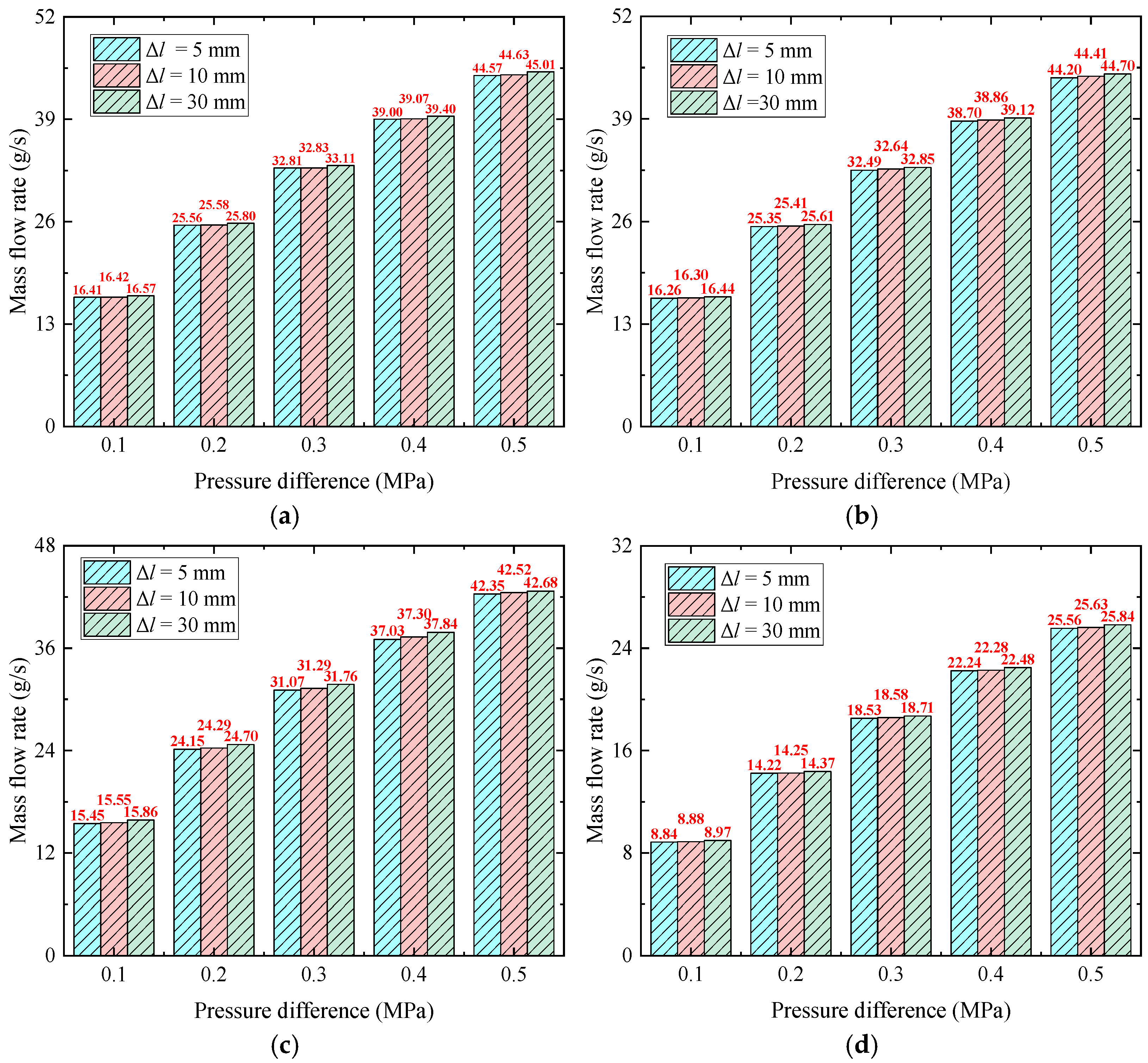
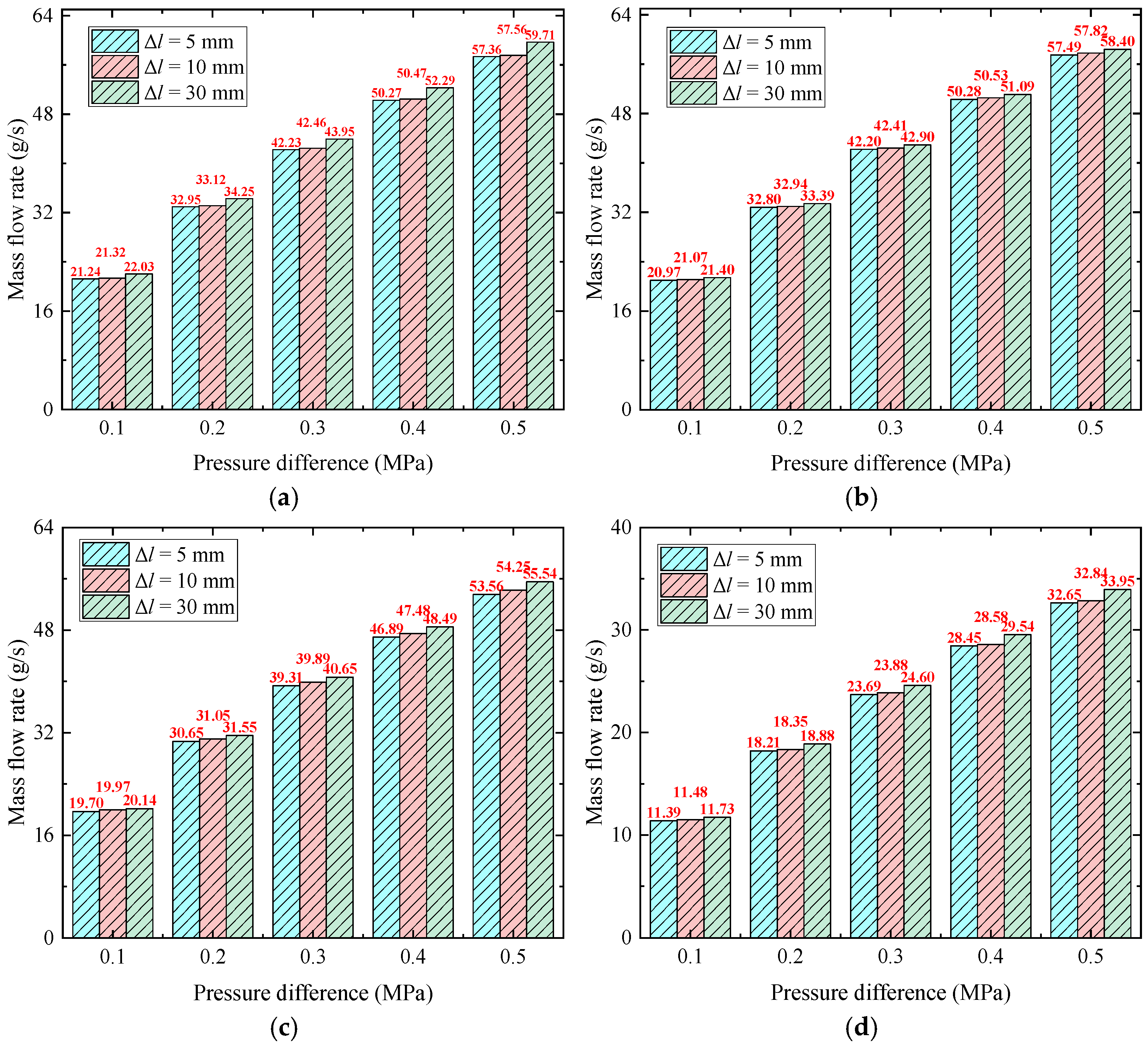
4.1. Internal Flow and Mass Flow Rate of Multi-Branch Oil Jet Nozzles
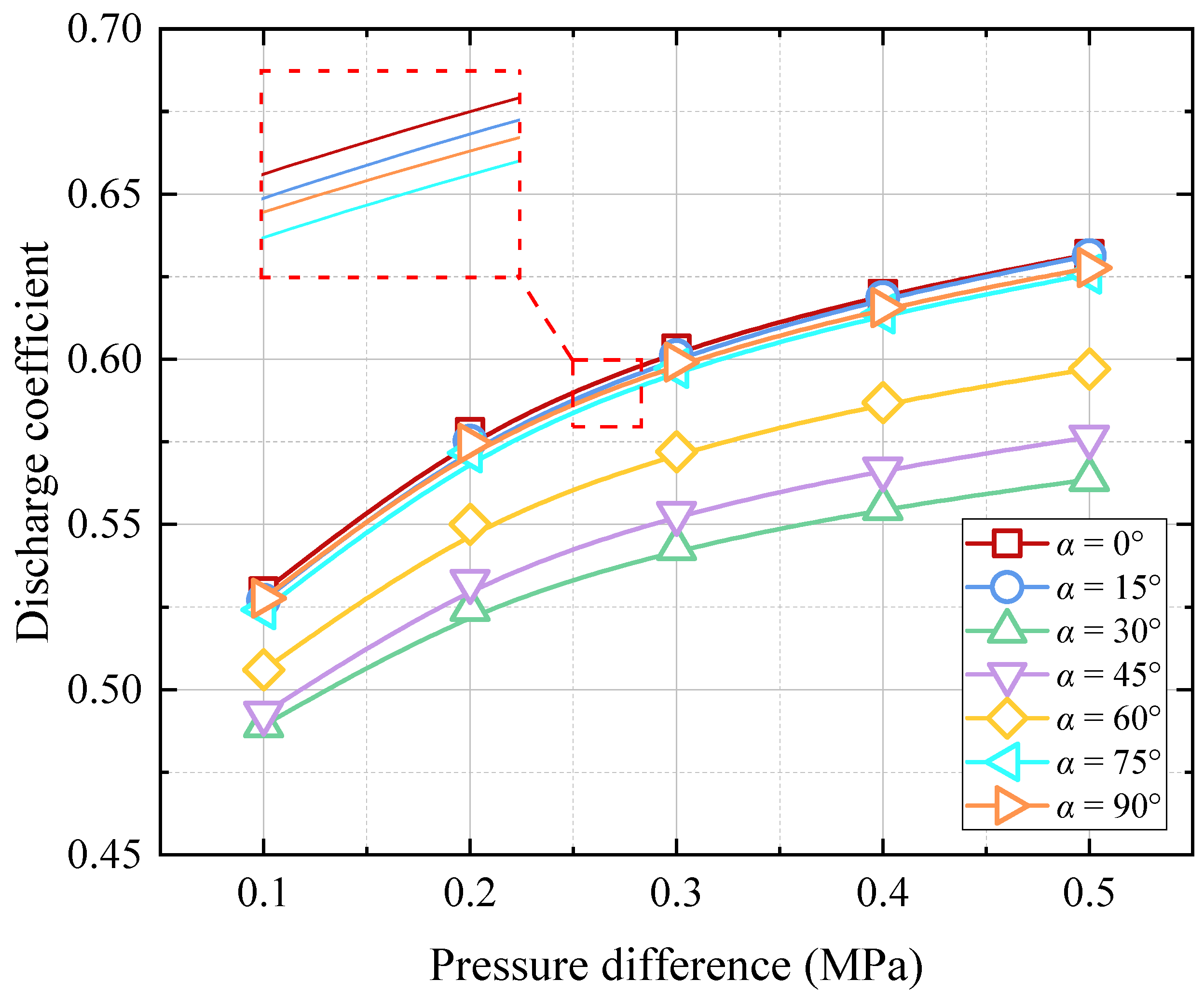
4.2. Flow Coefficient Analysis
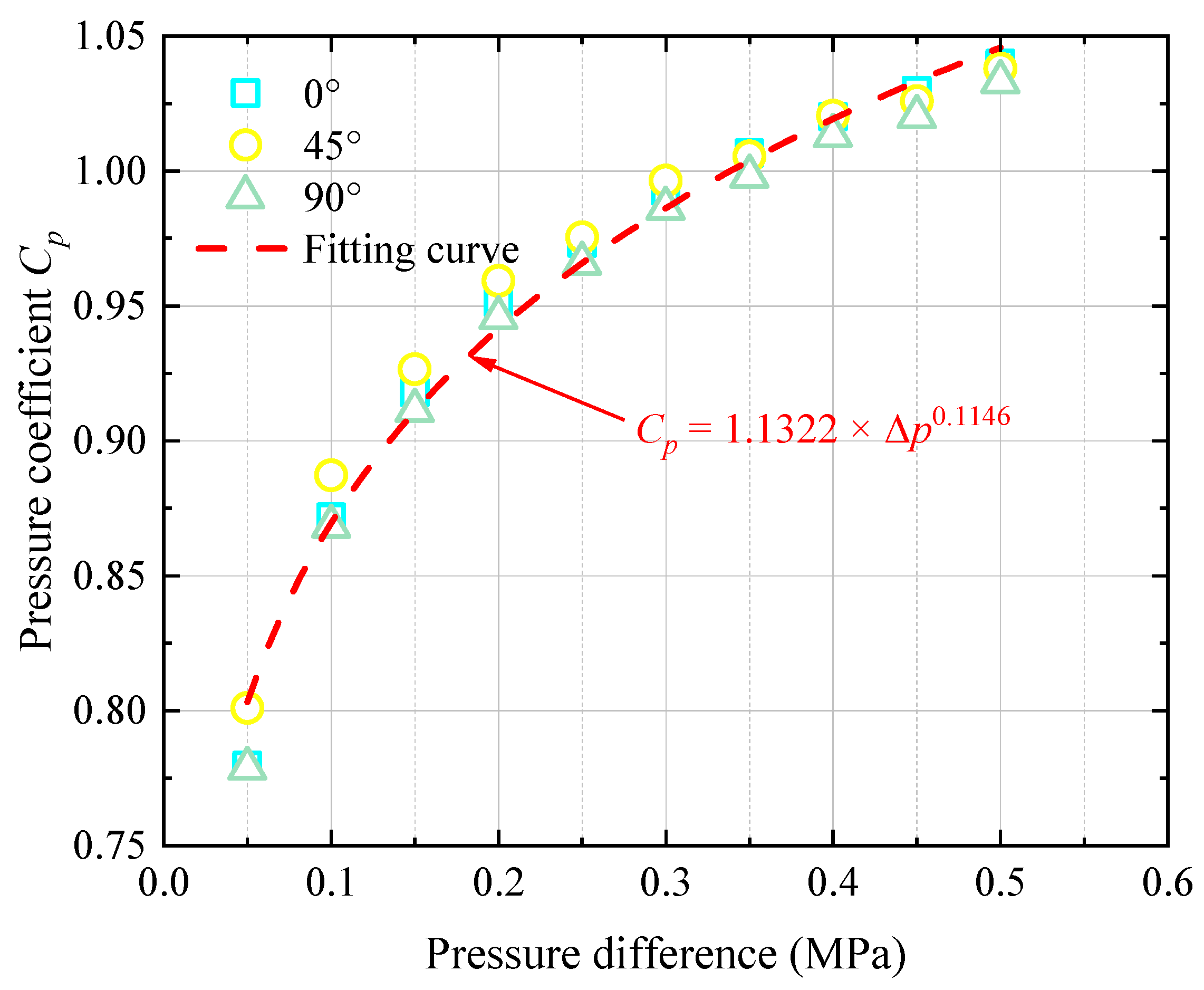
4.3. Verification of Corrected Discharge Coefficient
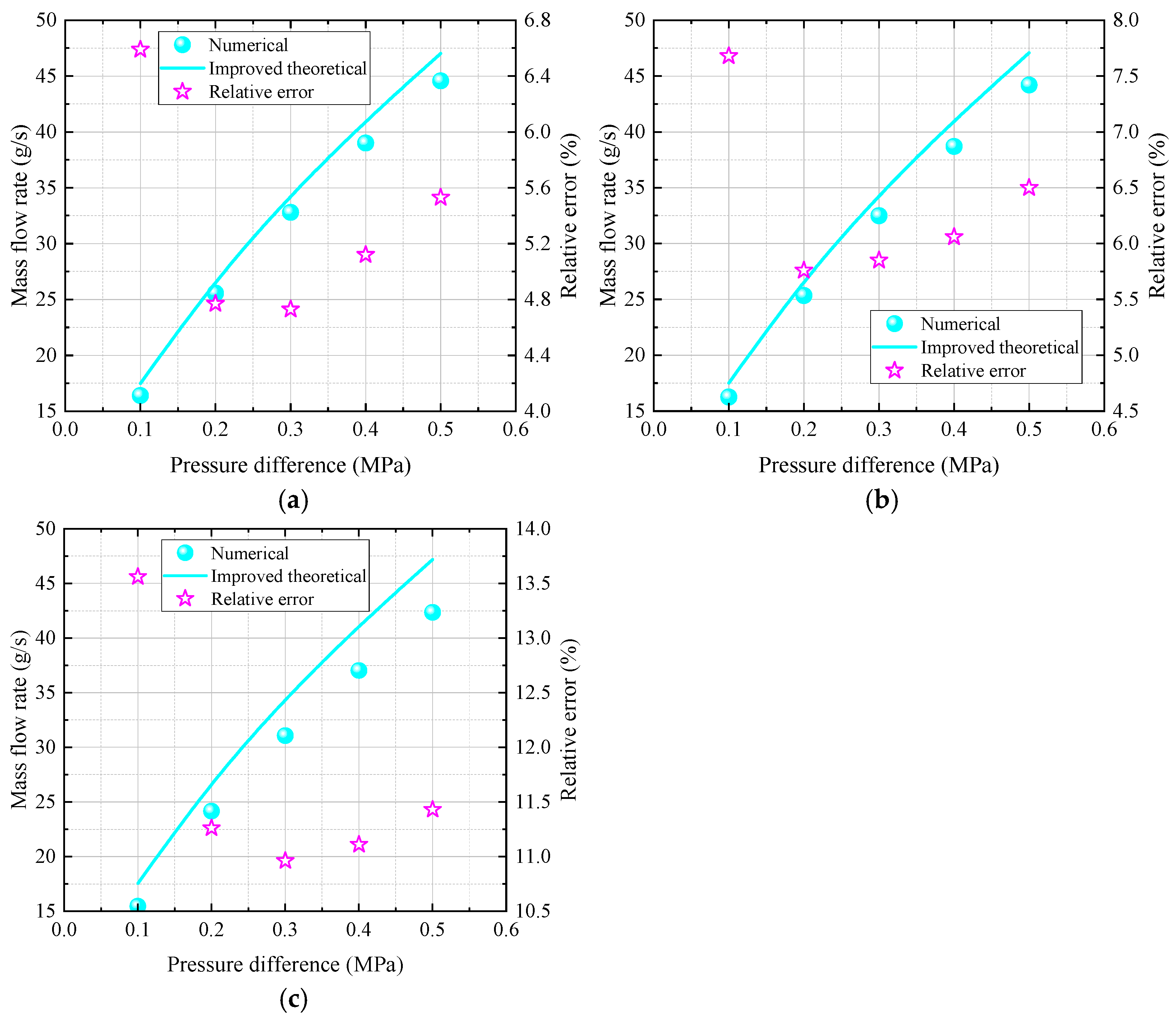
4.3.1. Verification of the Improved Method for Single Branch Nozzle
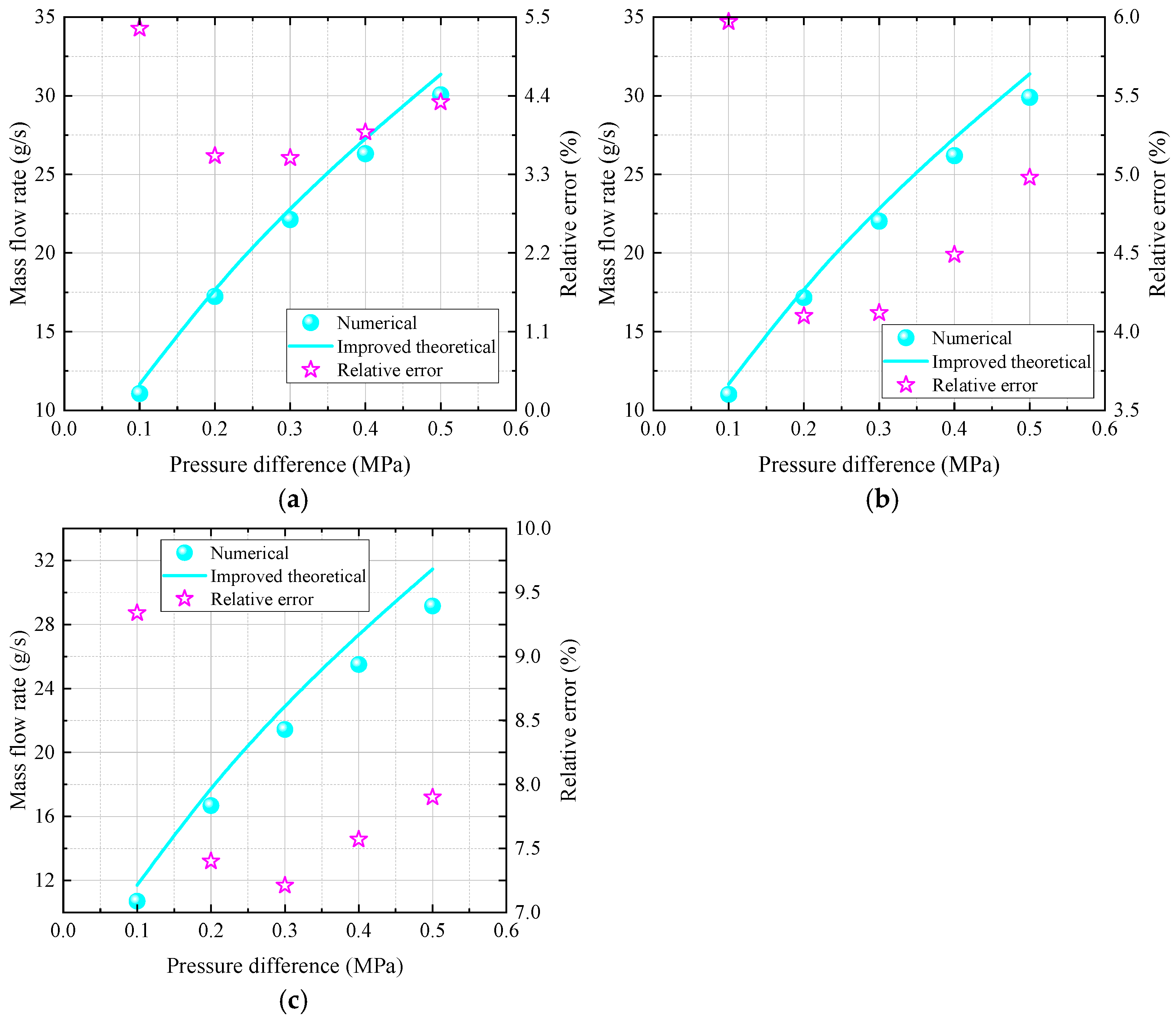
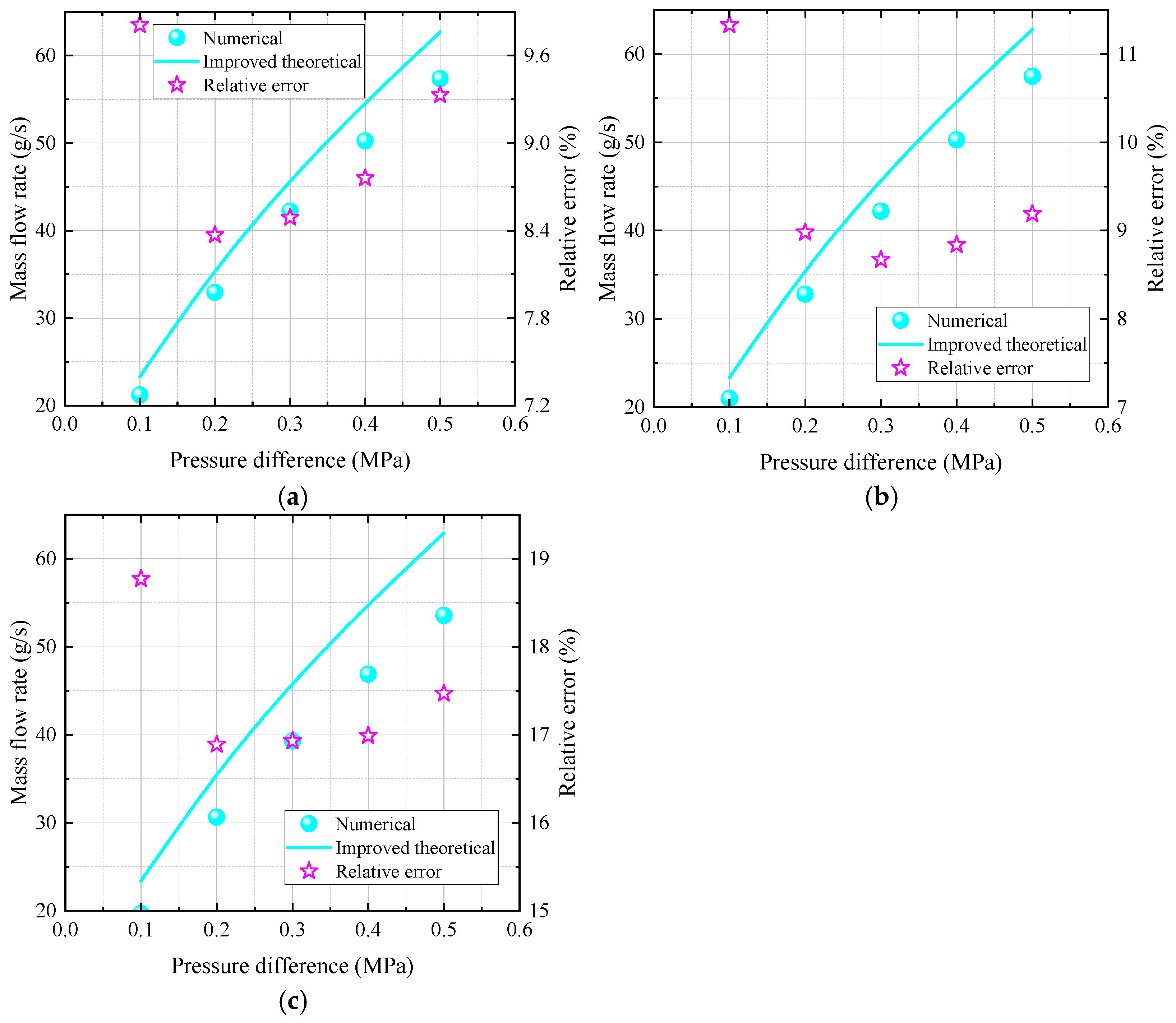
4.3.2. Verification of the Improved Method for Multi-Branch Nozzle
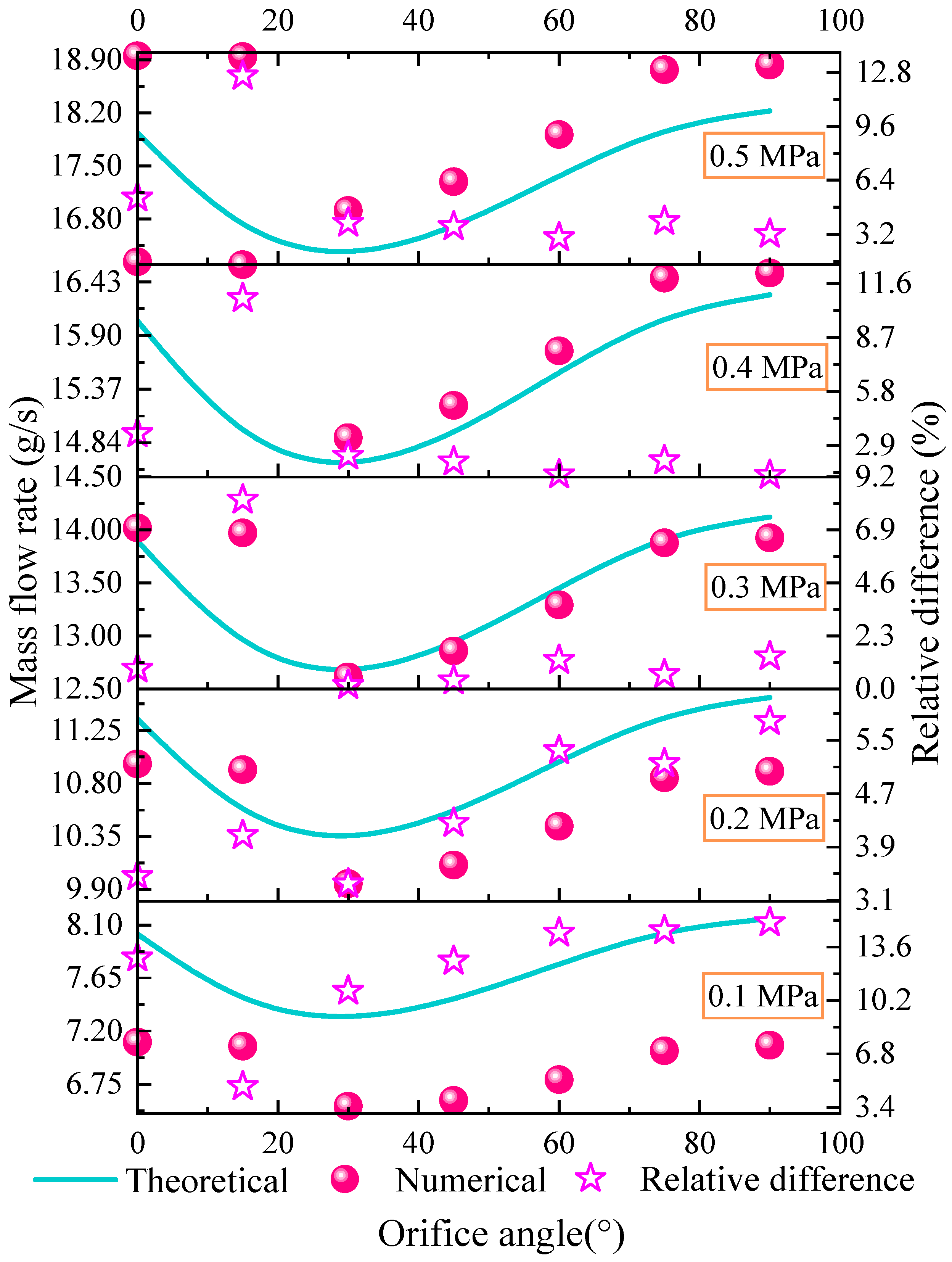
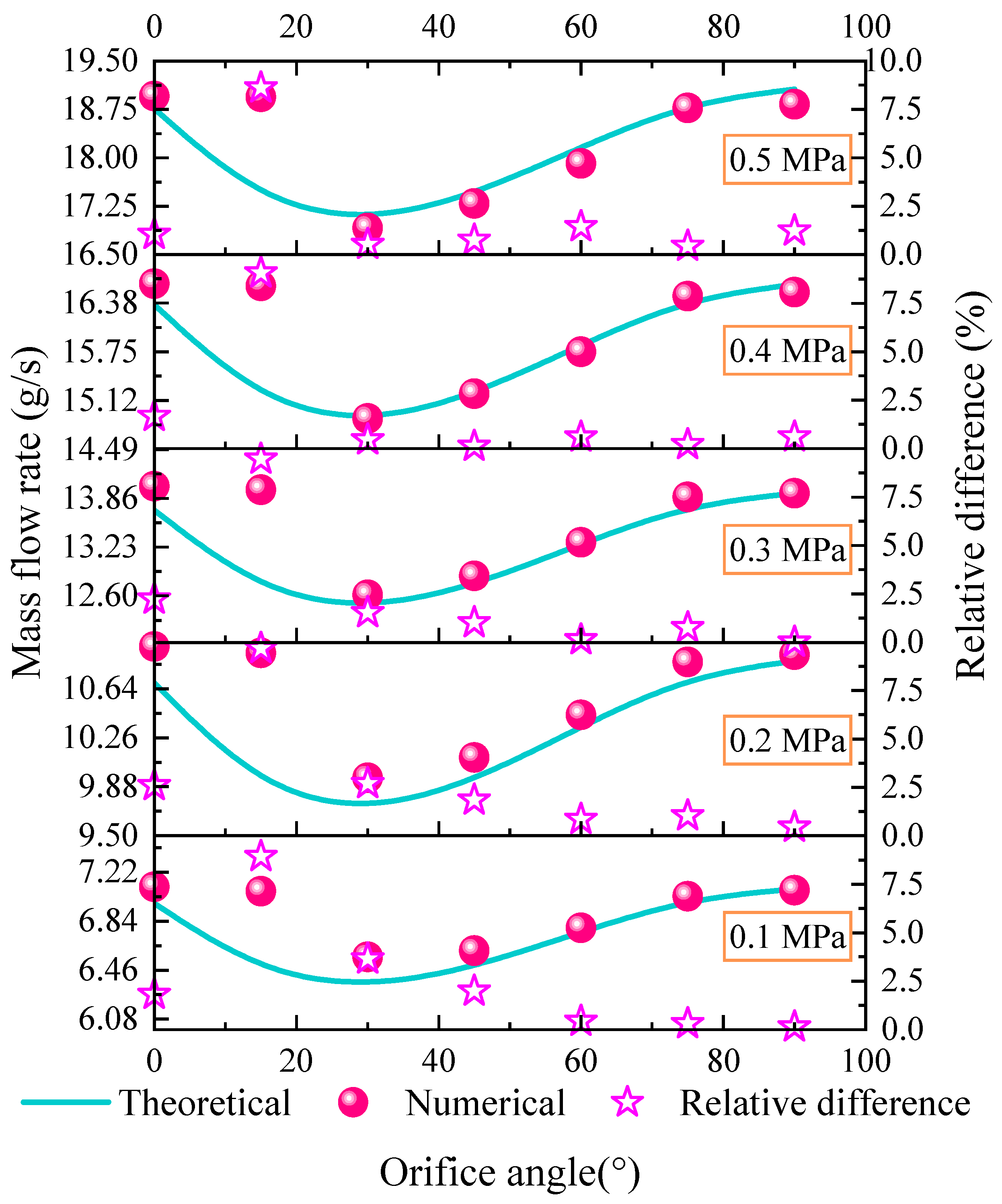
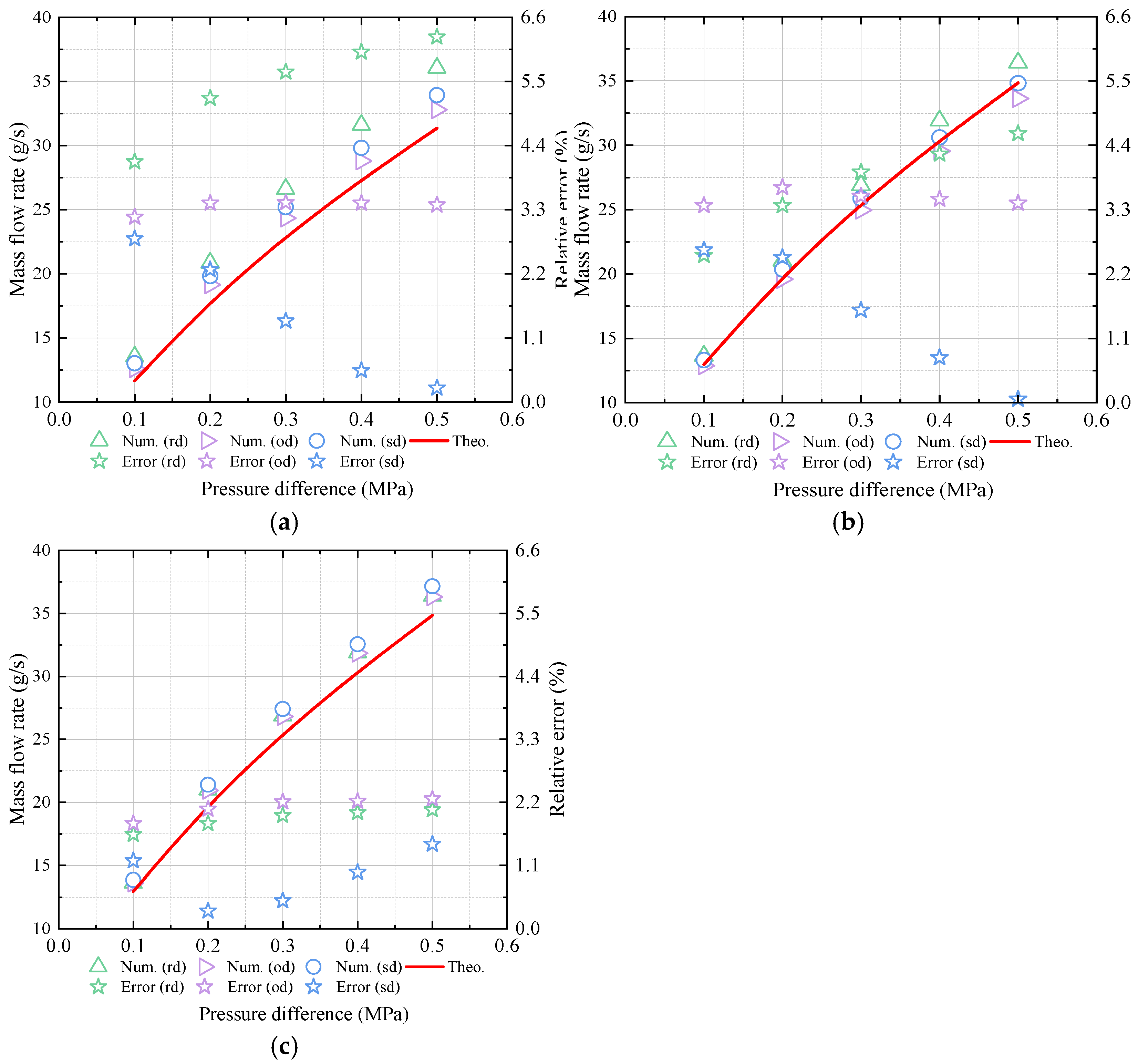
4.3.3. Verification for Dual-Branch Nozzle with Various Orifice Angle
5. Conclusions
- The theoretical equations considering the orifice angle and pressure coefficient obtained by the curve fit method exhibit a high accuracy. Compared to the original theoretical method not considering the pressure effect, the precision of the theoretical method improved in this paper is enhanced by over an order of magnitude. The average relative derivation between the calculated oil mass flow rate and numerical simulations is about 2%. These results indicate that the improved method can effectively predict the discharge coefficient under varying pressure and orifice angle conditions.
- As for the multi-branch nozzle, the spacing distance has an obvious impact on the total oil mass flow rate of the nozzle with two or more orifice exits, the total oil mass flow rate of the multi-branch nozzle is proportional to the number of branches (orifice) Nm. The overall trend of the calculated total mass flow rate also agrees well with the numerical results. Notably, the mass flow rate of the branch closer to the nozzle inlet is slightly lower than that of the branch farther from the inlet, likely due to the combined effects of the common chamber and frictional head losses.
- In terms of the dual-branch nozzle with different arrangement forms, the total mass flow rate is the largest for the nozzle adopting a radial arrangement, the next is the same and opposite direction arrangement. The improved theoretical method considering the pressure and orifice angle coefficient can predict the total mass flow rate pretty well with a maximum relative error not exceeding 6.3%. Additionally, the orifices are suggested to be radially arranged and appropriately away from the nozzle exit to slightly increase the mass flow rate during the preliminary design of the lubricating oil circuit.
- The assumption of incompressible flow and constant viscosity simplifies the model and is appropriate for the pressure conditions considered (0–0.5 MPa). However, these assumptions may not fully capture the complexities of flow behavior in real-world applications, particularly under higher pressure or temperature-varying conditions, where cavitation and viscosity changes could significantly impact performance. As such, while the results provide valuable insights, their applicability to more complex, high-pressure, or thermally dynamic systems is limited. Future work will aim to address these limitations by incorporating models that account for cavitation effects, temperature-dependent viscosity, and transient flow conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lichtarowicz, A.; Duggins, R.K.; Markland, E. Discharge coefficients for incompressible non-cavitating flow through long orifices. J. Mech. Eng. Sci. 1965, 7, 210–219. [Google Scholar] [CrossRef]
- Parker, D.M.; Kercher, D.M. An Enhanced Method to Compute the Compressible Discharge Coefficient of Thin and Long Orifices with Inlet Corner Radiusing. NASA STI/Recon Tech. Rep. A 1991, 93, 53–63. Available online: https://api.semanticscholar.org/CorpusID:118228991 (accessed on 18 August 2025).
- Buckingham, E. On physically similar systems; illustrations of the use of dimensional equations. Phys. Rev. 1914, 4, 345. [Google Scholar] [CrossRef]
- Deckker, B.E.L.; Chang, Y.F. Paper 7: An investigation of steady compressible flow through thick orifices. Proc. Inst. Mech. Eng. Conf. Proc. 1965, 180, 312–323. [Google Scholar] [CrossRef]
- Brain, T.J.S.; Reid, J. Performance of Small Diameter Cylindrical Critical-Flow Nozzles; National Engineering Laboratory: Glasgow, UK, 1973. [Google Scholar]
- STP-TS-084; Orifice Flow Coefficient Equation Comparison. ASME: New York, NY, USA, 2018.
- Kent, J.C.; Brown, G.M. Nozzle exit flow characteristics for square-edged and rounded inlet geometries. Combust. Sci. Technol. 1983, 30, 121–132. [Google Scholar] [CrossRef]
- Ohrn, T.R.; Senser, D.W.; Lefebvre, A.H. Geometrical effects on discharge coefficients for plain-orifice atomizers. At. Sprays 1991, 1, 137–153. [Google Scholar] [CrossRef]
- Chen, C.; Yang, Y.; Yang, S.; Gao, H. The spray characteristics of an open-end swirl injector at ambient pressure. Aerosp. Sci. Technol. 2017, 67, 78–87. [Google Scholar] [CrossRef]
- Desantes, J.M.; López, J.J.; Carreres, M.; López-Pintor, D. Characterization and prediction of the discharge coefficient of non-cavitating diesel injection nozzles. Fuel 2016, 184, 371–381. [Google Scholar] [CrossRef]
- Du, Z.; Huang, W.; Yan, L.; Dong, M. Impacts of jet angle and jet-to-crossflow pressure ratio on the mixing augmentation mechanism in a shcramjet engine. Aerosp. Sci. Technol. 2019, 94, 105385. [Google Scholar] [CrossRef]
- Yu, B.; Fu, P.F.; Zhang, T.; Zhou, H. The influence of back pressure on the flow discharge coefficients of plain orifice nozzle. Int. J. Heat Fluid Flow 2013, 44, 509–514. [Google Scholar] [CrossRef]
- Tharakan, T.J.; Rafeeque, T.A. The role of backpressure on discharge coefficient of sharp edged injection orifices. Aerosp. Sci. Technol. 2016, 49, 269–275. [Google Scholar] [CrossRef]
- Kontoulis, P.; Kaiktsis, L.; von Rotz, B.; Boulouchos, K. CFD modeling and experimental spray studies for different heavy fuel oil qualities with respect to large two-stroke marine engines. J. Energy Eng. 2019, 145, 04019014. [Google Scholar] [CrossRef]
- Tan, E.S.; Anwar, M.; Kumaran, P.; Indra, K.; Yoshikawa, K. Air assist atomization characterization of palm biodiesel through experimental investigation and CFD simulation. Biofuels 2017, 8, 571–577. [Google Scholar] [CrossRef]
- Ghadimi, P.; Nowruzi, H.; Yousefifard, M.; Feizi Chekab, M. A CFD study on spray characteristics of heavy fuel oil-based microalgae biodiesel blends under ultra-high injection pressures. Meccanica 2017, 52, 153–170. [Google Scholar] [CrossRef]
- Nowruzi, H.; Ghadimi, P. Effect of water-in-heavy fuel oil emulsion on the non-reacting spray characteristics under di erent ambient conditions and injection pressures: A CFD study. Sci. Iran. 2016, 23, 2626–2640. [Google Scholar] [CrossRef]
- Jakobs, T.; Djordjevic, N.; Fleck, S.; Mancini, M.; Weber, R.; Kolb, T. Gasification of high viscous slurry R&D on atomization and numerical simulation. Appl. Energy 2012, 93, 449–456. [Google Scholar] [CrossRef]
- Jiao, W.; Luo, S.; He, Z.; Liu, Y. Emulsified behaviors for the formation of Methanol-Diesel oil under high gravity environment. Energy 2017, 141, 2387–2396. [Google Scholar] [CrossRef]
- Nasim, M.N.; Qavi, I.; Jiang, L. Effect of varying internal geometry on the near-field spray characteristics of a swirl burst injector. Flow Turbul. Combust. 2023, 111, 641–674. [Google Scholar] [CrossRef]
- Brunhart, M.; Soteriou, C.; Gavaises, M.; Karathanassis, I.; Koukouvinis, P.; Jahangir, S.; Poelma, C. Investigation of cavitation and vapor shedding mechanisms in a Venturi nozzle. Phys. Fluids 2020, 32, 083306. [Google Scholar] [CrossRef]
- Nagy, P.T.; Paál, G. Modeling the perturbation growth in an acoustically excited plane jet. Phys. Fluids 2017, 29, 114102. [Google Scholar] [CrossRef]
- Rachakonda, S.K.; Goette, D.; Schmidt, D.P. Near-nozzle flash-boiling flow of iso-octane, methanol, and ammonia in the engine combustion network spray G injector. Phys. Fluids 2024, 36, 113371. [Google Scholar] [CrossRef]
- Bhatia, D.; Loukas, J.; Cabrera, A.; Lyras, K. A deep learning computational fluid dynamics solver for simulating liquid hydrogen jets. Phys. Fluids 2024, 36, 057120. [Google Scholar] [CrossRef]
- Wu, R.; Nie, S.; Ji, H.; Wang, Y.; Lin, L.; Yin, F. Effect of multi-parameter optimization of water-laser coupling device and nozzle geometry on the stability of water-guided laser beam. Phys. Fluids 2024, 36, 013620. [Google Scholar] [CrossRef]
- Payri, R.; Salvador, F.J.; Gimeno, J.; Garcia, A. Flow regime effects over non-cavitating diesel injection nozzles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2012, 226, 133–144. [Google Scholar] [CrossRef]
- Payri, R.; Viera, J.P.; Gopalakrishnan, V.; Szymkowicz, P. The effect of nozzle geometry over internal flow and spray formation for three different fuels. Fuel 2016, 183, 20–33. [Google Scholar] [CrossRef]
- Liu, H.; Cheng, H.; Dai, Y.; Zhu, X. Atomization characteristics of special-design pneumatic two-fluid nozzles for helicopter main reducers: A numerical and experimental investigation. Aerospace 2022, 9, 834. [Google Scholar] [CrossRef]
- Zhong, J.; Dai, Y.; Liang, C.; Zhu, X.; Xu, L. CFD investigation of air-oil two-phase flow in oil jet nozzle. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 10079–10089. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, Z.; Lyu, Y. Internal flow and discharge coefficient characteristics of oil jet nozzles with different orifice angles under non-cavitating conditions. Aerosp. Sci. Technol. 2021, 110, 106473. [Google Scholar] [CrossRef]
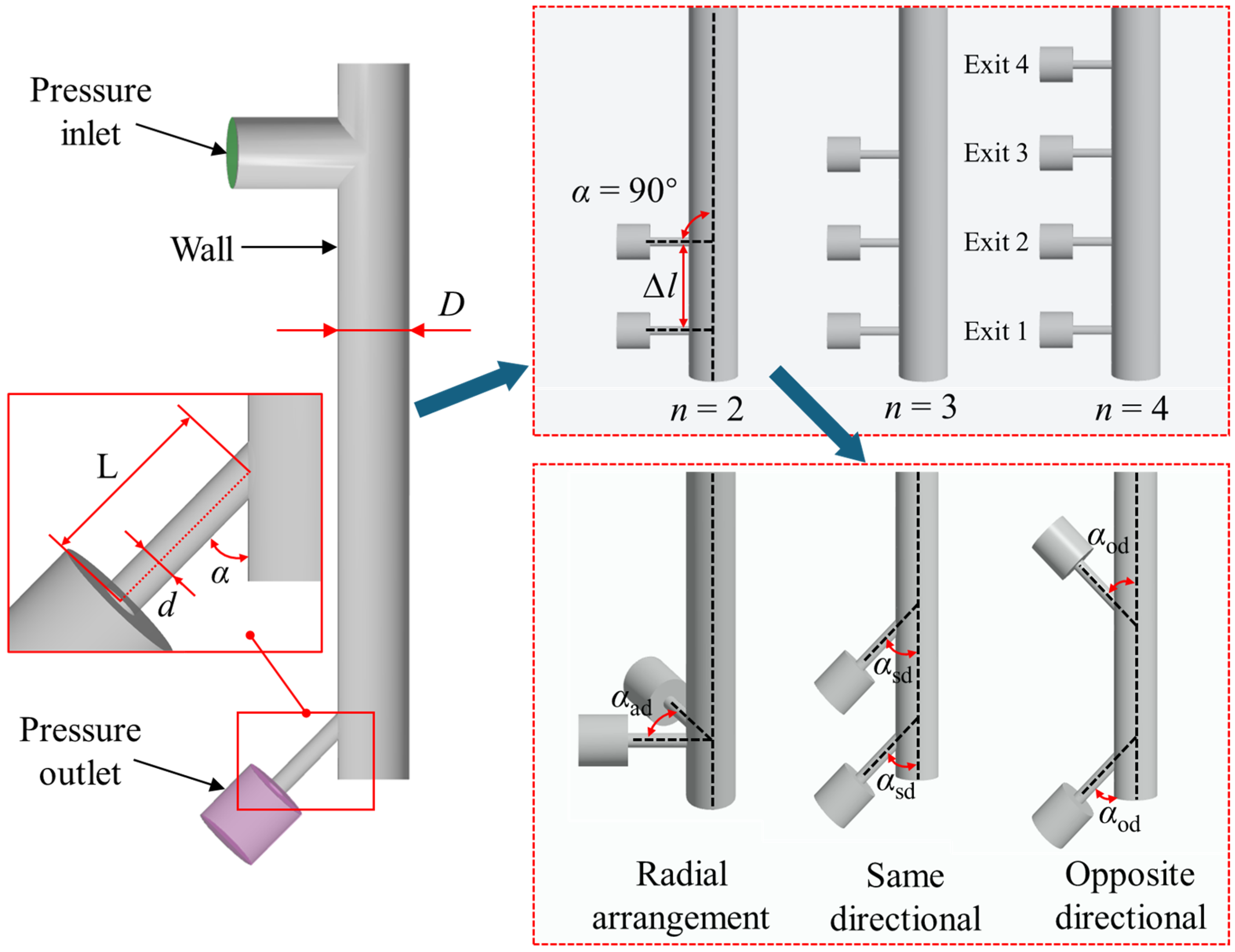










| Parameters | Value |
|---|---|
| Inlet diameter (D/mm) | 4.0 |
| Orifice diameter (d/mm) | 1.1 |
| Orifice length (L/mm) | 4.7 |
| Interval length (Δl/mm) | 10 |
| Orifice angle (/°) | 0~90 |
| Parameters | Value |
|---|---|
| Inlet diameter (D/mm) | 4.0~6.0 |
| Orifice diameter (d/mm) | 0.67~1.0 |
| Orifice length (L/mm) | 4.7 |
| Interval length (Δl/mm) | 5.0~30.0 |
| Orifice angle (/°) | 90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yang, X.; Wu, H.; Huang, X.; Dai, Y.; Zhu, X. Discharge Coefficient and Pressure Loss Characteristics of Multi-Branch Oil Jet Nozzles. Lubricants 2025, 13, 394. https://doi.org/10.3390/lubricants13090394
Zhang Y, Yang X, Wu H, Huang X, Dai Y, Zhu X. Discharge Coefficient and Pressure Loss Characteristics of Multi-Branch Oil Jet Nozzles. Lubricants. 2025; 13(9):394. https://doi.org/10.3390/lubricants13090394
Chicago/Turabian StyleZhang, Yanyang, Xinyuan Yang, Hongmei Wu, Xin Huang, Yu Dai, and Xiang Zhu. 2025. "Discharge Coefficient and Pressure Loss Characteristics of Multi-Branch Oil Jet Nozzles" Lubricants 13, no. 9: 394. https://doi.org/10.3390/lubricants13090394
APA StyleZhang, Y., Yang, X., Wu, H., Huang, X., Dai, Y., & Zhu, X. (2025). Discharge Coefficient and Pressure Loss Characteristics of Multi-Branch Oil Jet Nozzles. Lubricants, 13(9), 394. https://doi.org/10.3390/lubricants13090394







