A Hyperspectral Analysis-Based Approach for Estimation of Wear Metal Content in Lubricating Oil
Abstract
1. Introduction
2. Materials and Methods
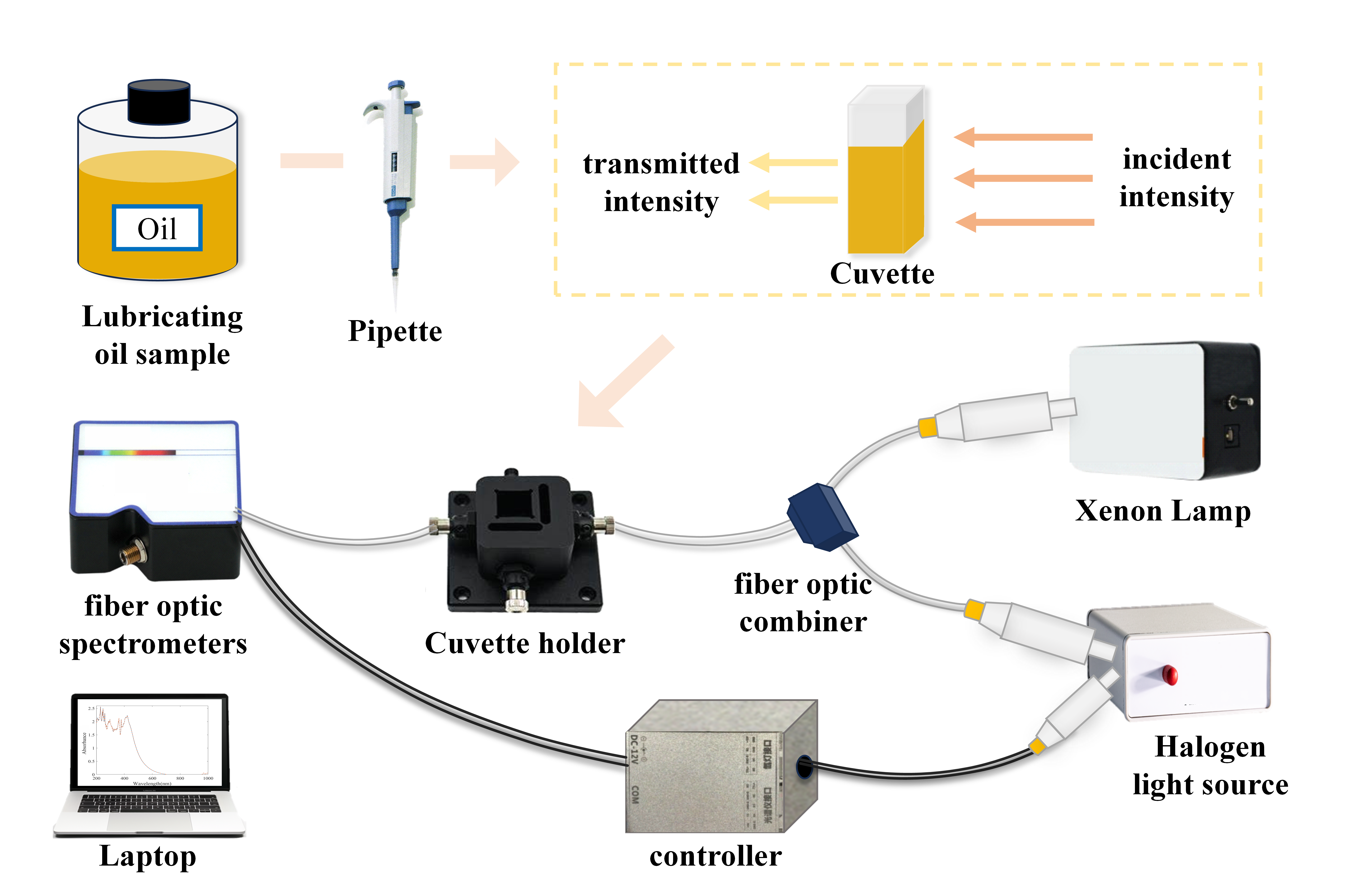
2.1. Lubricating Oil Sample Collection and Hyperspectral Data Acquisition
2.2. Methodology
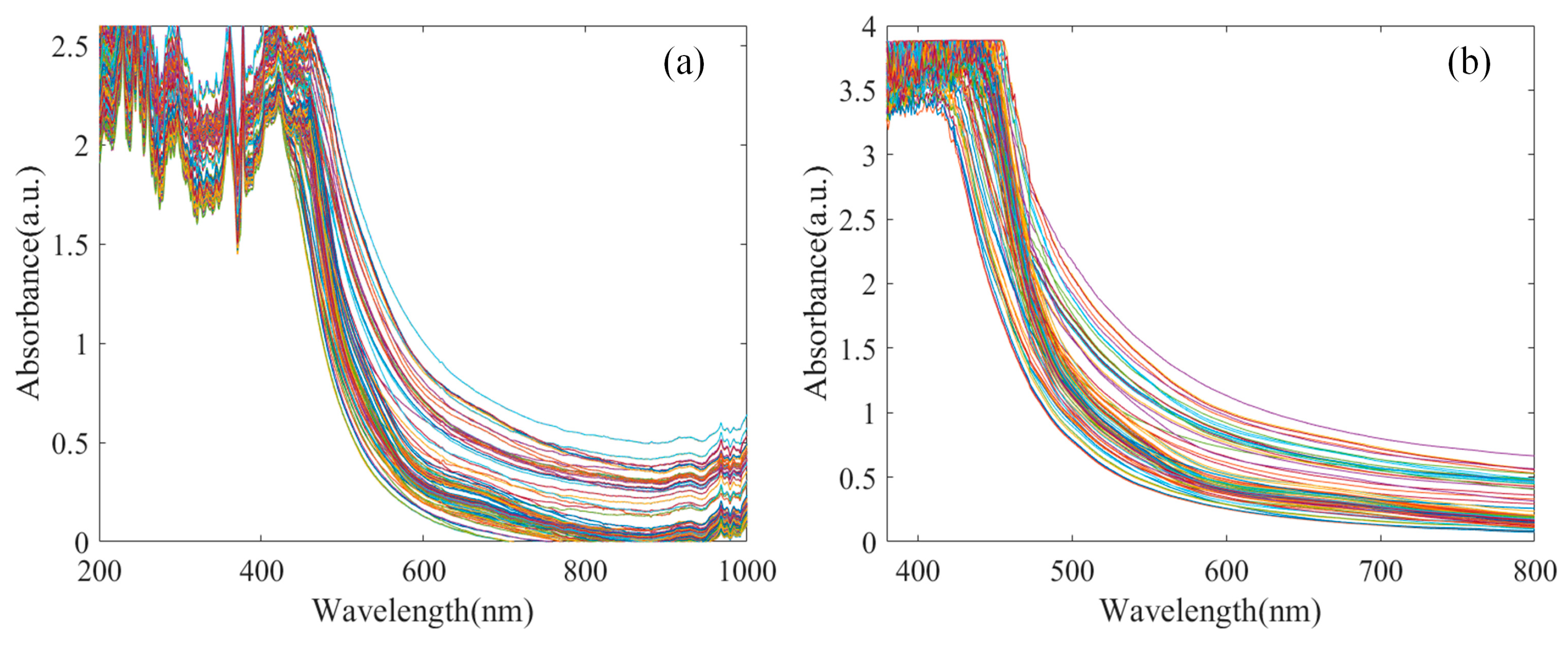
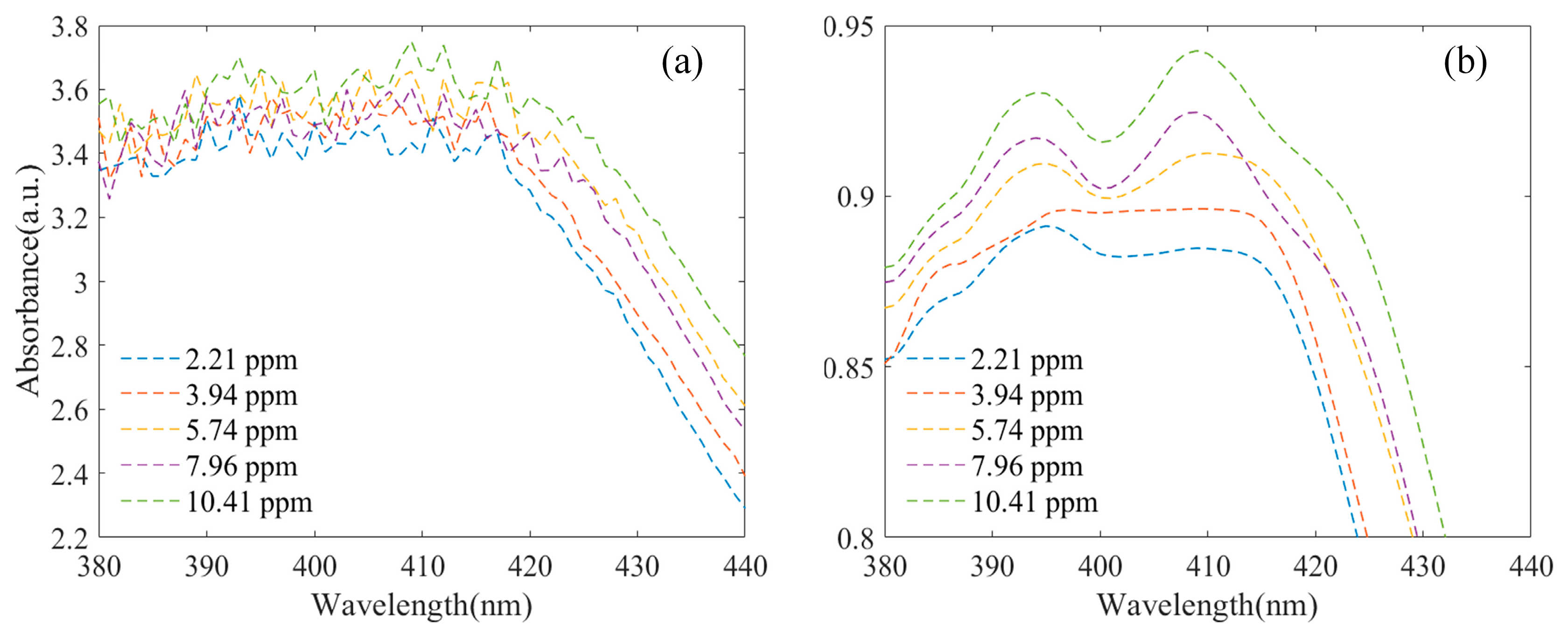
2.2.1. Spectral Preprocessing
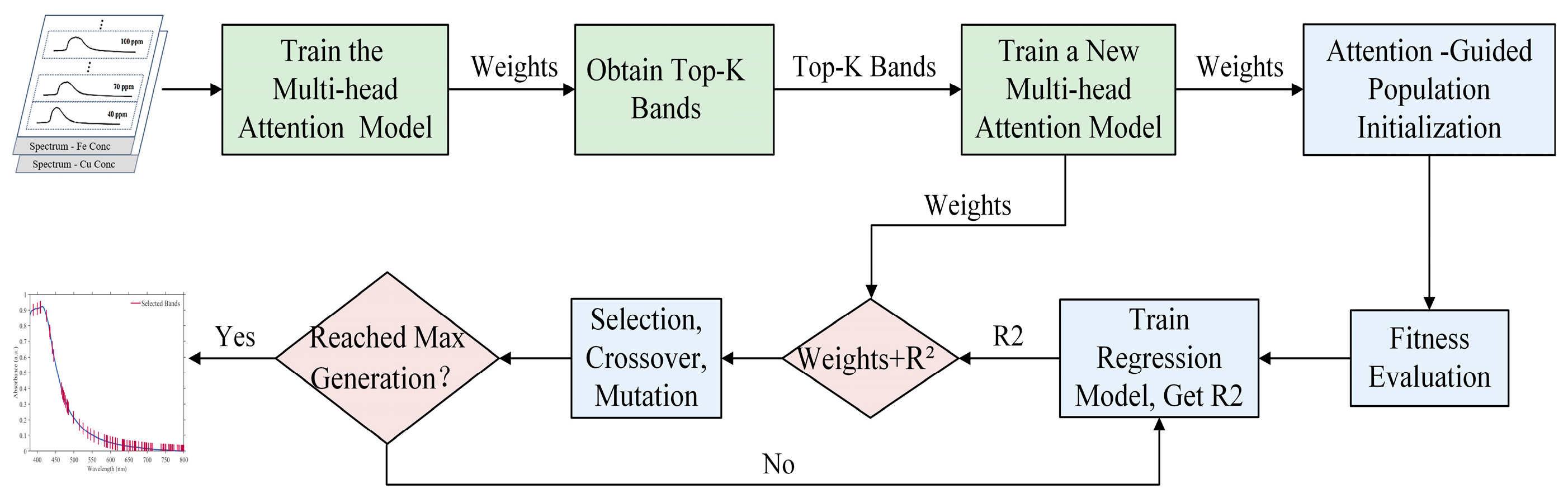
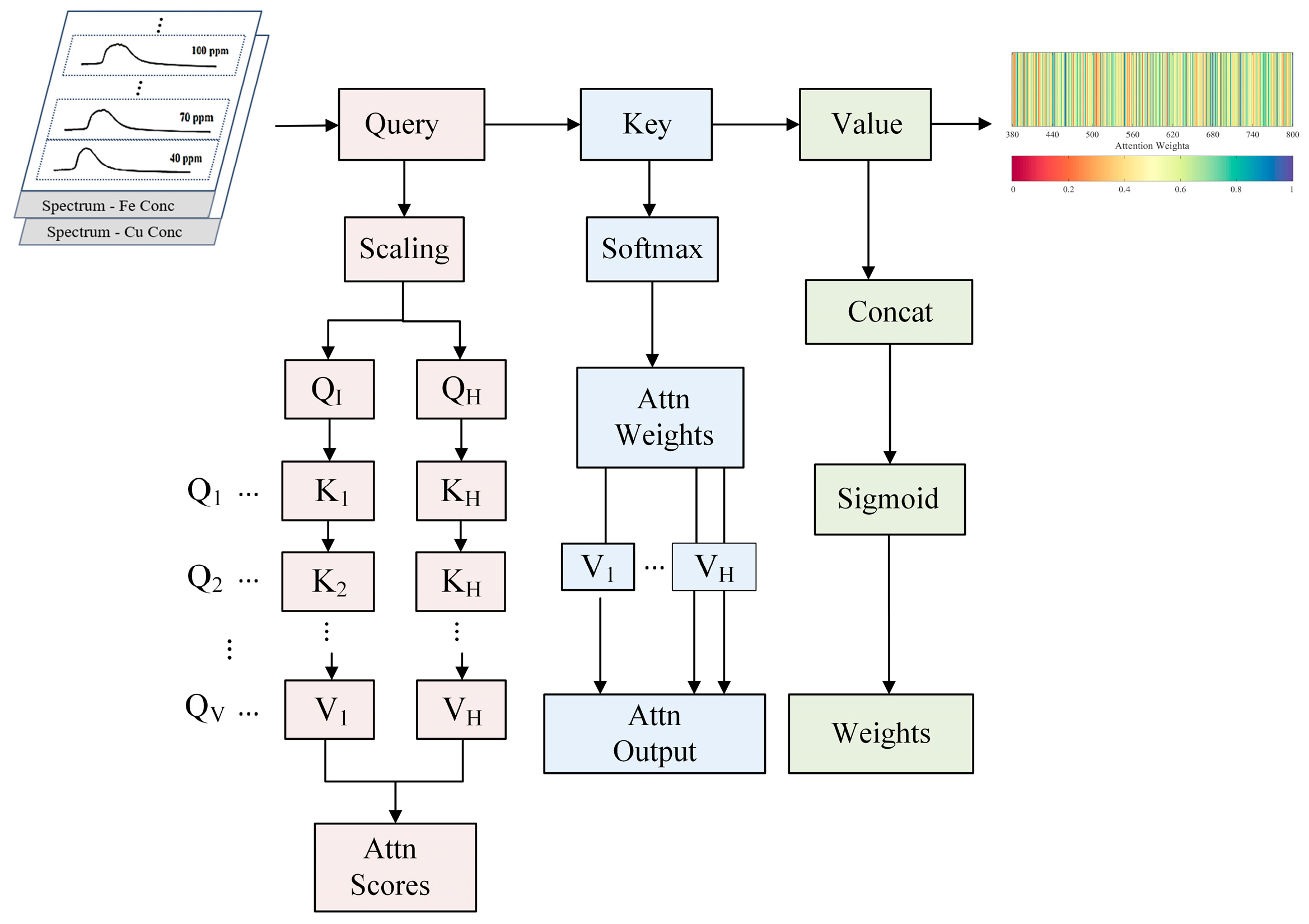
2.2.2. Multi-Head Attention Mechanism Enhanced Genetic Algorithm (MHA-GA)
- Multi-head spectral attention mechanism
- 2.
- Genetic algorithm
2.2.3. Regression Modeling Method
2.3. Model Evaluation Metrics
3. Results
3.1. Statistical Analysis of Wear Metal Concentrations in Lubricating Oil Samples
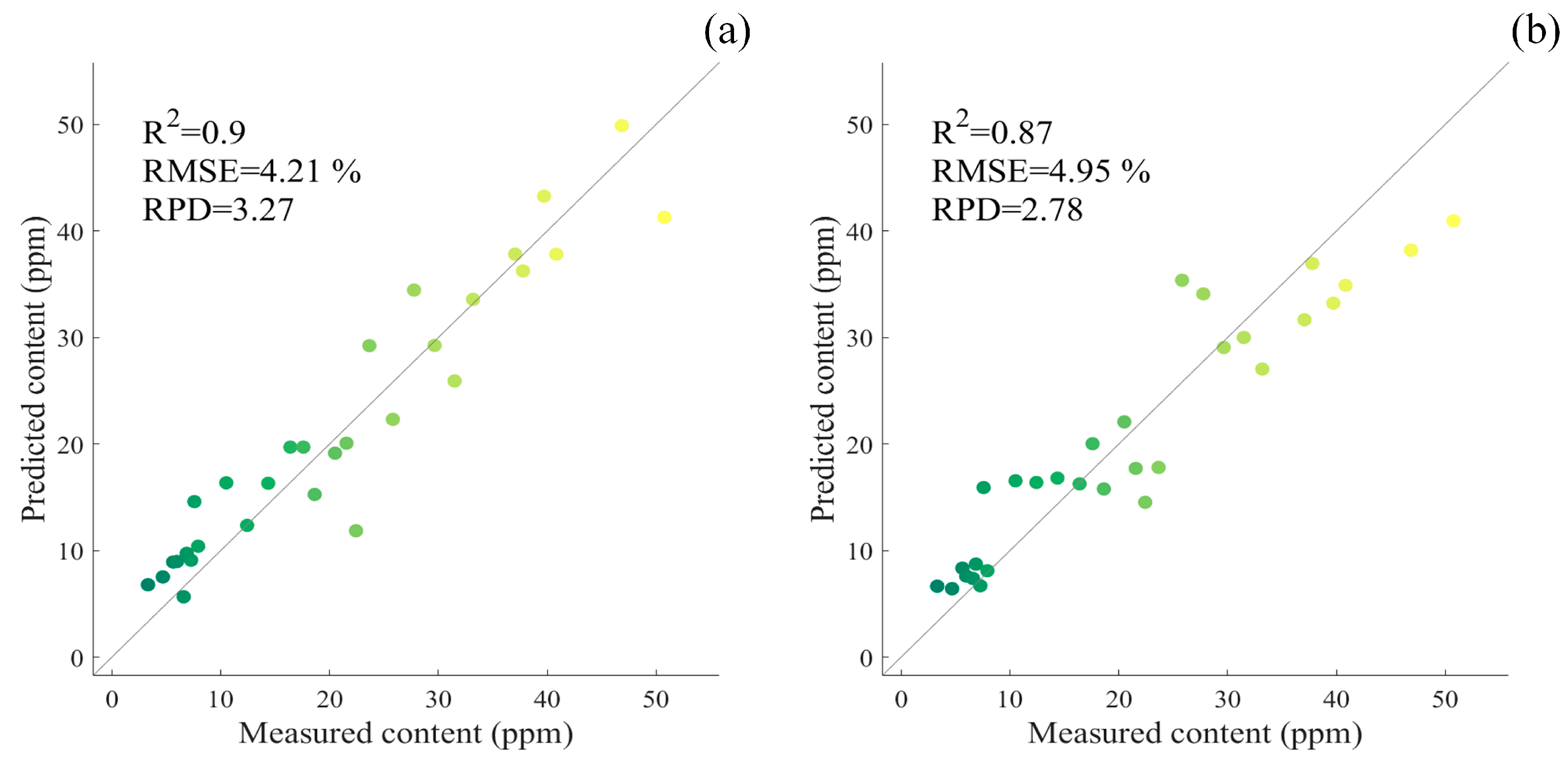
3.2. Performance Comparison of Modeling Methods in Estimating Fe and Cu Concentrations
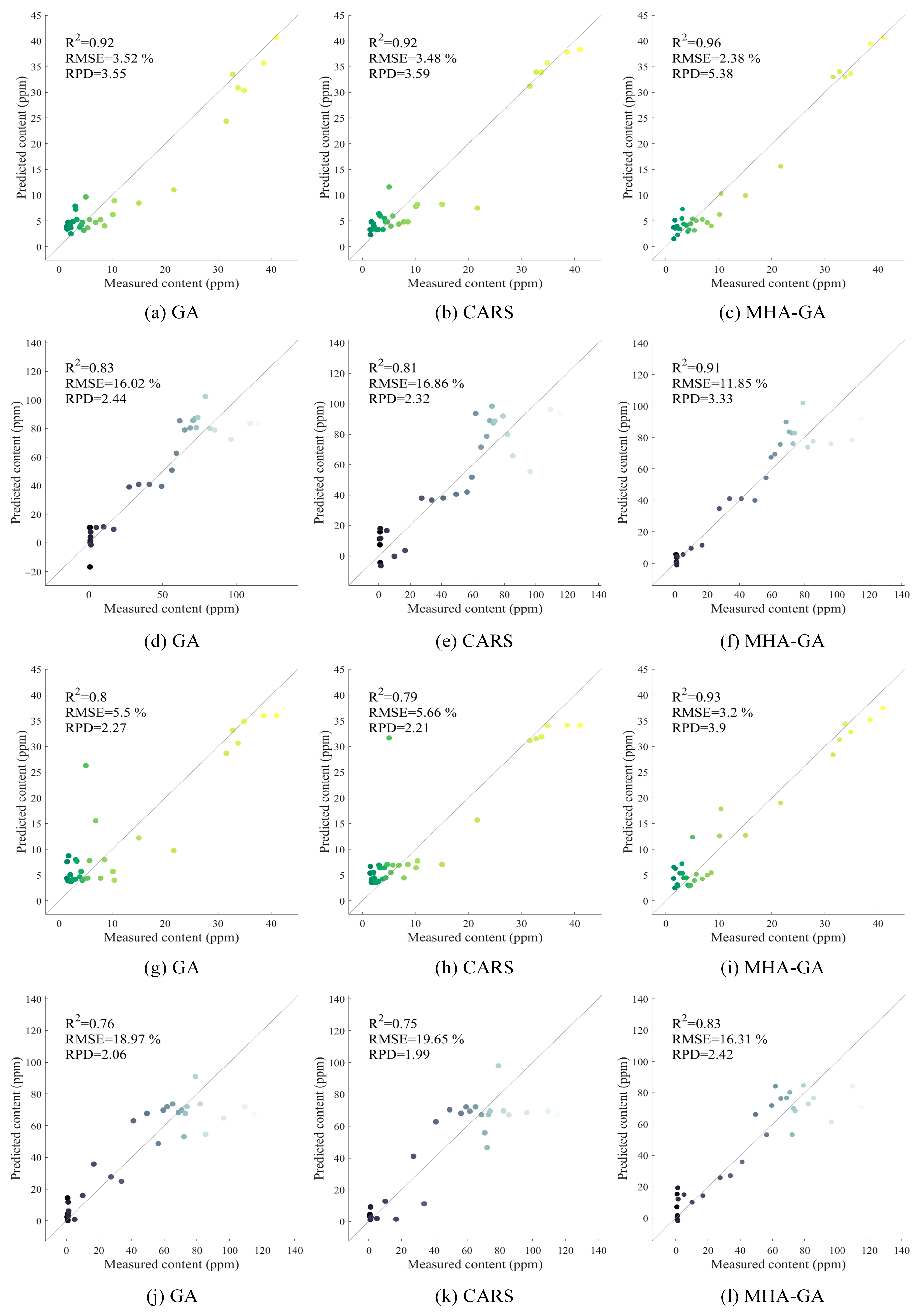
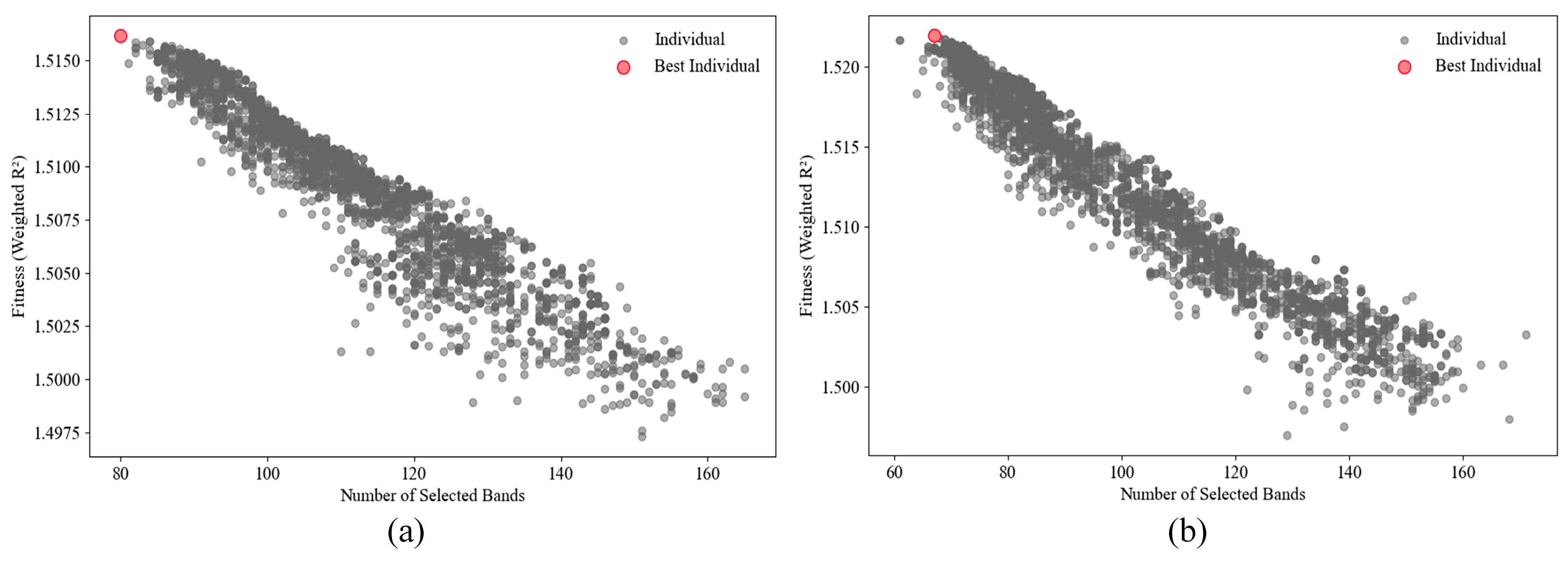
3.3. Effectiveness Analysis of MHA-GA Feature Extraction
4. Discussion
5. Conclusions
- Compared to traditional feature extraction algorithms, MHA-GA effectively reduces data redundancy and improves estimation accuracy. Specifically, MHA-GA retained fewer features for Fe and Cu prediction while covering metal-sensitive spectral regions. Compared to the traditional GA, the number of selected features for Fe decreased by 102 (Hach dataset) and 422 (GLT dataset), resulting in R2 values increasing from 0.92 to 0.96 and from 0.80 to 0.93, respectively. For Cu, feature counts were reduced by 99 (Hach dataset) and 477 (GLT dataset), and R2 improved from 0.83 to 0.91 and from 0.76 to 0.83, respectively.
- Among the three modeling methods evaluated (XGBoost, SVR, and RF), XGBoost demonstrated the best performance, achieving higher accuracy (R2 > 0.83) with fewer features. Its estimation accuracy for both target wear metals consistently surpassed that of SVR and RF, confirming its suitability for predicting wear metal concentrations in lubricating oil under high-dimensional and small-sample conditions.
- Hyperspectral data acquired with the Hach UV–Vis spectrophotometer yielded better modeling performance than the Progoo DS 10A-103 Hyperspectral lubricating oil intelligent detector which used GLT optical fiber spectrometer, primarily attributable to its higher spectral resolution and superior instrumental stability. Nevertheless, hyperspectral data from both instruments proved effective for estimating typical wear metal concentrations in lubricating oil, demonstrating the validity and reliability of the proposed approach. The overall results highlight the significant potential of hyperspectral technology as a rapid, in situ method for detecting wear metal elements in lubricating oil.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Taha-Tijerina, J.; Aviña, K.; Diabb, J.M. Tribological and Thermal Transport Performance of SiO2-Based Natural Lubricants. Lubricants 2019, 7, 71. [Google Scholar] [CrossRef]
- Zhu, X.; Zhong, C.; Zhe, J. Lubricating Oil Conditioning Sensors for Online Machine Health Monitoring—A Review. Tribol. Int. 2017, 109, 473–484. [Google Scholar] [CrossRef]
- Du, L.; Zhu, X.; Han, Y.; Zhe, J. High Throughput Wear Debris Detection in Lubricants Using a Resonance Frequency Division Multiplexed Sensor. Tribol. Lett. 2013, 51, 453–460. [Google Scholar] [CrossRef]
- Vähäoja, P.; Välimäki, I.; Roppola, K.; Kuokkanen, T.; Lahdelma, S. Wear Metal Analysis of Oils. Crit. Rev. Anal. Chem. 2008, 38, 67–83. [Google Scholar] [CrossRef]
- Tao, H.; Feng, W.; Yang, G.; Du, R.; Zhong, Y. A Wear Condition Warning Method for Wind Turbine Gearbox Based on Oil On-Line Monitoring Using Learnable Multi-Scale Convolutional Neural Network. IEEE Sens. J. 2024, 24, 35709–35721. [Google Scholar] [CrossRef]
- Shen, M.-X.; Dong, F.; Zhang, Z.-X.; Meng, X.-K.; Peng, X.-D. Effect of Abrasive Size on Friction and Wear Characteristics of Nitrile Butadiene Rubber (NBR) in Two-Body Abrasion. Tribol. Int. 2016, 103, 1–11. [Google Scholar] [CrossRef]
- Li, J.; Chu, X.; Liu, D. Rapid Determination of Chemical Compositions of Raw Materials and Intermediate Products of Lube Base Oil by near Infrared Spectroscopy Combined with Library Spectral Fitting Method. Microchem. J. 2024, 200, 110265. [Google Scholar] [CrossRef]
- Duyck, C.; Miekeley, N.; da Silveira, C.L.P.; Aucélio, R.Q.; Campos, R.C.; Grinberg, P.; Brandão, G.P. The Determination of Trace Elements in Crude Oil and Its Heavy Fractions by Atomic Spectrometry. Spectrochim. Acta Part B 2007, 62, 939–951. [Google Scholar] [CrossRef]
- Azcarate, S.M.; Langhoff, L.P.; Camiña, J.M.; Savio, M. A Green Single-Tube Sample Preparation Method for Wear Metal Determination in Lubricating Oil by Microwave Induced Plasma with Optical Emission Spectrometry. Talanta 2019, 195, 573–579. [Google Scholar] [CrossRef]
- García, M.; Aguirre, M.Á.; Canals, A. A New Multinebulizer for Spectrochemical Analysis: Wear Metal Determination in Used Lubricating Oils by on-Line Standard Dilution Analysis (SDA) Using Inductively Coupled Plasma Optical Emission Spectrometry (ICP OES). J. Anal. At. Spectrom. 2020, 35, 265–272. [Google Scholar] [CrossRef]
- Laza, A.; Orozco, E.; Baldo, M.F.; Raba, J.; Aranda, P.R. Determination of Arsenic (V) in Cannabis Oil by Adsorption on Multiwall Carbon Nanotubes Thin Film Using XRF Technique. Microchem. J. 2020, 158, 105265. [Google Scholar] [CrossRef]
- Palacio, C.; Rojas, K.; Triana, Y. Analysis of Diesel Engine Oils from 2.5L Engine Pick-up Trucks by Means of X-Ray Fluorescence. Rev. Fac. Ing. Univ. Antioq 2021, 104, 9–19. [Google Scholar] [CrossRef]
- Gondal, M.A.; Hussain, T.; Yamani, Z.H.; Baig, M.A. Detection of Heavy Metals in Arabian Crude Oil Residue Using Laser Induced Breakdown Spectroscopy. Talanta 2006, 69, 1072–1078. [Google Scholar] [CrossRef]
- Xu, B.; Liu, Y.; Yin, P.; Li, M.; Zhang, W.; Wang, Y.; Zhao, W.; Tang, J.; Duan, Y. Improving the Laser-Induced Breakdown Spectroscopy for Highly Efficient Trace Measurement of Hazardous Components in Waste Oils. Anal. Chem. 2023, 95, 18685–18690. [Google Scholar] [CrossRef]
- Mdluli, N.S.; Nomngongo, P.N.; Mketo, N. A Critical Review on Application of Extraction Methods Prior to Spectrometric Determination of Trace-Metals in Oily Matrices. Crit. Rev. Anal. Chem. 2022, 52, 1–18. [Google Scholar] [CrossRef]
- Vinić, M.; Aruffo, E.; Andreoli, F.; Ivković, M.; Lazic, V. Quantification of Heavy Metals in Oils with µL Volume by Laser Induced Breakdown Spectroscopy and Minimazing of the Matrix Effect. Spectrochim. Acta Part B 2020, 164, 105765. [Google Scholar] [CrossRef]
- Braga, J.W.B.; Junior, A.A.d.S.; Martins, I.S. Determination of Viscosity Index in Lubricant Oils by Infrared Spectroscopy and PLSR. Fuel 2014, 120, 171–178. [Google Scholar] [CrossRef]
- Li, X.; Zhang, L.; Zhang, Y.; Wang, D.; Wang, X.; Yu, L.; Zhang, W.; Li, P. Review of NIR Spectroscopy Methods for Nondestructive Quality Analysis of Oilseeds and Edible Oils. Trends Food Sci. Technol. 2020, 101, 172–181. [Google Scholar] [CrossRef]
- Wang, Z.; Deng, J.; Ding, Z.; Jiang, H. Quantification of Heavy Metal Cd in Peanut Oil Using Near-Infrared Spectroscopy Combined with Chemometrics: Analysis and Comparison of Variable Selection Methods. Infrared Phys. Technol. 2024, 141, 105447. [Google Scholar] [CrossRef]
- Holland, T.; Abdul-Munaim, A.M.; Mandrell, C.; Karunanithy, R.; Watson, D.G.; Sivakumar, P. UV-Visible Spectrophotometer for Distinguishing Oxidation Time of Engine Oil. Lubricants 2021, 9, 37. [Google Scholar] [CrossRef]
- Chen, P.; Liu, D.; Wang, X.; Zhang, Q.; Chu, X. Rapid Determination of Viscosity and Viscosity Index of Lube Base Oil Based on Near-Infrared Spectroscopy and New Transformation Formula. Spectrochim. Acta Part A 2023, 287, 122079. [Google Scholar] [CrossRef]
- Zhou, F.; Yang, K.; Li, D.; Shi, X. Acid Number Prediction Model of Lubricating Oil Based on Mid-Infrared Spectroscopy. Lubricants 2022, 10, 205. [Google Scholar] [CrossRef]
- Ma, W.; Gong, C.; Hu, Y.; Meng, P.; Xu, F. The Hughes Phenomenon in Hyperspectral Classification Based on the Ground Spectrum of Grasslands in the Region around Qinghai Lake. In Proceedings of the International Symposium on Photoelectronic Detection and Imaging 2013: Imaging Spectrometer Technologies and Applications (SPIE), Beijing, China, 25–27 June 2013; Volume 8910, pp. 363–373. [Google Scholar]
- Casasent, D.P.; Chen, X.-W. Waveband Selection for Hyperspectral Data: Optimal Feature Selection. In Proceedings of the Optical Pattern Recognition XIV, SPIE, Orlando, FL, USA, 21–25 April 2003; Volume 5106, pp. 259–270. [Google Scholar]
- Park, C.W.; Lee, I.; Kwon, S.-H.; Son, S.-J.; Ko, D.-K. Classification of CARS Spectral Phase Retrieval Combined with Principal Component Analysis. Vib. Spectrosc. 2021, 117, 103314. [Google Scholar] [CrossRef]
- Qiu, G.; Chen, B.; Lu, H.; Yue, X.; Deng, X.; Ouyang, H.; Li, B.; Wei, X. Nondestructively Determining Soluble Solids Content of Blueberries Using Reflection Hyperspectral Imaging Technique. Agronomy 2024, 14, 2296. [Google Scholar] [CrossRef]
- Zhao, H.; Bruzzone, L.; Guan, R.; Zhou, F.; Yang, C. Spectral-Spatial Genetic Algorithm-Based Unsupervised Band Selection for Hyperspectral Image Classification. IEEE Trans. Geosci. Electron. 2021, 59, 9616–9632. [Google Scholar] [CrossRef]
- Cernuda, C.; Lughofer, E.; Hintenaus, P.; Märzinger, W. Enhanced Genetic Operators Design for Waveband Selection in Multivariate Calibration Based on NIR Spectroscopy. J. Chemom. 2014, 28, 123–136. [Google Scholar] [CrossRef]
- Lin, S.; Ashlock, J.C.; Zhao, G.; Lai, Q.; Xu, L.; Zhai, C. Genetic-Simulated Annealing Optimization for Surface Wave Inversion of Shear-Wave Velocity Profiles of Geotechnical Sites. Comput. Geotech. 2023, 160, 105525. [Google Scholar] [CrossRef]
- Zhu, Y.; Lu, C.; Zhang, Y.; Jiang, W. Quantitative Method to Near-Infrared Spectroscopy With Multi-Feature Fusion Convolutional Neural Network Based on Wavelength Attention. Spectrosc. Spectr. Anal. 2024, 44, 2607–2612. [Google Scholar] [CrossRef]
- Yang, H.; Li, F.; Wang, W.; Yu, K. Estimating Above-Ground Biomass of Potato Using Random Forest and Optimized Hyperspectral Indices. Remote Sens. 2021, 13, 2339. [Google Scholar] [CrossRef]
- Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
- Lai, Q.; Yang, Z.; Yuliang, Y. Cost Analysis of Power Engineering Based on Improved Random Forest Algorithm. In Proceedings of the 2024 International Conference on Power, Electrical Engineering, Electronics and Control (PEEEC), Athens, Greece, 14–16 August 2024; pp. 1172–1177. [Google Scholar]
- Li, J.; Gao, Z. Setting of Class Weights in Random Forest for Small-Sample Data. Comput. Eng. Appl. 2009, 45, 131. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, S. Particle Swarm Optimization-XGBoost-Based Modeling of Radio-Frequency Power Amplifier under Different Temperatures. Int. J. Numer. Model. Electron. Netw. Devices Fields 2024, 37, e3168. [Google Scholar] [CrossRef]
- Li, J.; Liu, H.; Yang, Z.; Han, L. A Credit Risk Model with Small Sample Data Based on G-XGBoost. Appl. Artif. Intell. 2021, 35, 1550–1566. [Google Scholar] [CrossRef]
- ASTM D6595-22; Standard Test Method for Determination of Wear Metals and Contaminants in Used Lubricating Oils or Used Hydraulic Fluids by Rotating Disc Electrode Atomic Emission Spectrometry. ASTM International: West Conshohocken, PA, USA, 2022; pp. 1–6.
- Tulapurkar, H.; Mohan, B.K.; Banerjee, B. Transfomer Based Hyperspectral Dimensionality Reduction with Gabor Kernel CNN for Feature Extraction. In Proceedings of the IGARSS 2023—2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 7388–7391. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 6000–6010. [Google Scholar]
- Zounemat-Kermani, M.; Batelaan, O.; Fadaee, M.; Hinkelmann, R. Ensemble Machine Learning Paradigms in Hydrology: A Review. J. Hydrol. 2021, 598, 126266. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zhang, P.; Liu, X.; Zhang, H.; Shi, C.; Song, G.; Tang, L.; Li, R. Optimized SVR Model for Predicting Dissolved Oxygen Levels Using Wavelet Denoising and Variable Reduction: Taking the Minjiang River Estuary as an Example. Ecol. Inform. 2025, 86, 103007. [Google Scholar] [CrossRef]
- Zornoza, R.; Guerrero, C.; Mataix-Solera, J.; Scow, K.M.; Arcenegui, V.; Mataix-Beneyto, J. Near Infrared Spectroscopy for Determination of Various Physical, Chemical and Biochemical Properties in Mediterranean Soils. Soil Biol. Biochem. 2008, 40, 1923–1930. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhang, J.; Sun, M.; Zhu, R. Vegetable Sales Forecasting Based on XGBOOST Algorithm and Random Forest. In Proceedings of the 2024 International Conference on Computers, Information Processing and Advanced Education (CIPAE), Ottawa, ON, Canada, 26–28 August 2024; pp. 150–155. [Google Scholar]
- Zhang, Y.; Xia, C.; Zhang, X.; Cheng, X.; Feng, G.; Wang, Y.; Gao, Q. Estimating the Maize Biomass by Crop Height and Narrowband Vegetation Indices Derived from UAV-Based Hyperspectral Images. Ecol. Indic. 2021, 129, 107985. [Google Scholar] [CrossRef]
- Chen, Y. Research on the Prediction of Boston House Price Based on Linear Regression, Random Rorest, Xgboost and SVM Models. Highlights Bus. Econ. Manag. 2023, 21, 27–37. [Google Scholar] [CrossRef]
- Guan, Q.; Zhao, R.; Wang, F.; Pan, N.; Yang, L.; Song, N.; Xu, C.; Lin, J. Prediction of Heavy Metals in Soils of an Arid Area Based on Multi-Spectral Data. J. Environ. Manag. 2019, 243, 137–143. [Google Scholar] [CrossRef]
- Fang, J.; Tai, D. Evaluation of Mutual Information, Genetic Algorithm and SVR for Feature Selection in QSAR Regression. Curr. Drug Discov. Technol. 2011, 8, 107–111. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhou, J.; Huang, W. Attend in Bands: Hyperspectral Band Weighting and Selection for Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4712–4727. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, K.; Xu, D.; Yang, G.; Huang, H.; Nie, F.; Liu, C.; Yang, S. CuO Nanostructures: Synthesis, Characterization, Growth Mechanisms, Fundamental Properties, and Applications. Prog. Mater. Sci. 2014, 60, 208–337. [Google Scholar] [CrossRef]
- Bowles, J.F.W. The Iron Oxides: Structure, Properties Reactions Occurrence and Uses. Mineral. Mag. 1997, 61, 740–741. [Google Scholar] [CrossRef]
- Shi, T.; Chen, Y.; Liu, Y.; Wu, G. Visible and Near-Infrared Reflectance Spectroscopy—An Alternative for Monitoring Soil Contamination by Heavy Metals. J. Hazard. Mater. 2014, 265, 166–176. [Google Scholar] [CrossRef]
- Butsch, K.; Haseloer, A.; Schmitz, S.; Ott, I.; Schur, J.; Klein, A. FeIII, CuII and ZnII Complexes of the Rigid 9-Oxido-Phenalenone Ligand—Spectroscopy, Electrochemistry, and Cytotoxic Properties. Int. J. Mol. Sci. 2021, 22, 3976. [Google Scholar] [CrossRef]
- Nasse, J.-M.; Eger, P.G.; Pöhler, D.; Schmitt, S.; Frieß, U.; Platt, U. Recent Improvements of Long-Path DOAS Measurements: Impact on Accuracy and Stability of Short-Term and Automated Long-Term Observations. Atmos. Meas. Tech. 2019, 12, 4149–4169. [Google Scholar] [CrossRef]
- Lin, Y.; Gao, J.; Tu, Y.; Zhang, Y.; Gao, J. Estimating Low Concentration Heavy Metals in Water through Hyperspectral Analysis and Genetic Algorithm-Partial Least Squares Regression. Sci. Total Environ. 2024, 916, 170225. [Google Scholar] [CrossRef] [PubMed]
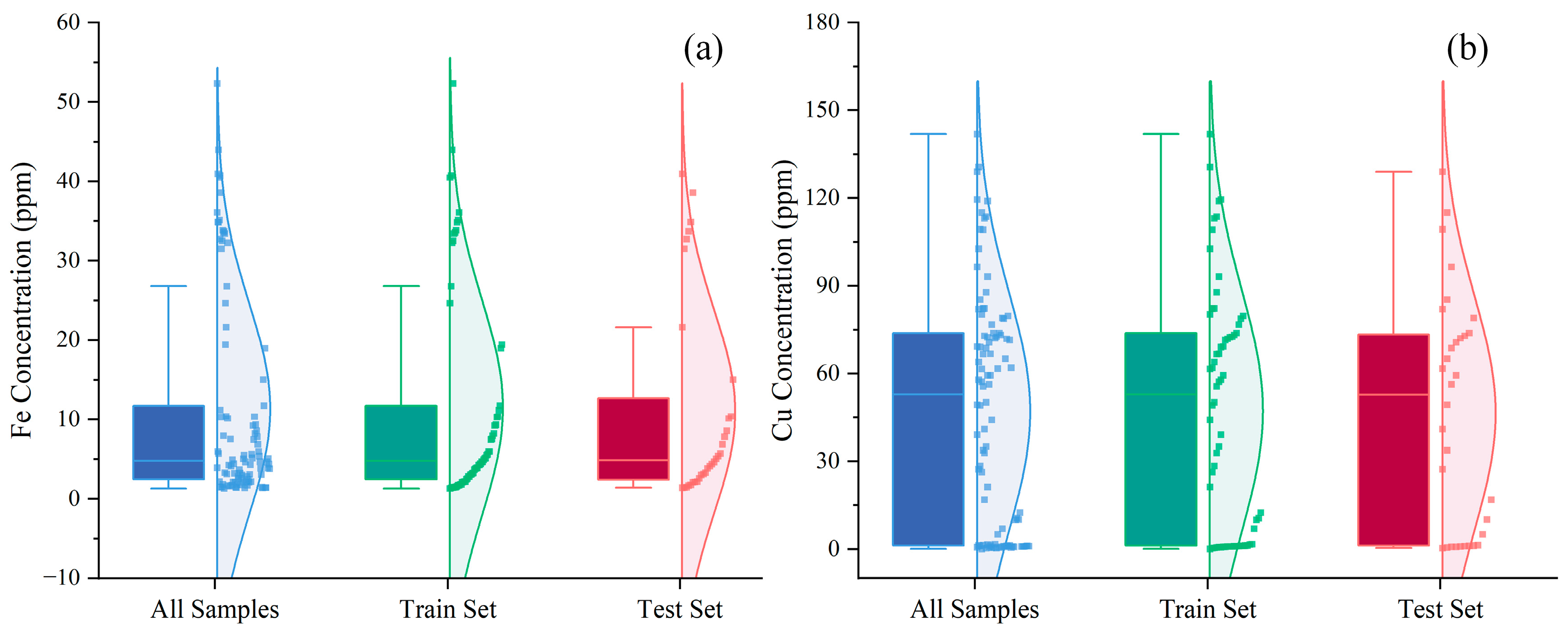


| Metal Type | Data | Max (ppm) | Min (ppm) | Median (ppm) | Mean (ppm) | SD |
|---|---|---|---|---|---|---|
| Fe | All Samples | 52.35 | 1.35 | 4.82 | 11.36 | 13.14 |
| Training Samples | 52.35 | 1.35 | 4.82 | 11.52 | 13.44 | |
| Test Samples | 40.98 | 1.44 | 4.87 | 11.03 | 12.51 | |
| Cu | All Samples | 141.96 | 0.13 | 53.00 | 47.08 | 40.20 |
| Training Samples | 141.96 | 0.13 | 53.00 | 47.32 | 40.70 | |
| Test Samples | 129.13 | 0.43 | 52.90 | 46.56 | 39.15 |
| Spectrometer | Metal Type | Modeling Method | R2 (c) | eRMSE (c)/(%) | eRPD (c) | R2 (v) | RMSE (v)/(%) | RPD (v) |
|---|---|---|---|---|---|---|---|---|
| Hach | Fe | SVR | 0.96 | 2.69 | 5.00 | 0.90 | 3.96 | 3.16 |
| RF | 0.98 | 2.04 | 6.58 | 0.90 | 3.93 | 3.18 | ||
| XGBoost | 0.99 | 0.34 | 40.02 | 0.96 | 2.38 | 5.38 | ||
| Cu | SVR | 0.95 | 9.45 | 4.31 | 0.85 | 15.06 | 2.62 | |
| RF | 0.96 | 7.75 | 5.26 | 0.86 | 14.63 | 2.71 | ||
| XGBoost | 0.95 | 9.38 | 4.34 | 0.91 | 11.85 | 3.33 | ||
| GLT | Fe | SVR | 0.97 | 2.39 | 5.62 | 0.78 | 5.83 | 2.14 |
| RF | 0.96 | 2.44 | 5.49 | 0.76 | 6.07 | 2.05 | ||
| XGBoost | 0.94 | 3.27 | 4.10 | 0.93 | 3.20 | 3.90 | ||
| Cu | SVR | 0.97 | 6.74 | 6.04 | 0.74 | 19.80 | 1.98 | |
| RF | 0.95 | 8.66 | 4.70 | 0.74 | 19.72 | 1.98 | ||
| XGBoost | 0.97 | 6.36 | 6.39 | 0.83 | 16.31 | 2.42 |
| Spectrometer | Metal Type | Feature Selection Method | Number of Features | R2 (c) | eRMSE (c)/(%) | eRPD (c) | R2 (v) | eRMSE (v)/(%) | eRPD (v) |
|---|---|---|---|---|---|---|---|---|---|
| Hach | Fe | GA | 182 | 0.99 | 0.96 | 14.06 | 0.92 | 3.52 | 3.55 |
| CARS | 88 | 0.97 | 2.29 | 5.87 | 0.92 | 3.48 | 3.59 | ||
| MHA-GA | 80 | 0.99 | 0.34 | 40.02 | 0.96 | 2.38 | 5.38 | ||
| Cu | GA | 166 | 0.97 | 6.68 | 6.09 | 0.83 | 16.02 | 2.44 | |
| CARS | 109 | 0.96 | 7.13 | 5.71 | 0.81 | 16.86 | 2.32 | ||
| MHA-GA | 67 | 0.95 | 9.38 | 4.34 | 0.91 | 11.85 | 3.33 | ||
| GLT | Fe | GA | 547 | 0.96 | 2.68 | 5.01 | 0.80 | 5.50 | 2.27 |
| CARS | 125 | 0.96 | 2.65 | 5.07 | 0.79 | 5.66 | 2.21 | ||
| MHA-GA | 127 | 0.94 | 3.27 | 4.10 | 0.93 | 3.20 | 3.90 | ||
| Cu | GA | 590 | 0.92 | 11.77 | 3.46 | 0.76 | 18.97 | 2.06 | |
| CARS | 227 | 0.95 | 8.47 | 4.81 | 0.75 | 19.65 | 1.99 | ||
| MHA-GA | 113 | 0.97 | 6.36 | 6.39 | 0.83 | 16.31 | 2.42 |
| Metal Type | Max (ppm) | Min (ppm) | Median (ppm) | Mean (ppm) | SD |
|---|---|---|---|---|---|
| Na | 60.59 | 1.46 | 19.96 | 21.45 | 14.60 |
| Mg | 24.99 | 11.97 | 19.74 | 19.49 | 2.90 |
| Al | 4.62 | 0.65 | 1.78 | 1.90 | 0.74 |
| P | 3.09 | 0.13 | 0.75 | 0.90 | 0.62 |
| B | 4.27 | 0.32 | 1.28 | 1.65 | 1.00 |
| Ni | 0.47 | 0.01 | 0.24 | 0.23 | 0.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Zhang, L.; Yuan, D.; Sun, X.; Tong, Q. A Hyperspectral Analysis-Based Approach for Estimation of Wear Metal Content in Lubricating Oil. Lubricants 2025, 13, 393. https://doi.org/10.3390/lubricants13090393
Li M, Zhang L, Yuan D, Sun X, Tong Q. A Hyperspectral Analysis-Based Approach for Estimation of Wear Metal Content in Lubricating Oil. Lubricants. 2025; 13(9):393. https://doi.org/10.3390/lubricants13090393
Chicago/Turabian StyleLi, Mengjie, Lifu Zhang, Deshuai Yuan, Xuejian Sun, and Qingxi Tong. 2025. "A Hyperspectral Analysis-Based Approach for Estimation of Wear Metal Content in Lubricating Oil" Lubricants 13, no. 9: 393. https://doi.org/10.3390/lubricants13090393
APA StyleLi, M., Zhang, L., Yuan, D., Sun, X., & Tong, Q. (2025). A Hyperspectral Analysis-Based Approach for Estimation of Wear Metal Content in Lubricating Oil. Lubricants, 13(9), 393. https://doi.org/10.3390/lubricants13090393






