Surface Property and Braking Reliability Analyses of YSZ Thermal Barrier-Coated Brake Disc of Kilometer-Deep Well Hoist

Abstract

A significant amount of heat is generated during the braking process of a kilometer-deep well hoist, which causes a large temperature rise and then thermal deformation and cracks in the brake disc. Thus, improving the surface performance of the brake disc is necessary to ensure reliable braking under high-speed and heavy-load conditions. In this paper, thermal barrier coating technology is applied to a brake disc, and the friction and wear characteristics of a yttria-stabilized zirconia (YSZ) thermal barrier-coated brake disc is studied. A coupled thermomechanical model of the hoist disc brake is established, and a temperature field simulation analysis of uncoated and coated brake discs under emergency braking conditions is carried out. Then, a surrogate model of the maximum temperature of the brake disc surface with respect to the random parameters of the brake disc is constructed based on a Latin hypercube experimental design and the Kriging method. The reliability of the brake disc under emergency braking conditions is estimated based on saddlepoint approximation (SPA), and the feasibility of applying a YSZ thermal barrier coating to a hoist disc brake is verified.

1. Introduction

Braking reliability is critical for the safe operation of mine hoists. Multiple pairs of disc brakes are used to achieve braking by creating friction between the brake shoe and the brake disc. However, the faster hoist speeds and larger loads required for kilometer-deep well hoists can increase the initial braking speed and load, posing a significant challenge for existing disc brakes. Additionally, emergency braking of the hoist generates a lot of heat on the contact surface, causing the temperature of the friction contact surface to rise rapidly, which can lead to the deformation and oxidation of the brake disc surface. These issues can significantly diminish the lifespan and reliability of disc brakes.

A disc brake works by creating friction between the brake shoe and the rotating brake disc. Thus, the temperature rise of the brake disc under thermal coupling effects has been extensively studied in recent decades. Popescu et al. [1] conducted a temperature simulation of mine hoist brake discs during emergency braking. Kepekci et al. [2] found that brake discs made of different materials with different heat transfer coefficients had significant differences in surface temperature and heat dissipation during braking. Wang et al. [3] examined the temperature evolution of train brake discs during high-speed braking and discovered that the temperature distribution on the friction surface initially formed a hot ring, which then expanded and persisted.

Belhocine and Wan [4] analyzed the thermomechanical behavior of the dry contact between the brake disc and pads during the braking process. They found that the temperature, Von Mises stress, and total deformations of the disc, as well as the contact pressures of the pads, increased with thermal stresses. Coupled thermomechanical finite element analyses of the brake disc and brake shoe were conducted in [5] to investigate their temperature and stress fields during emergency braking. Kalamegam et al. [6] carried out a systematic parametric comparison using a finite element analysis, which revealed the quantitative impact of material selection, groove orientation, and ventilation design on brake rotor disc performance. Zuo et al. [7] simulated the dynamic convective heat transfer and transient temperature field of a high-speed train brake disc by integrating fluid–structure interactions and thermomechanical coupling methods. Hong et al. [8] identified the cause of thermal cracking through a thermomechanical friction analysis of the disc and pad, and they verified their model using a dynamometer. Abdullah et al. [9] calculated the surface temperatures of the friction clutch disc and studied the thermal behavior of friction clutches during multiple engagements. Orlowicz et al. [10] analyzed the influence of different friction coefficients on braking torque and found that changes in friction coefficients during braking can alter the braking torque along the tangential and normal directions, leading to the early occurrence of “hot spots”. Yevtushenko et al. [11] developed a mathematical model to analyze the influence of changes in friction power over time on temperature, and they carried out a numerical analysis of spatiotemporal temperature distributions and heat flux intensities. Gigan [12] proposed a simulation approach for evaluating brake disc designs with respect to thermomechanical performance. Jin et al. [13] investigated the thermal behavior of friction discs in dry clutches during long-term slipping, using a two-dimensional transient thermal model based on the finite element method. Zhang et al. [14] created a flow model similar to the actual working conditions of a brake disc and examined the local and average convective heat transfer characteristics on the brake disc surface through experiments. They found that the convective heat transfer characteristics on the brake disc surface were determined by the diameter ratio of the brake disc to the train wheel. KIM et al. [15] conducted fatigue testing, a contact pressure analysis, and a thermal stress analysis on a brake disc made of GC25; established a linear relationship between temperature and stress changes; and evaluated the remaining life of the brake disc. Belhocine and Abdullah [16] used the thermal structure coupling method to simulate a transient thermal analysis and static thermal analysis of disc brakes with three different brake disc materials. Benhassine et al. [17] analyzed the isotropic and anisotropic thermoelastic behavior in multiple friction cycles of three kinds of disc materials using the finite element method. They found that the distribution of and change in temperature are very important for the contact pressure, stress field, and braking torque.

In addition to the challenges mentioned earlier, the randomness of the physical properties and material parameters of the brake disc can also affect the braking reliability of a mine hoist. In practical situations, most of these parameters are random variables. For example, the brake force and contact area of the friction pair between the brake disc and brake shoe can lead to uncertainty in the brake force. The coefficient of friction between the friction pairs, elastic modulus, and thickness of the brake disc are all random variables that have a significant impact on the braking reliability of the mine hoist. Therefore, the reliability of the brake system should be analyzed while taking into account the influence of parameter randomness on the heat transfer characteristics and temperature field of the brake disc. Lu and Yu [18] proposed a hybrid probabilistic and interval model to address the uncertainties present in a disc brake system. Li et al. [19] presented a fault diagnosis method for the hoist disc brake system based on machine learning, where the state of the brake system is determined by classifying data. Ren et al. [20] conducted probabilistic modeling and a reliability analysis of brake shoes by considering stress and temperature failure. Xu et al. [21] developed a disc brake that monitors the positive brake force in real time and has a certain brake fault diagnosis function. Yang et al. [22] carried out a reliability sensitivity analysis of automotive disc brakes, identifying multiple failure mode correlations.

One potential issue that may arise when conducting a brake disc reliability analysis is the nonlinear implicit limit state function problem caused by the complexity of the structure. However, due to the limitations of computing resources, a single finite element method is not suitable for reliability calculations that require large-scale sampling. To reduce the computational costs involved in a reliability analysis, the use of surrogate models, also known as metamodels, has become an effective approach [23]. In general, a metamodel is constructed by approximating a limited number of samples obtained from simulations using the design of experiments (DOE) method [24,25]. With an explicit, continuous, and smooth metamodel, the saddlepoint approximation method can be promptly used for reliability estimation [26,27]. There are currently many types of surrogate modeling techniques in the literature, as summarized in [28]. These surrogates fall into three major groups: geometric, heuristic, and stochastic models [29]. Among them, the Kriging metamodel stands out from the other surrogate models [30,31].

The main focus of this study is to analyze the braking reliability of a mine hoist with a coated brake disc using a thermal structural coupling analysis and an uncertainty analysis. The surface performance of a YSZ thermal barrier coating and the braking reliability of a coated brake disc for a kilometer-deep well hoist are examined. The rest of this paper is organized as follows: In Section 2, the thermal conductivity of three types of YSZ thermal barrier coatings is studied. The friction coefficient, wear resistance, and thermal deformation resistance of a YSZ thermal barrier-coated disc are examined under different pressure forces, speeds, and times. In Section 3, the parameters for a simulation analysis, such as the structural and material parameters and emergency braking parameters, are determined. The brake disc temperature field under emergency braking conditions is analyzed in Section 4. Then, a reliability evaluation of the brake disc under emergency braking conditions is performed in Section 5. Finally, the main conclusions of this study are summarized in Section 6.

2. Surface Performance Analysis of a YSZ Thermal Barrier Coating

2.1. Sample Preparation

As a type of low-alloy, high-strength steel, 16Mn is commonly used in mine hoist brakes and is chosen as the substrate material for brake discs. The material characteristics of 16Mn are presented in

Table 1. Material characteristics of 16Mn steel.

Properties	Tensile Strength (MPa)	Yield Strength (MPa)	Hardness (HB)
Values	470~630	≥345	150~160

. The dimensions of the sample substrate material are Φ30 mm × 7 mm and 20 mm × 20 mm × 5 mm.

To improve the surface performance of the brake disc, YSZ is chosen as the coating material. YSZ is a ceramic material with a high melting point and low thermal conductivity, making it a popular choice for coating aero-engine blades. In theory, YSZ coatings have good heat insulation properties, good wear resistance, and good oxidation resistance. By adjusting the Y₂O₃ content in YSZ powder, the crystal form of YSZ can be controlled to produce materials that meet specific requirements. In this study, samples with 10 wt.%, 8 wt.%, and 5 wt.% Y₂O₃ concentrations doped into YSZ powders are prepared using plasma spraying. These samples are referred to as Sample 1, Sample 2, and Sample 3, respectively. The prepared samples are displayed in Figure 1.

The WSM-3 non-asbestos brake shoe material commonly used in hoist brakes is chosen to form a friction pair with the above samples. An uncoated sample of the same size made of 16Mn steel is also selected for comparison and is referred to as Sample 4.

In this study, an MVF-1A multi-functional friction and wear testing machine is employed for friction experiments. The primary technical parameters are presented as follows:

(1)

Main shaft power: 1 kW.

(2)

Maximum measurable friction torque: 2.5 N·m. The maximum distance of the friction force arm is 50 mm, and the relative error of the friction torque indication value is ±2%.

(3)

Axial test force working range: 10–1000 N. The relative error of the test force indication value is ±0.5%.

(4)

Main shaft rotational speed range: 5–2000 r/min. The error of the main shaft rotational speed is ±1%.

The testing principle of the MVF-1A multi-functional friction and wear testing machine is that the friction pair is directly connected to the main shaft. The sample is fixed on the workbench. During the experiment, the main shaft exerts a normal pressing force. The brake shoe material comes into contact with the specimen and rotates. The main shaft is equipped with a pressure sensor, a friction force sensor, and a rotational speed sensor. All experimental data are collected and recorded by a computer. The experiment procedures are as follows:

(1)

Install the prepared friction pair and sample in their respective positions. Power on the device and the computer, check all components, and then enter the testing system.

(2)

To ensure better engagement of the friction pair and to approximate the actual working conditions more closely, perform preliminary grinding on the friction pair prior to commencing the friction experiment, and then conduct the friction experiment.

(3)

Set parameters such as the rotational speed, pressing force, and experimental duration in the testing system, and initiate the experiment.

(4)

After the experiment is completed, export the experimental data recorded by the computer.

Under the actual braking conditions of the hoist, both the pressure force and the initial braking speed will affect the braking effect. To closely simulate the real working conditions, the following test plans are proposed:

(1)

The influence of pressure force on the friction and wear characteristics of the friction pair

The wear rate, friction coefficient, and variance of the friction coefficient of the four samples in the friction test are investigated under the conditions of a constant initial braking speed and different pressure forces.

(2)

The influence of rotational speed on the friction and wear characteristics of the friction pair

The wear rate, friction coefficient, and variance of the friction coefficient of the four samples in the friction test are investigated under the conditions of a constant pressure force and different initial rotational speeds.

(3)

The influence of braking duration on the friction and wear characteristics of the friction pair

The wear rate, friction coefficient, and variance of the friction coefficient of the four samples in the friction test are investigated under the condition of an extended braking time, that is, multiple consecutive braking events.

To implement the above test plans while referring to the technical parameters of the friction testing machine, the pressure force is set to three values, namely, 100 N, 200 N, and 300 N, and the rotational speed is set to three values: 100 r/min, 200 r/min, and 300 r/min. Cross-experiments are conducted on four samples (three coated samples and one uncoated sample), totaling 36 groups, with each group’s test time being 5 min. Under the conditions of a pressure force of 300 N and a rotational speed of 300 r/min, multiple consecutive braking tests are conducted on the four samples, with each group’s test duration being 30 min.

2.2. Friction and Wear Performance Analysis of YSZ Coating

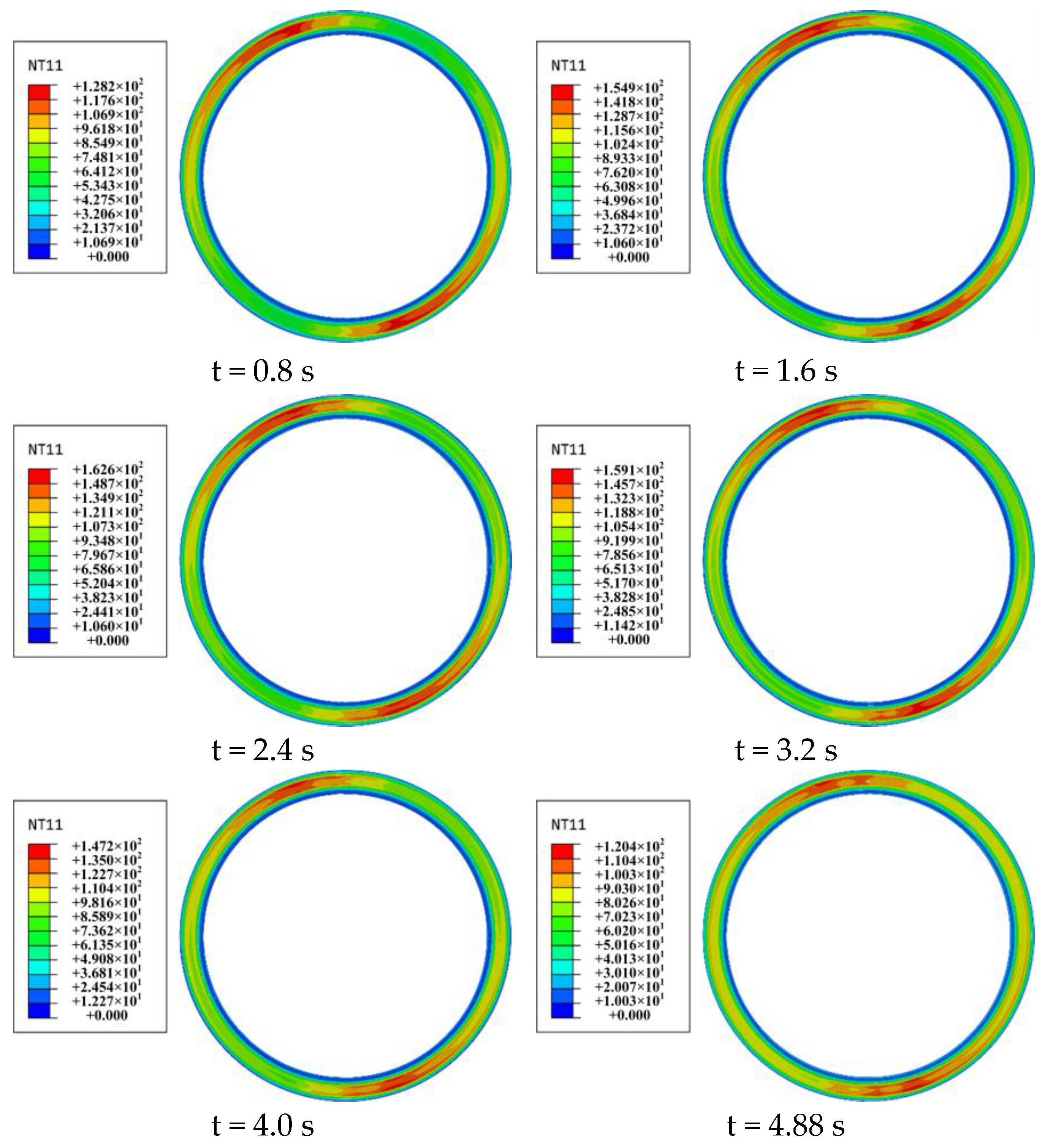
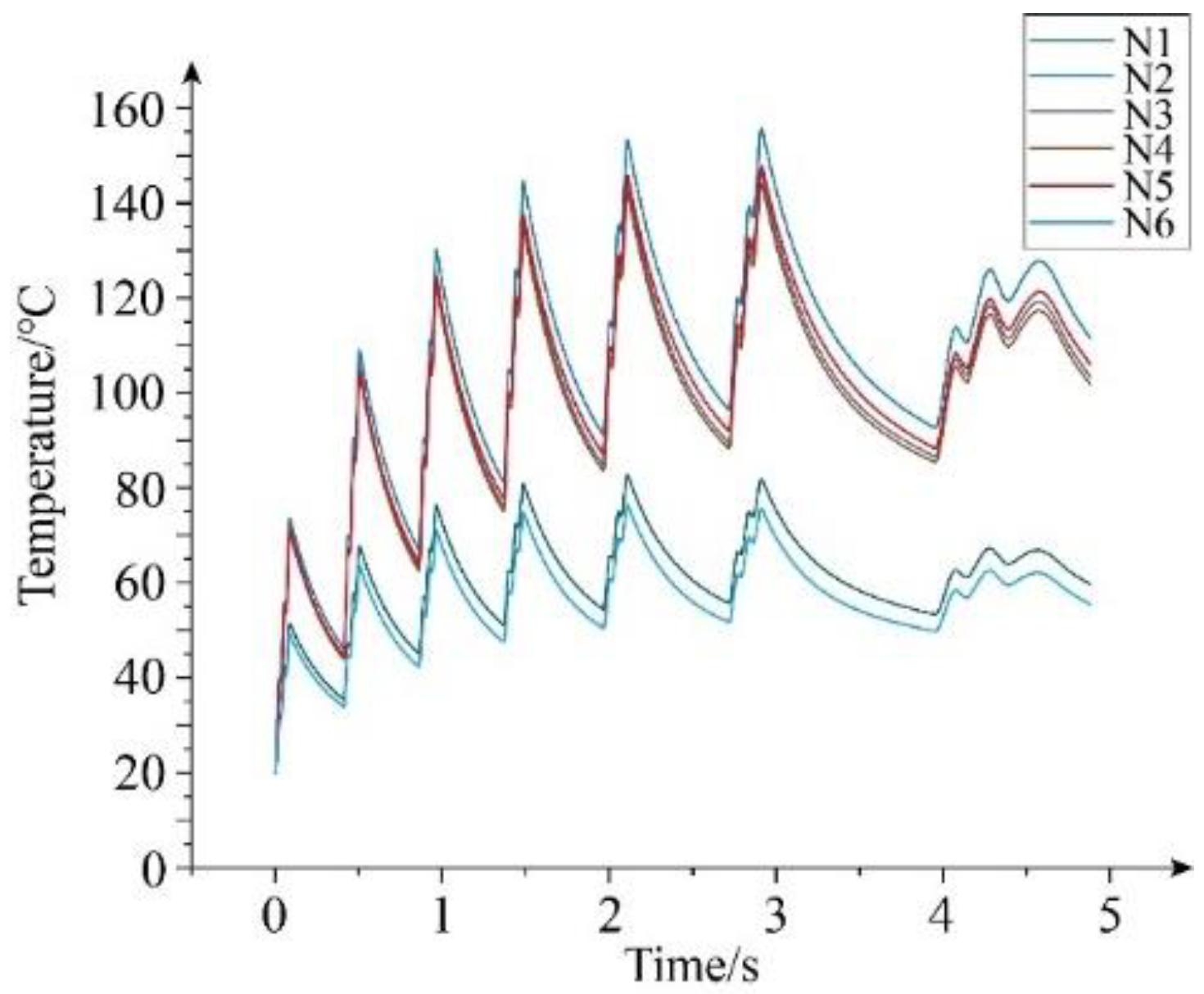
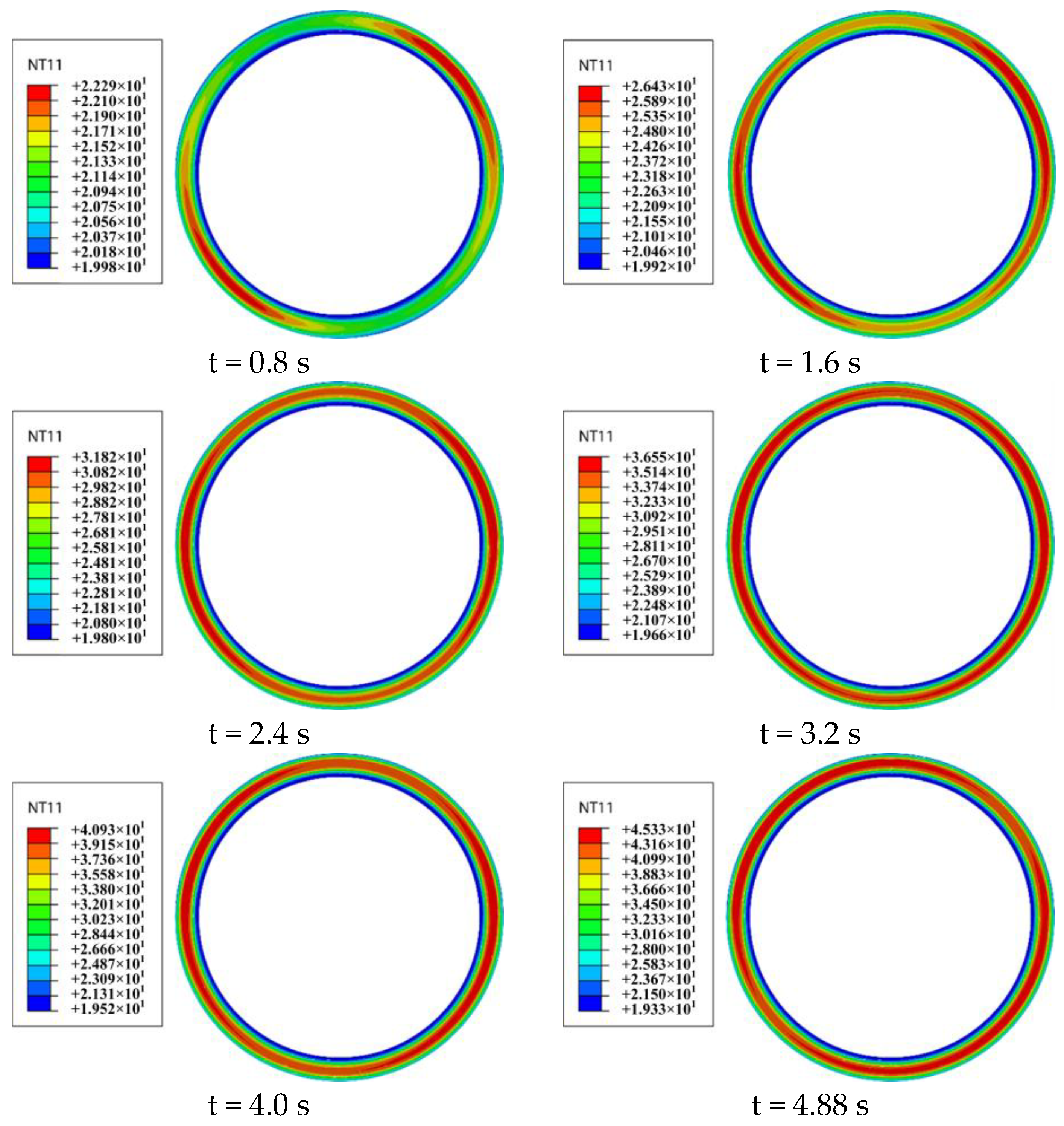
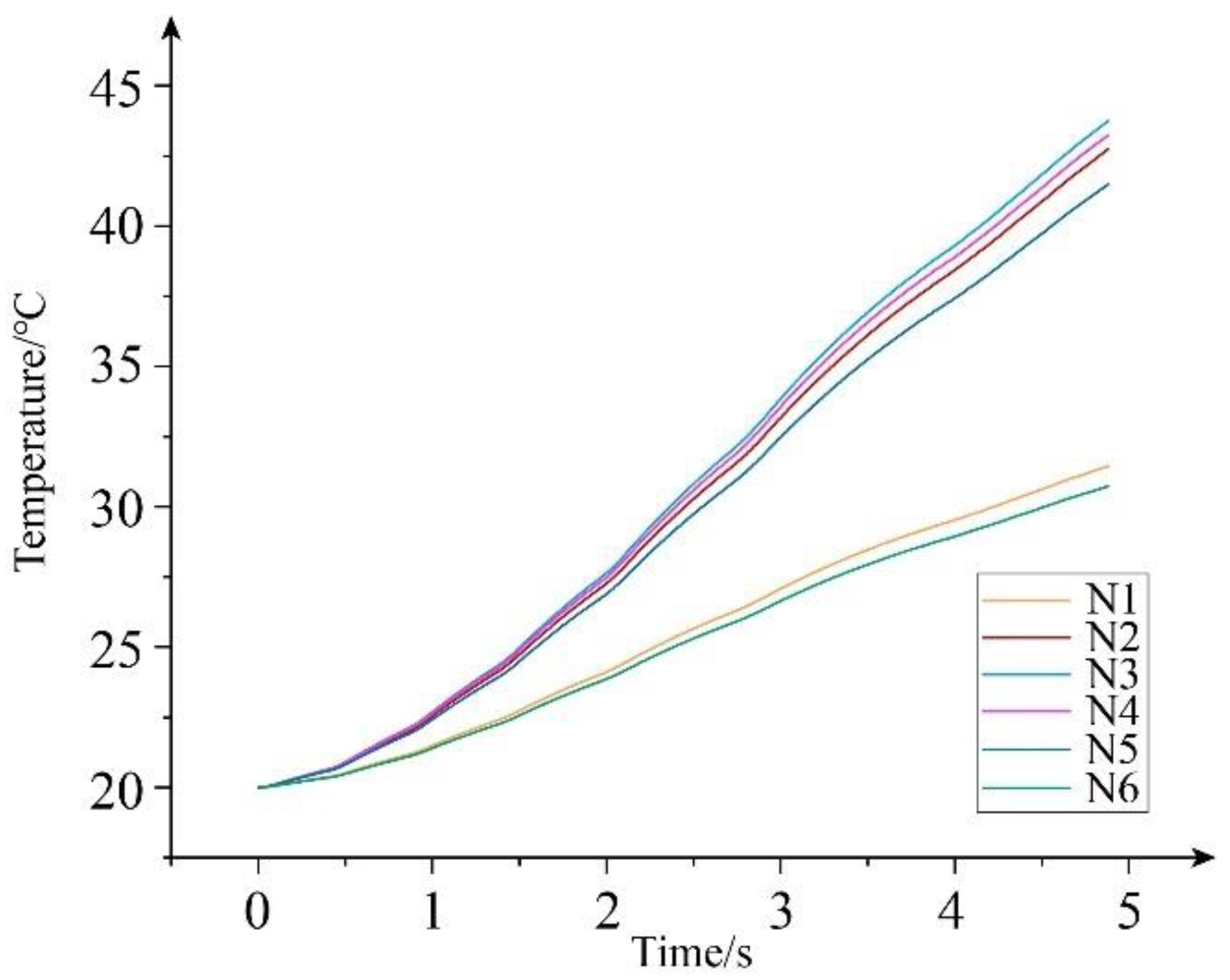
During the braking process of a mine hoist, a stable braking torque is necessary for safety. Therefore, to analyze the friction and wear performance of the YSZ coating on the brake disc, the friction coefficient, wear amount, and variance of the friction coefficient are selected as indexes to evaluate the friction and wear properties of the YSZ thermal barrier coating. Additionally, under the working conditions of a mine hoist, both the pressure force and initial rotational speed can affect the braking effect. Therefore, this study focuses on the friction and wear characteristics under various combinations of pressure force, initial rotational speed, and number of braking cycles.

2.2.1. Influence of Pressure Force on Friction and Wear Properties

The wear amount, friction coefficient, and variance of the friction coefficient are examined at different pressure forces with a constant initial rotational speed of 300 r/min (revolutions per minute).

• Wear amount analysis

The wear amount of each sample under these conditions is shown in

Table 2. Wear amount of each sample at 300 r/min.

Pressing Force	Sample 1 (×10−4 g)	Sample 2 (×10−4 g)	Sample 3 (×10−4 g)	Sample 4 (×10−4 g)
100 N	5	5	24	7
200 N	11	8	41	15
300 N	19	12	67	25

. As shown in the table, the wear amount and pressing force exhibit a positive correlation: as the pressing force increases, the wear amount also increases. The duration of the wear test is set to 5 min.

According to Table 2, when the pressing force is 100 N, the wear amount of Sample 1 and Sample 2 is the same at 5 × 10⁻⁴ g. Sample 3 and Sample 4 have wear amounts of 24 × 10⁻⁴ g and 7 × 10⁻⁴ g, respectively. In comparison, the wear amount of Sample 4 under a pressing force of 100 N is higher than that of Samples 1 and 2 but much lower than that of Sample 3.

At a pressing force of 200 N, the wear amount of Sample 2 is the lowest at 8 × 10⁻⁴ g. The wear amount of Sample 1 is 11 × 10⁻⁴ g, which falls between the wear amounts of Sample 2 (8 × 10⁻⁴ g) and Sample 4 (15 × 10⁻⁴ g). However, Sample 3 has the highest wear amount at 41 × 10⁻⁴ g.

When the pressing force is 300 N, the wear amounts of the four samples follow the same trend. Sample 3 has poor wear resistance, with a wear amount much higher than that of Sample 4. Samples 1 and 2 demonstrate superior wear resistance compared to Sample 4, and the wear resistance of Sample 2 is the best among the four samples.

2.

Friction coefficient analysis

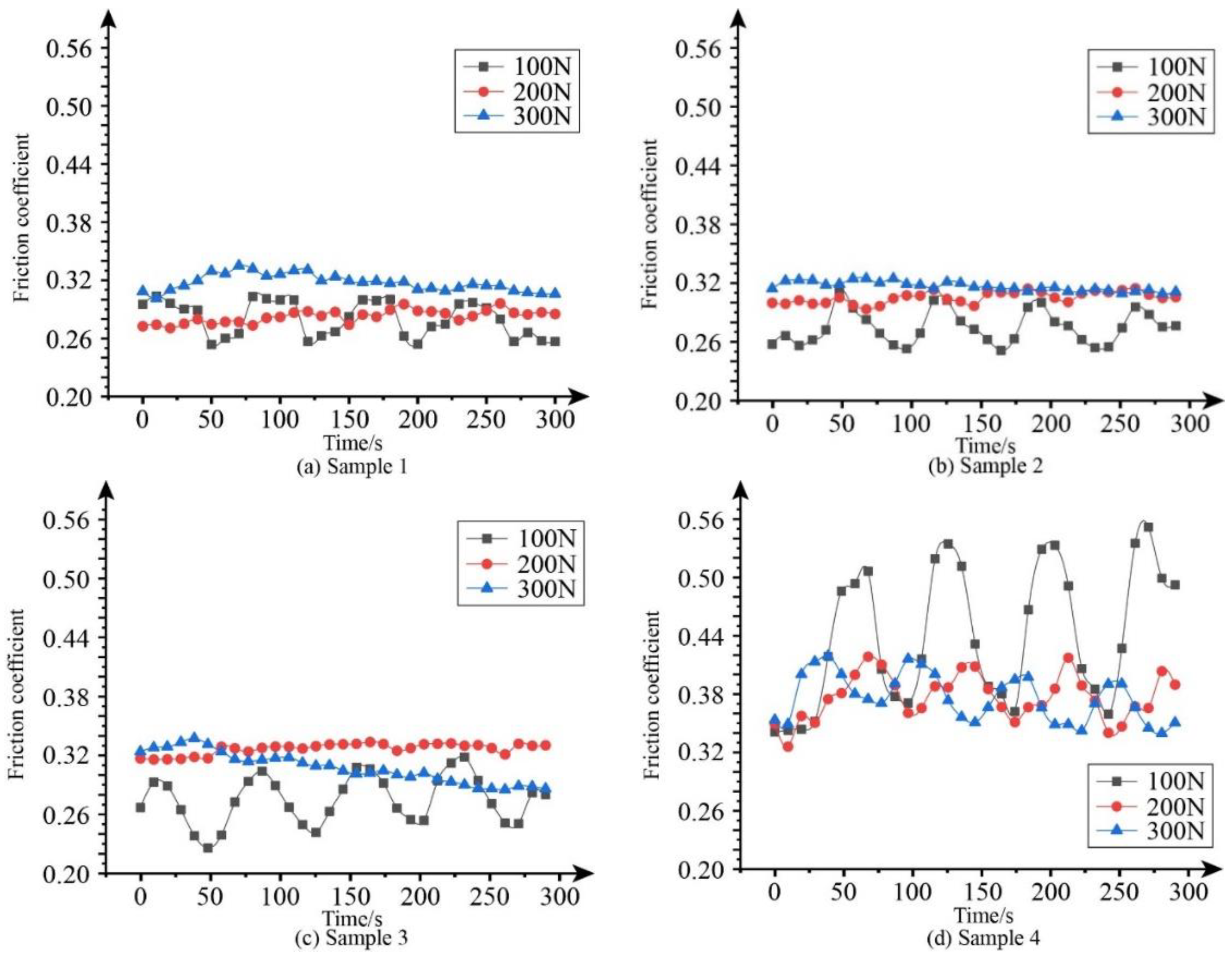
It is worth noting that changes in the friction coefficient can affect the braking torque during the braking process of a hoist, which will affect the effectiveness and safety of braking. As can be seen in Figure 2, the friction coefficient of each sample under different pressing forces at a rotational speed of 300 r/min is presented. The coefficient of friction is calculated by μ = F/P, in which F represents the measured friction force, and P represents the measured pressure force.

The friction coefficients of the four samples all show significant fluctuations under a pressing force of 100 N. The fluctuation degrees of the friction coefficients of Samples 1, 2, and 3 are similar, while the friction coefficient of Sample 4 fluctuates dramatically. When the pressing forces are set to 200 N and 300 N, the change in the friction coefficient of Samples 1, 2, and 3 is relatively stable, while that of Sample 4 fluctuates greatly.

In terms of the average friction coefficient, the four samples have values of 0.28, 0.27, 0.27, and 0.44 under a pressing force of 100 N, respectively. When the pressing force is 200 N, the average friction coefficient of the four samples is 0.28, 0.30, 0.32, and 0.37, respectively. When the pressing force is 300 N, the average friction coefficients are 0.31, 0.31, 0.30, and 0.37, respectively.

In conclusion, the friction coefficient of the three coated samples (Samples 1, 2, and 3) is lower than that of the uncoated sample (Sample 4), but the degree of fluctuation in the friction coefficient of the coated samples is lower than that of the uncoated sample. When the pressing force is 300 N, the friction coefficient of both Samples 1 and 3 increases at first and then decreases slightly, while Sample 2 exhibits relatively consistent friction coefficients.

3.

Friction coefficient variance analysis

Based on the results of the friction coefficient, the friction coefficient variance is also calculated to quantify the fluctuation degree of the friction coefficient.

The variance of the friction coefficient refers to the variance of the friction coefficient in the braking friction test, which is used to describe the stability of the friction coefficient during the braking process. Its expression is as follows:

$$S_f^2={\displaystyle \frac{{\left(f_1-{\overline{\mu }}_f\right)}^2+{\left(f_2-{\overline{\mu }}_f\right)}^2+\dots +{\left(f_n-{\overline{\mu }}_f\right)}^2}{n}}$$

(1)

where f₁, f₂,…, f_n represent the friction coefficients of each sampling point, n is the number of sampling points, and µ_f is the average value of all sampling points with friction coefficients.

The friction coefficient variance of each sample under different pressing forces is shown in

Table 3. The friction coefficient variance of each sample at 300 r/min.

Pressing Force	Sample 1 (×10−5)	Sample 2 (×10−5)	Sample 3 (×10−5)	Sample 4 (×10−5)
100 N	26.7	30.1	61	508.9
200 N	2.0	3.6	3.2	57.6
300 N	1.8	2.3	25.6	60.5

. The larger the variance, the more unstable the friction coefficient.

When the pressing force is 100 N, the friction coefficient variance of Sample 1 is the smallest, while that of Sample 2 is slightly higher than that of Sample 1. The friction coefficient variance of Sample 3 is twice that of Sample 2. The friction coefficient variance of Sample 4 is very large and 8.3 times that of Sample 3.

When the pressing force is 200 N, the friction coefficient variance of Samples 1, 2, and 3 is relatively small, while the friction coefficient variance of Sample 4 is relatively large. When the pressing force is 300 N, the friction coefficient variance of Samples 1 and 2 is small, while that of Sample 3 is large. Sample 4 displays twice the variance of the friction coefficients compared to Sample 3.

Additionally, under different pressing forces, the friction coefficient variance of Sample 1 and Sample 2 is relatively small, that of Sample 3 is slightly higher, and that of Sample 4 is much higher. In other words, the friction coefficient stability of coated Sample 1, Sample 2, and Sample 3 is better than that of uncoated Sample 4. Among the coated samples, the friction coefficient stability of Sample 1 and Sample 2 is the best, and the friction coefficient stability of Sample 3 is worse than that of Sample 1 and Sample 2.

2.2.2. Influence of Rotational Speed on Friction and Wear Properties

The impact of different rotational speeds on the friction and wear properties is analyzed at a constant pressing force of 300 N. As before, the wear amount, friction coefficient, and friction coefficient variance are studied.

• Wear amount analysis

The wear performance of each sample at different rotational speeds under a pressing force of 300 N is presented in

Table 4. The wear amount of each sample under a pressing force of 300 N.

Rotational Speed	Sample 1 (×10−4 g)	Sample 2 (×10−4 g)	Sample 3 (×10−4 g)	Sample 4 (×10−4 g)
100 r/min	11	5	11	11
200 r/min	13	7	32	13
300 r/min	19	12	53	25

.

The wear amount of each sample at the same rotational speed and a pressing force of 300 N is compared, as shown in Table 4. Obviously, the wear amount increases with the increase in the rotational speed, and the amount of wear is positively correlated with the rotational speed. The wear resistance of Sample 1 is equivalent to that of Sample 4 at relatively lower speeds, while the wear resistance of Sample 1 is slightly better than that of Sample 4 at high speeds. The wear resistance of Sample 2 is the best in the friction test, with the smallest wear amount at both low and high rotational speeds. The wear resistance of Sample 3 is the worst, while that of Sample 4 is the same at 100 r/min, but that of Sample 3 is the highest at 200 r/min and 300 r/min and is much higher than that of Sample 4.

In summary, compared to Sample 4, Sample 2 has the best wear resistance performance, followed by Sample 1, while Sample 3 has the worst performance.

2.

Friction coefficient performance

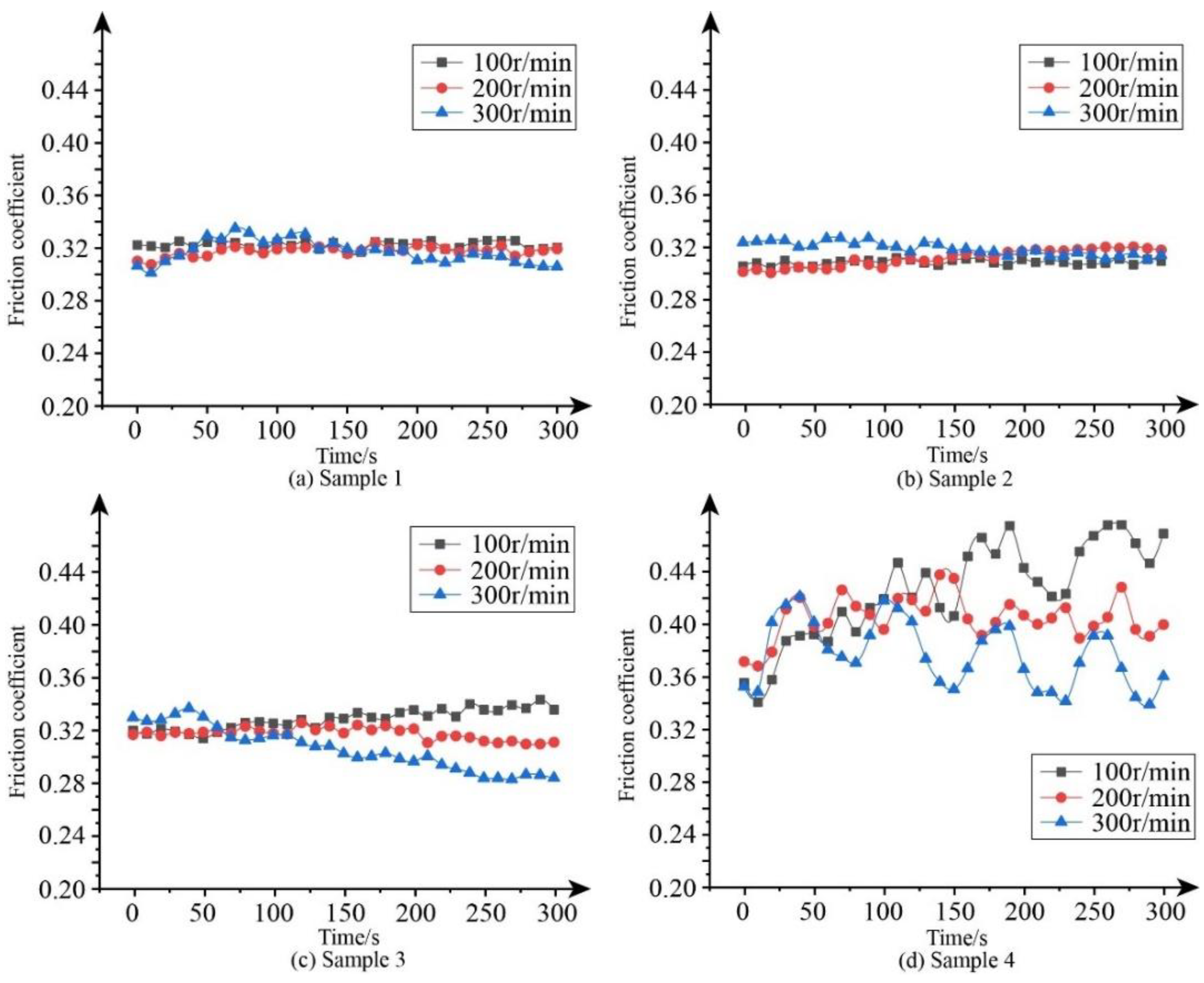
Figure 3 shows the friction coefficient of each sample at different rotational speeds under a pressing force of 300 N. The friction coefficient of Sample 1 and Sample 2 is relatively stable at different rotational speeds. For Sample 3, the friction coefficient increases slightly with time when the rotational speed is 100 r/min. When the rotational speed is 200 r/min, the friction coefficient is relatively stable. When the rotational speed is 300 r/min, the friction coefficient increases slightly at first but then decreases continuously. For Sample 4, the friction coefficient fluctuates greatly at different rotational speeds, and it is significantly higher than that of the other samples.

According to the above analysis, although the coating can slightly reduce the friction coefficient, it can also increase the stability of the friction coefficient. Sample 1 and Sample 2 show the best stability of the friction coefficient, while that of Sample 3 is poorer. Sample 4 has a relatively high friction coefficient, but it fluctuates greatly.

3.

Friction coefficient variance analysis

Table 5. The friction coefficient variance of each sample under a pressing force of 300 N.

Rotational Speed	Sample 1 (×10−6)	Sample 2 (×10−6)	Sample 3 (×10−6)	Sample 4 (×10−6)
100 r/min	7.8	4.0	57.1	1344.8
200 r/min	12.6	40.9	19.4	257.7
300 r/min	75.5	23.4	264.9	591.7

shows the friction coefficient variance of each sample at different rotational speeds under a pressing force of 300 N.

Compared to the coated samples, the friction coefficient variance of Sample 4 is the highest at all speeds, while the stability of the friction coefficient of the three coated samples is better than that of the uncoated sample.

When the rotational speed is 100 r/min and 300 r/min, the friction coefficient variance of Sample 2 is the smallest, indicating the best stability of the friction coefficient. The friction coefficient variance of Sample 1 is slightly higher than that of Sample 2. The stability of the friction coefficient of Sample 3 and Sample 4 is poor. When the rotational speed is 200 r/min, the friction coefficient variance of all coated samples is small, indicating a good stability of the friction coefficient.

In terms of friction coefficient stability, that of Sample 1 is the best, followed by that of Sample 2, and that of Sample 3 is poor. The stability of the friction coefficient of the three coated samples is superior to that of the uncoated sample.

2.2.3. Influence of Braking Times on Friction and Wear Performance

When the pressing force is 300 N and the rotational speed is 300 r/min, the effect of braking times on the friction and wear performance is studied.

• Wear amount analysis

Table 6. Wear amount of single friction test and continuous friction test of each sample.

Type	Sample 1 (×10−4 g)	Sample 2 (×10−4 g)	Sample 3 (×10−4 g)	Sample 4 (×10−4 g)
Single test	19	12	67	25
Continuous test	80	59	872	101

shows a comparison of the wear amount of each sample under single braking tests and continuous braking tests. It is evident that the wear amount of Sample 2 is the smallest among the four samples in both single and continuous braking, indicating the best wear resistance. The wear resistance performance of Sample 1 is slightly inferior to that of Sample 2 but better than that of uncoated Sample 4. The wear amount of Sample 3 is higher than that of Sample 4, indicating that the wear resistance of Sample 3 is even worse than that of the uncoated sample.

2.

Friction coefficient performance

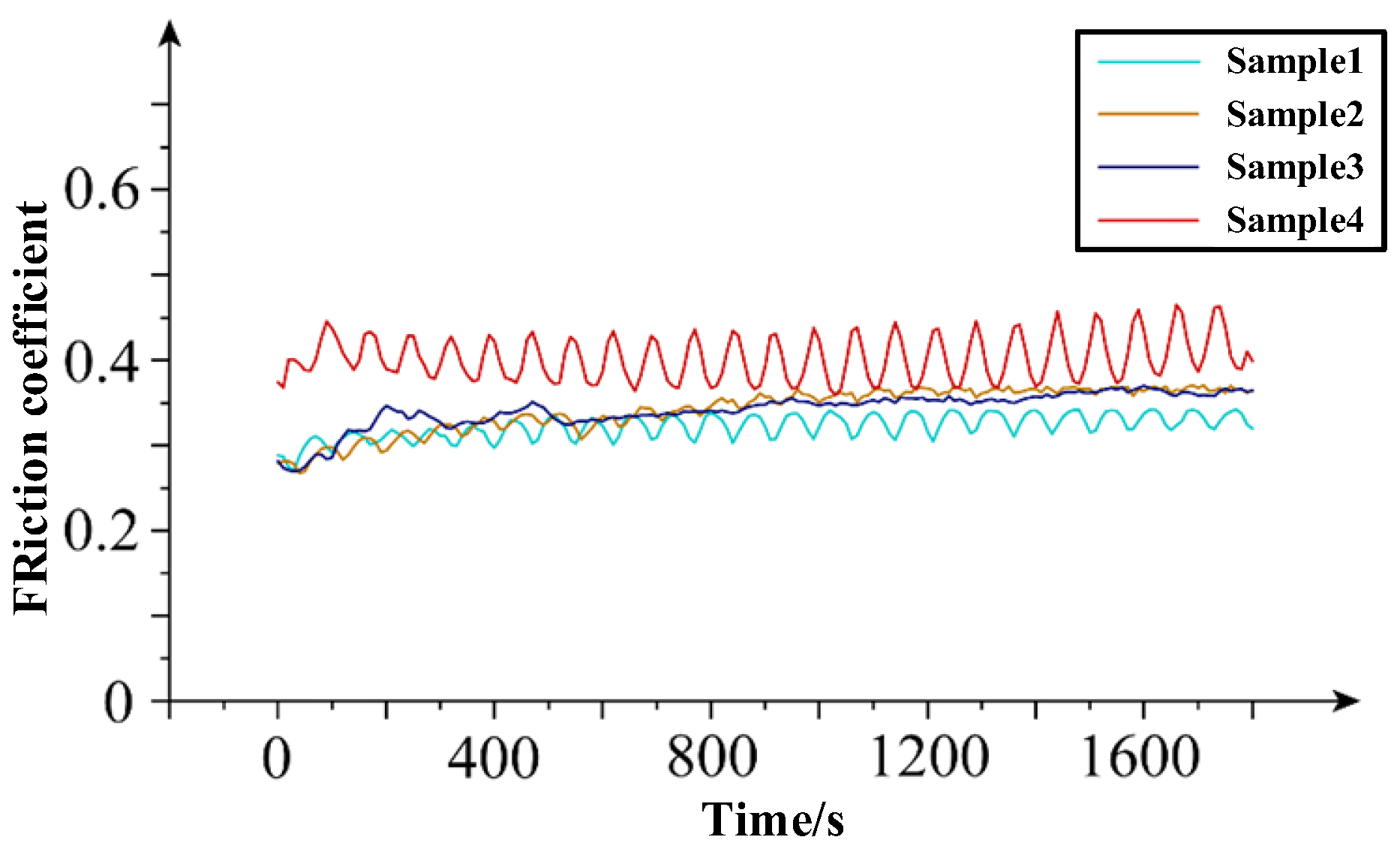
Figure 4 illustrates the variation in the friction coefficient of each sample in the continuous braking tests. It is evident that the friction coefficient of Sample 4 is higher than that of the other three samples throughout the test, and the fluctuation of the friction coefficient is also the largest. The friction coefficient curves of Sample 2 and Sample 3 are close to each other, showing a small upward trend throughout the test process. The friction coefficient curve of Sample 1 is nearly horizontal, but with small fluctuations. When compared with the single friction test, it is apparent that, in the continuous friction test, the value of the friction coefficient does not increase or decrease significantly, but the fluctuation degree of the friction coefficient increases to a certain extent.

3.

Friction coefficient variance analysis

Table 7. Variance in friction coefficient in single braking test and continuous braking test.

Type	Sample 1 (×10−5)	Sample 2 (×10−5)	Sample 3 (×10−5)	Sample 4 (×10−5)
Single test	7.4	2.3	25.6	60.5
Continuous test	21.0	68.7	43.9	67.3

shows a comparison of the friction coefficient variance between the single braking tests and continuous braking tests for each sample. The friction coefficient variance in the continuous braking tests for all four samples is higher than that in the single braking tests. The stability of the friction coefficient becomes worse with increasing braking times, resulting in greater fluctuations in the friction coefficient.

In the single braking tests, the friction coefficient variance of Sample 2 is the smallest, and its friction coefficient stability is the highest. However, in the continuous braking tests, the stability of the friction coefficient of Sample 2 is comparable to that of Sample 4, indicating that the fluctuation degree of the friction coefficient of Sample 2 increases significantly with increasing braking times.

Furthermore, the friction coefficient variance of Sample 1 in the single braking tests is higher than that of Sample 2 but smaller than that of Sample 3, while the friction coefficient variance of Sample 1 is the smallest in the continuous braking tests. The variation in the friction coefficient of Sample 3 in the single braking tests and continuous braking tests is at a medium level. The variation in the friction coefficient of Sample 4 is the largest in both the single friction tests and continuous braking tests.

2.2.4. Summary

The wear performance of Sample 2 was found to be the best among all samples, as indicated by it exhibiting the smallest mass loss in both the single and continuous braking tests. Additionally, the friction coefficients of Samples 1, 2, and 3 were found to be equivalent in the single braking tests. However, the friction coefficients of Sample 1 and Sample 4 exhibited periodic fluctuations in the continuous braking tests, while those of Sample 2 and Sample 3 remained stable. Furthermore, the friction coefficient variance of Sample 1 and Sample 2 was the smallest in the single braking tests, although it was slightly inferior in the continuous braking tests. Based on these findings, the coating material of Sample 2, i.e., 8 wt.% YSZ, was chosen as the coating material for the brake disc due to its superior wear performance, friction coefficient performance, and friction coefficient variance performance in the single braking tests.

3. Parameter Determination for Simulation Analysis

3.1. Structural and Material Parameters

A JKMD-5 × 4 (III) floor-type multi-rope friction hoist was selected as the research object. The main shaft of the hoist has a diameter of 5 m, and there are six disc brakes on each side of the brake disc. On each side of the main shaft device, there are six pairs of brake shoes on the brake disc, with an angle of 14° between each pair, as shown in Figure 5. The geometric parameters and installation dimensions of the brake disc and brake shoe can be found in

Table 8. Geometric parameters of brake disc and brake shoe.

	Internal Diameter (mm)	External Diameter (mm)	Thickness (mm)
Brake shoe	5000	5500	50
Brake disc	4800	5600	50

.

The materials of the brake disc and brake shoe were 16Mn steel and WSM-3, respectively, and the coating material was 8%Y2O3-ZrO2 (8YSZ). The density, specific heat capacity, and Poisson’s ratio of 8YSZ did not change with temperature, and the values were 5650 kg/m³, 450 J/(kg·K), and 0.23, respectively. The other performance parameters of 8YSZ under different temperatures are presented in

Table 9. Performance parameters of 8% Y2O3-ZrO2 coating material under different temperatures.

Material Name	Temperature (°C)	Elastic Modulus (GPa)	Coefficient of Thermal Expansion (10−6/K)	Thermal Conductivity W/(m·K)
	20	48	9.68	1.2
8%Y2O3-ZrO2	200	47	9.68	1.19
	400	44	9.78	1.18

.

The brake disc material, made of 16Mn, has a density of 7850 kg/m³ and a Poisson’s ratio of 0.3. These properties are barely affected by temperature. As shown in

Table 10. Thermophysical parameters of brake disc.

Temperature	Elastic Modulus	Thermal Conductivity	Coefficient of Thermal Expansion	Specific Heat Capacity
(°C)	(GPa)	(W/(m·k))	(10−6/K)	(J/(kg·K))
20	212	53.2	11.0	460
100	208	51.1	12.8	472
200	203	40.9	13.4	507
300	197	39.4	13.9	548
400	185	37.8	14.5	582

, the thermophysical parameters of the brake disc, such as the elastic modulus, thermal conductivity, thermal expansion coefficient, and specific heat capacity, change with the change in temperature. The material of the brake shoe is WSM-3, and its basic properties and thermophysical parameters are presented in

Table 11. Basic properties of WSM-3 brake shoe.

Density (kg/m3)	Poisson’s Ratio	Elastic Modulus (GPa)	Coefficient of Thermal Expansion (10−5/K)
2250	0.25	2.2	3

and

Table 12. Thermophysical parameters of WSM-3 brake shoe.

Temperature	Specific Heat Capacity	Thermal Conductivity
(°C)	(J/(kg·K))	(W/(m·K))
20	998	1.701
30	1004	1.706
60	1074	1.684
90	1168	1.701
120	1178	1.595
150	1224	1.562
180	1265	1.523
210	1295	1.489
240	1330	1.474
270	1347	1.458
300	1340	1.410

, respectively.

3.2. Parameters of Emergency Braking Condition

A deep well hoist is a type of hoisting equipment that is commonly used in mines with depths of 1000 m or more. These hoists are designed to improve the lifting speed and load capacity. In this case, it is assumed that the lifting height is 1000 m, the lifting speed is 20 m/s, and the load is 32 t.

The dynamic equation of the hoisting system during emergency braking can be expressed as follows:

$$M_d=M_{\tau }-M_j$$

(2)

where $M_d$ is the lifting maneuver torque, $M_{\tau }$ is the braking torque, and M_j is the static load torque.

The dynamic torque of the lifting system in the lifting process can be expressed as

$$M_d=\Sigma m{a}_{\tau }{R}_g$$

(3)

where $a_{\tau }$ is the braking deceleration, and $R_g$ is the radius of the hoist drum.

The braking torque of the lifting system during emergency braking can be expressed as

$$M_{\tau }=\mu NPS{R}_m$$

(4)

where $\mu$ is the friction coefficient, N is the number of brake shoes, P is the pressure force, S is the contact area between a single brake shoe and the brake disc, and R_m is the friction radius.

The static load torque of the lifting system can be expressed as

$$M_j=[KQ+C(H-2X)]g{R}_g$$

(5)

where $K$ is the resistance coefficient, Q is the effective load, C is the stiffness coefficient of the hoisting wire rope, $H$ is the height at which the lifting system needs to be lowered, $X$ is the height at which the lifting system has been lowered, and g is the gravitational acceleration.

From Equations (3)–(5), the braking acceleration can be deduced as

$$a_{\tau }=(M_z-M_j)/\Sigma m{R}_g$$

(6)

Then, the braking time of the emergency braking of the hoisting system can be obtained as

$$t_z=v/a_z$$

(7)

Regarding the rotating parts in the hoisting system, the displacement quality of each component is shown in

Table 13. Equivalent mass of lifting system.

Parameters	Equivalent Mass
Sheave wheels (kg)	39,400
Friction wheel mass (kg)	32,200
Main wire rope mass (kg)	54,511.2
Wire rope tail rope mass (kg)	47,066.7
Lifting container mass (kg)	78,000
Electric motor mass (kg)	9520
Effective load (kg)	32,000
Total displacement mass (kg)	292,697.9

.

According to the requirements of “Coal Mine Safety Regulations” and the hoisting system parameters obtained above, the emergency braking working condition parameters can be determined, which are shown in

Table 14. Parameters of emergency braking.

Parameters	Value
Hoisting speed (m/s)	20
Friction coefficient	0.3
Brake specific pressure (MPa)	1.6
Drum radius (m)	2.5
Braking torque (kN·m)	4000
Maximum static tension difference (kN)	400
Emergency braking deceleration (m/s2)	4.1
Emergency braking duration (s)	4.88

.

3.3. Convective Heat Transfer Coefficient

The contact surface between the brake disc and the brake shoe will produce a large quantity of heat during emergency braking. Heat will be transmitted from the brake disc surface to the air as the temperature of the brake disc surface rises. Therefore, the convective heat transfer coefficient is not a constant value at different speeds. The convective heat transfer coefficient of disc brakes is commonly calculated using Equation (8):

$$h_d=\left\{\begin{array}{c}0.70\left({\displaystyle \frac{{\lambda }_a}{d_a}}\right)R_e^{0.55},R_e\le 2.4\times {10}^5\\ 0.04\left({\displaystyle \frac{{\lambda }_a}{d_a}}\right)R_e^{0.8},R_e>2.4\times {10}^5\end{array}\right.$$

(8)

where $R_{\mathrm{e}}$ is the Reynolds number, and $R_e=v_a{\rho }_a{d}_a/3.6{\mu }_a$. $v_a$ is the speed of the brake disc, ${\rho }_a$ is the air density, $d_a$ is the outside diameter of the brake disc, and ${\mu }_a$ is the air viscosity.

According to the emergency braking conditions and Equation (8), the convective heat transfer coefficient of the brake disc can be transformed into the following relationship:

$$h_a=\left\{\begin{array}{c}11.98\times {(8-1.64t)}^{0.8},t\le 4.21\\ 6.74\times {(8-1.64t)}^{0.55},t>4.21\end{array}\right.$$

(9)

By fitting the above piecewise function formula, the approximate relationship between the convective heat transfer coefficient and time can be obtained, as shown in Equation (10):

$$h_a=-12.48t+65.43$$

(10)

3.4. Heat Partition Coefficient

Assuming that the brake disc and brake shoe materials are isotropic and have a uniform average temperature at their friction contact surface, it can be assumed that heat flow is continuous between them. The heat distribution on the friction surface during braking depends on the thermal resistance of both friction contact surfaces. Under steady-state conditions, the coefficient of heat partition can be expressed using Equation (11):

$$k={\displaystyle \frac{q_d}{q_s}}={\displaystyle \frac{\Sigma R_s}{\Sigma R_d}}$$

(11)

where $q_d$ is the heat flux to the brake disc, $q_s$ is the heat flux to the brake shoe, $R_d$ is the heat transfer resistance of the brake disc, and $R_S$ is the heat transfer resistance of the brake shoe.

Additionally, the following relationship exists in the contact area:

$$\left\{\begin{array}{c}{T}_1^{*}=T_2^{*}\\ q_d+q_{\mathrm{s}}=q\end{array}\right.$$

(12)

where $T_1^{*}$ and $T_2^{*}$ are the average temperatures of the contact surface of the micro-convex body in the contact area, and $q$ is the total heat flux generated by the friction surface.

Then, the coefficient of heat partition between the brake disc and brake shoe is

$$k={\displaystyle \frac{q_d}{q_s}}={\left({\displaystyle \frac{{\rho }_d{c}_d{\lambda }_d}{{\rho }_s{c}_s{\lambda }_s}}\right)}^{{\displaystyle \frac{1}{2}}}$$

(13)

where $\rho$ is the density, $c$ is the specific heat capacity, and $\lambda$ is the thermal conductivity.

By utilizing Equation (13) and considering the material properties of both the brake disc and brake shoe, we can calculate the heat distribution between these two components. The resulting values are summarized in

Table 15. Heat flow distribution of brake disc and brake shoe.

Material	Density $\mathit{\rho }$ (kg/m3)	Specific Heat Capacity $\mathit{c}$ (J/kg·K)	Thermal Conductivity $\mathit{\lambda }$ (W/m·K)	Heat Flux Distribution Coefficient (%)
WSM-3 brake shoe	2250	1004	1.706	12.41
Brake disc	7850	460	53.2	87.59

. The brake disc has high thermal conductivity and low thermal resistance, which means that 87.59% of the heat generated through friction is transferred to the brake disc, while only 12.41% is transferred to the brake shoe.

4. Thermal–Structural Coupling Analysis of Disc Brake Under Emergency Braking Conditions

4.1. Temperature Field Analysis of Uncoated Brake Disc

Based on the parameters determined in the previous section, a finite element model is established for the brake disc and brake shoe. Figure 6 shows the maximum temperature curve attained by the uncoated brake disc during emergency braking, with temperatures peaking at 163.4 °C after 2.3 s. Figure 7 illustrates the temperature contour of the uncoated brake disc under emergency braking conditions for a duration of 4.88 s.

As can be seen in Figure 6 and Figure 7, a significant amount of heat is generated due to surface friction on the brake disc immediately following the act of braking. Because the heat cannot spread into the air in a short time, heat accumulates rapidly, and the brake disc surface temperature rises rapidly. During the early stages of braking, the fast rotational speed of the brake disc causes the speed of heat diffusion to be slower than that of heat generation by friction, which causes the temperature of the brake disc to continue to rise. As the rotational speed of the brake disk gradually slows down, at 2.3 s, the rate of heat generated by friction is the same as that of heat diffusion, and the temperature does not rise any more. After 2.3 s, the speed of friction heat production is less than that of heat diffusion, leading to a gradual decrease in the brake disc temperature.

As shown in Figure 7, the temperature change nephogram reveals that the uncoated brake disc exhibits consistently high temperatures near the friction pair position, which gradually reduce over time. This phenomenon is primarily caused by the fact that the brake disc continues to rotate after the temperature of the contact surface of the friction pair rises. Simultaneously, due to the convective heat transfer of air, the maximum temperature gradually decreases with the rotation process.

To further investigate the surface temperature distribution of the brake disc under emergency braking conditions, six nodes are marked on the brake disc’s friction surface. As shown in Figure 8, these nodes are labeled N1, N2, N3, N4, N5, and N6 in the radial direction. The corresponding temperature variations of each node at different times are depicted in Figure 9.

As shown in Figure 9, the temperatures of the six nodes from N1 to N6 fluctuate greatly during braking, showing a “sawtooth” shape. This is because each braking point repeatedly passes through both the contact and non-contact areas, thus showing a repeated increase and decrease in temperature.

At the same time, the temperature of N1 and N6 is much lower than that of the other four nodes. The reason for this is that convective heat transfer and heat conduction exist at the same time during rotation at the edge of the frictional area, where N1 and N6 are located. The rapid diffusion of heat makes the temperature drop rapidly.

However, in the inner position of the frictional area, there is only heat conduction in the contact area. The heat diffusion speed and temperature drop are slow, and the temperatures at N2, N3, N4, and N5 are relatively higher. Additionally, as the heat generation conditions and heat dissipation conditions at the N2, N3, N4, and N5 nodes are similar, their temperature performance is also similar.

4.2. Temperature Field Analysis of Coated Brake Disc

Figure 10 displays the temperature curve of the YSZ thermal barrier-coated brake disc substrate at different times during emergency braking, reaching the highest temperature of 45.33 °C at 4.88 s. During the braking process, the temperature of the brake disc substrate with the coating rises gradually over time, but the maximum temperature is much less than that of the uncoated brake disc, which is 163.4 °C.

The temperature field of the brake disc substrate with a YSZ thermal barrier coating at each time during emergency braking is also analyzed, and a temperature nephogram is shown in Figure 11. The maximum temperature of the matrix is 22.3 °C at 0.8 s. As the braking continues, the temperature continues to rise, and, when it reaches 2.4 s, the area with a temperature difference of 1 °C from the maximum temperature connects as a complete ring, which indicates that the temperature difference of the substrate is relatively small during the braking process.

Similar to Figure 6, six nodes, designated N1, N2, N3, N4, N5, and N6, are arranged in the radial direction of the substrate. Figure 12 shows the temperature curve of each node on the coated brake disc substrate. The temperature of the six nodes rises gently, indicating that the heat dissipation efficiency of the substrate is stable. The temperature of N1 and N6 is lower than that of the other nodes because the heat input is less at the corresponding positions on the friction surface.

By analyzing the temperature field of the coated and uncoated brake discs, three main differences can be found through comparison. (1) The maximum temperature varies greatly, and the times taken to reach the maximum temperature are different. (2) The temperature fluctuation of the brake disc substrate with a YSZ thermal barrier coating is much lower. (3) The temperature distribution of the coated brake disc substrate is more uniform.

5. Reliability Evaluation of Brake Disc Under Emergency Braking Conditions

It is important to conduct an accurate assessment of the braking reliability of kilometer-deep wells. The reliability of the brake disc under emergency braking is examined by comparing the reliability of the coated and uncoated brake discs.

5.1. Stochastic Response Modeling

According to the real braking conditions of disc brakes, the brake specific pressure, friction pair area, friction coefficient, elastic modulus, and brake disc thickness are treated as random variables, and their statistical properties are presented in

Table 16. Statistical properties of random variables.

Variable	Name	Mean Value	Standard Deviation
L (Pa)	Brake specific pressure	1.6 × 106	9.35 × 104
S (m2)	Contact area of friction pair	0.48	1.5 × 10−2
f	Friction coefficient	0.3	1.7 × 10−2
E (N/m2)	Elastic modulus	2.09 × 1011	4.15 × 109
$\delta$ (m)	Brake disc thickness	0.05	5.2 × 10−4

.

According to the properties of the selected random variables, Latin hypercube sampling (LHS) is utilized to select the values of the random variables, and a Kriging model is employed to establish the functional relationship between the random variables and the temperature response. The temperature response functions with respect to the random variables of the uncoated and coated brake discs can be expressed as Equations (14) and (15), respectively:

$$T_1=h_1(L,S,f,E,\delta )$$

(14)

$$T_2=h_2(L,S,f,E,\delta )$$

(15)

5.2. Reliability Estimation Based on Saddlepoint Approximation

The SPA method can be used to estimate the output distribution of a multivariate function for a joint probability distribution of input random variables. For a joint PDF of input vector X, the moment-generating function (MGF) is defined as Equation (16):

$$M_X\left(t\right)=E_X\left\{\exp \left(tx\right)\right\}={\displaystyle {\int }_{-\infty }^{+\infty }\exp \left(tx\right)f_x\left(x\right)dx}$$

(16)

and the cumulant generating function (CGF) is

$$K_X\left(t\right)=\ln M_X\left(t\right)$$

(17)

Once $K_X\left(t\right)$ is available, SPA is readily applicable for estimating the probability of failure by the following equation:

$$P_{fSPA}=\mathrm{Pr}\left(X\le x\right)\approx \Phi (\omega )+\phi \left(\omega \right)\left({\displaystyle \frac{1}{\omega }}-{\displaystyle \frac{1}{v}}\right)$$

(18)

where $\phi$ is the PDF of a standard normal variable, and w and v can be calculated using $\omega =sign\left(t_0\right)\sqrt{2\left[c{t}_0-K_X\left(t_0\right)\right]}$ and $v=t_0\sqrt{{K^{″}}_X\left(t_0\right)}$, respectively. sign () is the sign function.

$$sign\left(t_0\right)=\left\{\begin{array}{ll}1,& t_0>0\\ 0,& t_0=0\\ -1,& t_0<0\end{array}\right.$$

(19)

Here, $t_0$ is the saddlepoint and can be solved by the following equation:

$${K^{\prime }}_X\left(t\right)=x$$

(20)

where ${K^{\prime }}_X\left(\cdot \right)$ and ${K^{″}}_X\left(\cdot \right)$ are the first and second derivatives of the CGF $K_X\left(\cdot \right)$, respectively.

The key problem to be solved in this paper is the thermal deformation and thermal crack caused by the high surface temperature of the brake disc. Thus, for a breaking reliability estimation of the brake disc, the performance functions of the uncoated and coated brake disc are respectively defined as

$$\left\{\begin{array}{c}{g}_1(X)={\mathrm{T}}_0-T_1\\ g_2(X)={\mathrm{T}}_0-T_2\end{array}\right.$$

(21)

where $X={[L,S,f,E,\delta ]}^{\mathrm{T}}$ is the random variable vector. T₀ is the limit temperature at which failure occurs, and T₀ = 192 °C.

Based on the saddlepoint approximation, the failure probabilities of the uncoated brake disc P_f1 and coated brake disc P_f2 are calculated as

$$\left\{\begin{array}{c}{P}_{f1}=1.105\times {10}^{-2}\\ P_{f2}=1.594\times {10}^{-21}\end{array}\right.$$

(22)

The results show that the failure probability of the coated disc brake under emergency braking conditions is greatly reduced. From another perspective, the probability that the internal thermal stress of the brake disc exceeds its material yield limit during emergency braking is also greatly reduced after the application of thermal barrier coating technology; that is, the possibility of thermal deformation or thermal crack failure of the brake disc is greatly reduced.

6. Conclusions

To enhance the reliability of the brake disc of a 1000 m deep well hoist, the thermal–structural coupling characteristics of the hoist brake under emergency braking conditions are studied. The surface performance and the reliability of coated and uncoated brake discs are compared. Several conclusions are summarized as follows:

(1)

Through friction and wear tests of YSZ coatings with different Y2O3 doping concentrations, taking the wear amount, friction coefficient, and friction coefficient variance as reference indexes, it is found that a YSZ coating with an 8 wt.% Y2O3 doping concentration has the best friction and wear performance among all the samples.

(2)

After conducting a thermal–structural coupling analysis on uncoated and coated brake discs during emergency braking conditions, this research compares the temperature characteristics of the two types of brake discs. It is discovered that the temperature fluctuation of the coated brake disc is much lower, and its temperature distribution is more uniform during the emergency braking process.

(3)

By comparing the failure probabilities of uncoated and coated brake discs under emergency braking conditions, it is found that the failure probability of the coated brake disc is greatly reduced, which means that the application of thermal barrier coating technology significantly enhances the reliability of the brake disc because the use of the coating significantly reduces the rise in frictional temperature.