Abstract
Water-lubricated bearings (WLB), due to their pollution-free nature and low noise, are increasingly becoming critical components in aerospace, marine applications, high-speed railway transportation, precision machine tools, etc. However, in practice, water-lubricated bearings suffer severe friction and wear due to low-viscosity water, harsh conditions, and contaminants like sediment, which can compromise the lubricating film and shorten their lifespan. The implementation of micro-textures has been demonstrated to improve the tribological performance of water-lubricated bearings to a certain extent, leading to their widespread adoption for enhancing the frictional dynamics of sliding bearings. The shape, dimensions (including length, width, and depth), and distribution of these micro-textures have a significant influence on the frictional performance. Therefore, this study aims to explore the coupling effect of different micro-texture shapes and distributions on the frictional performance of water-lubricated sliding, using the computational fluid dynamics (CFD) analysis. The results indicate that strategically arranging textures across multiple regions can enhance the performance of the bearing. Specifically, placing linear groove textures in the outlet of the divergent zone and triangular textures in the divergent zone body maximize improvements in the load-carrying capacity and frictional performance. This specific configuration increases the load-carrying capacity by 7.3% and reduces the friction coefficient by 8.6%. Overall, this study provided critical theoretical and technical insights for the optimization of WLB, contributing to the advancement of clean energy technologies and the extension of critical bearing service life.
1. Introduction
With the continuous development of global transportation and manufacturing industries, the performance demands for production and transportation equipment, such as large ships, submarines, high-speed railway systems, and precision machine tools, have risen significantly [1,2,3]. Sliding bearings, which are integral components of contemporary mechanical systems, are essential for supporting rotating elements, minimizing friction, and facilitating effective lubrication between moving components. These bearings are indispensable in such machinery [4,5]. In particular, water-lubricated bearings (WLB) are extensively utilized in high-speed rotating machinery due to their low frictional power consumption, efficient heat dissipation, environmental sustainability, and simple structural design [6,7,8,9]. However, the low viscosity of water poses significant challenges in establishing an effective liquid film under low-speed and heavy-load conditions. In such cases, the bearings predominantly operate under boundary lubrication or mixed lubrication regimes, leading to increased contact between the shaft and bearing. This will intensify wear and may lead to self-excited vibrations caused by friction, severely reducing the bearing lifespan [10]. Consequently, there is an escalating demand to enhance the wear resistance, load-carrying capacity, and fatigue life of WLB. Recent research have focused on friction reduction technologies in which various strategies have been introduced to minimize friction and wear during relative motion, among which biomimetic surface micro-textures are emerging as a particularly effective approach [11,12].
With the development of microfabrication technology, deterministic roughness, known as surface textures, has been introduced into the practical applications of bearings [13]. Emerging techniques such as 3D printing [14], laser surface texturing [15], chemical etching [16], fly cutters [17], and novel finishing methods [18] have enabled the precise fabrication of controllable micro-textures on the surfaces of sliding bearings. These micro-textures have been shown to significantly improve tribological performance by reducing friction, improving reliability, and lowering energy loss.
Previous studies have shown that the introduction of dimples or roughness near the inlet of sliding surfaces can generate additional pressure, thereby enabling the support of higher loads. Tonder [19] highlighted this benefit, which was confirmed by Cupillard et al. [20]. Kovalchenko et al. [21] demonstrated that laser surface texturing expands the contact parameters under hydrodynamic lubrication in terms of load and speed. Tala-Ighil et al. [13,22] investigated the influence of textures on the sliding bearing lubrication under steady-state conditions using a finite difference numerical model. Their findings suggested that increasing the size and depth of dimples enhances the load-carrying performance compared to smooth surfaces. Additionally, Jin et al. [23] developed a computational model to analyze lubrication and wear in textured journal bearings and revealed that surface textures can establish secondary lubrication.
Computational fluid dynamics (CFD) serves as a crucial analytical instrument for studying the lubrication characteristics of bearings. Yin et al. [24] utilized CFD to analyze the lubrication characteristics of radial bearings and found that placing textures in the primary bearing region enhances the load-carrying capacity, reduces frictional coefficients, and minimizes lubricant flow. Wang et al. [25] employed CFD software to compare the effect of texture distribution on the journal bearing performance, both with and without the consideration of cavitation effects. Their finding indicated that textures placed near the outlet of the convergent gap produced the most significant effects. Tao et al. [26], developed a simulation model to analyze the impact of various surface texture shapes and their spatial arrangements on the load-carrying capacity. Their results showed that in terms of load-carrying capacity, rectangular is better than trapezoidal, which is better than a circular arc, and triangular textures are the worst. The strategic arrangement of textures within the convergent wedge region was found to significantly enhance the load-carrying capacity.
Numerous scholars have explored the effect of surface textures on the bearing performance from diverse perspectives. Wang et al. [27] compared the performance of textured and smooth journal bearings across varying eccentricities. The results demonstrated that the impact of surface textures on lubrication behavior depends on eccentricity. Chen et al. [28] experimentally evaluated the comprehensive effects of surface texture density, depth, and distribution on the vibration and stability of radial bearings. They innovatively analyzed the impact of textures on the bearing dynamic characteristics. Galda et al. [29] performed experimental studies on the effect of micro-textures on bearing performance, concluding that micro-textures contribute to reduced friction during the start-up and shut-down phases of the bearing operation. Hao et al. [30] proposed an improved method utilizing electrochemical micromachining to fabricate micro-textures of varying dimensions on the inner surfaces of bearings, subsequently testing the stability of these textured bearings. Filho et al. [31] conducted experimental analyses on the impact of microtextured journals on bearing performance, revealing that the effect of textures could be beneficial or detrimental, depending on the motion direction of the journal. Xie et al. [32,33] executed CFD analyses on representative dimples, and the lubrication mechanisms of micro-interfaces and the variation in dimple structure parameters were elucidated.
This study aimed to investigate the influence of different micro-texture combinations on the bearing performance, particularly in the context of cavitation effects. Triangular, hexagonal, and linear groove micro-textures distributed in distinct regions were combined to form hybrid textured configurations. Three bionic micro-texture models were developed using CFD technology, with the load-carrying capacity and friction coefficient as the evaluation metrics. A systematic investigation of the hybrid arrangements of these textures at multiple locations was conducted to clarify their impact on the bearing behavior.
2. Materials and Methods
2.1. Governing Equations
Cavitation, which leads to the rupture of the water film, occurs when the water film pressure in the bearing’s divergent zone falls below the cavitation pressure. To incorporate the effect of cavitation, a mixture model is adopted, assuming the lubricant consists of gas and liquid phases. The continuity and momentum equations, shown in Equations (1) and (2), serve as the governing equations for bearing performance analysis [13].
where is the viscosity of the mixed phase, is the speed of the mixed phase, is the density of the mixed phase, and t is the time.
The water film thickness equation for sliding bearings is as follows:
where is the journal eccentricity, is the bearing clearance, is the total water film thickness, is the base water film thickness, is the texture-additional water film thickness, and is the water film thickness at the textured region.
The enhanced fully implicit-coupled algorithm, which is founded on the pressure-coupled equation, is employed to calculate the pressure and shear stress of the bearing water film. The bearing load-carrying capacity is obtained by integrating the water pressure over the area of the inner wall surface of the bearing:
where is the water film inner diameter and is the water film width.
The friction force of the bearing water film is obtained by integrating the shear stress over the surface area, and it can be calculated by the following formula:
The friction coefficient is the ratio of the friction force to the load-carrying capacity.
2.2. Three-Dimensional Geometric Model
The schematic diagram of the hydrostatic bearing is shown in Figure 1. Water enters into the bearing from the upper section and exits from both extremities. A fixed eccentricity ratio is utilized to demonstrate how microflow within textures impacts the flow in the bearing clearance. Since the bearing operates under load in practical working conditions, eccentricity exists. The fluid domain experiences a transition from a wider to a narrower configuration and subsequently back to a wider one. As the viscous lubricant flows into the wedge-shaped clearance, the wedge effect creates symmetric high- and low-pressure regions around the minimum water film thickness, as shown in Figure 2. The parameters of bearing geometry and boundary conditions used in the present study are listed in Table 1.
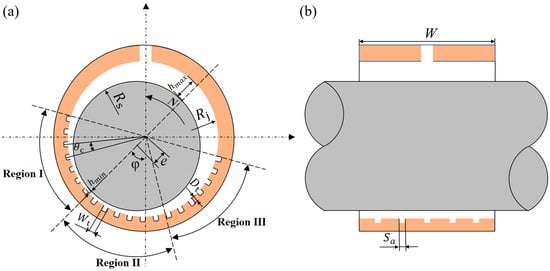
Figure 1.
Geometry of hydrodynamic journal bearing: (a) front view; (b) side view.

Figure 2.
Pressure distribution in the water film.

Table 1.
Structural parameters of the journal bearing.
In Figure 1, the flow of viscous water flowing into the wedge-shaped clearance results in the formation of symmetric high- and low-pressure regions surrounding the minimum thickness of the water film due to the wedge effect. The clearance is divided into three parts: Region I (Convergent Zone), Region II (Divergent Zone Outlet), and Region III (Divergent Zone Body). The parameters are defined as follows: means the bearing radius, means the shaft radius, means the bearing width, e means the eccentricity distance, means the attitude angle, means the texture space in the circumferential direction, means the circumferential width, means the texture depth, and means the axial width.
The water inlet is defined as the starting point at 0, with the inner wall surface being segmented in a counterclockwise direction. Using the maximum and minimum water film thickness as the boundary, texture regions are divided starting from 105 at intervals of 60, resulting in three regions: Region I (Convergent Zone: 75135), Region II (Divergent Zone Outlet: 135195), and Region III (Divergent Zone Body: 195255°), as shown in Figure 3.

Figure 3.
Expansion of fluid domain inside a journal bearing.
Inspired by the friction-reducing properties of biological skin, this study selected three types of biomimetic micro-textures: triangular (snakeskin-like), linear groove (earthworm skin-like), and hexagonal (lizard skin-like), as illustrated in Figure 4. The animal images in Figure 4 were generated by Chatgtp-4.0 (v4, OpenAI, San Francisco, CA, USA) to assist in expressing the configuration concept. The images were strictly selected by the team to be in line with the actual situation and are only used as an image enhancement method. To eliminate the influence of texture volume, the surface area and depth of the three micro-textures were kept identical. Schematic diagrams and specific parameters are provided in Figure 5 and Table 2.

Figure 4.
Illustration of the three biologically inspired surface textures.
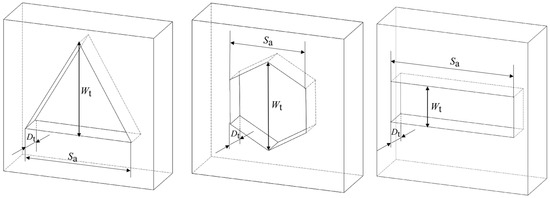
Figure 5.
Structure diagram of the three bionic textures.

Table 2.
Design parameters of the three textures.
2.3. Simulation Model
The water film model was developed using SolidWorks (v2021, Dassault Systèmes, Vélizy-Villacoublay, France). The parameters for the bearing model parameters are detailed in Table 1. After the water film model was built, the solid model was imported into Fluent (v2021 R1, ANSYS Inc., Canonsburg, PA, USA). The slice command was used to separate the water inlet from the textured part. Subsequently, the multi-zone method was applied in the meshing process, and the rotating water film was meshed with appropriate sizing for both the water inlet and the micro-textured regions. In the end, a mesh quality inspection was conducted. The geometric model is shown in Figure 6.
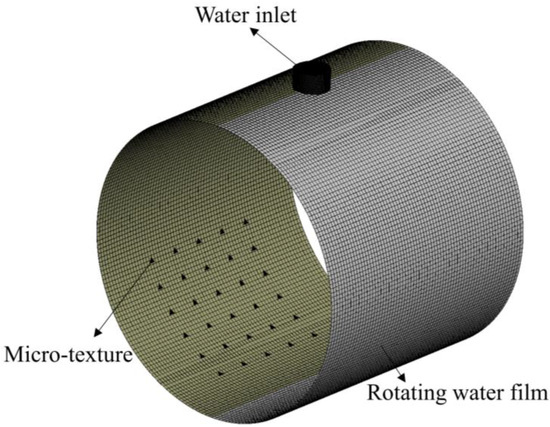
Figure 6.
Geometric model of the bearing water film.
2.4. Boundary Conditions and Solver Settings
The lubricant inlet located at the upper section of the bearing was designated as a pressure inlet, with an inlet pressure set to 0.103 MPa. The two ends of the bearing cavity were defined as the lubricant outlets, with the outlet pressure set to the atmospheric pressure. The inner surface of the bearing cavity was configured to function as a rotating wall, thereby simulating the rotational motion of the journal, while the outer wall was defined as a stationary wall. The rotational speed of the bearing was set to 1000 rpm. The material properties of the water and air are detailed in Table 3. The mass transfer mechanism is set to cavitation from the primary phase to the secondary phase. The cavitation model is set to the Schnerr–Sauer Model with vaporization pressure equal to 2340 Pa [34,35,36].

Table 3.
Material parameters of air and water.
The mixture model was employed to simulate the water–air two-phase flow. Considering the significant aspect ratio of the computational mesh, the fully implicit-coupled algorithm, based on the pressure-coupled equation, was implemented to ensure the convergence of the calculation results. The residual value was set to 1 × 10−6, and the water-phase volume change rates at the inlet and outlet were monitored. Convergence was achieved when the change rate was below 1 × 10−4 and both criteria were satisfied. Once the pressure was obtained, the shear stress of the bearing, the velocity distribution of the water film, the load-carrying capacity, the friction force, and the friction coefficient of the bearing were calculated through integration.
2.5. Mesh Convergence Analysis
The minimum water film thickness observed within the bearing cavity is 18.0 μm, while the bearing width measured at 90.0 mm, resulting in a significantly elevated width-to-diameter ratio. To ensure that the computational mesh remains undistorted and the simulation maintains stability, a globally structured hexahedral mesh was adopted, as shown in Figure 7. The fluid domain model was meshed in ANSYS Workbench (v2021 R1, ANSYS Inc., Canonsburg, PA, USA). A mesh convergence analysis was conducted to establish an optimal balance between accuracy and computational efficiency.
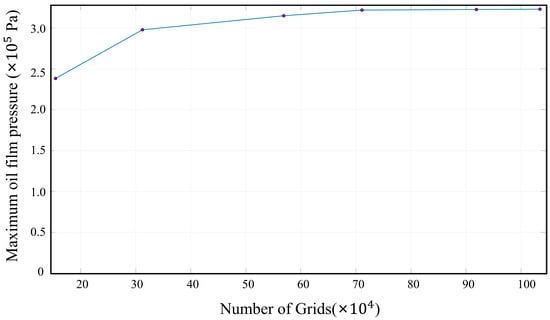
Figure 7.
Mesh convergence analysis for the water film model.
Six groups of comparative tests were carried out. As shown in Table 4, when the mesh number exceeded 918,908, the calculation accuracy became high, and the calculation speed remained acceptable. Therefore, in subsequent simulations, the mesh number was consistently set to a value greater than 918,908.

Table 4.
Maximum water film pressure with different mesh numbers.
3. Results and Analysis
3.1. Validation of Model Rationality
To validate the accuracy of the model used, a water-lubricated bearing model was created according to the description in Zhang’s article [34]. This model is characterized by a diameter and width of 80 mm, a relative clearance ψ of 0.1%, an eccentricity ratio of 0.6, and operates at a rotational speed N of 3000 r/min. The boundary conditions and solver settings of this study were applied to the model. Then, the water film stress distribution and the pressure distribution on the middle ring of the water film are compared with the result of Ref. [34]. The comparative results are illustrated in Figure 8. The analysis reveals that the maximum water film stress calculated using our model settings deviates by 1.13% from the reference results [34]. Furthermore, the circumferential pressure curves align well. Thus, the results from the model in this study can be considered reliable.

Figure 8.
Comparison of dimensionless pressure (P = pψ2/(η2πN)) distribution with Zhang’s result [34].
3.2. Effect of Single Micro-Texture Arrangement in Different Regions on the Bearing Performance
To analyze the effect of different micro-textures in various regions on the load-carrying capacity and friction coefficient of sliding bearings, three types of micro-textures (triangular, hexagonal, and linear groove) were arranged separately in Region I (Convergent Zone), Region II (Divergent Zone Outlet), and Region III (Divergent Zone Body). The load-carrying capacity and friction coefficient of bearing water films with different micro-textures are compared as shown in Figure 9. It is important to note that, in the majority of instances, the variation in shear force is typically less pronounced than the variation in load-carrying capacity. Therefore, according to Formula (8), there is often an inverse relationship between the coefficient of friction and the load-carrying capacity. And the hexagonal texture distributed in Region III has significantly enhanced the load-carrying capacity.
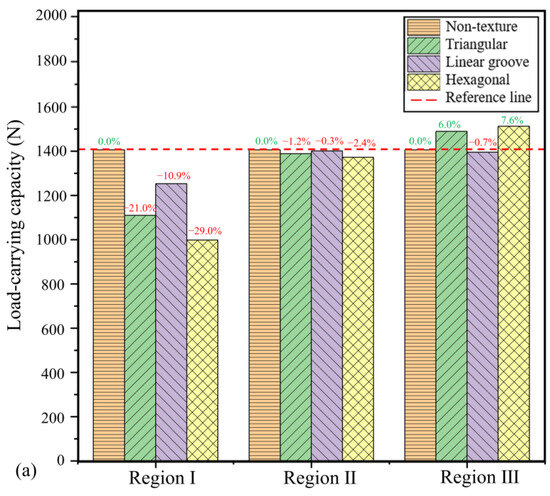
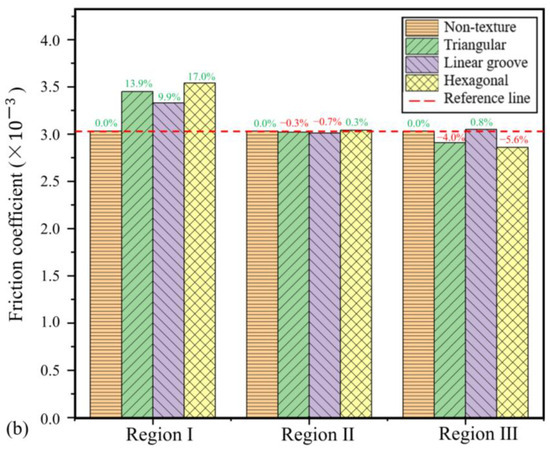
Figure 9.
Comparison of micro-textures in a single region: (a) load-carrying capacity; (b) friction coefficient.
As shown in Figure 9, the exclusive distribution of micro-textures within Region I (Convergent Zone) results in a decline in tribological performance. Specifically, triangular, hexagonal, and linear groove textures have been observed to exhibit reduced load-carrying capacity and increased friction coefficients. This detrimental effect stems from their positioning in the high-pressure zone, where the minimal water film thickness amplifies hydrodynamic inefficiencies.
Figure 10 clearly illustrates the circumferential static pressure of the water film on surfaces with different textures. This pressure is significantly lower than that of the smooth surface. In Figure 10a, the pressures of the three textured bearings are significantly lower than those of the smooth surface, and the load-carrying capacity associated with different textures aligns with the circumferential static pressure. Additionally, Figure 11 indicates that the texture in the convergent area enhances and concentrates the cavitation effect. Consequently, the compromised lubrication dynamics intensify both the reduction in load-carrying capacity and the increase in friction coefficient.

Figure 10.
Static pressure curve of water film with single texture distribution in different regions: (a) Region I; (b) Region II; and (c) Region III.

Figure 11.
Cavitation diagram of water film with single texture distribution in different regions.
The exclusive placement of micro-textures in Region II (Divergent Zone Body) demonstrates no statistically distinguishable effects on frictional performance compared to non-textured sliding bearings. Triangular, hexagonal, and linear groove textures show negligible differentiation in tribological behavior, while the load-carrying capacity and friction coefficient remain largely unaffected. As shown in Figure 10b, the static pressure of the water film is similar when the texture is exclusively located in Region II. However, there is a slight displacement of the entire high-pressure zone towards the cavitation region. Additionally, Figure 11 indicates a slight increase in the cavitation effect, leading to a minor negative impact. Overall, this configuration exhibits minimal functional impact on bearing performance.
When micro-textures are placed only in Region III (Divergent Zone Outlet), both triangular and hexagonal micro-textures enhance the load-carrying capacity and reduce the friction coefficient in comparison, compared with the non-texture water-lubricated bearings. The linear groove texture has a minimal effect on the performance but still shows an overall improvement. As shown in Figure 10c, when textures are distributed in Region III, the overall peak pressure values are similar. However, triangular and hexagonal textures induce a slight elongation in the regions of negative pressure, while the high-pressure region associated with the hexagonal textures experiences a minor anterior displacement. Figure 11 further indicates that the cavitation region becomes more elongated, resulting in a stabilization of the pressure gradient, with the shear region remaining relatively unaffected. These changes improve lubrication efficiency. Conversely, linear groove textures produce less pronounced cavitation elongation. Their cavitation zones remain relatively concentrated, creating negative effects. Consistent with the observation results of the hexagonal texture, Li et al. [37] emphasized that surface textures primarily improve the load-carrying capacity through hydrodynamic interactions: as lubricant flows into the surface grooves, its diffusion and convergence generate localized pressure build-up, thereby strengthening the hydrodynamic effect.
3.3. Effect of Mixed Micro-Textures Coupled in Two Different Regions on Bearing Performance
In order to investigate the effect of coupling different micro-textures in two distinct regions on the bearing performance, a total of 27 texture combinations were designed. In this study, the number 0 represents a non-textured region, while 3, 4, and 6 denote regions with triangular, linear groove, and hexagonal textures, respectively. The numbers from left to right correspond to Region I to III. For instance, the configuration labeled 304 indicates triangular textures in Region I, non-texture in Region II, and hexagonal textures in Region III. The results for coupled textures in Regions I and II, Regions I and III, and Regions II and III are presented in Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18, respectively.

Figure 12.
Impact of combined textures in Regions I and II: (a) load-carrying capacity; (b) friction coefficient.

Figure 13.
Static pressure curve of water film coupled with different textures in Regions I and II.
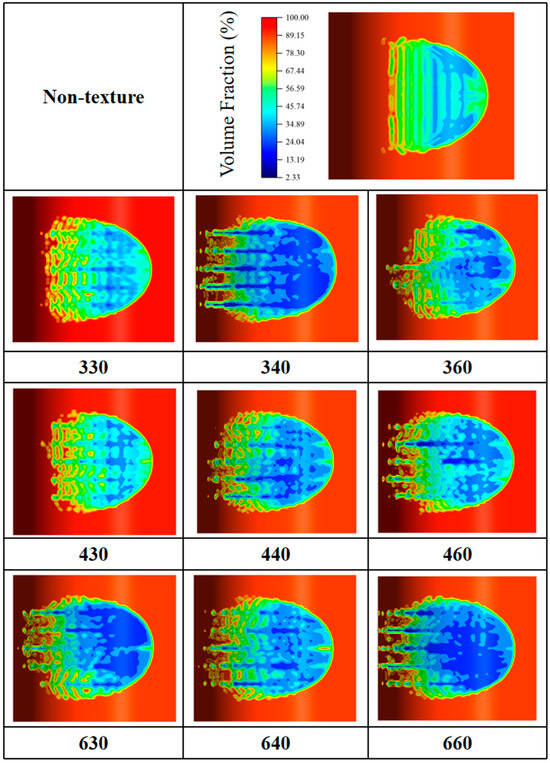
Figure 14.
Cavitation diagram of water film coupled with different textures in Regions I and II.
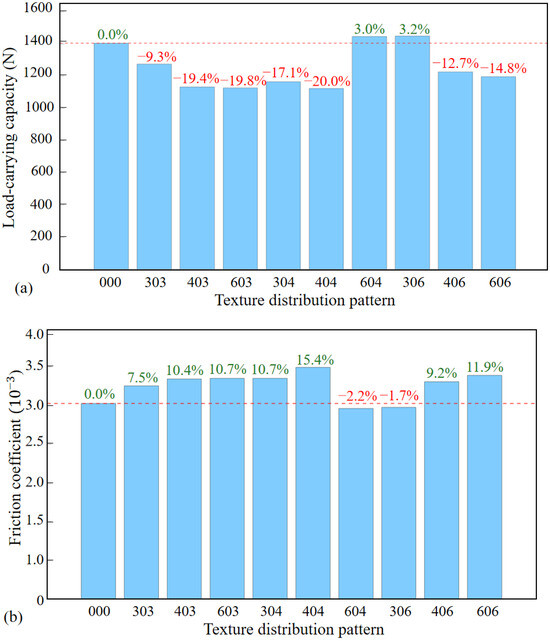
Figure 15.
Impact of combined textures in Regions I and III: (a) load-carrying capacity; (b) friction coefficient.

Figure 16.
Static pressure curve of water film coupled with different textures in Regions I and III.

Figure 17.
Cavitation diagram of water film coupled with different textures in Regions I and III.
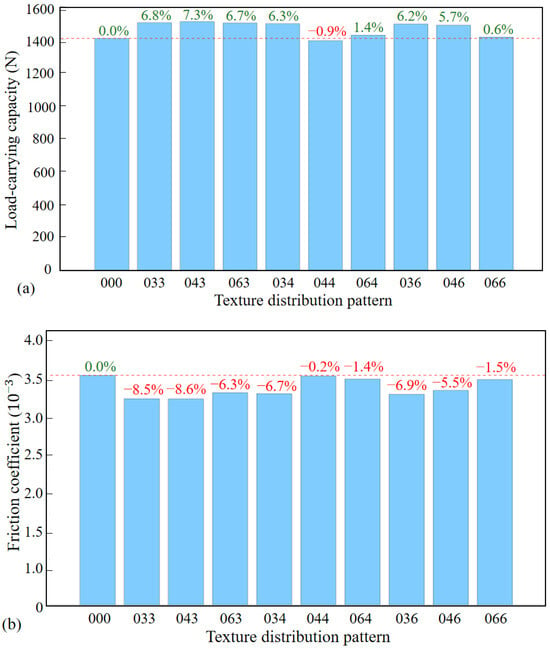
Figure 18.
Impact of combined textures in Regions II and III: (a) load-carrying capacity; (b) friction coefficient.
The coupling of micro-textures in Region I and II exhibits detrimental effects on the bearing performance. The implementation of triangular, linear groove, and hexagonal textures collectively led to the decrease in load-carrying capacity and the increase in friction coefficients. As shown in Figure 13, the micro-texture coupling present in Regions I and II weakens the dynamic pressure effect of the bearing, with the majority of the static pressure curve profiles exhibiting values lower than those observed in the non-texture. Furthermore, the analysis of cavitation depicted in Figure 14 reveals that the cavitation zone of the water film is situated nearer to the high-pressure zone, suggesting a more significant and severe occurrence of cavitation. Specifically, in the cases of 340 and 660, the degree of cavitation is extremely high and relatively concentrated, resulting in a significant decline in the load-carrying capacity. This coupling mechanism demonstrates a significant negative influence on the tribological characteristics.
The coupling of micro-textures in Region I and III yields selective performance outcomes. Only two configurations enhance the load-carrying capacity and reduce the friction coefficient: linear groove textures in Region I with hexagonal textures in Region III, and triangular textures in Region I coupled with hexagonal textures in Region III. In contrast, other configurations degrade the bearing performance, showing diminished hydrodynamic efficiency and elevated friction. As shown in Figure 15, this divergence underscores the critical dependence of tribological behavior on texture pairing strategies in high-pressure lubrication zones. As illustrated in Figure 16, the static pressure of the water film in the configurations of 604 and 306 is comparable to that of the untextured arrangement; however, the region of negative pressure exhibits a more gradual increase and a smoother profile. Furthermore, Figure 17 indicates that the cavitation phenomenon in the other configurations is both concentrated and pronounced, while the effects of dynamic pressure have not been adequately established. This leads to a marked reduction in load-carrying capacity and an elevation in the friction coefficient.
The coupling of micro-textures in Region II and III reveals distinct performance outcomes, the result is shown in Figure 18. Linear groove textures in both regions demonstrate a slight reduction in load-carrying capacity and a marginal decrease in the friction coefficient, exhibiting minimal influence on bearing performance. In contrast, other texture combinations lead to enhanced load-carrying capacity and reduced friction coefficients, collectively demonstrating an overall positive impact on tribological performance. As shown in Figure 19, in most arrangement schemes, the distribution of the positive pressure zone closely resembles that of non-texture. However, the presence of texture induces a coupling effect that leads to an expansion and a more gradual gradient of the negative pressure zone. Figure 20 provides a clearer visual representation, indicating that, in comparison to the non-texture scenario, the textured distributions in Regions II and III yield a more elongated negative pressure zone and a more continuous liquid film. This phenomenon facilitates a smoother transmission of shear force, thereby enhancing the load-carrying capacity and reducing the friction coefficient.

Figure 19.
Static pressure curve of water film coupled with different textures in Regions II and III.

Figure 20.
Cavitation diagram of water film coupled with different textures in Regions II and III.
3.4. Effect of Mixed Micro-Textures Coupled in Three Different Regions on Bearing Performance
This study conducted a systematic examination of the coupled effects of micro-textures on the bearing performance by designing 27 distinct combinations of triangular, hexagonal, and linear groove textures across Region I, II, and III. Figure 21 illustrates the load-carrying capacity and friction coefficient of the water film with textures coupled in Region I, II, and III. Analysis reveals that combining linear groove textures in Region I with triangular textures in Region II and III enhances load-carrying capacity and reduces the friction coefficient. Similarly, equipping all three regions with linear groove textures results in a slight decrease in the friction coefficient. However, most other combinations have a negative impact on the bearing performance. These results indicate that micro-textures need to be arranged rationally, as increasing texture distribution does not always improve performance.

Figure 21.
Impact of combined textures in Regions I, II and III: (a) load-carrying capacity; (b) friction coefficient.
4. Conclusions
This study aimed to explore the influence of micro-texture shapes and distributions on the tribological performance of water-lubricated bearings. Based on the cavitation effect, a CFD model of a water-lubricated bearing with three biomimetic surface textures was established. The study primarily aimed to elucidate the regulatory mechanisms that govern the synergistic effects of various textures across different regions on the pressure distribution of the water film, the morphology of cavitation, and the lubrication performance. Although previous studies have investigated the influence of a single micro-texture in different regions of the frictional performance, comprehensive studies on the combined effect of various micro-textures distributed across different positions, especially considering cavitation effects, are still limited. Based on the results presented in the present study, the following conclusions were obtained:
- When textures were placed in Region I (Convergent Zone), the load-carrying capacity of the bearing decreased, and the friction coefficient increased. The reason is that the convergent zone has the thinnest water film and the highest pressure, creating harsh operating conditions that negatively impact the frictional performance.
- The best frictional performance and optimal lubrication occur when textures are arranged in both Region II (Divergent Zone Outlet) and Region III (Divergent Zone Body). This effect is particularly significant when linear groove textures are used in Region II and triangular textures in Region III, resulting in a 7.3% increase in load-carrying capacity and an 8.6% reduction in the friction coefficient.
- Arranging textures in all three regions simultaneously has an overall negative effect on the frictional performance. This indicates that textures cannot be arbitrarily distributed across all regions and that increasing the number of textures does not necessarily lead to better performance.
- When textures are distributed in multiple regions, the negative effect of textures in Region I (Convergent Zone) on the frictional performance is significantly greater than the positive effects achieved by textures in the other two regions.
It should be noted that this study focused only on the primary convergent and divergent zones of water film formation in operational sliding bearings and selected only three types of micro-textures. However, many biological skins with beneficial friction and wear reduction need to be explored. The microscopic analysis of micro-texture and the sensitivity analysis of texture parameters, including depth, texture size, and distribution density, hold significant importance. Future research should conduct a pressure distribution assessment and parameter sensitivity analysis on the micro-texture of the optimized texture distribution configuration in sliding bearings. This will facilitate a deeper understanding of the texture coupling mechanism. Additionally, it is essential to explore more viable micro-texture geometries and examine the interactions of these textures on the friction and wear characteristics of sliding bearings.
Author Contributions
Conceptualization, X.T. and Y.L. (Yongtao Lyu); methodology, X.T. and Y.L. (Yunfei Lan); software, X.T.; formal analysis, X.T., Y.L. (Yunfei Lan), T.H., Y.X. and Y.L. (Yongtao Lyu); resources, Y.L. (Yongtao Lyu); writing—original draft preparation, X.T. and Y.L. (Yunfei Lan); writing—review and editing, S.B., M.Z., T.H., Y.X. and Y.L. (Yongtao Lyu); supervision, S.B., M.Z. and Y.L. (Yongtao Lyu); funding acquisition, M.Z., T.H. and Y.L. (Yongtao Lyu). All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key R&D Program of China (2024YFE0213500), the Open Fund of Science and Technology on Thermal Energy and Power Laboratory (TPL2022A01), the DUT-BSU Joint Institute Fund (ICR2303), and the Fundamental Research Funds for the Central Universities (DUTIO-ZG-202501).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
Author Tao He was employed by Wuhan Second Ship Design and Research Institute. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Xie, Z.; Li, J.; Tian, Y.; Du, P.; Zhao, B.; Xu, F. Theoretical and experimental study on influences of surface texture on lubrication performance of a novel bearing. Tribol. Int. 2024, 193, 109351. [Google Scholar] [CrossRef]
- Xie, Z.; Jiao, J.; Yang, K.; Zhang, H. A state-of-art review on the water-lubricated bearing. Tribol. Int. 2023, 180, 108276. [Google Scholar] [CrossRef]
- Fedorynenko, D.; Nakao, Y. Evaluation of thermal stability of ultra-precision water-lubricated spindle. Precis. Eng. 2023, 80, 127–137. [Google Scholar] [CrossRef]
- Shi, G.; Yu, X.; Meng, H.; Zhao, F.; Wang, J.; Jiao, J.; Jiang, H. Effect of surface modification on friction characteristics of sliding bearings: A review. Tribol. Int. 2023, 177, 107937. [Google Scholar] [CrossRef]
- Wang, J.; Shen, J.F.; Fan, Y.W. Static characteristics analysis of spherical hybrid sliding bearings. Ind. Lubr. Tribol. 2020, 72, 93–100. [Google Scholar] [CrossRef]
- Xiong, G.; Mao, Z.; Zhang, J.; Wang, Z.; Wang, H.; Jiang, Z. Coupled effects of misalignment and viscoelastic deformation on dynamically loaded journal bearings. Int. J. Mech. Sci. 2023, 251, 108347. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, S.; Lin, X. Study of dynamic characteristics of water-lubricated journal bearings using thermohydrodynamic cavitating lubrication model. Tribol. Trans. 2023, 66, 381–397. [Google Scholar] [CrossRef]
- Zhang, L.; Dong, C.; Yuan, C.; Bai, X. Frictional vibration behaviors of a new piezo-damping composite under water-lubricated friction. Wear 2023, 522, 204842. [Google Scholar] [CrossRef]
- Zhu, S.; Zhang, X.; Sun, J.; Wang, D. A study of misaligned compliant journal bearings lubricated by non-Newtonian fluid considering surface roughness. Tribol. Int. 2023, 179, 108138. [Google Scholar] [CrossRef]
- Gimeno, S.; Mescheder, H.; Quintana, I.; Gasion, A.; Arias-Egido, E.; Carbonell, A.; Carlos, M.; Ignacio, M.; Paredes, J.; Zalakain, I. Effect of different laser texturing patterns on rolling contact surface and its tribological & fatigue life behavior on 100Cr6 bearing steel. Wear 2023, 522, 204717. [Google Scholar]
- Xu, J.; Zhang, X.; Dai, J.; Yu, D.; Ji, M.; Chen, M. Biomimetic microtextured surfaces to improve tribological and antibacterial behaviors of 3Y-TZP ceramics. J. Mater. Res. Technol. 2023, 23, 1360–1374. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, T.; Liu, J.; Li, J. Study on synergistic friction between surface micro-texture and hot-pressing filling coal-to-oil soot solid lubricant. Surf. Coat. Technol. 2024, 489, 131167. [Google Scholar] [CrossRef]
- Tala-Ighil, N.; Fillon, M.; Maspeyrot, P. Effect of textured area on the performances of a hydrodynamic journal bearing. Tribol. Int. 2011, 44, 211–219. [Google Scholar] [CrossRef]
- Mourya, V.; Bhore, S.P.; Wandale, P.G. Comparative investigation on wear properties of 3D-printed textured journal bearings. J. Manuf. Process. 2023, 103, 337–353. [Google Scholar] [CrossRef]
- Etsion, I. State of the art in laser surface texturing. J. Tribol. 2005, 127, 248–253. [Google Scholar] [CrossRef]
- Lu, X.; Khonsari, M.M. An Experimental Investigation of Dimple Effect on the Stribeck Curve of Journal Bearings. Tribol. Lett. 2007, 27, 169–176. [Google Scholar] [CrossRef]
- Denkena, B.; Bergmann, B.; Keitel, M.; Wege, C.; Poll, G.; Kelley, J.; Pape, F. Process strategies for milling of dimples on tapered roller bearings. Prod. Eng.-Res. Dev. 2023, 17, 893–905. [Google Scholar] [CrossRef]
- Oliveira, J.F.G.D.; Bottene, A.; Franca, T. A novel dressing technique for texturing of ground surfaces. CIRP Ann.-Manuf. Technol. 2010, 59, 361–364. [Google Scholar] [CrossRef]
- Tønder, K. Inlet roughness tribodevices: Dynamic coefficients and leakage. Tribol. Int. 2001, 34, 847–852. [Google Scholar] [CrossRef]
- Cupillard, S.; Glavatskih, S.; Cervantes, M. Computational fluid dynamics analysis of a journal bearing with surface texturing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2008, 222, 97–107. [Google Scholar] [CrossRef]
- Kovalchenko, A.; Ajayi, O.; Erdemir, A.; Fenske, G.; Etsion, I. The effect of laser surface texturing on transitions in lubrication regimes during unidirectional sliding contact. Tribol. Int. 2005, 38, 219–225. [Google Scholar] [CrossRef]
- Tala-Ighil, N.; Maspeyrot, P.; Fillon, M.; Bounif, A. Effects of surface texture on journal-bearing characteristics under steady-state operating conditions. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2007, 221, 623–633. [Google Scholar] [CrossRef]
- Jin, L.; Yang, J.; Li, C. Numerical coupled model of mixed lubrication wear for textured journal bearing. Lubr. Eng. 2020, 45, 67–74. [Google Scholar]
- Yin, M.H.; Chen, G.D.; Gao, D.C.; Wang, L. Effects of three types of surface texture on the performances of journal bearing. J. Harbin Inst. Technol. 2016, 48, 159–164. [Google Scholar]
- Wang, L.; Guo, S.; Yin, G.; Wei, Y.L.; Yuan, G.T. Research on micro-textured journal bearing characteristics considering the effect of cavitation. Lubr. Eng. 2018, 43, 65–69. [Google Scholar]
- Nie, T.; Yang, K.; Zhou, L.; Wu, X.; Wang, Y. CFD analysis of load capacity of journal bearing with surface texture. Energy Rep. 2022, 8, 327–334. [Google Scholar] [CrossRef]
- Wang, L.; Han, Z.; Chen, G.; Su, H. Thermo-hydrodynamic analysis of large-eccentricity hydrodynamic bearings with texture on journal surface. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2018, 232, 3564–3569. [Google Scholar] [CrossRef]
- Yu, R.; Chen, W.; Li, P. The analysis of elastohydrodynamic lubrication in the textured journal bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 1197–1208. [Google Scholar] [CrossRef]
- Galda, L.; Sep, J.; Olszewski, A.; Zochowski, T. Experimental investigation into surface texture effect on journal bearings performance. Tribol. Int. 2019, 136, 372–384. [Google Scholar] [CrossRef]
- Hao, X.; Sun, H.; Wang, L.; Ali, Q.; Li, L.; He, N. Fabrication of micro-texture on cylindrical inner surface and its effect on the stability of hybrid bearing. Int. J. Adv. Manuf. Technol. 2020, 109, 1671–1680. [Google Scholar] [CrossRef]
- Filgueira Filho, I.C.M.; Bottene, A.C.; Silva, E.J.D.; Nicoletti, R. Static behavior of plain journal bearings with textured journal-experimental analysis. Tribol. Int. 2021, 159, 106970. [Google Scholar] [CrossRef]
- Xie, Z.; Yang, K.; He, T.; Jiao, J. Experimental and theoretical analysis on the nonlinear rotor-dynamic performances and vibration characteristics of a novel bearing-rotor system. Mech. Syst. Signal Process. 2023, 199, 110416. [Google Scholar] [CrossRef]
- Xie, Z.; Tian, Y.; Li, J.; Du, P. Lubrication performance of a novel double-film bearing: Theory & experiment. Tribol. Int. 2023, 189, 108958. [Google Scholar]
- Zhang, X.; Yin, Z.; Gao, G.; Li, Z. Determination of stiffness coefficients of hydrodynamic water-lubricated plain journal bearings. Tribol. Int. 2015, 85, 37–47. [Google Scholar] [CrossRef]
- Čech, J.; Sťahel, P.; Prokeš, L.; Trunec, D.; Horňák, R.; Rudolf, P.; Maršálek, B.; Maršálková, E.; Lukeš, P.; Lavrikova, A.; et al. CaviPlasma: Parametric study of discharge parameters of high-throughput water plasma treatment technology in glow-like discharge regime. Plasma Sources Sci. Technol. 2024, 33, 115005. [Google Scholar] [CrossRef]
- Xie, Z.L.; Ta, N.; Rao, Z.S. The lubrication performance of water lubricated bearing with consideration of wall slip and inertial force. J. Hydrodyn. Ser. B 2017, 29, 52–60. [Google Scholar] [CrossRef]
- Li, J.; Zhou, F.; Wang, X. Modify the friction between steel ball and PDMS disk under water lubrication by surface texturing. Meccanica 2011, 46, 499–507. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).