Extraction of Pavement Texture–Friction Surface Density Index Using High-Precision Three-Dimensional Images
Abstract
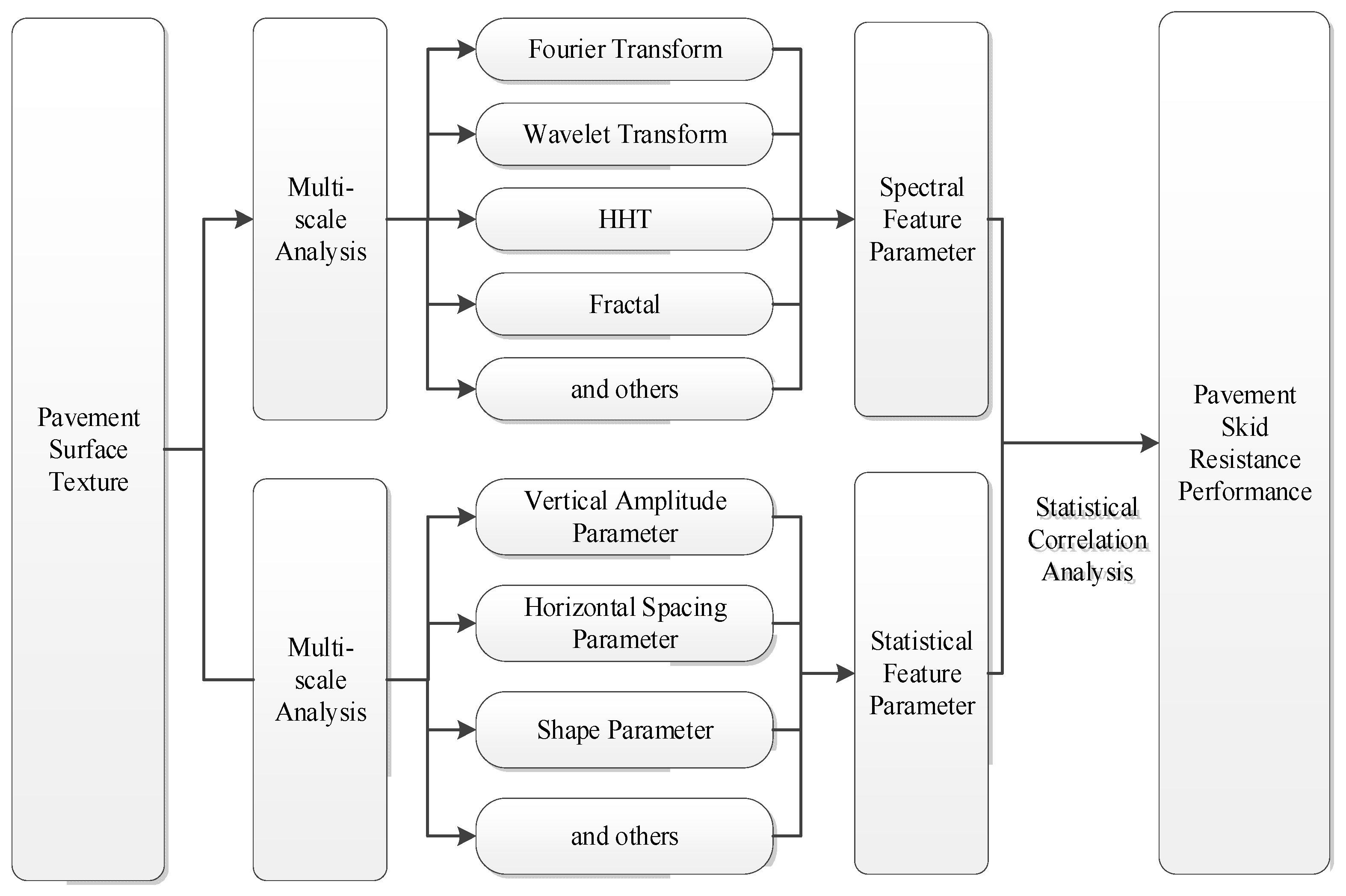
1. Introduction
2. Three-Dimensional Point Cloud Data Acquisition and Area Calculation
2.1. Testing Equipment
2.1.1. Pendulum Friction Tester
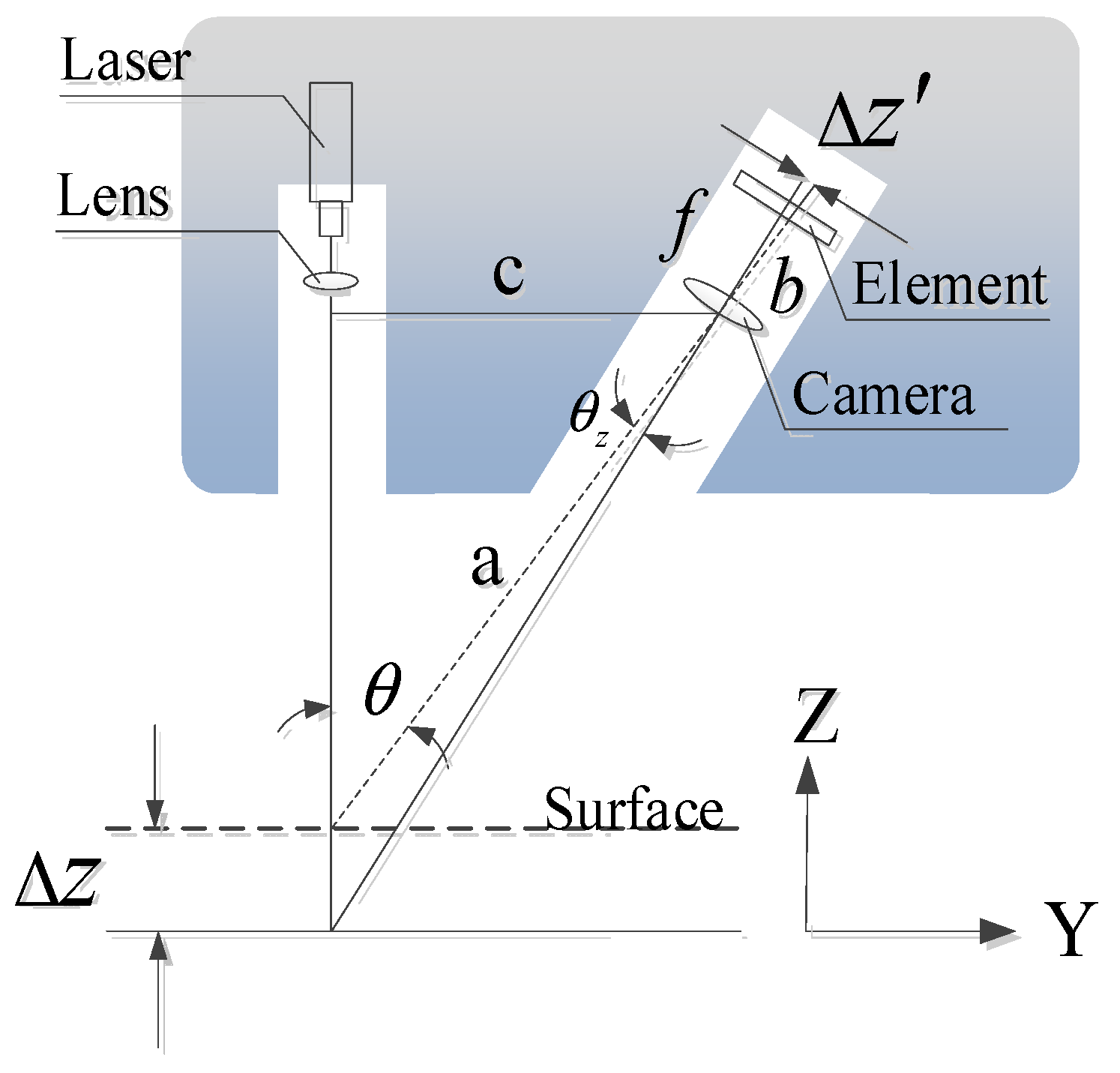
2.1.2. LS-40 Pavement Analyzer
2.2. Test Subject
2.3. Calculation of Area for Irregular Shapes in 3D Space
2.3.1. Existing Image Measurement Methods for Irregular Surface Areas
- (1)
- Integration method
- (2)
- Perturbation method
- (3)
- Projection method
2.3.2. An Area Calculation Method Based on High-Precision Pixel-Level Spatial Construction
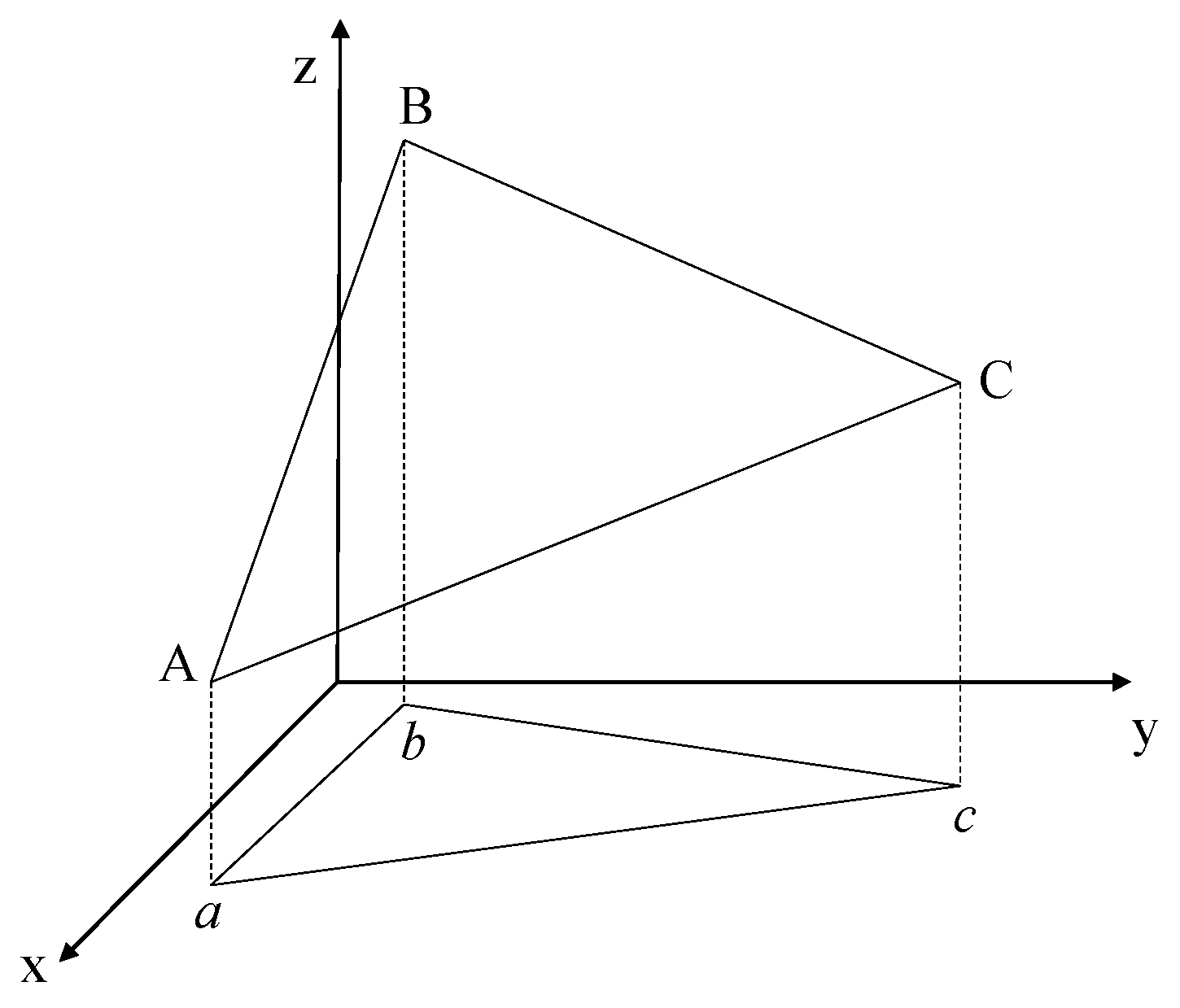
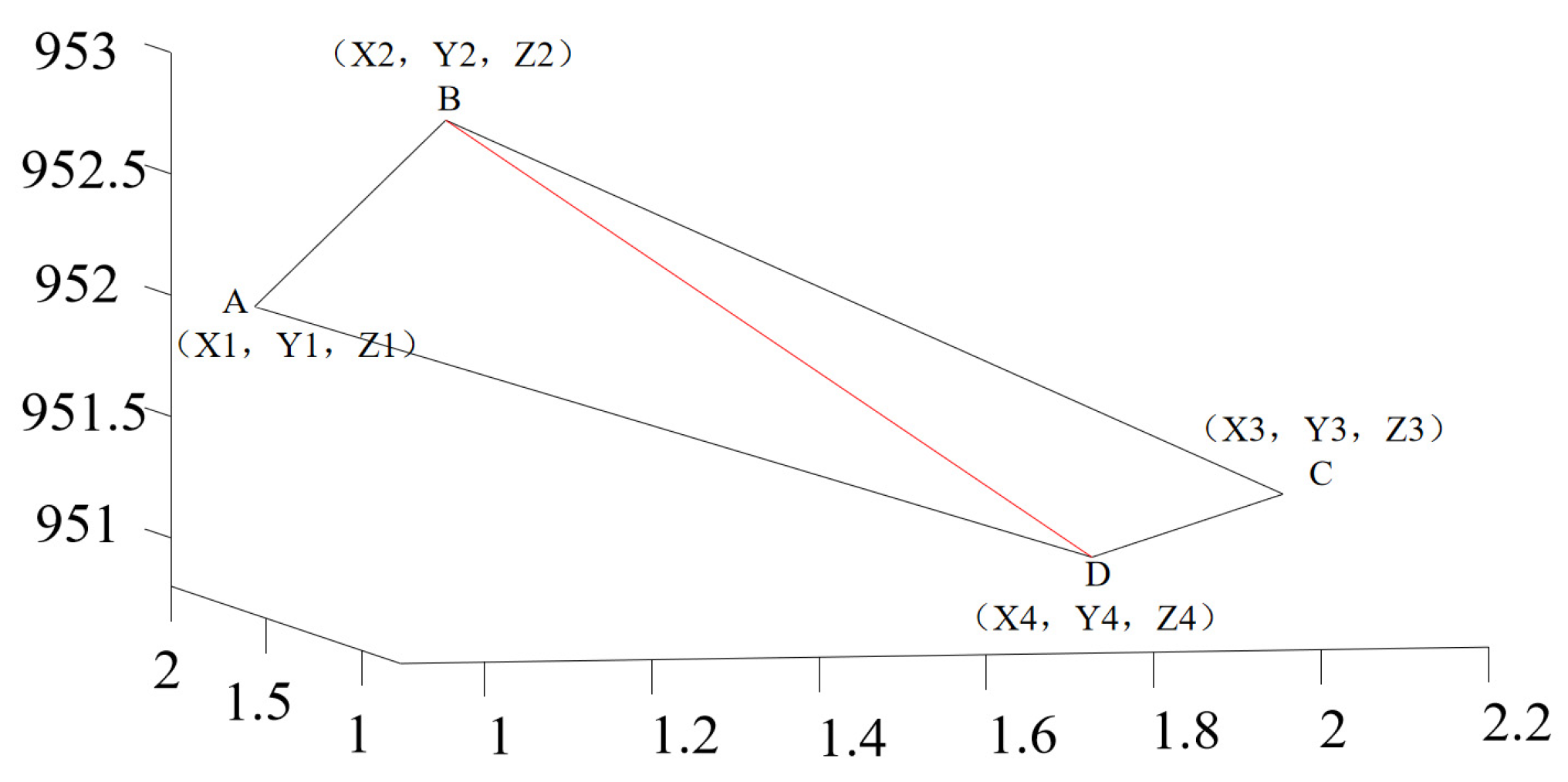
- Calculation of the Area of a Spatial Triangle
- 2
- Solving for the Surface Area of a 3D Surface
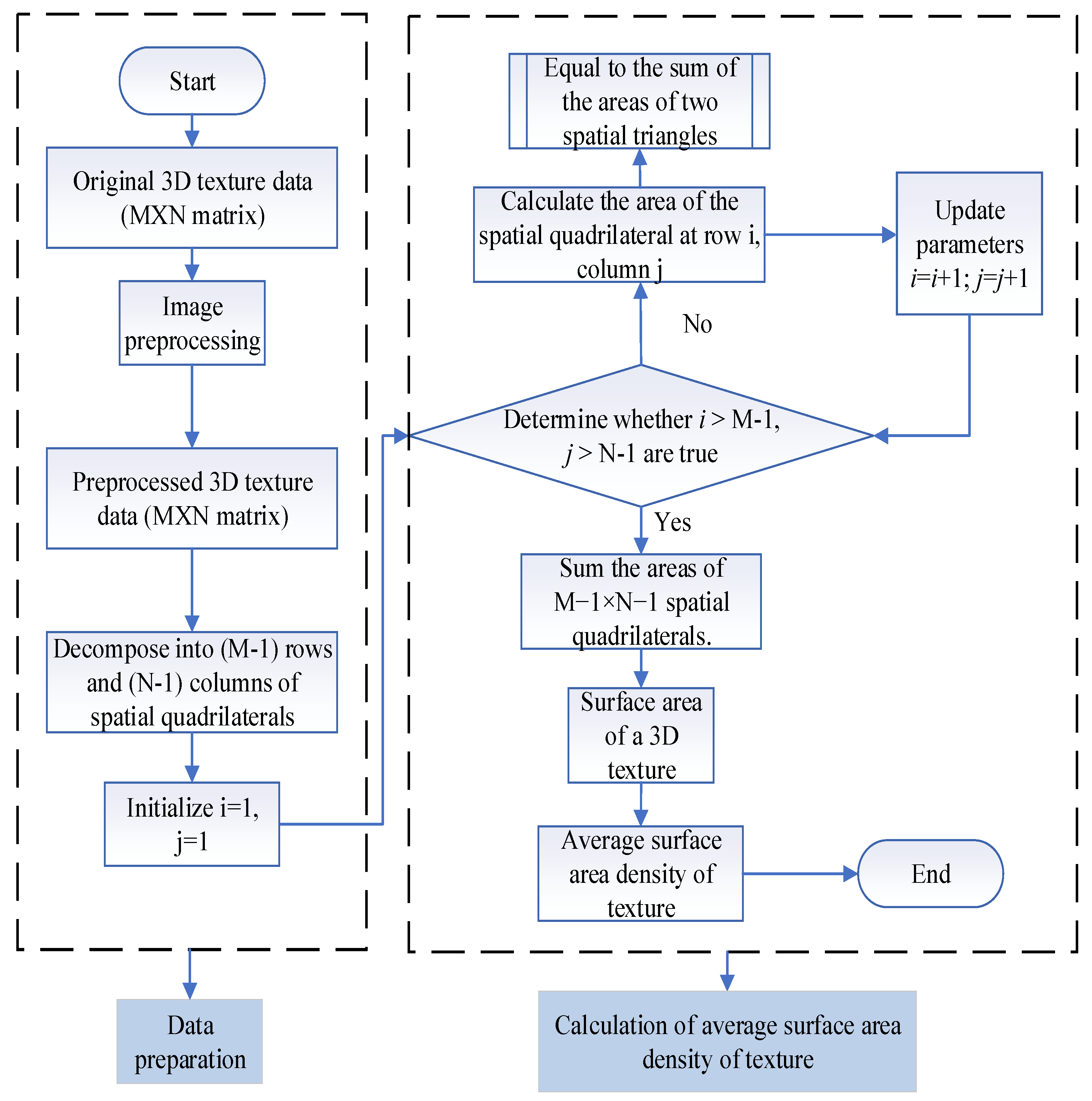
3. Mean Texture Surface Area Density
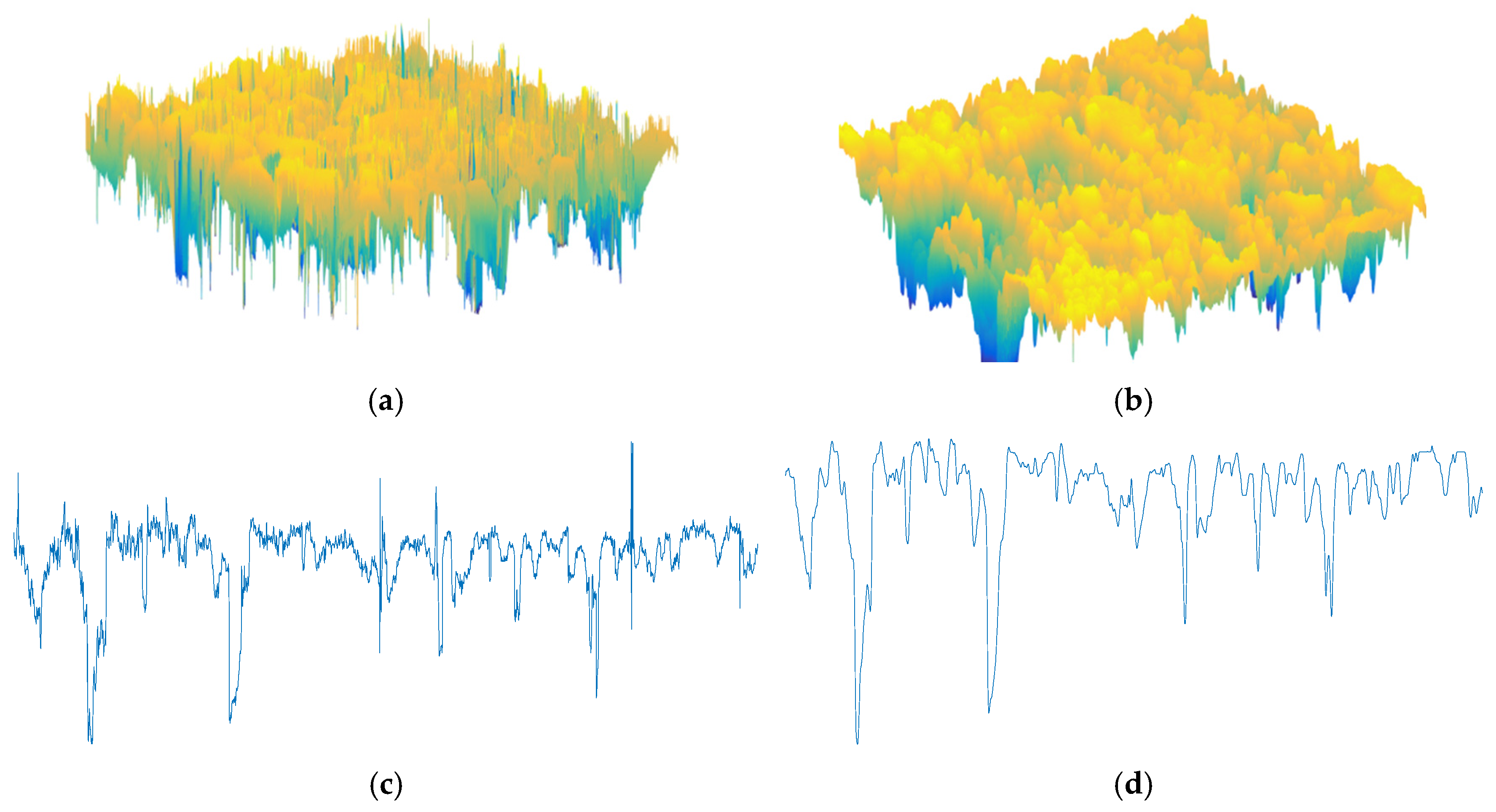
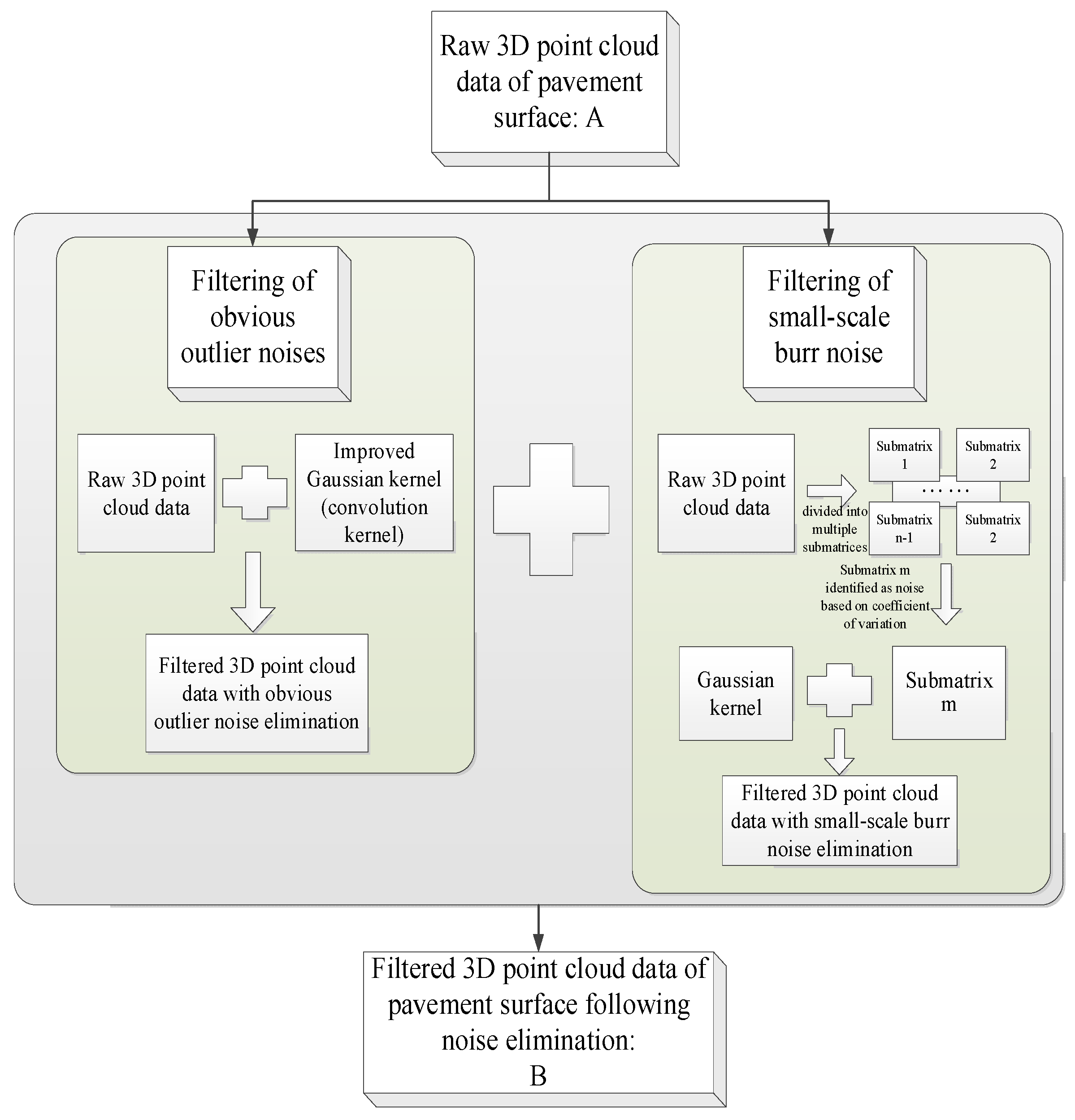
3.1. Image Preprocessing
3.2. Calculation of Average Surface Area Density of Pavement Texture
- (1)
- First, the spatial quadrilateral of the smallest computational unit was divided into two spatial triangles. Then, we calculated the areas of these two triangles, Sij1 and Sij2, using the following formulas:
- (2)
- The areas of the two spatial triangles are then added to obtain the area of the spatial quadrilateral computational unit Sij as follows:
- (3)
- The total surface area, S, of the pavement texture is calculated by summing the areas of the M spatial quadrilateral computational units as follows:
- (4)
- MTSAD of the pavement texture is the ratio of the textured surface area of the scanned region (S) to the area of the scanned region (SH) as follows:
4. Experimental Results and Analysis
4.1. Results of the Pendulum Friction Coefficient Test
4.2. Test Results of LS-40 Pavement Micro-Texture Structure
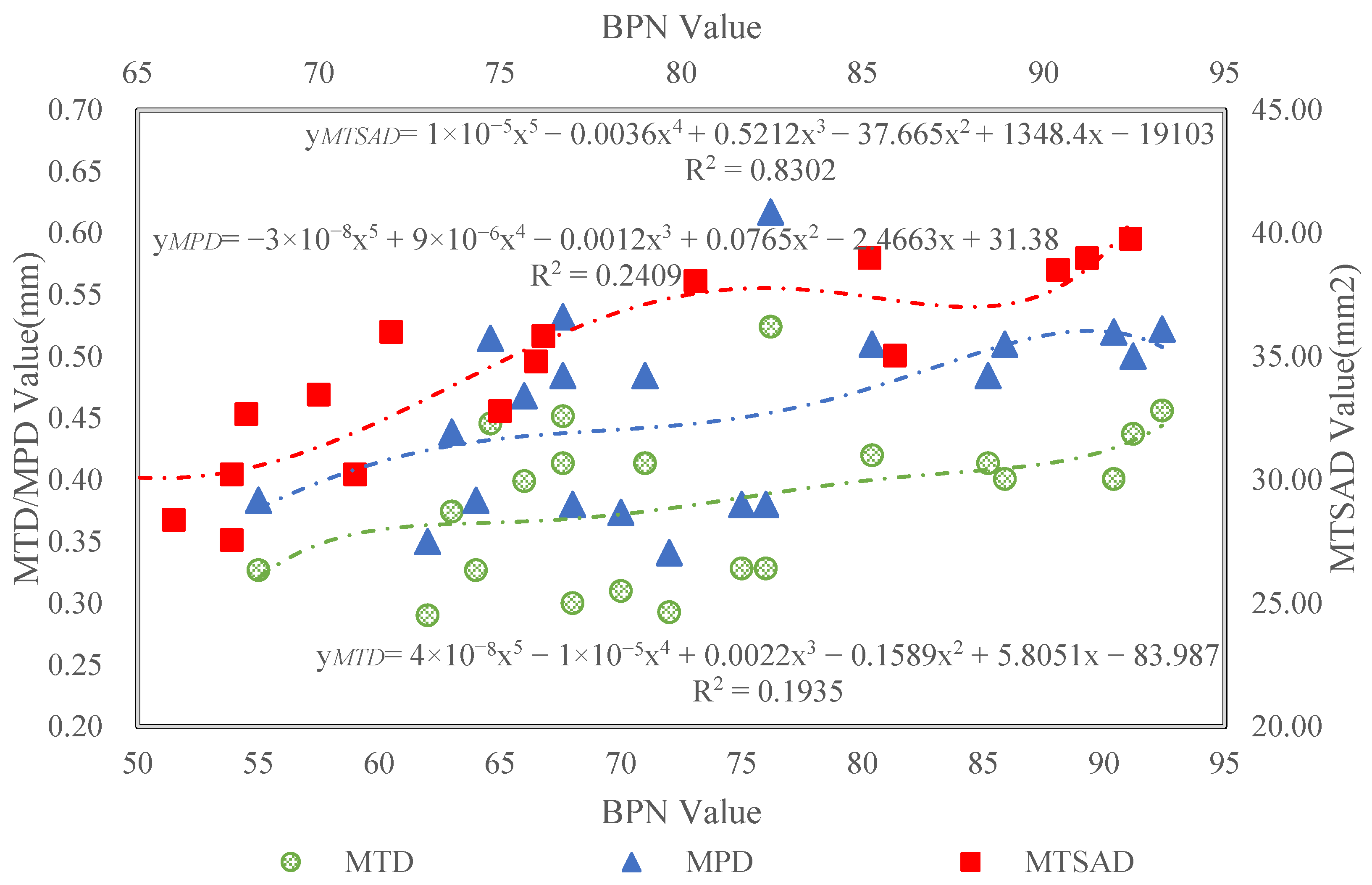
4.3. LS-40 Correlation Analysis
5. Conclusions and Recommendations for Future Research
- (1)
- Based on high-precision 3D point cloud data, a novel method for calculating the area of irregular shapes in 3D space is proposed using the mathematical concept of integration, which is applied to calculate the surface area of pavement textures.
- (2)
- Through polynomial fitting analysis of MTD, MPD, and MTSA with pavement friction coefficients BPN, the correlation coefficient between MTSAD and BPN is 0.8302, significantly superior to traditional indices (MTD, MPD). The results show that the novel 3D texture evaluation index MTSAD proposed in this study better characterizes the anti-skid performance of pavements.
- (3)
- Compared with traditional texture indices (MTD, MPD), the MTSAD contains 3D texture structure information and more accurately evaluates pavement anti-skid performance.
- (4)
- This paper uses 3D laser technology to obtain 3D point cloud data of pavements in a non-contact manner, indicating that non-contact methods can be used to detect pavement anti-skid performance in the future.
- (1)
- Deeply investigate whether the pigmentation of red/white/green pavements will change the physical properties of the surface, analyze the independent impact of pigmentation on texture or friction, and examine whether it may lead to data confounding risks.
- (2)
- Conduct extensive experiments on different gradations of asphalt mixture types (including pavements with high macrotexture) to further verify the applicability of the proposed approach and explore whether parameter and method adjustments are required for different material types.
- (3)
- Based on high-precision 3D pavement texture images, comprehensive evaluations and the research on 3D texture evaluation indices capable of characterizing anti-skid performance should be conducted in the future.
- (4)
- Three-dimensional laser detection technology can realize non-contact pavement detection. Therefore, intelligent evaluation methods for pavement inspection can be developed based on non-contact detection techniques in the future.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MTSAD | Mean Texture Surface Area Density |
| MTD | Mean Texture Depth |
| MPD | Mean Profile Depth |
| PIARC | Permanent International Association of Road Congresses |
| HHT | Hilbert–Huang Transform |
| 3D | Three-Dimensional |
| 2D | Two-Dimensional |
| PSD | Power Spectral Density |
| CRP | Close-Range Photogrammetry |
References
- Hall, J.W.; Smith, K.L.; Titus-Glover, L.; Wambold, J.C.; Yager, T.J.; Rado, Z. Guide for Pavement Friction: Final Report for National Cooperative Highway Research Program (NCHRP) Project 01-43; Transportation Research Board of the National Academies: Washington, DC, USA, 2009. [Google Scholar]
- Zhu, H.-Z.; Liao, Y.-Y. Present Situations of Research on Anti-skid Property of Asphalt Pavement. Highway 2018, 1, 35–46. [Google Scholar]
- Huang, X.; Zheng, B. Research Status and Progress for Skid Resistance Performance of Asphalt Pavements. China J. Highw. Transp. 2019, 32, 32–49. [Google Scholar]
- Kogbara, R.B.; Masad, E.A.; Kassem, E.; Scarpas, A.; Anupam, K. A state-of-the-art review of parameters influencing measurement and modeling of skid resistance of asphalt pavements. Constr. Build. Mater. 2016, 114, 602–617. [Google Scholar] [CrossRef]
- Mataei, B.; Zakeri, H.; Zahedi, M.; Nejad, F.M. Pavement friction and skid resistance measurement methods: A literature review. Open J. Civ. Eng. 2016, 6, 537–565. [Google Scholar] [CrossRef]
- Lei, Y.; Hu, X.; Wang, H.; You, Z.; Zhou, Y.; Yang, X. Effects of vehicle speeds on the hydrodynamic pressure of pavement surface: Measurement with a designed device. Measurement 2017, 98, 1–9. [Google Scholar] [CrossRef]
- De Luca, M.; Abbondati, F.; Pirozzi, M.; Žilionienė, D. Preliminary study on runway pavement friction decay using data mining. Transp. Res. Procedia 2016, 14, 3751–3760. [Google Scholar] [CrossRef][Green Version]
- Technical Committee on Surface Characteristics. Report of Technical Committee on Surface Characteristics; World Road Association (PIARC): Mrrakesh, Morocco, 1991; pp. 287–305. [Google Scholar]
- Dunford, A.M. Measuring Skid Resistance Without Contact: 2009–2010 Progress Report; TRL: Crowthorne, UK, 2010. [Google Scholar]
- Henry, J.J. Evaluation of pavement friction characteristics. In NCHRP Synthesis291; Transportation Research Board: Washington, DC, USA, 2000. [Google Scholar]
- Roe, P.G.; Sinhal, R. The Polished Stone Value of Aggregates and In-ServiceSkidding Resistance; TRL: Crowthorne, UK, 1998. [Google Scholar]
- PIARC. Report of the Committee on Surface Characteristics; Permanent International Association of Road Congress (PIARC) XVIII World Road Congress: Brussels, Belgium, 1987. [Google Scholar]
- ASTM. ASTM E965—15 Standard Test Method for Measuring Pavement Macro-Texture Depth Using a Volumetric Technique; American Society of Testing an d Material: West Conshohocken, PA, USA, 2019. [Google Scholar]
- Sabey, B.E. Pressure distribution beneath spherical and conical shapes pressed into a rubber plane, and their bearing on coefficient of friction under wet conditions. Proc. Phys. R. Soc. 1958, 71, 979–988. [Google Scholar] [CrossRef]
- Forster, S.W. Aggregate Microtexture: Profile Measurement and Related Frictional Levels; Report FHWA/RD-81/107; Federal Highway Administration: Washington, DC, USA, 1981. [Google Scholar]
- Do, M.T.; Tang, Z.; Kane, M.; de Larrard, F. Evolution of road surface skid-resistance and texture due to polishing. Wear 2009, 266, 574–577. [Google Scholar] [CrossRef]
- Zelelew, H.M.; Khasawneh, M.; Abbas, A. Wavelet-Based Characterisation of Asphalt Pavement Surface Macro-Texture. Road Mater. Pavement Des. 2014, 15, 622–641. [Google Scholar] [CrossRef]
- Villani, M.M.; Scarpas, A.; de Bondt, A.; Khedoe, R.; Artamendi, I. Application of Fractal Analysis for Measuring the Effects of Rubber Polishing on the Friction of Asphalt Concrete Mixtures. Wear 2014, 320, 179–188. [Google Scholar] [CrossRef]
- Hartikainen, L.; Petry, F.; Westermann, S. Frequency-wise Correlation of the Power Spectral Density of Asphalt Surface Roughness and Tire Wet Friction. Wear 2014, 317, 111–119. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, H.; Cai, J. Tire-pavement friction modeling considering pavement texture and water film. Int. J. Transp. Sci. Technol. 2024, 14, 99–109. [Google Scholar] [CrossRef]
- Kane, M.; Rado, Z.; Timmons, A. Exploring the Texture-Friction Relationship: From Texture Empirical Decomposition to Pavement Friction. Int. J. Pavement Eng. 2015, 16, 919–928. [Google Scholar] [CrossRef]
- El-Ashwah, A.S.; Abdelrahman, M. Comparative analysis of empirical decomposition algorithms in predicting tire-pavement friction from asphalt surface textures: A Hilbert–Huang transform (HHT) analysis. Discov. Civ. Eng. 2024, 1, 89. [Google Scholar] [CrossRef]
- Kogbara, R.B.; Masad, E.A.; Woodward, D.; Millar, P. Relating surface texture parameters from close range photogrammetry to Grip-Tester pavement friction measurements. Constr. Build. Mater. 2018, 166, 227–240. [Google Scholar] [CrossRef]
- Kanafi, M.M.; Kuosmanen, A.; Pellinen, T.K.; Tuononen, A.J. Macro- and micro-texture evolution of road pavements and correlation with friction. Int. J. Pavement Eng. 2015, 16, 168–179. [Google Scholar] [CrossRef]
- Kanafi, M.M.; Tuononen, A.J. Top topography surface roughness power spectrum for pavement friction evaluation. Tribol. Int. 2017, 107, 240–249. [Google Scholar] [CrossRef]
- Hu, L.; Yun, D.; Liu, Z.; Du, S.; Zhang, Z.; Bao, Y. Effect of three-dimensional macrotexture characteristics on dynamic frictional coefficient of asphalt pavement surface. Constr. Build. Mater. 2016, 126, 720–729. [Google Scholar] [CrossRef]
- Li, Q.; Yang, G.; Wang, K.C.P.; Zhan, Y.; Wang, C. Novel Macro- and Microtexture Indicators for Pavement Friction by Using High-Resolution Three-Dimensional Surface Data. Transp. Res. Rec. J. Transp. Res. Board 2017, 2641, 164–176. [Google Scholar] [CrossRef]
- Qian, G.; Wang, Z.; Yu, H.; Shi, C.; Zhang, C.; Ge, J.; Dai, W. Research on surface texture and skid resistance of asphalt pavement considering abrasion effect. Case Stud. Constr. Mater. 2024, 20, e02949. [Google Scholar] [CrossRef]
- Tan, Y.; Xiao, S.; Xiong, X. Review on detection and prediction methods for pavement skid resistance. J. Traffic Transp. Eng. 2021, 21, 32–47. [Google Scholar]
- Dong, S.; Han, S.; Zhang, Q.; Han, X.; Zhang, Z.; Yao, T. Three-dimensional evaluation method for asphalt pavement texture characteristics. Constr. Build. Mater. 2021, 287, 122966. [Google Scholar]
- Dong, S.; Han, S.; Su, J.; Han, X. Three-dimensional evaluation method for asphalt pavement surface texture and analysis of its calculating boundary conditions. Mater. Rep. 2023, 287, 1–20. [Google Scholar]
- JTG 3450—2019; Field Test Methods of Highway Subgrade and Pavement. Ministry of Transport of the People’s Republic of China: Beijing, China, 2019.
- Lin, D.-J. Study on solution of area of curved surface. J. Zhejiang Univ. Technol. 2000, 28, 10–14. [Google Scholar]
- Chen, J. Research on land Mapping Technology Based on GPS and Land Management Information system. Master’s Thesis, Zhejiang University, Hangzhou, China, 2013. [Google Scholar]
- Cao, J. Research on Surface Area Image Measurement Technology. Master’s Thesis, Southwest Petroleum University, Chengdu, China, 2012. [Google Scholar]
- Liu, B.-Z. Design of Three-Dimensional Surface Land Area Measurement System Based on GPS. Master’s Thesis, Southwest University, Chongqing, China, 2017. [Google Scholar]
- Ding, S.; Yang, E.; Wang, C.; Ji, Y.; Lei, K.; Zhang, X. Three-Dimensional High-Precision Laser Non-contact Detection of Asphalt Pavement Surface Texture. J. Southwest Jiaotong Univ. 2020, 55, 758–764. [Google Scholar]
- Ding, S.; Yang, G.; Wang, K.C.P.; Yang, E.; Zhan, A. 3D Imaging based pavement texture evaluation. Int. J. Pavement Eng. 2023, 24, 2077942. [Google Scholar]



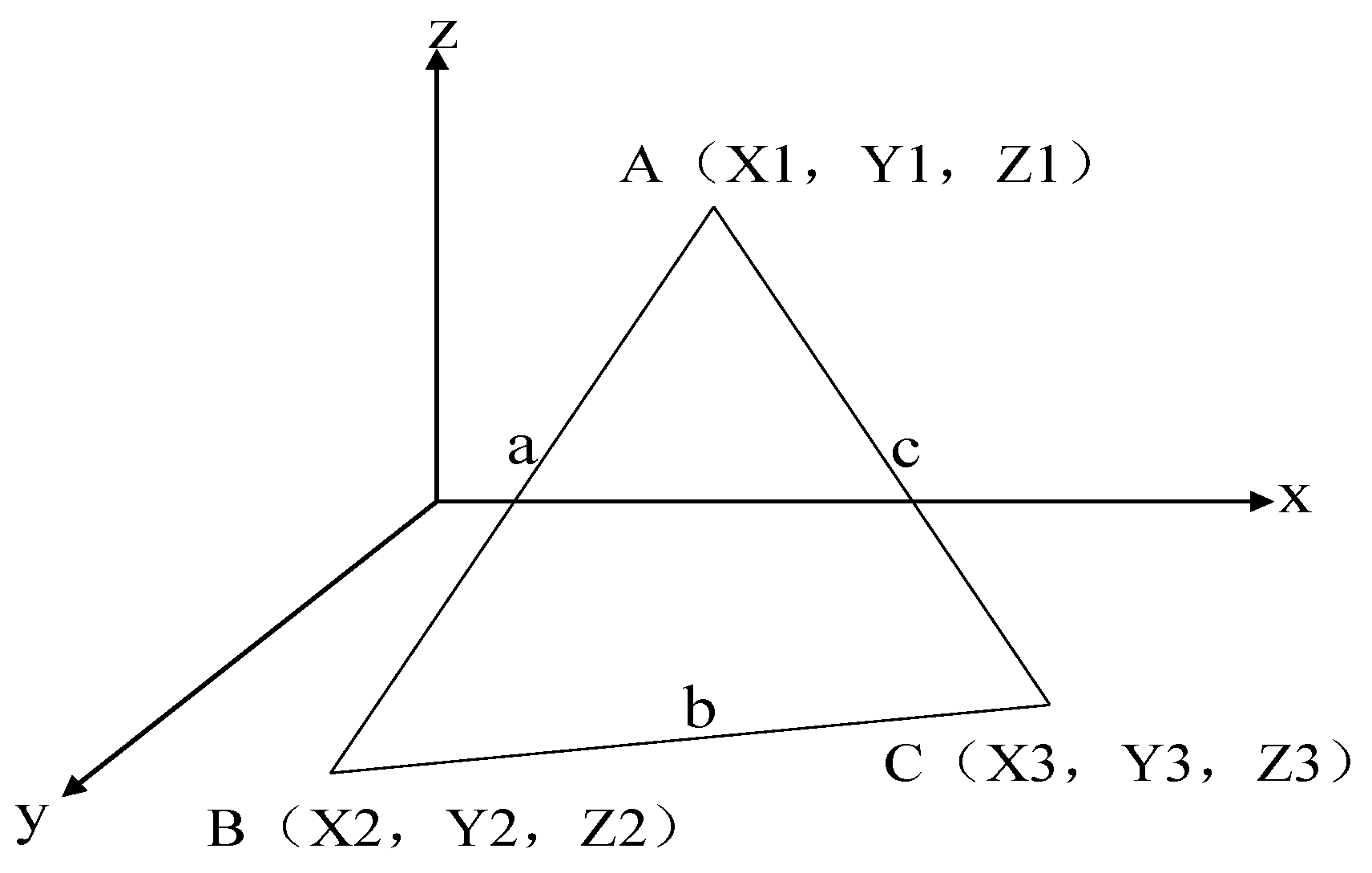


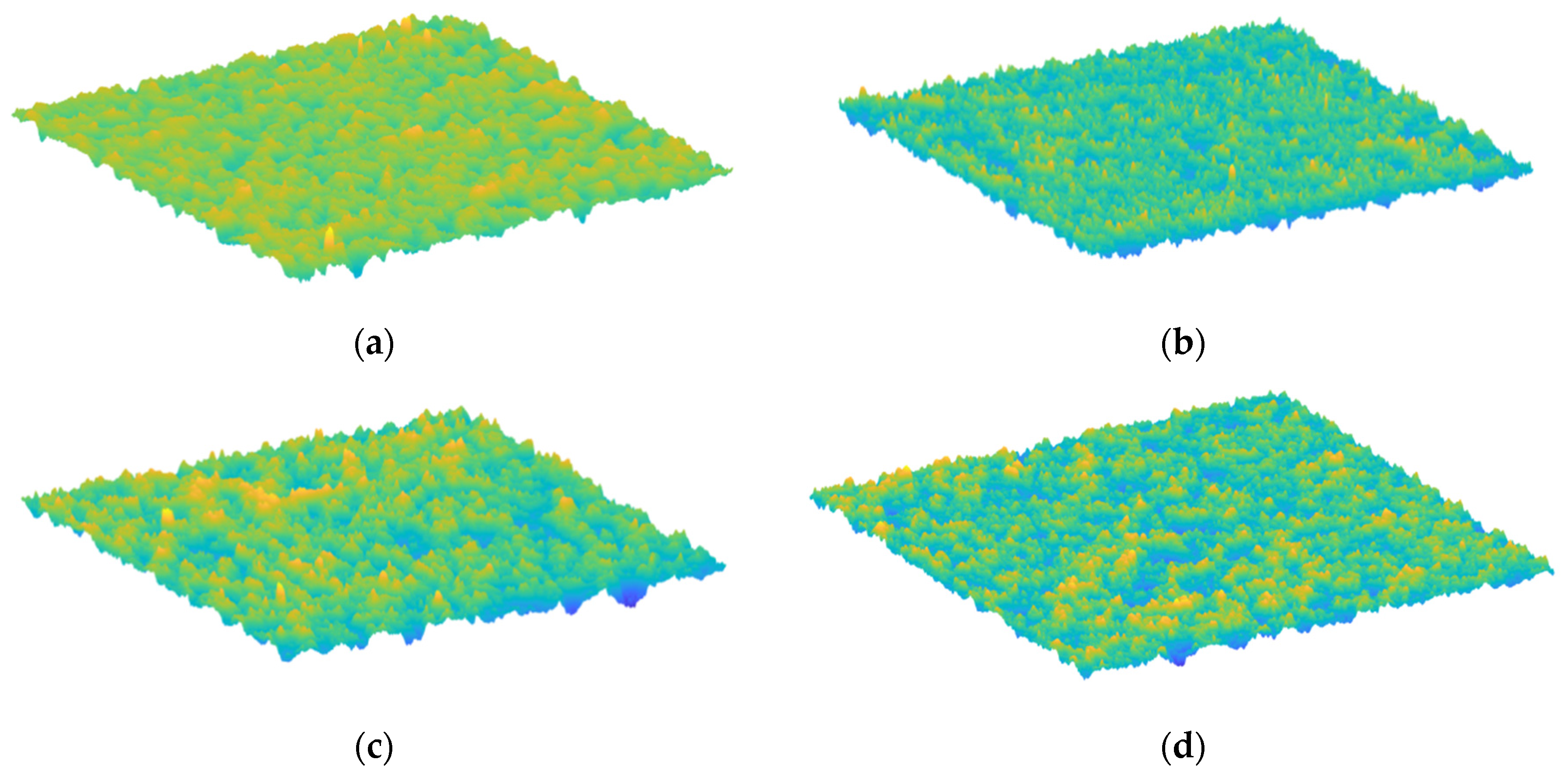
| Index | Region 1 | Region 2 | Region 3 | Region 4 | Region 5 |
|---|---|---|---|---|---|
| Temperature (°C) | 28 | 29 | 28 | 28 | 28 |
| Temperature Correction Factor | 2.8 | 3.2 | 2.8 | 2.8 | 2.8 |
| Friction Coefficient BPN20 | 78.8 | 71.2 | 60.8 | 64.8 | 72.8 |
| 78.8 | 69.2 | 60.8 | 66.8 | 74.8 | |
| 74.8 | 69.2 | 60.8 | 66.8 | 74.8 | |
| 76.8 | 69.2 | 62.8 | 68.8 | 74.8 | |
| 72.8 | 71.2 | 64.8 | 70.8 | 76.8 | |
| Mean | 76 | 70 | 62 | 68 | 75 |
| Standard Deviation | 2.61 | 1.10 | 1.79 | 2.28 | 1.41 |
| Coefficient of Variation | 0.03 | 0.02 | 0.03 | 0.03 | 0.02 |
| Index | Region 1 | Region 2 | Region 3 | Region 4 | Region 5 * |
|---|---|---|---|---|---|
| Temperature (°C) | 31 | 32 | 32 | 32 | 33 |
| Temperature Correction Factor | 3.8 | 4.1 | 4.1 | 4.1 | 4.4 |
| Friction Coefficient BPN20 | 63.8 | 70.1 | 64.1 | 64.1 | 70.4 |
| 65.8 | 72.1 | 64.1 | 64.1 | 70.4 | |
| 61.8 | 72.1 | 66.1 | 64.1 | 72.4 | |
| 61.8 | 74.1 | 64.1 | 64.1 | 72.4 | |
| 61.8 | 74.1 | 68.1 | 64.1 | 70.4 | |
| Mean | 63 | 72 | 65 | 64 | 71 |
| Standard Deviation | 1.79 | 1.67 | 1.79 | 0.00 | 1.10 |
| Coefficient of Variation | 0.03 | 0.02 | 0.03 | 0.00 | 0.02 |
| Index | Region 1 | Region 2 | Region 3 | Region 4 * | Region 5 | Region 6 |
|---|---|---|---|---|---|---|
| Temperature (°C) | 31 | 31 | 33 | 30 | 28 | 33 |
| Temperature Correction Factor | 3.8 | 3.8 | 4.4 | 3.5 | 2.8 | 4.4 |
| Friction Coefficient BPN20 | 65.8 | 75.8 | 66.4 | 55.5 | 84.8 | 68.4 |
| 63.8 | 75.8 | 66.4 | 53.5 | 86.8 | 66.4 | |
| 63.8 | 75.8 | 68.4 | 53.5 | 82.8 | 66.4 | |
| 63.8 | 77.8 | 68.4 | 53.5 | 84.8 | 68.4 | |
| 65.8 | 75.8 | 68.4 | 53.5 | 86.8 | 68.4 | |
| Mean | 64.6 | 76.2 | 67.6 | 53.9 | 85.2 | 67.6 |
| Standard Deviation | 1.10 | 0.89 | 1.10 | 0.89 | 1.67 | 1.10 |
| Coefficient of Variation | 0.02 | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 |
| Index | Region 1 | Region 2 | Region 3 | Region 4 | Region 5 |
|---|---|---|---|---|---|
| Temperature (°C) | 34 | 33 | 33 | 28 | 33 |
| Temperature Correction Factor | 3.8 | 4.1 | 4.1 | 4.1 | 4.4 |
| Friction Coefficient BPN20 | 86.7 | 88.4 | 92.4 | 90.8 | 78.4 |
| 84.7 | 90.4 | 92.4 | 92.8 | 82.4 | |
| 86.7 | 90.4 | 90.4 | 90.8 | 80.4 | |
| 86.7 | 90.4 | 88.4 | 92.8 | 78.4 | |
| 84.7 | 92.4 | 92.4 | 94.8 | 82.4 | |
| Mean | 85.9 | 90.4 | 91.2 | 92.4 | 80.4 |
| Standard Deviation | 1.10 | 1.41 | 1.79 | 1.67 | 2.00 |
| Coefficient of Variation | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 |
| Bridge Deck Pavement | Index | MTD of Pavement Texture | MPD of Pavement Texture | MTSAD of Pavement Texture | BPN20 |
|---|---|---|---|---|---|
| Cheng’an-Yu Ginkgo Bridge (White) | Region 1 | 0.33 | 0.38 | 34.80 | 76 |
| Region 2 | 0.31 | 0.37 | 33.46 | 70 | |
| Region 3 | 0.29 | 0.35 | 32.23 | 62 | |
| Region 4 | 0.30 | 0.38 | 32.67 | 68 | |
| Region 5 | 0.33 | 0.38 | 32.80 | 75 | |
| Shaxi Woye Bridge (Green) | Region 1 | 0.37 | 0.44 | 31.13 | 63 |
| Region 2 | 0.29 | 0.34 | 36.00 | 72 | |
| Region 3 | 0.40 | 0.47 | 28.37 | 65 | |
| Region 4 | 0.33 | 0.38 | 29.17 | 64 | |
| Region 5 | 0.41 | 0.48 | 30.22 | 71 | |
| Xindu Golden Phoenix Bridge (Green) | Region 1 | 0.45 | 0.51 | 29.74 | 64.6 |
| Region 2 | 0.52 | 0.62 | 35.84 | 76.2 | |
| Region 3 | 0.45 | 0.53 | 27.56 | 67.6 | |
| Region 4 | 0.33 | 0.38 | 29.17 | 53.9 | |
| Region 5 | 0.41 | 0.48 | 39.00 | 85.2 | |
| Region 6 | 0.41 | 0.48 | 30.22 | 67.6 | |
| Yurui Bridge (Red) | Region 1 | 0.40 | 0.51 | 35.04 | 85.9 |
| Region 2 | 0.40 | 0.52 | 38.52 | 90.4 | |
| Region 3 | 0.44 | 0.50 | 38.99 | 91.2 | |
| Region 4 | 0.46 | 0.52 | 39.78 | 92.4 | |
| Region 5 | 0.42 | 0.51 | 38.07 | 80.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, N.; Ding, S.; Chen, X.; Ai, C.; Yang, H.; Wang, J. Extraction of Pavement Texture–Friction Surface Density Index Using High-Precision Three-Dimensional Images. Lubricants 2025, 13, 288. https://doi.org/10.3390/lubricants13070288
Mao N, Ding S, Chen X, Ai C, Yang H, Wang J. Extraction of Pavement Texture–Friction Surface Density Index Using High-Precision Three-Dimensional Images. Lubricants. 2025; 13(7):288. https://doi.org/10.3390/lubricants13070288
Chicago/Turabian StyleMao, Niangzhi, Shihai Ding, Xiaoping Chen, Changfa Ai, Huaping Yang, and Jiayu Wang. 2025. "Extraction of Pavement Texture–Friction Surface Density Index Using High-Precision Three-Dimensional Images" Lubricants 13, no. 7: 288. https://doi.org/10.3390/lubricants13070288
APA StyleMao, N., Ding, S., Chen, X., Ai, C., Yang, H., & Wang, J. (2025). Extraction of Pavement Texture–Friction Surface Density Index Using High-Precision Three-Dimensional Images. Lubricants, 13(7), 288. https://doi.org/10.3390/lubricants13070288




