Investigating Film Thickness and Friction of an MR-Lubricated Journal Bearing
Abstract
1. Introduction
2. Materials and Methods
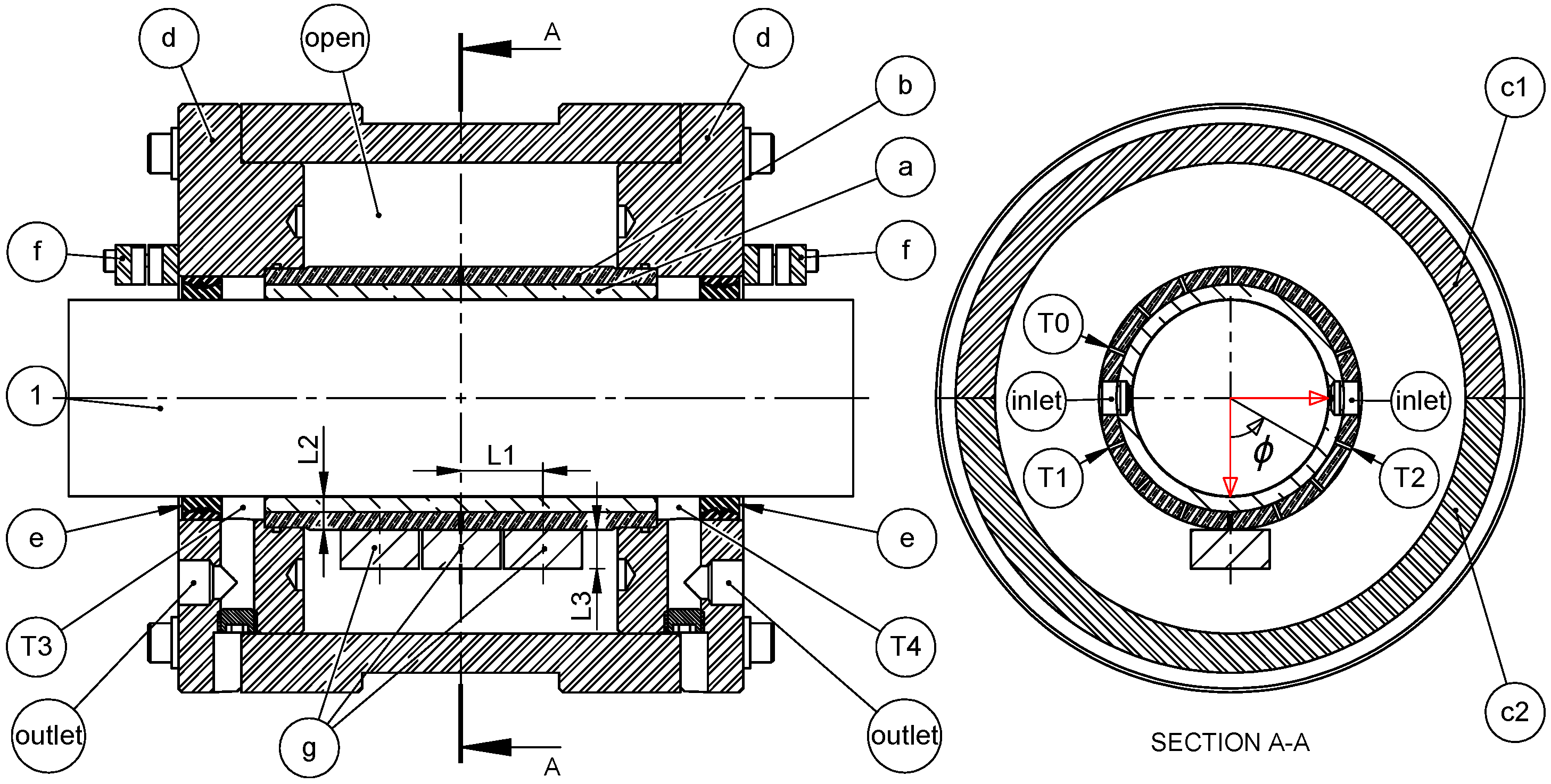
2.1. Experimental Setup
2.2. Experimental Procedure
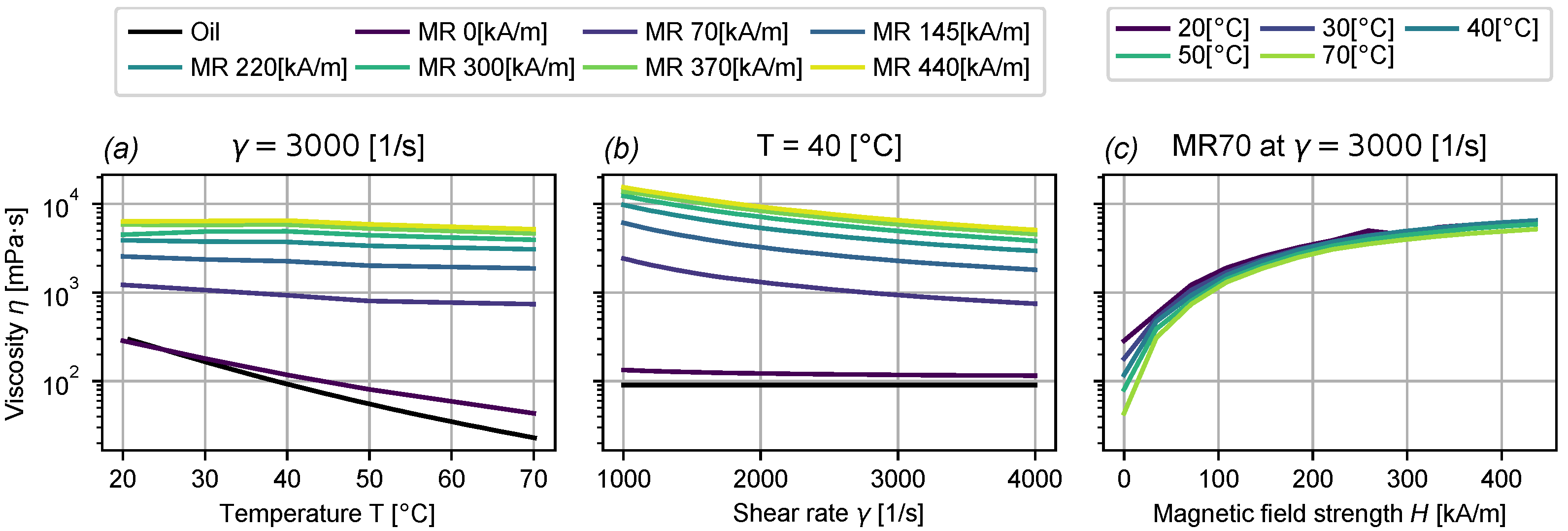
2.3. Lubricant Properties
2.4. Numerical Model
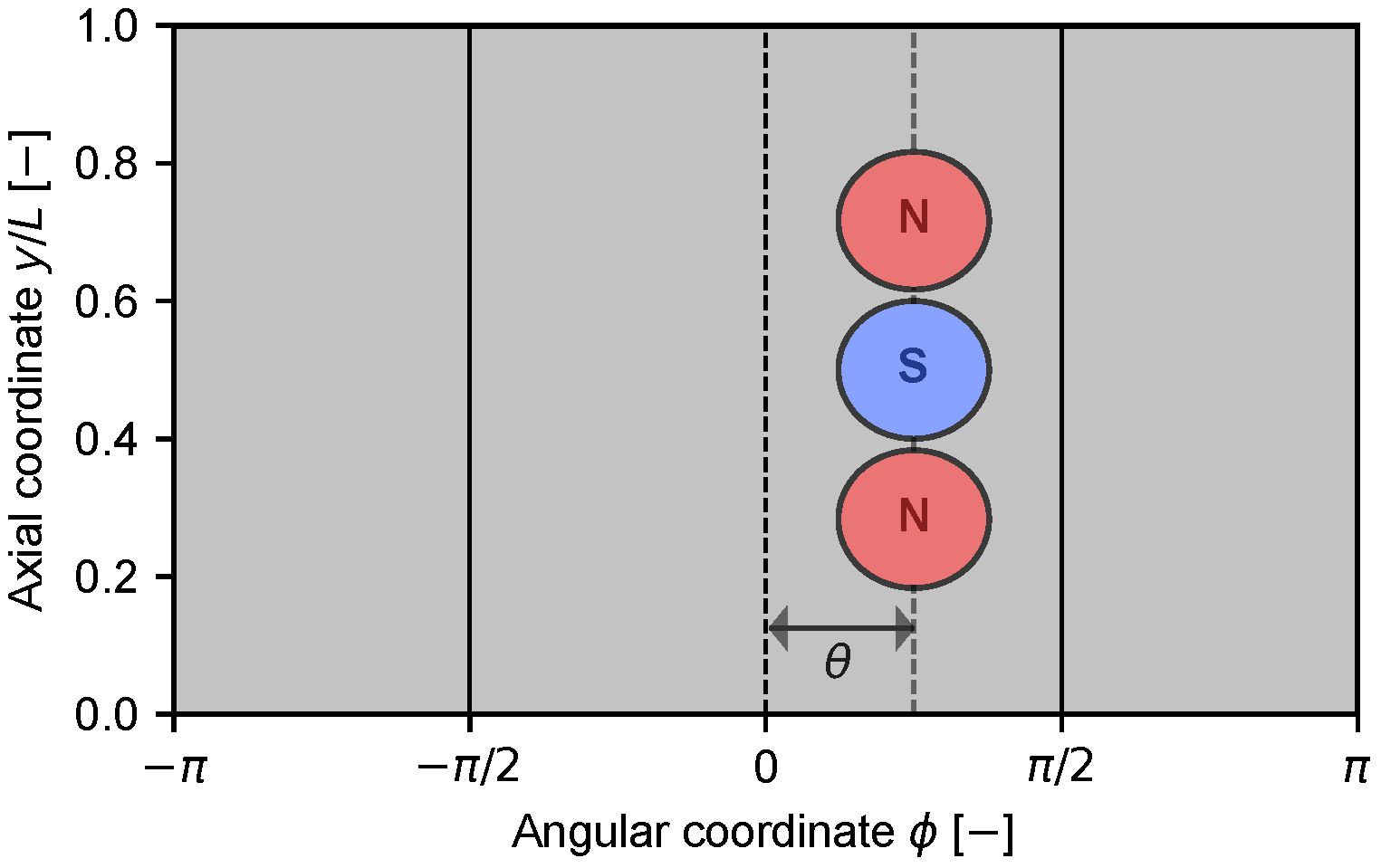
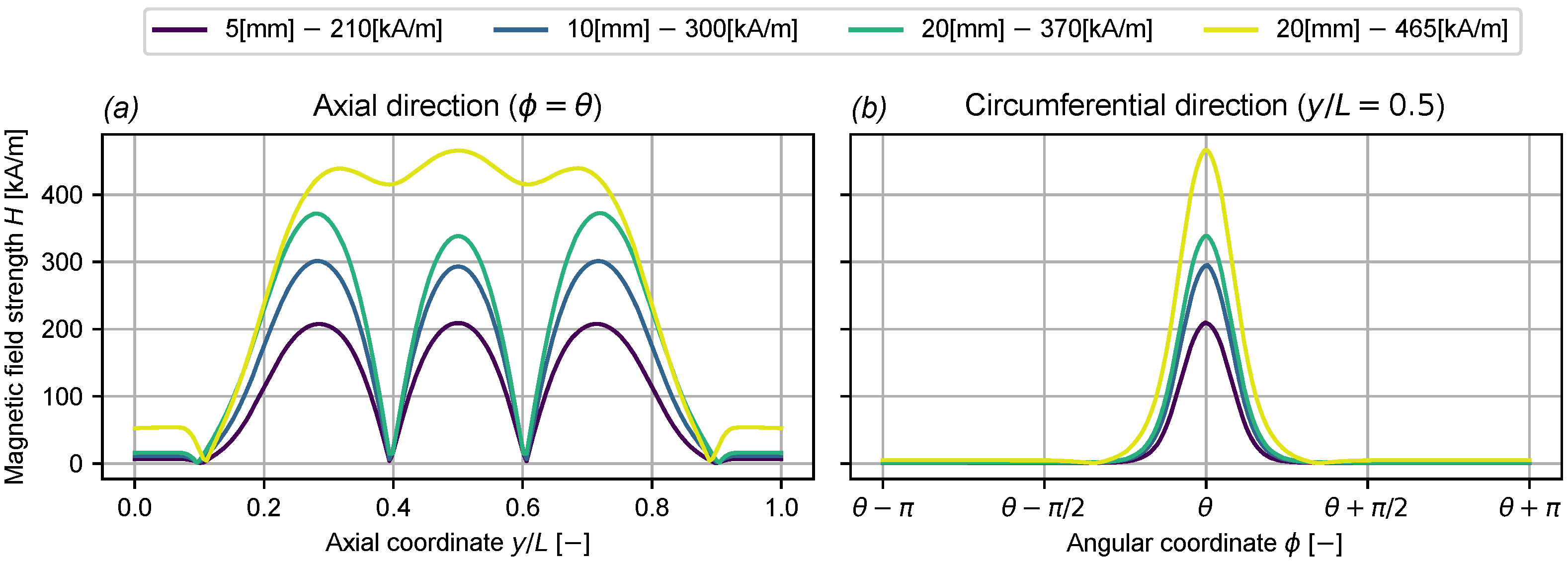
2.4.1. Magnetic Field Calculation
2.4.2. Software Implementation
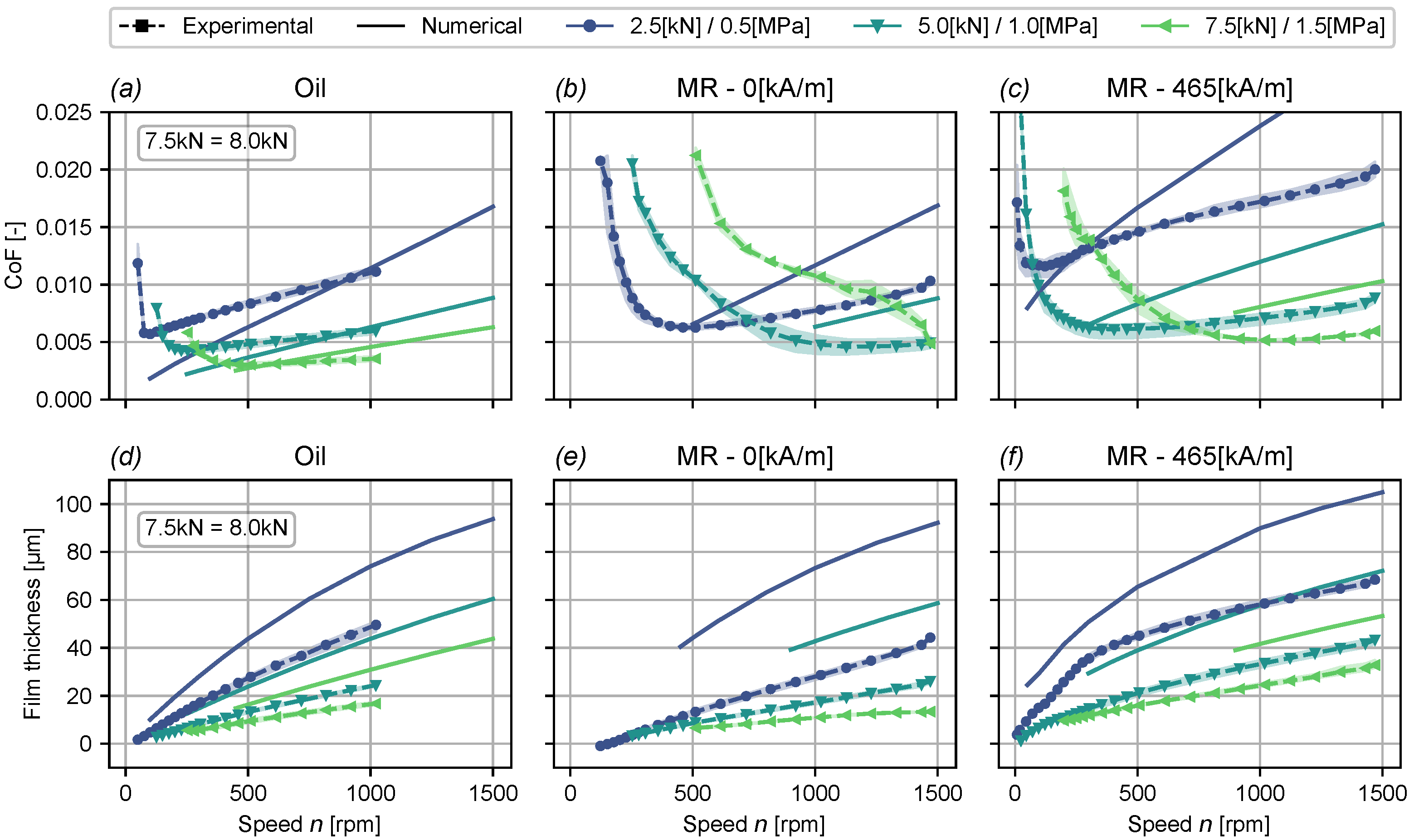
3. Results and Discussion
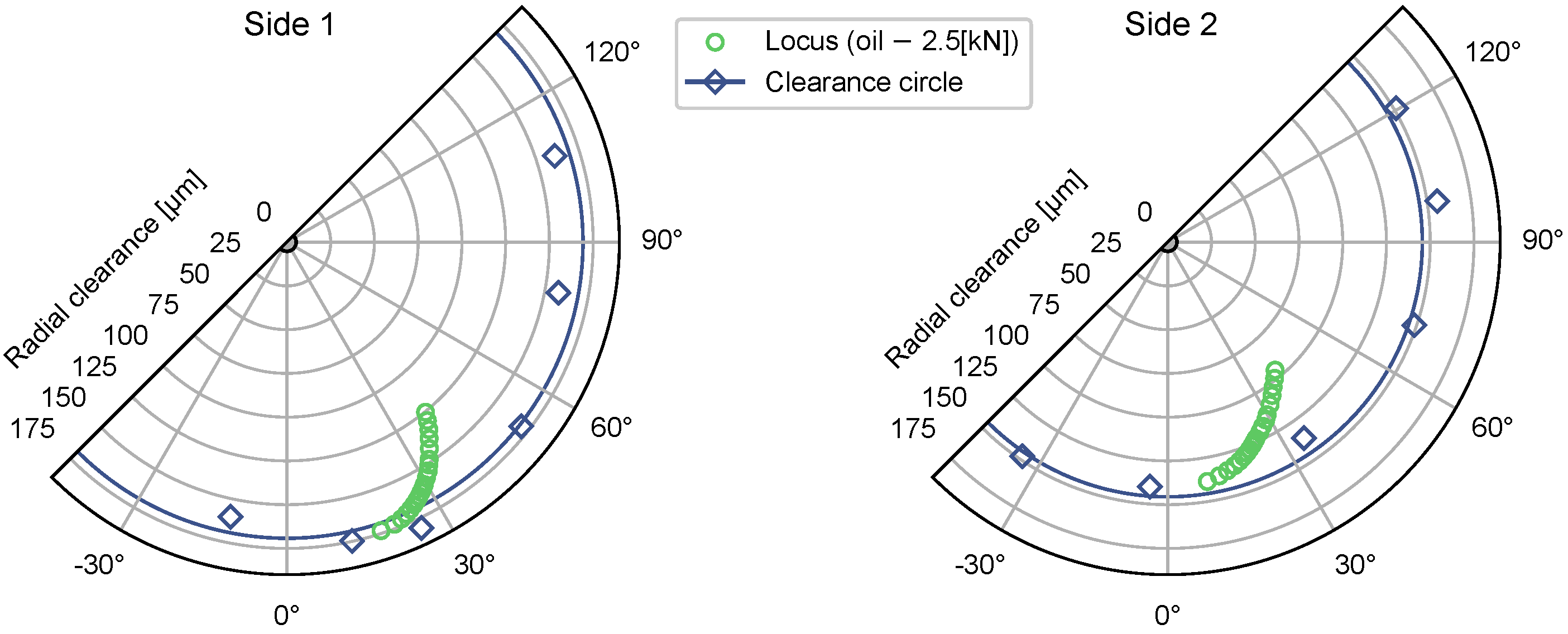
3.1. Magnet Angle Optimisation
3.2. Varying Magnetic Field Strength and Load
3.2.1. Magnetic Field Strength Variation
3.2.2. Load Variation
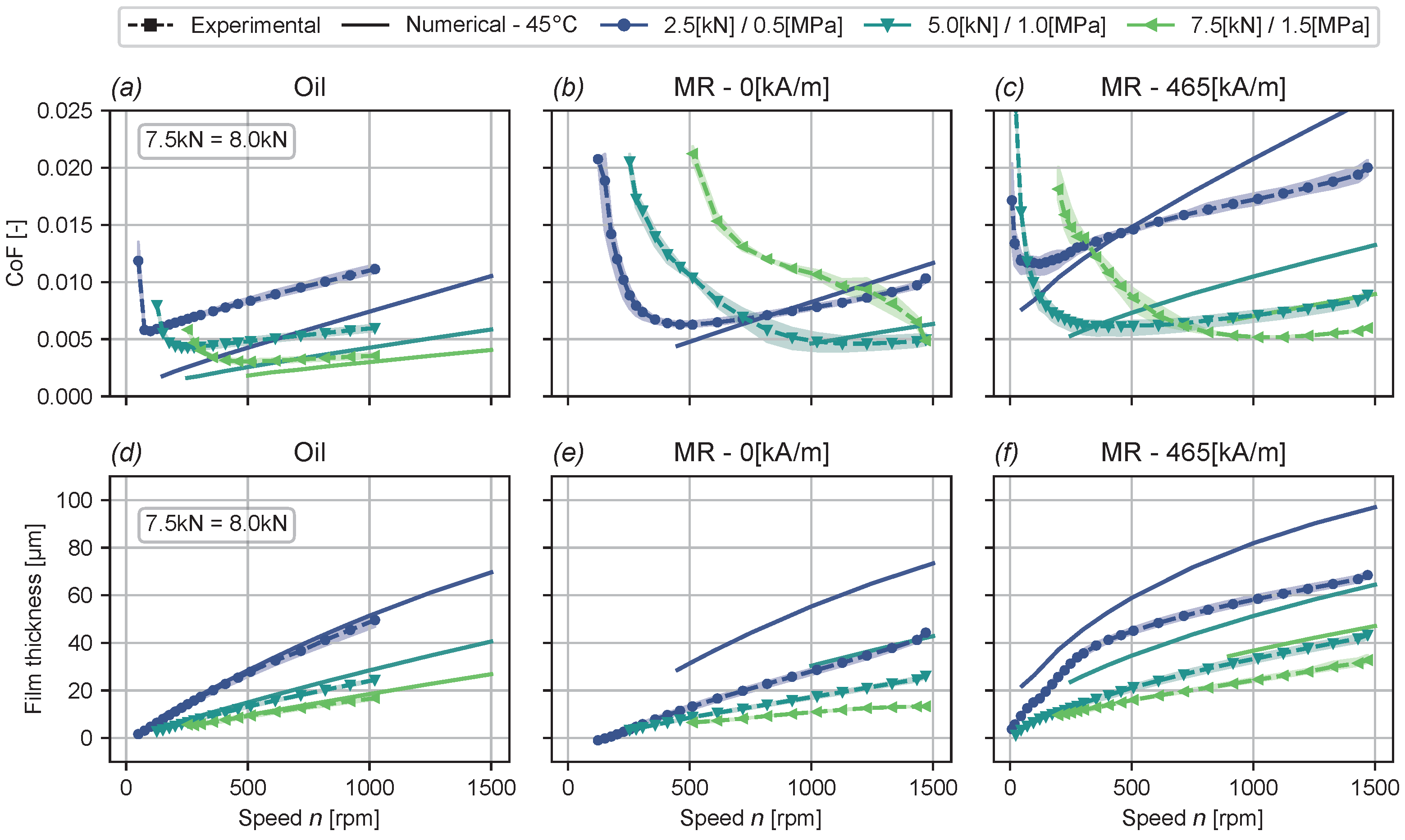
3.3. Discussion on the Numerical Model
- The model overpredicts both the friction coefficient and the film thickness for all operating conditions, independent of the type of lubricant.
- The model underpredicts the increase in film thickness due to an increase in magnetic field strength with the MR-lubricated bearing (Figure 9e,f).
- The model does not predict any differences between oil and unmagnetised MR lubrication, even though the experimental results clearly show that such a difference exists (Figure 9d,e).
3.3.1. Bearing Sleeve Shape Errors
3.3.2. Film Temperature
3.3.3. MR Fluids at Very High Shear Rates
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bossis, G.; Volkova, O.; Lacis, S.; Meunier, A. Magnetorheology: Fluids, Structures and Rheology. In Ferrofluids: Magnetically Controllable Fluids and Their Applications; Odenbach, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 202–230. [Google Scholar] [CrossRef]
- de Vicente, J.; Klingenberg, D.J.; Hidalgo-Alvarez, R. Magnetorheological fluids: A review. Soft Matter 2011, 7, 3701–3710. [Google Scholar] [CrossRef]
- Ahamed, R.; Choi, S.B.; Ferdaus, M.M. A state of art on magneto-rheological materials and their potential applications. J. Intell. Mater. Syst. Struct. 2018, 29, 2051–2095. [Google Scholar] [CrossRef]
- Choi, S.B. Thermal Conductivity and Temperature Dependency of Magnetorheological Fluids and Application Systems—A Chronological Review. Micromachines 2023, 14, 2096. [Google Scholar] [CrossRef]
- Eshgarf, H.; Ahmadi Nadooshan, A.; Raisi, A. An overview on properties and applications of magnetorheological fluids: Dampers, batteries, valves and brakes. J. Energy Storage 2022, 50, 104648. [Google Scholar] [CrossRef]
- Klingenberg, D.J. Magnetorheology: Applications and challenges. AIChE J. 2001, 47, 246–249. [Google Scholar] [CrossRef]
- Ghaffari, A.; Hashemabadi, S.H.; Ashtiani, M. A review on the simulation and modeling of magnetorheological fluids. J. Intell. Mater. Syst. Struct. 2015, 26, 881–904. [Google Scholar] [CrossRef]
- Gertzos, K.P.; Nikolakopoulos, P.G.; Papadopoulos, C.A. CFD analysis of journal bearing hydrodynamic lubrication by Bingham lubricant. Tribol. Int. 2008, 41, 1190–1204. [Google Scholar] [CrossRef]
- Dorier, C.; Tichy, J. Behavior of a Bingham-like in lubrication flows. J. Non-Newton. Fluid Mech. 1992, 45, 291–310. [Google Scholar] [CrossRef]
- Wada, S.; Hayashi, H.; Haga, K. Behavior of a Bingham Solid in Hydrodynamic Lubrication—1. General Theory. Bull. JSME 1973, 16, 422–431. [Google Scholar] [CrossRef]
- Bompos, D.A.; Nikolakopoulos, P.G. CFD simulation of magnetorheological fluid journal bearings. Simul. Model. Pract. Theory 2011, 19, 1035–1060. [Google Scholar] [CrossRef]
- Laukiavich, C.A.; Braun, M.J.; Chandy, A.J. A comparison between the performance of ferro- and magnetorheological fluids in a hydrodynamic bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2014, 228, 649–666. [Google Scholar] [CrossRef]
- Zapoměl, J.; Ferfecki, P. A new concept of a hydrodynamic bearing lubricated by composite magnetic fluid for controlling the bearing load capacity. Mech. Syst. Signal Process. 2022, 168, 108678. [Google Scholar] [CrossRef]
- Bompos, D.A.; Nikolakopoulos, P.G. Rotordynamic Analysis of a Shaft Using Magnetorheological and Nanomagnetorheological Fluid Journal Bearings. Tribol. Trans. 2016, 59, 108–118. [Google Scholar] [CrossRef]
- Wang, X.; Li, H.; Meng, G. Rotordynamic coefficients of a controllable magnetorheological fluid lubricated floating ring bearing. Tribol. Int. 2017, 114, 1–14. [Google Scholar] [CrossRef]
- Sahu, K.; Sharma, S.C. A Simulation Study on the Behavior of Magnetorheological Fluid on Herringbone-Grooved Hybrid Slot-Entry Bearing. Tribol. Trans. 2019, 62, 1099–1118. [Google Scholar] [CrossRef]
- Sharma, S.C.; Kumar, A. On the behaviour of roughened conical hybrid journal bearing system operating with MR lubricant. Tribol. Int. 2021, 156, 106824. [Google Scholar] [CrossRef]
- Vaziri, S.A.; Norouzi, M.; Akbarzadeh, P.; Kim, K.C.; Kim, M. Thermohydrodynamic analysis of magnetorheological conical bearings with conjugated heat transfer. Sci. Rep. 2024, 14, 20596. [Google Scholar] [CrossRef]
- Hesselbach, J.; Abel-Keilhack, C. Active hydrostatic bearing with magnetorheological fluid. J. Appl. Phys. 2003, 93, 8441–8443. [Google Scholar] [CrossRef]
- Guldbakke, J.M.; Hesselbach, J. Development of bearings and a damper based on magnetically controllable fluids. J. Phys. Condens. Matter 2006, 18, S2959. [Google Scholar] [CrossRef]
- Bhat, A.K.; Vaz, N.; Kumar, Y.; D’Silva, R.; Kumar, P.; Binu, K.G. Comparative study of journal bearing performance with ferrofluid and MR fluid as lubricant. AIP Conf. Proc. 2019, 2080, 040008. [Google Scholar] [CrossRef]
- Urreta, H.; Leicht, Z.; Sanchez, A.; Agirre, A.; Kuzhir, P.; Magnac, G. Hydrodynamic bearing lubricated with magnetic fluids. J. Intell. Mater. Syst. Struct. 2010, 21, 1491–1499. [Google Scholar] [CrossRef]
- Vaz, N.; Binu, K.G.; Serrao, P.; Hemanth, M.P.; Jacob, J.; Roy, N.; Dias, E. Experimental Investigation of Frictional Force in a Hydrodynamic Journal Bearing Lubricated with Magnetorheological Fluid. J. Mech. Eng. Autom. 2017, 7, 131–134. Available online: http://article.sapub.org/10.5923.j.jmea.20170705.01.html (accessed on 23 March 2025).
- Moles, N.C. Actively Controllable Hydrodynamic Journal Bearing Design Using Magnetorheological Fluids. Ph.D. Thesis, University of Akron, Akron, OH, USA, 2015. [Google Scholar]
- Lampaert, S.G.; Quinci, F.; van Ostayen, R.A. Rheological texture in a journal bearing with magnetorheological fluids. J. Magn. Magn. Mater. 2020, 499, 166218. [Google Scholar] [CrossRef]
- Quinci, F.; Litwin, W.; Wodtke, M.; van den Nieuwendijk, R. A comparative performance assessment of a hydrodynamic journal bearing lubricated with oil and magnetorheological fluid. Tribol. Int. 2021, 162, 107143. [Google Scholar] [CrossRef]
- van der Meer, G.H.G.; Quinci, F.; Litwin, W.; Wodtke, M.; van Ostayen, R.A.J. Experimental comparison of the transition speed of a hydrodynamic journal bearing lubricated with oil and magnetorheological fluid. Tribol. Int. 2023, 189, 108976. [Google Scholar] [CrossRef]
- Wodtke, M.; Litwin, W.; van der Meer, G.H.G.; van Ostayen, R.A.J. Wear tests of a hydrodynamic journal bearing lubricated with magnetorheological fluid. 2025; submitted for publication. [Google Scholar]
- Litwin, W. Experimental research on marine oil-lubricated stern tube bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 233, 1773–1781. [Google Scholar] [CrossRef]
- Liquids Research Ltd. Magneto-Rheological Fluids. Available online: https://liquidsresearch.com/en-GB/document_download-58.aspx (accessed on 27 November 2024).
- Anton Paar Netherlands B.V. The Modular Compact Rheometer Series. Breda, The Netherlands. Available online: https://www.mtbrandao.com/files/products/MCR_1.pdf (accessed on 24 March 2025).
- Hemmatian, M.; Sedaghati, R.; Rakheja, S. Temperature dependency of magnetorheological fluids’ properties under varying strain amplitude and rate. J. Magn. Magn. Mater. 2020, 498, 166109. [Google Scholar] [CrossRef]
- Zschunke, F.; Rivas, R.; Brunn, P.O. Temperature Behavior of Magnetorheological Fluids. Appl. Rheol. 2005, 15, 116–121. [Google Scholar] [CrossRef]
- Mörée, G.; Leijon, M. Review of Hysteresis Models for Magnetic Materials. Energies 2023, 16, 3908. [Google Scholar] [CrossRef]
- Petrescu, L.; Cazacu, E.; Petrescu, C. Sigmoid functions used in hysteresis phenomenon modeling. In Proceedings of the 2015 9th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 7–9 May 2015; pp. 521–524. [Google Scholar] [CrossRef]
- van der Meer, G.H.G.; van Ostayen, R.A.J. Efficient solution method for the Reynolds equation with Herschel–Bulkley fluids. Tribol. Int. 2025, 204, 110460. [Google Scholar] [CrossRef]
- Dowson, D. A generalized Reynolds equation for fluid-film lubrication. Int. J. Mech. Sci. 1962, 4, 159–170. [Google Scholar] [CrossRef]
- Alakhramsing, S.; van Ostayen, R.; Eling, R. Thermo-hydrodynamic analysis of a plain journal bearing on the basis of a new mass conserving cavitation algorithm. Lubricants 2015, 3, 256–280. [Google Scholar] [CrossRef]
- COMSOL AB. COMSOL Multiphysics® Version 6.1. 1986–2025. Stockholm, Sweden. Available online: https://www.comsol.com/ (accessed on 23 March 2025).
- Litwin, W. Water-Lubricated Journal Bearings, Marine Applications, Design, and Operational Problems and Solutions; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar] [CrossRef]
- Leung, W.C.; Bullough, W.A.; Wong, P.L.; Feng, C. The effect of particle concentration in a magneto rheological suspension on the performance of a boundary lubricated contact. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2004, 218, 251–263. [Google Scholar] [CrossRef]
- Wong, P.L.; Bullough, W.A.; Feng, C.; Lingard, S. Tribological performance of a magneto-rheological suspension. Wear 2001, 247, 33–40. [Google Scholar] [CrossRef]
- Sahu, K.; Sharma, S.C.; Ram, N. Misalignment and Surface Irregularities Effect in MR Fluid Journal Bearing. Int. J. Mech. Sci. 2022, 221, 107196. [Google Scholar] [CrossRef]
- Lohner, T.; Ziegltrum, A.; Stemplinger, J.P.; Stahl, K. Engineering Software Solution for Thermal Elastohydrodynamic Lubrication Using Multiphysics Software. Adv. Tribol. 2016, 2016, 6507203. [Google Scholar] [CrossRef]
- Becnel, A.C.; Hu, W.; Wereley, N.M. Measurement of magnetorheological fluid properties at shear rates of up to 25,000 s−1. IEEE Trans. Magn. 2012, 48, 3525–3528. [Google Scholar] [CrossRef]
- Hu, W.; Wereley, N.M. Behavior of MR fluids at high shear rate. Int. J. Mod. Phys. B 2011, 25, 979–985. [Google Scholar] [CrossRef]
- Wang, X.; Gordaninejad, F. Study of magnetorheological fluids at high shear rates. Rheol. Acta 2006, 45, 899–908. [Google Scholar] [CrossRef]




| Property | Symbol | Value |
|---|---|---|
| Bearing length/shaft diameter | L/D | 100 mm/50 mm |
| Nominal radial clearance | 155 μm | |
| Shaft/bearing material | C45 steel/Polymer | |
| Shaft/bearing surface roughness | 0.4 μm/0.4 μm | |
| Max. load/specific pressure | / | 7.5 kN/1.5 MPa |
| Speed range | n | 0–1000/1500 rpm |
| Lubrication groove radius/length | 1 mm/100 mm | |
| Lubrication groove radius/length | 0.3 L/min−1 | |
| Average inlet temperature | 32 °C | |
| Average film temperature | T | 36 °C |
| Polymer Young’s modulus | 2.2 GPa | |
| Polymer hardness (shore-D) | 83 | |
| Polymer thermal expansion coefficient | 6 × 10−5 mm/(mm°C) | |
| Applied load accuracy | ±30 N | |
| Distance sensor accuracy | ±0.15 μm | |
| Friction coefficient accuracy | ±3.12 N/Wa | |
| Thermocouple accuracy | ±1.5K | |
| Centre-to-centre distance magnets | L1 | 20.8 mm |
| Distance magnet–film | L2 | 9 mm |
| Magnet diameter/length | dm/L3 | 20 mm/5,10,20 mm |
| Magnet remanence | Br | 1.29–1.32 T |
| C | Unit | ||||
|---|---|---|---|---|---|
| 6605 | 5.151 × 10−6 | 1.601 × 105 | 5013 | ||
| K | Pa·sm | 210.3 | 1.007 × 10−5 | 2.553 × 105 | 210.7 |
| m | - | 0.9614 | 1.039 × 10−5 | 1.570 × 105 | 1.992 |
| °C−1 | 3.638 × 10−2 | 3.785 × 10−5 | 0 | −4.260 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
van der Meer, G.; van Ostayen, R. Investigating Film Thickness and Friction of an MR-Lubricated Journal Bearing. Lubricants 2025, 13, 171. https://doi.org/10.3390/lubricants13040171
van der Meer G, van Ostayen R. Investigating Film Thickness and Friction of an MR-Lubricated Journal Bearing. Lubricants. 2025; 13(4):171. https://doi.org/10.3390/lubricants13040171
Chicago/Turabian Stylevan der Meer, Gerben, and Ron van Ostayen. 2025. "Investigating Film Thickness and Friction of an MR-Lubricated Journal Bearing" Lubricants 13, no. 4: 171. https://doi.org/10.3390/lubricants13040171
APA Stylevan der Meer, G., & van Ostayen, R. (2025). Investigating Film Thickness and Friction of an MR-Lubricated Journal Bearing. Lubricants, 13(4), 171. https://doi.org/10.3390/lubricants13040171





