Dynamic Analysis of Dual Parallel Spring-Supported Tilting Pad Journal Bearing
Abstract
1. Introduction
2. Modeling
2.1. Governing Equation
2.2. Solving Strategy
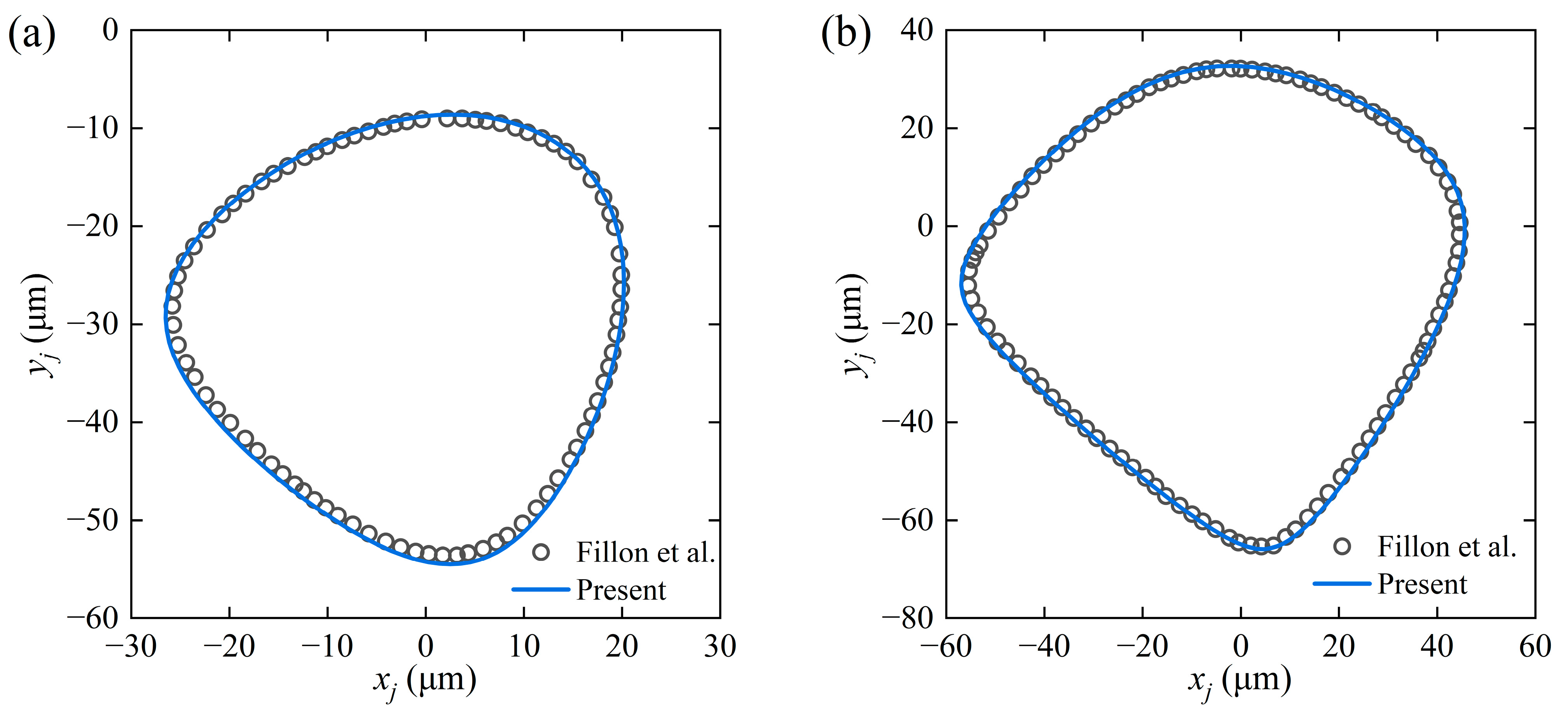
2.3. Model Validation
3. Results and Discussion
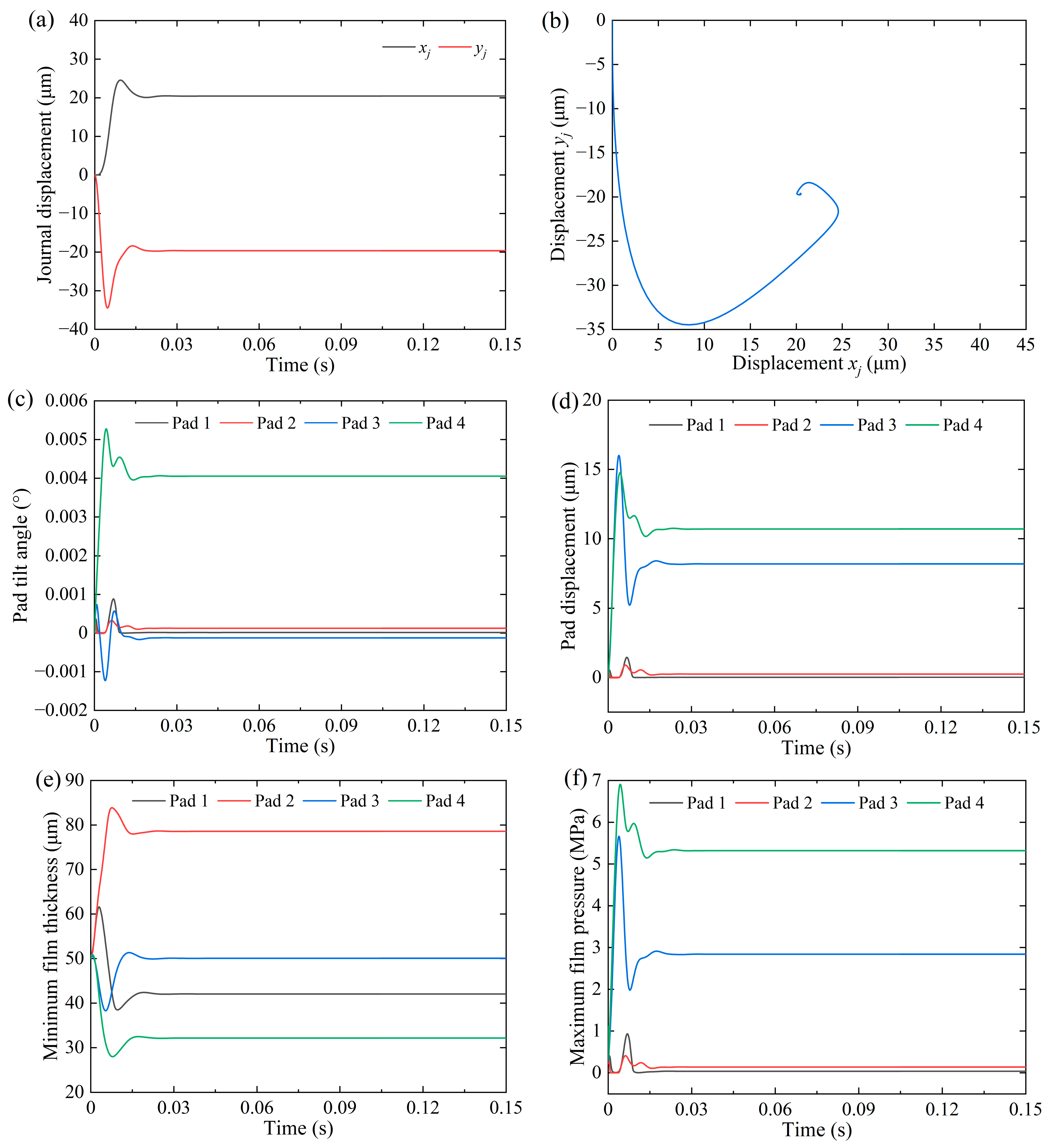
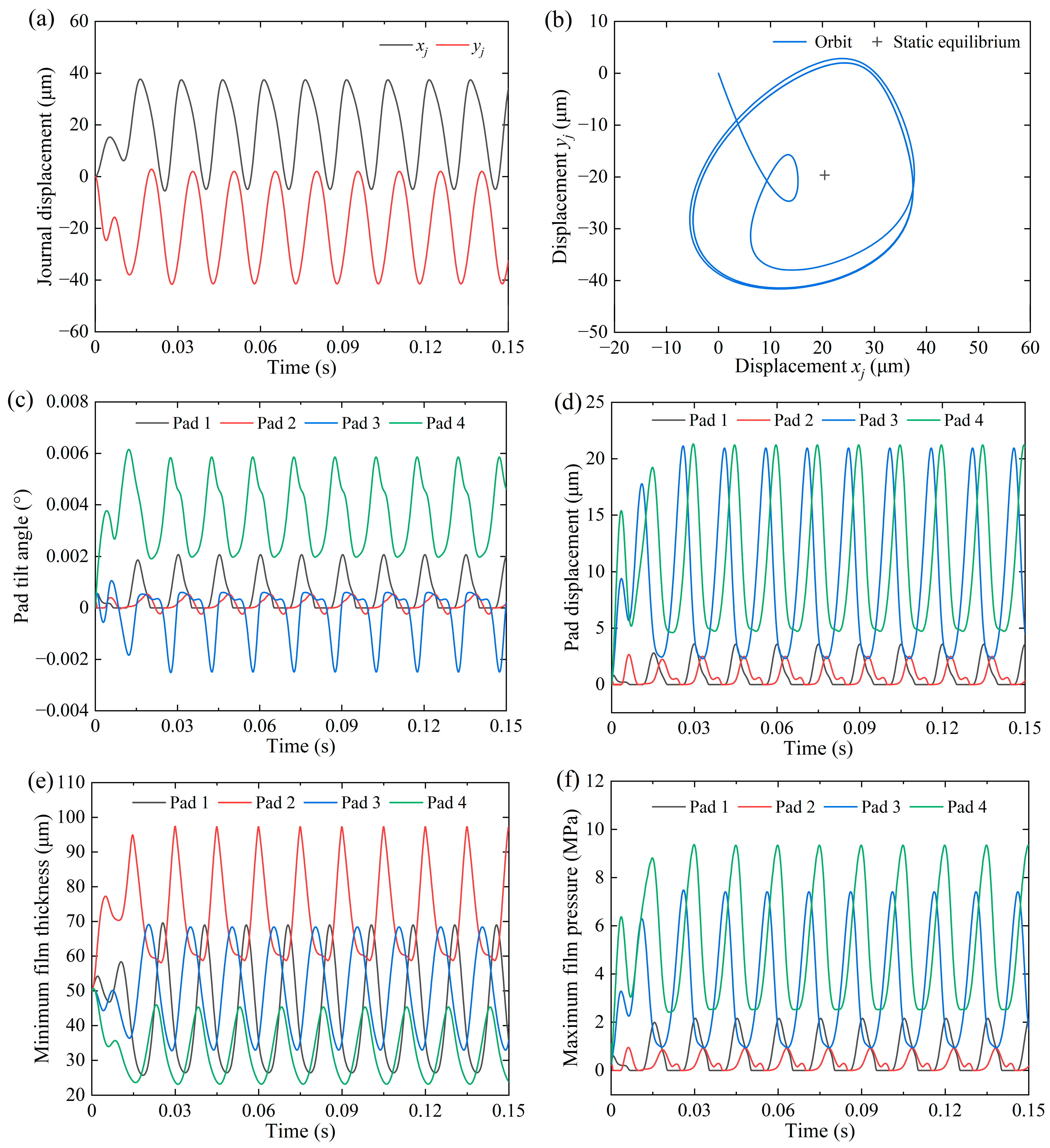
3.1. Dynamic Response with and Without Unbalanced Load
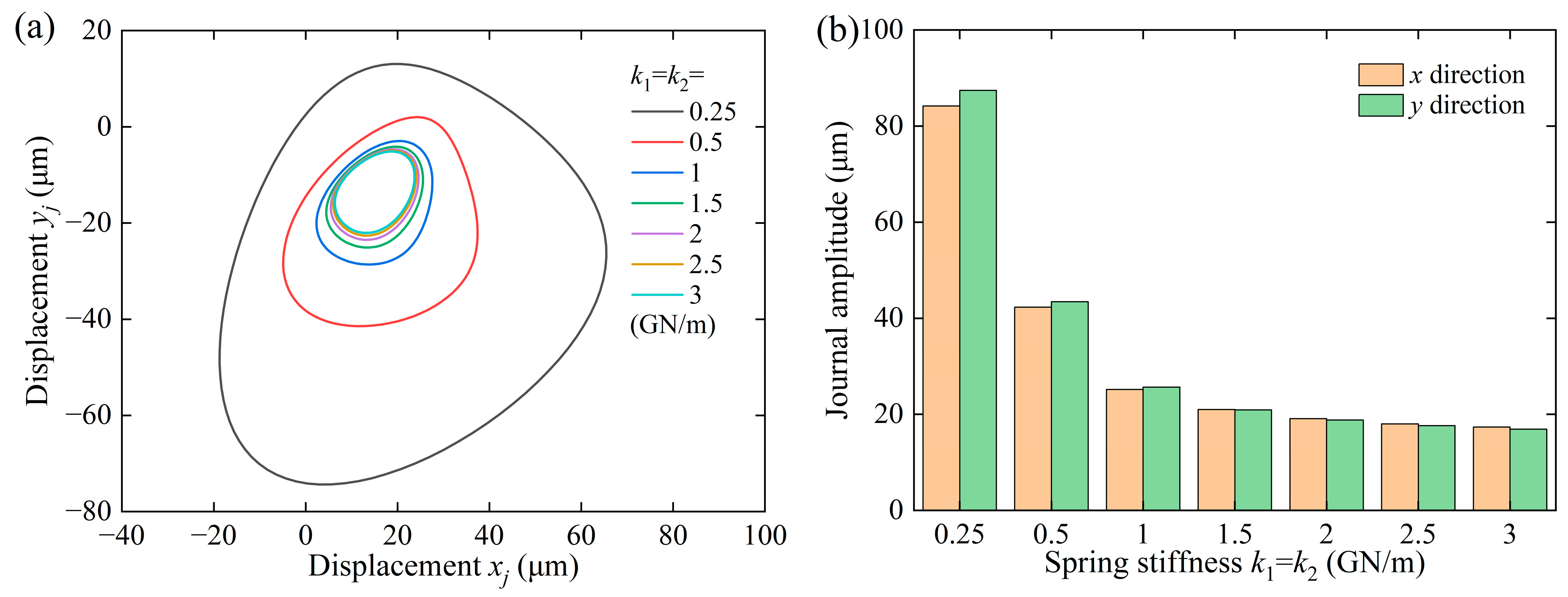
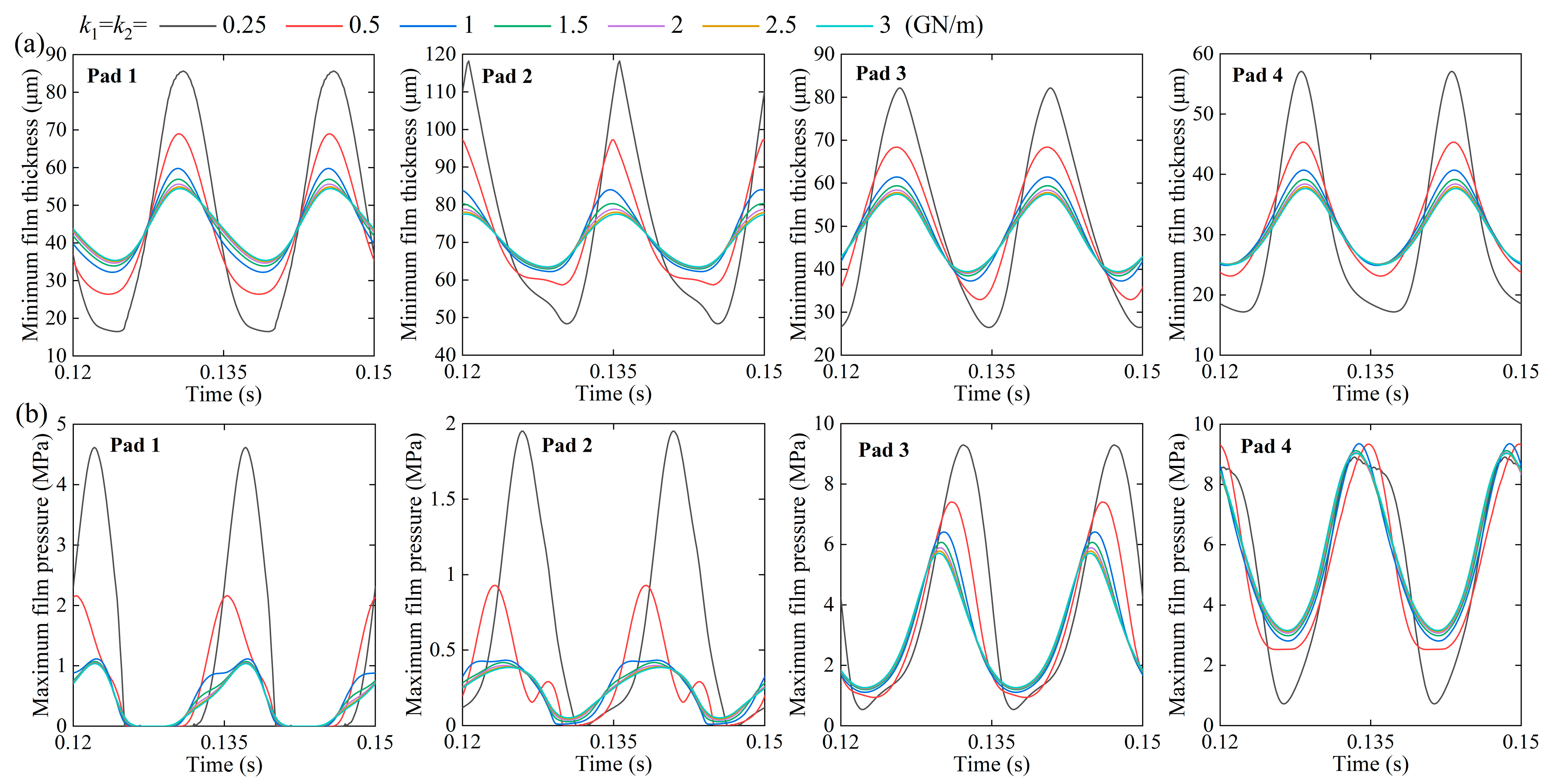
3.2. Effect of Spring Stiffness
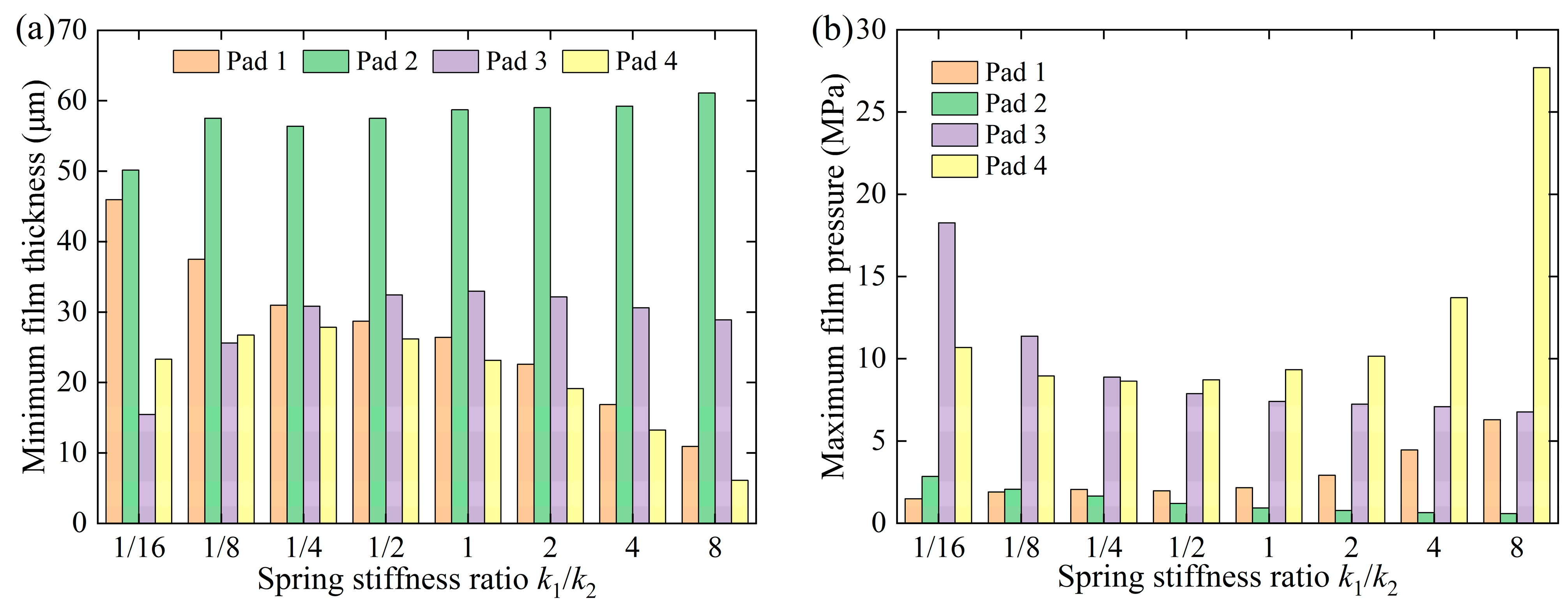
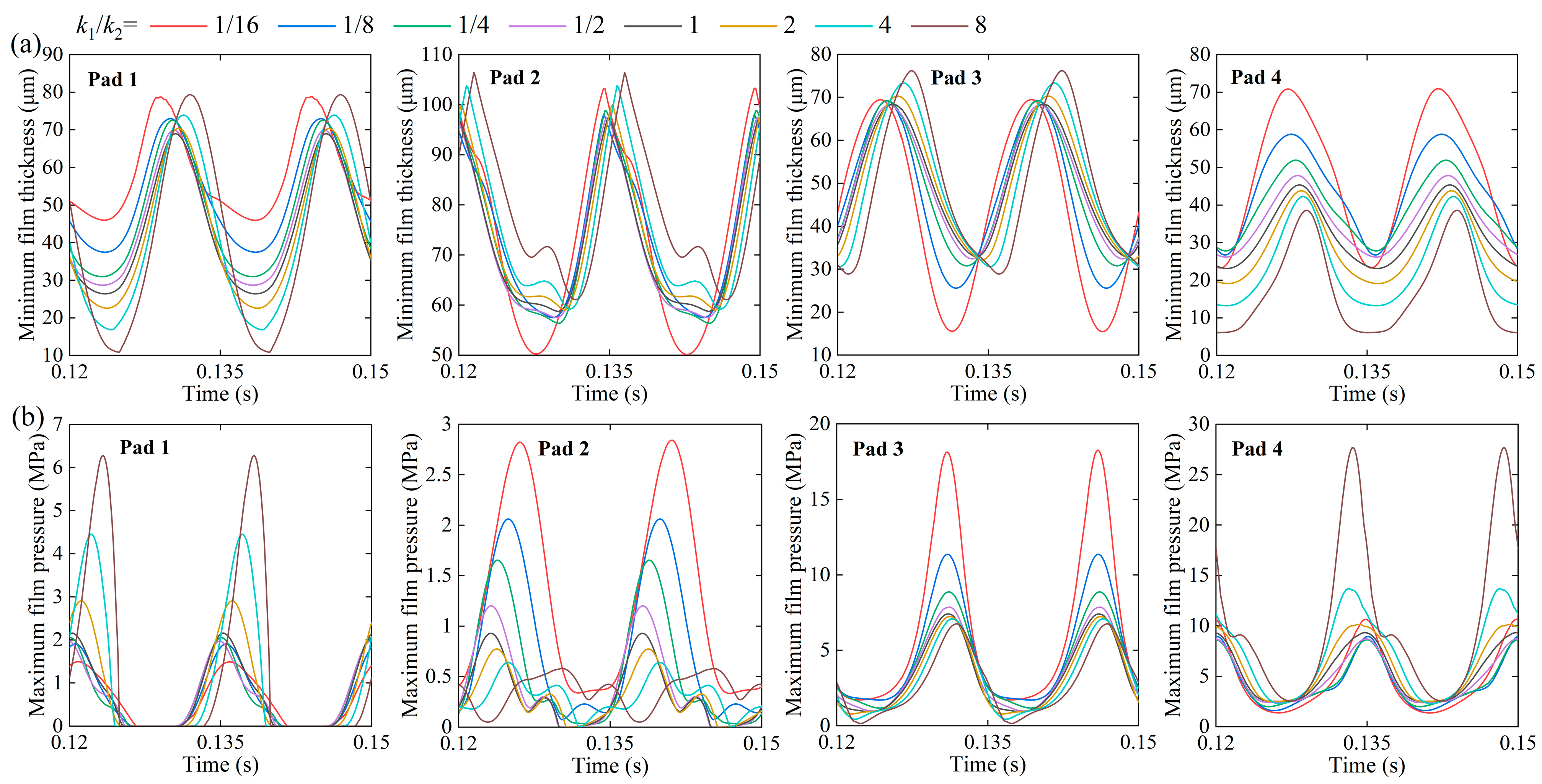
3.3. Effect of Stiffness Ratio
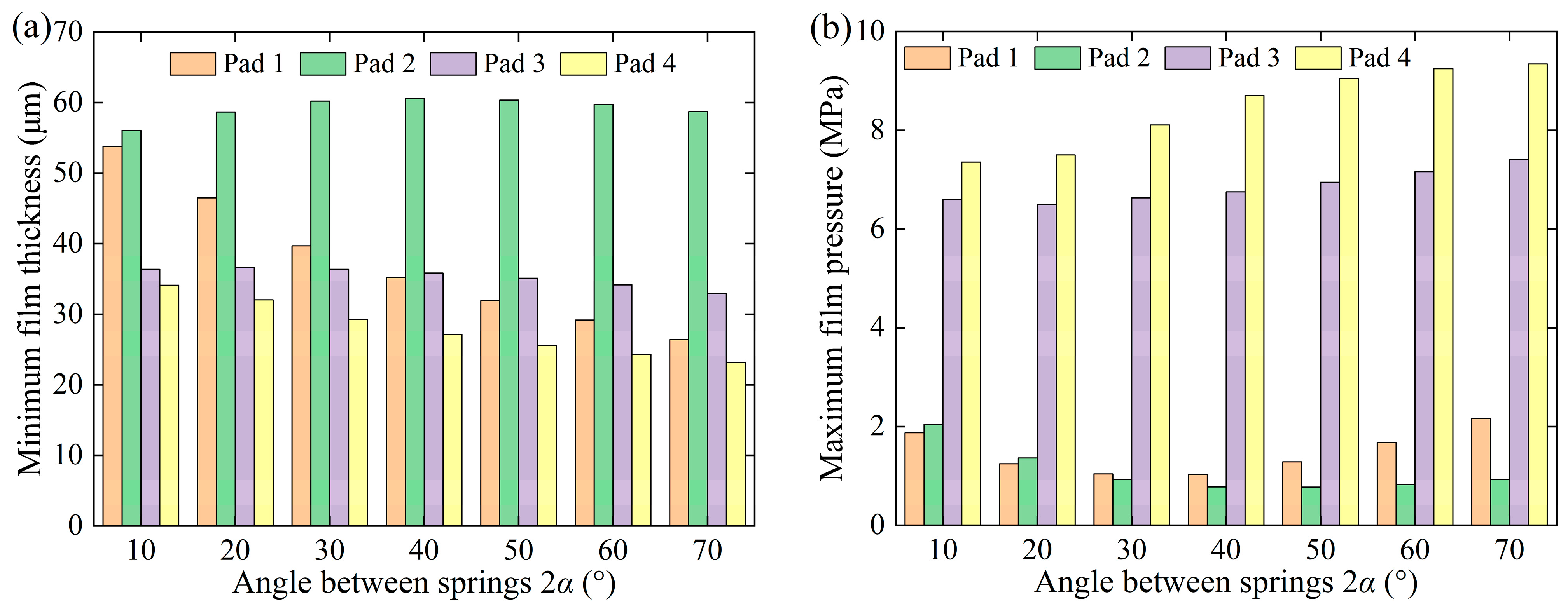
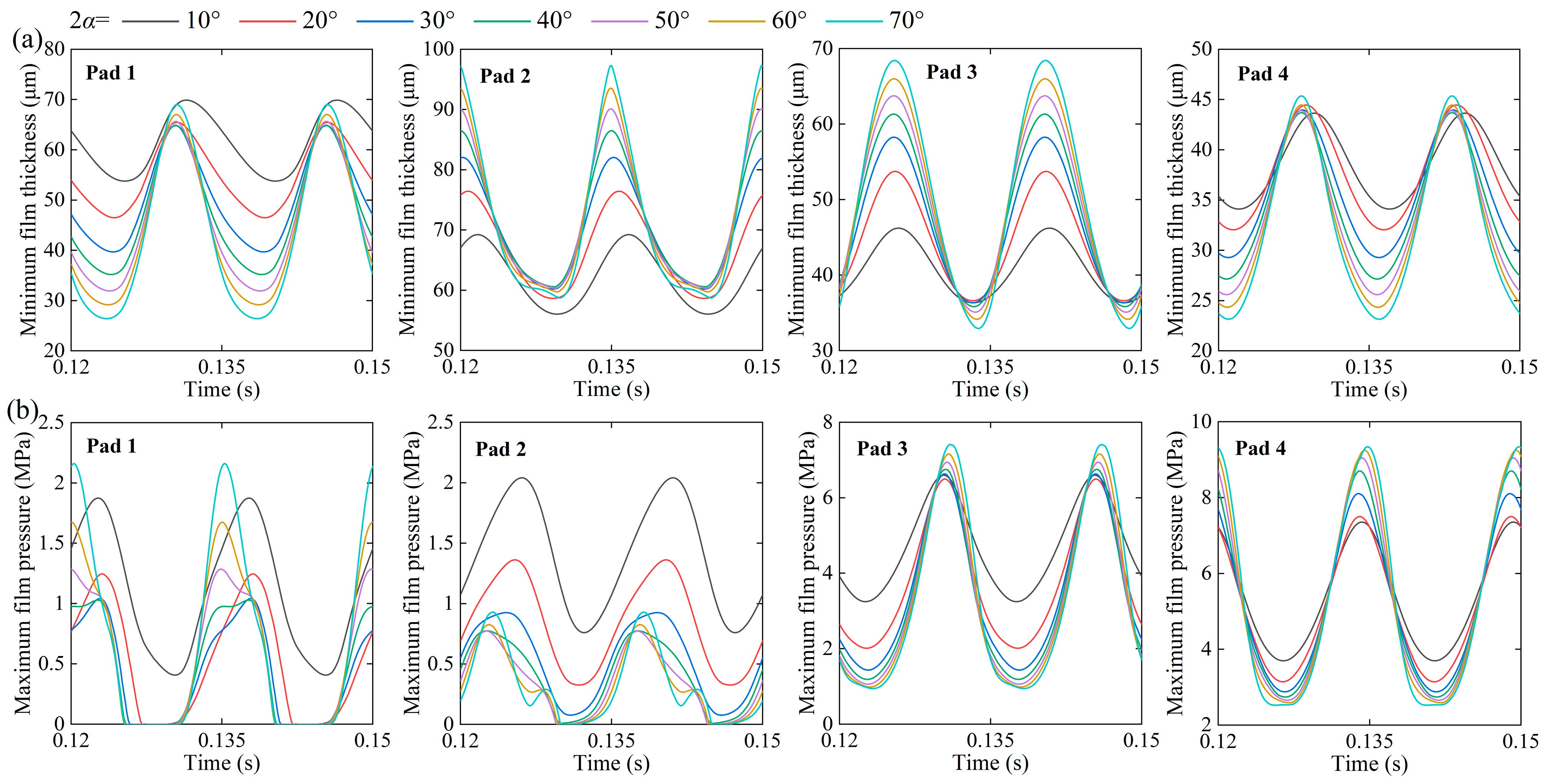
3.4. Effect of Angle Between Springs
4. Conclusions
- The journal whirl center of the DPSTPJB stabilizes in the fourth quadrant with a specific attitude angle. Pad 4 serves as the primary load-carrying pad, while pad 3 acts as the secondary load-carrying component.
- With increasing spring stiffness, the journal center orbit gradually contracts, the journal amplitude progressively decreases, the bearing’s minimum film thickness increases and stabilizes, and the bearing’s maximum film pressure exhibits negligible variation.
- An optimal stiffness ratio exists that minimizes the journal amplitude, maximizes the bearing’s minimum film thickness, and minimizes the bearing’s maximum film pressure. For larger stiffness ratios, both the minimum film thickness and maximum film pressure occur on pad 4. Conversely, these critical parameters manifest on pad 3 when smaller stiffness ratios are employed.
- As the included angle increases, the journal center orbit gradually expands, the attitude angle of the journal whirl center progressively increases, the journal amplitude gradually rises, the bearing’s minimum film thickness continuously decreases, and the bearing’s maximum film pressure steadily increases.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rendl, J.; Dyk, S.; Smolík, L. Nonlinear dynamic analysis of a tilting pad journal bearing subjected to pad fluttering. Nonlinear Dyn. 2021, 105, 2133–2156. [Google Scholar] [CrossRef]
- Zhang, F.; Ouyang, W.; Hong, H.L.; Guan, Y.S.; Yuan, X.Y.; Dong, G.N. Experimental study on pad temperature and film thickness of tilting-pad journal bearings with an elastic-pivot pad. Tribol. Int. 2015, 88, 228–235. [Google Scholar] [CrossRef]
- Liu, S.Y.; Xiao, Z.H.; Yan, Z.Y.; Chen, Z.J. Vibration characteristics of rotor system with tilting-pad journal bearing of elastic and damped pivots. J. Cent. South Univ. 2015, 22, 134–140. [Google Scholar] [CrossRef]
- Chen, S.T.; Yang, S.J.; Zhou, Q.; Hou, Y.; Lai, T.W. Numerical study on tilting pad journal gas bearing with variable stiffness springs. J. Mech. Sci. Technol. 2015, 29, 3059–3067. [Google Scholar] [CrossRef]
- Jin, Y.Z.; Chen, F.; Zhang, F.; Yuan, X.Y. Nonlinear dynamic performance of tilting-pad journal bearing with adjustable elastic pivot design. Tribol. Int. 2019, 136, 533–547. [Google Scholar] [CrossRef]
- Huang, G.Y.; Wang, X.J.; Qin, X.; Zhu, L.M.; Yi, S.X. Experimental investigation of dynamic behavior of rotor system with a novel double layers flexible support tilting pad bearing. Adv. Mech. Eng. 2022, 14, 16878132221116482. [Google Scholar] [CrossRef]
- Wu, Y.Y.; Zhang, W.W.; Yi, S.X.; Wang, X.J.; Qin, Y.Y.; Peng, S.X. Theoretical and Experimental Study of Flexible Structure Tilting Pad Bearings Considering Deformation. Lubricants 2024, 12, 284. [Google Scholar] [CrossRef]
- Wang, J.W.; Han, S.C.; Zhang, H.X.; Li, H.; Wang, P.; Feng, K. Experimental and theoretical investigation on rotodynamic characterization of porous tilting pad bearings with hermetic squeeze film dampers. Mech. Syst. Signal Proc. 2024, 218, 111548. [Google Scholar] [CrossRef]
- Armentrout, R.W.; Paquette, D.J. Rotordynamic Characteristics of Flexure-Pivot Tilting-Pad Journal Bearings. Tribol. Trans. 1993, 36, 443–451. [Google Scholar] [CrossRef]
- Suh, J.; Palazzolo, A.; Choi, Y.S. Numerical Modeling and Analysis of Flexure-Pivot Tilting-Pad Bearing. ASME J. Tribol. 2017, 139, 051704. [Google Scholar] [CrossRef]
- Plantegenet, T.; Arghir, M.; Jolly, P. Experimental analysis of the thermal unbalance effect of a flexible rotor supported by a flexure pivot tilting pad bearing. Mech. Syst. Signal Proc. 2020, 145, 106953. [Google Scholar] [CrossRef]
- Koondilogpiboon, N.; Inoue, T. Nonlinear Vibration Analysis of a Flexible Rotor Supported by a Flexure Pivot Tilting Pad Journal Bearing in Comparison to a Fixed Profile Journal Bearing With Experimental Verification. ASME J. Eng. Gas. Turbines Power 2021, 143, 091007. [Google Scholar] [CrossRef]
- San Andrés, L.; Tao, Y.J. The Role of Pivot Stiffness on the Dynamic Force Coefficients of Tilting Pad Journal Bearings. ASME J. Eng. Gas. Turbines Power 2013, 135, 112505. [Google Scholar] [CrossRef]
- Dang, P.V.; Chatterton, S.; Pennacchi, P. The Effect of the Pivot Stiffness on the Performances of Five-Pad Tilting Pad Bearings. Lubricants 2019, 7, 61. [Google Scholar] [CrossRef]
- Zhang, F.; Yin, P.; Liu, Y.Y.; Wang, J.M. Numerical and experimental study on dynamic characteristics of tilting-pad journal bearings considering pivot stiffness in a vertical rotor system. Ind. Lubr. Tribol. 2021, 73, 1275–1285. [Google Scholar] [CrossRef]
- Shin, D.; Palazzolo, A.B. Tilting Pad Bearing Pivot Friction and Design Effects on Thermal Bow-Induced Rotor Vibration. ASME J. Tribol. 2021, 143, 121804. [Google Scholar] [CrossRef]
- Ciulli, E.; Forte, P.; Antonelli, F.; Minelli, R.; Panara, D. Tilting Pad Journal Bearing Ball and Socket Pivots: Experimental Determination of Stiffness. Machines 2022, 10, 81. [Google Scholar] [CrossRef]
- Jin, Y.Z.; Niu, Q.L.; Qu, Y.P.; Yuan, X.Y. Pivot Stiffness Effect on Transient Dynamic Characteristic of Tilting Pad Journal Bearing-Rotor System Passing through Critical Speed. Lubricants 2023, 11, 125. [Google Scholar] [CrossRef]
- Peixoto, T.F.; Tuckmantel, F.W.D.; Daniel, G.B.; Cavalca, K.L. Effect of direct injection and pivot stiffness on the static performance parameters of tilting pad journal bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2023, 237, 1487–1510. [Google Scholar] [CrossRef]
- Wagner, L.F. Tilting-Pad Bearings-The Contact Flexibility of the Pivot. Lubricants 2023, 11, 189. [Google Scholar] [CrossRef]
- Betti, A.; Forte, P.; Panara, D.; Ciulli, E. Investigation on Pivot Rolling Motion Effect on the Behavior of Rocker Back Tilting Pad Journal Bearings. Appl. Sci. 2023, 13, 5563. [Google Scholar] [CrossRef]
- Tofighi-Niaki, E.; Asgharifard-Sharabiani, P.; Ahmadian, H. Nonlinear dynamics of a flexible rotor on tilting pad journal bearings experiencing rub-impact. Nonlinear Dyn. 2018, 94, 2937–2956. [Google Scholar] [CrossRef]
- Kim, S.; Palazzolo, A.B. Pad-Pivot Friction Effect on Nonlinear Response of a Rotor Supported by Tilting-Pad Journal Bearings. ASME J. Tribol. 2019, 141, 091701. [Google Scholar] [CrossRef]
- Ciulli, E.; Forte, P. Nonlinear Response of Tilting Pad Journal Bearings to Harmonic Excitation. Machines 2019, 7, 43. [Google Scholar] [CrossRef]
- Jin, Y.Z.; Chen, F.; Xu, J.M.; Yuan, X.Y. Nonlinear dynamic analysis of low viscosity fluid-lubricated tilting-pad journal bearing for different design parameters. Friction 2020, 8, 930–944. [Google Scholar] [CrossRef]
- Li, Q.; Tang, X.H.; Zhang, S.; Wang, Y.J.; Xu, W.W.; Wang, Z.B. Dynamic Response Analysis of Tilting Pad Journal Bearing Considering Fluid-Structure Interaction. J. Appl. Fluid Mech. 2021, 14, 1827–1837. [Google Scholar]
- Hojjati, M.; Navazi, H.M.; Haddadpour, H. Nonlinear vibrations of a rotor on nonlinear tilting-pad-journal-bearings. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 168. [Google Scholar] [CrossRef]
- Dyk, S.; Rendl, J.; Bulín, R.; Smolík, L. Influence of detailed ball-and-socket modelling on tilting pad journal bearings dynamics. Nonlinear Dyn. 2023, 111, 8155–8171. [Google Scholar] [CrossRef]
- Cao, Z.W.; Guo, H.L.; Cheng, Z.Y.; Men, R.; Zhang, Z.Y.; Wang, T.Y. Nonlinear dynamics characteristics of a tilting pad journal bearing supported turbocharger. Nonlinear Dyn. 2024, 112, 16941–16961. [Google Scholar] [CrossRef]
- Wang, L.W.; Xiang, G.; Han, Y.F.; Yang, T.Y.; Zhou, G.W.; Wang, J.X. A mixed visco-hyperelastic hydrodynamic lubrication model for water-lubricated rubber bearings. Int. J. Mech. Sci. 2025, 286, 109887. [Google Scholar] [CrossRef]
- Pan, F.P.; Ouyang, W.; Ning, C.X.; Dong, X.W. Wide-area film thickness measurement method of water-lubricated polymer bearing based on ultrasonic reflection coefficient phase. Measurement 2025, 242, 116121. [Google Scholar] [CrossRef]
- Xiang, G.; Goltsberg, R.; Etsion, I. Role of intermolecular potential in adhesive wear behaviors for elastic-plastic spherical microcontacts. Tribol. Int. 2024, 199, 110054. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Hu, F.; Ouyang, W.; Ning, C.X.; Sheng, C.X. An Ultrasound-Based In Situ Monitoring for Water-Lubricated Thrust Bearing Wear. IEEE Sens. J. 2025, 25, 2921–2933. [Google Scholar] [CrossRef]
- Song, C.S.; Zhang, R.H.; Zhou, Y.; Tan, J.J.; Zhu, C.C. Transient analysis of non-uniform tilting-pad journal bearing for wind turbine main shaft under dynamical loading. Mech. Mach. Theory 2024, 203, 105792. [Google Scholar] [CrossRef]
- Liu, Q.L.; Ouyang, W.; Li, R.Q.; Yang, J. Experimental exploration on the nonlinear dynamic behavior of marine propeller shaft-bearing system. Ocean Eng. 2024, 310, 118595. [Google Scholar] [CrossRef]
- Yang, T.Y.; Xiang, G.; Cai, J.L.; Wang, L.W.; Lin, X.; Wang, J.X.; Zhou, G.W. Five-DOF nonlinear tribo-dynamic analysis for coupled bearings during start-up. Int. J. Mech. Sci. 2024, 269, 109068. [Google Scholar] [CrossRef]
- Fillon, M.; Desbordes, H.; Frene, J.; Wai, C.C.H. A global approach of thermal effects including pad deformations in tilting-pad journal bearings submitted to unbalance load. ASME J. Tribol. 1996, 118, 169–174. [Google Scholar] [CrossRef]
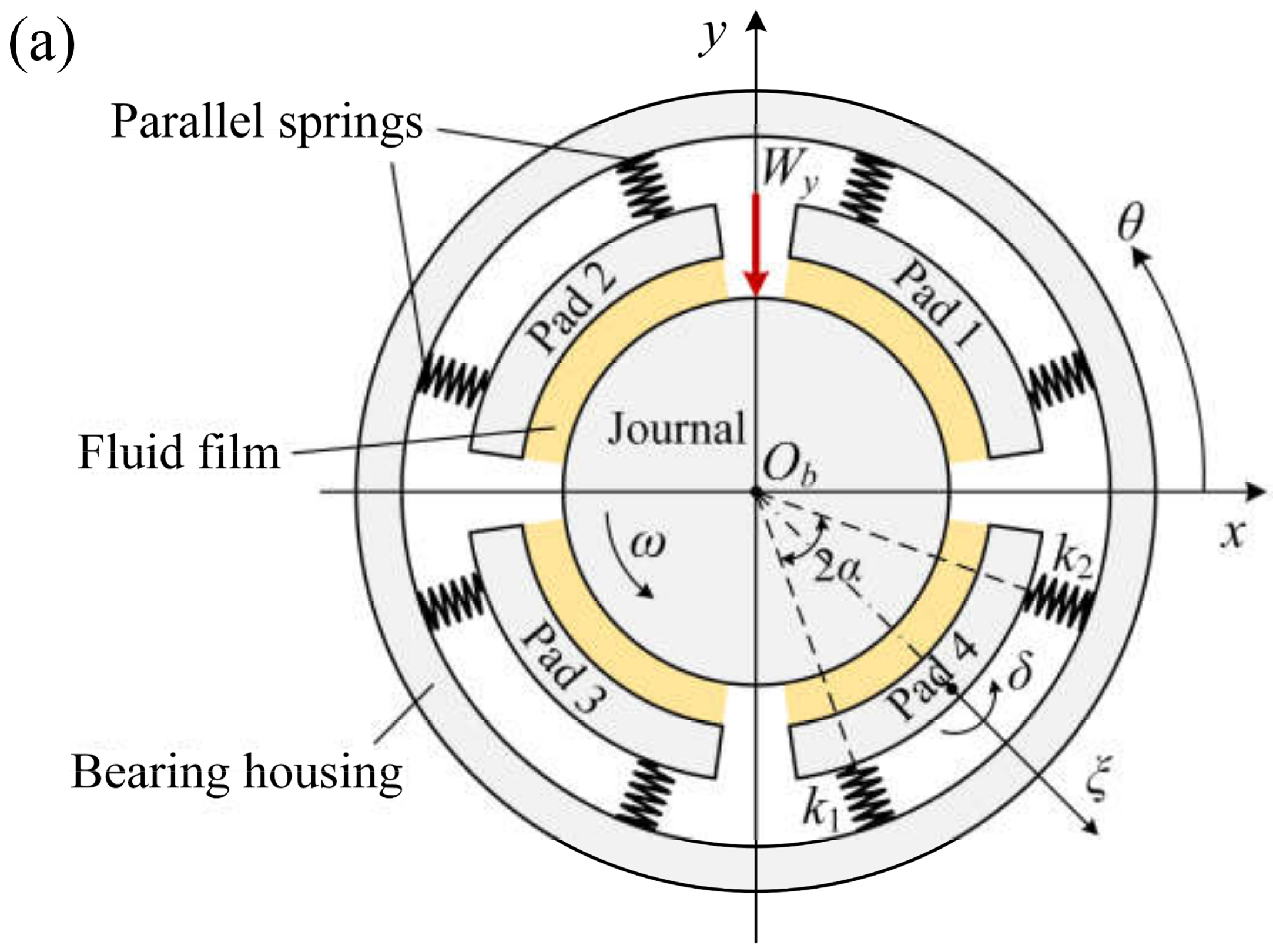
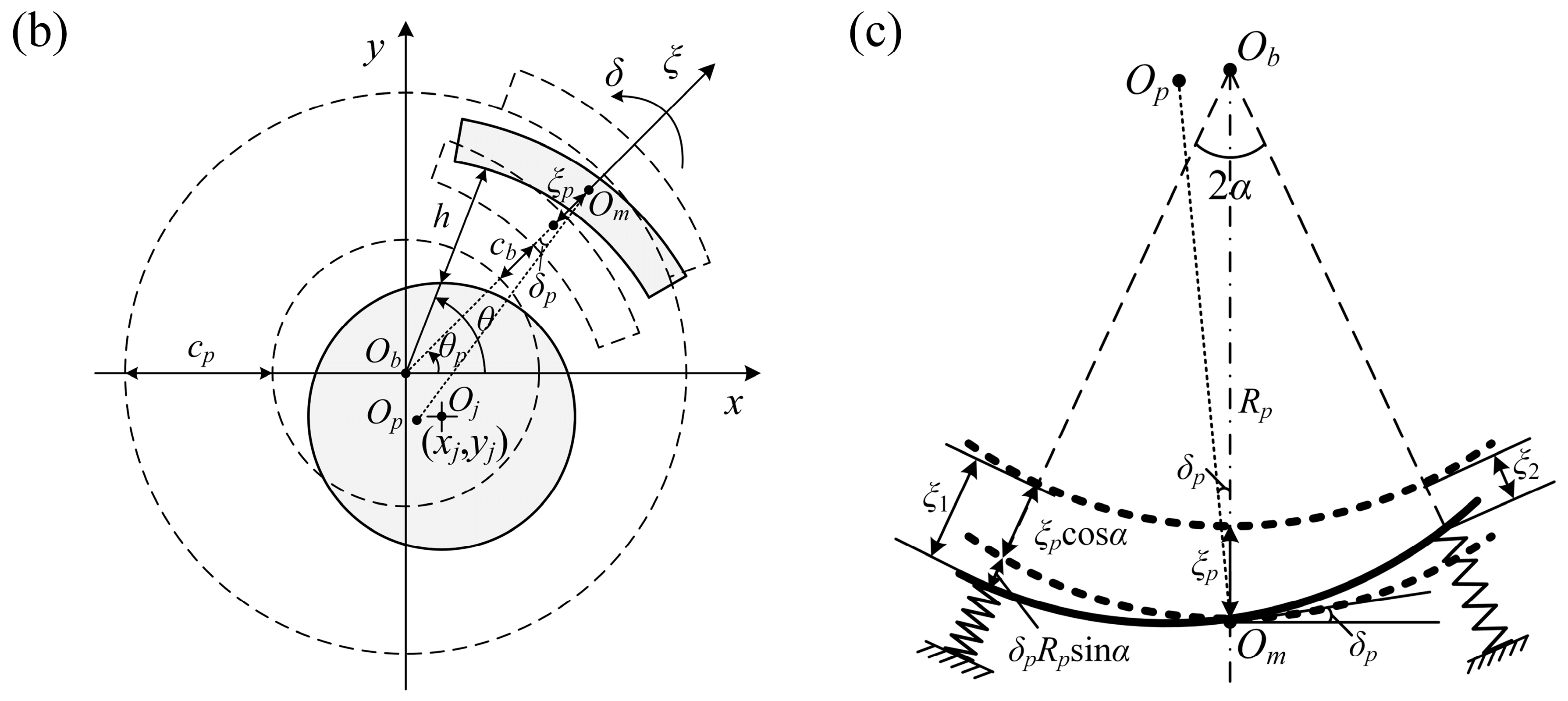



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Journal radius (R) | 50 mm | Bearing length (L) | 70 mm |
| Radial pad clearance (cp) | 100 μm | Radial bearing clearance (cb) | 50 μm |
| Pad arc angle | 75° | Lubricant viscosity (μ) | 0.03 Pa·s |
| Pad mass (mp) | 0.8632 kg | Pad moment of inertia (Ip) | 6.1686 × 10−4 kg·m2 |
| Polar coordinate of pad mass center (Rp, θp) | (70 mm, 45°/135°/225°/315°) | Journal mass (mj) | 1000 kg |
| Unbalance mass eccentricity (eu) | 20 μm | Static load (Wy) | 10,000 N |
| Rotational speed | 4000 rpm | Spring stiffness (k1, k2) | 0.25–3 GN/m |
| Spring stiffness ratio (k1/k2) | 1/16–8 | Angle between springs (2α) | 10–70° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Y.; Wang, Z.; Zhao, X. Dynamic Analysis of Dual Parallel Spring-Supported Tilting Pad Journal Bearing. Lubricants 2025, 13, 120. https://doi.org/10.3390/lubricants13030120
Jin Y, Wang Z, Zhao X. Dynamic Analysis of Dual Parallel Spring-Supported Tilting Pad Journal Bearing. Lubricants. 2025; 13(3):120. https://doi.org/10.3390/lubricants13030120
Chicago/Turabian StyleJin, Yingze, Zhicai Wang, and Xuefei Zhao. 2025. "Dynamic Analysis of Dual Parallel Spring-Supported Tilting Pad Journal Bearing" Lubricants 13, no. 3: 120. https://doi.org/10.3390/lubricants13030120
APA StyleJin, Y., Wang, Z., & Zhao, X. (2025). Dynamic Analysis of Dual Parallel Spring-Supported Tilting Pad Journal Bearing. Lubricants, 13(3), 120. https://doi.org/10.3390/lubricants13030120





